圆内接正多边形的画法
我们来玩转圆内接四边形的性质,经营用所谓的圆的内接四边形呢,就是四个顶点均在同一个圆上,他有什么性质呢?圆内接四边形的对角是互补的,我们来看这个图,这边的这个角一,他的对角呢,就是这边的这个角二, 因为呢,这个四边形他的四个点均在同一个圆上,所以他就是圆的内接四边形了。以后这个性质就可以得出来,角一他与角二互补,角一加角二对就是一百八十度。当然另外的一组对角也是这样的,这边的这个角三跟这边的对角角四,他俩加起来同样是一百八十度, 他有个推论,就是圆内跟四边形的一个外角等于他的内对角,什么意思呢?我们来看角二的这个零补角,你可以看到就是他的一个外角,那么这个外角他跟角二是互补的呀,因为呢,跟角二是零补角吗?而角一跟角二也是互补的,这样的话呢,我们根据同角的补角相等,也就可以达到 这个外角呢,就等于他这个内对角,也就等于这个角一。这个推动呢,是很好理解的。下面我们解释一下为什么他的对角是互补的原因就是圆轴角定理啊。那你可以看到这边我给你标一个,这个是暗法,他的是圆心角, 那铜壶所对的圆周角呢?等于他所对圆形角的一半,这里的这个角二是不是就是爱法的一半啊?也就是二分之一爱法。然后这边的这个角呢,我给他标为是背他吧。那么他是哪一个壶所对的呢?是一个优壶所对的, 是不是这一段优虎所对的呀?这段优虎所对的圆心角就是背他,他所对的圆周角呢?你看看是不是角一,因此这里的角一呢,就应该是背他的一半,也就是二分之一背他。 我们验证一下,角一加角二啊,角一加角二,角一呢,就是二分之一,背他,角二呢,就是二分之一挨法,他俩加到一起,把那二分之一提取出来,也就是二分之一。括号里 阿尔法加上贝塔,而阿尔法加贝塔呢,是不是就是围绕着圆心转了一周圈,这不就是一个周角吗?所以他是三百六十度乘以二分之一,那也就是一百八十度了,这就是角一加角二,他是对角互补的原因了, 让你们操练一下。第一,如图四边形 abcd 是半圆的那些四边形 ab 是直径,别看他说是半圆的,他跟是整个圆的那些四边形是一回事,你即使把那半个圆给他补上来的话,你会发现,你看这不一回事吗?反正 abcd 这四个顶点呢,都在这同一个圆上,因此他一定会满足 对角互补这样的性质的。角 a 跟角 c 是对角,加起来一百八,角 b 跟角 d 呢,加起来是一百八,然后 dc 胡等于 bc 胡,好,这相等的胡,他们所对的圆心角相等,所对的斜相等,所对的圆周角是不是也是相等的啊?这就是那个五量关系定理啊。然后角 c 呢,等于 一百一十度啊,这个角是一百一十度。我们紧接着就想到他的对角了,对,他的对角就是这边的角 bad, 那应该是多少度?得是七十度吧,因为呢,他俩互补,这角 abc 啊,这个角是多少度? 求这个角的话呢?我们看一看有角 bad 跟这个角能不能发生关系啊?那要把这个等壶给他用上了,用上的话可以把那个七十度的角刚求出来,这个 给他一分为二啊,因为呢,这样一分分出来的两个相等的圆珠角,这两个圆珠角加到一起呢,是七十度,这样的话呢,各占一半了,也就都是三十五度。 而这个三十五度的圆轴角,他跟这边的这个角臂有关系,在同一个直角三角形里边,为什么说他是直角三角形呢?原因就是直径呢,直径对直角,既然他是直角的话,那直角三形的两个锐角就互于这个三角形 ab 四呢,是直角三角形, 脚臂呢,跟这边的这个三十五度的脚呼于九十度减去三十五度,就可以得到脚臂的度数,对,就是五十五度。所以这道题答案就出来了,我们看一看这道题啊,他利用了哪些知识点?首先呢,就是圆的内结四边形对角互补这条性质, 然后呢,就利用了直径所对的圆珠角是九十度,还有呢,就是等弧对的圆珠角下等。 好,这个立一,你 get 到的同学,欢迎回复个六例二,如图, abc 在原欧上角 bod, 他呢等于一百度,问的是角 abc 的度数,很多同学一激动说,对角互补呀,那他是一百度,他就是八十度,这就大错特错了,为什么呢?因为这个四边形 abco, 他并不是圆的内结四边形, 圆的那些四边形要求四个顶点都得在圆上,你看这个污点,他就没有在圆上,对不对啊?所以你不能上来运用圆的那些四边形的性质,那要想运用怎么办呢?也好办,比如说 咱们就在这边呢,来找一个点给他凑凑数吗?这不就是三缺一的事吗?我们给他找到这么一个点啊,比如说这个点我在极为点地,你现在看一看,这会就凑齐了吧。哎, abcd 这四个点是不都在这个圆上?既然都在这个圆上的话,他就符合了圆的内向四边形的性质了。对角互补呀, 那这边的这个角 abc, 他就跟这边的我们构造的这个角地,这才是对角,是吧?他就互补,可是角地是多少度呀?角地是多少度,他是圆周角,就要看看他所对的核呀。另一个圆周角定理,你看这个核 ac 啊,一条核所对的圆周角等于他所对圆心角的一半, 这个壶 ac 对着的圆形角就是这个一百度的角,对着圆轴角呢,就是把角地啊,说明角地呢,就是一百度的一半,对,他就是五十度,他是五十度的话,内接四边形对角互补,那么这个角 abc 跟着五十度加起来是一百八,有一百八呢,去掉 他是不是就得到了他为一百三十度了?所以这个题答案就是一百三十度,这是第一个方法啊,我们运用了三缺一给他补上的一个,给他凑数,凑出来了一个圆的内加四边形,如果要是硬一点我就不补,能不能行呢?也可以,怎么来看呢? 这个围绕着点欧有一周角三百六,对吧?这个三百六呢?去掉这一百,还剩二百六。二百六是哪一个角?就是这边的这个大大的角超过了平角的啊,这个就是二百六十度的一个角,这个二百六十度的角就是圆心角,对不对啊?他的壶啊,他是由 u 壶 adc 所对的, 他照样还是满足圆珠角定理的啊,就是这个壶所对的圆珠角,你看看是谁?不就是咱们要求的这个角 abc 吗?对吧?啊,那这个角 abc 呢,就等于他所对圆心角的一半,这个圆心角呢,不就是二百六吗? 百六十度的一半,你看看是不是一百三呀?殊途同归,两个方法是不是都可以啊?啊,你要不习惯于说用这么大的一个角啊,竟然也可以适用圆珠角的话,超过一百八十度的角,没以前呢,哎,都不做使用,现在用一用的话,发现也是很美妙的。好,这个第二,咱们感觉到很美妙了,两个方法咱都会了啊, 那欢迎回复个六六。那三,如图,四边形 abcd 内接于元欧,这会来了真正的内在四边形了,那他的对角就会互补点一在对角线黑色以上 有 ec 等于 bc 等于 dc 啊,这里呢?啊,我们找一找, ec 呢是这条边,然后 bc 是这条边, dc 是这条边,里面呢有等摇三角形,你像 cbe 这个呢,就是等摇三角形,对不对啊?等边对等角啊,那就可以得到这一个角,他呢就会跟这边这个角就是相等的,然后还有呢, bc 跟 cd 相等,你看他俩也构成了一个等幺三角形,那就是这边这个角跟这边这个角是相等的。等边对等角还有一点呢,就是 bc 跟 cd 呢,他俩是弦相等的,弦所对的 u 胡和列胡分别相等,于是呢,可以得到这里的 bc 这条胡,他呢跟 cd 这条胡这两条列胡是相等的, 那么等壶呢?又想到所对的圆珠角是相等的啊,那这里面的这个角和这个角,我们再突然标一下,这是角三,这个呢是角四,这两个角呢,是相等的。 里面的那么多个相等的角啊,我们看一看的话,量有点多,你也可以设餐,比如说呢,角三角四呢,我就不计为角三角四了,我就都计为一个量,我就记得他们都是阿尔法, 这样的话,一看图呢,就知道这两个角是相等的角了,对吧?我们还可以用阿尔法代表师啊,代替更多个角,比如说他是二 f, 那么这个对角呢,是不是就一百八十度减二 f 呀? 因为人家是内结四边形,他对角是互补的。第一个问题,热角 cbd 是三十九度角, cbd 就这个角,他要是三十九度的话,那么这边这个角是不是也就是三十九度啊?因为等边都能角吗?上面球的是哪个角呢?角 bad 球的角 bbd, 这不就是二 iphone 吗?啊,我可以间接来来求他的对角行不行啊?因为呢,原来那些四边形对角互补他的对角好球啊,因为他的对角啊,跟这两个三十九度的角在同一个三角形里边 啊,那内角和呢,就可以求出来。这个,其实呢,他是等要算的顶角,写下过程,因为 bc 等于 dc, 所以等边对等角就可以得到角 cdb, 它呢等于角 cbd, 角 cbd 呢?第一问给了个度数是三十九度,所以这两个角呢,都是三十九度,因此呢,角 bcd, 呃,由内角和就可以得出来是一百八十度,减去 两个三十九度,也就等于啊,一百零二度,一百零二度,又因为 abcd 呢,这个四边形内结于元欧,所以我们要求的那个角 bad, 他呢就等于一百八十度,减去我们求得的角, bcd 减去他的对角,一百八十度,减去一百零二度,那就等于七十八度。好,第一个问题呢,就是啊,此处运用了圆的内结四边形对角互补进行了一个球角度。 第二天我们求证角一等于角二,那我们就分析分析角一、角二分别在哪些三角形里边,把三角形的内角、外角都给他考虑进来,你像角一呢,他就在这个三角形 在这个三行当中,可是这边这个连点都没有标注,对不对啊?当然也可以标注上,标注上的话,你会发现这个角是多少,咱也不知道这个角怎么来表示,也不知道。这里呢,并不是让我们把角一角的度数取出来,所以第一个问题给的这个度数啊,只适用 作为第一题。啊,我们第二题呢啊,这里没有任何一个角的度数,所以我们必须得找中间的桥梁,这个中间的桥梁是什么呢?我们得需要一个参照单位,其实呢就是一个设餐思想,我们可以给他设餐,找这样的中间桥梁,让参数起到一个牵线搭桥的作用。 参数呢,还有一个好处就是使的里面角的数量呢,从个数上给它降下来。你像那两个 i 法角,其实呢它是两个角,可是呢,我们用一个 ia 法就替换了,包括这个角 我还是用阿尔法的,代瑞士就是二,阿尔法不也替换了吗?这个脚我可以用阿尔法代瑞士来表示的话,就是一百八十度减去二,阿尔法这里面呢,变来变去的啊,其实呢,阿尔法这个量没有增多, 里面的位置量就这一个,就是这个参数,当然呢,必要的时候你可以再设一个参数,你只要设了参数,他总比里边的角的总个数要少啊。比如说呢,我们这 bc 跟 ec 他俩相等,到目前呢,还没有用一用,对不对?他俩相等的话,不妨呢,咱就上这个角呢,哎,我背他行吧。啊?等边对等角吗?这个角我稍微背他,是不是这边的这个角,哎,他也是背他呀,等边对等角。 那么再来看这里的这个角一,我们可以用埃法呀,或者贝塔的代号是来给他表示,表示这个角是贝塔,这个角是多少呢?这个角呢?其实是埃法,为什么呀?因为我们这里呢, cd 壶跟 bc 壶相等,相等的壶所对的圆轴角相等,或者说你用这个铜壶所对的圆轴角相等也一样。 cd 所对着的圆周角,是不是这边的埃法就是角 cad 啊,他还对着一个就是角 dbc 像在圆当中啊,我们在倒角的时候要充分的观察胡对着谁对着哪些圆周角,同伙所对的圆周角都相等, 所以既对着这边这个角,也对着这边这个角,这不就说明这两个角相等了吗?那他也是二法,那他是背他背他减二法便是角一了,如果角二也是背他减二法,那我们就赢了,他是不是呢?角二在这个三角形 abe 里边,他这里面呢有一个二法角,哎,看到有一个外角,是不是就这个背他角呀? 那么三型的外角贝塔等于和他不相邻的这两个内角的,和贝塔呢,就等于角二加 iphone。 那么一等量,哎,一转换的话,角二呢,也就等于这个外角贝塔减去这个内角 iphone 了,这不就正出来了吗?这是一个方法啊,你不上餐的话也可以。你就这么来说,角二呢,就是角 bec, 减去这边这个角, 然后角一呢,就是由这个角减去这个角,然后你再证明这两个式子当中的被减和减出相等啊,他呢,跟他是相等的,等于等等角,然后呢,他呢等于他, 他又等于他,所以呢,这样等他带换过来也可以,只不过呢,有的同学那种情况可能就招架不了了,原因呢,就是一小会就晕了,被他蒙,哎,整蒙了,亮的太多了,咱们就是射餐吧。好,我们就射这里的这个角 cbe, 他呢等于背他, 然后角 bac, 他的等于 i 法,因为已知的这三段相等,那么根据等面对等角,先得出来这个角 ceb, 他呢,就跟我们所设的那个角 cbe 相等,说明他也是贝塔。 然后呢,根据五量关系定理啊,两条相等的弦所对的圆珠角也是相等的。还有呢,就是铜壶和等壶所对的圆珠角相等,这些呢,五个量当中有一组量相等,其他的四个都是相等的,那么我们由这三个相等 其中的 bc 跟 cd 这两条弦相等,那你可以由这两条弦所对的圆周角就相等,或者你转到壶上来也可以啊,就是 bc 壶相等的弦呢,所对的 u 壶和列壶分别相等,也可以用这个。 好,那这两个壶相等,这两条壶相等的话,所以就可以得到这边的这个角 dac, 他也就等于角 bac, 角 bac 呢,我们稍微的是 ipha, 这说明这个角 dac 也是阿依法,那还有就是角 cbd, 他呢等于角 cad, 所以他也是 iphone, 这是同虎所对的圆珠角,这几个角都表示完了吧,那么因为这里的角一,你可以看到它呢,就是角 cbe, 减去角 cbd, 也就是贝塔减去 i, 因为这个角就是背的,这个角就是爱法。然后角二,我们再看一看,他呢,就是这个外角 ceb, 然后减去角 cab, 减去这个内角, 那也是贝塔减去 rf, 你看都是贝塔减二法,从而呢,角一也就等于角二。这是我给你以涉餐法为例写的一个步骤,你要不涉餐的话,你就从这个地方继续往后证明他俩相等,证明他俩相等就行了,还是利用我们的那关系定理就可以正出来。 总之把关于语言当中的这些角的等量代换或者是倒角问题呢,我们就是练眼睛观察力的一个非常好的啊一种锻炼方式。那你就看看相等的嫌疑,但出现的话, 那就看看他们所对的啊,等弦对着的优胡列胡的问题。然后如果出现了等胡,那我们就要看 看一看他们所对的弦,所对的圆心角,所对的圆中角,包括后面的弦心句。当然这道题呢,一般不涉及到弦心句,弦心句呢,就是啊,圆心到弦的那个垂线段的长度,或者圆心到这条弦的距离,称之为是弦心句。 其实这也恰恰是原这块的题目好的地方,因为你不停的变换视角去观察的时候,一会哎,看一看他对着谁,他既对着这边又对着这边 啊,我们就会有一个又一个的意外的发现。再比如说 bc 胡,他对着这边的这个角 bac, 他还对着这边的角 bdc, 你会发现这个角 bdc 呢,他也是 if。 这会呢,你再放眼看一看,整个的图里面已经标注了四个 if 了,对不对啊?已经标注了四个 if 了, 然后呢,你会看到更多的啊,当然,你还可以看到这个角跟这个角是下等的,只不过呢,这两个角呢,都是 ab 虎所对的, 他呢,我们不是用埃法来表示的而已,也不是背他表示的。当然了,能不能用背他来表示的?能,你看这个三角形 bce, 他的两个底角都是背他一百八十度减去两个底角,不就是这个顶角了吗?所以一百八十度减去二背他就是这个角了, 那所以这边这个角也是一百八十度减去二背他,对吧?这样我们就会发现呢,在题目当中越来越多的角啊,那比如说这边这个角 acd, 这个角,他会跟角一角二拼成的这个角有相同,为什么呀?因为他们都是 ad 虎所对的圆周角,借助于这个图呢,我们就把它看的越透彻越明了。 好了,这个丽莎呢,咱们有所收获的同学感觉到还很好玩了,那就欢迎回复个六六好了。下面总结一下这个专题呢,我们就研究了圆的内结四边形啊,就是四个顶点均在圆上的,所以一定要看清,他得四个顶点均在圆上,只有三个行不行呢?不行 不行的时候想用,那你就得三缺一,就再找一个凑个数,凑成四个顶点聚在原上,他满足了,这样的话,他的内加四边形对角就会互补, 否则他叫啊,就没法用对角互补。另外呢,他这个推论呢,其实有些同学学,有些同学不学,原内接四边形的一个外角等于他的内对角,这个呢,非常的好,正应呢,每个外角都跟相邻的内角呢。是啊,离不角的关系是互补的关系, 跟他相邻的这个内角跟他的对角呢,也是互补的关系。根据同角的补角相等,也就可以得到这个推论了。好了,这个专题就为大家讲讲到这里,再见。
粉丝1.3万获赞5.2万
相关视频
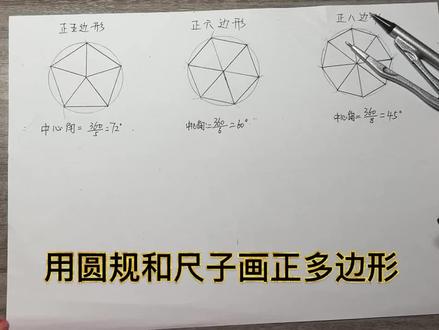 02:43查看AI文稿AI文稿
02:43查看AI文稿AI文稿好,同学们现在看一下,老师这里画了正五边形、正六边形、正八边形,那我们怎么借助半圆齿和圆规画出这些图形?首先我们要是画正五边形,那我们先画一个圆, 先画一个圆,然后我们先画圆心,任一个边,圆心和圆上身一个点,画一条半径。好,这里我们今天学习的是正多边形,这个角是中心角, 那这一圈是三百六,他是正五边形的话,那个这个中心角算出来就是七十二度,这时候我们就把圆规的这个半圆尺的圆心和这个半圆尺的圆心和这个圆心重合, 重合以后这条边和我们刚才画的半径重合,看半径重合,重合好以后我们找到七十二度,这里找这是七十,七十的话是七十一,七十二是到这好 轻轻的画一个点,然后用尺子,好,这样子好,把这半径画出来,到这就是七十二度。这时候我们也可以继续和圆形重合, 然后七十边和这个半径重合,这样去画七十二度。那有圆规的话,我们都知道震动这些中心角都是相等的,他所对的弦也相等,所以我们可以借助圆规好,圆心放在这,然后量出这个长度。好,这么长度好,根据相同的圆心角所对的弦相等,这样子画 好,那这样量的时候,这个长度也是一样长的啊。好,我们现在把这五个边连接起来,连接起来, 好,他就是一个正无边形,然后如果有需要的话,我们把这些半径再都连接起来。好,接下来我们画正六边形,正六边形,那我们先画一个圆。 好,我们先来,现在来看这个正六边形,那中心角是六十度,而这两条是半径,半径相等,等腰三角形。有一个角是六十度的,等腰三角形是等边三角形,也就是说正六边形的半径和边长是相等的, 那么针对于这个圆来说,这个弦和半径是相当的,所以我们不这时候画正六边形的时候就不需要两脚气了。好,那么圆规放到这儿任一个点好,然后我们选择这样子画胡好,再根据这个焦点继续画胡 好,这是痘痘一点就出来了,我们在 用尺子把这些关键点连接起来,好,这六边形就出来了。
431小敏@ 01:25查看AI文稿AI文稿
01:25查看AI文稿AI文稿五边形的对称轴怎么画?今天我们来教大家画五边形的对称轴,先来画出一个正五边形,确认一个点,然后我们来找到七十二度的角, 然后我们将这五个点连接起来, 然后我们来画他的对称轴。 我们的五兵型总共有五个点, 我们用每一个点经过欧点做对边的垂直线段,就是我们的对称轴, 像这样我们五边形的五条对称轴就完成了。
354文儿书画课 09:01
09:01 20:56
20:56 11:26
11:26 09:07
09:07










