宝山小学六年级上册数学几何图比赛题
粉丝14.2万获赞44.9万
相关视频
 00:30
00:30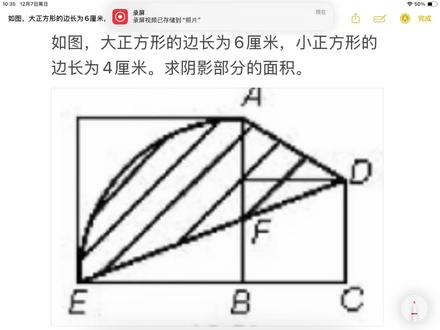 05:12查看AI文稿AI文稿
05:12查看AI文稿AI文稿hi, 六年级的小朋友们大家好,今天梁老师给大家带来了一道求阴影部分面积的题目,因为这一部分,嗯,比较重要,在以后的学习中遇到的比较多,所以呢,我们尽量把它吃透,尤其是阴影部分的重叠和图形的加加减减。 好,我们来看这道题,大正方形的边长为六, 单位是厘米,小正方形的边长为四四厘米。好,让你求的是这个阴影部分的面积。 好,我们来看一下这个阴影部分,它是一个不规则图形,然,老师一直在强调,遇到自己没有学会的图形,我们要把它转化为学过的图形来进行计算。那么这个不规则的图形我们看一下,分析一下你可以把它放在哪一个大图里面?好,思考一下, 我们是不是可以把它放到这样一个图形里面。 好,你想到了吗?那么这样一个图形,其实我们可以把它分割成两个我们学过的图形。好,我在这里再连一下,因为这两个是直角, 所以这个它就是一个九十度的扇形。好,我们看这边是一个直角梯形,那也就是说,嗯, 这个上行的面积加上这个直角梯形的面积,但是它并不等于阴影部分。那其实我们这样连线以后,你就会发现,这个图形被我们拆解的就很容易了。扇形的面积加上这个梯形的面积,再减去三角形 c、 d、 e 的 面积,是不是正好就是这个阴影部分的面积了?怎么样, 你想到了吗?好,同学们,这里面会涉及到几个面积的计算公式,我们来看一下。首先扇形的面积,我们知道扇形的面积公式,它是等于 圆的面积公式,乘三百六十分之扇形的角度 n, 那 么在这里 n 是 等于九十的,三百六十分之九十其实就是四分之一。好,我们还用到梯形的面积公式, 等于上底加上下底乘高除以二。好,这里还用到了三角形的面积公式,三角形 d、 e、 c, 三角形等于 底乘高除以二。好,我们刚才已经分析过了,这个阴影部分的面积,它就等于这个九十度的扇形面积,再加上这个梯形的面积,然后减去 三角形 c、 d、 e 的 面积。好,那么我们直接代入公式就可以了,因为它的已知条件已经够我们求出这三个图形面积了。首先我们来看扇形,扇形,我们要知道扇形的面积首先要求圆的面积,这个 大的正方形的边长正好是扇形所在的这个圆的半径,那么我们再看这个梯形,梯形的上底就是这个小正方形的边长,下底就是这个大正方形的边长,而它是直角梯形,它的这个高也正好是小正方形的边长。 好,我们先把这个梯形它是等于上底加上下底,乘高除以二,再加上这个扇形的面积。 我们先写圆的面积,三点一,四乘六的平方,九十度的扇形其实就是四分之一了,乘四分之一。好,再减去这个 白色的这个空白部分三角形的面积,三角形的面积是底,它的这个底是小正方形的边长,而它的这个高是大小正方形的边长之和。底乘高 六加四。好,这边不好写了,再除以二。好,我们来计算一下, 等于十乘四除以二,加上三点一,四乘六的平方,再乘四分之一,减去四十除以二。注意啊,这个地方老师没有写出来,他是六加上四, 再乘上他的底,再除以二,再除以二是这样子的好,最后等于多少呢?二十八点二六 平方厘米。好,同学们,呃,我们一起来总结一下。像这样的一个不规则图形,我们把它放到了一个规则的图形里面,而这个规则的图形,它是我们学会了扇形和梯形面积组合而成的,那么组合以后,我们发现多了一个三角形的面积,而三角形 e、 c、 d 的 面积,我们知道底,知道高,那也很容易求出来。所以我们又是把一个不规则的硬部分面积转化成了我们学过的图形的面积来进行计算。小朋友们,你们掌握了吗?今天这道题目就到这里喽,再见!
12神兽伴学攻略
猜你喜欢
- 18.5万俊俊大师兄
















