粉丝1.1万获赞3.6万
相关视频
 16:11145肖老师数学笔记
16:11145肖老师数学笔记 20:07查看AI文稿AI文稿
20:07查看AI文稿AI文稿同学们大家好,今天我就和同学们共同开启正弦函数、余弦函数的图像这节课的学习。三角函数是我们学习的一类新的基本出档函数,按照函数研究的方法,在学习了三角函数的定义之后,接下来我们应该研究什么问题了呢? 同学们说的对,应该继续研究三角函数的图像和性质了。请同学们思考一下,之前我们研究指数函数,对数函数的图像和性质的思路是怎样的呢? 我们就是先明确了函数的定义,然后利用定义研究函数的图像,再利用函数的图像研究函数的性质。 之前我们已经学习了三角函数的定义,所以接下来我们就要来研究三角函数的图像。 那请问同学们绘制新函数图像的基本方法是什么呢?是的,绘制一个新函数图像的基本方法就是描点法。 那么根据三角函数的定义,需要绘制正弦函数在整个定义域上的函数图像吗?其实选择哪一个区间即可呢? 根据三角函数的定义,单位元上任意一个点在圆周上旋转一周以后又回到原来的位置,即三呀二法加二 k 派等于三呀二法。同样 q 三二法加二 k 派也等于扣三二法,其中 k 是整数, 所以我们可以先画出正弦函数在 b 区间零到二派的图像,再画出正弦函数,再定 抑郁而上的图像就可以了。那么现在我们就先一起研究如何绘制出正弦函数的图像。既然描点法是画函数图像的基本方法,对于正弦函数,大家想取哪些点,怎样描点画图呢? 有的同学说可以对于次变量,在必须间零到二派上随意的取一些值,然后利用计算器选出函数值,再在平面直角坐标系上秒点连线。大家觉得这样做图可行吗? 这样做图应该可以做出正前函数在 b 区间零到二派上图像的大致形状。但是对于正前函数,不论是角的弧度数还是正弦直,都会出现一些五里数,如果利用计算器 所图,明显不够精确,而且也没有利用到三角函数的定义,所以同学们你能寻找到更加精确而且利用到了三角函数定义的方法吗? 好,我们来进一步思考。要想绘制一个函数的图像,首先就需要准确绘制图像上的一个点, 所以对于正弦函数在 b 区间零到二派上认取一个值 x 零,我们该如何借助单位元确定正弦函数值三呀 x 零,并且准确的画出点替 x 零,三呀 x 零呢? 同学们请看图。在平面直角坐标系中画出以圆点为圆心的单位圆,单位圆与 x 轴正版轴的焦点为 a 一零。在单位圆上将点 a 绕着点 o 旋转, x 零弧度至点 b。 根据弧度制的定义,阿尔法弧度数的绝对值等于弧长 l 比半径 r, 单位员内半径为一,所以此时 x 零既是角 aob 的大小,同时也是弧 ab 的长度。 而根据正弦函数的定义,此时点闭的纵坐标 y 零即为赛因 x 零, 所以我们可以以 x 零为横坐标,而以外零为纵坐标画点就可以得到函数图像上的一个点 tx 零。 saying x 零, 那现在我们已经学会了绘制正弦函数图像上的某一个点,那么同学们你能制定一个 方案,画出正前函数在 b 区间零到二派的图像吗? 对于这个问题,同学们有很多不同的方案,现在我们就来逐一分析。有的同学说可以在 b 区间零到二派内认取一些横坐标的值,之后按照上述的方法逐一绘制点,再用光滑的曲线连接起来。 但是同学们请注意,如果我们对 x 零随意的取值,那么 x 零可能会出现有理数、无理数,这样就不容易在 x 轴上准确的定位。 再有根据弧度至的定义,此时 x 零的值是弧 ab 的长度,那么不容易平移,所以在单位员上想定位 x 零弧度角的中边时,就存在了一定的困难。 所以有同学提出,那么我们就不要对 x 零随意取值了,可以取像一、二、三弧度等这样的值,再按照上述方法绘制函数图像 一、二、三等。这些弧度数在 x 轴上确实可以准确的定位了,但是在单位员上想定位这些弧度角的中边时,仍然存在上数的问题,我们还是不容易准确定位点地的位置。 又有同学提出,那么不如我们取比较熟悉的这些特殊角,比如六分之派、四分之派、三分之派等等。 在 b 区间零到二派内的这些特殊角确实是大家比较熟悉的, 在 x 轴上也比较容易定位,但是在单位员上又该怎样确定点臂的位置呢?究竟我们应该取哪些特殊角,怎样取特殊角才能使得作图既简便又准确呢? 有同学提出了改进的方案,我们可以在 b 区间零到二派内取等分点,这样做图既简便又准确, 请同学们一起看图。首先我们可以把 x 轴上 b 区间零到二派这一段分成十二等份,从而使 x 零的值分别为零、 六分之派、三分之派一直到二派这些特殊角,而他们所对应的角的中边与 单位员的焦点,同样将圆周十二等分。我们可以再按照上述方法依次的画出点。 tx 零赛呀 x 零 同学们,现在就请大家和我一起来做出正前函数在 b 区间零到二派的图像。 首先我们将 x 轴上 b 区间零到二派这一段四等分,再将每一个子区间三等分,从而将 x 轴上 b 区间零到二派这一段等分成了十二份。 然后以坐标原点为圆心,做出单位圆 这些特殊角的中边,同样将圆周十二等分,这样我们就得到了 零到二派内这些特殊角的中边与单位员的焦点。现在我们就来秒点,首先散引零等于零,所以正弦函数的图像过点零零。我们再来看六分之派, 六分之派角的中边与单位员的焦点的纵坐标即为 saying 六分之派,所以我们可以以六分之派为横坐标,以这个点的外之为纵坐标描点,从而就得到了六分之派。 saying 六分之派这个点。 我们再来看三分之派,三分之派角的中边与单位员交点的重坐标即为赛印三分之派,所以我们以三分之派为横坐 坐标,而以这个点的外值为纵坐标描点,就可以得到点三分之派,下印三分之派,以此类推。用同样的方法,我们就可以依次做出 b 区间零到二派上所有对应点的位置, 然后用光滑曲线将这些点连接起来,从而我们就得到了正弦函数在 b 区间零到二派上的图像。 同学们,老师在这里利用信息技术,可以在 b 区间零到二派上取足够多的点,并且将这些点用光滑的曲线连接起来,就可以得到比较精确的正弦函数在 b 区间零到二派的图像了。好,同学们请看,这就是正弦函数在 b 区间零到二派的图像,它是一段连续光滑的曲线,那么根据函数 y 等于赛亚 x 在 b 区间零到二派的图像。同学们,你能想象出挣钱函数在定义域而上的图像吗?你的依据是什么?请你画出该函数的图像。 根据公式一,我们知道撒野阿尔法加二 k 派等于撒野阿尔法,其中开始整数,所以 函数 y 等于赛 x 在每一个形如二 k 派到二倍 k 加一派,其中 k 是不为零的整数。这样的必须间内, 他的图像应该与正弦函数在 b 区间零到二派的图像形状是完全一致的。从而我们就可以不断的将正弦函数在 b 区间零到二派的图像向左向右平移二派的单位,就可以得到正弦函数在定义域而上的图像了, 这就是正弦函数在定音域而上的图像。正弦函数的图像叫做正弦曲线,它是一条波浪起伏的连续光滑曲线。 那同学们,有时啊,对于函数的研究,能够快速又比较准确的做出他的简图,往往起着特别重要的作用。那么你能否画出函数外等于三呀? x 在 b 区间零到二派内图像的简图吗? 在确定图像的形状时,应该抓住哪些关键点呢?请同学们观察正线函数 在地区间零到二派的图像。我们可以看到这里起关键作用的几个点,正是最大指点、最小指点以及曲线与 x 轴的焦点。因为有了这几个点就可以确定曲线的形状了,所以我们就以这几个点为关键点描点作图, 他们的坐标依次为零零二分之派、一派零、二分之、三派负一以及二派零。 一般的,在精度要求不高时,我们可以先找出这五个关键点,再用光滑曲线连接起来。这种方法非常的简便实用,它称为五点法。 同学们,现在我们已经能够做出正前函数的图像了,请问你能做出 鱼玄函数的图像吗?有的同学说,那我们就和之前一样,利用鱼玄函数的定义,借助单位元描点作图吧。 但同学们请思考一下,如果我们仍然采用之前的方法,此时在单位员上点臂的横坐标为扣三 x 零,那么如果我们要做鱼选函数,以点臂的横坐标为点替的纵坐标,画图时这个坐标还那么容易使用吗? 显然不再容易使用了。那我们还能找到什么更简便的方法吗? 由三角函数的定义,我们知道正弦函数与选函数是一对密切相关的函数,诱导公式就已经表明了,余选函数和正弦函数是可 可以互换的。所以你能否通过已经得到的正弦函数的图像,通过图像变换的方法得到鱼悬函数的图像呢? 有同学马上想到了这个诱导公式, y 等于扣三, x 等于三眼,二分之派减 x。 但同学们请注意,这个公式里 x 的前面有负号,同时有二分之派又涉及到平移,所以图像变换是比较复杂的,不容易操作。那我们有没有形式更加简洁的诱导公式可以使用呢? 有的同学又想到了这个有点公式,扣下 x 等于 saying x 加二分之派。这个公式确实简洁了很多。同学们初中时学习过图像平移,我们知道 将正弦函数的图像向左平移二分之派个单位长度就能够得到余弦函数的图像了。 同学们请看图,我们可以将正弦函数图像上的点都向左平移二分之派个单位。比如将零零点平移到负二分之派零, 将二分之派一平移到零一,将派零平移到二分之派零等等。从而将正选曲线上的每一个点都向左平移二分之派个单位就得到了鱼选函数在定义域而上的图像。 而鱼悬函数在地狱而上的图像叫做鱼选曲线,它是与正弦曲线具有相同形状的波浪形曲线。 我们都知道曲线是由点构成的,那同学们,你能利用点的坐标来解释这种平移变换吗?我们一起来分析。设函数 y 等于 cx, 图像上任意一个点为 m, n 即 cm 等于 n, 则在函数 y 等于 say in x 加二分之派上,当 x 加二分之派等于 m 时,即 x 等于 m 减二分之派时,函数值同样也为恩, 所以函数 y 等于散呀。 x 加二分之派的图像上就有一个对应点,它的坐标为 m 减二分之派 n, 那我们看到将点 m n, 凭一道点 m 减二分之派 n, 显然 是将这个点向左平移了二分之派个单位。同时我们又是在正弦函数图像上任意取的一个点,所以说明正弦函数上的所有点都向左平移了二分之派个单位,从而我们就用点的坐标进一步解释了这种平移变换。 那同学们,类似于五点法做正弦函数的图像,我们又该如何做出余弦函数的简图呢? 思考这个问题啊!我们首先应该思考选取哪个区间研究这个问题比较合理。 那么根据鱼选函数的定义,我们可以知道仍然需要取长度为二派的区间,再根据鱼选曲线的特点,他关于外轴对称,所以我们不妨取一个关于外轴对称的 区间,这样我们取 b 区间复派到派就比较合理了。那么请同学们观察鱼旋函数在 b 区间复派到派上的图像,我们取哪几个点为关键点呢? 哎,仍然应该取最大指点、最小指点以及曲线和 x 轴的焦点。 他们的坐标依次为,负派负一、负二分之派零、零一、二分之派、零派负一。 现在我们已经能够做出正弦函数和鱼群函数的简图了,那么同学们,请大家和我一起看这个例题,请你用五点法画出下列函数的简图。 我们先来看第一个函数 y 等于一加三 x, x 属于 b 区间零到二派,我们应该取哪五个关键点呢? 由于是给赛 x 的值加了一个单位,所以我们可以取和正弦函数相同的五个关键点, 然后求出每一个对应的赛 x 的值,之后再求出一加赛 x 的值,之后根据表格描点,然后用光滑的曲线将他们连接起来,就得到了这个函数在 b 区间零的二派的图像。 我们将它和正弦函数在 b 区间零到二派的图像对比一下,可以发现,对于每一个 x 而言,横坐标不变时,纵坐标加了一,所以本质上是 将正弦函数在 b 区间零到二派的图像向上平移了一个单位而得到的。 好,我们再来看第二个函数, y 等于负抠赛 x, x 属于 b 区间零的二派,我们又该取哪五个关键点列表呢?由于这里是给抠赛 x 取了相反数,所以我们仍然可以取和余选函数相同的五个特殊点, 仍然为最大指点、最小指点以及零点,然后求出每一个扣三 x 的值,再求出负扣三 x, 根据表格秒点,然后用光滑的曲线连接起来,就得到了 y 等于负口三 x 在 b 区间零到二排的图像, 我们将它和鱼旋函数在 b 区间零到二派的图像对比一下,可以发现,对于每一个 x 横坐标不变,而纵坐标取了相反数,所以本质上是将鱼旋函数在 b 区间零到二派的图像关于 x 轴对称而得到的。 同学们,最后我们回顾一下这节课的内容,请大家思考一下以下问题。一、我们是如何做出正弦曲线和鱼弦曲线的? 首先,我们通过等分 b 区间零到二派等分单位员的方法,借助单位员和正弦函数的定义,做出了正弦曲线,然后将正弦曲线向左平移了二分之派 个单位得到的鱼旋曲线。二、如何用五点法做出正弦函数鱼弦函数的简图呢? 一般在精度要求不高时,我们可以采用五点法来做函数的简图。这里一般取的是最值点以及曲线与 x 轴的焦点。 三、做函数图像有哪些基本方法呢?正如我们这节课做正弦曲线和鱼弦曲线时用到的两种方法,分别是描点法和图像变换法,这也是我们做函数图像常用的两种重要方法。 这是这节课的作业,请同学们课下完成。最后我想送给同学们两句话,数学是打开科学大门的钥匙,数学是人类思考中最高的成就。希望同学们喜欢数学,热爱数学。同学们再见!
1487名师课堂 03:39查看AI文稿AI文稿
03:39查看AI文稿AI文稿大家好,这个视频我们利用图像来动态演示,用鱼弦线来画鱼弦汉字的图像。 好在这个图中呢,我们看一下有一个单位圆绿色的,然后呢圆上一点,一通过一点做 s 轴的垂线,这点是 f, 那么在三角形 e b f 中,角 e b f 这个角,他对应的对边是 e f, 那么他的另一边呢,是 b f。 根据余学函数的定义 coss 角,我试一下 coss 角 eb f, 他的定义应该为 b f b b e, 这是余雅涵的定义, 那么我们就把 b f 叫做余弦线,并且 bf 有方向的,和做正选函数的图像类似, 我们要研究的是角 bf 这个角和 bf 的关系,在直角这个戏中把它展现出来, 角 ebf 把它化为弧度,展现在 s 轴, b f 呢,应该展现到 y 轴,但是呢,他和 s 轴重合。那么我们要利用一条直线,就是 yds 这条 四十五度的直线,把它对应到外轴上去。好,我们通过 f 点做 s 的垂线,与外面 s 这条直线求于 m, 那么我们知道 m f 和 b f 是相等的, 然后通过平移 fm 到 f t n 这个地方,我们就知道了 f p, l n 这一条就是余弦线的直。那么在途中这三条红色的线都是代表了余弦的直。来看一下余弦直的变化, 从零开始, 这时候呢,鱼线线 b f 等于一 f, 撇 m 的值也为一。好,这是初始值,就是说扩散零度等于一, 我们开始变化 好,大家可以看到,随着角 e b f 的增大,扩散的直 b f 再减小, 减小,从一开始减小。继续, 当 ebf 这个角大于九十度的时候,余弦线 b f 为负向的余弦值是负值,继续, 当这个角达到一百二十度的时候,库穗为负一于全的最小值,继续, 当一天画到二百七十度的时候, 库线池漂移帘继续。 好,那么这一个完整的周期已经结束,大家看一下。 好,谢谢大家。
89济南冰浩企业店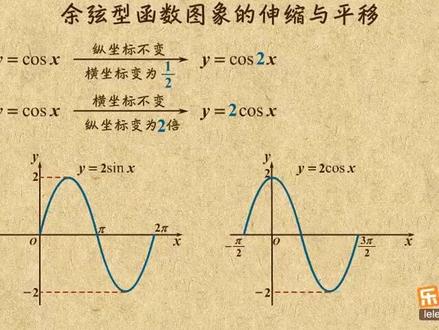 02:41查看AI文稿AI文稿
02:41查看AI文稿AI文稿这个视频我来给你讲讲鱼先生函数的伸缩与平移。总的来说,他和正先生函数是一样一样的。咱举起来看一下。 先看伸缩变换,比如要把 y 等于 cosex 变成 y 等于 cose。 二 x 咋变呢?还记得三 x 的变换吧,在 x 前面成了二,那就是把图像像这样横向压缩。对于 cosex 也是一样,在 x 前面成了二,也是把图像这样横向压缩。 所以,要从 y 等于 cosax 变化到 y 等于 cosairx, 就得让所有点的重坐标不变,横坐标变为原来的二分之一。 刚才是在 x 前面乘了二,你已经知道咋变化了。如果我改成再扣三前面乘以二,你知道咋变吗?还是想想三 x 的变换吧。在三前面乘了二, 那就是把图像像这样纵向拉伸。对于科三, x 也是一样,在科三前面乘以二,还是把图像像这样纵向拉伸。所以,要从 y 等于 cos x 变到 y 等于二倍, cos x 就得让所有点的横坐标不变,纵坐标变为原来的两倍。 看来,对于鱼先行寒暑的伸缩变换。在 x 前面成了几,你就把所有点的纵坐标不变,横坐标变为原来的几分之一。在扩散前面成了几,你就把所有点的横坐标不变,纵坐标变为原来的几倍。 好了,看完伸缩变换,再来看看平移变换,其实没啥新的东西,还是这八个大字,左加右减,上加下减。比如要把 y 等于 cosax 变成 y 等于 cosax 加四分之派,你就只要把他的图像往左平移四分之派就成。如果 要把 y 等于扩散, x 变成 y 等于扩散 x 再加一,你就只要把它的图像往上平移一个单位就成,确实很简单吧。不过我还是要再提醒一下,如果是把 y 等于扩散 rx 变成 y 等于扩散 rx 加四分之派, 你还得把这个二先提出来,再看平移了多少。显然要得到他的图像,得把 y 等于扩散二, x 往左平移八分之派。 总的来说,鱼先函数的平移还是左加右减,上加下减。不过如果 x 前面有系数,在做左右平移时,系数要先提出。 好了,就讲到这里总结一下。这个视频我就给你讲了余弦型函数图像的伸缩与平移,它的变换规则和正弦形函数的变换一模一样, x 前面成系数就让横坐标变成几分之一, 前面成系数就让动作标变为几倍。至于平移变换,还是左加右减,上加下减。好了,本姑娘就讲这么多,赶紧刷题去吧!
85初高中数学老师 17:01查看AI文稿AI文稿
17:01查看AI文稿AI文稿同学们好,我是董老师,我们继续来讲三角函数的第六节,余弦函数的图像与性质。 之前我们是讲的正悬函数的图像与性质,这两个啊,正于悬函数图像,他们是长得是几乎本来就是一模一样的,只是位置不一样,所以呢,他的性质也是几乎一样的,只是一个横坐标,有点区别。 因此咱们学这节课,我们进度会快一点啊,同学们一起需要认真的听。我们先来看语选函数图像, 我们之前是学了一个诱导公式,所以呢,这里面相当于啊,用诱导公式,可三 ex 就等于三应 x 加二分的判,因此三应这 个函数我们知道,我们现在已经知道三 ex 图像怎么得到这个函数呢?很明显,我们利用平移变换就行了,是不是利用左加右减就行了啊,向左平移二分之派个单位就行了,就会得到三 ex。 所以呢,余弦函数的图像与正弦函数图像,只需要将正弦函数图像向左平移二分之派克单位即可啊,向左平二分之派克单位即可,得到的图像就知道就叫做余弦曲线。 正面是他的图像啊,跟正选曲线他几乎是图形状是一一样的,只是位置不一样啊啊,那我们该如何画余选函数的图像呢?跟前面是一样的, 也是利用五点法来画余弦函数图像啊,因为余弦函数他也是周期函数,因此我们只需要在一个周期内啊,比如在零到二派内画他的图像就行了。后面的我们只需要向左拼音或向右拼音整数个周期就行了啊, 他的五个关键点分别为哪五个关键点呢?其实跟正义学函数的一样,横坐标都是零,哎, 二分之派派二分之三派,二派,然后呢,后面的纵坐标啊,纵坐标就有一点不一样,纵坐标其实就是直接将横坐标带路过去算出的函数 数值就就可以了。虽然我们之前在学习正学函数的画法的时候,我只要求你们记乘坐标分别 是零,二分之派,派二分之三派,二派。这五个点,那么重左标就是相对应的函数值就行了啊,这五点,这五个点,我这个没标出来啊。好,这是这五个点啊,这是余弦函数的图像, 余弦函数的性质哎,性质也是跟前面的一样的,操作就是看图像总结出他的一个性质就行了啊。首先看定律,定律没啥说的,直接是 整个时数值域,我们发现他最大值是一,最小值是负一,因此值意是负一到一最大值。我们发现这当 x 等于零的时候会取得最大值, x 等于零的时候,他会取得最大值。但是呢,这里面是我们一个周期内的一个啊,最大值点 啊,我们只需要在这个 x 啊加上一个周期的整数倍就行了。所以零加上二踢派,其中 k 属于 z, 当 x 等于二 k 派的时候,那么 y 就会取得最大值的是一同理最小字。我们找一个,你会发现当 x 等于派的时候,哎,在一个周期内说等派的时候取得最小值啊,然后同理也是加上周期的整数倍,二 k 派, k 属于对 他会起到最小值啊,最小值。再来看他的一个周期,他是一个周期函数周期跟前面是一样是二派啊,单调性,我们也是看一个周期内的东西啊,一个周期,我们看一下在这个周期,在零到二派这个周期,我们发现啊,零到派, 单调地铁,派到二派时候单调地震,因此我们可以这样说,在第一二象限连续的一、二象限是为单调地铁,连续的三、四象限为单调地 真可不可以说函数在第三周起,第三项线为单调递减呢?其实这个说法是错误的,你只能说在单独的, 因为第三象限每个象限是吧,都要用逗号隔开就行了啊,这个是由于不能用并解啊,单调的声音说派到二派啊,派到二派,因此我们在这里面 派到二派,然后呢,在两端同你跟前面一样的操作,加上周期整数倍,加上二 k 派,加上二 k 派啊, k 属于 z 在零到派,零到派,所以单调递减的, 然后呢,加上周期的整数倍啊,所以呢,我们这里稍微改一下,就是二 k 派的啊,派加二 k 派属于单调递减,这是一个他的增减性,都是由图像可以看出来的啊。再来看他的一个基友性,根据图像我们发现他是一个偶函数啊,偶函数, 关于歪轴对称关于歪轴对称,那这个里面啊,余弦函数其实也有很多对称轴以及对称中心。对称轴,我们看一下对称轴, y 轴是一条对称轴,这个数啊,你看这里面是派, x 等派的时候也是一条对称轴, x 等二派的时候也是对称轴,因此他的对称轴是 x 等于 k 派,这个属于 z 啊, k 属于 z。 对称中心呢,对称中心 只需要与 x 轴的焦点就行了。我们发现这里面对称中心是 k 派加二分之派啊,你可以总结规律啊,这个比较总结,比较讲好,总结我就不多说了,后面都是 k 属于 z 啊, 这是一个对称轴和对称中心锋利。在余弦函数里面,我们发现当 x 取得他的对称轴的时候,他的函数值会取得最值,要么取得最大,要么取得最小。那对称中心呢?也是以 x 轴的焦点 与安卓焦点通通为对称中心啊,这个跟前面的正悬函数是一样的啊。啊,我们把 余弦函数的一个基础知识学习吧,我们再来看一些辨析题啊,判断题。第一个,余弦函数图像是关于原点对称啊,第一个 不对啊,对,我们刚刚说的他是关于 y 轴对称,关于圆轴对称,是一个 g 函数啊。第二,于选函数,他的图像可由三 ex 图像向右平移。哎,向右就不对了,我们刚刚说的是向左平移,这就是错的啊,所以要改成左 三。在同一坐标系列,余弦函数与正弦函数它的图像完全相同,只是位置不同,这个是对的啊,是对的。 第四,正弦与弦有相同的周期,最大值、最小值以及相同的单调圈啊。前面周期是一样的,最值也是一样的,但是 单调曲线是不一样的,所以这个是错的啊,是错的啊。再来看第一题,这个前面是辨析题,这个看第一题,他说他说要画简图,哎,简图我们 还是找点描,然后连线就行了啊。这里面找的点,我们横坐标,记住刚刚的五个点就行了。 坐标零二分之派派二分之三派,二派,然后带过去算,我们发现这个函数值,比如 s 带连过去是二分之一减一二分之一, 二分之派过去是负一,好算出他的函数值,在,然后呢,在那个直角坐标心里面秒点。第二点是零,负二分之一,然后呢是二分之派,负一 派负二分之三,然后呢二分之三派负一,二派负二分之一,将这五个点连起来即可啊,这,这个就,这就是他的一个函数图像啊,这个没什么太多说的。再看第二题,这是一个解不等式问题啊,解不等式解这些不等式的话,我们也 可以利用函数图像来解啊,或者啊,利用单位语言,我因为我们这节课学的是函数图像,因此我们用函数图像来解啊。 好,来看第一个,这个要外大于等于二分之一,外大于等于二分之一。同理,我们只需要在一个周期里来解就行啊,一个周期我们先画外等二分之一这根直线,外等二分之一这根直线啊,这边用红色直线画啊。 我们找周期的时候,我们可以这样来找啊,可以这样找,正面复派到派,别说这里面是不是一个完整的周期啊, 我们在这个周期列解就行了。对呢,两个点坐标,因为这是划分之一,因此我们可以很容易求得这个,其实这个点横坐标是负三分之派这个点对呢,是三分之派,因 是外大于等二分之一,我们可以解到啊,意外,由图像可知啊,他的一个结节就是 x 属于正面,是外要大取上方就行啊,就是 负的三分之派到三分之派,又因为他是一个周期函数,因此我们只需要在端点两边同时加上二 k 派就行了啊,这里面能取到的就必须这样,是二 k 派减去三分之二,到二 k 派加上三分之派, 也说属于 z 啊,也属于 z, 这是第一问,再看看第二问,要外大于等于外大于等于负二分之一,小于等于二分之根号三啊。那么我们来看一下,画两条直线啊,画两条直线,负二分之一大概在这啊, 发动机大概在这二分之根号三大概在这。同理,我们也是在一段周期内来解就行了啊,一段周期,我们还找刚刚那个周期,也说找这一段周期就行了啊, 找这一段周期,从这段周期我们发现他要这个函数值夹在正面,因此我们发现说这一段啊,这段函数对应的横坐标,以这段函数对应的横坐标啊,左边这一段对应的横坐标是 x, 属于投资, x 是属于。我们先来看第一段啊,第一段是因为是负二分之一,因此这个对应的是其实是负的三分炸牌啊,负三分炸牌,那正面对应的是二分之二三,对呢,是负六分之派, 负的三分之二判啊,然后呢,到负的六分之判并上,我们再看第二段,第二段同理 是二分之根号三,对应的是六分之派啊,到这边是三分之二派啊,三分之二派。 然后呢,在每个端点两边同时加上奥克派就行了,我们叫奥克派啊,后面这属于这这个东西千万不要忘,忘了就肯定会被扣分的啊。好, 这个立条咱们就是利用图像法先在一个周期内解就行了,然后呢,在端点两边同时加上周期的整数倍啊,就行了啊。再看立体三,立体三,这个我们之前其实本质还是利用一个换元法, 零 t 是等于可三应 x, 则 t 的范围,他是属于 t, 是属于负一到一,所以呢,这个函数就 变为 y, 所以等于负 t 的平方加 t 啊。很明显,他的一个对称轴是等于二分之一,所以 t 等于二分之一的时候,外有最大值 是等于带二分之一过去是等于负十分之一加二分之一啊,所以是四分之一,负一是离对称轴更远的。 t 等于负一的时候,那么他就使得最小值啊,最小值带过去是等于 二啊。水第一个他的一个最大只是四分之一,最小的是发啊,这第一个第二个也是一样的,换元法 a, t 是等于可三 x, 那么 t 的范围就不再属于负一到一了,因为 x 给了范围,这个范围正好跟前面第二题类似,是属于负 二分之一到二分之一啊,二分之一到二分之一啊,那此时这个函数外就变成,所以 y 说等于三 t 的平方减四, t 加一啊,他的对称走啊,踢走需要等于三分之,这边是三分之二,所以 y 式等三 t 方减四 t 加一,这个对称轴不在这个范围,那明显在对称轴左边,通通在左边为单调递减,再负二分之一到二分之一为单调递减。 所以呢,他的一个最小值当 t 等于二分之一时,外的最小值那就等于带带过去是四分之三减一 是等于负四分之一。 t 等于负二分之一的时候,外有最大值是等于四分之三,加上三是等于四分之 十五,因此他的最大值就等于四分之十五了啊,这是也是利用换元法,换元就变成一个二次函数了,就比较简单了啊。 再来看第四题,他说要求下列函数的定域和直遇,这个第一个定域还是就直接一减二三, x 大于点零,那么 c 三 ex 小于等于二分之一,小于等于二分之一,我们可以解在一个周期内减就行了啊, 此时我们可以写到, x 是属于啊,三分之派到三分之五派啊,三分之派到三分之五派,然后呢,两边同时加 搭上奥迪派就行了啊。有的同学不知道这个三分之派三分之五派怎么来的,同学们可以看一下那个图像啊,图像,我们看正面图像啊,我们 们看这里面的图像啊,我们看这里面图像,此时其实你相当于在这个周期内解就行了啊,在这个周期内解就行了,我们找到二分之二分之一对应的,所以要下方这个对应的就是三分之派,这个对应的其实是三分之五派 商住派。因此你会发现在这个周期内是三分之派到三分之五派,然后呢,两边加上周期的整数倍就行了啊。啊, 这是定域啊,紫玉,紫玉就比较简单了啊,这个比较简单,我们看一下啊,紫玉,因为一减二和三 ex 一定要大于等于零,但是呢,他的最大值可上一次取负 一的时候,我们就可以取到他的最大值是等于三的,所以直遇那就是零到根号三结为所求啊,零到根号三结为所求。 再来看第二个,第二个,第二个也是一样的,这个对数增数,我们这个三亿啊,增数二可上亿, x 减根号上要大于零,因此我们解答是多少呢? 三应 x 是大于二分之根号三的,我们是根号三,在一个周期内解,我就太多叙述了,我们可以觉得 x 是属于二分之根号三,对应的是一个六分之派,或者说负六分之派,所以是 负六分之判啊,六分之判这一个周期内结。就是啊,然后加上周期的整数倍,都是加上二 k 判,后面 k 属于 z, 这是定律。 直遇呢?直遇我们知道二可三应 x 减去根号三,它肯定是属于零的。最大值是几啊?最大值数的二减根号三啊, 减高上啊,这可以等啊,这可以等。所以呢,这个落个函数外,函数他是有最大值的,他是单调递增啊,单调递增他是有最大值的,所以 子欲,子欲为,这个是复吴雄,因为那个左边是零啊,打那个二减跟号三啊,二减跟号三,这是他的子欲,子欲还是比较好求的啊。子欲啊, 这个是第四题求定义值一问题。余学函数,他的图像与性质,我们学起来一定要跟正学联系起来,其实大部分我们见到的都是正学函数啊,正学函数对于解不等式问题,这是 一个难点,多利用图像啊,然后找周期,我们,我们刚找周期,在一个周期内的时候,这个周期其实会变的啊,有的时候我们找的是复派到派, 有的找时候我们找找的是连道派,这个周期啊,我们这个是会变的。所以呢,同学们一定要注意,什么时候使用这个啊,哪个方便就用哪个啊。
451咚铛铛 02:41查看AI文稿AI文稿
02:41查看AI文稿AI文稿这个视频我来给你讲讲鱼弦型函数的伸缩与平移,总的来说,它和正弦型函数是一样一样的。咱具体来看一下。先看伸缩变换,比如要把 y 等于 coss 变成 y 等于扩散二 x 咋变呢? 还记得赛 x 的变换吧,在 x 前面成了二,那就是把图像像这样横向压缩。对于扩散 x 也是一样,在 x 前面成了二,也是把图像这样横向压缩。 所以要从外等于抠下 x 变化到 y 等于扩散二 x 就得让所有点的纵坐标不变,横坐标变为原来的二分之一。 刚才是在 x 前面乘了二,你已经知道咋变化了。如果我改成在 q 三前面乘以二,你知道咋变吗?还是想想三 x 的变换吧。在在前面乘了二, 那就是把图像像这样纵向拉伸。对于扩散 x 也是一样,在扩散前面乘以二,还是把图像像这样纵向拉伸。所以要从外等于扩散 x 变到 y 等于二倍。扩散 x 就得让所有点的横坐标不变,纵坐标变为原来的两倍。 看来,对于于先行函数的伸缩变换,在 x 前面乘了几,你就把所有点的纵坐标不变,横坐标变为原来的几分之一。 在扩散前面乘了几,你就把所有点的横坐标不变,纵坐标变为原来的几倍。好了,看完伸缩变换,再来看看平移变换,其实没啥新的东西,还是这八个大字,左加右减,上加下减。 比如要把 y 等于 coss x 变成 y 等于扩散 x 加四分之派,你就只要把他的图像往左平移四分之派就成。如果 要把 y 等于扩散, x 变成 y 等于扩散 x 再加一,你就只要把他的图像往上平移一个单位就成,确实很简单吧。不过我还是要再提醒一下,如果是把 y 等于扩散, r x 变成 y 等于扩散, r x 加四分之判, 你还得把这个二先提出来,再看平移了多少。显然要得到他的图像,得把 y 等于扩散二, x 往左平移八分之判。总的来说,于先函数的平移还是左加右减,上加下减。不过如果 x 前面有系数,在做左右平移时,技术要先提出。 好了,就讲到这里总结一下。这个视频我就给你讲了鱼弦型函数图像的伸缩与平移,它的变换规则和正弦型函数的变换一模一样, x 前面呈系数就让横坐标变成几分之一,扩散 前面成系数就让动作标变为几倍。至于平移变换,还是左加右减,上加下减。好了,本姑娘就讲这么多,赶紧刷题去吧!
3024数学王子特训营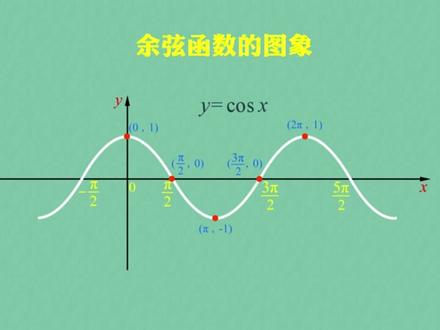 02:15查看AI文稿AI文稿
02:15查看AI文稿AI文稿我们已经学过正显函数的图像 y 等于三 x, 是这样一条过远点的波浪线。 这个视频我们来看一下余弦函数 y 等于 cosax 的图像,还记得诱导公式吗? 扣三 x 等于三,括号内二分之派加 x。 可以看出,只要把这个 x 加上二分之派,就是扣三 x。 从图像上看,就是把三 x 的图像向左平移二分之派个单位得到, 因此这个图也就是余弦函数 y 等于 cosax 的图像了。余弦函数的图像叫做余弦曲线。 从余弦函数 y 等于 cosax 的图像上也可以发现五个关键的点,分别是零一、二分之派、零派负一而 分之三派零以及二派一。与正弦函数的五点做图法一样,我们也可以用五点做图法做出余弦函数的图像。比如用五点法做函数 y 等于 cosan 括号内二 x 减三分之派。在区间零到派上的图像 同样先列出表格,领 cos 后面的二 x 减三分之派等于零二分之派、派二分之三派及二派,列出相应的函数值,然后得到对应的 x 的值。由于题目要求是在零到派上的图像,因此需要舍去最后一个点, 图像一般从零开始,因此我们找出 x 等于零时,得出相对应的函数值,在平面直角坐标系中描出这几个点,最后用光滑的 曲线连接起来,这样就得到函数 y 等于 cosan 括号内二 x 减三分之派的图像了。这就是五点做图法。首先领 cosan 后面的值分别等于零二分之派、派二分之三派和二派, 然后再分别求出对应的 x 的值以及整个的函数值。这里要注意题目中给出的 x 的范围,从而对点做出相应的取舍,再进行描点,最后用光滑的曲线连接起来即可。好了,这个视频就讲到这里,下节课。
100不正经2️⃣ 06:17查看AI文稿AI文稿
06:17查看AI文稿AI文稿这节课我们一起来做一下鱼线函数图像练习题来看看。练习题一,画出 y 等于负的可算 xx 属于零到二派的图像,这样图像该怎么样的画呢?我们通常采用五点法,按五个关键点,然后呢我们再列表, 当 x 值分别为零二分之派、派二分之三派两倍派的时候,科三研 x 值呢?它是为一零负一零一,但题目问的是 y 等于负的科三前面有个负号,他的还是图像,而且 x 的取值范围呢,是零到二派,必须减。 接下来我们再多练一行,是负的可算 x, 它对应的函数值分别为负一零一零负一 x 值呢?还是不变?那么五个点分别为 x 等于零的时候,那么负的可算 的值呢?是等于负一 x 等于二分之派的时候,负的可算的指呢?是等于零, x 等于派的时候,那么负的 可算 x 值是等于一 x 等于二分之三派,那么负的 x 值是等于零。 x 等于二派的时候,对应的函数值是等于负一。我们把这五个点 把它描出来,然后用光滑的曲线把它们连接起来。是这样的一个函数图像,紫色这一条五个点,我们用红色把它标记出来了。 y 等于负的个三 x, x 属于零到二排,必须填,这是用描点法。 接下来我们看一下练习题二,判断 x 平方减去个三 x 等于零的根的个数为多少个?这样的题该怎么样来做呢?有些人说我直接来解放乘 x 平方等于个三 x, 但是这样来求解呢? 不是很好求 s 平方等于扣三 x, 直接写方程不是很好求,我们利用第二种方法,另外是等于 x 平方,另外一个函数呢,是 y 等于扣三,以 x 画出他们两的函数图像。画出图像以后呢,我们看他们图像的焦点的个数有几个焦点,那么他跟的个数就有几个。 y 等于 s 平方,它是一个二次函数,比较好画。 y 等于可算。 x 呢,它是一个鱼形函数,我们刚学过,那么我们画出他们俩的函数图像,大概是这个样子的。从图中我们可以看出他们的焦点个数是有两个 好,那么它的根的个数呢,也是两个,这是类似。第二,接下来我们看一下类似。第三,下列函数图像相同的是哪一个? a 选项 y 等于个三, x 与 外等于快,加上一个字,那么要判断他们的函数图像是否相同,只要判断他们化解以后呢,函数是否一致。首先我们回忆一下之前所想的诱导公式的时候呢,积变偶不变,符号看象限这样的口诀,积变偶不变, 符号看相线。 所谓即变偶不变,就要讨论餐饮和餐饮 弹性的二分之 k 派加减 r 法这样的情形,当 k 为基数的时候,那么就要变腮影变成口腮影,弹性的变成可弹性的。 如果 k 是偶数的时候呢,我们不需要变相应还是相应和相应还是相应符号看象限呢?通常情况下,我们会把阿尔法看成是一个 角,看成是一个锐角,于二分之 k 派做运算以后呢,看他是在第几个象限。如果是在第一象限正前于线正切都是正的,我们再来回忆一下,如果是第二象限呢,只有正弦是剩的。 第三项线呢,只有正切和鱼切,他们俩是正的。第四项线呢,只有鱼弦,他是正的。根据这个我们再来做这个题。 a 选项, y 等于可算, x 与 y 等于可算,以派加上 x, 这里呢,是二分之派的偶数变,所以不变。但是当 x 为锐角的时候,加上派是在 第三项线,所以为负的,那么这里是 y 等于负的,和三 ex 他们还是不一样,那么图像也必定不一样。第二个呢, y 等于三, ex 减去二分之派,这边呢 除外。等于三引二分之派减去 x, 刚好想差一个符号,那么这边几个符号出来呢?因为我们有讲过,三引负的 x 是等于负的,三以 x, 那么这边是等于负的。三引 x 减去二分之派。 我们也可以根据机变偶不变符号,看向线,把它化解一下。 x 减去二分之派, x 是在第一象线一个锐角,那么减去二分之派呢,必定在第四象线。三印在第四象线是为负的,所以是负的 cosin x, 那么这边呢,三引二分之派减去 x, 二分之派减去 x, 必定还在第一上限,那么是正的,正的即变偶不变,这里是二分之派的基数变,所以变成可相应,这边是可相应 x, 而这边呢,是负的,可相应 x, 所以也是不一样。第三个 y 等于三,一个四与 y 等于三应付的 x, y 等于三以负的 x, 刚才有讲是等于负的三以 x, 所以也是不一样。最后一个 y 等于三应两倍派加上一个词与 y 等于三,一个四,三以, 也就是正弦,他是以二派为周期的周期函数,所以加上他减去他,不影响他们俩是一样的。最后答案选 d 选项。 最后我们来做一下小结。这节课呢,我们主要讨论呢,雨险还是 y 等于块三 x x 属于二,他的图像 y 等于 c x, 他的图像该怎么样画呢?我们是根据三以 x 加上二分之派来画的,因为 快三 ex 是等于三 ex 加上二分之派,我们首先画出 y 等于三 ex 他的函数图像。 然后呢,根据左加右减,上加下减,这里是加上 s, 后面加上二分之拍,那么整个还是图像是向左,在他的基础上是向左平移呢?二分之派, 然后得到这样的函数图像,大概是这样的一条曲线,最大值是一,最小值是负一。关于外主对称,好,这节课我们就讲到这。
161滴答课堂









