初中数学沪科版角的平分线画法ppt
粉丝6.9万获赞27.3万
相关视频
 00:29查看AI文稿AI文稿
00:29查看AI文稿AI文稿这个宝藏网站可以让任何知识动起来,而且操作非常简单。就比如初中数学中经典的角的平分性问题,你只需要上传课本照片,输入你的想法,很快就可以得到一份可交互、可下载的模拟动画。通过调整 pm 两点的位置, 探求角平分线上点的距离关系,不仅可以拖拽互动,右侧还有运用知识点的讲解,无论是哪种形式,他都可以帮你实现。这个网站甚至还有上万个现成的教学动画免费共享,评论区留言免费使用。
278刘老师AI教学分享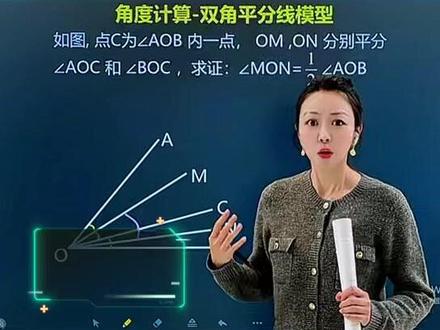 02:54查看AI文稿AI文稿
02:54查看AI文稿AI文稿初一数学一共有五大亚洲难点,其中角度计算这里动脚问题一定会在我们期末出最后一道亚洲大题,这里的技巧性非常强, 像这种角度计算的分类讨论问题,看似难,其实是有技巧的,我今天一句口诀带你搞定这种角度计算对应的亚洲题,这个口诀就叫做神龙摆尾,一半,一半又一半,我会给大家具体的去推导。这个结论怎么用?应用的场景是什么? 那有关于角度计算啊,老师也把近三年常考的这些易错的压轴题做了一个总结,如果咱们孩子做这种题,经常漏答案,没有思路,几何题这种模型的思维还都没有的话,做题慢,答不完试卷。 哎呀,这个分题型练习一定是必须要做的了,考前把所有的题型归类总结方法,再去带着孩子刷题,这样才能事半功倍好不好? 下面我们就来一起看一下啊!这个模型叫做双角平分线模型。什么意思?看好了, o m 平分角 a o c 这两个黄角相等, o n 呢?平分角 b o c 这两个绿角相等。想让你求证 m o n 等于二分之一的角 a o b 这道题很典型,它让你找的是角的和差关系, 而对应这个角 m o n, 你 发现了吗?它不就等于一段小黄加一段小绿吗?那这个小黄是什么呀?哦,这个小黄对应不就是哎这个角 m o c 吗?小绿不就是对应角 n o c 吗?而 m o c 等于什么? 你会发现题干当中根本没跟你说 moc 有 关的信息,所以这需要我们有一个思想,叫做化位之角为已知角。已知信息是啥呀?是这些角是题干当中告诉你的,所以 moc 能不能往这些角上去做转化呀? 可以啊,它不就是二分之一的角 a o c 吗?同理,它不就是二分之一的角 b o c 吗?所以二分之一提出来,这不就是角 a o c 再加上角 b o c 吗?对不对?扎完了之后你会发现,哎, 这不就是大角 aob 吗?所以这不就等于二分之一的角 aob 了吗?所以你发现了吗?双角平分线模型和双中点模型正面的思路是一样的。首先第一步,小黄小绿来帮忙, 用相同的符号条件上图表示相等的角,接下来做二分之一替换,把未知角向已知角上做转化。接下来我们用角的和差关系既可以得出答案, 那这道题呢?我想给它变一变,如果我把点 c 是 角内部一点,去掉角点 c 就 为平面内任意一点,那这个时候这个结论还成立吗?那如果不成立的话,又有几种情况呢?
585依依老师讲初中数学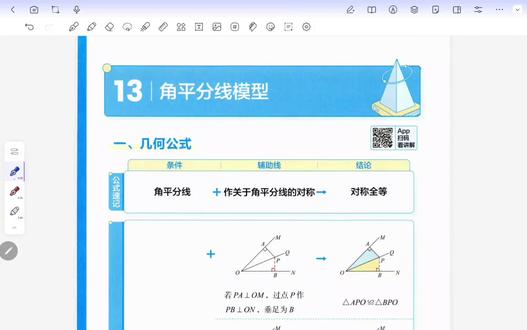 36:32查看AI文稿AI文稿
36:32查看AI文稿AI文稿hello 宝子们,今天给大家录一期全等三角形之角平分线模型。首先看条件,顾名思义,那条件肯定是要有角平分线,对吧?辅助线怎么做呢?辅助线有三种做法, 第一种做法,看这个图形 o p, o p 是 角 m o n 的 角平分线,那么过点 p 向角的两边, o m 和 o n 分 别做垂线, 这样就可以得到上面这个三角形 o a, p 和下面这个三角形 o b p, 它两个是全等的。 全等的判定条件非常简单,首先这两个角相等,这里有九十度,还有一条公共边是 o b, 通过角角边就可以判定上面这个三角形和下面这个三角形全等。 这种辅助线呢,应该是我们经常常用的,因为角平分线上的一点到角两边的距离是相等的,对吧?好,这个角平分线我们就讲到这里,看第二个辅助线。第二个辅助线 o q 还是角 m o n 的 角平分线,我们过点 p 做一条垂直于 o q 的 直线,然后交 o m, 交 o n, 分 别于 a 点和 b 点, 这样的话呢,我们就得到了这个线段 ab。 那 么三角形 oab 就是 等腰三角形,为什么是等腰呢?因为我们知道等腰三角形三线合一,这里角平分线,这里有垂直,那么很显然 ap 就 等于 pb, 然后 o a 也等于 o b。 好, 结论也是一样,三角形 o p 啊, a p o 和三角形 b p o 是 全等的。判定方法是这里是角平分线,这两个角相等, 公共边加九十度等角,通过角边角就可以判断上面三角形 o a, p 和下面三角形 o b p 是 全等的。 在我们平时的做题当中啊,第一类辅助线大家一般都会做,那第二类辅助线呢?往往不容易想到,所以往往我们在看到角平分线加九十度的时候,要想到这一类辅助线,然后把它条件写在这里。 大家平时在做题的时候,一定要注意看到角平分和垂直,要想到做第二类辅助线,接着看第三类。第三类的话呢,比较简单,就是在 o q 还是角平分线,在一条边上有一个, 有一个 o b, 那 么在另外一条边上呢,取一个 o a 和 o b 相等,或者说在一条边上有 o a, 在 另外一条边上呢,取 o b 等于 o a。 都一样,也一样可以得到三角形 o a、 p 和三角形 o b、 p 是 全等的,判定条件是 这两条边 o a 等于 o b, 角平分线加一个公共边是边角边,来判断这两个三角形是全等的。 好,接下来有一个补充,这个补充并不是这个讲义当中的,我是想说啊,看到角平分线往往还有第四种做辅助线的方式,就是过点 p 做一条平行线, a p 平行于 o n, 这样的话呢,可以得到三角形 a, o p 是 一个等腰三角形。首先角一和角二相等,是因为 o p 是 角平分线,然后角二和角三相等,是因为两只线平行内错角相等,那么角一和角三相等了,等角对等边,所以 o a 等于 ap。 好, 讲到这里,那我们接下来看例题。第一,如图,在三角形 a、 b、 c 中, b d 平分角 a、 b、 c 这两个小角相等,角 a 等于两倍的角 a、 d, b、 ab 等于六,这条边等于六, cd 等于七。那我们来把已知条件写一下, ab 是 六, cd 是 七,求 bc 的 长,那通过这个已知条件我们就知道,我们知道是 ab, 那 应该把 ab 转化到 bc 这里,所以做的辅助线是在 bc 上面截去一点使得,比如说是 e 吧, 使得 b、 e 等于 a e, 然后连接 d、 e, 那 么 b、 e 也就是六,对吧?然后这里呢,也就是角 a 跟角 a 是 相等的,角 a 等于这个角的两倍,那么角 b、 e、 d 也就等于角 a, 角 a 又等于两倍的角 a、 d、 b。 两倍的角 a、 d、 b。 我 们知道,这样做完辅助线 b、 e 之后啊,取 b、 e 等于 ab 之后呢? 上面这个三角形和下面这个三角形就全等了,既然全等的话呢,哎,这个角和这个角是相等的,那么角 a、 d、 e 也等于两倍的角 a 也等于角 b、 e、 d。 也就是说角 a、 d、 e 和角 b、 e、 d 是 相等的,这两个角相等了,那么等角的补角相等,所以这个角和这个角也就相等了,那么 c、 d 等于七, c、 e 也等于七,那么 六加七等于十三,所以这题选二, b。 再看例二,第二题,已知在等腰直角三角形 a、 b、 c 中,那么这两个小角都是四十五度, a、 b 等于 a、 c。 角 a 等于九十度 b、 d。 平分角,平分角 abc、 a、 b、 c。 好, 这两个小角都是二十二点五度, c、 e 垂直于 b、 d。 标了垂直符号,求证 b、 d 等于两倍的 c、 e。 这里是 b、 d, 这里是 c、 e。 那么对于这个图形啊,我们要想到角平分线这个模型当中的第几个模型啊?第几个辅助线是第二个辅助线,因为看到垂直,这里有垂直吧,这里有角平分线,我们要想到怎么样想到 a 延长,延长这条边,然后呢,延长 c、 e, 这样呢,假设交于点 f, 点啊,这样做完辅助线之后呢,我们肯定知道 f、 e 和 c、 e 是 相等的了,因为这里是垂直,这里是角平分线,所以三线合一,知道 b、 e 既是三角形 f、 bc 的 高线也是角,平分线也是中线,那么点 e 就是 f、 c 的 中点。 题目让我们证明 b、 d 等于两倍的 c、 e, 那 两倍的 c、 e 也就是 f、 c 吧,所以这个题目目前就转化成了证明 b、 d 等于 等于 c、 f。 那 我们注意到三角形 a、 b、 d 和三角形 d、 e、 c 组成了一个八字形,这里是九十度,这里是九十度。那么角 a、 b、 d 这个角肯定和这个角是相等的,我们标一下。 好,那接下来在三角形 a、 b、 d 和三角形 f、 a、 c 当中, a、 b、 a、 b 和 a、 c 是 相等的,这里两个锐角是相等的,这里有九十度,这里也有九十度。我们通过角边角就可以判断这个三角形 a、 b、 d 和这个三角形 a、 c、 f 全等,那么 b、 d 等于 c、 f, 也就是 b、 d 等于两倍的 c、 e 了。 好,这里我将这个题目做了一个简单的总结,主要证明呢,分为三步,第一步是做辅助线,第二步呢,是证明三角形 b、 e、 f 和三角形 b、 e、 c 全等得到 e、 f 等于 e、 c。 第三步呢,是证明三角形 a、 b、 d 和三角形 a、 c、 f 全等,所以 b、 d 等于 c、 f, c、 f 又等于两倍的 e、 c, 这样就完成了证明。好,这是一个整体的过程啊,接下来我们再往后看, 接下来就是看真题了。如图,在三角形 abc 中,角 abc 这个角等于两倍的角 c、 a、 d 和 b、 e 分 别是角 b、 a、 c 和角 abc, 那 这两个角相等, 这两个角相等,又因为角 a、 b、 c 等于两倍的角 c, 所以 角 c 等于角 a、 b、 e 也等于角 e、 b、 c, 那 么等角对,等边,所以 b、 e 和 e、 c 就是 相等的了。 三角形 a、 b、 e 的 周长是二十二, a、 b、 e 的 周长等于 a、 b 加上 b、 e 加上 ae, 我 们知道 b、 e 和 ec 又是相等的,那么转化一下, a、 b 加上 ec 加上 a、 e 等于二十二, ec 加 a、 e, 它就是 ac, 所以 ab 加上 ac 等于二十二。好,这个角平分线 b、 e 用过了, ad 还没有用,对吧?知道 b、 d 等于四,知道这里是两倍的角 c, 那 很显然,我们想到 结一个 f, 这个点是 f, 使得 a、 f 等于 ab, 那么三角形 a、 b、 d 和三角形 a、 f、 d 就是 全等的了,因为角啊,因为边角边,对吧?边角边全等之后呢?那么 b、 d 等于四, d、 f 呢?也等于四, 这里是角 a、 b、 d 等于角 af d, 角 a、 b、 d 等于角 a、 f、 d 等于两倍的角 c, 角 a、 f、 d 又是三角形 f、 d、 c 的 外角,它等于两倍的角 c 又等于角 c 加这个角,所以这个角和角 c 是 相等的。 好,是这样,那么 df 等于四, fc 也等于四。题目让我们求 ab, 那 么设 ab 为小 a 吧。通过上面这个式子,我知道小 a 加上 ac 等于二十二, ac 又可以表示成,因为 ab 也等于 af 嘛,也等于小 a, 所以 小 a 加上小 a, 再加上 fc, fc, 是 啊, 四等于二十二,那么小 a 等于二十二。减四除以二等于十八除以二等于九。哎,这题是九好,这题我觉得整体的转化还是比较有意思,大家可以好好看一看,再看第二题。 如图,在三角形 a、 b、 c 中, a、 d 是 角平分线,且 a、 d 把三角形 a、 b、 c 的 面积分成三比七的两部分。我们知道, 我先画一个三角形啊,任意一个三角形,这是三角形 a、 b、 c, 跟这个图形是没有关系的,假设有一点 d、 d, 随便标吧,在这吧。 好,那么 a、 d 就 把三角形 a、 b、 c 分 成了三角形 a、 b、 d 和三角形 a、 d、 c 左边和右边这两个三角形, 那 s 三角形 a、 b、 d 比上 s, 三角形 a、 d、 c 面积之比,就等于上面面积等于二分之一 b、 d, 那 三角形 a、 b、 d, 它底边是 b、 d, 高是多少呢?我们过点 a 向 b、 d 所在的直线,也就是 bc 所在的直线做垂线,假设这个垂足是 e, 乘以 a、 e 再除以二分之一。三角形 a、 d、 c 的 面积是二分之一, d、 c 也乘以高,同样是 a、 e 二分之一没了, a、 e 没了,就等于 b、 d 比上 dc。 通过我举的这个例子,我们就知道一个三角形底边上面有有一点,将这个底边分成两条线段,一个是 b、 d, 一个是 d、 c, 那 么左边这个三角形比上右边这个三角形的面积之比,就等于 底边的边长之比,能理解吧?好,那这个三角形 abc、 bc 边上有一点 d, 将这个 bc 线段分成了 c、 d 和 db, 那 么上面这个三角形 c、 a、 d 和下面这个三角形 d、 a、 b 面积之比,就应该等于底边之比。好,我们设这个是 上面三角形 a, 那 cad 它的面积是三 s, 那 下面就就是七七 s, 很 显然它辅助线做法就是我取一个嘛,取一个是 f, 点嘛,使得 af 等于 ac, af 等于 ac, 那 么三角形 cad 和三角形 fad 是 全等的, 那么三角形 d、 a、 f 这个的面积也就是三 s, 那 这半边呢?就是七 s 减三 s 是 四 s, 是 吧?好,那这个七 s 我 就不要了, 这是三 s, 这是四 s。 这个时候我们看,相当于在三角形 d、 a、 b 当中一条线 d、 f 将三角形分成了两部分,左边的和右边的,那么左边的面积和右边的面积之比就是 底边线段 if 和 f、 f、 b 之比,所以那也就是三比四嘛。 题目说 ac 等于五,那么 af 也就是五,所以 af 比上 f、 b 就 等于三比四, af 等于五,所以 f、 b 等于几? f、 b 等于四五,二十除以三, 那么 ab 呢? ab 等于 a, f 加上 f、 b 等于五,加上三分之二十,等于三分之十五,加二十是 三十五,所以是三分之三十五。好,通过这个题目,我们知道面积之比等于底边之比好用了两次吧?用了两次,再看第三题, 三角形 a、 b、 c、 a、 b、 c 面积是十六,大的是十六, ad 平分,这是平分,然后 ad 垂直于 b、 d, 看到平分,看到垂直,我们想到什么?就是模型二还是模型二,延长, 延长, b、 d 交 ac 于点于点, e 还是三角形 a、 b、 e, 就 得到一个等腰三角形是吧?角相等,公共边垂直垂直是 a、 s、 a, 所以 ab 等于 a、 e, 然后问的是 a、 d、 c 的 面积是多少? 我们看,那这个是 s 一 啊,标一下,这个是 s 一, 三角形 a、 b、 d 的 面积是 s 一, 三角形 a、 e、 d 的 面积就也就是 s 一, 而且我们知道 b、 d 和 d、 e 是 相等的,根据上面那个结论, 三角形 d、 e、 c 底边上有个点 d, 那 连接 d、 c, 就 将三角形 b、 e、 c 分 成了两个三角形,一个是 e、 d、 c, 一个是 d、 b、 c, 那 这个三角形面积和它的面积之比就等于 底边之比,那底边是一比一,所以这两个面积,这个三角形面积和这个三角形面积是一样的了。 所以这个是 s、 r 的 话呢,那这个也是 s、 r 题目呢是 a、 d、 c, a, d、 c 就 等于 s, 一 加 s r, 我 们知道两倍的 s 一 加上两倍的 s r 就 十。三角形 a、 b、 c 的 面积等于十六,那么一倍的 s 一 加一倍的 s、 r, 不 就是除以二吗?就是八。这题选二 b 第四题啊,如图,在三角形 a、 b、 c 当中, bc 等于十, ac, ac 减 ab 等于四, ad 是 角平分线, cd 又有平分又有垂直啊,这题目还是跟刚才一样,延长 ab 延长 cd 好,假设是焦点为 f 点,那通过三线合一的话,角平分线高线,那很显然 d 是 f、 c 的 中点,我就不再说是怎么证明的了啊,可以往前面再看一看,现在知道这两条边相等了,然后 af 等于 ac, 那 么 ac 减 ab, 其实就是 af 减 ab, 写一下 a, f 减 ab 就 等于 b、 f 吧, abf 就是 个定值啊,等于四,这就比较高兴。求三角形 b、 d、 c、 b、 d、 c 的 面积,在这里 我们还知道 dc 等于 df 的 吧,我求这个三角形 bdc 的 面积,其实就是求三角形 bfc 的 面积,因为这条边等于这条边嘛,所以这个的面积等于这个的面积。好,现在的目标就是求 s 三角形 b、 f、 c 的 最大值,因为它等于两倍的 s 三角形 b、 d、 c。 那 怎么求呢?我们知道 b、 c 边是十吧, b、 f 呢?等于定值四。 求这个三角形 b、 f、 c 的 面积,就是过点 f, 我 们可以把 b、 c 看成底,对吧?过点 f 向 b、 c 所在直线做垂线, 做垂线,假设垂足是啊 e, 那 它这个面积啊,就等于二分之一 b、 c 乘以一个什么 f、 e, 对 吧?底乘高等于二分之一,乘以十,乘以 f e 等于五倍的 五倍的 f e。 但是这个图形是不定的吧,因为 f 点是一个动点嘛,是不是?所以 那这个求这个面积的最大值,也是求 fe 的 最大值。 fe 什么时候最大?我们看这个直角三角形,直角三角形 e、 f、 b 这条边斜边是固定的四,在直角三角形中,斜边肯定是比两条直角边要长的,所以 fe 是 怎么样? fe 是 小于四的,什么时候能等于四呢?就是点 e 和点 b 重合, 点 b 和点 b 重合的时候,那么 f、 e 就是 f, e 就 等于 f, b 就 等于四,所以它是小于等于五乘以四的,等于二十,那这个大的三角形面积是 最大值是二十,三角形 b、 d、 c 呢,是它的一半,所以最大为十,这里选四 d。 接着看第五题,已知 c 是 角 m, a、 n 的 角平分线上一点 a, c 平分这个角角 b、 c、 d 的 两边, b、 c、 d 的 两边就是有一个点 b 和点 d 分 别在这个射线上,好角 abc, 这个角 abc 和角 adc, 这个角 是互补的。过点 c 做垂线 c, e 垂直于 ab, 垂足是 e e。 问,在这个图形 e 当中啊,求证 b, c 等于 dc, 那 么通过这个图形和已知条件,我们知道它的辅助线做法,应该是这个讲义当中第一种辅助线做法就是过角平分线上的一点向角两边做垂线。那我把这个图形放大一点。好,我们过点 c 向 a、 n 做垂线,假设垂足是 f, 那 根据定理啊,角平分线上的一点到角两边的距离相等,所以 c、 f 和 c、 e 是 相等的。我们又知道这个角角 a、 d、 c 和这个两弧的是 互补的吧?那角 a、 d、 c 和这个角组成了一个平角,那它们也是互补的,所以角 a、 b、 c 等于角 f、 d、 c。 角 a、 b、 c 等于角 f、 d、 c。 那 么在三角形 c、 f、 d 和三角形 c、 e、 d 当中,九十度九十度相等,是吧? 这两个弧的两个弧的锐角相等,且 c、 f 等于 c、 e, 那 通过角角边我们就能判断三角形 c、 f、 d 和三角形 c、 e、 b 全等了,所以 cd 和 c、 b 就 相等了。 所以第一问就这名结束了,难度不大。好,那我接着清一下屏幕,说第二题在第二题当中啊,当点如图二,当点 e 在 线段 a、 b 的 延长线上时,好, e 在 线段 a、 b 的 外面了,探求 a、 b, 这是 ab, ad 在 这里和 be 之间的关系。那辅助线做法应该还是一样的吧,还因为这里有 c、 e 垂直于 am, 很 显然还是过点 c 向 an 做一条垂线,哎,做一条垂线, 假设垂直度是 f, 依然可以得到三角形 c、 a、 f 和三角形 c、 e、 a 是 全等的, 这个角角 abc 和角 a、 d、 c 和这个角是互补的,角 abc 呢? 和这个角也是互补的,所以我们可以测到同角的补角相等,也就是角 bce。 这个角和角 啊,不是 bce 啊, cbe 这个角 cbe 和角 a n a d, a, d, c 和这个角是相等的。看直角三角形 cfd 和直角三角形 c, e ceb 有两个锐角相等,九十度九十度相等。然后还有一个是 c, e 等于 c f。 还是那个定律,角平分线上的点到角两边的距离相等, 就可以得到三角形 c、 f、 d 和三角形 c、 e、 b。 是 全等的判定呢?还是 a、 a、 s 判断完了之后,题目上证呢?是要求的是 a、 d 和 a、 b、 b、 e 之间的关系。我们通过第一个全等我来写一下,第一个全等三角形 a, c、 f 全等于三角形 a, c, e, a, c, f 和 a c, e 全等,直到 a、 f 等于 a、 e。 第二个全等三角形 c、 f, d, c, f, d 全等于三角形 c、 e、 b。 我们可以知道 f, d 等于 b, e, f, d 等于 b e。 那 么看 a, d, a, d, 它等于 af 加上 f、 d 的, 对吧?那 af 呢?等于 a e, a, f 等于 a e, 所以 等于 a, e 加上 f d, a, e 等于什么? a, e 等于 ab 加 b, e 等于 ab 加上 b e 再加上 f d 呢? f, d 也等于 b e, 所以 a、 d 等于一倍的 a, b 加上两倍的 b e。 那 这个第二小问就解决了啊,难度也一般般。再看最后一题, 最后一题如图,在如图三,在图二的条件下,角 m a, n m a n 这个角是六十度连接 b, d 连接了 b, d 左角 a, b, d, a, b, d 的 角平分线 b, f 交 a, c 于点 o 连接 d, o 交 ab 呢?于点 g, b, d, 这里是二 f d, 这里是四,求 d, b 的 长好,那对于这个题目,我相信大家如果不会做,肯定卡在这第三问上了,对吧?第三问,我先通过几个问题来带大家,带大家去看一下这个题目是怎么做的。首先第一个问题, d g 平分角 a, d b 吗?这就是第一个问题,这里是 d g 角 a, d, b 是 这里,那这两个角相等吗?这是我的第一个问题。接着问第二个问题,这个六十度怎么用? 角 d, a, b, d, a, b 等于六十度,哎,怎么用,对吧?好,我们先说第一个问题。第一个问题肯定是平分的, 平分怎么证明呢?我来说一下证明过程。我们过点 o 向向 ab 做垂线,假设这个点是 abcd f 吧, f 也有了点设是点 g 啊,也有了 g 啊,好烦。 h 假设是 h, 那 过点 o 向 a, d 做垂线, a, d 做垂线,一个是 h m 也有了 p, 对 吧?再过点 o 向这边做垂线,向 b, d 做垂线,假设是 q, 好 为为什么要这么做?我们知道 a o 平分角 d, a, b, f b 平分角 a, b, d, 那 么我们过点交点都是 o 吗?我们过点 o 向角两边做垂线,是吧?然后呢,过点 o 向角两边做垂线,很显然, o, o, h 和 o p 和 o q 都是相等的,因为角平分线上的点到角两边距离相等, a, o 平分角 d, a, m 这个 f b 平分角 abd, 所以 这三条线段都是相等的。哎,我们看一下,因为以 o p 等于 o q, 我 们又知道到角两边距离相等的点在这个角的角平分线上,也就是 d o 平分角 a, d, b。 第一个证明结束了,好,证明结束了之后证明这两,那其实就是想得到这两个角是相等的,那我们来标一下,这两个角是相等的, 那接下来为了证明这个,为了求 d、 b 等于多少,我们知道 d、 f 是 四了,在 d、 b 上面取一点,假设是 k k, 这个点是 k, 取 d k 等于 d、 f, 也就等于四了, 那么整个这个 d、 b 就 知道了一个边长是四,那我求出 k、 b 就 可以了,是吧?那我们看三三角形 o、 k、 b 和三角形 o、 g、 b 是 不是全等的呢? 可能我们猜测是全能的,我们现在要证明一下,是吧?在证明之前看一下这个问题,角 d、 a、 b 怎么用?看一下这个图形啊?我画一下这个形,这是什么形?哎,这是我们这个讲义当中,呃,六十九个模型当中的飞镖形,是吧?飞镖形, 假设这个角是角一,那它也是角一,这个角是角二,这也是角二。我们知道两倍的角一加上两倍的角二,再加上角 d、 a、 b 等于一百八十度,因为是三角形 d、 a、 b 三角形内角和两倍的角一加两倍的角二,加这个角六十度等于一百八, 那这个代入六十度,那所以角一加角二等于一百八十度,减六十度,再除以二等于多少度等于六十度。好,看,这个三角形, 它加它是六十度,那这个角多少度?肯定是一百八,减去角一角二,那这个角是角 d、 o、 b 是 一百二,角 d、 o、 b 等于一百二十度。好,这就是它的用法。推出来角 d、 o、 b 等于一百二十度,知道角 d、 o、 b、 d、 o、 b 是 一百二十度,那么 f、 o、 d 和角 d、 o、 b 组成了一个平角,推出来角 f、 o、 d 等于一百八十度,减一百二十度等于六十度, 这个角是六十度。我们通过刚才做取了 d、 k 等于 d f, 那 么角 d o k 这个角也是六十度。 角 d o k 等于六十度,整个角 d、 o b 是 一百二十度,那么角 k、 o b 这个角也是六十度, 所以角 k、 o b 等于六十度。然后还是看角 f o d。 因为角 f o d f o d 和角 g o b 是 对顶角吧, 这里是对顶角,所以角 g o b 也等于六十度。 角 g o b 等于六十度,是通过对角得到的。那么我们看在三角形,在三角形 k o b 与三角形 g o b 当中,哎,角二等于角二,但我这写不规范啊,你看出来这角平分线对吧?题目说了,对角二和角二是相等的,然后 b o 等于 b o 是 公共边角 k o b, 角 k o b 等于角 g o b 等于六十度。我们就通过 角边角角边角得到三角形。三角形 k、 o、 b 全等于三角形 g o b 判定的是 a s a 判定完了之后,那么 k b 就 等于 g b。 推导出来 k b 等于 g b, g b 是 二,那整个 b d 整个 b 啊, b d 就 等于 d k 加上 k b, d k 等于 d f 四, 再加上二就等于六。所以这题如果不会做,我相信肯定卡在 这两个问题当中了。第一个问题很简单,有的同学会说,这一眼看出来这个 d o 就 平分角 a d a d b。 因为我们课本上写了,就是三角形每一个内角的角平分线重合得到一个交点,但是我们得证明, 我们得证明,证明的方法就是过点 o 向每一个边都做垂线,通过角平分线上的点到角两边的距离相等得到 o p 等于 o h 等于 o q, 那 么 o p 等于 o q, 所以 再通过到角两边距离相等的点,在这个角的角相等,这是第一个,第二个,这里是六十度,六十度通过非标形 推出来这个角等于他加他加他。当然了,你也可以直接像我刚才写的这样,得出这个角 d、 o、 b 等于那一百二十度。非标题啊,一定要证明啊,但是考试不能直接用啊,除非是选择填空题。知道这里是这里知,知道这里是一百二十度之后呢? 通过角 f、 o、 d 和这个和这个角一百二十度互补,我们就知道这里是六十度。然后通过两个三角形全等,直到角 d o k 这里等于六十度。又因为这里是一百二十度,减去这个六十度,得到 k o b 等于六十度。目的就是想知道 k、 o b 等于 g、 o b 这两个角都等于六十度。角 g o b 是 怎么等于六十度的呢?它和角 f、 o、 d 是 对零角,所以最后通过 a、 s、 a 判断出来这两个三角形全等,所以把 g、 b 等于二转到,转到这个 k、 b 等于二,然后四加二就等于六。这题是 写起来还是比较麻烦的啊,自己好好去。嗯,去再去讲一遍,最好能自己去录个视频讲一遍,看看自己讲的是否流畅,然后再把这个完整的过程写一写。好,那今天的视频就录到这里,谢谢大家。
 04:33查看AI文稿AI文稿
04:33查看AI文稿AI文稿洞角问题是初一数学期末考试的常见压轴题类型,今天我们来系统梳理其中一种重要模型,双角平分线模型,帮助大家彻底掌握这类问题的解析方法。这个模型通常分两种情况,我们逐一来看。 第一种情况, op 在 角 aob 内部。首先要提醒大家注意,很多初一同学刚开始做几何题的时候,容易只是盯着条件和图形看,不在图上做标记,这样往往很难找到思路。所以我们要掌握的第一个技巧就是 把题目信息清晰地标注在图上。我们一起来标一标,说角 aob 等于一百二十度, o p 为角 aob 内的一条射线,那么 o p 就 把角 aob 分 成了两部分,角 aob 和角 bop。 其中 o m 是 角 b o p 的 角平分线,那么这两个小角它的度数就相等。我们可以设它为 r 法,它也是 r 法 o n 平分角 a o p, 那 么这两个小角它的角度也一样。继续设它俩的角度是 b, 它 当然设度数为 x y 也可以。这时可能有同学会问,那设了两个未知数是要列方程吗?而且 o p 它不是固定的,而法贝塔也就不是一个确切的数,这怎么解? 哎,这个问题非常好,这就引出了我们要掌握的第二个思想,设而不求 我们先用阿尔法北塔表示出相关角,再寻找他们与已知条件的关系。在表示和计算的过程中,他们往往会自然抵消,最终只留下我们需要的那个数值, 相当于起到一个桥梁的作用。我们来操作一下要求的这个角 m o n 是 不是可以用 r 法贝塔表示出来,哎,角 m o n 就 等于 r 法加贝塔。再看已知条件中的角 a、 o b 是不是等于这四个角的和呀?那就是阿尔法加二北塔等于一百二十度。好,两边同时除以二,阿尔法加北塔就等于六十, 所以角 m o n 是 不是就等于六十度呀?由此我们可以总结,当射线 o p 在 角 a o b 内部的时候,这两条角平分线 o m 和 o n 形成的加角 m o n 就 等于整个角 a o b 的 一半。 第二种情况, o p 在 角 a o b 的 外部,角 a o b 还是一百二十度。此时 o p 和角 a o b 的 两个边形成了两个角 a o p 和 b o p om 平分角 b o p, 就 说明这个角和这个角度数一样,我们还是设为 r 法 o n 平分角 a o p, 那 就说明这个角和这个角的度数一样,我们还是设为被它。 观察一下要求的这个角 m o n 能不能用 r 法被它表示出来,是不是就等于被它角减去这个 r 法呀?好,角 m o n 就 等于被它减去 r 法。 我们再看已知条件里的角 a o b, 它是不是这个整个的大角减去角 b o p 好, 那就是二倍,它减去二,而法等于一百二十度, 两边同时除以二倍,它减去,而法就等于六十度,所以角 m o n 就 等于六十度。 结论,当射线 o p 在 角 a o b 外部的时候,这两条角平分线 o m 和 o n, 它们形成的加角 m o n 也等于整个角 a o b 的 一半。 两种情况结论一致,无论 o p 在 内部还是外部,双角平分线所加的角始终等于圆角的一半,这就是我们常说的洞中有镜, 可以记一个口诀,双角平分线,一半,一半又一半。希望通过这次讲解,你能掌握这种模型的思考方法和步骤,我们下期再见。
416张云数学思维 04:26
04:26 02:41查看AI文稿AI文稿
02:41查看AI文稿AI文稿初一期末考试押注题一定会考角度动态问题,我们一起来看这道题。已知角 a o b 等于一百二十度,射线 o m。 从 o 点开始,绕着 a 点顺时针旋转,速度是十二度每秒,到 o b 结束。在旋转的过程中, o n 始终平分,角 a o m。 试问二倍的角 b o n 减去角 b o m 的 值是否是一个定值?这是一个非常典型的动角问题,一定是初一期末压轴题中最最最难的题型。今天韩老师带你彻底学会动角问题解析的两 个步骤,一分钟解决压轴题。同时关于角度动态,所有题型优中选优,韩老师已经全部整理到了这套角度动态,七大培优提分必刷专题中,给孩子练一练,期末考试拿满分! 那解决冻脚问题的时候,我们只需要关注两个步骤,第一个步骤就是学会去表示冻脚。在表示冻脚的时候,我们会发现运动的射线是 o m, 速度是十二度每秒,那我不妨设运动时间为 t, 那 咱们的角 a o m 永远是速度乘时间为十二 t 度,所以我们就将动角用含有 t 的 式子表示出来了。那由于 o n 始终平分,角 a o m, 那 所以我就可以得到角 a o n 等于角 m o n 都等于六 t 度,因为它就是角平分线各分得一半。 那么接下来我们要的是角 b o n 给它表示出来。角 b o n 的 表示方法有两种,第一种是角 m o n 加角 b o m, 第二种是用一百二十度减去六 t 度,那就是可以用角 a o b 减角 a o n 就是 一百二十度 减去六 t 度,那么还要角 b o m, 那 我们再来表示一下,角 b o m, 就是 用整个角 a o b 减去角 a o m, 就 等于一百二十度减去十二 度。那当我们把要用的角都表示出来了,我们就可以直接进入到咱们的第二步,把题目中的关系给它列出来。而这道题给的关系就是要去找二倍的角 b o n 减去角 b o m 的 值,那我们直接代入计算, 二倍的角 b o n 就是 二倍的一百二十度,减去六 t 度,再减去角 b o m, 就是 一百二十度,减去十二 二 t 度。这里我们进行一下计算,二百四十度减十二 t 度,减一百二十度,再加十二 t 度,那正负十二 t 度一抵消,最终等于一百二十度。一个定值,也就意味着它的值是一个定值,并且等于一百二十度,你听懂了吗?
853韩佳老师数学~ 04:32查看AI文稿AI文稿
04:32查看AI文稿AI文稿每天一道必考题,考试多考二十分,今天我们一起来学习八年级上册三角形账结比较喜欢考察的一个模型,叫做双角平分线模型,我们一起来看一下图 如图一,则图一, b、 p、 c、 p 是 三角形 a、 b、 c 的 角平分线,两条角平分线交于点 p 了都角平分与角 p 的 数量关系。第二个呢是三角形 a、 b、 c、 b、 p 是 平分角 a、 b、 c 的 p c 是 平分角 a、 c、 d 的, 也就平分了。一个外角相当于一个内角和一个外角的角平分线的交点交于点 p, 同样求角 a 和角 b 的 数量关系。图三的话切个还是一样,只不过这回事,三角形 a、 b、 c 的 两个外角的平分线交于点 p, 依然求角 a 和角 b 的 数量关系。这就咱们典型的一个双角平行,第一个是双内角,第二个是以内以外, 第三个是双外角。先看第一个在求角的关系的时间,我们一般要先找到它们的联系在哪。在三角形中,角平分线 b、 p 平分角和 d、 c 的 说明,这两个角角相等,角 a、 b、 p 和角 c、 d、 b 相等。 同理,角 a、 c、 p 和角 b、 c、 p 也是相等。那还有一个需要利用的就是三角形的内角和角 a 加上角 a、 b、 c 加上角 a、 c、 b 等于一百八十五。那其实我们就可以从这儿入手,三角形 b、 c、 p 这里面也是可以用三角形内角和的, 那我们就一点点去转它。先从角 p 开始,我们列出来角 p 所包含的关系是角 p 加上角 p b、 c 加上角 p、 c、 b 等于一百八十吨。同样,我们再求出来角 a 所在的直角形的关系,角 a 加上角 a、 b、 c 加上角 a、 c、 d 也等于一百八十吨。 再把它角平分线用上,这里面的 a、 b、 c 应该是角 b、 t、 c 的 两倍,角 a、 c、 b 应该是角 p、 c、 d 的 两倍。如果把它当成式子一,把它当成式子二,那我一次乘以二呢? 再减去二十,是不是就能把这两个相等的角减掉?一是乘以二,减去二十,一是乘以二呢,就是二倍的角 p, 二倍的它,二倍的它这边就变成了三百六十度,上下相减这两下,这两下变没了。因为二倍角 p b、 c 呢,等于角 abc。 同理,二倍角 p c、 d 也等于角 a、 c、 d。 减一下得二倍的角 p, 减去角 a 等于二倍的一百八,减去一个一百八,还剩一个一百八,所以角 p 就 等于九十度,加上二除以一的角 a, 这就是咱们第一个乘法的结果。我们再看第二个界线,第一个方法,只需要把角 a 和角 p 所在三角形满足的一些数量关系列出来,再用角平面线的数量去过渡一下就可以。第二个是在外角,那我们在用数量关系的时候,可以用外角定 就三角形的外角等于它不相邻的两个内角的和。哎,我们可以用它来设一设角 v、 c 等于角 a、 b、 c 加上角 a, 这个关系是零九,包含的角 a、 角 p c、 d 其实还是三角形 b、 p、 c 的 外角。 那我也可以用一下外角角 p c、 d 就 等于角 p b、 c 加角 p 这个数字里面就含角 p, 生了含角 a。 再看看上下这两者之间的关系,角 a、 c、 d 和这个角 p c、 d 是 刚好又是二倍的关系,这个角 a、 d、 c 和角 p、 e、 c 又是二倍关系,因为它们两个都是角平分线, 这是一乘以二,再减去一了乘以二,我们看它成二倍,它成二倍, 它也是二倍。如果这个二倍的角 p、 c、 d。 等于角呀 a、 c、 d。 二倍的角 p b、 c 又等于角 a、 b、 c。 那 上下一减,六点钟了,二倍呢?角 p 减去角 a 等于零,角 p 就 等于二分之一的角 a。 第三个是双外角角 p 要加三角形 p、 b、 c。 格,可以先把三角形的内角顶点切列于 角 p, 加上角 p b、 c, 再加上角 p c、 d, 等于一百八十度。这时候我们可以用这两个外角试试。角 p 加上二分之一倍的二倍的角 p b、 c。 时候就变成了 e、 b、 c。 二倍的角 p c、 d 就 变成 f、 c、 d 等于一百八。根据外角定律,角 e、 b、 c。 是 等于角 a 加上角 a、 c、 b 就 等于角 a 加上角 a、 b、 c。 那 相当于他们俩加一块,是不是相当于是角 a、 c、 b。 加角 a、 b、 c。 加二倍的角 a, 其中一个角 a 和他们两个能组成一个三角形。内角和, 那它就应该等于角 p 加上二分之一倍的一百八十度。加上角 a 等于一百八,角 p 等于九十度。减去二分之一的角, 这就得到了角 p 和角 a 的 关系。这三个就是咱们常见的双角平行中的三种形式,可能会出到一个大字母,同学们下去可以仔细研究一下,有什么问题可以在评论区给我留言。
12数学思维杨老师 01:30查看AI文稿AI文稿
01:30查看AI文稿AI文稿初衷几何模型之角平分线定律什么是角平分线定律?我们首先能想到的是书上的那句话,角平分线上的点到角两边的距离相等。 那么如果我们把角平分线放到三角形里,比如在三角形 a、 b、 c 中, a、 d 是 角 bug 的 角平分线,我们就能得到 a、 b 比 b、 d 就等于 a、 c 比 c、 d, 那 么我们把这个书上没有的定律就叫做课外补充的角平分线定律。 为什么会有这个特殊的定律?它是怎么来的呢?我们来证明一下。先做辅助线,做 d 垂直 ab 垂足为点 e 做 d, f 垂直 a、 c 垂足为点 f 做 m 垂直 bc 垂足为点 m。 首先我们根据角平分线易得到 d 等于 d、 f。 开启等面积法,我们分别用两种底和高把三角形 a、 b、 d 和三角形 a、 d、 c 的 面积表示出来,两个三角形面积一比,这么一看能约分, 我给他们约分约分约分约分约分约分,就得到了最简单的 a、 b 比 b、 d 等于 a、 c 比 c、 d, 是不是很神奇?那么我们来看看怎么记住这个定律,不要用错。在三角形中内角角平分线的两侧,左边的上比下就等于 右边的上比下,这么是不是就好记多了?中考十五题和二十三题遇到角平分线遇到会有奇效,点个关注呗!
24张数学讲初中 10:07查看AI文稿AI文稿
10:07查看AI文稿AI文稿下面我们来共同学习与三角形的角平分线有关的三个常用公式。首先我们来看一下第一个公式,两条内角平分线相交而成的钝角公式如图所示, b、 d 平分角 abc, c、 d 平分角 a、 c、 b。 那 么请确定角 a 和角 d 的 数量关系,并说明理由。那么此时角 d 就是 两条内角平分线相交而成的钝角,它和角 a 的 关系是怎样的呢?那么不难发现, 因为 b、 d 和 c、 d 分 别平分两个内角,我们可以分别假设角 c、 b、 d 等于阿尔法,那么角 a、 b、 d 也等于阿尔法角 d, c、 b 等于贝塔,那么角 d c、 a 啊,也等于角贝塔。 那么因为在三角形 b、 c、 d 中,我们的角 d, 它利用内角和公式等于一百八十度减去括号阿尔法加贝塔作为第一个式子, 那么在三角形 abc 中,我们的角 a, 它等于一百八十度,减去二倍的括号阿尔法加贝塔作为第二个等式, 那么对第二个等式进行移项之后,可以得到二倍的括号阿尔法加贝塔等于一百八十度减角 a, 然后方程两边同时除以二,可得阿尔法加贝塔等于九十度,减去二分之一角 a, 然后把这个式子作为三代入到一当中去。 然后呢,我们的角 d 就 等于一百八十度,减去括号九十度,减去二分之一角 a, 这样区块号合并成这样之后,可得角 d 等于九十度,加上二分之一角 a, 这样我们就可以得出两条内角平分线相交成的钝角等于九十度,加上二分之一角 a。 那 么我们熟练这个公式之后啊,做选择和填空题的时候就可以拿来直接使用。我们再来看第二个 一条内角平分线和外角平分线相交成的锐角公式。那么如图所示, b e 平分角 abc c e 平分角 a c m。 那 么请确定角 a 和角 e 的 数量关系,并说明理由。 那么不难发现,因为 b e 和 c e 分 别平分角 a、 c、 m, 那 么我们也可以像刚才一样,假设角 a、 b e 和角 c、 b e 的 度数都为二法,那么角 a、 c e 和角 m、 c e 呢? 都为 beta。 那 么利用三角形外角的性质,角 a、 c、 m 是 三角形 a b c 的 外角, 外角等于和它不相邻的两个内角的和,我们就可以得到二倍的角 beta 等于角 a 加上二倍的 alpha, 那么角 e c m, 它又是三角形 b c、 e 的 一个外角,所以被它它又等于角 e 加上角 r 法。 那么这个时候我们对第一个式子进行变形,可得角 a 等于二倍的贝塔减去二倍的阿尔法。提取共音式二括号里面就是贝塔减阿尔法。而对于第二个式进行变形,可以得到角 e 等于贝塔减阿尔法。这样的话,我们就会发现,我们的角 a 最终是等于 角 e 的 两倍,或者说角 e 等于二分之一角 a, 也就是说一条内角平分线和外角平分线相交而成的锐角角 e 是 等于角 a 的 二分之一的。 那么在这个题目的证明中,啊,我们使用了三角形外角的性质。好了,我们再来看第三个公式,如果是两条外角平分线相交而成的锐角会怎么样呢?那么如图所示, b f 平分角 p b c c f 平分角 bcq, 则角 a 和角 f 的 数量关系是怎样的,并说明理由。 那么这个题目啊,我们也要用到三角形外角的知识。首先有角平分线的性质可得,我们如果假设角 p、 b、 f, 同学们假设角 p、 b、 f 等于角 c、 b、 f, 它们呢,都等于 alpha, 那么角 q、 c、 f 和角 b、 c、 f 呢,都等于 beta, 那 么因为利用外角的性质啊,我们这个角 p、 b、 c 是 三角形 a、 b、 c 的 外角可以得到二倍的角二法等于角 a 加上角 a、 b、 c, 那 么这两个式子分别命名为一和二。 我们如果把一和二这两个式子相加的话,不难发现,二阿尔法加上二倍塔,它就等于这四个角的和。 那么这四个角当中,我们把后三个角进行组合,你会发现后三个角 a、 c、 b、 角 a 和角 abc, 它们三个其实是一个三角形的角和等于一百八十度,这样再加上角 a 等式两边同时除以二阿尔法加贝塔就等于九十度加上二分之一角 a, 那 么又因为在三角形 b、 c、 f 当中,阿尔法加贝塔还等于一百八十度减去角 f, 那么这样根据等量代换,我们的九十度加二分之一角 a 就 等于一百八十度减去角 f, 这样一项可得,角 f 就 等于九十度减去二分之一角 a, 那 么角 f 啊,就是三角形两个外角平分线相交而成的一个锐角,它就等于九十度减去二分之一角 a。 下面我们来看一下利用公式的应用解决问题。如图所示,在三角形 a、 b、 c 中,角 a 等于五十六度,这里 角也等于五十六度,那么 b、 d 和 c、 d 分 别平分角 abc 和角 a、 c、 b, 而 m、 n 还有 q 分 别是 d、 b、 d、 c 和 b c 的 延长线上的点。我们的 b、 e 啊,它平分的是角 e、 b、 q, 那 么 c、 e 平分的是角 b、 c、 f、 b、 c、 n。 那 么这样以来的话,我们可以看到往下还有两条角平分线, b、 f 和 c f 分 别平分角 e、 b、 c 和角 e、 c q。 问我们角 f 最终是多少? 那么这个图啊,我们可以看到它包含着我们刚才所说的那三类图。第一,同学们可以看到,我们利用他们的结论,首先,在三角形 a、 b、 c 中有两条内角平分线,相交所成的钝角叫 d, 那么利用公式,角 d 就 等于九十度加上二分之一角 a, 角 a 是 五十六度,那么九十加上五十六的一半是二十八度,这样等于一百一十八度,这是角 d 的 度数。而此时啊,我们如果再仔细观察的话,不难发现, 擦掉 ab 和 ac 之后呢,这里面有三角形 btc 完了之后有它的两个外角, 他两个外角之后呢,他们的角平分线分别是 b、 e 和 c e。 那 么很明显,大家可以看到这里 b、 e 和 c e 分 别平分的角是 m、 b、 c 和角 b、 c、 n。 所以 啊,利用我们第三个公式,就可以得到角 e 的 度数和角 d 度数的关系,角 e 就 等于九十度减去二分之一角 d, 这样就可以用一百一十八度除以二,这样得五十九度,这样再用九十度减去五十九度,就可以算出角 e 的 度数等于三十一度。 那么我们再来看这个地方的一组条件,角 f 是 怎样来的呢?它其实是三角形 bce 的 一条内角平分线 bf 和它的外角平分线 cf 相交而成的一个角,所以利用公式二可以得出角 f 等于角 e 的 二分之一,这样三十一度的一半就是十五点五度。那么在这个地方啊,我们 题目当中就综合应用了我们刚才所提到的三个公式,那么这些公式啊,在我们做选择或填空题的时候,都是可以拿来直接使用的,那么熟记它们,并且能够熟练的掌握它们的证明方法, 对我们做一些几何题还是非常有帮助的,同学们,你理解了吗?
16看见花盛开 05:19查看AI文稿AI文稿
05:19查看AI文稿AI文稿大家好,我是王志鹏,屏幕前的你如果是一名八年级的学生,是否还在因为角平分线的问题而苦恼呢?考试的时候是不是感觉题目似曾相识,错过却又做不出来呢? 今天我就用一条视频帮你把角平分线全都讲清楚,让我们一起进入探求环节吧! 好,我们先来看到探求一两内角平分线形的问题,如图, b、 p、 c、 p 分 别平分角 abc, 角 a、 c、 b。 求证,角 p 等于九十度加二分之一角 a, 证明因为角 a 加角 abc, 加角 abc 等于一百八十度。这里呢,我们是运用了三角形的内角和定力, 所以角 abc、 加角 abc 等于一百八十度减角 a 运用等式的性质,两边同时减去角 a。 因为 b p 平分角 abc c p 平分角 a、 c、 b, 所以 角一等于二分之一角 abc, 角二等于二分之一角 abc, 所以 角一加角二等于二分之一括号角 abc 加角 abc 等于。那么我们把角 abc、 加角 a、 c、 b 替换成上面一算出来的一百八十度减角 a 就是 二分之一括号一百八十度减角 a 等于九十度减二分之一角 a。 好, 最后,因为角 p 加角一加角二等于一百八十度。 再次运用三角形的内角和定力,所以角 p 等于一百八十度。减括号角一加角二等于一百八十度。减掉, 把角一加角二用这个替换掉减括号九十度减二分之一角 a 等于九十度加二分之一角 a。 这样这个结论就被我们证明出来了。 接下来是探求二疑内角疑外角平分线形的问题,以及探求三两外角平分线形的问题, 那么这个留给大家自己去思考了,答案附在视频的末尾,有能力的同学一定要自己探求后再看答案验证哦! 最后我们来总结一下,如图, b p。 平分角 a、 b、 c, b m。 平分角 c, b c d c m。 平分角 b c f c n。 平分角 a、 c、 d。 则我们可以得到以下的六个结论,结论一,结论二,结论三,分别是探求一、探求二,探求三得出来的结论。 结论四,角 e、 b、 c。 加角 f、 c、 b 等于一百八十度加角 a。 好, 那么角 e、 b、 c。 加角 f、 c、 b。 我 们可以看成三百六十度减去 角 abc 与角 a、 c、 b 的 和,那么角 abc 加角 a、 c、 b 又可以替换成一百八十度减角 a, 最后算出来就是一百八十度加角 a。 结论五,角 bpm 等于角 pcm 等于九十度。那么这里想必大家七年级应该都学过叫做零补角的角平分线互相垂直 证明过程,大家可以简单思考一下。 最后一个结论,角 b、 p、 c。 加角 m 等于一百八十度。那么这里分别可以用结论一和结论三中的数字来推来替换, 最后算出来的结果就是一百八十度。 怎么样?和角平分线有关的问题你听懂了吗?希望大家今后在学习中能够灵活运用这些知识,那我们就下次再见喽,拜拜!
71草木
猜你喜欢
- 2821秒杀小数








