反对称矩阵的秩有什么性质
粉丝7.7万获赞55.1万
相关视频
 08:47查看AI文稿AI文稿
08:47查看AI文稿AI文稿好,我们呢来总结一下反对式矩阵的性质,那么什么叫反对式矩阵呢?首先啊,如果能够满足 a 的 转制加 a 等于个零的话,那么呢,就称 a, 它为反对称矩阵。 好,就说明什么呢?就说明满足 a i j 等于个负的 a j i 的 形式, 这个结果啊,那么呢,有什么性能呢?看第一个啊,第一个,如果说我的矩形的话,他这个反转的矩形的话,说明什么呢?说明满足对角线元素均为零 啊,均为零的,为什么呢?因为对圆心的话都是满足什么呢?满足 a i i 的 呀,对不对?那么 i 和这相等的时候,不就说明 a i i 等于一个负的 a i i 吗?是不是它们俩相等,说明什么呢?说明就满足 a i i 就 只能取零啊? 来,我们看第二个,就是说,如果啊,它是一个基础阶段化, 那么这个时候就满足 a 的 行列式是为零的,为什么要这样子呢?你们看啊,首先的话呢,如果是一个反的式的话,它满足 a 等于一个负的 a 的 转制的,是不是?那我这样子两边同取行列式,就满足 a 的 行列式,等于个 负的 a 转的行列式,那么我的 a 的 话是个 n 接的吧。好,就等于一个负一的 n 次方乘个 a 转的行列式啊, 那么 a 转换成和 a 转换成是一样的啊,就等于多少呢?负一的 n 次方乘个 a 的 行列式是不是这样的?来,你看啊,那么如果说当满足我的 n 的 话,它为二 k 加一的时候,是个基数啊,是个基数,那么负一的 n 次方就是个负一啊,所以说就满了,什么情况呢?好, 就满足 a 的 行列式等于一个负的 a 的 行列式。因此可得满足 a 的 行列式是为零的啊,是为零的,这是我们的第二条。来,我们看第三条啊,第三条, 第三条什么样呢?就是说啊,对于任意的 x 而言。 好,那么呢,均有 x 转至 a x, 它是等于零的,为什么这样呢?你看啊,首先你要知道什么呢?知道这是 x 转至 a x 的 话,它是啥呀?它是一个数啊, 对不对?它是一个数啊,那么这样啊,我现在两边去转制,可以吧?那啊,我这样子,则就满足 x 转制 a x, 它等于个 x 转制 a x, 我 再去转制啊,数去转制是相等的,对不对?那么呢, 等于多少呢?等于一个 x 转制 a 的 转制 x 呀,那么因为满足 a 转等于负 a 是不是等于一个负的 x 转至 ax, 对 不对?你看这个地方,它和它是相等的,对吧?前面多个符号说明什么呢?那么不就满足 x 转至 ax 等于零了吗?好,来,我们看下第四个。第四个什么东西呢啊?就是说,对于矩阵一加 a 来说的话,它为可逆矩阵的, 那么怎么证明呢?我们来通过一个反证法来证明一下。 好,首先啊,先假设 e 加 a 啊,它满足不可逆 啊,那么如果不可逆的话,说明什么呢?不就说明存在 x 不 为零啊,不为零能够使得什么呢啊?使得 e 加 a x 等于零这个方程组成立吗?对不对?是不是其实方程组啊,成立啊,有非零解。那你看啊,我现在这样子,那么如果是个零的话, 应该等于个多少呢? s 转至乘个零的吧,而又满足 e 加 s 等于零啊,那么我能不能这样写,等于个 s 转至乘多少呢?乘个 e 加 a x 是 可以的吧,现在我给它写开啊,那么不就满足 s 转至 x 加个 s 转至 ax 吗?好,那么我刚刚得出来,满足 s 转至 x 等于零,在这呢, 所以说等于多少呢?不就满足 x 转折 x 的 形式吗?来,你看啊,那么现在的话, x 转折 x 啥东西啊?它是我们向量模的平方啊。好,如果说一个模长为零的话,说明什么呢?说明我的向量只能零向量啊。好, 则就说明 x 的 话呢,是为零向量的呀,这和我们的体感矛盾了吧,对不对?矛盾了吧,我展示的是存在 x 不 为零,而它是为零的呀,所以说矛盾。 因此的话呢,就满足我的一加一是可逆值啊,这是这个。来,我们看第五个。第五个啥东西呢?好,就是说 a 的 特征值 好,只能为零或者是虚数的。 那么为什么这样呢?我们看一下啊,刚刚我们是不是说了,满足一加 a 可逆,对不对?那么如果一加 a 可逆的话,说明什么呢?说明也满足 k, 一 加 a 也是可逆的, 我们可以通过上面的方法类推是不是?那么如果肯定的话,就满足 k, 一 加一的行列式是不为零的呀。那么如果满足不为零,说明什么呢?不就说明负 k 它就不是特等值吗? 那么负 k 不是 特等值的话,我的 k 是 个实数啊,对不对?说明什么呢?说明满足特等值是虚数的呀。 好,并且也可能取到零。为什么呢?因为这个地方如果我的 n 是 个基数的话,就满足行列式为零啊。那么如果行列式为零的话,说明什么呢?说明满足特征值为零对不对?好,因此就说,当满足 n 为基数的时候, 好,特征值的话呢,为零的 好,因此可得就满足 a 的 特征值的话呢,只能是零或者是虚数的呀,并且我们要知道什么呢?知道的是啊,对于我的实数系数方程来说的话呢,好写这儿, 那么呢,虚根它一定是成对出现的。 所以说啊,如果题刚中出现什么呢?出现了 a 为三阶 非零反对称整数的话, 好,那么就满足 a 的 值是为二的,为什么呢?因为三是一个基数,满足特称值一定有零, 而我的 a 的 话呢,它是非零的,满足值等于一,那么因为 a 是 个反对称啊,我的零和虚根只能是特称值,对不对?并且虚根成对出现,因此的话呢,满足值为二就可以了。
105考研数学超超 04:14查看AI文稿AI文稿
04:14查看AI文稿AI文稿好,我们看下这道题啊,他说 a 的 话呢,是一个三阶非零的反对的矩阵。好,那么 b 的 话是个方阵,并且满足 a b 减一的质为一,那么 b 有 哪是对的?看啊, 他们都是判别我的两个方程是否有零解的,对不对?那么看什么呢?看质啊,看质啊,并且都是个方阵,判别什么呢?判别行列式就行了, 对不对?那你看啊,那么这个地方的话,他说什么呢? a 是 一个三阶非零的反对正矩阵,那么说明什么呢?说明满足质为二, 为什么为二呢啊,我前面是讲讲过的啊,大家可以去看一下。好吧,来,那么并且啊,满足 b 的 话呢,是个方正,三阶方正。还有就是说 ab 减的质为一来看啊, 我们通过它分析,如果满足 ab 减 a 的 质等于一的话,它说明啥呢?不就满足多少呢?满足 a 乘个 b 减一的质是为一的吗? 是为一的吗?好,你看啊,它们里面是相乘的关系,对不对?有个不等式啊,什么不等式?就是说啊, r a 加 r b 减 n, 它是小等于 r a b 的, 有这个不等式啊,对不对?好,你看啊,那么如果往里面套的话,它不就满足这个关系吗? a 乘个 b 减 e 的 值,它是大等于 r a 加个 r, b 减 e, 再减去个 n 的 呀,减去 n 的 吧,而我的 n 的 话是个三 a 的 值的话呢,是 v 二的,说明啥呢?不就满足 b 减一的值,它是小等于二的吗?来看一下啊, b 椅子呀,我带进去呗,你看啊,则 b 减一为几呢?就是 a 减一,五一好, 零一零,再是二 b 二的。来看一下这个值的话,可能是比二要小吗?或等于吗?来看这个地方,我取一个二阶指示,可以吧? 二阶只是不为零啊,证明什么呢?来写着 b 减 e 啊,它呢,存在二阶,只是它是不为零的呀,那么不就满足 b 减一的质是大于二的吗?你看一下啊,我两边都要满足因子的话呢?好,就只需要满足 b 减的质为二就行了呀。那么如果满足 b 的 质为二的话,我的质不满质,说明什么呢?就满足 它行列是为零啊,对不对?行列是为零啊,怎么算呢?我就按照第二行展开一下不就行了吗?好,因此可得 就满足二倍的 a 减一,再减二是等于零的。可得 a 就 等于二点, b 等于多少呢?就等于个二五一零二零,然后呢,二 b 三点好,有它了吧?现在我算行列式啊,你看 b 的 行列等于多少呢?我按照第二号展开一下,就是二乘多少呢?乘个二一,再是二三点 好,那么结果就等于多少?等于个二乘个二乘三减二的结果等于个八。满足不为零,说明啥呀?说明满足我的 b 可逆啊,因此就说明 b 的 话呢,至为三的,至为三。那么如果为三的话,说明啥?说明我的 b x 的 话呢? 等于零,它仅有零解。 仅有零解,对吧?我们前面说了呀, a 的 值为二,对不对?说明什么呢?就说明 a s 等于零的话呢,它是有非零解的呀。 啊,那么这个题选哪一个呢?选 b 选项是不是?
517考研数学超超 02:18
02:18 03:33查看AI文稿AI文稿
03:33查看AI文稿AI文稿最近很多模拟卷里边都涉及到了对反对称矩阵性质的考察,那么在这里呢,静静老师给大家总结一下反对称矩阵到底有哪些性质。考试碰到了直接去用 n 阶矩阵 a, 如果是一个反对称矩阵,那么矩阵 a 应该是长成这样,主对角线元素全为零,其余位置的元素一定是关于主对角线元素互为相反数的, 所以就有小 a r j 加上小 a j r 一定得零,这是从元素上来看,那如果从矩阵上来看的话, a 加上 a 转置一定等于零矩阵。所以但凡题目里面出现了矩阵 a 加上 a 转置得零矩阵,或者说 a 转置等于负的 a, 那 么这道题考察的一定是反对称矩阵的性质。 性质如下,第一个,如果 n 是 一个极数的话,那么 a 的 行列式一定是零。我们可以去计算一下 a 的 行列式,也就可以等于负的 a 转置的行列式。其中这个负一 取 n 字方,再乘以一个 a 转至的行列式。因为 n 是 个基数,所以照样是负一倍的 a 的 行列式, a 的 行列式本身就是个数,这个数等于它的相反数,那么这个数只能是零,所以 a 的 行列式必然为零。 第三条,对于任意的一个向量 x, 甭管它是不是零向量,一定会有 x 转至乘以 a 乘以 x 一定等于数字零。注意,这个你可以给他看成一个二次型了,那么二次型的结果一定是个数,这个表示数字零。既然是个数,我们可以算一下,这个数字一定可以等于这个数字本身的转至,所以我们主动给他取一个转至, 于是就有他就可以等于 x 转至 a 转至再乘以 x, 其中 a 转至又可以用负 a 来代,那么他就变成了负的 x 转至 a, x 这个数字等于它的相反数。好了,这个数也只能是零。于是就有对于任意的向量 x 都有 x 转至乘以 a 乘以 x 的 数字零。第四条 k e 加 a, 只要 k 不 为零,这样的一个矩阵一定是可逆的。很多题里边只要看到了,都可以直接用,那就有 e 加 a 可逆, e 减 a 可逆, a 减 e 可逆等等,这一系列的矩阵通通都可逆。来证一下,可以用上面的第三条来证。这里的第四条题目说它一定可逆。我们不妨假设这个矩阵不可逆,如果不可逆的话,那么 我一定能够找到一个非零向量 x, 使得这样的其次限行方程组,它是有非零解的,这个非零解呢,就是 x, 因为系数矩阵不可逆。那接着我们就可以去计算构造上面这个二次型啊,有 x 转至乘以一个零向量,其中这个零向量我就用 k 加 a 乘以 x 来代。 括号打开第一项就是 k 倍的 x 转至乘以 x, 加上第二项, x 转至 a x。 前面的第三条说了,对于任意的一个向量, x 都有 x 转至 a, x 一定是零向量,那代入之后,一定就有 k 乘以 x 转至乘以 x, 它得是零向量了。 又因为前面说了,这个 k 是 不为零的,那就只能有 x 转至乘以 x 为零,说明这个向量的内积才为零吧,其他向量的内积都不为零。而前面又 设的这个 x 是 非零向量,那就说明咱们推出来矛盾了,只要推出来矛盾,就说明这个假设是错误的。说明 k e 加 a, 只要 k 不 为零,必然可逆。 好,最后第五条,因为第四条里头的 k e 加 a 一定可逆,那就意味着 k e 加 a 的 行列式一定不为零,说明矩阵 a 的 特征值肯定不能是负 k, 而这里头的 k 取的很普通,不为零就行了。 k 不 为零,说明负, k 不 为零,那就意味着矩阵 a 的 特征值肯定不能是负 k 不 能是负 k, 说明不能是所有的非负值,非负的数。只要是非负的数都不能取, 那么课堂值呢?他就只能取零或者是纯虚数。注意哦,纯虚数一般都是成对出现的呀,比如说零加减 i, 零加减二 i, 那 么 a 的 质就表示非零特征值的个数,非零特征值的个数成对出现,所以 a 的 质就只能是偶数了。以上呢,是反对称矩阵的几个性质考试碰到了。
421考研数学静静 10:36查看AI文稿AI文稿
10:36查看AI文稿AI文稿a 考研数学结构就是我,今天呢,我要给大家讲一个反对称矩阵的性质, 如果问你反对称举证有什么性质?如果你什么都不知道,那好,今天这个视频一定要坚持看完,考研考到你就牛逼了,因为这个性质你知道就知道,不知道就是不知道,考场上没有时间去推导,而且你也推导不出来,你信不信?哎,同学们来做一下这个例题, n 结实矩阵 a 写成括号 a i g 的形式啊,这是我们举重的一种表达形式啊, 满足 a i j 加 a j i 等于零,下列命题中正确的是。首先,这个表达什么意思啊?这个表达的就是反对称正的意思,比如说我们举证 a 呢,它是一个二阶的啊,这就是 a 一一 a 一二 a 二一 a 二二,那由于 a i j 等于 a j i, 所以如果 i 等于一, j 等于二的话,那么 a 一二加 a 二一应该等于零,所以可以把 a 二一换成负的 a 一二,对不对? 其次,我们再看,如果 i 和 j 相等的话,那是不是说明 a i i 加 a i i 等于零啊?那是不是说明 a i i 就等于零啊?说明主对衡元素是零。 那你看这个情况下, a 的转制是什么? a 的转制是不是零?负的 a 一二 a 一二零啊, 它是不是等于负的 a 呀?对不对?好,所以我们反对认证呢。首先,第一个性质是 a 转制等于负的 a, 写成代数形式就是 a i g 加 a g i 等于零,这是一个刺激,一个信号啊,看到 a i g 加 a g i 等于零,它就是反对证证。其次,反对证证, 主对角线元素必须都是零, 对不对?其次,我们除了主对角线元素之外啊,跟着主对角线对称那种元素都得是叉个符号啊。好,接着我们来看反对称,这 一定是可逆矩阵吗?同志们,一定可逆矩阵吗?可不可逆?咱们对这个式子呢?两边同时取一个行列式, a 转制行列式等于负 a 整体行列式,对不对?而 a 转制行列式就是 a 的行列式, 负 a 整体的行列是是负一的, n 次方乘 a 的行列是,这时候 n 呢? a 是 n 阶矩阵啊。那也就是说, a 的行列是减去负一的, n 次方的, a 的行列是是等于零的。 如果 n 等于二 k 加一, 如果 n 是二 k 加一,则 a 的行列是减去负一的,二 k 加一,次方乘 a 的行列是, 是不是等于零?那这种情况下,这是啥?这是负一,那实际上是加了,是不是推导出来 a 的行列式呢?等于零,这说明什么?说明如果我们矩阵 a 的接数是一个基数的话,那它一定是不可逆的。 那么有同学问了,哎,杰哥,如果 n 是偶数的话,你这个也什么都得不到啊。 n 是偶数的话,那不就 a 的行列式减 a 的行列式,这是一个横等式吗?那它到底是不是可逆呢?那这种情况它是可以可逆,也可以不可逆, 你懂吗?但是只要我们 n 是一个基数,当 n 为基数的时候, 我们 a 的行列是一定是零,我们 a 呢?它一定不可逆, 所以他说 a 是可逆矩阵,这个不对吧?好,所以一不正确。 所以现在就知道咱们反对深圳是不是在有些情况下是不可逆的,有些情况下是可逆的。打个比方, 比如说 a 就是零,零负一一,这个时候 a 的行列是就是一个一,对吧? a 它是一个二阶的,而且呢,它不可逆,它可逆啊。第二个, e 加 a 是不是可逆?举止 e 加 a 是不是肯定取证呢?我们这个特征制也整不出来,我们以后再去证明是不是,是否是肯定取证中呢?可以尝试用方针组的想法去理解。 他说是肯定取证,那我就反正反反正吧。同志们啊,会不会啊,你看啊,我假设 假设 e 加 a, 它不可逆, 既然一加一不可逆,那么一定存在一个非零销量 x, 使得一加一乘 x 等于零啊,你看,一加一乘 x 等于。这个方程组由于吸引人不可逆,所以它一定有非零减嘛,它肯定是有无穷多减嘛。那好, 现在呢,我们来看啊,我们用这个菲林的这个项链 x 啊, 你看好了, we're on, 它去成一个零向量啊, we're on 它去成一个零向量,那么 x 转制成一个 x 呢?肯定是零了, 对不对?好,那我把这个零呢,用这个代换,因为 e 加 a 乘 x 是零嘛啊,所以 x 转制成 e 加 a 乘 x 依然是等于零的啊。啊,那这个情况下呢, 我们把它写成 x 转至 e, x 加 x 转至 a x, 可以吧?好,接下来呢,你想要把证二证明完,现在有点扯住蛋了,我必须要把另外一个结论告诉你,也就是咱们这个 mit 三,所以我们先来到 mit p 三,命题三正确不正确?我相信之前肯定有知道的同学啊,知道同学扣个一啊。命题三正确不正确,正确的话正确扣个一啊,不知道的话扣个二。命题三是正确的啊,只要举证 a 是反对证证,则 x 转至 a, x 一定是零。 为啥呢? x 转置 a x, 它既然是一个数字,那么对一个数字去转制它,还是 还是它本身对不对好?那么这个时候呢? x 转至 a 转至 x, a 转至又是负 a, 所以 x 转至负 a x, 它又等于 x 转至 a, x 等于负的。 x 转至 a x, 所以 x 转至 a x 呢,是等于零的。所以 三十正确的啊!从三十正确基础上,我们再回到咱们的二,这个东西呢,是咱的零啊,零不用管了。那 x 转至乘 x, 注意啊,这是一个非零限量的内积,它一定大于等于零。取等号的条件是 取等号条件是我们 x 必须是一个零项量。但现在呢,我们已经知道 x 转制成 x 等于零了,所以咱们 x b 是一个零项量。 但是我们这里面说的是什么存在非零项量 x 使得 e 加 x 乘 e 加 a 乘 x 等于零啊?但我们推出来的是矛盾了啊,那说明假设错误,说明 e 加 一定是可逆矩阵啊。所以二正确,三正确。所以一个反对成正加一个单位正,一定是一个可逆矩阵,它本身不一定可逆,但是加一个单位正义一定可逆。另外, x 和 z x 一定是零。 好,接着我们看第四个,如果 a 不是零矩阵,则 a 不可能合同于一个非零对角矩阵。 对的四是正确的。为什么呢?我们合同 合同是什么?是十对称矩阵 与十对称矩阵合同。 非时辰证矩阵与非时辰证矩阵合同。 你看我们矩阵 a, 它既然是一个反对称阵,那反对称阵一定和一个反对称阵合同,它不可能和一个时阵阵阵合同,而菲林对角矩阵,对角矩阵是一个时阵阵矩阵,对不对啊?所以第四个呢,是正确的啊,所以 a 不可能和一个菲林对角矩阵合同的,对吧?只要 a 不是零矩阵。 好,那这个题目命题正确的,就是我们的二三四好做对的同学,弹幕扣个六六六 啊,让大家都知道你把这个题目做对了。然后呢,今天学到的同学啊,下面一定要去复习把这个备注啊。有一说起来,反对证,举证什么性质?第一个反对证,举证主的元素肯定都是零。第二个反对证,举证 x 转至 a x 这个二字音,结果一定是零。第三个反对认证,只有当接触是一个基础的时候,他才是一个。呃,这个,这个,这个不可逆矩阵,其余情况下有可能可逆,有可能不可逆。接着再说,一加 a 一定是, 可你去这吗?你把这背住啊,以后遇到类似的题目马上就能写出来,考研考的就是结论,你考上没有时间去推,对不对? 好,这个就是咱们今天杰哥教给大家的啊,如果视频对大家有帮助的话,一定要给杰哥一个三连点赞,投币、转发、收藏,多多支持杰哥创作啊,就是你说你呢?
1019考研数学杰哥(线下)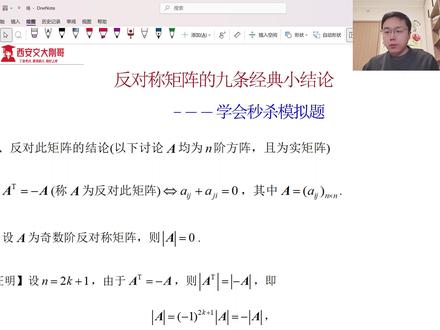 25:38
25:38 00:40
00:40 04:45查看AI文稿AI文稿
04:45查看AI文稿AI文稿等于二的对称矩阵可以表成二个至等于的对阵局阵之和。要想解决这个问题,我们呢需要用到对称局的一个重要结论。 在二字形里面,我们学过任何对称矩阵都合同于对角形。那下面我们利用这个结论来证明这个问题。是 a 是 对称矩阵 志伟 r。 因为 a 是对称矩阵,所以存在可逆矩阵 c, 使得 c 的转至乘 a 乘 c 合同与对角形。 因为 a 的痣是 r, 所以这里的每一个 d i 都不是零。 那下面我们 把后面这个矩阵可以分解成二个字为一的矩阵之和。 下面我们因为这个 c 是可一可逆的,我们呢可以把 c 全部移到后面去, 再利用这个矩阵的分配率, 我们呢可以把这个乘机进行展开, 再根据转至和逆,他们之间是可以交换的,我们就可以得到。 那么很容易发现这其中的这每一块 都是对称,举针 切至都是一。
43高等代数题解 14:22
14:22 02:44查看AI文稿AI文稿
02:44查看AI文稿AI文稿二零一四道题,他说假设三阶矩阵 a 的特等值是二,那么打一等于,那么打二等于六是 a 的二重特等值,然后呢?阿尔法一,阿尔法二,阿尔法三都是矩阵 a 属于特等值,六的特等值。 好,好,第一位让我们求 a 的另一个特征值和相应的特定项量,叫他,哦,他的志是二啊,是吧是吧?好,然后第二位让我们求取答 a 好题怎么做? 那你拿到之后啊,首先是不要把这个条件往特等值上面去翻译,那你看,说三阶十对称举证 a 的质是二, ra 等于二,好,这个翻译过来表示什么?是零为 a 的特等值,这些整体啊,他的考察的深度啊,他的考察深度和我们平时讲的其实是不是要低多了, 是不是这样容易多了啊?零是 a 的特征值,然后呢?另外两个是不是告诉你了,那么在一等于,那么零六是二层特登值,是不是一定一共就三个特登值,那就都有了,所以说则 a 的特登值六六 零,就这三个,然后呢?然后你再想,他告诉你六的三个特效量,哎,你说六怎么会有三个呀?你说老师,你问的是个啥问题?他别说三个了,他补充多个都有。哎,你这三个他线性相关就没事了啊,但是他线性无关的有几个?线性无关的是不是只有两个?对,你这三个里面你会发现啊,三个整个他是线性相关的,但是线性无关的好,不能挑出两个 好,是这样,好,就说呢,这是第一个啊,首先我们要注意到,接下来我们要求什么呢?就要求零的特征项量,因为二重特登值六有两个线性无关的特征项已经找到了,不用再找了,那么我们是不是在找零的特征项就可以了?好,零的特征项量怎么找?借助于什么呀?借助于正销来找就行,是不是?好,我们这样啊,假设零的 特征销量 beta 等于 x 一 x 二 x 三 t, 是不是?好,那所以说呢?所以说我们则返一 t beta 等于 off 二 t beta, 是不是? 这个贝塔和阿尔法一、阿尔法二都正交好,那么拿过来是什么呢?好,这几是一加 x 二,然后呢? x 一二 x 一加 x 二加 x 三。好起,这个会写了吧, 其基础解析啊,是负一负一,你这个等于被他这就完事。那你注意,第一问怎么写啊?第一问,你这么写,哎,你说则 属于增值六的特等销量是什么?是 k 一,阿尔法一加 k 二,阿尔法二,好,其中一 k 二不全为零。好,属于增值一的特等销量为 k 三倍的贝塔啊,其中 k 三 啊,我自己看到了,这不算酒吧啊,我自己看到的啊,这就做完了?反球举证 a, 独立举证 a 头上讲。没有啊,昨天晚上讲了一个,你现在屁都写出来了,屁怎么写啊?屁怎么写?屁就写阿尔法一,阿尔法二,还有 对角矩阵,写什么?对角矩阵写六六零啊,好,这个 a 等于 number, 拼命啊,这个自己算吧,是不是?这个我现场在这给你算一遍,是不是没啥意义?没没,没啥意义啊,看下答案啊,我不给你算答案。这个。好吧,看这个。
199展鹏考研





