物理必修二曲线运动思维导图好看
粉丝1023获赞4499
相关视频
 15:52查看AI文稿AI文稿
15:52查看AI文稿AI文稿各位同学大家好,今天这节课我们开始学习一下 b 修二,也是高中物理的第五章抛体运动里面的第一节曲线运动和第二节运动的合成与分解。 在初中阶段和 b 修一我们研究的是匀速直线运动和匀变速直线运动。物体运动的轨迹都是直线,但现实生活中 物体运动的轨迹不是直线的例子比比皆是,比如教材上给我们举的这两个例子,抛出去的篮球,攻转的地球等等等等。 所以我们把运动轨迹为曲线的运动,称之为曲线运动。我们知道直线运动的运动方向和轨迹一致,那曲线运动的速度方向是向哪边的呢? 比如思考一下这两个常见的装置,一个是打磨金属的那个沙沙龙,想想他飞出来的火红色威力怎么运动。还有一个是令球, 想想他被扔出去以后的运动轨迹,怎么判断沙龙打磨出的炙热威力和飞出去的令球在任意时刻或者任意位置的运动方向。 教材上给我们设计了这么一个实验,通过这个实验观察做曲线运动物体的速度方向。如图,在水平桌面上放一张白纸,白纸上摆一条有几段稍短的弧形轨道组合而成的弯道, 使表面沾有红色。印尼的钢球以一定的出速度从弯道的 c 端进入。钢球从出口 a 离开后,会在白纸上留下一条运动的痕迹,这个痕迹它记录了钢球在 a 点的运动方向。 拆去一段轨道出口,改在 b 点,用同样的方法可以记录钢球在 b 点的运动方向。通过实验,我们可以确定做曲线运动的物体在某一时刻或某一位置的速度方向, 但是要书面描述出这一瞬间的速度方向。对,明确一个数学上的概念,曲线的切线,圆的切线。初中我们就学过和半径垂直,那任意曲线的切线呢?它的方向应该怎么画? 比如黑色的这条曲线,在曲线上任意取两个点,把任意这两点的点相连,相连的这条直线,比如 ab 一、 ab 二、 ab 三, 这条直线就叫做曲线的一条割线,所以割线就是一条线段,或者是两点之间的距离。设想 b 一 点,沿曲线逐渐向 a 点靠近,比如到 b 二、 b 三、 b 四,这条割线的位置也就发生了变化。 当 b 一 特别特别靠近 a 点时,比如到 b 点,这条割线就叫做曲线。在 a 点的切线相当于长度区域零时的割线就是这个点的切线。用到了极限思维, 或者在这个位置画一个极小的圆,切线和半径垂直,也可以得到切线都是极限的思想方法。最后可以得出结论, 做曲线运动的物体在某一点的速度方向,沿曲线在这一点的切线方向,且速度方向时刻在改变,因为速度是矢量,不管是大小变还是方向变,则速度都在变,所以 曲线运动一定是个变速运动。第三个知识点,做曲线运动的条件。物体做曲线运动时,由于速度方向时刻改变,则速度时刻改变,当它为不等于零,物体的加速度一定不为零。根据流动电压定律,物体所受合力也一定不为零。 那物体受什么样的力才会做曲线运动呢?我们看看这个实验,把磁铁放在不同的位置,则磁铁对钢球的作用力就不同,因为物体的运动情况是由受力决定的。 当钢球受力不同的时候,观察一下钢球的运动轨迹。通过大量实验可以概括出三种运动情况,第一种,受力与速度方向相同时,钢球做加速直线运动。第二种,受力与速度方向相反的时候,物体做减速直线运动。 第三个,受力与速度方向不在一条直线上时,物体就做曲线运动。或者可以想想,平时走路,你正常向前走,有人从后面推的时候走的快了,但轨迹还是直线, 有人从后面拉走的慢了,甚至后退,运动轨迹还是直线,但有人在侧面推的时候,运动轨迹就不是直线了。所以通过大量实验可以得出物体做曲线运动的条件。 从动力学的角度分析,做曲线运动的条件就是运动物体所受核外力的方向跟它的速度方向不在同一条直线上,物体就做曲线运动。 从运动学的角度看,做曲线运动的条件是,当加速度方向跟它的速度方向不在同一条直线上时,物体就做曲线运动。或者也可以概括为,物体的速度不等于零,且速度方向与合力方向不共线。 做曲线运动的物体,合力一定不为零,因为根据流动的定律,物体所受合力为零时,要么静止,要么匀速。直线不可能做曲线, 那物体所受和外力有什么作用效果?比如把合力沿速度方向和垂直速度方向分解,沿速度方向的分力 f、 x 和速度在一条直线上改变速度的大小 和速度方向垂直的 d、 f、 y 则改变速度的方向。所以当合力方向与速度方向的夹角为锐角的时候,沿速度方向的力与速度方向相同物体就做加速曲线运动,如图,甲, 当合力方向与速度方向的夹角为直角的时候,这个力只改变速度的方向,不改变速度的大小,物体做速律不变的曲线运动,如图,以 当合力方向与速度方向它们的夹角为动角时,分解完沿速度方向的力与速度方向相反,物体做减速曲线运动,如图。饼, 不管是加速、减速还是速度不变,力都指向轨迹的凹侧或者内侧。概括完一句话,力和速度加轨迹,也就是轨迹总是在力和速度之间。 所以曲线运动总共有这些特点和知识点。首先,曲线运动的轨迹为曲线,折线,不属于曲线。其次,曲线运动速度的方向沿轨迹的切线方向。速度的方向时刻在变,变化 大小可变可不变。所以曲线运动一定是个变速运动,加速的恒定就是匀变速曲线,加速度不恒定就是非匀变速曲线。第三点, 曲线运动一定有加速度,所以合力一定不为零,并且物体所受的合力指向轨迹的凹侧或者内侧。最后,力和速度加轨迹,速度方向是这一点的切线方向。受力指向轨迹的内侧,则轨迹一定在力和速度之间。 曲线运动的降解、运动的合成与分解我们先思考一下这个问题。人在流动的河水中,始终保持头朝正前方游向对岸,人会在对岸的正前方到达还是会偏向上游或者下游?到达对岸 或者岸边的观察者看到的游泳者是怎么怎么运动的?为什么?这个问题应该都知道,答案肯定是偏向下游到对岸,因为人走的时候水也走, 水对着游泳者沿水的方向也在运动,所以相当于人有两个速度,一个是自己向前游的速度,一个是水冲着游泳者沿水方向的速度,所以岸边的观察者看到的游泳者是斜着运动的。 我们继续看一下教材上给我给我们的这个实验,探索蜡块的运动。这一个封闭长约为一米的玻璃管内注满清水,水中放一个红色蜡块小圆柱体 a, 将玻璃管的开口端用橡胶塞塞紧,把玻璃管倒置。如图一,蜡块 a 沿玻璃管上升因为粗重的知识点,蜡块的密度比水的密度小,所以它会浮起来。 如果在玻璃管旁竖立放一个刻度尺,可以看到拉快上升的速度大致不变,即拉快近似的做匀速直线运动。在拉快匀速上升的同时,将玻璃管紧贴着黑板,沿水平方向向右匀速移动。如图,丙音。 观察拉快的运动轨迹和运动情况是怎么样的呢?并尝试求下拉快的运动轨迹和运动的速度。 要确定那块的运动轨迹,首先要确定任意时刻那块的位置。我们以那块开始匀速运动的位置为坐标,原点凹,以水平向右的方向和竖直向上的方向分别为 x 轴和 y 轴,建立平面直角坐标系。 若以 y x 表示玻璃管向右移动的速度,以 v y 表示那块沿玻璃管上升的速度,则有 水平方向的位置 x 等于 y, x 乘 t。 竖直方向的位置 y 等于 y 乘 t。 两式相比, y 比 x 就 等于 y, y 比 y x, y 等于 y, y 比上个 y, x 乘 t, v, y 与 y x 都不变,比值则不变。记 y 等于 k, x, 则那块的运动轨迹为一条过圆点的直线,那块的路程 s 等于根号下 x 方加 y 方,方向为抬进的 c 塔,等于 y 比上个 x 那 块的速度 v 就 等于根号下 y, x 的 平方加 y 的 平方,速度的方向为抬进的 c 塔,等于 y 比上个 y x。 像纳块这样,我们将纳块实际的运动称为核运动,把 x 轴、 y 轴两个方向上的运动称为分运动。已知分运动求核运动的过程叫做运动的合成。已知核运动求分运动的过程叫做运动的分解。 和我们学的力的合成与分解一模一样,当时学力的时候就说了,所有的矢量运算法则都是一样的,速度是矢量,所以和力的处理方法也就一样。 合运动与分运动遵循的关系也是等效代替的关系,效果一定是相同的。分解原则一般根据运动的实际效果分解,也可以正交分解处理方法用平行四边形法则或者用三角形法则。 运动的合成与分解可以。合成与分解都有哪些物理量呢?运动的合成与分解指的是 v e x 速度 v 加速度 a 的 合成与分解。比如第一个图 v e 的 合成,第二个图速度的合成,第三个图加速度的合成。 这些物体量都是矢量,遵循的都是平行四边形法则或者三角形法则。特别强调一下,运动的合成是为一的,分解是有多种可能的,坐标系见的不一样,分解出的结果就不一样。第四个知识点, 和运动与分运动的关系。第一个,等时性,和运动和分运动经历的时间相等。第二个独立性,各分运动之间独立进行,互不影响。第三个等效性, 各分运动叠加起来的效果与和运动有相同的效果。第四个,同体性, 各分运动与核运动是同一个物体的运动,所以运动的合成与分解是将复杂问题化繁为简的一种方法,也是处理曲线运动最常用的方法。 所以以后处理曲线运动最先想到的方法就是通过运动的合成与分解,化曲为直,把曲线运动分解开,就变成我们熟悉的直线运动。 初中我们学的是匀速直线运动,必修一,我们学的是匀变速直线运动,把我们之前学过的各种运动合成一下,看看都做什么运动。 第五个知识点,两个不共线的运动的合成,前提是不共线,别忘了这两个运动不共线,比如两个不共线的匀速直线的运动,合一下,看合运动是什么运动?看上面这个图, v 一 和 v 二都是恒定不变的,都做匀速直线运动,只有速度,没有加速度。以 v 一 和 v 二为零边,只能画出一个平行四边形,有唯一解, 并且没有加速度。所以两个不共线的匀速直线运动的和运动一定是匀速直线运动。下种情况,一个匀速直线运动和一个匀变速直线运动的和运动是什么运动呢? 这两个运动还是不共线?看下下边这个图。比如水平方向做匀变速直线运动,水平方向既有出速度又有加速度。数值方向做匀速直线运动,只有速度,没有加速度。 这两个速度的核速度方向是右上的核加速度方向。水平向右核速度方向和核加速度方向不共线,物体做曲线运动, 但加速度又是恒定的,所以一个匀速直线运动和一个匀变速直线运动的核运动一定是匀变速曲线运动。 最后一种两个不共线的匀变速直线运动的核运动是什么运动呢?比如两个匀加速直线运动, 如果这两个物体出速度均为零,一定是匀加速直线运动,因为静止的物体会沿合力方向运动,则速度方向和加速方向共线,物体做匀加速直线运动, 如果出速度都不为零,如果和加速度与和速度共线,物体就做匀变速直线运动,物体就做匀变速曲线运动。 最后,确定和运动的轨迹方程。首先建立 x y 轴直角坐标系,将物体的运动分解为相互垂直的 x 方向的运动和 y 方向的运动。 其次,分析物体在 x 方向的运动,得到物体在水平方向的位置 x 随时间变化的关系,比如 x 等于 f t。 同理, 分析物体在 y 方向的运动,得到物体在数值方向的位置 y 随时间的变化关系。假设 y 等于 g t。 最后,根据运动的合成与分解的等时性原则,水平数值函数关系式中的 t 是 完全相同的,消掉 t 就 可以得到关于 y 和 x 的 函数关系式。比如 y 等于 h, x 去曲线运动,运动的合成与分解。这两节课的知识点就这么多,涉及到的题型咱们下节课再继续,谢谢大家。
0物简理清 04:09查看AI文稿AI文稿
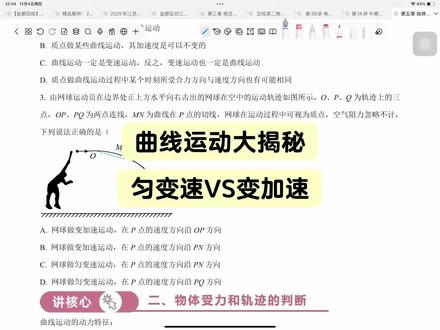
04:09查看AI文稿AI文稿好的,同学们,我们来看一下接下来这道选择题。质量为两千克的质点在 x o y 平面内做曲线运动,在 x 方向的速度图像 和 y 方向的位仪图像分别为啊,如图一和图二所示, x 方向是速度图像, y 方向呢,是位仪图像啊,他给的是两个不同的图像, 则下列说法不正确的。是啊,这是一个非常规的问题,他让我选择的是不正确的,同学们要注意啊,通常看到这种非常规的题目啊,我建议同学们呢,都要把它圈出来,保证你在下面分析的时候不会犯错啊。 a 选项, 质点的出速度大小为五米每秒,那质点的出速度应该指的是它水平方向速度和数值方向速度的和速度,对吧?那 x 方向出速度 t 等于零的时候,出速度是三,对吧? 那 y 方向呢? y 方向它的位移是随着时间均匀减小,所以它速度是横速度,对吧?斜率是肯定的,就等于什么呀,等于 四米每秒,而且应该是它的位移在减小,所以它的速度应该是负值。它 v y 的 方向应该是朝着 y 轴的负方向,对吧?那么我们只看大小的话, s 方向的初速度是三米每秒, y 方向的初速度大小是四米每秒,勾三股四弦五,所以它的初速度是五米每秒。 a 选项说法是正确的,不能选,他说选的是不正确的啊。 b 选项,质点所受到的核外力为三流顿, 那 y 方向它是做匀速直线运动,所以 y 方向不受到力。 x 方向呢? x 方向速度在逐渐增加,从三米每秒增加到六米每秒,所用时间是两秒,所以 x 方向的加速啊,应该是等于一点五米每二次方秒,对吧? 那它的质量是两千克,所以 x 方向所受到的力呢,就是 ma, 等于三流动没问题,因为 y 方向做匀速直线运动, y 方向不受到力 啊,和外力为三流动是对是对的,然后做的是匀变速曲线运动。那数值方向做的是匀速直线运动 啊,水平方向做的是一个初速度不为零的匀加速的运动,所以他肯定是做曲线,对吧?做曲线,也就说他的核外力方向和什么呀,和他的这个 速度方向啊,是不在同一条直线上,对吧?注意啊,我说的速度是 x 速度和 y 速度的一个和速度,不是指他单独的 x 速度或者是单独的 y 速度,所以他肯定是做匀变速器运动,他是一个类似于平抛一样的,对吧?类似一个平抛啊, 那 c 选项两秒末质点速度大小呢?为六米每秒。两秒末 y 方向的速度大小依然是四米每秒,对吧? x 方向的速度大小呢?是六米每秒,然后再 这个用勾股定,你算一下,四的平方加上六的平方,再开根号,肯定呢是大于六的,所以 c 选项这个说法是错误的。 d 选项两秒内质点的为一大小约为十二米。那两秒内我们分别去计算一下,什么呀?它 x 方向的为一大小和 y 方向的为一大小在什么呀? 再去用勾股定律算一下呗。那我们来看一下啊, x 方向的为一大小是多少啊?不就是求这个梯形的面积吗?三加六乘以二,再除以二是九米,对吧? 那 y 方向的位移呢?两秒末他的位移大小是八米,对吧?所以呢,是九的平方再加上八的平方再开根号。啊, 差不多呢,是约为十二米,没有问题。 d 选项说法是正确的。那这道题让我们选择的是说法不正确的选项,应该是哪一个不正确的是 c 选项,对吧?啊,所以这道题就选择第三个选项, c 选项。
 06:43
06:43 46:42查看AI文稿AI文稿
46:42查看AI文稿AI文稿好,这节课呢,我们来讲这个平抛运动中的追击和相遇,那么平抛运动呢,它也可能不是什么单独研究一个研究对象的,它有可能呢是多个研究对象放在一起,然后呢去寻找它们之间运动的对应的关联性。 那么平抛运动中的追击相遇呢,其实最早研究的时候是什么?是二战时候的这个反导系统, 但是那个时候的防盗系统呢,没有现在的这个什么他的主动动力,他可以跟踪啊,雷达这个什么电子线控啊,这些东西啊,都没有那么先进,所以呢,都是靠他的惯性指导,对吧?好,那所以呢,这个问题是个古老的问题了,但是古老的问题他有研究的对象和研究的意义, 为什么呢?它的意义在于它将承前启后啊,对以后的这个动力学的研究是有帮助的。那么具体的我们应该怎么去研究它,那我们还是要从它的具体案例开始分析, 好吧?好,那所以呢,这一刻呢,我们大致要从这个平抛运动中的追及和相遇的一系列的关系上呢,来进行分析啊和研究。那我们看看他大概会分成哪几类,而这几类在进行研究的时候又有什么样子,他的一些特点。好吧, 好,第一个我们来看一下关于啊平抛运动,啊平抛和谁呢?和啊直线运动之间对应的坠机相遇 啊,整这样子,那么这个时候呢啊,他就比较简单啊,当然了,这个地方呢,我们大致要说一下啊,再简单的东西呢,你得把它概括掉。那么比如说我们也举个例子来说,假设啊,在一个地面上的某一个高度处, 然后呢,这个地方呢?给他啊,有这个啊,丢炸弹了,对吧?飞机甩出了一个炸弹 啊,我们把它射成小球吧,好吧,这个不然话太暴力了啊,这个小球平抛出去了,假设它的出速度呢为为零,然后呢,这个高度呢?有多少嘞?这高度呢?告诉你呢,是为 h 了。 那么现在呢,在地面上跟它同一个数值位置处呢,有另一个小球在这个编号啊, a 球和 b 球, 那么在 a 球抛出的时候呢,与此同时也把 b 球呢水平的给它推出去了,那么如果我们不考虑地面啊,它是什么,它是光滑的,它没有摩擦力,不考虑摩擦,那么这个 b 球推出的速度要满足什么条件才会 啊?让他和 a 球能够相遇啊?教你求这个速度 v, 那 么这道题目呢?当然了,如果要是很熟悉的同学一看哦,你就知道。但是我们这样稍微分析一下,第一个,我们仍然是把 a 的 运动呢,他的轨迹给他画出来, 那就是说 a 呢,抛下来的时候是在这里,对吧?你要想让 b 球和 a 球相遇呢,那应该是要在这个位置给它相遇了,对吧?因为这它在着地的时候,它在空中的时候, b 球呢,它贴着地面跑,肯定不能 和 a 碰撞啊,相遇,对吧?好,所以了,这个时候应该是在他落地的这一瞬间,他们才能相遇的。好,那你讲这后面还弹起呢啊,弹起那个我们就算了啊,我们只讲他的平抛和他相遇的过程,那这个他平抛的什么啊?最末尾的一个位置吗? 好,那么这个时候呢,你发现平抛运动的物体,他的运动,我们是把它分成两段的,对吧?哪两个运动呢?一个是水平方向上的匀速直线运动,一个是数值方向上的自由体运动。 那么由于水平方向上是匀速直线运动,那么你 ab 如果想相遇的话,那自然就要形成什么,就要形成他们在水平位置的任意位置处的同步, 因为两个都是匀速的喽,那你要如果不同步的话,就没有办法相遇了,对吧?那就长这样子啊,一直是维持数值位置过程中的同步关系,我们把它图画一下,对吧?好,这一画你就知道了,这个位是多少了呀? 这个位多少了,这个位不就为零了吗?对吧?好,他长这样子了,当然了,这里给他画虚线, 对吧?维持同步呢,最终这个球落地了,那么自然你就砸中了,对吧?好,所以来你能得到这个 v 是 等于为零的。哎,这是它的第一种情况, 但是往后呢,问题就先显得稍微复杂点了,为什么呢?因为真实的情况下,地面是不可能没有摩擦的,对吧?所以呢,地面可能会产生让这个壁球运动过程中减速的这么一个效果,那也就是说地面呢,和壁球之间有动摩擦因素没有。 好,这变成了第二类问题了,对吧?刚刚是匀速直线,现在 b 球呢,推出去之后,它将什么?它将有一个阻力, 以使得它接下来要做减速运动了呗。好,那么现在这个球的这个位置呢,那就是 b 球在做接下来减速运动过程中的什么?它的出速度。 好了,那我们来分析一下这个时候他应该怎么去求解? 那么追击相遇问题呢?他的大的框架和基本思想仍然是跟我们前面讲的什么那个,呃,执行运动是一样的, 他仍然要从两个基础维度上来进行考虑。哪两个基础维度呢?第一个就是位关系或者是路程关系啊,我们每次在讲相遇问题的时候,总是在 不停的重复这个问题,那么还有什么呢?还有时间,对吧?你要从这两个时空的维度上去分析他们如何相遇的,你考虑速度和加速度呢?是没有办法考虑的,因为只有这两个关系才是最直观的关系。 那么 a 抛出去之后,仍然做自由落体喽啊,不做自由落体,做平抛运动了,那么它下落的位置啊,我们画出的轨迹,假设还在这个位置,我们把它收一 p 点, 那么 b 呢,就要在什么?在 p 这个位置要和 a 相遇, 那么相遇的条件就有了,如果 a 抛出的同时, b 开始运动了, 那么这个时候呢,你就要分析出他们什么,他们到达这个屁位置的等时性啊,他们时间又一样,不然的话,谁先到谁后到,那就没有办法相遇了,对吧?好,所以呢,第二个,你要考虑他们时间维度上的等时关系, 那有了这个等时关系呢,那就好分析了。怎么分析呢?因为自由落体啊,把它的平抛运动的数值方向上呢?自由落体呢,是可以去解决这个时间问题的,对吧?好,所以呢,我们来解一下解, 那么 a 求下落的时间呢?那自然就可以写成是 h 等于二分之一 g t 的 平方,对吧?那所以嘞,这个时间 t 就 给你算出来了也,根号下二 h 比上 g, 说明啥?说明你的 b 到达 p 这个位置的时候,那一定要是什么?要是等于这个时间 t 的, 但是 b 运动到 p 这个位置的时候呢,它的位移多大嘞?哎,这个位移呢,你也要从平抛运动的这个角度来把它算出来,因为为什么?因为这个平抛运动它可以分解成两个方向上的运动, a b 相遇,不仅仅是它们在时间上一样,它们在空间位置上还要维持一样,对吧?好,所以呢,这个时候你发现 party 运动的它的研究的相遇问题是要从两个维度上来同时考虑的。我把它写一下啊,写到后面, 写到哪了?写到这下面,跑腿运动,它不仅要在 x 方向上就水平方向了啊,要维持等时间啊,等时间中的 t 啊, t 啊, x 距离,那我们写大 x 啊,这个 x 的 距离要维持一致,而且呢,在外方向上, 他也要在考虑等时间的什么?竖直方向,哎,这写大写的话,它的一致, 对吧?谓语的一致。所以呢,解 party 运动的这一相遇,是要从两个维度上去同时考虑他们这个之间对应的关系的。 反义词呢?回归到这道题目,它的水平为一,那自然 x 就 等于什么?等于为零去乘以这个时间 t 喽,所以来等于为零乘以根号下二 h 去比上 g, 没问题吧?啊,为零等于啊,为零乘以根号下二 h 比上几。那么这个时候就确认了 b 的 出末之间的对应状态关系。出是什么?从 b 点由 a 的 正下方开始动的,而且同时开始动的 末位置在哪呢?末位置就是 a, 它的水平方向上移动的微一啊,那所以就搞清楚了,这个时候你要确认的是,这个 b 移动的微一就是 x, 只不过他应该写成是 v t, 然后呢,减去加速度产生的这么一个值,对吧?好,接下来你就要把它加速度能加速多少嘞?加速度好求的根据受力分析 啊,当然了,你熟悉的已经马上可以得到答案了啊,好,画一下,它受 mb 值受到地面的支持力, 当然了,还要受到地面的摩擦力,与它运动方向相反。那么根据牛顿第二定律呢,你马上就能猜到它所受到的合力就是你的小 f 喽,那小 f 自然等于 m n 喽, n 等于 mb 喽, 所以呢,等于它的啊,加速度关系对吧?好,把这个 a 给它弄出来。 那所以呢,解得这个 a 值是等于缪记的,呃,和 mb 没关系。所以呢,这个 b 的 质量可以不告诉你,对吧?好,那么接下来呢, x 可以 把它带进去算了, x 呢,是为零,乘以根号下二倍的 h 比上 g 的 等于 v, 要求的乘以时间 t, t 呢,在这对吧?啊,根号下二 h 比上记还要减去二分之一乘以 a, a 是 缪记乘以 t 平方啊,把根号打开 好了,这就好球了吧。那么稍微的化解一下啊。稍微化解一下,那么就可以写一下。写成是什么呢?我直接想分母上哈,那当然就是这个了, 分子上呢,自然就是这个喽。 啊, g 约掉了,二分之一也约掉了,哎,对对对,这个变得比较好, g h 对 吧?好,稍微化解一下,变成的是 y 以零去加上 g h 乘以它的倒数, g h 乘以它的倒数呢?那么 h 乘进去就约掉了,对吧?那所以变成的是 g 去乘以根号下 啊, h 给它乘进去啊,那么变成的是二分之 g h, 好 了,看,就是这个值啊,这个再化解,没什么化解头了,对吧?好,所以呢,这个解出来了,这是它的第二个产生的这么一个问题。 第二个,好,那你说那可能还有存在什么情况呢?可能存在的 b 会提前运动,或者是 b 会滞后运动,对吧?会存在这么一个问题,那么这个问题呢啊,假设 b 提前了 a t 零时间运动 啊,提前了,或者是 b 呢?它滞后于 t 零时间啊,滞后于 a t 零时间运动,那么再来分析他们相遇时 b 的 出速度的关系的话,这个问题呢,就留给你们课后自己去讨论了,好吧,这难度不是特别大,减法的思想仍然来自于微移关系和时间关系的 二维啊,两个维度上他的这个统一性。好,那么我们往后讨论什么? 往后讨论的是 party 和 party 之间它们的相遇,对吧?一开始我们研究的是什么 party 和和直线运动对应的关系,但是实际上呢,这个还是比较简单的。那所以我们要讨论的是两个平抛物体的相遇。 好,我们要研究这个,那么两个平抛物体的相遇的关系呢?那么可能就来的比什么一个抛体和一个直线它们对应的这个关系要来的稍微倒要复杂一点了,对吧?因为呢,原来是考虑一个物体运动的奥维, 现在呢,你要两个物体中的二维关系呢,都要给它讨论出来。好,那我们也来分析一下,那比方说第一种情况是这样子的,假设啊,这还是水平地面, 现在呢,在水平地面的某一个高度处啊,这个位置处,假设这个高度多少嘞?高度呢?仍然为 h 啊,好,在这里给它画成虚线啊,好,有个小球,小球看成正点 啊,以某一个水平出数为零,给他抛出了。好,那么然后呢?然后如果这个地方在这个什么啊,这个点,把它定为啊,这把它定为 o 一 点,好吧?啊,这定为 o 二点, o 二点呢?这个地方呢,也有一个,他的上方有个小球也水平抛出了,但是这个时候有个问题啊,我们稍微画一下,假设这个小球他在的位置是在这个位置处,好,画一下啊,画成虚线, 那么我们把这个称为 h 一 撇的高度,如果是 h 大 于 h 一 撇了,对吧?你的图上能看得出来,那么假设呢,在抛出 a 球的同时,把这个 b 球呢,也以某一个速度 v 给它抛出了, 好,那我就想问,如果 h 和 h 一 撇足够大,也就是说他们在相遇之前呢,是不考虑他们会着地的,对吧?我们只考虑他们在空中的问题,那么分析 a 和 b 会不会相遇 啊?给你们思考一下这个问题,如果这个高度足够大,就他们一直处在空中不相遇呢,就不让他着地,对吧?那么就问这个过程中, a 和 b 如果是同时抛出的,那么 ab 有 没有可能会相遇啊?问这个问题 会不会有没有可能?有没有可能?哎,对,这个时候好像是没有可能的,而你想为啥嘞?因为我们讲过, party 运动的相遇一定是要考虑什么啊?考虑水平位移和数值位移的两个维度上的,它们的时空观的相,它的相关联性。 那么这个地方我们只考虑哪方向呢?我们可以不考虑水平方向,对吧?啊?你讲这个 a 在 b 的 后方,那么 a 的 速度大点,是不是就可以去砸中抛出的 b 了呢?好像不一定啊,不见得 为啥,因为在数值方程上,你发现 ab 他 们始终是运动同步的,但是呢,他们有高度差呀,我们马上画一下啊, a 到 b 之间,他有个高度差,因为 h 是 大于 h 一 撇的喽,所以这个地方呢,存在一个德泰 h 是 等于哎,这个知道, 对吧?我把它画出来,那么画出来之后,你就会发现它存在一个巨大的问题。什么叫巨大的问题呢?你能明显感觉到,如果是两个球 把它一高一低的放在了同一个数值线上,让它们同时下落啊,就从这地方开始下落了,你觉得这两个球他们能相遇不? 他们不可能会相遇,能接受吧?为什么呢?因为它的加速为 g, 它的加速也为 g, 它们是什么啊?同步运动的,也就是说在未来的任意 t 时间 产生的运动的结果,那么都会使得它们之间距离维持了这个高度差得大 h 一 撇, 这能想象到吧,他们是什么啊?维持同步的两个铁球同时落地吧,那你一高一低的,肯定最后高度差是一样的,始终维持住了这个高度差。好了,那么说明什么问题? 说明什么问题?说明了一个巨大问题,你这个 a 和 b 两个球是没有办法在之后的运动过程中啊,能够碰撞到到一起了。 好,那你说那怎么办呢?那我可以把这个 b 的 高度给他放到什么和你的 a 的 高度一样的高度处啊,那他们维持了啊,这个没划到一起,把它划过来啊, 好,把它放到同样一个高度处,那么这个时候他们再抛出去,是不是就可能会相遇了嘞?那只要为零大于为肯定能相遇,这个没有问题吧, 对吧?啊,这不用解释吧,因为它们在数值方向上维持了同步水平,方向上呢,只要 a 能追上 b, 那 么只要高度足够高,它们一定在落地之前是能相遇的, 所以这个呢,不是我们要分析的这个具体过程。好,那因此我们把这个问题,如果想要去让 a 和 b 在 不同高度处抛出之后还能相遇的话,那我们要一步步把它做简化关系。那所以呢,我们先简化成什么样子呢? 先简化成这样啊,画一下假设这是同一个来画黑笔啊, 同一个数值线,在这根数值线上呢,给它放置了高低不同的两个小球啊,我们从这个角度开始先讨论这个相遇的问题啊,那么也标号啊,这是 a 球,这是 b 球, 那么现在告诉你呢, a 球如果抛出的话,它是以为零的速度给它抛出的。好,我们仍然不计空气阻力啊,现在告诉你呢, ab 之间的高度差呦, ab 之间的高度差呢?告诉你了,是等于好 h 了啊。啊,这个高度差为 h, 那 么他们所处在的高度呢?足够高,也就是 ab 在 相遇之前不会着地,对吧?好,仍然满足这个条件。好了,那么第一个问题问, 基于这个模型,分析一下, a 先抛出还是 b 先抛出才有可能相遇,还是同时抛出 好,你会发现呢?同时抛出应该不可能,对吧?我们刚刚分析了,同时抛出,数值方向上他们始终维持同步,所以数值方向上是没有办法他们挨在一起的。 那所以嘞,只有让什么让 a 在 数值方向上能够起步一定的速度,再去释放 b, 那 么接下来 a 才有可能追上 b 喽,是这个道理吧,所以这个地方一定是先 先什么?先抛出一个 a 球 好,那么这个地方问题就来了呀,那么如果抛出的时候, b 球的抛出速度 把它设为是 v 的 话,那么第一个问题是, a 球抛出后多久 b 球就要抛出了, 是不是可以一直等待下去?比如说啊,我抛出 a 等待了好久好久好久好久,我再把 b 给它放出去,那么是不是它仍然可以有相遇的可能性?这个我们来分析一下。 那么分析成什么样子呢?分析成,我们先把 a 的 他的轨迹给你画出来,对吧?啊?这个是个无限轨迹,因为高度足够高嘛。那么现在问题来了,现在问题是我们把 b 的 水平高度呢,给他做一条辅助线 啊,把它放在这个同样的高度上。问题来了,如果 a 现在下落到了 b 的 高度的下方,比如说,到这里啊,你再去释放 b, 那 么 ab 有 可能相遇,有没有可能? 这个好像不可能了,分析一下,为什么呢?因为我们仍然从数值方面考虑啊, 数值方向上能相遇,水平方向上才有可能探讨,对吧?那么数值方向上,他们在高度处变成了这样子了, a 已经落到了 b 的 下方了, 那么再去释放 b 的 时候,数值上面的他们的这个相遇可能性就不存在了。为什么?因为在数值方向上这个时候, a 已经获得了一个出一个出速度了,对吧? 那么你这个时候再去释放 b, b 在 数值方向上的速度是等于零的哟,但是他们加速度也一样, 那也就是说,在一个 a 有 出速度的情况下, b 却没有出速度,接下来加速都一样的情况下的时候, b 怎么可能在数值方向上能够再去追上 a 呢? 不可能啊。那么接下来在数值这个方向上,根据前面学的自由落体运动,你会发现,这个 a 如果在 b 的 高度下方时候, b 在 释放呢?那么 a 呢?在数值方向上将始终相对于 b, 做什么啊? 匀速直线运动,呵,能分析的出来吧?能分析出啊,加速一样喽。那么如果我们以 b 为参考线, a 相对于 b 的 加速就等于零,但是 a 有 出速度呀,所以 a 相对于 b 一 直做匀速直线运动啊。 好了,那所以呢,这个时间差得差 t, 它就必须是什么?是 a 在 落到 b 的 上方的时候, b 要释放出去才行,这个没有问题吧?好,所以嘞,得大 t 应该小于,等于什么呢? 等于什么? a 落到 b 的 上方吗?啊,等于可能都不行,对吧?因为等于呢,你接下来 a 有 速度了,那 b 也追不上了,所以是小于啊,他不能取 b 区间小于根号下二 h b 成 g 的, 对吧?也就是说,你的 a 球呢,要落在这一点之前, b 就 要抛出了。好,所以得差 t 呢,要满足这么一个条件。 好,那下面就变简单了,我们给出一个 a 抛出后, t 零时间内啊,这个时间 b 再抛出, 当然了, t 零满足什么条件现在已经清楚了吧? t 零满足条件不就得差 t 满足条件吗?对吧?好了,那么问这个 b 抛出的出速度 v 要满足什么条件才能让 a b 相遇呢?那么这个地方呢,你要什么?你再要把 b 的 轨迹再画一下, 对吧?好,画出轨迹才能找到几何关系啊,否则你哪来的几何关系呢?我们画一下啊,只有这样子,他们才能够形成什么轨迹上的交叉,轨迹有交叉才有可能相遇啊,那所以相遇的位置也就给你找到了,在哪呢?不就在这吗? 对吧?好,我们把这点呢,把它定义为 p 点,那么接下来就是要去计算 这个计算的过程,仍然要从两个维度上去考虑,当然了,这两个维度不是 x y, 因为 x y 两个维度,我们刚刚考虑了这两个维度指的什么?是位置和空间的它哦,位置和时间的关系, 你必须要是相同时刻在相同的位置上,它们才能相遇啊,那所以来要分析两个运动的两个方向维度上的它们的运动关系。 所以啦,先把 a 的 运动的位移给它分解成数值和水平的, 然后呢,再把 b 的 位移给它拆分成数值和水平的。 啊,水平卫衣一样,对吧?啊,这你能看出来了,那么所以这个时候呢,你要分析这个卫灵啊,那可能就好球了。那我们先来分析一下第一个 经过 t 零时间之后, b 在 释放的,那我们先来分析一下 a 下落的这段时间,那我们把这一段呢高度差,这段高度啊,就 a 下落的高度呢,称为 h 一, 好解, h 一 等于什么呢? h 一 自然等于二分之一 g 乘以 t 平方,那这 t 就是 a 下落的时间, 那么与此同时,在这段时间里面呢, a 的 水平位移了,那自然就是这一段长喽,那把它设为 x, 那 所以呢,这个 x 呢?那就等于什么啊?为零去乘以 t 啊,好了,直接写等于啊,为零 乘以 t 是 根号下二 h 笔记的,对吧?啊,一看就知道, 那么现在呢,现在的问题是,你的 b 是 延迟梯形时间释放的,对吧?那所以嘞, b 下落的高度,如果我们把它看成是 h 二的话, 那么 h 二在几何关系上就是你的平面,几何关系上,你一眼就能看出它应该等于什么, h 一 减去 h 的 v, 对 吧?所以等于呢,二分之一 g 好, 时间上什么关系? 时间上,后续的运动时间肯定是相等的,但是 b 延时于 a 多少时间啊? t 零时间,所以呢, b 的 运动时间是要比 a 的 运动时间短 t 零时间的吗?所以你乘以的是这个关系, 对吧?但是,但是啥嘞?但是它的水平为一,要和 a 的 水平为一维持一致啊,对吧?你能图上能看出来吗?那所以来写一下啊,为零乘以根号下二, h 比上 g, 这不水平为一吗?那么自然等于什么呢?等于啊,这个地方的 v 啊, b 的 速度去乘以这个时间喽, 对吧?这不它运动的时间吗?好了,那么这个时候呢,你发现它可以求了,好,我们来求一下啊,求一下这个 v v 呢?那自然就等于什么?等于这边去除以它喽,所以呢,就可以写成是 v 零啊,根号下二 h 除以 g, 然后再去除以 t 减 t 零, 而 t 刚刚已经算过了,在这,对吧?在这,所以把它带去变成的是为零,根号下二 h 比上 g 去除以来这个时间 t 呢,是等于根号下二 h 比上 g 减 t 零的 好,就变成这样子了。然后变成这样子之后呢,由于我没有给具体数据啊,分析一下为何为零谁大啊?为何为零?谁大?为何为零?明显是为大, 对吧?为什么呢啊?你能明显感觉到把这个值给它除下去嘛,对吧?除下去之后呢,就变成一减去一个值了,对吧?你这两边不是一样的吗?除掉 一减去一个值,说明下面的是一个小于一的值哦,小于一的值,那么明显 v 就 要大于 v 零二。所以呢,在下方抛出的小球 啊,如果要和上方的小球呢,能够相遇的话,那么你抛出的时候它的时间要延迟一段,但是不能超过什么呢?高度差,这个时间的它的关系,对吧?也就不能少啊,这个时间时间延迟的时间长度呢,不能超过更换下二 h b g, 其次呢,它的速度还得大一些,对吧?速度小了,它们可能在轨迹上都没有办法相遇,对吧?你轨迹都交叉不了啊。 好,所以啦,这是我们讲到的这第一种情况啊,从我们上面一开始讲的最基本的问题,把它延伸成了第一个特殊情况,是在同一个同一个数值面上,对吧?然后在上下呢,同一个维度上水平抛出的啊,这个时候怎么相遇的?好, 我把这问题呢再稍微修改一下。改成呢啊,和我们刚刚差不多的啊,慢慢递进啊,改成差不多的呢,那就是两条数值线了喽,那我们画一下啊,假设呢,这是一条数值线, 然后呢,在这里给他放了一个小球,让小球呢,抛出的时候,他的出速度仍然是为零啊,这是 a 球, 那么现在告诉你呢,这个情况下呢,是这样子的,这个 b 球在哪呢? b 球呢?在这条数值线上,只不过呢, b 球现在比 a 球要稍微高一些啊,这画的画太过来了啊,等下这图不好画了,我把它移过去 啊,移近点啊,然后图画的老大的,等下看不清楚了,对吧?啊,把它移近点啊,这是虚线,两条不同的数值面上 啊,这里有小球对吧?好,小球,把它涂黑,这是 b 球啊,然后呢,让他以某一个出速度是 v 的 速度给他抛出去了, 好了,变成这样子,那么现在告诉你呢啊,这个地方呢,就存在了什么啊,不止,不只是啊,他们的什么数值高度有差,他们水平之间还有 v 关系。所以啦,给他标出来啊,标一下, 告诉你呢,他们水平之间的这个宽度呢啊,宽度为 d。 好 啊,好,标出来了啊,宽度为 d, 然后呢,他们的数值高度差呢?那不就这一段吗?告诉你呢,为 h。 好 了,那么接下来你自己分析一下啊,分析一下这个是 a 球先抛还是 b 球先抛还是同时抛? 同时抛,我们刚刚分析了,不可能,对吧,因为数值方式上维持同步了,那就不可能相遇了,他们有高度差,所以应该是谁先抛出啊, 谁先抛出啊?哎,你想都别想,一定是高的那个先抛,因为高的那个不先抛的话,数值方向上就不可能能追得上,对吧?所以呢,一定是 b 先抛。同理,分析一下, b 抛出后延时多少时间内, a 就 要抛出, 延迟多长时间啊?哎,对,延迟了,还是更换下二 h b g 啊?也就是说,你的 t 零值呢?仍然是要小于更换下二 h b g 的, 这能接受吧?因为,为什么呢?因为 b 如果抛到 a 的 下方之后, b 再 a 再抛出去的时候,这个 a 就 不可能再追上 b 了, 对吧?好,所以啦, t 零时间仍然是小于它。好了,现在告诉你啦,给了一个 t 零, t 零引致,当然了, t 零满足条件是小于这个值,对吧?好,那么再问,再问, b 球抛出的初速 啊,还是求 b 的 速度要达到什么条件?这个时候 a b 才有可能相遇,当然了,高度足够高,就是说在他们相遇之前,我们不让他着地,对吧?好,这个时候怎么分析? 这是怎么分析那一样的,第一步干啥啊?第一步想的已经看清楚了,对吧?做轨迹嘛。啊, b 抛出的轨迹假设长这样,那么 a 抛出的轨迹呢?要想和 b 相遇嘞,那就要长这样, 哎,它有交叉点才有可能相遇,对吧?所以我们把这个相遇的位置呢,设为 p。 好,那么从这个角度,你已经能能看出什么了?从它的轨迹上,你就能看出 a 和 b 的 抛出速度谁大? 呵呵,能看出他吧,当然是 a 大 了,对吧? a 的 抛出速度大,为什么呢?因为曾经我们讲过两个抛物线的抛物线轨迹方程的, 还记得吧,我帮你推导一下啊,以它抛出位置建立坐标系的坐标原点,那么它的轨迹方程呢? y 是 等于负的二分之一记 x 平方比为零平方的, 对吧?那么开口越大的,说明他前面的这个系数的值要越小,那你如果说速度越小啊,什么前面呢,这个值就会变得什么变得越小呗,越小开口不就什么 开口就小了啊,开口就大了,对吧,能理解吧,速度越小,前面的值越大越大,就说明它开口小,对吧?这不是你二三数在初中说的吗? 哦,没有忘吧? o z 不 解释了,可以吧? o z 可以 不解释了啊,这个东西你要搞不清楚了你,你回忆一下初中的这个值结构 好了,那么抢到车里了,接下来问题就好解决了,对吧?您已经判定出位零肯定大于位了喽,那然后呢?然后一样的做抛体运动,肯定要分解来进行求解,所以呢,把它的运动给它分解成 啊数值和水平方向哎,换个颜色啊,数值 和水平,对吧,那 a 呢,也一样的不宜呢,把它分解成数值啊和水平 啊,把它分解成两个了,那么接下来不就要算了吗?那么先算什么?先算这个?先算 b 吧啊,一样的,先算 a, 先算 b 都行啊,只要你开心就好。好吧好,那我们来解一下解, 那么这个时候呢啊,这个 b 来下落的时间可以写成是把这段距离设为 h 一 好,所以写成呢, h 一 是等于二分之一 g t 平方,对吧?那么同样的它的水平不一呢?那就是这一段 我们把它设为 x 一, 那么 x 一 嘞,等于什么呢?等于 y e 去乘以这个 t 喽。 t 直接写根号下二倍的 h e 笔记, 对吧?那这里呢? v 解不出来,为什么 x 一 多大不知道, h 一 多大你也不知道,因为 t 是 设出来的,对吧?所以你不得不再去分析 a 好, a 呢下落的高度,我们把它设为 h 二 好写下 h 二呢,等于二分之一 g 啊,我们刚刚讲了, a 是 延迟于 b t 零时间抛出的,对吧?所以它的时间呢,应该就是 t 减 t 零喽, 没错吧?那么它的水平位移呢?把它设为 x 二好了。 那所以啦, x 二自然等于啊,它的速度为零去乘以它的时间,时间不这一段吗?那时间这一段呢?那仍然可以写成是根号下两倍的 h 二去比上 g 好 了。然后呢?然后你就想去找出对应的关系啊,你要解什么?你要解这里的 v, 要解这里的 v 就 要解除十啊。这个 h 一 要解除 h 一 就要解除 t, 要解除 t 就 要解除这里的啊 h 二,对吧?要解除这里的 h 二, 那么你要找到它对应的关系喽,那么这里的四个方程都没有联系,你看到没?所以接下来你刚刚是利用时间的等式形的, 所以接下来要使用什么?要用空间上他们的位移或者路程的对应的几何关系来列方程。那我们来列一下,首先, h 一 减去 h 二是等于啥? h, 对吧?那把它带去,那就是二分之一 g, t 方减去二分之一 g 乘以乘以什么 t 减 t 零啊?的平方是等于 h 的 喽, 对吧?好哎,这一列你马上就能看出来,这个 t 好 像可以减了,对吧?啊? t 可以 减了,然后呢? 然后,然后水平方向上的 v 一 你也能列出来了? x 二减 x 一 等于 d 的, 对吧?那我也把值给他带进去,那就是什么 v 乘以根号下两倍的 h 一 去比上 g 减去,哎,不对,这是这是这是这个哦, x 一 我减反着了啊 啊,对对对啊,重重重新写 x 二 x 二在这是 v 零根号下两倍的 h 二笔记,对吧?减去 v 根号下二倍的 h 一 笔记是等于 d 的。 那不管怎么样,我们先把什么先把 t 零搞出来再讲,对吧?好, t 搞出来, h 解出来, h 解出来, v 就 解出来了,所以算算这个式子先。 那么这个式子呢?先把什么先把?你要求的是,求的是 t, 所以 先把这个式子给它啊,二分之一 g 给它除过去,变成 t 平方, 减去 t 平方,加上两倍的 t 零 t, 然后呢?减去 t 零平方,对吧?等于二 h b g 啊,约掉了啊,原来它是一个一次方程啊,它它好好伪装了啊。 t 解出来了,那就等于等于什么啊? t 零平方加上二, h 比 g 除以二 t 零。 所以呢,算一下这个 t 值就等于二分之 t 零加上 h 比 g t 零。 好了, h 给你算出来了,对吧? h 在 哪?不在这吗?把 t 给它带进去, h 等于二分之一啊,二分之一呢? g t 平方。哇,这还搞个平方 好。然后 h 二也算出来了, h 二等于二分之一 g t 减 t 零,他减 t 零,直接写,那这个二分之 t 零减 t 零不是负的吗?所以是 h 比上 g t 零 减二分之 t 零的平方,对吧?好了,那所以啦,这个 v 终于给你算出来了,写下。那么 v 呢,自然就写成是啥啊?稍微写下啊,那就是,那就是 v 零,根号下二倍的 h 二比基 减 d, 然后呢,去乘以啊,它前面把这除过去了,所以乘以它的倒数,对吧? g 比上二维的 h 一, 好,稍微的化解一下,等下让你好算啊,对吧?稍微化解一下,那么把它乘进去,乘进去呢,就变成是括号标号啊,乘进去 g 约的二约的,所以是 v 零,根号下 h 二比 h 一 减去 d 乘以根号下 g 比上二倍的 h 一。 好带数据,所以啦,解得未知,等于啥呢?等于为零乘以它们俩相处啊, h 二除以 h 一, 所以是根号下 根号下二分之 g 全部约掉了,平方也可以打开了,没有根号了,对吧? 好,所以啦,变成是什么? h 比上 gt。 零,二分之 t 零。下面呢是 h 比上 gt。 零加上二分之 t 零啊,这 t 零啊,还要减去呢,后面的 d 乘以根号下,这 h 一 也给它开出来了, 对吧? h 一 给它搞出来,搞出来了,那下面呢?写一下,那就是 d 比上 啊,这个 h 一 的下面的这部分, t 零加 h 比上 g t 零, 根号里面呢,就变成的是根号下 g 比上二还要乘以二分之一, g 没有了,对吧?哎呦,根号全给搞光掉了,好,为零可以算了 啊, v 可以 算了啊,稍微算一下,那么然后通分呗。通分怎么通分呢?先把啊,它们分母是一样的,那分子相减 写下啊, h 比上 g t 零,加上 t 零比上二。上面呢,就写成的是 v 啊,写下写成什么呢? v 零 h 比上 g t 零, 减去二分之为零 t 零,然后减 d 零啊,减 d 啊,化减化减化减啊,不化减太丑了啊,上下同乘以两倍的 g t 零,那所以呢,这是二 h 减去 g t 零,平方上面呢,变成的是二倍的,为零 h 减去 v 零, g t 零,平方减去两倍的 g d t 零。 好,没什么好化解的,这是你的最后答案,对吧?好,那你想为什么花这么长时间去计算呢?那么请同学们在这个阶段上要重视计算啊,以后你们读大学到读这个研究生,那么计算能力很重要,因为你在实验室里要处理数据啊, 对吧,虽然有计算机辅助,但是呢,有些数据你可能心里也要明白了,对吧,你要对数据敏感,包括呢,有些东西呢,你可能做出这个实验了,数据分析不出来,你可能都不知道结论在哪, 对吧?好,所以呢,这个一定要对计算要上心。好,那这是我们讲的这节课呢,他的什么这个平抛运动中的追击和相遇问题, 那么平抛中的这些相遇问题呢,我们刚刚讲了,一定要从两个维度上考虑,对吧?两个维度上能够解除它对应的解的,那么这类问题呢,才是解决抛体运动相遇的它的核心啊,两个方向,对吧? 两个方向和两个维度, x y 水平,数值方向和空间和时间的两个维度来进行考虑。 当然了,题目还有很多,我们在这地方呢,没有办法一一例举完了,对吧?没有办法一一例举完了。 那么什么猎人打猴子的问题啊,对吧?或者是等等等等,那么这些问题呢,希望各位啊,在各种资料上自己再去这个什么寻找啊,然后呢,自己去多思考, 那么有什么问题呢?希望大家给我留言,或者是想想听什么样的这个题目的啊?你也可以给我留言。好吧,我们这节课暂时先上到这地方啊,下次再见。
9谱史哥














