所有的函数都是线性的
粉丝1.6万获赞11.2万
相关视频
 01:57查看AI文稿AI文稿
01:57查看AI文稿AI文稿任性得分是什么鬼?财务人、营销人会脱口告诉你,业绩考核用的呀!如果你追问该怎么算,他们可能会烦躁的挠挠日渐稀疏的头发,甩给你一句,没空!还有几个考核没算? 没关系,我这个月的考核算完了,努力用一分钟的时间教会你计算线性得分。上个例子 要根据员工销售目标的完成进度来计算得分。得分规则是这样的,进度大于等于百分之百, 得六分,进度等于八十,得基础分三分。进度在百分之八十到九十九之间,在三分的基础上限行得分。如果进度小于百分之八十,就不得分。 计算线性得分, if 函数是首选,我们开始写公式,等于 if 括号,如果进度大于等于百分之百,得六分线套一个 if。 如果进度大于等于百分之八十,在三分的基础上线性得分。那么我们先写一个三分,三分基础上加完成进度减基础进度百分之八十, 除以基础进度到百分之百之间的差值,也就是百分之二十,再乘以剩下的分值,六分减三分还是三分。如果进度小于百分之八十,就不得分零。 一共出现一个,两个 if, 所以最后是两个括号,也可以直接敲回车,让 excel 自动补全括号,装机填充,全部搞定。你学会了吗?关注我,让你的 excel 飞起来!
1435Excel飞起来 01:37
01:37 01:18
01:18 10:16查看AI文稿AI文稿
10:16查看AI文稿AI文稿当我们有了多元现行回归的目标函数之后,那下面呢,我们来看一下如何把它转换成矩阵或者项链的形态,也就是把这个式子里的一些项,看看能不能把它合并成一个项链或者矩阵,画的一个表现的形态。然后呢,在他的基础上,我们再求解 咱们线性回归模型的一个最优解。然后在这个式子里呢,我们可以看到暂时没有出现一个矩阵或者项链啊,但是我们现在想尝试把几个项呢合并成一个项链或者矩阵的形态, 那为了做到这一点呢,首先咱们来定一下啊,几个项链或者矩阵。首先我们来定一个矩阵叫做 x, 大写 x, 然后呢我们定一个大写的 x 矩阵为如 下的形式, 这里第一行 x 幺幺, x 幺二,一直到 x 弯弯地, 这是咱们第一个样本的特征。然后第二行呢,那就理所当然的可以得到 x 四二幺 x 四二二一,直到 x 二 d, 这是第二个样本,那以此类推, 那最后一个样本我们总共有 n 个样本,所以呢咱们最后一个是 x n 一, x n 二一,直到 x n d。 然后下面我们再定一个变量叫 w, 项链为 w, 那 w 呢?它是个项链, 是包含咱们参数的一个项链,然后参数我们有 w 一到 w d, 因为总共有第一个特征,所以我们把它写一下 w 一 w 二一直到 w d, 所以我们对于这个 w 参数来讲,他总共有第一位, 所以啊,我们可以写成这种形式。然后呢下面其实除了 w 之外呢,我们还有一个参数叫 b, 但是呢我们我们现在想做一个处理,就是我不想把 b 单独拿出来作为一个项链作为一个参数,而是呢希望把这个 b 呢融合到咱们整个的这个项链里面,就是在 w 项链里面呢,把这个 b 也考虑进来,所以呢我们决定在这个项链里面加一个新的项链叫 b, 但是呢为了啊跟他的名字啊稍微有点一致性,所以啊我们把这个 b 呢在这里面写成 w 零的形式, 然后呢我们把参数融合到了这里面,所以我们在 x 这个矩阵里面也需要做类似的操作,那他做什么样的操作呢?我们在 x 这个矩阵的低列全部用一来填满, 所以这这里的一呢其实对应到是咱们这个 b 或者是 w 零,然后下面呢我们试着乘以下 x 和 w, x 矩阵 乘 w 就是他俩乘一下,那我们来看一下他等于多少呢?首先咱们这个矩阵的大小,我们看一下多少, n 乘上低加一, n 乘上低加一,因为总共我们有低列,但是我额外多出了一个,多出了一列,所以呢 n 乘上低加一,然后这个项链我们知道它的大小其实是低加一 乘上一,因为我只有一列,所以这两个呢是我们可以可乘的,因为这尾这个纬度和这个纬度是一致的,所以最后我得出来的 x w 他的大小,其实我们也知道他是 n 乘一的一个大小,这是我们根据矩阵的乘积乘法 啊得到的一个性质,所以他的大小呢是 n 乘一,也就是一个项链,所以他其实就是一个项链, 那到底是什么样的一个项链呢?那我们试着可以通过惩罚的运算来计算一下,那首先我们来看一下这里的第一个项,就是第一行第一列的项, 那这里的第一行第一列怎么得出来的呢?其实就是第一,咱们这个矩阵的第一行,然后他的这一列也就是第一列, 那么把它画一下第一行第一列, 那也就是一乘上 w 零加上 x, 一乘上 w 一 x 一,二乘上 w 二,一直到 x 五万 d 乘上 w d, 那我们把它写写在这里面, 所以一一乘上 w 零,然后一一乘上 w 零,其实就是 w 零 加上 x, 一乘上他 x 幺,二乘上他 x 万 d 乘上 w d, 所以把他们全部加起来啊,那我们可以通过一个加法的这个符号来表示,那 j 等于一到 d, 因为我我要乘第一个枪,需要做一个循环,然后呢我乘的是每个 x y j 乘上他的一个 w 值,所以 w j, 所以这个是咱们的第一项,那类似的我们可以推出来,那最后一项呢,也是 w 零加上 j 等于一 到 d x n j 乘上 w j, 所以从这个结果里面是不是可以可以看到一个有趣的现象,就是这个值,这个值 恰好是不是跟咱们这里的这个指示对等的呢? 就是这个部分和这个部分,你大家可以看一下是不是一个对等的。唯一的不一样点在于 w 变成了 b, 就是 b 变成了 w 零。那这块我们刚才说过,就是我们可以认为这里的 w 零其实就是一个 b, 是一个参数,那剩下的应该是没有变化的。 而且那这个部分其实就是我们通过一个线形模型预测出来这个纸,所以这个部分我们可以把它表 表示为 why why i had, 那 那这个项链其实就是我们的一个预测的项链,所以我们把它表示为 y 一 hat, y r hat, 一直到 y n hat, 所以 x 乘上 w, 最后得出来的是咱们的这个预测的强量。然后我们现在想计算的是 咱们这个预测项链跟我的真实值之间的一个啊误差平方,那这里的下标应该是 y i, 所以这两块我们应该怎么去表示?所以我们已经有了他,所以我们要计算的呢,无非就是他和 真实值 w 一 w 二一直到 wn 的 差异,也就是他减去他的平方,加上他减去他的平方,加上一直加到 yn 减去 yn 的平方。然后我们把这个项链把它表示为 y 的形式,用这个 y 来表示咱们这个响亮,所以我们想要的误差呢?是这样的,误差 l 等于 y 一预测值减去 y 一的平方, 一直加到 yn 预测值减去 yn 的平方,但是我们现在知道 个呢,是通过 x 乘上 w 来表示的,那这个呢,是用通过 y 来表示的,那我们现在想能不能通过这两个来表示咱们这个目标函数?其实可以的,我们可以回想一下, 就是 l two 范数平方的一个概念,那我们是不是可以通过把这个式子可以通过 x w 减去 y 的二范数的平方来表示呢? 因为这两个相减,其实就是这两个相减,就说每一个 y 一,我们可以试着试试着做一下,那 x w 减去 y 等于多少?那他减去 y 呢?等于 y 一预测值减去 y 一, y 二预测值减去 y 二,一直到 y n, 预测值减去 y n, 所以他们的相减就是他。 然后现在呢,为了得到他,其实就是每个平方加一下就行了,那这个呢,其实刚好可以通过 l to 范数的平方来实现,那这个这块如果不清楚,可以啊看一下相关的视频。所以最后呢,我们得到的现行回购的目标函数就是这个, 所以接下来我们需要优化的就是这个值,让这个值最巧化的 w 到底是多少?只要我们把这个 w 求出来,其实等同意我们求解了原来的多元现行回馈目标函数里的 w 和 b, 因为我把 b 融合到了这个 w 里面,所以下面呢,我们想求解 w 就是要针对这个目标函数来去考虑就可以了,让这个目标函数最小化的 w 应该是多少,那这个就是我们的现行回归的它的一个解。
261文哲聊AI 08:02查看AI文稿AI文稿
08:02查看AI文稿AI文稿三角函数从入门到精通,今天胡老师当着大家所有人的面,挑战七天,带大家吃头糖,讲完糖行不行?行,今天咱们先从上帝视角带你们梳理清楚整个三角函数,我们核心要抓哪些重点, 帮你把体系先建立起来, ok 吗? ok, 好, 咱们三角函数注意啊,一共是从三大方向去攻克它, 第一大方向就是我们最近在讲的跟基础概念有关的东西,基础概念是三角函数的地基,是所有你后续学习的基础。那到底抓啥? 第一个叫啥?叫任意角,非常好,弧度制 你得知道呀,从初中到高中,我们的角度的定义发生了改变和拓展,怎么拓展?为什么要拓展?对吧?拓展出来之后出现了什么角?正角、负角和菱角都是怎么被定义的? 包括弧度值,为什么要产生弧度值?怎么快速去计算扇形的面积,扇形的周长,包括这里常见的二级结论, 你只要但凡用点心,这里都能够学的很好,考试不会丢分的。这第一个,第二个关键在于三角函数的定义, 包括三角函数线,三角函数线, 你这里搞不明白你后续要学的一切的公式,就只能死记硬背了,对吧?甚至有的公式你背过了,你不会用,所以这里打好地基是很重要的。 这搞不清楚诱导公式就是死记硬背吗?是不是知道好给诱导公式打下了坚实的基础啊?第一个是概念的方向,第二个九大组必会的公式,一定要 熟练推导,而且要知道他们之间的关系,闭上眼睛咔呲咔呲咔呲都能写出来,每一组公式之间,哎呀,他们之间有什么联系,有什么进阶的关系?你把这些能搞定,你的体系不就出来了吗?是吧? 九大组公式,除了诱导公式之外,除了同角关系之外,剩余的七个 对应到教材里面的什么位置,三角横等变换。我专门要说一下他为什么,因为很多老师是按照教材的顺序去讲的,把这之后了,而有的老师会提前讲他 为什么要提前讲,为我们后面学三角函数其他的图像做铺垫,所以我们在后面给大家讲课的过程中,也会把整个公式全放一个体系里面给你讲透的,你后面学图像问题才能够游刃有余好不好?好好,第三个大的方向, 三大图像写清楚啊,三大图像六个性质,你看我们三角函数都学了啥?就是这些, 包括图像的一些变换,这是你理解三角函数的关键,也是我们考试的重点。 那么每一个图像我们都怎么去研究它的?来把当年研究函数的 那些点在这里重新再研究一遍。我们函数里面当年都研究了什么?想一想,定义域,定义域,值域,再研究一遍,每个图像都这么研究一遍。 第二个叫什么值域?还有什么单调性,基偶性,还有呢?哎呀,这写不下了,怎么办呢?写这 周期性,还有什么对称性,对称性全选一遍,那我这得怎么考呢? 定域考你复合函数,定域的问题,直域怎么考?你注意。哎呀,给你加一个区间, 这都是考试要考的。有区间的指域怎么求?哎,我无区间的指域怎么求?哎,我二次有关的指域怎么求?给你范围,让你去求一些参数方向, 而且考试经常会考大家去大题考大题,考某一问下一个单调性,单调性怎么考?你一模一样的给区间,无区间考二次考,求餐 下一个基友性教材里面我们学到的是哎呀三考三具备基友性的,但是考试考你的是正弦型。 乍一看,哎呦没有什么鸡偶性问题,怎么变成鸡,怎么变成藕?不要死记硬背哦,它的本质是诱导公式,所以我刚才说你前面搞不明白,你往后面去学,你发现学不到根上 还有下一个什么性质?周期性,简单的周期,大家都会带一个公式,关键是你要能拉开差距,考你什么周期?考你一些给绝对值带周期,让你求周期的 还考你什么?考你一些变态的周期问题。那函数你根本就不认识,还考你什么?还考你一些动态周期问题。 求 omega 也是高考考试的重点,连续考了很多年了, 在我们同步当中考大题也考小题,大家不用怕周期,这里我们都有对应的方法和大招,后面都会讲到对称性,简单的让你求对称轴,求对称中心对吧?已知对称轴,求参。已知对称对称中心,求参。我刚说的这些都是基本功, 你要想跟别人拉开差距,那这里就会考到,除了基础的之外,他会结合咱们函数前面讲过的抽象函数的表达式去考你, 所以你前面的基本功如果没有打好,你这里可能有点难度,前面基本功打得好,这里是轻松拿捏的。当然还有最后一个问题,其实专门说一下什么问题?零点问题。 期末考试在大题当中经常和复合函数综合在一块,考你一个最后一道题,那高考当中是以小题为主了。胡老师根据我们历年的考试,把三角函数给大家拆解成了期末必会的, 期末必会的, 从基础概念到整个进阶的综合,从图像变换到每一个性质的考法,手把手带着大家一个一个去攻克这些题型,跟着胡老师学员整个系列,那么三角函数这个模块妥妥充一百三,没有任何问题。 大家可以留三角函数,我把对应的同类型的题目安排给大家拿走打印,跟着老婆的课学起来好不好?好好。
3953老胡模型数学 03:43查看AI文稿AI文稿
03:43查看AI文稿AI文稿哈喽,大家好,我今天给大家讲一下线性回归,用 xl 怎样能做出一个线性回归的函数,我们用这个例子,那我们现在就是看一下就是广告收入和他这个营业输入他们到底之间有什么关系?我们大家就看一下他是成正比,那我们具体的用数据表现出来,首先我们 选择这两页数据,然后我们再找到插入,插入以后我们再找到散点头,我们找到散点头以后,那我们把这些线删掉,让我们头清清晰一些,然后我们这个点,嗯, 我们添加上趋势线,我们就把他的趋势线添加出来了,我们看着趋势线,他是点状的,那我们把它改一下,同学改,把它改成 线型的,实心的,把改成实心的颜色,我们改成深蓝色,好看一些,然后我们再加上他的那什么显示公式,然后再显示 r 平方, x 是我们的广告,应该说是 y, 所以就是说这两类数据做出了回归方程式,也就是 y 等于一七十八点零五 零 t 五点 x, 加上七千九百三十点四,然后 r 二平方, r 平方代表的是呃,百分之九十三点二七的 y 可以被 x 解释,那我们就把点赞先人回购就做出来了, 那我们可以验证一下我们这个方法到底对不对,就可以用 forcass 函数,嗯,对了,我这里说一下,这一百我们代表是广告 x, 那我们用 forcass 函数, 然后我们输入 x 值,这里就代表广告,然后你看他需要第一个是 knowing why, 那就是营业收入,然后还有 knowing x 他的广告, 然后我们就可以看下,在广告投入一百的情况下,他有一一万五千七百三十七的呃营业收入,那我们看一下一百五十,那我们呃就直接复制公式吧。我们要做的就是先把这个 c 四到 c 十五固定一下, 当然你可以直接按住 f 四,因为我现在录屏没办法按 f 四,他是没有作用的,我只能一个一个的美颜符号一个一个打。 ok, 然后我们回车一下,然后我们 ctrl 加 c, 然后我们再 ctrl 加微,我们就看一下,如果广告是一百五,营业收入就是一万九千六百四十一,如果广告是两百,那我们的营业收入是两万三千五百四十五点四, 那我们可以用我们就是我们刚才回顾的方程式来验证一下福克斯的函数,那我们一样的就是七十八点七五,也就是他的斜率乘以一个一百,再加上他的拮据,提前九百三十点三五。 嗯,那我们一样的最好在这里,因为下面还有两个数据吗?那我们需要在这打上美颜符号,方便我们对公式的复制下。广告是一百的情况下,和上面我们用 focars 函数算出来的那个值是一样的,然后我们 ctrl 加 c, 然后我们 ctrl 加微,那我们如果是广告投入是一百五十,那我们的收入是一九六四一点六,和我们 freecast 函数算出来是一样的两百同里。那好了,我们今天就到这里,如果大家有什么问题可以给我留言,然后我会尽量给大家解决的。行,谢谢大家,再见。
445一起学法语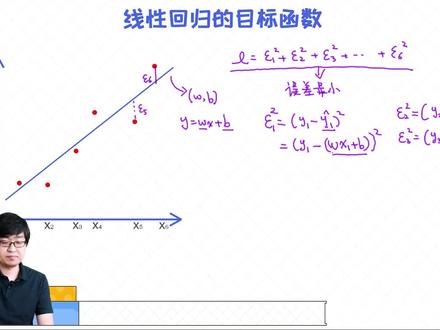 03:34查看AI文稿AI文稿
03:34查看AI文稿AI文稿所以 l 我们怎么表示?可以把它表示为原来是 f 四零一到 f 四六的平方之和,那现在呢,就变成了咱们这些平方之和啊,我们重新做一个整理,那 l 呢,那就 y 一减去 wx, 一减去 b 的平方,加上 y 二减去 wx 减去 b 的平方,然后呢,再加上 y 三减去 wx, 三减去 b 的平方,然后一直加到咱们的第六个样本, y 六减去 w, x 六减去 b 的平方。然后我们把这个式子呢,稍微做一个简化。 那简化的过程,我们可以通过一个符号来表示这个叫散的符号,因为我们这里面是咱们的下标,从一开始二三四一直到六,都是一个循环的方式。所以呢,那这种啊,就是 加法累积累加之和呢,可以把它用这个符号来表示,这个叫累加之和。然后呢,这里的 i 等于一到六,也就是咱们的下标,其实从一开始到六,然后那这个部分呢,可以表示为 y i 减去 w, x i 减去 b 的平方。 当然这个式子呢,也可以把它表示为换一个位置,因为是有平方,所以我们可以把它啊,就是换个位置,就是 wx a 加上 b 减去 y i 的平方,那他俩是相等的, 所以最终我们得到了这个式子,所以 l 等于他,所以误差我们把它表示成了 w 和 b 的一个参数。然后现在接下来我们要做的事情,无非就是我要去最小化误差,也就是我要去最小化咱们这个函数, 那最小化这个函数之后呢,我们当然可以求出其中的 w 和 b 了。然后呢,这里的 l 我们也把它叫做目标函数,其实任何的模型呢,它都具有一个目标函数的, 那目标函数就类似于我们有一个目标,其实我们人生都是有目标的,那有了目标你才有一个行动的动力,而且你沿着这个目标去前进, 那整个模型的训练的过程,无非就是要去帮助咱们的模型达到这个目标。所以这里的啊,这个 l 呢,就大家要记住这个叫目标函数。 然后我们接下来做的事情,无非是让我的目标在这里呢变得越来越小,让他最小的 wb 到底是什么样的?我们要把它求出来,所以这里的 wb 就是我们的参数。然后呢,这里的 l 呢,我们也可以把它表示为 l, wb, 因为我的误差呢,是跟 wb 相关的一个函数,所以我们一般也可以这么写。然后呢, x 等于把它写出来, a 等于一到六, 然后呢 w x i 加 b 减去 y i 的, 所以最终我们得到了啊这样的一个式子。那当然啊,假设我们有十个样本,那这里的六应该把它改造成十,然后假设我们有 n 个样本,那这里的六呢,就把它写成 n 就行了。
191文哲聊AI 02:19查看AI文稿AI文稿
02:19查看AI文稿AI文稿我们来看几个常见的几位函数,那最简单的几位函数呢?我们把它叫做线性的几位函数啊,这个叫 linear activation function, 那线性的接完数呢?我们可以这么理解,刚才说了,接完数我们把它叫做 h, 然后 那这里的线性意味着 h a, 那 a 呢?是咱们基物函数的输入,你可以认为是 productivation 之后的输出,然后它等于我们可以这么定义,就是它等于 a, 所以你可以看到线性的今晚数呢,他等于我们没有做任何的事情,我们只是把信号呢直接传递给下一层了,所以我的 posex 这个操作没有做任何的事情。然后呢, 线性的计划函数,我们可以在这里面画一下,所以这个函数呢,其实你可以理解成就是 y 等于 x, 所以啊,你画完之后其实得到的是这样的一条线,那这里的夹角是四十五度,因为它的斜率是等于一的, 然后这个线条呢,我们把它叫做 h a 等于 a 吧,然后这是 s 轴,是 a, 然后呢这个 y 轴的话就是 h a, 那这样的线型函数,那有什么特点呢?那第一个我们一起来看一下。那第一个特点呢,他是没有边界的,所以在这条线上 他是没有任何的边界,所以我可以取无穷无穷大,所以呢,我们把它叫做 no bond, 他没有边界。 然后第二个特点就是说因为线性线性的计划来说,他其实没有做任何的事情,就是加加不加是无所谓的, 所以只是他把信号就直接给你通过了,对吧?就像一个高速公路一样,我就直接让一个车辆通过,那这个时候呢?其实相当于啊,这个收费站没有做任何的事情,就是直接让所有的车辆通过了。 所以从咱们鸡窝函数的角度来讲,那这种函数呢?啊,其实意义不是特别大,所以我们不是特别的感兴趣。好,那这是线性的鸡窝函数。
86文哲聊AI 07:49查看AI文稿AI文稿
07:49查看AI文稿AI文稿哈喽,大家好,今天继续给大家带来表格自己的分享,我们今天要分享的案例同样来自一位同学在群里面的提问,他说,老师,我有一个数据,想要达到百分之九十九点五以上的可以得到满分,达到百分之九十九的得三分之一的分值, 那么九十九到九十九点五之间是线性得分,九十九以下的是不得分。我们这个满分可以用一来表示,如果对这个表达不是很理解的话,在这里我给大家稍微把关系再梳理了一下, 也就是说这个地方它实际上来讲的话是三块,第一块达到百分之九十九点五的达满分,一分, 在百分之九十九以下的百分之九十九以下的,那么得了什么零分。 那么第三个是什么?是百分之九十九到九十九点五这个区间,他是给一个线性得分。那么看到这里很多人就不太理解了,那么我们首先要搞清楚的是什么是线性得分, 所谓这个线性得分呢?实际线性它是一个数学的概念啊,是我们讲的数学线性方程。呃,线性方程的话呢,是有一个这样一个公式,就是我们讲的 y 等于 k, x 加 b 这个关系, 那么这地方的 k 啊,我们把它是不是叫叫旋律吗?啊?叫旋律,简单的讲呢,就是这么个意思,就是说得分与你实际达成的征服它有一个系数关系,怎么去理解它?好,在这里呢,我继续说一下,也就是说当你达 百分之九十九的时候,他是得了三分之一的分值吗?满分就是一吗?所以呢,我这里给他换算一下,你说当你达到百分之九十九的时候,你的基础分是零点三三分,这没问题啊。好,如果说当你达到了百分之九十九点一,也就你你的这个征服增加了零点一,那么你该得到多少分呢? 这该得多少分呢?好,关键问题在这个地方把这个搞明白了,你这个线性得分这个关系搞明白了,这个题目就不难了。好,在这里吧,我继续说。 因为你的总分是一分,那么你这中间九十九到九十九点五, 总共是有征服,是有五五个征服五段,我们叫五段,那么每一段要增加多少分呢?在这地方注意基础的是零点 三三,你的总分是一,那么你剩下的分值是把一减去零点三三,这里有个叫零点六七,这是你在这个区间 你能够可分配的分数,那每一个征服多少呢?因为我刚说有五五五个征服五段嘛,所以在这个地方,我们把你的这个零点六七除以五,得到一个数字叫零点一三四,这个是你每一个征服你,你得加上这个 分值的啊,他是有这么一个系数的关系。所以呢,这地方我们根据这个线圈方程我们来口头理解一下啊。那也就是说 我零点一一是多少分?增加一个分值多少是把你的基础的零点三三是吧?零点三三任基数加上我增加了多少?增加了一个嘛? 增加增幅是一吗?那么我们是增一是多少?零点一三四吗?数据这个关系,你当你增加了一个年份值就这么多, 那么也就是说当你达到这个比例的时候,你的分数是零点十六分,好,以此类推,那么我们是九十九点二呢,那么这关系什么?这关系嘛?还是你的基数是吧?再加上什么征服二 k, 这个就刚说了,这是斜率啊,就所谓的这个征服乘以你的干嘛? 你这个地方叫零点一三四,是两个零点一三四,哎,这是你的九十九点二分,以此类推。当你后面 不断的增加一个的时候,也就是我们的哪个把这个二变成三,三变成四,是不是所以最后我们会有一个这样的一个分子结果出来,好,这就是我们刚刚讲到了叫线性得分的一个关系, 我把这层关系理解了之后,那么现在回到这个题目上来,好,比方说我这里有有一点 你所考核的分数,那么我如何把这个需求表达出来呢?这位同学,他知道用易辅函数写,那么易辅函数在我们前面的视频我们是讲过很多次的。 好,那么这个题目难就难在我刚讲这个线性得分,他可能不是很好理解,把这个理解了,这个题目就迎刃而解了,该怎么写呢?我们一起来完成一下。等于 if, 当你的这个条件对你考核的得分是什么?是小于 九十九,百分之九十九以下,好,得到什么零分?逗号,没问题啊,中间继续继续判, 如果你是九十九到九十九点五这个区间,所以这个时候要注意了,就是你要大于等于百分之九十九,同时你还要满足小于九十九点五这个区间,那这个时候怎么写呢?这个时候我们需要记住,记住 and 函数 啊, and, and 是逻辑与哦,两个函数同时满足。好,当你的这个得分是大于等于九十九,注意一下,这个九十九 是要包含的啊,包含同时你还是要小于小于九十九点五,注意这个九十九点五不包含,所以我没有等于。 好,这个部分其实代表的就是逻辑与的关系,就说你的考核分是正好是这两个分数之间之间,怎么办?好,就把刚才表达的给写上去是什么?就是 是你的基础分数,对吧?基础是零点三三分吧,加上什么?加上哦,括弧,加上什么?加上 你的考核分,减去基础,基础比例是百分之九十九,对吧?好,乘以 每一段分的系数征服多少?零点一三四吧,乘一点三四。但这次大家注意一下,你这个时候比例减下去之后,他应该是一个比方,这是九十九点一,他算出来时候应该是零点零零一,我们说的这个征服关系,这个斜率的话,他是个学率的话,他是一个征服,是一个整数关系啊。 所以在这个地方大家千万要注意一下,我们应该还要把它乘一个,乘一个一千啊,因为我们是要征服是一二三,他是这样一个关系嘛,所以这个时候要注意 好,到这里为止最后一个是满分了,就大于九十九点五以上了,满分满分之一就可以了。好,这个时候几重判断,一重判断,两重判断。好,那后面有两个跨弧。好,如果没问题,我回车把它放大一点。 好,九十八,小于九十九,得零分往下。九十九点三,九十九点三,九十九点三,是不是零点七三啊?那这是保留,这是保留两位小数,这是保留一位小数,三位小数了啊,好,没有问题,继续, 九十九点六六,按,到底是一分,对不对?没毛病,九十九零点三三啊,好,继续往下。九十九点五应该是什么? 不包含标志一,是不是?好,继续往下拉。没问题啊,这样拉下来之后你会发现,哎,确确实实就达到了我刚才讲的那个效果啊,应该没有问题。 好,所以这个题目实际上来讲的话,他的难点不在于这个义务函数怎么写,而在于我们中间这个线性得分他该怎么去表达。好,实际上他是一个,呃,数学啊,逻辑思维的一个社交,一点数学的知识点在里面。好,是不是很简单呢?不知道你听懂了没有,不过对你有用,记得点个赞哦,谢谢大家。
168DUO.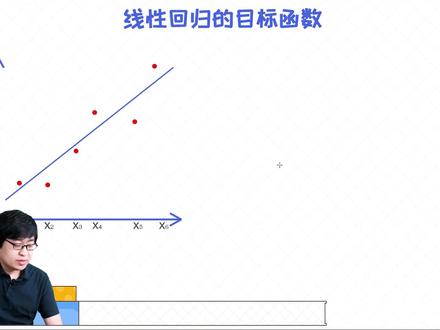 04:20查看AI文稿AI文稿
04:20查看AI文稿AI文稿现在呢,我们已经知道给另一个线条的情况下,我们应该怎么去表示一个误差了,或者怎么去计算这个误差。所以对于这条线以及咱们六六个点来讲,那我们的误差啊,之前也说过,那对这个点来讲,他的误差呢叫 f 四六六, 这个点呢叫 f cloun 五,所以整体的误差我们用 l 来表示,所以 l 呢啊,他是 fcloun 一的平方加上 fcloun 二的平方,加上 fcloun 三的平方,一直加到 fcloun 六的平方。 然后接下来呢,我们来讨论一下,那这样的一条线我们应该怎么去寻找?当然我们可以拧合非常多的线,那我们可以画这样的,也可以画这种,也可以画比如说这种,那在所有的线条当中,我们应该选择什 什么样的一条线?那其实这个问题可能很多人已经有了答案,什么答案呢?就是我们需要寻找的一条线呢?其实可以选择为让误差最小的那条线,行不行是可以的, 所以这个就是我们要寻找最好的那条线的一个依据,就是这条线我们想寻找的一条线呢,就是想让咱们这个误差值 变得最小,就是让他变得最小。误差最小的一条线是我们想寻找的那条线,那咱们怎么去寻找这条线? 其实在高中的数学里面,我们知道一条线在一维的环境下,它是由两个参数来组成的,一个叫 w, 一个 叫 b, 所以啊,这条线的参数有两个,一个叫 w, 一个叫 b, 然后呢一条线呢,我们经常可以把它表示为 y 等于 wx 加上 b 的形式,所以寻找一条线其实等同于我们来寻找两个参数,一个是 w, 一个是咱们这个线条的偏音量叫 b, 那接下来我们用如何去解决啊?这个问题呢?那这里的误差呢?我们已经给出来了,所以我们需要寻找的这条线,就是让这个误差最小的那条线,然后同时呢我们想寻找的就是 w 和 b 这两个参数, 所以我们接下来能做的事情就是说我如何把 w 和 b 跟我的 l 做一个关联,如果想做关联,那核心的问题是我们需要把 f 表示成 w 和 b, 他的一个函数。好,那下面我们来看一下,假设我想表示其中的一个,比如说 f clow one, 那 fcl one 呢?我们也知道 他,或者我们看一下 f 二五万的 f 二一的平方,那 f 二一我们可以把它表示为 y 一,减去 y 一下次的平方,然后这里的 y 是他的一个真实的值,就是我们已经给出来的, 然后这里的 yhit 呢,他是一个预测值,但是我们要知道 yhit 呢,实际上是通过我们这条线来预测出来的, 也就是说当 x 一给定的情况下,而且我知道这条线的啊,这个斜率是 w, 然后呢偏音量是 b, 所以我们可以预测出他的歪址,所以 实际上这里的 w i 就可以把它表示为 wx 一,加上 b, 然后呢最后加一个平方,也就是这里的 w 一的预测值,实际上 就是这个纸,然后这里的 wb, 我们正好是想求出来的那两个参数, 那依次类推那 f 四二的平方,我们也可以把它表示为 y 二,减去 w x 二加 b 的平方, 然后呢 f 四六三的平方也是一样的,那这就 y 三减去 wx 三加上 b 的平方,所以 l 我们怎么表示?可以把它表示为原来是 f 四零一到 f 四六的平方之和,那现在呢?就变成了咱们这些平方之和啊,我们重新做一个整理。
282文哲聊AI 14:46查看AI文稿AI文稿
14:46查看AI文稿AI文稿三角函数和的变换,一个视频全搞定,无论是二位角公式,降米公式,还是两角和差公式,我都给你们整理好了搞笑的口诀,那我们开始上课吧! 我们先来看到第一个提醒哈,两角和差公式非常的简单,一定要熟记我的口诀,对于正弦公式来说,它是非常正义昂然的, 所以说,只要是正号展开,他还是正的,他不改变,我是负号展开我还是负的,我不改变,我不搞那些花架子。而对于他的口诀来说嘞,我们撒野阿尔法加贝塔,记住了,帅哥加哥帅!如果是撒野阿尔法减贝塔,这是帅哥减哥帅。 而对于弦公式来说,他就很多余了,他就非常的邪魅一笑了,所以他的符号展开绝对是不一样的,他就要反着来哈,你是正派,那我就是反派。所以说这里的正号展开是符号,这里的符号展开是正号。所以 cosine arvonne 贝塔,他对应的口诀是 哥哥减嫂嫂,而 cosine alpha 减倍,它对应的是哥哥加嫂嫂。咱们再来看到正接公式,它是不是由正弦和余弦组装得到的,所以说它是一正一斜的,咱们的分子展开来哎,保持符号不变,而咱们的分母展开来,它就要变符号了, 同理,这里是加号,咱们的分子展开也是加号,同理,咱们的分母就是负号的,而此时哈,我们怎么去记公式呢? tangent alpha 减贝塔,咱们的分子是 tangent 减 tangent, 咱们的分布是一加 tangent 乘 tangent, 而咱们 tangent alpha 加倍呢,咱们的分子就是 tangent 加 tangent, 咱们的分母呢,就是一减 tangent 乘 tangent, 我 们就全部记住了哈,大家不要着急记笔记哈,这里的口诀呢,以及后续的口诀题型我都整理好了,大家一定要领取了,之后呢,多复盘几次,点击我的主页这里去撩就可以领取了。 我们来看到第一个题目哈,已知撒眼乘撒眼等于三倍, cosine 乘撒眼则不用看,我们先把左边全部给它展开,撒眼放在这保持不动,这里是撒眼减,所以它变成了帅哥减哥帅,帅的话,这里就是二分之根号三乘哥 杰哥帅,这个样子非常的简单,然后右边来是等于三克,然后再乘上,这里是相加,所以是帅哥加哥帅,帅哥哥的话就是二分之二,三加哥帅,好这个样子的, 我们再继续来跟大家说一下哈,你在做选填的时候呢,一定要记得化简,我们把三以内写成是 s, 把 cosine 写成是 c, 这样你就可以节省很多时间。我们把左边展开哈,就是二分之根号三倍 s c, 再减去二分之一倍 s 方,等于右边的 二分之三倍,根号三的 s c, 再加上二分之三倍的 c 方,哈,就这个样子。然后呢,我们去化解一下,就会得到根号三倍 s c 再加上 c 方,它是等于负二分之一的, 然后此时哈,你看,我们要求的是一个二倍角,所以呢,我们是肯定要把这两个东西给它画成二倍角的。 而咱们 s c 怎么化成二倍呢?是不是我在这乘一个二就可以了呀?乘一个二嘞,它就可以化成咱们的撒眼二 alpha 了,对不对? 而这个 c 方嘞,我们就要用降幂公式了,给它化成是二分之一加科撒眼二 alpha 了哈,所以这里就是二分之一加上二分之科撒眼二 alpha 等于负二分之一的好,我们再去整理一下 二分之根号,三倍三眼二反,再加上二分之一倍科三眼二反等于负一的好。此时我们写成塞科加科塞塞眼课,这是科的话,也就是咱们的六分之一选 a 选项。 我们来看到二倍角公式哈,他是最最最畅考的,没有之一。首先是三眼二反,他没有什么花折,他就等于二倍塞扩 两个帅哥哈。但如果是 cosine 二法,他的花招可多,他花招最多,他有三个花枝,首先呢,是最大的花枝,这 cosine 方减去三眼方,所以他是在沟通什么?沟通一个一次方和咱们的二次方之间的一个非常重要的桥梁。 同时嘞,咱们的 cosine 方和三眼方还可以继续再去写,因为 cosine 方他加三眼方,他是不是等于一的呀? 所以如果说咱们把三衍方写成是一减科三衍方,它就会变成二倍科三衍方减一了。而同理,我们把科三衍方写成是一减三衍方的话,那么它就会变成什么呢?它就会变成一个一减二倍三衍方呢?我建议大家不要直接推哈,直接背 怎么背嘞哈?首先科三衍方减三衍方是非常常背的,而后面这两个东西怎么背嘞?你思考一下, 我们的科三眼和科三眼,它是一个宗族的对不对?那么肯定我在搞平方的时候,肯定是科三眼在前的,而三眼它是不同宗族的,那么我在搞这个展开的时候,它肯定是靠后的, 所以说它们在结构上就有对称性,一个是二倍方减一,一个是一减二倍方,就给大家记住了。我们再来看最后一个 tangent 的 阿尔法,它是更简单的哈, 因为你给它直接拆成是 tangent 的 alpha 加 alpha, 然后呢,咱们的分子还是正好就是 tangent 的 alpha 加 tangent alpha, 一 直二倍 tangent alpha, 而咱们的分母嘞是一减了,减什么呢? tangent 的 alpha 乘 tangent alpha 一 直是 tangent 方二法,就给它记住了。 我们看到这道题哈,已知 cosine theta 等于负五分之三,它又告诉了 c 塔角的范围,一定是为了让你求出来, sine theta 为多少呢?为五分之四,然后呢,它在二分之 pi 到 pi 之间,所以 sine theta 它肯定是大于零的,所以我们求对了,我们再看后一句话, sine 二 sine theta 加四分之 pi 肯定是要给它展开的,对吧? sine 加它展开是什么?帅哥加哥帅,也就是帅 哥加哥帅的这个样子的。所以你看我这儿要求的是什么?求的是一个撒野二 c 塔和一个科撒野二 c 塔, 而撒野二 c 塔它等于多少呢?它是不是等于二倍帅哥的,对吧?也就是等于二乘上负五分之三,乘上一个五分之四的,而这里的科三以二 c 塔嘞,你怎么求啊? 非常的简单,你可以写成是科塞也方减三也方,你也可以写成是二倍科塞也方减一的,也可以写成是一减二倍三也方的哈,给大家求出来。所以最后答案呢,它是等于负五十分之三十一倍根号二的。 我们来看到降倍公式哈,它其实是我们刚才二倍角公式的一个延伸,为什么呢?因为科塞也二法,它是不等于二倍科塞也方减一的, 而它又等于咱们的一减二倍 sine 方阿尔法的。那你来看第一个十字,我如果说把一给它搞过去,则此时来二倍 cosine 方阿尔法,它是不等于 cosine 二阿尔法加一等,而此时 cosine 方阿尔法,它是不就等于二分之一加 cosine 阿尔法了,对吧? 而咱们这一个式子嘞,我们就可以写成是二倍 sine 方二法,它是等于一减 cosine 二法的,而 cosine 方二法,它就等于二分之一减 cosine 二法的。那怎么去记忆嘞?其实非常非常的简单。 怎么做呢?就是你想哈,我的降倍公式是跟我的二倍角公式对应的,那它背后的大 boss 一定是 cosine 二法。先记住了, 然后你再举呗,我一个对称过来是二分之一加,一个对称过来是二分之一减,这里就填上了个大 boss 就 可以了。而谁是加谁是减呢?那加肯定是同宗族的呗。我的 cosine 方二法和 cosine 二法, 我们俩是同宗族的呀,肯定是一加,而咱们的三也和 cosine 它是不对负的,所以它是一减就记住了。我们来看这道题啊, cosine 方,那马上就用咱们的向量公式, 它就会变成什么二分之一加,科撒眼里面这一坨重上一个二,就是二倍的四分之 pi 减 alpha 的。 好,我们给大家展开一下,这是二分之一加,科撒眼里面就是二分之 pi 减 alpha 的。 哎,这个东西是什么呀?由诱导公式哈,它就会变成 sin 阿尔法,就是二分之一加 sin 阿尔法,所以它就等于右边的五分之三的,此时你解出来咱们的 sin 阿尔法来,它就是等于五分之一的 over 了。 我们来看到第四个题型哈,给值求实,很多老师在这里讲的太难了,其实非常的简单哈,只要他给你什么值,你当成整体去做,你就避免了说,哎,我先给他展开,我也给他合起来,你多此一举干什么呢?我不管三七二十一,我就去令这一坨整体为 t 呀, 则此时我的 alpha, 它就等于 t 减六分之八,而题目给的条件,它就变成了三点 t, 它等于三分之根号二的。 那么后面这一坨我要求的 cosine r 减三分之二牌怎么办嘞?我们先把 r 法替换掉,替换成 t 减六分之派,再减去三分之二牌,给它展开,变成 cosine r t 减三分之派, 减三分之二牌,这里就会变成什么减派呀,对吧?我减去一个派了之后,你就会发现,哎,再由右导公式,它是不是变成负 cosine r t 了呀? 然后呢,我们有的是 sine t 等于这么多,那我肯定是由 sine 的 二倍角公式,也就是一减二倍 sine 方 t 呀,所以里边儿就是一减二,乘上三分之二的平方也是九分之二的,所以最后算出来是负九分之五的 over。 我们来看到第五个题型哈,给值求角其实也非常的简单,只是要去判断这个角的范围。已知 cosine alpha 为这么多, gamma alpha 加 beta 为这么多,然后呢? alpha 和 beta 都是在零到二分之派之间求角 beta 的 值,这个应该怎么做嘞?你就直接写成 gamma beta 等于三眼阿尔法加贝塔,你肯定要把题目条件都给用上,对不对?阿尔法加贝塔,我再减去一个阿尔法不就可以了吗?我这里是塞减,那就变成了帅哥减哥帅,也是帅哥 减哥帅。那我们来观察一下啊。哎,这一个是已知的,是十四分之五倍根号三的,而这里科三阿尔法也是已知的,是七分之一的, 而这里来我们是不知道的。而这个三眼阿尔法来,我们是可以求出来的,因为我们的阿尔法是在零到二分之外之间,则此时来三眼阿尔法,它就等于根号下一减科三眼方阿尔法哈算出来嘞,它就是等于 七分之四倍根号三的,算出来了。那我们再来看科三眼阿尔法加贝塔怎么做嘞?有同学说,唐老师直接用根号下一减三眼方阿尔法加贝塔就可以了。 行,宝贝,为什么?因为我们的阿尔法贝塔都是在零到二分之二之间,则阿尔法加贝塔它是在零到派之间的, 则此时我算出来科三也阿尔法加贝塔,它可能是正的,也可能是负的,所以在这还需要去判别它究竟是正是负。哎,那我应该怎么去判别啊?其实非常的简单, 大家看哈,我们的 sine alpha 加 beta, 它是不是等于十四分之五倍根号三等,而咱们的 sine alpha, 它是等于多少嘞?是等于七分之四倍根号三等,其实也就是十四分之八倍根号三等。 你就会发现不对呀,我加上一个角之后,我反而 sine 值变小了, 什么意思呀?什么意思?我们来画一下 sine 的 图哈,然后呢?我们 sine x, 它在零到派上是这样一个图像的,我们可以确定的是,我们的 alpha 角肯定是在这里的, 对不对?然后我们呢,我们的 alpha 加倍,它可能是在对称轴的左边,也可能是在对称轴的右边,如果说它在对称轴的左边,那么 alpha 加倍它在这里,则此时 sine alpha 加倍,它是肯定要大于 sine alpha 的, 因为在对称轴的左边,它是单调递增的,对不对?但 此时出现了大逆转,我们的撒眼阿尔法加贝塔,它是小于撒眼阿尔法的,就说明啊,它其实已经跑到哪里了,跑到这里去了,它甚至比这个对过来还要更小啊, 对吧?所以你就可以说明,咱们的阿尔法加贝塔,它肯定是在二分之派到咱们的派之间的, 那么 cosine 算出来就一定是个不止不扣的负数啊,对吧?所以在这呢,我们就怎么去写,我们就直接写成 cosine alpha 加贝塔,它就应该是等于根号下一减 cosine alpha 加贝塔的平方的,但是外面还要再加一个负号哈,所以你算出来它是等于负十四分之十一的,好,带进去一下哈,最后的答案呢,它就是等于负十四分之十一的, 所以给值求角,它的关键因素在哪里?在你要去确定这个角的范围,我最后算出来到底是正还是负,这个是需要商量的。 那我们最后是不是得到了三倍,它是等于二分之根号三的,又因为 beta 它是在零到二分之派之间,所以 beta 它肯定就等于什么呢?等于三分之派了。 over。 我们来看到辅助角公式哈,这一个函数化成这样一坨东西怎么化嘞?这里有二倍角,这里有一个一倍角,肯定是要把一倍角用降倍公式换成二倍角的。 我们后面这一坨哈写成什么?是不是二分之一加二分之一加什么大 boss, 就是 cos 二 x 的, 对吧?然后呢,我们前面保持不动,后面来写成是一加 cos 二 x 的。 好,这两坨东西我放在一块儿, 也就是根号三倍撒也二 x, 再加上克萨尔 x 加一等。此时我提一个什么出来,提一个根号下这个的平方就是三,这一个一的平方就是一等,所以提的是根号四也是二出来。提一个二出来之后嘞,里面还剩下 三也二 x 乘上二分之,根号三,再加上科三也二 x 乘上二分之一,再加一个一等,所以里边就是塞科加科塞塞克,这里是克,也就是咱们的六分之 pad。 然后呢,再加上一个一,最后呢,就已经写成这样一个形式了,它适用于做大题的时候。 如果你还想查看更多的数学解例程序,以及更多的数学题分方法,一定要点击我们的主页这里群哦。
1106北大糖的魔法数学
猜你喜欢
最新视频
- 5.2万小阿文数学








