三角函数符号判断
三角函数这个个现象中的符号应该怎么去看呢?今天呢我们来给大家讲一讲我们呢图上呢有我们的三扣三,以及我们的添减的一个三角函数,很多老师呢会教你叫做一权杖,二证弦,三证揭,四余弦。那么今天呢,老师教大家一个全新的方法, 一分钟解决了事情,那么我们大家都希望做一个怎么样对社会有用的人才,那么人才的才怎么写呢?我们是一横一竖 一撇好看,这个材质代表的什么呢?一横代表的是我们晒晒,在我们的第一第二线线里面,它为正,一竖呢是代表的抠晒,抠晒呢在第一和第四现象为正,而天甲呢是一和 三摄像,代表积极撇。所以说只要我们对做社会有用的人才,只要记住这个材质,你就可以记住了我们这个图像,关注小青老师了解更多知识。
粉丝5365获赞2.0万
相关视频
 08:55查看AI文稿AI文稿
08:55查看AI文稿AI文稿这节课我们一起来学习三角函数值的符号,首先来看一下正弦与弦正切值,再割相线的符号。 那么我们上节课学习了有关任意角的三角函数的第一,我们先来复习一下他的第一的一个情况,先给出一个直角坐标系,然后呢,给出一个单位元,所谓单位元,也就是他的半径是等于单位长度。现在呢,角二法的中边,他与单位元有一个交点,这是角二法, 他的焦点呢是 p 点。我们给出 p 点的横坐标是 x, 中坐标是外,那么得出减二法的三个三角函数,三应儿法是等于屁点的重坐标外,可三应儿法呢,是等于屁点的横坐标 x 胎记的耳法是等于屁点的重坐标,比上横坐标,因为 x 作为分母,所以 x 不能等于零。那么 现在他的三个三角函数得出来了。我们来看一下正弦与弦正切直在各相线的符号是什么样子呢? 正弦它是与外有关,所以只要在外轴的正半轴,也就是在第一第二象限,那么三应耳法都是大于零的。而在外轴的副半轴呢,第三第四次象限呢?那么三应耳法都是小于零的, 那么我们得出三以耳法,一二象限大于零,三四象限是小于零,外轴正半轴大于零,外轴负半轴呢,是小于零。 好,再来看一下口相印耳法的一个情况,口相印耳法他是与 x 有关,那么在 s 的正半轴,也就是在第一第四象限的时候呢,口相应阿尔法是大于零,而在 s 的负半轴呢,第二第三象限的时候,他是小于零。那么我们得出一和四象线口相应 大于零,二三象限,可三二八是小于零,他们俩就出来了。现在看一下胎记的阿尔法是等于外,比上 x 不能等于零。那么看一下,只要外和 x 他们是同号的时候,同号他们必定大于零,而一号呢,一号就小于零, 同号要么同为正,这里 x 和 y 都为正。而第三项线呢, x 外都为负。 第二象限是 x 为负,外为正。第四象限呢, x 为正,外为负。所以我们得出第一和第三象限,弹吉尔法是大于零。 第二、第一、四象线胎形的耳法是小于零,这是有关正弦与弦正切直在各项线的符号的一个情况。我们得出一个口诀,一、全正。第一象线全是正的。第二将线呢,是正,弦是正的。而 第三象限呢,是正切是正的。第四象限呢,是鱼弦,他是正的。接下来我们做一下例子题,根据中边所在的象限,确定下列三角函数的符号是什么样子,是大于零,小于零,还是其他的情况?现在看第一个胎形的三分之十一派, 三分之十一派,我们先把它画一下,三分之十一派是等于两倍的派,加上三分之五派。这样的情况, 那么因为他是弧度值,所以我们在坐标系里边也把它标成弧度值的情况,这是零弧度,这是二分之派,这是派,这是二分之三派。这边呢是两倍的派,两倍的派加上三分之五派。好, 这里得出两倍的派,还要加上一个三分之五派。三分之五派的话,那么是在第四项线 中边落在了第四象限。第四象限,我们刚才回忆一下,第一象限是全正,第二象限呢,只有正弦是正的。 第三象限呢,只有正切是正的。第四象限呢,只有鱼弦是正的。好,那么这里是第四象限。第四象限的话,他是正切,正切他是负的,所以他是小于零。 第二个,三应负的四分之派,三应负的四分之派。再怎么样来求呢?我们同样来看一下,因为这里是负的,负的我们就顺时针标,刚才是正的,我们就逆时针标好,这里负的话,这里是零 度,因为也是弧度值。这里呢负的二分之派,这里呢是负派,这里呢负的二分之三派,这里负两倍的派。那么顺时针标负的四分之派 是不是也在第四象限?在第四象限的话,来看一下第四象限,这里是正弦,而只有余弦是正的,所以他也是小于零。第三个,胎性的两百五十度和科三应负达三百五十度,他们俩相乘以后是什么样的情况? 因为这里是角度痣,所以我们也标称角度痣,他现在两百五十度。好,我们逆时针标零度,这里呢就用度数来标九十度,一百八十度,两百七十度,这里呢是 三百六十度,两百五十度。在这里的一个情况大概是这里好。第三象限。第三象限,而且是胎记,胎形的阿尔法呢,胎形的两百五十度,他是大于零的,第三象限,他是为正。再来看一下,可算以负 的三百五十度,负的三百五十度,那么我们要顺时标,这里呢,负的九十度,这里呢是负的一百八十度。负的两百七十度,负的三百六十度,好,回到了这里,那么顺时针来标是这样的一个情况,他的中间落在了第一项线,第一项线都是正的, 这里为正,这里为正,正正相乘以后呢,还是正的,所以大于零,这是有关 mist。 接下来我们看一下第二判断,三与一和三与二抬进了三,他的一个正负 一二三都是弧度,不是很好算,我们把它掌握角度。一弧度约是等于五十七度的样子,两弧度呢,约等于一百一十四度,三弧度约等于一百七十一度。那么这三个角我们就比较好找,看一下他们的中边,第一个五十七 七度的中边是在这里,第一象限。第二个呢,一百一十四度,他的中边在第二象限。 第三个一百七十一度,他的中边也在第二象限。第二象限现在一百一十四度,求的是科三一,一百七十一度呢,求的是弹性,弹 好。胎记呢,只有在第三象限和第一象限为正,那么在这里呢,是为负。第二象限可塞印呢,只有在第一象线和第四象限为正。而在第二象线呢,也是为负。塞印呢,在第一象线是为正的,塞印、可塞印以及胎镜的在第一象线都为正, 三个相乘,负负正两个负变成正,那么相乘以后是正的。看下第二个相应儿法是等于五分之三,可相应儿法是等于负的五分之四。这样问, 阿尔法在第几象限?我们来看一下。第一象限是全正,第二象限呢,只有正弦为正。第三象限呢,只有正铅为正。第四象限呢,只有余弦,它是正的。 三应儿法,他是正的,可三意儿法是负的,三意儿法是正,可三意儿法是负,那么他就是第二项。先 第三题,若三角形 abc 的两角满足三 a 和三 a b, 他是小于零的,那么现在问这个三角形是什么样的三角形?我们看一下三角形 abc 随便画的哈。 三角形的内角和他是等于一百八十度,所以不管是 a 还是 b 还是 c, 他们的角度肯定是大于零度,小于一百八十度,那么在大于零度小于一百八十度 之间,三应 a 他都是大于零的。一个大于零的数乘上扣三硬币,他是小于零的,所以说明他是小于零,这样扣三硬币他是小于零。是不是在第二象限的时候,在小于一百八十度,只有在第二象限的时候才会小于零, 将他小于零,所以这个角他就是在这个第二象限,那么他是大于九十度,将大于九十度,那么这个三角形呢?是钝角三角形,这是练习第二。 最后我们做一下小节,这节课呢,我们学习了三亿耳法和三亿耳法以及胎心的耳法,他们的值在各项性的一个正负情况。 先看正弦,正弦在第一象线和第二象线,也就是在外轴的正半轴,他是为正,外轴的负半轴呢,是为负。 而口香印呢?余弦是在 x 轴的正半轴是伪正,而在 x 轴的负半轴为负。 正确,他是当 x 和 y 同号,这是同正的时候和同负的时候,那么他们是为正的。而一号的时候呢?比如说这里 x 小于零, y 大于零,这里是 x 大于零, y 小于零,他们是一号的时候呢,他就是负的。 最后我们得出口诀,第一项线全正,第二项线呢,只有正弦是正的,第三项线呢?只有正切是正的第四项线呢?只有余弦是正的。好,这节课我们就讲到这。
1239滴答课堂 25:54查看AI文稿AI文稿
25:54查看AI文稿AI文稿哥们,诱导公式知道是什么吗?诱惑什么?诱惑公式有多诱惑? 鸡变藕不变,请我炸酱面。行同学再来一年吧。啊,好嘞,讲一下诱导公式,其实这一章呢,你理解之后啊,特别的简单,什么都不需要背,你看我给你出的这些题啊,都这么长,为什么呀?就为了折磨?呃,就为了让你们学会 懂了吧,特别简单是吧,听完这堂课啊,你应该说是都可以会了。来,首先第一句话啊,基变偶不变。 那什么意思呢?什么叫基变不变啊?这个基指的就是基数加上一个字,倍,这个偶呢,指的是什么?哎,对喽,偶数倍。 什么叫基数倍啊?一三五七九,偶数倍呢?二四六十是不是?那是谁的倍数啊?你要记住了,是九十度,或者说什么二分之派的倍数 的几倍。举例子,二百七十度是它的几倍,是三倍,这是不是就叫做基啊? 那如果是派,是他的几倍,注意了,是两倍,这个不要错啊,初学者很容易错,这是偶,哎,老师,为什么?这不是一个派吗?但是说的是二分之派的几倍,这就是第一句话,即变偶不变,你就学完了, 看好啊,我要给你举例子了,就拿第一道题来举啊,这是不是有一个二分之派,这是几倍,这是一倍, 一倍积变。哎,老师,这个变是什么意思啊?就是把 sun 啊变成 cosin, 那 如果原来题里面写的是 cosin 呢,就变成什么 cosin, 这里边你看啊,因为是一倍积变,所以我要把 cosin 变成什么 cosin, 然后干嘛啊?然后直接把 alfa 抄下来 就完事了。哎,你说老师,二分之派呢?二分之派让我用几遍,五遍给弄没了。那你再来啊,看着,我再给你写一个都擦掉啊。 sun 二分之派,剪了发,哎,你说老师毁了,这有个符号啊,没关系,还是第一句话,即便 cosin, 然后呢? g 变, o 变,直接抄啊, cos 阿尔法。注意了,此时这个正符号对于我来说, 干嘛我根本就不看,就是我眼里啊,根本就没有符号,就我就直接抄下来,再来啊,三负二分之派加阿尔法,你说老师毁了,这是负的, 没关系啊,是不是正符号在我眼里根本就没有,是不是一倍啊?积变 直接抄,哎,老师再来一个负二分之派,减 alph 干嘛 cos 啊? alph? 为什么积变, cos 变成 cos, 然后呢?符号根本不看,直接抄下来, 这就叫第一句话,既变偶不变符,呃,就没了啊。但是这个问题出在哪了?你看这四个式子是不是一不一样啊?但是为什么结果一样呢?因为咱们还没有写完,就要说到下一句话了,叫做什么?符号看象限, 符号看象限,这句话是什么意思呢?首先啊,咱们先画一个象限, 第一项线,第二项线,第三项线,第四项线,然后写什么呢? s, c, t, st, c, 这是我惯用的一个写法啊,这个 sin, cos and tan 呢,就是代表这些字母。什么叫 s, c, t 啊?就是第一项线啊,第一项线,这个 sin, cos and tan 呢,都是正的。 第二项线呢,只有什么是正的? sin 是 正的,第三项线呢,只有 tan 呢,是正的。第四项线呢,只有 cos 是 正的。这个东西啊,其实是根据这个 就是三角函数的图像总结出来的,你看看,这是 sin 的 图像,你看零到派是不都是正的呀? 就这么着来的,你呢?我呢?这,这是什么?小孩们还跟我说过什么全是天才。这个也可以啊,也挺好,就是你爱怎么记怎么记,反正我比较喜欢的就是 s c t s t c, 就 用这个字母就都来了, 全是天才是什么意思啊?第一项现在是全就都有,然后是天才,这么着就来了,是天才。那你看着啊, 哎,老师,这句话什么意思?就是符号看相线啊,你说这个我已经懂了,什么叫符号看相线啊?看好了,无论这个阿尔法啊,就是当你在用这个公式的时候,这个阿尔法无论是多少度的角啊,它就是一亿度负一万度,无论你爱多少度多少度啊,一律看作是锐角, 就是一律看作是锐角,只要我用这个公式就给他当做锐角。这时候你就想了啊,二分之派加上一个锐角,也就是说九十度加上一个锐角啊,是第几象限?你说老师,我好像就是说反应不过来了啊,你可以人为的啊,你就让这个阿尔法是多少度啊?一度 或者说十度都行,你不就好算了吗?你想想啊,九十度,假如说啊,九十度加上一个,这个,这个十度是不是一百度呀? 那你想一百度是不是第二象限散第二象限是不是还是正的?就说啊,这个东西它是什么?它是正的,所以说我前面这个符号啊,也得是正的,所以散二分之派加阿尔法就是 cos 阿尔法,懂了吗? 再来啊,再来,哎,你说老师,咱,咱看第二个啊,散二分之派减了法。首先我第一句话啊,咱们刚才用的第一句话叫做即变无穷,写出来了也是 cos 了法。那你看啊, 二分之派减了法,也就九十度,九十度减去一个什么。我说了啊, alfa 都是什么角?都是锐角,那我就让 alfa 多少度,十度行不行?你想想九十度减十度, 八十度第几项线?第一项线三是不是还是正的?所以前面还要加什么号?正号。所以啊,还是什么? cos 阿尔法?看啊,这个是 cos 阿尔法,这个也是什么 cos 阿尔法。再来啊,咱们刚才又说了这个了, 微乱啊,只能说是微乱写在这啊,散负二分之派加 r 法等于什么?积变偶变考散 r 法,我直接抄了。然后呢, r 法多少度啊?十度,这是多少度?负九十度负九十度加十度是多少负八十度负八十度是递减相减 第四象限。第四象限只有谁是正的? cosine 是 正的, cosine 是 正的,那我这 sine 就 应该是什么?就应该是负的。所以啊,注意了啊,原来这个函数是正的,你看啊,原来这个函数是正的,我就要在前面加什么号?正号, 但是加正好就跟没加一样,所以不管了。原来我这个函数是什么号是负的,我就要在前面加什么号?符号,所以你看啊,这个东西的最终结果变成了什么?负 call 三阿尔法,你能不能听懂现在?所以说啊,这个符号看象限看的是什么啊?这个符号看的是什么?是看的,原来这个函数就是原来这个式子正还是负,原来这个式子是正,就比如说这个啊,是正,它前面都是加正号, 如果原来这个式子是负,哎,老师,为什么负啊?因为 sin 负八十度,第一次相切,它是负的,所以我要在前面加什么号?负号。那你再来啊,咱们还有一个是什么?嗯,这呢,哎,不行了,乱的我都不行了,重写啊, 三二分之二减 alpha, 那 这个哦,负,这有个负啊,我给你出了四种情况。那你就想啊, 首先第一步,基变哦不变, cos alpha 直接抄下来的。然后呢, alpha 多少度啊?是十度,这个是多少度?负,九十度,负九十度减十度,是不是负?一百度负一百度,第几项线?第三项线, 第三项线,只有谁是正的?只有 t 是 正的。但是我这道题是不是这是 s 呀?所以说它是负的,所以说前面就要加一个什么号符号,听懂没有? 这就是奇变偶不变符号看象限就学完了,剩下的就是说什么,就是解决这些题, 你说老师我好像没有看太懂啊,那咱们做题来啊,做题 第一题, sin alpha 加上二分之派。首先啊,二分之派是不是 g 啊?直接写 cos alpha, 然后呢, alpha 加上二分之派,第几项线?第二项线,第二项线。原来我这个东西是不是正的呀,所以前面啊,不需要进行任何的变化,加上什么 cos 二分之派,减 alpha, 二分之三派,这是不是积啊?因为是几倍三倍,所以积变偶不变,直接抄啊。 sum alpha, 但是没完呢,积变偶不变,符号看象限,二分之三派减 alpha, 二分之三派是不是在这啊?减一个 alpha 啊,就是减去一个锐角,应该是第几象限?第三象限。 老师,为什么你要转不过来弯啊?你就干嘛二分之三派,二百七十度减去 alpha, 减去一个锐角,也就是减去十度,是吧?二百六十度。那你就想着第几象限?第三象限,第三象限, cosine 是 不是应该是负的?所以我要在前面加一个什么号 符号能跟上吗?所以啊,分子就变成什么了,就变成 cosine 减 sine, 分 母呢? sine 加 alphine, sine 加 alphine 是 什么? pi 是 基变,偶不变,所以就是 sine alphine。 老师,为什么? pi 是 不是偶数是两倍,所以偶不变? sine 还在,还写成 sine alphine, 抄下来 符号看下线 pi 是 多少度? pi 是 一百八十度,加上一个 alpha, 是 不是第三象限?第三象限只有 t 是 正的,所以这个东西是什么?是负的?所以我要在前面加上一个什么号符号,也就是它啊,这个东西变成什么?负的?向量 f。 再然后啊, cosine 负 alpha 等于什么?等于 cosine alpha? 老师,为什么?因为 cosine 图像长这样,它是偶函数,偶函数是什么? f x 等于 f, 负 x, 就 相当于直接把这个符号怎么拿掉, 所以 cosine 负 alpha 就是 cosine alpha。 那 你看啊,分子是 c 减 s, 分 母呢?也是什么? c 减 s。 最后答案 一,就这么着。那第二题,散派减 alpha 即变偶,偶不变散 alpha 符号看下线,派减 alpha, 一 百八十度,减去一个锐角,第几项线?第二项线,所以这个散还是什么正的不用管。下一个 cosine 二派减法怎么办啊?记着啊,只要出现二派,直接删掉 cosine 出现二派 cosine 或者说 sin 呢? 只要出现了二派就能直接删掉。老师,为什么?其实这是因为什么? cosine 和 sin 这个图像呢,都是以二派为最小正周期, 所以呢?加减二派为最小正周期。所以呢, cosine 六派 就是 cosine 零。为什么加减二派都无所谓,我就加减几个二派,三个二派, cosine 七派就等于 cosine 派。为什么呀?因为我减去一个什么六派,加减二派都无所谓。所以啊,你看着这个 cosine 二派, cosine 二 pi 减 alpha 就 等于 cosine 负 alpha 就 还等于什么 cosine alpha。 因为咱们上道题说了啊,是偶函数,所以这个东西啊,就是 cosine alpha 啊,分子写成啊, cosine alpha 前面那个是什么?奇变?偶不变算 alpha, 再看后边啊, cosine 负 alpha 加上二分之三派来 是不是积呀?因为是三倍,所以啊,积变 sum alpha 就 直接抄啊,不用管正负号。然后二分之三派 减去 alpha, 也就是减去一个锐角二百七十度啊,减去一个锐角,你每次转换不过来,你就给它转换成角度二百七十度,减去一个锐角,是不是还是正的还是负的?是不是负的呀? 所以啊,要在前面加个什么号?符号也就这啊, sine alpha, 把符号提前,再然后看分母,分母干嘛积变 sine alpha, 然后二分之派减 alpha 是 第几项线?第一项线,第一项线, cosine 是 不是正的?所以说前面不需要加任何符号, sine 负派减 alpha, 基变偶偶偶不变 sin alpha。 然后呢,符号看象限负派啊,在哪?负派是不是倒着走啊?这是负一百八十度,这是负一百八十度啊, 然后他说什么呢?再减去一个锐角,你比如说减十度,就是负多少度,负一百九十度,一负一百九十度,是不是跑这来了?第二象限,第二象限人家原来是不是就正大,所以不用管。所以这,这还是什么 sin alpha 刚刚刚刚直接消掉了。所以啊,这堆一化简是什么?负的 cosine alpha? 人家问你什么呢? f 三分之派就是 f 六十度啊, cosine 六十度是不是二分之一啊?最后答案负二分之一,就这么着, 能不能听懂?就每道题啊,都这样,你说你把这种就这一大串的题会了再考你什么三二分之三派加 r 法,那多简单呀。那这个呢?接着话讲啊, sin pi 加 alpha, 积变 o 不 变 sin alpha, 但是没完啊。 pi 加 alpha 是 第几象限?哎,我听见你说的了啊,你说第三象限,嗯,第三象限它是不是应该是负的啊?所以要在前面去干嘛?加个符号,然后 cosine 三 pi 加 alpha, 我直接写成什么?我直接写成 cosine pi 加了吧。哎,老师,为什么呀?因为我说了啊,能够加减什么?加减二 pi, 我 这么着写是不是相当于把这个角给它变小了就好算,懂了吗? cosine pi 加了吧,来基变偶偶偶偶不变, 是不是 cosine alph 再然后没完呢啊? cosine pi 加 alph 就是 既变偶不变 cosine alph, 但是没完。符号看象限 pi 加 alph 是 不是还是第三象限?第三象限它是什么?它是不是负的?所以我要在前面干嘛?加个符号? 哦,这儿还是乘法,所以把这儿啊,把这儿删了就得了,也就是负三 alpha 乘以负的 cos alpha, 然后呢? cos alpha 二分之派加 alpha, cos alpha 二分之派加 alpha, 写这儿啊,积变 cos alpha, cosine 二分之派加了法。符号看象限,二分之派加上一个锐角是不是第二象限?第二象限 cosine 是 什么?是负的,所以要在前面加一个什么号符号,也就是负的三 alpha, 这就是分子 符号,看象限啊,要看原来这个函数,就原来这个是正的还是负的,如果是负的,就要给你得出来的这个结果, 加个符号再来这啊,三二分之五派减 alpha, 我 直接写成三二分之派减 alpha, 为什么呀?因为我减去了一个什么二分之四派, 三二分之派减 alpha 来积变 cosine alpha 符号看象限,二分之派减去一个锐角是不是还是第一象限?第一象限它是不是还是正的?所以啊,就直接写 cosine alpha, 然后 散负派减 alpha 积变,偶偶偶偶不变是吧?散 alpha 直接抄,然后呢?负派减 alpha, 没事啊,忘了你就画图。负的一百八十度,我是不是得这么着走,哎,走着走着到这了,负一百八十度,他说减了法减去多少度,减十度,负多少度,负一百九十度,是不是跑这来了?然后怎么记得刚才说过呀, 也就是说第二项线它是不是正的啊,正的就不用管了,就直接把这个化简的结果直接往上抄 sin alpha, 那 你看啊,看着啊,这个哒哒复为正了对不对?然后 sin sin cosine, cosine 消掉了,所以最后答案啊,负的 sin alpha 有 没有学会啊?你看咱们这其实做了一百道题了,是不是继续 一定要学会啊?你学会了,你这种东西你说根本忘不了,你要没学会呢你,你这道题蒙对了,下道题你可能蒙不对了,再来啊,第四题,哎,你说老师我聪明了啊,我直接碰见二排,我直接给删掉行吗?没问题,你删掉之后是不是算负 r 的 话, 这时候就来了啊, sum 负 alpha 等于负的。 sum alpha 为什么?因为因为它是奇函数。咱们刚才说啊, cos 负 alpha 等于什么?等于 cos alpha, 因为它是因为,为什么这么着写?因为它是偶函数。那这个东西呢?它是什么? 奇函数,你也可以怎么记啊?就奇函数,直接把这个符号干嘛?哎,提出来了简单不?奇函数就提符号,偶函数干嘛消符号。 嗯啊,继续给我讲,累了都。这个啊,这是什么?负的? sine f。 然后呢?看啊,该来看这个了, 基变,偶偶偶,怎么着?偶不变,也就是它是变成什么 cosine alpha 先抄下来啊,还没完呢,基变不变符号,看象限派加 alpha。 第几象限,第三象限,第三象限 cosine 是 不是负的,所以要在前面加个什么符号? 我说的有点快啊,再来看这啊,哎。积变,所以是什么? sum alpha 符号,看相线二分之派加 alpha 是 不是第二相线,第二相线 cosine 是 不是应该是负的?注意了啊,看,原来是正的还是负的啊。 cosine 是 负的,所以我要在前面加上什么号,哎,符号, 这个 二分之十一派减 alpha, 我 立马写成,什么 cosine 二分之三派减 alpha。 哎,老师,为什么呀?因为我刨出个什么二分之八派,然后你看这个啊,基,基基是吧?基变三 alpha, 二分之三派减 f。 二是第几象限?二百七十度减去一个锐角,二百七十度减十度,二百六十度二百六十度,第几象?第三象限,第三象限 cosine 是 不是负的?因为第三象限只有 t 是 正的,所以我要在前面是干嘛加个符号。哎呦,怎么这么多呀, 然后呢?看分母啊,这这这个分子刚刚弄完 cosine 派减 alpha, 基变。哦哦哦,不变 cosine alpha, 但是没完啊。派减 alpha 是 不是第二项线?第二项线 cosine 是 不是负的,所以在前面加个什么号符号? 然后这个三三三派减 alpha 怎么办?我直接写成三派减 alpha, 因为我去掉了个什么二派派减 alpha, 积变 o 不 变 没完呢啊?派减 alpha 是 第几项线?第二项线符号开箱线,咱们还得用呢啊,第二项线它是不是正的,所以不用管了,就还是这个结果,就还是这结果啊, 然后这个,哎呀,积变偶 不变 sine alpha 直接超。然后呢?符号看象限啊,负派是不是负一百八十度啊?负一百八十度,再减去一个锐角减十度。负负负负负多少度?负一百九十度,第几象限?第二象限,所以它还是什么 sine alpha? 那这个呢?行啊,我已经看,我已经知道你说出来了。二分之派加 alpha 是 不是基 变 cosine alpha 符号看象限,二分之派加 alpha 是 不是第二象限?第二象限 cosine 本身就是什么正的,所以这儿不用改啊。 cosine alpha, 来吧,这都什么玩意啊,负负负负,是不是这个上面没符号了,然后干嘛? 呃,这个这个,这上边记着啊,上边就没符号了。那我给你写写吧。嗯, s 乘以 c 乘以 s 乘以 s, 下边什么负? c s s c 所以 啊,你看,咱就消了 c c 一 消, s s s s 一 消,所以最后答案啊,是负的贪占特阿尔法,因为 s 除以 c 不是 t 吗?懂了吗?是不是觉得老简单了现在。 然后这个第五题不中了啊,我也要不中了,这个三阿尔法减二零二五派,我立马啊,我立马写上三,阿尔法减,呃,派, 为什么呀?因为我把二零二四个派干嘛给去掉了?就是阿尔法减派, 能懂吗?就是加减三百六十度啊,加减三百六十度都能去,我就相当于加了一个二零二四 pi, 然后这个呢? cosine 写成什么?二分之 pi 减 alpha。 为什么呀?因为我去掉了一个什么二分之八 pi 分母写成什么? cosine 负 alpha。 为什么呢?因为我把二零二四派直接干嘛去掉了。 tanthan, 我 写成什么?写成 tanthan alpha, 哎,老师,这是为什么呀?很简单啊,还是根据周期来决定呢。我刚才说为什么这个加减三百六十度可以呢?因为 sine cosine 的 周期是三百六, 摊着的呢,它是加减派就可以,因为它的周期就是派。注意了啊,摊着的是加减派就可以了,所以我直接就消掉了。那你看啊,咱接着化简。 阿勒法减派即变。哦哦哦,不变算阿勒法,抄下来符号看一下下。阿勒法减派。阿勒法多少度啊?你就当做是锐角是吧。十度十度减一百八十度,是不是负的? 一百七十度啊,第几象限?第三象限,所以是负的啊,所以在前面加一个什么符号?那 cosine 二分之派减的法呢?积便是吧。 cosine 二分之派减的法,第几象限?还是第一象限,所以不用改啊,分子看着啊,分子就变成什么 负的三乘以三分母呢? cosine 负 alph, 哎,你说对了,是不就是 cosine alph, 所以 就 cosine 啊,然后呢?再来这个还是 t t 就 写在这儿, 怎么做怎么接着化简呀。啊,这就简单了啊,看着啊,我直接从这分开。这不就出答案了吗?看着啊, s 除以 c 前面加个符号乘以什么呀? t 分 之 s, s 除以 c。 不是 t 吗?负 t 乘以 t 分 之 s 就 等于负的 三就得了。这就是即变哦。不变啊,符号看象限诱导公式所有的考点了。就是你把这题都学会啊。你这回头看你那卷子上那个单个的那题你卷子上怎么出你单你卷子上也就出个这个。那你是不是都会了?都给我讲冒烟了。
4725单招数学邪修 02:12查看AI文稿AI文稿
02:12查看AI文稿AI文稿这个视频由我来讲讲有角球三角函数符号三引二发等于外比根号 x 方加外方。由于根号 x 方加外方一定是大于零的,那三应奥尔法的正负就和外的正负相同,所以当阿尔法是第一、二相近角时,外大于零, 命的三以奥尔法都是正的。当阿尔法是第三、四象限角时,外小于零,那三以奥尔法也是负的,所以三以奥尔法在各项线的正负是这样的。接着看考三以奥尔法,分母显然大于零,所以考三以奥尔法的正负和 x 是相同的。 当阿尔法在第一、四象限时, x 大于零,对应考塞尔,奥尔法也大于零。当阿尔法在第二、三象限时, x 小于零,对应考塞尔,阿尔法就是负的, 这就是考森林阿尔法在各项线的正负。最后看开这个阿尔法,他的正负和 xy 都有关系。 当阿尔法在第一、三项线时, xy 同正或者同负时,笔直都为正,也就是开进的阿尔法都为正。当阿尔法在第二项线时, xy 一正一负, 第四相见时,也一正一负,笔直都是负的,所以胎记的阿尔法都为负。像这样,只要知道一个角是第几象性角,咱就能判断出这些三角函数值的正负。 比如已知讲阿尔法是第二项线叫,那么三引阿尔法乘靠 ceel, 阿尔法乘。胎记的阿尔法的符号是啥呢?要判断这个算式的符号,咱得分别判断这三个 符号。先看三眼二法,他以二相线为正,三、四相线为负,而二法是第二相线角看第二相线,所以三以二法是正的。再看考三以二法,他一四为正,二三为负, 看第二象限,所以靠三亿阿尔法为负。最后看开俊的阿尔法,他一三为正,二四为负,第二象限也是负的,他们三个相乘,这两负刚好得正,所以整个算式符号为正。
154高中数学小郑老师 07:19查看AI文稿AI文稿
07:19查看AI文稿AI文稿大家好,这个视频我们来讲一下诱导公式,这个诱导公式你如果就要记的话,是需要记九组公式的,很麻烦,所以我们把它化成一句话叫纵变横不变, 符号看象限。当然有些同学学的是什么既变偶变符号看象限一样不没有大的区别,横变纵不变,就是我们等会再去确定那个记几象限的时候,会相对来说会方便一点,本质上没有大的区别。 那这个诱导公式有什么用呢?其实目的就是化解,把负的化成正的,把大的什么化成小的,尽量都把它化到什么一个锐角。这个结论都给大家总结出来,放在这里,那我们去详细来讲解一下这个纵变偶变具体 怎么用。这个纵变偶变里面的纵指的就是外轴的什么轴线角,横指的就是 x 轴的轴线角。符号呢,要去看原来它所在的那个什么,因为变完之后我们把它当做锐角是不是都是正的, 那就看它是不是就没有意义了。再来看这里面会出现加和减,加法呢,就是我们逆时针去转这个角,减法呢就是顺时针走就行了。所以只要你去 明白这一点,我们具体去解析的时候其实也很简单,那具体使用还得看例题,看第九题,阿尔法 bet 的 中间关于外周对称,让我们去求这个值,那好了,你既然给了我这个阿尔法和 bet, 关于外周对称,之前我们学过关于外周对称,这阿尔法和 bet 之间是不是有这样的关系?阿尔法加 bet 是 不是等于二 k 加一倍的什么 pi, 其中这个 k 要属于什么?属于 z, 对 吧?那这就是关于外种,那前面你学的明白了,那后面我们用直接用这个结论就行了。那现在我们来看一下这两个是不是都需要化解?先来看前面这个三是什么二分之五派, 二分之五派我们减去一个 r 法,如何来用诱导公式进行化解?首先看 二分之五派,因为它超过了二派,所以我们交给周期直接给它减一个二派是不是变成二分之一了?它和二分之一派这个是等价的,那二分之一派是不是它属于纵坐标?纵坐标是不是变函数名怎么变?这前面是什么 c, 我 们变考 c, 所以 我们就先给它写成考 c 什么 算法?然后我们再来看一下二分之派减去个算法,他是不要顺时针走,顺时针一走是不是就走到了第一项线?他是正的,所以这个画出来他就是这样的,所以最终的结果就等于什么三分之一,对吧? 然后我们来看我们要求的这个考塞是什么 better, 因为 better 和 alpha 之间有这么一个关系,那我们可以把我们这个就给它换掉,见到见到 beta 我 们可以给它用谁换?用二 k 加一派 减去 alpha, 是 不是给它换掉就可以了?换掉之后呢,我们发现这里出现了这个什么二 k 加一派,所以我们要用诱导公式 对它进行化解,这个就是派的什么基数倍,派的基数倍就落在了 x 轴的什么负半轴, x 轴负半轴,那首先横坐标,横是不变的,所以它就等于 cos 什么 r 法。然后我们再来看 这个负 x, 除了负半轴再减去一个 r 法,是不是顺时针走?这么一走是不是就走到第二项形了?第二项形的原来是余弦值,所以是负的,这里我们添上符号是不是?行,那到这一步之后,你看一下负的 cosine r 法,而 cosine r 法 我们前面是不是已经求出来了?所以它就等于负的什么三分之一,最最终的结果就选 b 选项 好了。接下来咱们来看第十题角。 abc 是 三角形的内角,那内角的话,这肯定要用到我们之前学的这个结论,就是三角形的内角和是不是等于一百八,那高中现在我们把它转化成弧度值,那也就说 a 加上 b 加上 c, 是 不就等于什么 pi 是 吧?那现在看这些选项里面有 a 加 b 有 c, 对 吧?当然还有 b 加 c, 这里我们可能要对它进行什么变形,那比如说,那你要 a 加 b, 那 a 加 b, 它和 c 有 什么关系?不就等于 pi 减去 c 嘛?那以此类推,你这 b 加上 c 是 不是就等于什么派减去 a, 对 吧?那现在我们来看一下,根据这个我们来一个选项一个选项来进行化解。那考塞括号谁 a 加上 b, 是不是见到它用什么派减 c 换它就等于派减 c 对 不对?好了,派减 c, 我 们来看一下如何用诱导公式来进行化解。派是不是 x 轴的负半轴,那是不是横不变,那它就不变函数名,所以先写成 cosine, 谁 考点 c, 然后再来看派减去了 c, 对 吧?减就顺时针走,顺时针一走,这个是不是走到第二项线?第二项线看原来的余弦是不是负的,那这里是不要添一个符号,它是不是等于负的 考点 c, 所以 a 选项是不是就不对?然后我们再看 b 选项, b 选项是 c, 谁括号 a 加上什么 b, 它就等于 c 括号 pi 减 c, 对 吧?也是一样,看 x 轴的什么负半轴横不变,你就先写成 sin c, 对 吧?然后再来看这个 pi 减 c, 是 不是刚才说了,我们减就顺时针走,就走到了第二项弦,正弦是不是正的,所以它就等于 sin c, 所以 b 选项 也不对。那 c 选项和 d 选项这个你看一下, c 选项只是二分之 a, 其他的是不是都是什么一倍的?那 d 选项这个呢?相对来说会比 c 选项容易化解,我们先从 d 选项入手,那我们先来看一下这个 c 什么括号二分之 b 加 c, 它等于什么来是一样,见到 b 加 c, 我 们可以用派减 a 给它换掉,对吧?那换一下,那这是不是就是 c 括号二分之谁派 减去 a, 对 吧?减去它之后,我们再给它化解一下,它就得到了 c 括号二分之派,减去一个二分之 a, 是 吧?到了这步之后,我们来看出现了二分之派 y 轴的什么正半轴,那纵是不要变函数名,那首先变函数名,把 sin 变,是不是考 sin, 所以 它就等于考 sin 二分之 a, 再来看 二分之派减了二分之 a, 外轴的正半轴顺时针走,是不是走到了第一象限?那第一象限的正弦是正的,所以这里 不变号,所以最终它的结果就是 cosine 二分之 a, 那 这个结果是不是就是正确的选项?至于说 c 选项,因为这个我们一个是二分之一倍的 a, 其他的都是一倍的,这个我们就不去化解它了。
122数学何思维 16:01查看AI文稿AI文稿
16:01查看AI文稿AI文稿鸡变偶不变,符号看象限!这句话听了无数遍,到底是什么意思?怎么运用?快叫上学习达子!十六分钟跟着小树一起拆解口诀,核心,吃透诱导公式,掌握使用方法,实战三类高频体型,全程无废话,帮你彻底搞懂诱导公式! 欢迎来到小树老师的数学课堂,接下来我们将会用十五分钟时间带着大家快速记住所有诱导公式,并熟练掌握诱导公式的使用技巧。首先我们先来看一下第一组公式啊,我们要记住第一组公式的话,我们要先记住一句话,就是任意角 加上或者是减去二 k 的 整数倍,它的三角函数值是不变的,所以说我们这个 r 法加二 k 的 正弦值呢,它就等于我们的散引 r 法。我们的这个 r 加二 k 的 余弦值呢,它就等于我们的 r 法。这期函数比较特殊啊,因为它的周期是派,等我们后面讲函数图像的时候你就知道了,就是它的 r 法加 k 的 函数值呢,它就等于我们的它的 r 法。那么大家可能就会有一个问题说,老师,那我知道这个公式有什么用呢?我先问大家一个问题啊,请问三三分之派等多少?大家是不是都知道它等于二分之根号三,没问题吧?好,问题来了,请问在三 三分之十九派等于多少,你会发现你不知道了吧,为什么呀?因为三分之十九派特别大,那么有没有什么样的方式可以把它变小呢?哎,有,第一组一个公式就这个作用,我们可以把一个特别大的角通过加减二派的整数倍把它变小,它就等于多少呢?它就等于我们的塞三分之十九派,怎么样?你 直接给他减去一个三分之十八派。为什么是三分之十八派?因为三分之十八派它等于多少?它等于六派呀, 等于我们的二派的三倍,是不是相当于是我们二派的整数倍三角函数值怎么样不变,它就等于我们的在三分之派,等于我们的二分之根号三。所以你会发现诱导公式是不是很好使?接下来我们来看一下诱导公式的第二组公式。同样你要记住第二组公式的话,你要先记住一句话,就是正弦是奇函数,余弦是 偶函数。这个地方呢,有一个记忆的方法叫做震机,大家都去过牙科医院吧,在牙科医院当中呢,有一个学术名词叫震机,所说震弦是基函数,余弦是偶函数,它是基函数的话,那它是不是就满足我们基函数的定义? f 负 x 等于什么呀?等于我们的负的 f x, 所以 说我们就可以知道哦。 find 负 r 等于多少?等于我们的负的 find r 法。而由于我们的这个余弦是偶函数,所以说 cosine 负 r 等于多少,它就等于我们的 cosine r 法。同样的给大家举个例子啊, find 三分之派,你刚是不是讲到过等于多少?等于二分之三,对吗? 那么请问 find 负三分之派等于多少呢?根据我们刚刚所讲的的诱导公式,它是这样数,我们可以把这个符号怎么样放在外面,它就等于负的 find 三分之派就等于多少?就等于 我们的负的二分之二三,这就是我们诱导公式的前两组公式。紧接着我们来看一下诱导公式的剩下两组公式啊,这两组公式呢,看似特别繁杂,但是实际上我们只需要记住其中的两个,就能够记住剩下所有的公式。我们先来看一下第三组公式,我们只需要记住这个三元派减 r 发的结果是多少,那么剩下的三个呢,就可以根据它内在的规律全部都给记下来。 记住这个第一个公式呢,大家需要先记住一句话,就是互补的两个角,它的正弦值是相等的,什么样的两个角是互补的,其实就加起来等于派呗,那就是我们的派减 r 法与我们的这个 r 法,所以说散引派减 r 法就等于什么?它就等于我们的散引 r 法。那么为什么说我们记住这第一个公式,下面的三个公式你就都知道了,因为只有第一个公式, 他前面的符号以及后面的三角函数名呗。那么你就记住 只有 sin 派减,而法化减之后的结果是正的,剩下的下面三个全部都是负的,这样符号你是不是就不会搞混了?然后大家在自己看这个辅导书的时候,有没有听过一句话叫积变偶不变呢?那这个积和偶指的是什么东西呢?它其实指的是前面的这个派,和 这个派有什么关系呢?你会发现这个派呢,它可以写成是二分之派,乘上一个二,这个二是个什么数啊?是个偶数,这个偶指的是我们刚刚公式里面的那个偶变的,那个偶不变指的是三角函数名不变。如果说前面是正弦, 后面就是正弦,前面是余弦,后面就是余弦。所以由此你可以把下面三个的三角函数都可以写出来。前面是正弦的吧,那第二个空呢,就等于散减而法, 而最后两个呢,自然就是我们的过散而法。所以说是不是就是我刚给大家讲到的,你只需要记住,散减派减而法等于正的散减而法。后面的三个公式是不是都知道了? 因为只有第一个是正号,后面三个呢,都是负号。同样的方法,我们可以用来记忆第四组公式,因为只有第一个扩散二分之派加尔法,它的符号是负的,剩下的三个呢,都是正的。所以你是不是只需要记住第一个公式就好了? 然后回到我们刚刚那个口诀,积变偶不变。我们刚刚是不是讲到过,你看前面的这个二分之派,它可以写成什么呀?它可以写成我们的二分之派乘一啊。这个一是个什么数?是一个基数,这个基对应的就是我们的基变, 比如他的三角函数名会发生变化,如果前面是余弦的话,那后面就是正弦。同样的道理,如果前面是正弦呢?后面就是余弦。所以说整个的这八个公式,我们是不是只需要记住前面这两个公式就好了?接下来呢,我们就带着大家去证明一下 四组的第一个公式,要证明这个扩散二分之二加 r 等于负的散元 r 的 话,本质上其实还是要借助我们在上一个视频给大家讲到的三角函数定义来 证明我们的三角函数是在一个单位里面定义的。我们说如果说这个角 r 的 中边,我们 单元相交了,假如说交于 p 点,这个 p 点坐标呢,我们可以写为 x y, 我 们过这个 p 点呢,做一个垂线下来,假如说这个垂足呢,是 p 一 撇,那我们就可以知道怎么样。哎,我们的萨因阿尔法,它其实对应的就是我们的纵坐标 y, 而我们的扩散阿尔法呢,它对应的就是我们的横坐标 x, 而我们的 tangent 阿尔法呢,它就等于我们的 y b x 吧。这是我们在上一个视频上面是不是讲到过的,如果说有同学不知道的话,我建议你去看一下我们的上一个视频, 三角函数定义的解释都讲的非常清楚,那么我们这个时候接下来就需要思考另外一个问题了,就是请问这个二分之派加而法与这个而法是什么关系?我们是不是讲到过逆时针旋转是正角加了一个二分之派,相当于这个中边怎么样?逆时针旋转了二分之派个单位就是多少单位, 九十多个单位,那我们给他画一下这个图像,把它中边怎么样旋转了,我们的九十度就是二分之派加而法的中边与我们的单位原交于 q 点,我们 同样的道理过 q 点呢,做一个 x 轴垂线,假如说垂轴是 q 一 撇,你会发现一个特有意思的事情,是什么呢?就是这个红色的三角形和这个绿色的三角形是怎么样? 是全等的,因为它们角度一样怎么样边长也是一样长的,所以说这两个三角形怎么样全等,那么全等有什么好处呢?就是对应边是一样的,我说长度是一样长,但是你会发现怎么样 q 点的横坐标应该是负的吧,就这个 q 点的横坐标是多少? 是负外啊,要注意符号,那么纵坐标呢,自然就是 x, 所以 我们可以把这个 q 点的坐标给它怎么样写出来?横坐标是负外,纵坐标是 x。 根据我们的三角函数定义,我们就可以知道扩散这个二分之派加 r 法怎么样,它就等于我们的负外啊, 横坐标嘛,它就等于我们的负的,在 r 法就证明完了。同样的道理,大家也可以用这个方法呢去证明我们其他的所有的诱导公式,感兴趣的同学呢,可以把你的证明过程发在你评论区,我可以帮你看一看。讲完了诱导公式的记忆和证明方法之后呢,接下来我们要给大家讲一讲诱导公式的三种 成考题型。先看第一种题型,就是利用诱导公式求值。这几道题呢,我建议大家可以先暂停,自己做一做,然后再来听我讲。首先我们先来看一下第一道题啊,我们要求这个三分之二零二四派的正弦值, 会发现这个三分之二零二四派怎么样,是不是特大呀?特别大的角,咱们是不是并不在我们的所要去背的那个三角函数表里头,所以我们就要想一个办法把它变小一些,有没有什么样的方式可以把它变小?有的就是刚刚讲的第一组公式,任何一个角加上或者是减去二派的 整数倍的三角函数值是不变的,所以它就怎么样,它就等于我们的 side, 三分之二零二四派减去一个三分之二零二二派,那么大家可能就会问了说,老师,为什么是三分之二零二二派啊?这个三分之二零二二派到底是怎么来的?很简单,因为三分之二零二二派 等于什么呀?它等于六百七十四 pi 呀?它是不是等于三百三十七?乘上一个二 pi 是 不是我们的二 pi 的 整数倍?我们刚是讲到过,加上或者是减去二 pi 的 整数倍,它的三角函数值不变的,所以它就直接等于我们的 side 三分之二 pi。 我 们之前是不是给大家讲过零到 pi 的 三角函数值, side 三分之二 pi 等多少? 二分之高三直接就能出结果了。同样的道理,我们来看一下第二个,他不是让你求这个扩散负的三分之十派吗?三分之十派怎么样?挺大的,我们就要想办法给他变小一些,能给他变小,我们只需要给他加上一个多少来着三分之十二派就好了。 为什么是加上一个三分之十二派呢?因为这是距离他最近的二派的整数倍四派吗?是不是它就等于多少?它就等于我们的扩散三分之二派就等于多少呢? 等于我们的负的二分之一。可能会有同学说,老师呢,我要是记不住扩散三分之二败怎么办?那就建议大家看一下我们的上一个视频。我们在上一个视频里面其实是给大家详细的去讲了一下怎么去快速记住我们的三角函数,而第三题和第四题呢,我们就给他留置练习, 大家可以把你们的答案发在评论区,帮大家看一下你是否做正确了。讲完了诱导公式的第一种题型之后呢?接下来我们给大家去讲诱导公式的第二种常用考法,就是利用诱导公式来进行化解。下面这道题好像看起来特别复杂,就是一大堆乱七八糟的公式堆在了一起, 实际上你把每一个公式呢单独分开来看的话,它就没有那么复杂了。我们先来看第一个式子,扩散二分之七派减 r 法。这个二分之七派减 r 法呢?你是没法直接用我们刚刚所讲的公式化简的吧。为什么呀?因为二分之七派太大了, 那你就要想有没有哪个公式可以把一个比较大的角变小。刚刚是不是讲过了?可以啊,任何一个角加上或者是减去二派的整数倍,它的三角函数值是不是不变?因为这样的原理的话,我们就可以怎么样直接给他减去一个二分之几派。二分之八派吗? 这个地方减去的是二分之八派,不是二分之六派。为什么呀?因为二分之八派等于四派啊,四派是二派的整数倍吧,它的值是不变的,所以它就等于我们 一开始的二分之七派减二派的余弦值。你进一步,它就等于我们的扩散负 r 法。减去二分之派。我们是不是讲到过余弦是什么函数?余弦是偶函数啊,所以它就等于我们的扩散二分之派 加 r 法。因为是不是说到过只有它是 负的?紧接着我们再来看一下第二个式子,就是贪念的阿尔法,加上一个派,它就等于多少?它就等于我们的贪念的阿尔法。为什么呀?因为我们讲到过正切比较特殊啊,正切的周期是派,所以说贪念的阿尔法加派呢?它就等于贪念的阿尔法。我们在后面给大家讲正切函数图像的时候,你会发现也能够再次去强化这个概念,就是正切函数的 周期就是派。我们再来看一下第三个式子,就是这个扩散二派减阿尔法这个二派吧。我们是不是一直在 重复一句话,就是任何一个角加上或者是减去二派的整数倍,它的三角函数值是不变的,就是我们可以直接减掉一个二派,它就等于多少呢?它就等于我们的扩散负。而法。我们又说到过余弦是个什么函数,一个偶函数符号可以怎么样?直接扔掉它就等于我们的扩 散而法。这样子的话,我们是不是把我们的分子都化简完了呀?我们再来看一下分母啊,就是这个扩散而法呢,加上这个二分之五派,这个二分之五派是不是同样的有点大? 我们把它变小,减去一个二派的整数倍就好了,所以说它就等于扩散 r 加上二分之五派,减去多少?减去二分之四派就好了,因为二分之四派就是我们的二派呀,它就等于我们的扩散二分之派加上 r 法等 于多少?它是不是就等于我们的负的三眼 r 法,最后呢,是不是还剩下了一个三眼?二分之三派加 r 法,同样的道理我们可以怎么处理?我们可以给它减去一个二分之四派呢?因为二分之三派有点大, 等于多少呢?它就等于 sine 哎, r 减去一个二分之 pi 就 等于多少呢?就等于我们的负的 sine 二、分之 pi 减 r。 为什么要提个负号出去?因为我们讲到过正弦是一个奇函数,我们有符号呢,要把负号提到外面去,它就等于多少呢?它就等于负的 cosine r。 这样子的话,我们是不是把分母的式子呢都给它写完了,那么由此我们就可以得到我们的 原式,它就等于什么呢?你分子分母分开给它带进去啊,那就是我们的负的散减 r 法,乘上一个贪婪的 r 法,这个地方一定要仔细点,别写错了啊,再乘上一个扩散 r 法,因为咱们刚刚不是化简完了吗?你看这是负的散减 r 法吧,这是贪婪的 r 法。这个地方是不是我们的扩散 r 法我们都给它带进去了吧,而分母 去看一下,别忘了人家这个地方还有个平方啊,那所以它就等于什么呢?负的 sine alpha 的 平方再乘上一个多少呢?乘上一个负的扩散 alpha。 我 们都知道这个正切等于正弦,比于弦嘛,所以我们会发现它约分约掉了之后呢,就等于一个扩散 alpha 呢?分 之一这地方他是不是告诉你 r 的 取值呢?六分之派,所以他就等于多少呢?我们的扩散六分之派分之一。扩散六分之派等于多少?等于二分之根号三。那最终结果呢?就等于我们的二分之根号三分之一,就等于我们的三分之二倍根号三。最后呢,我们来给大家讲一讲,在诱导公式这个板块当中,确儿八十对于大家来说有一定难度体现 是构造法的应用,为什么说这种题型对于大家来说有一定难度呢,因为你会发现我们之前所讲到那种利用六道公式直接化简的方法呢,在这道题当中不太现实了,为什么?因为你会发现这些角度呢?都是三分之派、六分之派和三分之二派,它并不是我们刚 公式当中所讲到的二分之派呀,二派呀,派呀这种非常规整的公式里面现成的角度,对吧?那在这种情况下我们应该怎么办呢?大家记住了啊,以后遇到类似于这样的题型的时候,一定要去思考一下,就是这些角它相互之间有没有可能存在一些什么样的内在关系?什么意思? 比如大家来看一下,你看这个第一个角是多少?是我们的三分之派加 x, 也说这两个角虽然说不是标准意义上的诱导公式,但是你会发现他们俩怎么样 加起来等于二分之派。你观察一下,这个三分之派减 x, 加上一个我们的这个六分之派加 x, 它是不等于二分之派啊,这不就和我们的一个公式能够关联上了吗?而你再看一下,我们的这个三分之派减 x 和我们的什么呀?和我们的这个三分之二派加 x, 它能怎么样?所以说这个三分之派减 x 和我们的这个三分之二派加 x, 它也是有关系的,加起来等于派呗。那么由此我们就可以借助他们整体上所存在的一些关系去使用我们的导公式。为了简洁一点呢,我们把这个式子呢给大家化简一下,我们另前面这个角呢为 r 法哎, 这个角呢为 beta, 这个角呢为伽玛哎,你就会发现,怎么样你会发现这个阿尔法加上这个 beta 是 不是等于二分之派?这没问题吧?刚刚是不是写过了紫色的笔记?而这个阿尔法加上这个伽玛呢?是不是等于派?有了这样的一个准备工作之后呢?我们就可以把这道题简化一下,可以简化成什么呢? 它可以简化为已知向量阿尔法等于三分之派,阿尔法加上这个伽玛呢?等于我们的派,然后让求什么呢? 求这个 sine beta 减去一个 cosine gamma。 你 这样处理之后之后呢,你会发现这个题就没有那么复杂了吧,因为这个 alpha 加 beta 等于二分之派,所以这个 beta 等于多少?它就等于二分之派减去 alpha 吧。那则我们的这个 sine beta 呢?它是不是就等于 sine 二分之派 减 alpha, 这不就是我们的诱导公式吗?它就等于我们的 cosine alpha 没问题吧?而我们的这个 gamma 呢,它是不是等于我们的 pi 减去 alpha, 则我们的这个扩散伽马,它就等于扩散派减阿尔法就等于多少?就等于我们的负的扩散阿尔法。所以你必须要对诱导公式的最基础公式呢足够的熟悉,所以原式就等于多少?它其实求的就是扩散阿尔法减去一个负的扩散阿尔法,它的值让,其实就是让,求什么呢?急求我们的二倍扩散阿尔法的值呗。 怎么去求这个扩散算法的值呢?你会发现他是不是前面告诉了你,这个散样法等于三分之六啊?我们都知道有一个公式叫做同角关系呗,那就是散方 r 法加上一个扩散方 r 法 是不是等于一啊?你要带进去之后呢,就可以得到这个扩散方 r 法呢,等于多少?等于三分之一?那么问题来了,扩散 r 法等于三分之一,请问他开放之后应该是取正数呢还是取负数 地方?大家要注意点细节,因为它告诉你这个 x 的 范围是零到二分之派吧,在第一项线对吗?那么我们的这个三分之派减 x, 因为它的正弦值等于三分之二六大于零,所以说三分之派减 x 是 不是也在第一项弦? r 方是第一项弦角, 它的正弦和余弦都是正数,所以说由此呢,我们就可以知道这个扩散 r 法它是大于零的,那么则我们的这个扩散 r 法呢,就等于我们的正的 三分之根号三, ok 吗?就是最终这个结果等于多少?等于二,乘上一个三分之二倍根号三就做完了。那么这个第二题呢,我们就给大家留声,课后练习,大家可以在你的聊天框里面发出你的答案,我来帮你看一看 你是否真正掌握了这种解题技巧。以上呢,就是我们关于各道公式的三种常考题型,希望对于大家的学习会有帮助。下一期我们将会带大家去了解三角函数的基本抽象性质,关注我带你掌握更多的数学知识。
5622秒杀小数 17:46查看AI文稿AI文稿
17:46查看AI文稿AI文稿三角函数的图像性质和我们后期各种含有正余切的不等式复合函数、最值求导以及圆锥曲线章节都有着十分紧密的联系,所以基础图像内容的掌握就显得尤为重要。 首先,我们看这样一个大波浪一样的玩意儿,它叫做正弦函数 y 等于 sine x。 而除此之外,这样的一个外形好像也是一模一样的波浪的一样的玩意叫做余弦函数 y 等于 cosine x。 当然,还有一个长得比较奇特的是正切函数呃,先选哪个?好嘞, 这两玩意长得像,我们就先研究他们俩。哎,我发现呀,这波浪虽然看着吓人, 但是他根本上却是这种小的半壶一个一个重复拼接而成的,那我是不是只要把这一个小半壶研究明白了,每一部分也就都清楚了呀? 好,既然他的表达是是 y 等于塞眼 x, 那 么图像上任取一个点 p, 横坐标为 x, 纵坐标便是赛隐 x。 可是问题来了,他的图像为什么会呈现这样一个像对称的弧形一样的玩意呢?这里就不得不搬出我们的常驻嘉宾单位员来了。 在此之前,聪明的你已经了解到,对于一个大小为 x 的 角度,它的中边与单位圆的交点 q, 它的纵坐标就是 x 的 正弦值。 而当我们把视线转向右边的途中,横坐标为 x, 对 应这样的长度纵坐标,也就是 sine x 正弦值, 他们俩之间会不会有啥特别的关系啊?看左边,对于锐角 x, 随着 x 的 增大,点 q 在 上升,那么他的纵坐标正弦值也在变大。 看右边的图,在弧形的前半段,随着横坐标 x 的 不断增大,纵坐标 sin x 也在变大, 这两个 x 的 大小是一模一样的,只是说呢,一个作为角度,一个作为长度存在,而 x 一 样了, p、 q 两点的正坐标 sin x 也就一样了,可以用一条线进行贯穿。 比如,咱们先研究 x 属于零到二分之派的开区间大于零小于九十度的情况, 也就是左边图中点 q 只在第一象限上升的情况。好的,让 x 的 值无限趋近于零作为起点,随着 x 的 增大, p q 两点都在上升,可是他俩会一直这样上升吗? 没错,并不会的,因为马上随 x 逐渐靠近二分之派,也就是九十度这个点, q 便会到达圆的最高点,那么相应的,右边图中的 p 点自然也到达了最高峰。 那么这个高度是多少呀?没错,正是单位圆的半径大小等于一,此时的 x 等于二分之派,也就是九十度。 那么右边的 x 也是二分之派,正好是这样一段红色实线的长度,正好是波峰的横坐标。 好的,再接下来,随着自变量 x 的 继续增大,为什么图像开始递减了呢?我们还是两个图像一起来看。 随着 x 的 继续增大, q 点开始沿着圆下滑,和 q 点等高的 p 点呢,也开始下滑,一直下滑。下滑?滑到哪呢? 一直滑到 q 点的纵坐标为零了,此时的 x 恰好是一个平角半圆。咱们说一派一半圆, x 刚好等于一个派, 右边的 x 对 应红色实线,他也等于派一个派的横向跨度刚好对应一个半弧。不过嘞,这好像还没完, 当 x 大 于派之后,还有图像,并且是这样一个完全复制翻折过来的半弧,我们还是可以两个图像一起来看。 单位圆上的点 q 它还在继续下降,那么右图中的 p 点它也会同步下滑,但啥时候是个头呀?是的,当 q 点触碰到单位圆最低点的时候,右边图中的 p 点也会到达。拨鼓, 此时的 x 等于二分之三派,对应拨鼓的横坐标。最后图像又是怎么递增回去的呢?相信你一定想到了 此时的 x 等于二派一个完整的圆。到这里,我们便推出了无尽重复的正弦函数中的一个完整的周期, 其他部分就是不断的复制粘贴,首尾相接,这样便可以得到一个完整的正弦函数 y 等于 sin x 的 图像。 并且呀,图像一直都被前置在外等于一和外等于负一两条直线之间,当然可以取到边界点。我们把视角放大了看, 一正一负两个半弧相邻拼在一起,就是一个完整的周期,也就是最小正周期。一个半弧是一个派,那么一个最小正周期呢,便是两个派了。 好的,再说这个函数,它有对称轴吗?图像是无穷左右延伸的,所以啊,任何一条贯穿波峰或者波谷的竖直线都是正弦函数的对称轴,不用考虑对称轴左右图像的长度问题。 并且啊,相邻对称轴之间的距离都是派,比如这其中一条对称轴是 x 等于二分之派, 那么二分之派加派,二分之派加二派,二分之派加三派,二分之派加四派等等。 x 等于二分之派加上整数倍的派,都是对称轴。同时呢,二分之派减掉整数倍的派也是的。 所以啊,对称轴的一个通用表达式就是 x 等于二分之派加 k 派, 二分之派是其中的一条,加上一个 k 派就覆盖了所有的情况。 不过这里千万注意的是, k 是 一个整数,他不是正整数,因为减掉几倍的派和加上几倍的派都是可以的。好的,说完了对称轴,你说他有对称中心吗?思考一下, 没错,不仅有,还有无数个图像与 x 轴的所有焦点都是对称中心派,二派,三派,所有的整数倍的派都是对称中心的横坐标。 k 派都好零,这里边的 k 他 还是要注意是整数,而不是正整数。 好的,到这里说完了正弦函数 y 等于塞沿 x 的 这么多性质,我们回过头来简单的总结一下。 首先,定义域为 r, 整个 x 轴上都有图像。再说直域为负一到一的 b 区间,因为它的图像呀,永远都只在外,等于负一和 y 等于一之间波动来回 最小正周期。 t 等于二派,两个半弧拼接而成,一派一半弧。 再说,对称中心是所有的焦点,焦点的横坐标呢? x 等于 k 派。 不过需要注意的是,对称中心是一个点,千万不要只写一个横坐标就结束了。而对称轴呢,竖直贯穿所有的波峰波谷, 当然, y 轴不在其中,因为正弦函数是一个奇函数。好的,说了这么半天的正弦函数,如果我要研究余弦函数,这些结论需要全盘推翻吗? 这里是并不需要的,我们只需要把图像在原本正弦函数的基础上向左平移二分之派个单位长度就可以了。 为啥呀?因为塞隐 x 加二分之派等于 cosine x, 这个借助上一节所学的诱导公式可以推理得到,左加右减, x 加二分之派就是向左平移二分之派个单位长度就可以得到余弦函数了, 它是一个偶函数,但是波形外观和正弦函数是一模一样的,所以定义域值域最小正周期都是完全不变的。只有对称轴和对称中心的横坐标需要简单的互换一下位置, 但是对称中心依然是所有的交点,对称轴依然是贯穿所有的波峰波谷的数值线。 不过对于余弦函数这样一个偶函数来说,外轴他也是对称轴了。好的,说了这么老半天,也该拿出一道题目来检验检验了。 首先, x 属于零到二派的开区间,要解这样一个不等式,我们还是借助图像来辅助求解。 蓝色图像是 y 等于 sin x 的 全貌,但是题目中他只要零到二派这个开区间之内的图像,也就是这样一个完整的周期,其余部分通通拿掉。 好。 y 等于 cosine x 对 应于弦值,但是他还带了一个绝对值,这个怎么画呢? 我们还是先把里边的余弦函数给他画出来,就是在正弦函数图像的基础上,向左平移二分之派个单位长度得到余弦函数,再结合定义域零到二派的开区间,只保留对应的区域。 接下来戴上绝对值,这个应该咋办呀?没错,把副半折的部分通通翻折上来,这样就可以了。现在题目明确了,在零到二派的开区间上求蓝色曲线高于红色曲线的部分, 那是不是就只有这样一个狭窄的开区间符合题目的要求呀?好的,方向明确了,但是 x 一 和 x 二又应该怎么求呢? 在图像中看, x 一 x 二正好对应红蓝曲线的交点横坐标,所以赛引 x 一 等于 cosine x 一 的绝对值,赛引 x 二的绝对值。 那么 x 一 和 x 二之间又有什么区别呢?他们俩中间竖着隔着一条, x 等于二分之派, 也就是 x 一 小于二分之派, x 二大于二分之派。现在方程就好解了, x 一 是锐角,所以 cosine x 一 的绝对值可以直接拿掉, 进而算出 x 一 等于四分之派。 x 二呢,是一个钝角,所以 cos 以 x 二的绝对值等于 cos 以 x 二的相反数,进而解出 x 二等于四分之三派。 而咱们的答案呢,就是 x 一 到 x 二的开区间。这样一道题便成功的解出来了。 接着看第二题,要解一个含有正切值的不等式。可是正切函数的图像又有什么特点呢? y 等于 tan 减 x, 它长这样挺吓人的,它被无数条虚线分割成了无数个单体,而每一个单体又刚好对应一个最小正周期。 t 等于 pi, 相邻虚线之间的距离也是派。并且呀,你会发现他的图像在数值方向上可以无限延伸,上天入地,没有正余弦函数那样的限制值域为 r。 但是嘞,他的定义域就有不少的限制了,所有的虚线都不能取 x 等于二分之派,二分之三派,二分之五派以及负二分之派,负二分之三派等等等等。 定义域是 x 不 等于二分之派加 k 派, k 取全体整数。 接着正切函数的对称中心依然是曲线与 x 轴的所有焦点, k 派逗号零,只不过呢,他没有对称轴,一条也没有。 好的简单了解了正切函数的性质之后,我们再回到题目当中,一个玩意的正切值大于等于负一,小于等于根号三, 且不管正切符号里边是个啥,如果一个数的正切值大于等于负一,小于等于根号三,比如这个数就是 c, 它暂时给它替换掉, 那么符合题目要求的曲线范围便是所有标黄的部分。毕竟要大于等于负一,小于等于根号三,必须在两条红线之间,那么横坐标 c 塔的取值范围自然是黄色曲线的横向跨度了。 但是一下子研究这么多个,确实有些看不过来。咱们从中挑出一个来,比如在负二分之派到二分之派的开区间上的这一个。 既然解析式是 y 等于贪婪 x, 那 么曲线上的点自然就要满足对应的关系, 而这里的点 p, 他 又刚好是上边界 y 等于根号三和曲线的焦点,所以纵坐标正切值等于根号三,进而可以算出横坐标等于三分之派, 下边界 y 等于负一与曲线的交点 q 也是同样的道理,纵坐标正切值等于负一,进而可以算出横坐标为负四分之派。那么现在在这一周期内, c 塔角它的左右边界就都完美搞定了。 这个时候,我们再把曲线放回原本的大的重复周期当中,相邻周期之间的间距都是 pi, 那 么在刚刚单拎出来的周期中,左边界负四分之 pi, 右边界三分之 pi, 组成这样一个符合题目要求的 b 区间, 那么整体加个派就可以得到第二个成立的区间,第三个,第四个等等等等。不过呢,有没有一个表达式可以把所有这些符合题目要求的黄色区间都一次性表达出来呢?思考一下, 哎,还真有这样一个,在我们最开始求出的负四分之派到三分之派的 b 区间的基础上,发生 k 派的左右平移,便可以包含所有的情况。当然呢, k 属于 z, 可以 取全体整数。 现在咱们知道了,只要 c 他 角属于这样一个 b 区间,他就是符合题一的, 当然呢,还没有完 c 它角是换元之后的结果,千万要记得要换回二分之一 x 加六分之 pi, 这才是题目的要求。这样一个不等式,解开之后便可以得到最终的答案。
2.0万加数 10:52查看AI文稿AI文稿
10:52查看AI文稿AI文稿各位同学,你们好,今天我们来讲任意角的三角函数,我们来看一下这个图形,看一下右下角这个图形, 我们仍然沿用之前象限角的那种定义方式,将一个角的矢边 和我们的 x 轴的非负半轴重合,就是顶点在原点,然后以正半轴为矢边,我们做一个阿尔法角, 在这个角的中边上取一点 p, p 点,我们给给到坐标 x y, 那 p 点到原点 o 的 距离, 我们用小写的字母 r 表示,那我们就可以得到。我们根据勾股定律可以得到这个 r 就 等于什么呢?根号下 x 的 平方加上 y 的 平方, 感兴趣的同学哈。呃,可以去推导一下, r 等于根号下 x 的 平方加上 y 的 平方。那既然是一个点到圆点的距离,那肯定是大于零的啊,这你们要知道的,那就会有如下的定义, 正弦我们定义为,就这个任意角 r 法的正弦,我们就定义为,我们取的这个点的 纵坐标和这个点到圆点的比值就是 y 比 r, 那 余弦就是我们取得这个点的横坐标和这个点到圆点的比值就是 x。 比 r, 那 正切就是 这个点到的重坐标和这个点的横坐标的比值就是 y b x。 当然这个点取在任意的位置,只要不和原点重合啊,它是都是可以的啊,要在中边上去取。 嗯,具体的推导过程,感兴趣的可以私底下去推导一下。那再补充一下其他的三个三角函数啊。 第一个与切科探进的阿尔法啊,科探进的阿尔法,上面这几个你们以前都学过,都会读的,我就不再讲了哈。科探进的阿尔法等于我们正确的倒数就是探进的阿尔法分之一, 正歌萨克阿尔法,萨克阿尔法等于什么呢?正歌等于鱼选的倒数 cosine 阿尔法分之一,那鱼歌呢?克萨克阿尔法,克萨克阿尔法,它等于正选的倒数 萨尔法分之一哈,大家对着这三个稍微补充记一下就行,来,我们来看一下例题, 我们来看例题一哈,已知角阿尔法的中边经过这个点,求这个角的正弦余弦还有正切值,我们该怎么去求呢?我们看见这样的题,我们就要求取的这个点,它其实就是我们取的点到圆点的距离,怎么求啊? 来看一下是不是等于横坐标的平方加纵坐标的平方,再看什么算数平方根,那我们就写下呀,这个地方的 r 对 应的 r 就是 根号下 负三的平方加上四的平方等于几啊?根号下九加上十六等于根号二十五,也就等于五。好, r 出来了,那 sin r 法那是不等于 y 比上 r 就 什么重坐标四,比上 距离五就是五分之四,那余弦呢? cosine r 法就等于什么横坐标负三比三, r 五就是负的五分之三,那正切探进的 r 法就等于什么呢? 重坐标四比负三等于负的什么?三分之四,这是我们的 定义对不对?定义题的考的考法,那我们再来看例题二,若角阿尔法的中边落在 y 轴正半轴上啊,那这个时候我们就画下图呀, 中边落到这是圆点,这是 x 轴,这是 y 轴,是不是落在这个部分呀?啊,取个点, 并且中边上的一点屁的坐标是什么?是五,那他的坐标是不是零?五?那我们又来求三幺二法和扩散二法,那怎么去求啊?也是和上面一样,先算 r, r 就 等于什么?根号下 零的平方加上五的平方等于根号二十五就等于几啊?五,那 sine r 法就等于什么?五比五就等于一,那 cosine r 法呢?就等于什么?零比五等于什么零? 好,这就是我们三角函数的一个定义的题的考点,我们接着来看第二个知识哈, 三角函数值符号的规律。我们知道 sin 阿尔法等于 y 比上 r, cosine 阿尔法等于什么? x 比上 r, 贪婪的阿尔法等于 y 比上 x。 并且我们还知道在各个象限内他的点的坐标的正负情况,第一象限就是正正,第二象限就是负正,第三象限就是负负,第四象限就是正负。我们根据 x 和 y 的 正负情况啊,我们知道 r 一定是大于零的, 那就可以推导出以下的表格哈,他有个记忆的口诀啊,就是我们看红色字体部分, 正选上为正,余选亦为正,正切看一三。那其他没有提到的呢?就是都是负。什么叫正选上为正啊?就是当时我们一个三角函数是正选的时候,只要是上面的结果就一定为正,就第一第二项线正弦为正。 咳咳咳,那余弦一为正呢?同理就是余弦的第一和第四弦弦弦为正,正弦呢?就是什么啊?第一和第三,那剩下的是不都是负啊? 好,这是我们的三角函数值的符号规律。来,我们来看一下对应的立体。我们知道一个角阿尔法等于二百一十度,求看这他的正弦与弦正确的符号。那阿尔法是第几弦角啊?我们画一下呗。 从这个地方开始到这地方是不一百八,这是一百八。十度,转到二百一,转到这是不二百七。十度啊,他是没到二百七,所以他是第三象限角。第三象限角的正弦为正为负啊,正弦上为正,那下面是不是为负余弦呢? 那是不是右边为正,左边就为负正切呢?一三,什么为正对不对?这是我们的第一题。第二题,我们来看一下余弦,一个角阿尔法的余弦值啊,是负数。什么正弦值是正数?那请问角阿尔法所在的象限是第几象限?那我们就判断一下 余弦是不是右边为正,这是余弦啊,那左边是不是就为负?所以他只可能是什么第二或者是第三象限角,那正弦呢? 是不是只会在第一和第二象限?什么为正?那第三第四象限是不是为负?这是我们的正弦。 那综上所述,我们是不是只会又余弦,又要是负数的,又得正弦是正数的,是不?只会是什么第二项弦?于是角阿尔法是第几弦角,第什么二项弦角, 理解了吧?好,我们来再看第三个知识哈。呃,书本上给了很多的角的,但是在这个地方我们就只需要记一下这几个特殊值的就行,其他的我们后面学习诱导公式以后可以自己去推导就可以了。 首先啊,我们来看一下,当然记这一表你也可以去背背的了,就背,背不了也有简编的办法去背的啊,我们会画两个三角形就可以了。第一个,这是三十度的角 啊,这是六十度的角,这是直角,那么三十度所对的这个边呢?我们视为一,那斜边是不是二三十度所对的直角边是斜边的一半,再用勾股定律算出来,这条边就是几啊,就是根号三, 然后正选就是对边比斜边与选临边比斜边正确就是什么对边比临边,咱去慢慢比,算一下就算出来了。那四十五度呢? 是不也一样?这是四十五度,那这是不是也四十五度?这是不是等腰直角三角形?所以这边是一,这边是一,这边是吧?根号二,然后自己用定义去比一下就可以了哈。好,我就不再往下讲了哈。来,我们看一下这道题。好, 三倍三也六十度,减 cos 三也三十度,再加 tan 四十五度,它等于多少?我们就分别去看一下。三影六十度,那三影六十度,我们是不是画个有六十度的什么三角形?这是六十度, 这是一,这是根号三,对不对?那三影是不是六十度的正弦是不是就对边比上斜边,所以等于什么啊?根号三比上二好,那余弦呢?三十度的余弦呢? 那这是六十度,这是不是三十度?那是不就是零边?它的零边?根号三比上斜边二啊? cosine 三十度等于二分之根号三,那碳晶的四十五度呢? 那是不是就画一个等腰直角三角形就行了呀?啊?这四十五度,这是一,这是一,这是根号二。那贪心的四十五度是不是就是四十五的对边一比上一等于什么?一,那全部带进去,所以我们的原式啊, 它等于多少呢?是不是就三乘上二分之根号三,减去什么 二分之根号三,再加上什么一,那全部算下来就是 什么二分之三倍,根号三减去二分之根号三加上一,那是不等于这个减,这个就是二分之二倍根号三,就是根号三加一。好,最后的结果就是根号三加一。好,今天的课就讲到这个地方。
30带技能的数学 02:21查看AI文稿AI文稿
02:21查看AI文稿AI文稿数学,三角函数里的这些符号到底怎么读?这是一个英语图,我经常收到的评论和私信问题,所以今天我请来了我的兄弟数学图。 先说他,也就是他的缩写,这是个开音节单词,末尾一不发音,而字母 i 发本来的音,所以整个词读作 sign, 而他实际上就是嗓音前加了个前缀扣,写作这样,所以读这个词,只要把嗓音前面读出前缀扣就可以了。口嗓音,请注意,他在英文中的读法是重音在第一个音节,而不是咱们大多数人读的扩散音。 下一对也和刚才有点像,他就是 tangent, 他就是 cotagent。 但是注意这次有个不同, cotagent 有三个音节,重音在 倒数第二个,也就是中间这个 tangent 还有一个不同,那就是 tangent 不光是三角函数上常用的,在英语日常用语中也有一席之地。有个短语叫 go off on a tangent, 或者 go off at a tangent, 直接翻译就是从一条切线走开,你能猜到是啥意思吗? 其实很形象,从切线离开,意思就是不再顺着原来的轨迹走了。那不就是离题了,偏离原来思路了吗?比如, while explaining the best way to cook carrots i went off on a tangent to talk about the weather。 当我在说明怎么烹饪胡萝卜最好吃时,突然开始谈论起了天机。看出来了吧,我这么做就是典型的 going up on a tangent 偏离主题。想想看你生活中的老师、同学、老 老板、同事,甚至你自己是不是经常干这种事啊?好,再看最后一对, second 也有人读 second, 所以这个字读 cosicant 或 cosicant。 注意这里 s 后面的 e 发音是 e 而不是 a, 所以不是 second 和口 second。 出于求生欲,我要说明一下哈。以上是英文世界三角函数的读法,仅供与外国人交流使用,请不要拿着这个去纠正他人,尤其是你数学老师的读音, 咱们学数学的时候,专注于数学本身就好。当然,如果你把这个视频转发给数学老师,想必他不会介意的。
88是小doro呀 01:10查看AI文稿AI文稿
01:10查看AI文稿AI文稿同学们,你们不会还在用这种正正负负正负负正的方法在记忆三角函数值的正负吧? 天呐,太麻烦了,孙老师呢,教给你一句口诀,让你可以迅速的记住他们。这句口诀叫什么呢?听好了,叫都是天才,什么意思呢?不是夸你们啊,我们一起来看一下, 在我们的平面直角坐标系中呀,我们说对于第一象限的角来说,都有哪些三角函数值是正的呢?是不是我们的三也贪正的和扣三都是正的,那就都写上那第二项线我们三也为正, 第三项线谈枕头为证,第四项线扣三为证。哎,怎么理解都是天才呢?第一项线 大家都是正的,然后后面看二三四,是不是他们是是天才的 手字母呀?哎,那我们就记住了,都是天才哎,是不是记住口诀,让你不再纠结。
2257讲数学的暴躁孙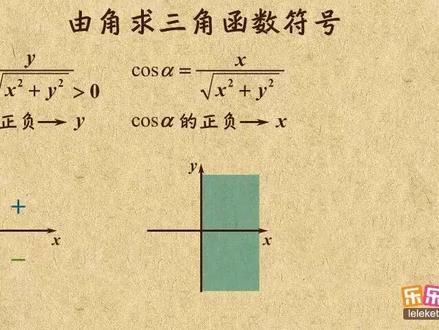 03:45查看AI文稿AI文稿
03:45查看AI文稿AI文稿这个视频我来讲讲,由角求三角函数符号。上回讲到,赛尔法等于 y 比根号 x 方加外方,由于根号 x 方加外方一定是大于零的,那赛尔法的正负就和 y 的正负相同。 所以当阿尔法是第一、二项现象时,外大于零,对应赛阿尔法都是正的。当阿尔法是第三、四项现象时,外小于零,那赛阿尔法也是负的,所以赛阿尔法在各项线的正负是这样的。 接着看口塞阿尔法,分母显然大于零,所以口塞阿尔法的正负和 x 是相同的。当阿尔法在第一次上线时, x 大于零,对应口塞阿尔法也大于零。 当阿尔法在第二、三象线时, x 小于零,对应口塞阿尔法就是富的,这就是口塞阿尔法在各象线的正负。最后看贪骏查阿法,他的 正负和 x、 y 都有关系。当阿尔法在第一、三项线时, xy 同正或者同副时,笔直都为正,也就是餐具茶阿法都为正。当阿尔法在第二象线时, xy 一正一负,第四项线时,也一正一负,笔直都是负的,所以摊俊茶阿法都为负。 像这样,只要知道一个角是第几项线角,咱就能判断出这些三角函数值的正负。比如一只角阿尔法是第二项线角。那么 sionr 法乘口塞阿法乘潘俊茶阿法的符号是啥呢? 要判断这个算式的符号,咱得分别判断这三个的符号。先看赛阿尔法,他一、二项线为正,三、四项线为负,而阿尔法是第二项线角,看第二项线,所以赛阿尔法是正的。再看口三阿尔法,他一、四为正,二三为负,看第 二项线,所以口三阿法为负。最后看贪骏查阿法,他一三为正,二四为负,第二项线也是负的,他们三个相乘,这两副刚好得正,所以整个算式符号为正。 刚才的题目是直接告诉你角的象限,你可以直接判断。有时候题目会含蓄一点,比如告诉你角阿尔法等于二,再求这个算式的符号。那咋求呢?只知道阿尔法等于二,那得先判断他是第几项线角呀。 先看坐标系,零到二分之派是第一项线,二分之派到派是第二项线。由于派约为三点一四,二分之派就约为一点五七,所以二就在二分之派和派之间,也就是在第二项线。 知道了阿尔法是第二项线脚,用老方法判断就行。和刚才一样,还是第二项线脚,所以结果也一样。像这样, 如果只知道角,那就先得判断角的象限,再判断三角函数值就行。不过有时候题目的条件更含蓄,比如角 f 的中边在直线 y 等于负三 x 上,那你能判断犯案阿尔法成贪正常阿尔法的符号吗? 先看看直线五二等于负三 x 中边可能在第二项线和第四项线,那就得分开讨论一下。 当东边在第二象线时,看塞阿尔法,他在第二象线是正的。在看贪军强阿法,他在第二象线是富的,他俩一正一负相成后,结果就是富的。 当中边在第四象线时,看塞尔法,他在第四象线是负的。再看贪骏塔尔法,他在第四象线是负的,所以相乘后,负负得正。你看,遇到这类中边在直线上的题目,你就要注意,直线上的中边会有两个位置,得分 别讨论。好了,以上就是这个视频的全部内容,关键记住三甲函数在各项线的符号塞阿尔法的符号要看外一二象线为正,三四象线为负。 口三阿尔法的符号要看 x, 一、四上线为正,二三向线为负。 tangine xrf 的符号要看 x 后外以三向线为正,二、四向线为负。怎么样,你学会了吗?如果学会了,就速速刷题去吧!
50数学大师 04:14查看AI文稿AI文稿
04:14查看AI文稿AI文稿零基础速通三角函数本节课我们直击高一上重点内容,三角函数的概念与定义。温馨提示,本节课过于基础,学霸可以直接划走主播今天只带想提分但基础差的同学,只要你想学,什么时候都不晚。这节课来跟他去讲一下三角函数的概念与定。 我们说三角函数在高中是摆在一个直角坐标系当中去研究的,我们首先把一个角把它给找到,你看这是中边,这是 r 法角,对吧?那我怎么样去定义三角函数呢?首先我们知道由于在这个直角坐标系当中,它的中边肯定是会过某个 点的,而这个点屁,我们可以把它定义成 x, y, 好, 那我把垂直边把它给做出来之后,这一段边的长度恰好代表的是就是这 p 点的纵坐标 y 打横代表的是不就是这个 p 点的横坐标 x, 我 们用勾股定律是不根号下的 x 方加 y 方,那么我把这一段定义成 r, r 是 等于根号下的 x 方加上 y 方的。好,那么我我们有这样的定义的时候,那我怎么样去算 sine? cosine 可得整数,我要去算 sine。 r 法是对比斜是吧?我们写出来是不是 y 比上什么呢?斜边就是根号下的 x 方加 y 方,我们都知道这是等于 r 吧,所以我们写下应该是等于 r 分 之 y 口算,写出来应该是等于零比斜,那写出来是不是 x 除以啊?那么 tan 减法是对比零吧,也就是说 y 可 x 做一个比值,所以我就可以得到这是 y 比上 x。 那 么在这里一定要保证一个点就是它的斜边啊,肯定是个正数才可以啊,我们以前学过三角函数,在初中是不是都是正数?在高中它是可正可负 负的,那问题就是这个三眼拉法是正是负,你可以发现它是受什么控制,它是不是受它的, y 就是 它的纵坐标控制, y 是 正的,那整个式子很明显是正的,因为我没有加绝对值嘛。 y 是 负的,那整个式子是不是就负的?对 于口塞来说,它是受 x 控制, x 是 正的,口塞 alpha 就是 正的, x 是 负的,口塞 alpha 是 不是就是负的?那最后我们再来看一下天枕,天枕受什么控制,你可以看到它是不是受到 x 和 y, 它之间的比值的关系,换句话说,它们同号就意味着它是正数,同号比一下就变成正数, 一号比一下其实就是负数。所以在这里我们就可以得到一个结论,如果我们要去研究三角函数的正负应该怎么去研究?首先我们可以分四个象限,第一象限我们可以发现三是正还是负, x 和 y 和 x, y 是 不是都是正数?所以第一象限三样勾三样跟 ten 是 不是都是正数?好,那我们来看一下第二象限。第二象限当中三样很明显是个正数,而我们知道此时它的 x 是 不是应该是个负数, 所以我们就可以得到口算就变成负数,而由于是一号,所以看成写下来应该也是个负数吧。那么接下来我们一起来看到第三象限, y 是 不是小于零, x 是 不是也小于零?所以对于这两个来说, sin 跟 cosine 是 不是都是负数?而由于它们是同号,所以 y 比上 x, 最终得到的是不是还是一个正数? tan 写下来应该也是个正数?好,我们来看一下我们的第四象限, y 应该是小于零, x 是 大于零的,所以 tan 是 个负数, cosine 是 个正数,而由于它们是一号, tan 是 不是也是个负数? 那么这就是我们对于高中来说三角函数的一个最基本的定义。好,那接下来我们来看一些相关的题型啊。他说如果 sin alpha 是 正数, tan 乘 alpha 是 小于零,他要问角 a 的 中边位于多少项向量? sin alpha 大 于零,大于零是不是要么是一项线,要么是二项线?摊选 alpha 小 于零是不?要么是二项线,要么是四项线,对吧?最终上所述就是,如果他们同时成立,他应该在第几项线?很明显答案选的是 b。 我们再来看到下一个问题,他说如果 sine 的 绝对值比上 sine x 是 等于负一的话,则角 x 它所在的象限应该是多少?如果我想要比值等于负一的话,那么是不是就意味着 sine x 它必定是小于零? 由于我现在知道 sine x 是 小于零,它等于负一,那么就意味着角 x 它应该是在第几象限,它是不是应该是在第三或者是第四象限?因为我们知道 sin x 它是在第三或是第四象限的时候是个负数,对吧?所以我们这道题目就很简单,把它给找到,学会了的话,大家来看一下这道题,打出你的答案。苦练十年,不如名师指点!每周我都会在抖音粉丝群分享独家的大招资料,需要的话大家可以进群领取。
12.8万数学君







