五上数学植树问题的封闭图形怎么做
封闭图形无外公就是这三种,我们先来看第一个,这是一个什么圆形啊?也就是说在这个圆形周围去值数的话,能值多少颗? 我们来看,我们先来数一下这一共是多少颗?从这开始一二三四五六七八,一共是八颗数,对吧?我们把封闭图形如果转换成不封闭的图形,也就说两边都装,两边都不粘,或者说只粘一端,它属于是这三种里边的哪一种情况?我们画图来看一下, 假设我把这个粘成一条线,从这开始粘好,这是最开始的,这, 这是这一颗,对吧?好,我往后画,我们刚才数一二三四五六七八八棵树,一二三四五六七 八。我们来看一下我到这个八棵树这之后,他这是不是还有一段的间距?是,我是不是要把这一段间距给画下来?是,但是这段间距这没有树了,因为再有树就成了刚开始的这一棵树了。 那所以我们现在这种情况来看的话,它属于是哪一种情况?在一端只在一端,我们来看是不是只在了这边这一端, 这边没有那只在一端的时候。棵树和间距数的联系是什么?等于间隔数,棵树等于间隔数,是不是有几个间隔就有几棵树? 我们来数一下,是不是一二三四五六七八,一共是八棵树吧?数一下间隔一二三四五六七,这是不是也是?所以它一共也是 八个间隔数吧?所以它的棵数等于间隔数。我们球封闭图形的时候,其实就是球只栽一端。
粉丝1.9万获赞10.0万
相关视频
 02:09查看AI文稿AI文稿
02:09查看AI文稿AI文稿在正六边形的花坛周围等间距栽树,我们画出来这个六边形,六个顶点各栽一棵,我们画一下一、二、三、四、五六。好, 那一共栽了四十八棵,问每边栽多少棵树?好多孩子说一共是四十八棵树,有六条边,那直接用四十八除以六,等于是八颗,这样做对吗?这是错的, 它错在哪里?我们来看一下这个六边形,它属于是一个封闭图形,我们说过封闭图形,它属于是指在一端的情况,那我们把这六条边给展开来看一下,假设我从这里开始,这是第一棵树, 然后这条边,然后这是第二棵树这条边,这是第三棵树这条边,第五棵树这条边,第六棵树 这条边。那我发现如果我用四十八除以六得出来的八里边只包含了这边一棵树,但是并没有这边的树, 我用另一个颜色表示出来,并没有这边的树,那所以我还应该用八再加上这边的这一棵树,也就是再写八加一等于九颗,这样才是完整的算式。那除了这种方法还有没有其他的方法?我们再来看一下 同样是这个正六边形,他说在六个顶点上各栽一颗,也就是栽了是六颗,一共是四十八颗,我减掉这六颗,还剩四十二颗。啊,那我把这六颗给划掉,划掉,那他现在剩的就是中间的这些数, 然后我再用四十二除以,一共是六条边,等于是七颗,那这七颗就是中间的这七颗。 但是这七科里边他并没有算到我刚才划掉的这两科,所以我最后还应该再用七加二等于十九科,这才是完整的算式。所以我们在做题的时候不可以直接用四十八除以六。
 05:04查看AI文稿AI文稿
05:04查看AI文稿AI文稿大家好,学习植树问题第四节,化蛰为直复习导入学校开展校园文化建设。我们班的植树任务是在一条八米长的小路的一旁, 每隔两米栽一棵树,可以怎么栽?这道题没有明确值数类型,需要分不同的情况解答。解题步骤,先求间隔数,再求值数棵数。 总路长是八米间隔数,我们就用总路长除以,每隔两米栽一棵树,就是除以株距等于四个间隔。 看第一种类型,两端都栽,间隔数加一等于值数,棵数八除以二,这是在求间隔数,再加一等于五棵。 如果两端不栽,间隔数减一等于值数,棵数八除以二减一等于三棵。 如果一端栽一端不栽,直数棵数等于间隔数八除以二等于四棵。 这是我们之前学过的这节课学习第三张伯伯准备在圆形池塘周围栽树,池塘的周长是一百二十米,如果每隔十米栽一棵,一共要栽多少棵树? 池塘是圆形,池塘圆是封闭曲线。和前面我们学过的一条路线上直数有什么联系呢? 一起来分析一下类比前面学过的直数问题。如何解决这个问题呢?可以通过画图分析。 举例,先在周长四十米的圆上栽树,每隔十米栽一棵, 有四个间隔,种了四棵树。再来看,在周长八十米的圆上栽树,每隔十米栽一棵, 有八个间隔种了八棵树,都是间隔数等于值数棵数。我们发现值数棵数等于间隔数, 值数棵数等于间隔数,和我们在一条路线上,值数的一端栽一端不栽的情况相等。 如果把圆拉直成线段,你能发现什么?我们来看拉直成线段, 正好是一端栽一端不栽的情况。间隔数等于值数棵数。 由此我们推出封闭曲线上的值数问题。用图形周长除以珠距等于间隔数,等于值数克数,求出了间隔数,也就是求出了值数的克数 来解决。例三,周长是一百二十米,轴距是十米,弦球间隔数 一百二十除以十等于十二,十二是十二个间隔。由于是间隔数等于值数棵数,这个间隔数就是最后的棵数十二棵。答,一共要栽十二棵树。 这里要注意,封闭图形不止原一种,我们前面学过的长方形、正方形、平行四边形、三角形、梯形等都是封闭图形。 来总结一下在封闭曲线上直数的问题。将封闭图形划分为直后, 它和在一条线段上一端栽一端不栽中,棵数和间隔数的关系是一样的,都是值数,棵数等于间隔数。
52燕子老师讲数学 07:12查看AI文稿AI文稿
07:12查看AI文稿AI文稿我们来看这个题的信心,他说要带一个圆形,跟我们前面的直线形都不一样,对不对?直线形有头有尾,而圆形他是连在一起的。好,再看在他的周围来种出池塘的洲长是一百二十米,哎,同志们,洲长 周长是这个圆的一圈的长度,一圈的长度好,接着如果每隔十米再来猜一颗,好,按照我们左边学的,我们这些信息应该一一对。为什么周长就是我们学的总长一遍,周长就是我们学的总长,对,总长就是几米。一, 一百二十米。好,对了,每隔十米栽一棵,这里呢十米栽一棵就是我们说的对,就是我们的间距,所以间距是十米。那我们求 棵树,求棵树,那么怎么来做呢?昨天我们讲的时候都是通过画图,今天老师依然也是用画图的方式来让大家理解。 画图好,一百二十米呢,稍长,我们我们给他分段,分成小一点的来研究,我把它对,好,我们先给他分成四十米来研究的时候,我们看他说每隔十米一方,对不对?所以我画,我画这个圆圈的周长就给它定为四十米。那么这个时候我们在四十米的上面来种树,那我先在这个位置种一棵树, 这个位置种一棵树,那我就要隔十米,然后再种第二棵,第二棵又隔十米,然后种第三棵,第三棵又隔十米,然后再种第四棵。哎,刚好第四棵种完之后又隔十米,刚好就是我们原来的 第一棵。那么我们图画好之后,我们来找看看他故意的这棵树是多少。好,咱们打了,先从这里一棵树, 一棵树对应一个箭头,再来一棵树对应一个箭头,再来一棵树对应一个箭头,一棵树对应一个箭头。有几个箭头? 一个间隔四个间隔。那有几棵树?四棵树。同学们,什么情况?它是什么?这棵树与我们的间隔数是一样的,相等的,它是巧合吗?不是。再来,我们再来看,这五十米怎么样呢? 好,一棵我们一起说,两棵、三棵、四棵、五棵。好,一棵我们一起说五十米 上面,我们来看五十米上面一个端点,对了,以这个为端点,我们从这里开始数,一颗对应一个和一颗对应,一个间隔,一颗对应一个间隔,一颗对应一个间隔,一颗对应一个间隔。 几个几个,五个间隔。错了,间隔几棵树?五棵树。哎,他们俩还是相等的好,你看呢?六十米呢?把它分成几个间隔?六个间隔。好,那 六个间隔从这里开始,一个间隔,两个间隔,三个间隔,四个间隔, 五个间隔,六个间隔,一二、三、四、五六,在六个间隔上面来种树。好看,这里一棵树、两棵树,三棵、四棵、五棵、六棵。好,再来数一下看看。 一棵树对应一个天鹅,一棵树,一棵天鹅,一棵树,一棵天鹅。一棵树,一棵天鹅,一棵树,一棵天鹅,一棵天鹅。几个有几个箭头呀?六个,六个箭头就有六棵树,还差是相等的, 这是巧合吗?不是。为了吸引大家,一定不是老师带了一个小道具啊,作为小道具。好,现在同学们,你们看老师手上他就是我们的第一个图形,几棵树,四棵树,四棵树好,看着四棵树,然后呢, 我把它沿着,我以这棵树为端点,我给他沿着这个位置给他打开,打开,哎, 打开之后取了什么一一端来这,来这来这。哎, 你们看这是小河吗?我们看我们把四棵树的一个圆形给它打开之后,它变成了什么?一堆开,一堆不开,大声一点,什么一堆开,一堆不开。对,其实它就是一端摘一端不摘的 习惯,跟我们昨天学的直线型上面种树一端栽一端不栽是一样的,好,看清楚吗? 老师,你别干活了,啊啊啊啊, 好朋友们,那其实我们封闭图形上面来求它的棵数,其实就可以换成什么,我们直线图上面的一瓜开,一瓜不开是一样的,就把它转成一个问题去求就可以了。所以它棵数等于什么? 棵数等于一个数。对,好,那你可以写完再,你应该是可以写这里是是还有哪里的意思呀?树,你的树。 那么接下来我们通过观察发现他就是一关栽,一关不栽的问题,那我们就可以得出他的规律,那就是 通数等于间隔数,他就是等于间隔数。那接下来就非常简单了,你只要把间隔数给他求出来就可以。间隔数等于什么?打平 箭头数等于总长除以间距,总长除以间距 除以间距。好,再继续返回图中,总长是一百二十一百二十,间距是一十几十除以等于十二棵树。 哎呀,在原形上面来种树,把它转换成我们一边栽一边不栽,有问题,那他就是棵树等于箭头数。同样的, 如果他问我们总长呢?他给我们什么棵数呀?总长呢?总长等于箭头数,等于箭头数和树成间距数,成间距 好,没问题吧?同学们,没有,你看这对于你们昨天学的很好啊。所以今天我们把这个知识点从昨天迁移到新知识上读出来了。所以同学们,圆形封闭图形上面重数其实都不难。当然我们还要想想 除了圆形还有哪些叫封闭图形啊?小方形,这角形,这角形,哦,还有其他的,还有其他的或者什么多边形都可以这样来做。那现在我们的这个新课就说完了。嗯,没问题吧?没问题。
15木易老师 01:15查看AI文稿AI文稿
01:15查看AI文稿AI文稿哈喽,大家好,我又回来了。很久没讲题了,今天来讲一道值数问题的封闭图形。我们先来读一读题目。一个长二十米,宽十米的水池, 要在水池边种树,树的间隔为十米,需要几棵树才够。这一个水池的长是二十米,宽是十米, 我们要求出间隔数才能知道要种几棵树是因为在封闭图形中间隔数等于棵树, 我们要求间隔数。第二,先求他这个水池周长。周长是什么呢?周长是这一个图形围绕他一圈的总长度,算他的周长,需要把他两个宽两个长加起来,我们列式为 二十乘二加十乘二等于六十单位米,我们知道了它的周长是六十米,然后我们用六十米来除以十米,就可以知道它的间隔数。六十除以十等于六个 棵数等于间隔数。我们这里知道了间隔数是六,那他需要准备的棵数也是六。最后来写答语,这道题你学会了吗?记得在评论区告诉我你的答案哦。
 01:06查看AI文稿AI文稿
01:06查看AI文稿AI文稿我们学习直数问题中一端栽一端不栽的情况,我们来观察图,如果我们只栽一棵树的话,我们会发现一棵树对应一个间隔,栽两棵树呢?两棵树对应两个间隔, 栽三棵树呢对应三个间隔,所以我们会发现栽树的棵数等于间隔。 还有一种题型跟它是相同的,就是一个封闭图形,假设这个圆的周长是四十米,每隔十米栽一棵树,那么我栽了四棵树,同样也有四个间隔, 所以封闭图形跟一端栽和一端不栽的情况是用同一个方法,那么就是用路长除以周记。我们来看题,一个圆形池塘周长六十米,在池塘周围每隔五米栽一棵树要栽多少棵? 在题中非常明显的一个字眼,圆形的池塘,圆形的池塘,我们就能想到它是一个封闭图形,所以我们就可以用路长去逐一注句,所以是六十除以五等于十二颗。
26教数学的赵老师 02:42查看AI文稿AI文稿
02:42查看AI文稿AI文稿今天我们进入五上最后一个单元值数问题的学习,我们一起看一下五星学霸的思维题。 我们先看一下第一题,这是一个圆形的场地,实际上就是封闭图形值数问题。我们讲解一下五星学霸第三关练思维的这三道题, 我们一起读一下题。在操场圆形场地的周围,五一班的二十名同学在老师的带领下一起玩丢手绢的游戏,开始的时候,他们每两个人之间的间隔是两米, 玩了一会,有十二名同学被淘汰,剩下的人继续玩。所围成的圆大小不变,问,间隔应该改为几米?我们分析一下这道题。这是一个圆形的场地,我们先画一个圆形,也就是是一个封闭图形,它就属于值数问题中的在封闭图形内的值数问题。 我们知道在封闭图形的值数问题中,值数的颗数,也就是这道题所说的人数,它就等于间隔数。 那这个间隔数是怎么求的呢?就是用总周长,就是整个总距离除以间隔的长度,这个每一个间隔是多长? 那题目告诉我们,一共有二十名同学,他们的间隔是两米,也就是说我们可以把这个圆形的总周长求出来,它就等于圆人数 乘以圆间隔数圆间隔长度,那么圆人数是二十名同学,每个人之间的间隔是两米,就是二十乘以二等于四十米。 那解答这道题的关键是什么?是淘汰了十二名同学之后,他们所围成的圆大小不变,这个大小不变就是说圆的总周长是不变的, 不管人数减少了多少,他们围成的这个圆周长是不变的,那么我们就可以把这个现在的人数给求出来, 根据条件,现在的人数等于原来的二十人,减去淘汰的十二人,现在就是八人,这八人还是围了这么大的圈,就是周长不变,那我们就可以把现在的间隔数给求出来了,现在的间隔长度就等于这个总周长 除以现在的人数,总周长呢,依然是四十米,现在是只有八人了,所以现在的间隔就变为五米了,那这道题就解答出来了, 所以答间隔应改为五米。解答这道题的关键点就是抓住总周长不变,那么它的人数变了,间隔的长度变了,但是总周长不变,我们就可以用总周长除以现在的人数求出现在的间隔数。记得点赞关注哦!
33煊和花教做题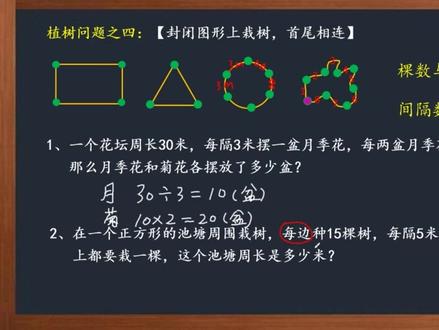 04:57查看AI文稿AI文稿
04:57查看AI文稿AI文稿植树问题的第四种类型,也就是在封闭图形的线路上栽树,首尾相连,这是一个长方形,现在在它的四个角上面各栽了一棵树,也就是有四棵树,很明显有四个间隔, 这个三角形每个角上面栽了一棵树,就有三个间隔。再来看这一个圆形, 首先我们在这个圆形上栽三棵树,那这里就有三个间隔,四棵树就有四个间隔,那五棵树五个间隔,六棵树就有六个间隔。这是一个不规则的图形,比如说在一个湖的周围之树, 一棵树就只有这一个间隔,两棵树,三棵树,四棵、五棵、六棵、七棵、八棵,这八棵树就有 一二三四五六七八,也就八个间隔。不管是规则的图形还是这个不规则的图形,只要是封闭的图形的周围指数,那么我们都可以得到 颗数跟间隔数一样多,也就是间隔数等于颗数。现在来看这样一道题目,一个花坛周长三十米,就是指的封闭图形一周的长度,全长三十米,每隔三米百亿瓶月季花。 我拿这幅图形做比较,这个三米就是指的两盆月季花之间的距离,我们称之为间距,同样这两个之间也是三米。每两盆月季花之间又摆两盆菊花,这是什么意思呢?就说这是月季花,这是 月季花,这之间又摆两盆菊花,同理,这两盆之间呢也摆两盆菊花,换言之就是一个间隔就有两盆菊花。 最后要求月季花和菊花各摆放了多少盆,刚刚已经分析过,他是一个封闭的图形,所以这种题目我们就不需要去考虑加一减一的问题,直接运用全长除以间距 三十除以三得到十,那么这个十就是指的十个间隔。既然是十个间隔,由于他们是完全相等,所以就有十盆花, 直接得到月计划就有十盆。刚刚我们已经分析过,一个间隔就摆两盆, 两个间隔就摆四盆菊花,同理,十个间隔就摆十乘二,也就是二十盆菊花, 那么菊花就有二十盆。最后口答就可以了。再看下一题, 在一个正方形的池塘周围栽树,每边种十五棵树,每隔十五米种一棵,四个角上都要栽一棵,最后要求周长树三比一。这同样是在封闭土地当中栽树, 如果告诉这个周边一共种了十五棵树,那这个题目就简单了,那十五棵树就十五个间隔,所以十五个间隔乘五就得到七十五米,周长是七十五米。但是这个题目他不是总共种了十五棵树,他是每边 种十五棵树,同时四个角上面都要栽一棵。那很明显,我就要先求出一圈,也就是一周一共要种多少棵树。这个题目既然是每边十五棵树,我首先用十五乘四,得到六十棵, 但是他又说四个角上都要栽一棵,很明显四个角上的这个树啊,他就重复了,你看这一棵树 既在这一条边上,又在这一条边上,那么他就算了两次,因此四个角上的四棵树呢,都算了两次, 也就是多数了一遍,所以我们要减掉十颗,那这个时候呢,就只有五十六棵树了。当然也可以采用什么思路呢? 用十五,首先剪去一颗,把这一颗先剪掉,我们从这个位置开始算 十四棵树,那么这一边呢也是十四棵树,这里呢也是十四棵,同理这个位置还是十四棵,那一共就有四个十四,总共五十六棵树,这样就没有重复,五十六棵树就有五十六个间隔, 然后根据间隔数乘间距就得到全长。那么五十六个间隔乘一个间距五米,就可以得到这一圈的周长,也就是二百八十米。最后我们答池塘的周长是二百八十米。
137程老师 00:59
00:59 01:19查看AI文稿AI文稿
01:19查看AI文稿AI文稿小可爱们上课啦,今天呢,我们一起来研究封闭图形的植树问题,正方形四周种树,每边种四颗, 四个角都种,一共要摘多少棵树?那么这种题啊,我们应该怎么做呢?是不是正方形有四条边,每条边四颗,所以四四十六颗呢?当然不是,那么应该怎么做?那我们就要来画图,塑形结合,轻松解决。 四个角老师已经都种好了,那要保证每一边四棵树的话,那我中间只能留下两棵树。 好,那么同学们看一下,老师已经画完了,我每条边都中四颗,而且我四个角都还中数了。那现在如果你每条边都按四颗来算的话,那我们来把它画起来,这条边你按四颗来算,这一条边你也按四颗来算,如果你全部每条 边都按四颗来算的话,那么你就会发现有四条边,所以四乘四总共就有十六棵树。但是你发现没有,这里有一个问题,这四个角上的这四棵树啊,被你重复多算了一次, 重复多算了一次啊,这四棵树,所以我们就要把它给剪掉,所以真正他种的就是十二棵树,同学们要注意啊,重复的我们一定要把它给剪掉,听懂了吗?
3523燕纯老师 01:00查看AI文稿AI文稿
01:00查看AI文稿AI文稿有个正方形的池塘,边长为二十五米,沿着池塘的边,每间隔五米摘一棵柳树,四个角都摘,一共要摘多少棵柳树呢? 今天我们来分析一下这张图。这是一个正方形的,如果是封闭的图形,那棵树等于间隔数,一边有二十五米,每间隔五米种一棵树。最简单方法,二十五除以五等于五棵树每边,然后乘以四边四个边,然后四乘以五等于二十颗。 第二种方法就是二十五直接乘以四等于一百,这就是就是算他这四条边总共有多少米,非常好。然后再除以每间隔五米种一棵树,就等于一共要种多少棵树,一共要种二十棵树。这道题讲完了。
 04:48查看AI文稿AI文稿
04:48查看AI文稿AI文稿上个视频说到,狗蛋小队又一次抵挡住了黑心公爵的狂风,但是他们暗中发现,黑心公爵居然贼心不死,布下了一个圆形魔法阵,整圈的长度是四百二十米, 然后只要在这个圆上每隔七十米安一个黑心大风扇,就能发动超厉害的黑心龙卷风,风力强到可以把树木连根拔起。那这一次黑心公爵要安几个风扇呢? 狗蛋讲,虽然这是个圆形魔法阵,可以知总长度四百二十米,每隔 七十米安个风扇,这看起来很像是个植树问题啊。我们先来画个图看看,这个圆就代表魔法阵,我们随意挑个点作为起点,每隔七十米安风扇,就是每七十米分一段, 我们用总长度四百二十米除以每段的长度七十米得到,一共要分六段,段间的这些点就是安风扇的地方。那你觉着一共要安几个风扇呢? 答案选 b。 六个图上虽然分成了六段,可一共也只有一二三四五六这六个点,每个点上都要安一个风扇,那就一共要安六个 风扇。为啥图形分成了六段,却只有六个点呢?这是因为这回我们分的是一个封闭图形,圆形 而非之前的线段。这就又改变了点和段的对应关系。在原型中,第一个点对应第一段,第二个点第二段继续下去, 你看不多不少,点和段刚好一一对应,也就是说点数等于段数。 哎,点数等于段数?我们之前在学习只栽一端的值数问题时,也有点数等于段数,莫非他俩之间有什么迷之联系吗?这时喵大师突 突然出现,把这个圆在起点前剪开,然后慢慢拉直。你来仔细观察一下,这一下就变成了线段中的哪种情况呢? 不难选吧,是 b 法院展开后就是一端有一端没有的情况,所以点数的确等于段数。而且有了这种剪开的方法,我们拿到其他眉头眉尾的封闭图形,也能发现类似的情况。 比如你看这个周长八十米的正方形,每隔十米栽上树,就像这样,我们选择一个点剪开再拉直,是不是变成了纸在一端的情况?再比如这个已经栽上树的 长方形,选个点剪开再拉直,也是只栽一端的样子。所以小结一下,面对这类封闭图形的植树问题,通过把一个点剪开再拉直,问题就变成了线段上只栽一端的情况。 那相应的计算过程也是同样的两步,首先用总长度除以每段的长度得到段数,再通过点数等于分段数就得到答案了。 掌握了这种新情况,狗蛋小队打算用喵大师的鸡蛋阵法应对。这个鸡蛋阵法是个封闭的圈,总长五百六十米,需要每隔八十米立上一个风力转向器,那么一共要立即 几个呢?答案选 b。 对于这个封闭的圈,我们就能看作是直线上只在一端的情况, 所以计算时,先用总长五百六十米,除以间隔八十米就能得到段数七段,接着点数等于段数也是七,一共要立七个。 最终在狗蛋小队的努力下,龙卷风成功转向,把黑心公爵给卷走了。
627人教版刘少 01:51
01:51 01:59查看AI文稿AI文稿
01:59查看AI文稿AI文稿说一下这个支数问题中封闭图形上支数这种怎么办? 封封闭图形就是比如说在游泳池,嗯周围,嗯修建路灯,或者是嗯在雨塘周围支数这种类型 其实用图形很能够明白的看出来,他不管是椭圆、椭圆形还是圆形,当他你看假设这是这是,这是一个圆形,你把这个圆形或者椭圆形吧,你把它打开之后, 打开之后他是不是就是属于那种就是一端栽树,一端不栽树那一种类的? 所以遇见这道题,你就按照咱上个视频讲的第三种情况,就是说啊,一端不栽树的方法去求能栽了多少棵树,棵树就是间隔数, 就是每个间隔有多少个间隔,有多少间隔就种多少棵树。当遇见这种环形了,椭圆形了啊, 他就是或者是不老规则的,但是他叫属于这种密闭型的图形,在这种图形上指出你只要知道周长, 知道周长了之后,他告诉你中长,周长之后,你知道每隔多少米在一阔啊,那你求出来间隔数,周长除以,嗯就相隔多少米的米数处求出来间隔数,间隔数就是要种的树的棵数。
30三个宝贝儿的妈
猜你喜欢
- 4537曦竹Z
最新视频
- 2852稣岐


![AI赋能五上数学位置、可能性、植树问题期末复习 #五年级上册数学期末复习课件[话题]# #位置可能性植树问题[话题]# #位置可能性植树问题[话题]# #植树问题复习课[话题]# #五年级上数学期末复习[话题]# #五年级数学期末复习[话题]# #位置与可能性[话题]# #植树问题课件[话题]#](https://p3-pc-sign.douyinpic.com/tos-cn-p-0015/ogKU7vAPI0iRQ5LAbyBwV2iTBPCImv7A5IaCL~tplv-dy-resize-origshort-autoq-75:330.jpeg?lk3s=138a59ce&x-expires=2083226400&x-signature=5ByKJMUI0Iv%2B2owN%2BZAOhhvAT64%3D&from=327834062&s=PackSourceEnum_AWEME_DETAIL&se=false&sc=cover&biz_tag=pcweb_cover&l=202601081841561A5B3F2329BDDB7C966F)


