二年级图形与几何102页讲解
上个视频你已经认识了四边形家族,这个视频咱再来认识一下三角形家族,这是三角形,这也是三角形,它的两边相等,那就是等腰三角形。比如这个和这个都有两边相等,所以也都是等腰三角形。 这个三角形有一个角是直角,那就叫做直角三角形。同样,这个和这个都有一个直角,所以也都是直角三角形。 如果等腰三角形的另一条边也和这两条边相等,也就是三边都相等,那就是等边三角形,也叫正三角形。看三边都相等了,那一定有两边相等,所以他其实也是特殊的等腰三角形。 还有个比较特殊的等腰直角三角形,他有相等的两边同时还有一个直角,所以是特殊的等腰三角形,他并不是等边三角形。 三角形家族的关系你已经认识了,那你能判断出这些图形当中哪些是等腰三角形吗?要找等腰三角形,只要找到相等的两边就行。这个和这个以及这个都有两边相等,所以都是等腰三角形。 这个和这个三边都不相等,所以不是这个和这个以及这个也都有两边相等,所以也都是。 以上就是这个视频的全部内容,关键得掌握三角形家族之间的关系。等腰三角形和直角三角形是两类特殊的三角形, 其中等边三角形是特殊的等腰三角形,而等腰直角三角形既是特殊的等腰三角形,也是特殊的直角三角形。怎么样,明白了吗?如果明白就赶紧去做题抢金币吧!
粉丝1444获赞2886
相关视频
 11:57查看AI文稿AI文稿
11:57查看AI文稿AI文稿图形与几何图形与几何这一部分,本学期我们主要学习了长度单位、角的初步认识、观察物体三单元的内容。 长度单位主要包括认识厘米和米,以及认识线段两部分内容。角的初步认识主要包括角的含义、角的分类以及画角三部分内容。 观察物体主要包括从不同的位置观察物体或立体图形,以及用推理解决简单的问题。那么接下来我们就详细看看每一部分的内容。 好,首先回顾一下长度单位这一单元的内容。先来看认识厘米和米。 小海和爸爸在测量同一张课桌时,都是用闸做单位,量得的结果为什么不一样? 那是因为人的手有大小之分,所以不同的人量得的结果也会不同。因此在测量物体的长度时,统一长度单位很有必要。这时我们就认识了厘米和米。 好,那先回顾一下,什么时候用厘米做单位,什么时候用米做单位呢? 米和厘米谁大谁小?他们之间的近率是多少?怎样测量一个物体的长度? 好,一起来看。我们在测量比较短的物体的长度时,用厘米做单位。尺子上每两个相邻刻度之间的长度是一厘米。 还记得生活中哪些物体的长度大约是一厘米吗?哎,对了,比如食指宽大约是一厘米,田字格宽大 约是一厘米,图钉的长大约是一厘米, 米是比厘米大的长度单位。测量比较长的物体的长度时,通常用米来做单位。那一米有多长呢? 课桌桌面的长大约是一米,衣柜这个面的宽大约是一米,教室黑板面的宽大约也是一米, 米和厘米之间有什么关系?一米里面有一百个一厘米,所以一米等于一百厘米。 好,咱们来看看下面这支铅笔的长度是几厘米?怎么测量它的长度? 对,首先把尺子的刻度零对准铅笔的一端,然后看铅笔的另一端对着几铅笔就是几厘米,这里铅笔的右端对着八,所以是八厘米。 那我们还学习了线段,那么想一想,什么是线段?线段有什么特点?怎样画一条线段呢? 我们通过一道题来回顾一下线段的特点,下面哪些是线段? 第一条、第三条都是线段,只有第二条不是线段。为什么呢?对,因, 因为线段是直的,可以量出长度,很明显第二条是弯的。 你能画出一条和下面这一条一样长的线段吗?首先要量出这条线段的长度,把线段的左端与尺子的刻度零对齐,右端在刻度五的地方,所以这条线段长五厘米。 接下来就是画一条五厘米长的线段。哎,怎么画? 先确定一个端点,尺子的刻度零与端点对齐,然后从刻度零开始画起,画到刻度五的地方,最后标出右侧端点。 那还可以怎么画?还可以在刻度零和刻度五的地方各画一个点,然后再用尺子把这两个点连起来,同样得到一条五厘米的线段。 再来看角的初步认识有关的内容,回顾一下角各部分的名称是什么?按角的大小分为哪几类?怎样知道一个角是不是直角?怎样画一个角? 一起来看,角是由一个顶点和两条边组成的,现在延长角的这两条边角变大了吗?角没有变大,角的大小只与两条边张开的大小有关, 与编的长短无关。接着看,直角是一种特殊的角,三角尺上最大的角是直角,而且所有的直角大小相等。 要想知道一个角是不是直角,直接用三角尺的直角比一比,锐角比直角小,钝角比直角大,所以锐角小于直角,小于钝角。 知道了各种角,那经过下面的这个点,怎样画一个角?哎,从这一点起,我们用尺子向一个方向画一条线,再从这点起,用尺子向另一个方向画一条线,就组成了一个角。 注意,画角时,角的两条边必须从同一个顶点引出。那又该如何画一个直角呢?第一步,先画一个点做顶点, 从这个点起画一条直线。第二步,把三角尺的直角顶点与这个点重合,三角尺的一条直角边与这条线重合。 第三步,从顶点起,沿直角尺的另一条直角边画一条线,最后必须标上直角符号。 最后看观察物体。你知道下面的三个图形分别是从哪个位置观察得到的吗?要判 判断图形是从哪个位置看到的,需要根据观察者的位置,抓住被观察物体各部分的特征进行判断。这三个分别是从正面、侧面、上面观察得到的。 从不同的位置观察同一物体或立体图形时,看到的图形可能是相同的,也可能是不同的。 如果我们观察立体图形,看到的一个面是圆,哎,这个立体图形可能是什么? 想一下,从正面、上面、侧面观察长方体和正方体,看到的图形只有长方形或正 方形,这两种情况不会看到圆。那球呢?我们知道球从各个位置观察,看到的图形都是一样的,都是一个圆,所以这个立体图形可能是球。 那圆柱呢?圆柱从正面和侧面观察,看到的图形都是一样的,是一个长方形或正方形, 但从上面看看到的是一个圆,所以这个立体图形也可能是圆柱。 根据观察到的图形猜测所观察的立体图形时,应根据立体图形的特征进行分析。 符合条件的立体图形有时不止一个。好图形。与几何有关的知识暂时复习到这里,我们来看几道典型题目。 第一题,在括号里填上厘米或米。我们知道,较短的物体用厘米做单位,较长的物体用米做单位,所以小百的身高是一米六十二厘米, 黄瓜长二十厘米,教学楼高十二米。第二题,先量出线段的长度,再画一条比他长三厘米的线段。首先量出这条线段的长度,线段与尺子平放在一起, 起一端与刻度零对齐,另一端对着刻度四。所以这条线段长四厘米,比四厘米长三厘米的线段长七厘米。然后画一条长七厘米的线段, 尺子的刻度零与端点对齐,然后从刻度零画到刻度七的地方,最后标出右侧端点 好。第三题,数一数有几个角,几个直角?想一想,再说一说自己是怎么数的。 我们可以先数出单个的基本角,看这个图,基本角有十二个,再数有两个 基本角组成的合成角一、二、三、四合成角有四个,并且都是直角。 第四题,连一连右边三幅图分别是谁看到的? 好,我们按照一定的顺序进行观察。先看小百,他站在汽车的前面,看到的是汽车的正面,应该是第二幅图。 再看小川,他站在汽车的侧面,看到的是汽车的一侧,应该是第一幅图。最后看小华,他站在汽车的后面,看到的是汽车的 后面,应该是第三幅图,你都掌握了吗?
38心飞翔520 06:46查看AI文稿AI文稿
06:46查看AI文稿AI文稿好,今天我们继续整理四上的内容,我们今天整理的是第二、第三、第五单元的内容,他们其实都属于图形与几何的内容。我们先看第二单元内容,公顷和平方千米其实它是属于面积单位,那面积单位呢?之前我们也接触过,我们从小到大就是平方厘米、平方分米、平方米、公顷、平方千米, 我们看一下他们面积单位之间的进率是多少。平方厘米和平方分米相邻的进率是一百。平方分米到平方米是一百平方米到公顷呢,他们之间的进率是一万。 公顷和平方千米它们之间的进率是一百,所以我们在做这个公顷的时候一定要注意啊,公顷它是一个面积单位, 根据我们之前说的小单位换算,大单位我们要除以进率,大单位到小单位我们要乘进率。还有注意点,平方米和平方千米之间的进率其实就是一万乘一百,也就是一百万, 所以这样的话你可能更为系统化。那我们想一想这些是面积,其实还有一个边长,我们看一下这几个面积单位它所对应的正方形的边长 都是多少,那一平方厘米它所对应的正方形的边长就是一厘米,平方分米就是一分米,平方米就是一米公顷,注意它的正方形的边长是一百米,平方千米它的边长是一千米或者是一千米。 公顷和平方千米它最基本的这些知识你要知道还有一个考点,就是公顷和平方千米的应用,那公顷、 平方千米和平方米它们之间可能有的同学会混平方米,在这三个面积当中它是最小的,其次公顷,最后是平方千米,所以平方千米是大的面积单位,常用于像区,就是某某区、市以及省、国家,还有海洋、陆地这些大的面积。而公顷 宫廷呢,主要用于像公园,对吧?这个是我们经常考的宫廷,它常用于公园。接下来我们就学的第三单元的内容。第三单元的内容我们有线,我们开始学的就是线。那线我们可以分为线段、射线、直线,要清楚这三个概念,那线段、射线、直线,它们都是直的,对吧?那线段它有两个端点, 注意啊,他们是端点,就是两个端,两端还有两个端点,这叫三段。射线有一个端点,直线没有端点,这是三个的区别。这里呢给大家补充几个题目啊。比如说常考的就是画一个图,让你去数他的线段有几条,射线有几条,直线有几条, 那我们看这个图啊,他们线段有几条,那你就找两端有端点的,对吧?你像这个是一个,这个是一个,这个是一个,对吧?所以他的线段是有三条啊,线段三条, 射线呢?射线我们可以看其中一个,比如说我们看这一条,这条,你会发现它这个端点在这,那么它这一条是射线,那它这边是不是也是射线?所以它一个点就有两个,两条射线,那这个点呢?也是它这么延长过来,它是不是先射线,这样也是射线,所以一条线它是有四条射线,那么它是不是有三条,所以它是有十二条的射线。 直线呢?直线两端没有端点,所以它就是三条, 这是成口的数线段的。接下来我们看角板块的内容,首先第一个是它的定义,定义成口它是由一个点引出的两条射线,它有端点,对吧?但是在角里边它不叫端点,这个角里边它是叫顶点 啊,有一个点引出的两条射线所组成的图形叫做角,这两条射线在这里称为边,对吧?这个和这个叫边,这个就是角,注意它这个是射线。 还有就是两角,你要会使用两角器进行两角画角,画角的时候注意标角的符号和度数, 我觉得两角和画角其实需要注意的一个点就是一定是从零度,从零度的刻度线开始 开始去数啊,这个一定要注意。那么分类从小到大角的分类给大家梳理出来,锐角、直角、钝角、平角、角,锐角,它是一个大于零度,小于九十度的直角,是等于九十度,它有一个非常明显的标志,能看出来就是相应的这个直角符号,它只要有这个直角符号,就说明它是九十度的角。 钝角大于九十度,小于一百八十度,平角等于一百八十度,角等于三百六十度。平角和轴角作为重要的内容,它是绕端点,这个射线绕端点旋转,平角是旋转半周, 所以它是一百八十度。周角,它是绕端点旋转一周,它是三百六十度。啊。直角、平角、锐角,它们的关系你要知道,一个平角等于两个直角,一个周角等于四个直角等于两个平角,它常出的题就是这个类型的,我们可以看一下,比如让你求角一角二角三角三,这是个直角,很明显角三就等于九十度,那么角二呢? 角三加三十度,加角二是一百八十度,所以角二就等于一百八十度,减去九十度,减去三十度,它就等于六十度。 角一和三十五度构成一个平角,那么角一就等于一百八十度,减去三十五度等于一百四十五度。接下来我们看最后一个板块内容就是平行四边形和梯形,最开始是两条直线的位置关系,在这里一定要注意,两条直线在同一平面内, 它的位置关系是相交与平行啊,你不能说平行、垂直、垂直,它是相交的一种特殊形式啊,相交分为垂直,还有其他普通的这种相交,所以说你要注意这个垂直,它是相交的特殊形式。两条直线的位置关系一定是相交与平行,这个是一错。把垂直放到这 垂直的里边,重要的内容是画垂线以及画垂线段。 画垂线你一定要注意,它是要出头的,并且要标上这个直角的符号。垂线段它是点到线的距离,也就是垂直线段最短,这个不出头, 这是垂线和垂线段的区别啊,这个是个重点。平行线段就平行四边形和梯形,你要知道它什么是平行,什么是梯形。平行四边形是两组对边分别平行的四边形,其实它延伸出来的是对边平行并且相等,不仅平行并且还相等。 这里边也伸出两个图形,正方形、长方形、正方形、长方形、正方形、长方形都是特殊的平行四边形,因为长方形它一拉它的对角就会变成平行四边形。平行四边形它有一个特性,就是易变形。 梯形它是只有一组对边平行的四边形,它分直角梯形和等腰梯形,它们两个也有一个共同的重点,就是画高, 画高的时候要注意三个点,第一个点虚线高一定用的是虚线,第二个点要标上这个直角符号,第三写这个高字 四上同相于几何,主要的内容就是这些,这些基础的点一定要会。
18墨山乡水 01:11查看AI文稿AI文稿
01:11查看AI文稿AI文稿今天要分享的是小学数学思维应用 判断题,把一根二十厘米的小棒分成整厘米长的三个小段,围成三角形,最长的一段不能超过九厘米。我们用逆向思维解答这道题,假设最长的一段超过九厘米,比如是十厘米,那么 另外两段长度之合为二十减十,等于十厘米。此时另外两段长度之合 等于最长边不满足三角形。任意两边之合大于第三边的条件,不能围成三角形。当最长的一段是九厘米时,另外两段长度之合为 为二十减九,等于十一厘米。因为十一大于九,满足三角形三边关系,可以围成三角形。所以把一根二十厘米的小棒分成整厘米长的三个小段,围成三角形, 最长的一段不能超过九厘米。该说法正确,你答对了吗?如果本视频对你有帮助,记得点赞关注哦!
 02:29查看AI文稿AI文稿
02:29查看AI文稿AI文稿同学们,欢迎来到陈老师的课堂,今天我们要学习二年级第二讲数数图形一、 我们已经认识了线段、角、三角形、长方形等基本图形, 当这些图形重重叠叠的交错在一起时,就构成了复杂的集合图形。要想准确的记述这类图形中所包含的某一种基本图形的个数,就需要仔细的观察, 灵活的运用有关的知识和思考方法,掌握数图形的规律,才能获得正确的结果。 来看一下例题,数出下面图中有多少条线段。同学们要正确解答这类问题,需要我们按照一定的顺序来数,做到不重复,不遗漏。 从图中可以看出,从 a 点出发的不同线段有三条,分别是 ab、 ac、 ad。 从 b 点出发的不同线段有两条,分别是 b、 c、 b、 d。 从 c 点出发的不同线段有一条 c、 d。 因此,图中一共有三加二加一等于六条线段。 来看一下练习题,数出下列图中有多少条线段。仔细观察这幅图,从图中可以看出,从 a 点出发的不同线段有四条,分别是, a、 b、 a、 c、 a、 d、 a、 e。 从 b 点出发的不同线段有三条,分别是 bc、 b、 d、 e。 从 c 点出发的不同线段有两条,分别是 c、 d、 c。 从 d 点出发的不同线段有一条 d、 e。 因此,图中共有四加三加二加一等于十条线段。同学们,你学会了吗?
24跟着陈老师学数学 01:05
01:05 00:15查看AI文稿AI文稿
00:15查看AI文稿AI文稿如图,两个正方形如此摆放,边长分别为八和六。求阴影部分的面积。思考五秒钟。
 12:31查看AI文稿AI文稿
12:31查看AI文稿AI文稿同学们大家好,欢迎进入知交会教育广场。今天我们复习的主题是图形与几何。 这节课我们将从以下四个方面展开,一是理清关系,二是触类旁通,三是反思评价,四是拓展延伸。 下面进入第一环节,理清关系。 这个剪角问题想必大家并不陌生,它是数学书第六单元认识图形第一课时认识角的最后一道练习。 我们一起来回顾一下当时是怎么做的。 当时我们是从左边这条边减到上面这条边,减去左上角这个小角,此时还剩下几个角,一起数一数 一二三四五,还剩下五个角。 我们也可以从一个顶点出发,减到对面的这条边,减去一个小角, 还剩下几个角,一起数一数一二三四,还剩下四个角。 我们还可以从一个顶点出发,减到另一个顶点,减去一个角,一起数一二三,还剩下三个角。 同样都是减去左上角这个角,剩下角的结果却是不同的。角的个数与什么有关系呢?其他图形适用吗? 带着这几个问题,我们一起进入第二环节,触类旁通。 这是一个正方形,老师给它变一变形,去一条边,就变出了一个三角形, 再变一变,增加一条边,就变出了一个五边形。 如果这两个图形的纸张减去一个角,还剩下几个角呢?请同学们按下暂停键尝试一下吧。 我们一起来看三角形。减去一个角,可以从一条边减到另一条边,减去一个角,还剩下一二三四个角。 也可以从一个顶点出发,剪到对面这条边,剪去一个角,还剩下一二三三个角。 五边形呢,可以从一条边减到另一条边,减去一个角,同学们,真快!是呀,还剩下这样的六个角, 也可以从一个顶点出发,减到对面这条边,减去一个角,同学们,速度真快!剩下五个角, 还可以从一个顶点出发,减到另一个顶点,减去一个角,此时还剩下四个角。 通过操作,我们知道三角形有这样的两种剪角方法,五边形和正方形一样,有三种剪角方法。 老师把前面的这三种图形的剪角情况罗列成一张表格,请同学们仔细观察思考。 剪角有哪几种方法,角的个数有什么变化?此外,还有什么发现?请同学们按下暂停键思考一下, 聪明的你一定有了不少发现。我们一起来看。第一页, 都是从一条边剪到另一条边,我们把这种方法定义为边对边 角的个数。我们逐个来看,三角形原来是三个,剪完后剩四个角, 正方形原来是四个角,剪完后剩五个角。五边形,原来五个角,剪完后剩六个角,角的个数再增加。 再看第二列,都是从一个顶点出发,剪到对面一条边,我们把这种方法定义为顶点对边 角的个数。三角形由原来的三个,现在还是三个。正方形,原来四个,现在还是四个。 五边形原来五个,现在还是五个,角的个数是不变的。 再看第三列,正方形和五边形,这里都是从一个顶点减到另一个顶点,减去一个角,我们把这种方法定义为顶点对顶点, 善于观察的你一定发现了,发现了三角形这个位置,顶点对顶点的方法是不能使用的,原来呀,顶点到顶点就是三角形的边 角的个数。我们来看正方形,原来四个,现在减完后剩三个。五边形原来五个,现在剩四个,角的个数再减少。 此外,我们还可以发现,角的个数与新的图形边的条数是有关系的, 角有几个,边的条数就是几条,所以我们知道角的个数与新图形边的条数是一致的。 同学们可真厉害呀,发现了不少规律。带着刚才的发现,我们一起进入第三环节反思评价。 通过前面两个环节的学习,我们知道剪角可以有边对边,顶点对边,顶点对顶点,三角形除外这三种方法。 此外,我们还发现角的个数与新图形边的条数是一致的。带着我们的发现,我们一起进入第四环节拓展延伸。 同学们,这是一个六边形,如果减去一个角,还剩下几个角呢?你们还敢挑战吗?请按下暂停键,动手试试吧! 下面我们一起来看一下这位同学的说题。 用剪刀剪去一个角,用虚线表示减法。我们来看第一个六边形,下面 我们要在括号里填写,还剪掉一个角,还剩多多少个角,那么我们就可以试着用边对边的方法。 那么剩下的我们看一下有多少个角,一二三四五 六七,所以下面这个括号里填七。再来看第二个六边形,还是还是同样 减去一个角,把剩下的角填在括号,那我们括号里,那我们可以,这次可以顶点对一对边, 那么我们再数一下剩下的有多少个角,一二三 四五六,还是六个不变,括号里就填六。再来看第三个六边形, 那么我们这次可以用顶点对顶点的方式来剪, 那么来看一下后面还剩下多少个角,一二三四五,所以这个括号里填五。以上是今月份的说题, 你们的想法与结果和他的一样吗?真了不起,为聪明的自己点个赞吧! 同学们,这节课我们一起复习了图形与几何中的剪角问题, 在平时的学习当中,我们也可以试着这样说题来提升自己的数学语言表达能力。这节课我们就先学到这里了,同学们,再见!
 00:50查看AI文稿AI文稿
00:50查看AI文稿AI文稿二上数学思维题,我们来看一下一个三角形的花园,在每条边上种十五朵花,三个顶点都种上,共要种多少朵?三角形就有三条边,每条边种十五朵,那么一共要种 十五乘三等于四十五朵花,他说三个顶点都种上,那么这三个顶点都种重复了,那我们实际上是要用四十五减三等于四十二朵, 所以我们一共是种了四十二朵花,你学会了吗?像这类二上数学的全套必备知识点概念老师已经汇总好了,想要领取的回复九八五。
21湛江钟老师讲数学 02:28查看AI文稿AI文稿
02:28查看AI文稿AI文稿小朋友们,老师上一个视频发的题目你们做了吗?会不会做呢?我们今天一起来公布一下答案。题目是这样的,一个小正方形和一个大正方形的组合图形中求三角形 a、 b、 c、 e 部分的面积,同时告诉你, 小正方形的边长为六,大正方形的边长为八。那我们怎么求呢?这里会用到一个非常关键的信息,叫做在一组平行线中任意移动三角形 a、 b、 c 的 边长为八。那我们怎么求呢?这里会用到一个非常关键的顶点 a, 任意移动位置所组成的三角形面积是相等的。举个例子,在三角形这个 abc 中,它的面积是不是 底乘高,然后除以二,对吧?那我们的高呢?我们已经用红线做的垂直线画出来了,那它的面积求出来。那你把这个 a 移动到 a 一 的位置,会发现 a 一 和 bc, 它的面积同样是底边, bc 乘高, 这个三角形也是同理。由此我们可以知道,一组平行线中任意移动三角形 a、 b、 c 的 顶点 a 的 位置,它们的三角形面积是相等的。那我们会用到这个关键信息啊,在这,我们在这组合图形里找一组平行线,同时呢包含我们三角形 a、 b、 c, 我 们看一下找哪里合适呢? 正好发现 bc, 它是小正方形的对角线。同样的道理,我们在大正方形连接 a、 d 对 角线,咦,这个时候发现我们三角形 abc 正好在 bc 和 d、 a、 d 这条这组平行线中,对不对?那正好 bc 呢?还是顶边 a 是 顶点, 那我们刚刚说了,顶点 a 的 位置任意移动,它们所组成的面积是不是相等的呀?所以我们把 a 移动到点 d 的 位置 a 看一下这个三角形, 三角形 b、 d、 c 的 面积是不是和三角形 a、 b、 c 的 面积是一样的?因为它们同样都是用底边 b、 c 乘它们的高高的话,我们需要做一条垂直线啊,都是一样的长度,所以它们这两个三角形面积是相等的,所以我们只需要求出这个三角形的面积,就可以求出 阴影部分的面积,那这个三角形你们可以观察一下,正好是小正方形面积的,哎,一半,那我们就可以求出来阴影部分的面积就等于我们小正方形的面积除以二。那小正方形的面积为边长乘边长,六乘六,再除以二,等于三十六除以二, 那我们阴影部分的面积就是十八,同学们听懂了吗?你们做对了吗?
 00:29
00:29 00:15查看AI文稿AI文稿
00:15查看AI文稿AI文稿如图,两个正方形如此摆放三角形 o、 c、 g 的 面积是六,求阴影部分的面积,思考五秒钟。
13趣味数学几何 02:36查看AI文稿AI文稿
02:36查看AI文稿AI文稿这是一道刚刚考完的期末考试题,求图色部分面积单位是厘米观察图,这是直角,这是直角,那说明这条边和这条边是互相平行的,那也就是说这个四边形,它是一个直角梯形 图色部分的面积,它就等于直角梯形的面积,然后减去这个 扇形的面积,再减去这个空白三角形的面。那直角梯形的面积怎么算呢?梯形的上底是十,下底是二十,由于这个十呢正是扇形的半径,所以这部分也是十,它也是扇形的半径, 这个角是四十五度,这角是九十度,那说明这个角呢,也是四十五度。那这个三角形就是一个等腰直角三角形,这条腰长是二十,那这条的腰长也是二十, 所以这个直角梯形的勾就是十加二十等于三十。然后呢,我们用 上底加下底的和乘勾除以二,来算出梯形的面积。上底是十,下底是二十,上底加下底的和乘勾勾是十加二十的和,然后再除以二, 它等于四百五十平方厘米,就是这个梯形的面积。然后我们分别再算出这个扇形的面积和这个等腰直角三角形的面积相减就可以了。来,我们先看扇形的面积,扇形的半径是十, 那整圆的面积就是三点一四乘十的平方。由于这个圆形角是九十度,所以它的面积等于整圆面积的四分之一,我们再给它除以四,等于七十八点五 平方厘米。再看二二的面积呢,底是二十,勾也是二十,所以它的面积就等于底乘勾,然后再除以二等于二百平方厘米, 那图的部分的面积就等于梯形的面积是四百五,减去扇形的面积七十八点五,再减去直角三角形的面积是二百,得到的图的部分的面积是一百七十一点五平方厘米。
59数思领跑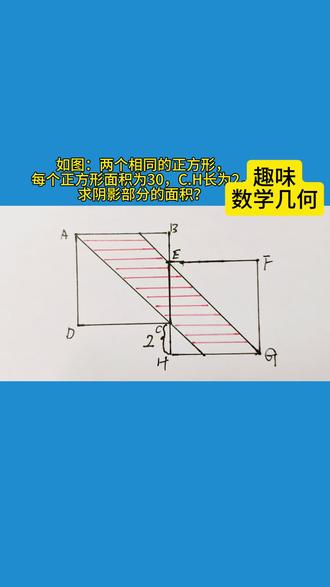 00:15查看AI文稿AI文稿
00:15查看AI文稿AI文稿如图,两个相同的正方形,每个正方形面积为三十, c h 长为二,求阴影部分的面积。思考五秒钟。
11趣味数学几何 00:15
00:15 01:14查看AI文稿AI文稿
01:14查看AI文稿AI文稿斜边十周长二十四,求直角三角形面积,只知边和不知乘积?学霸都卡壳的几何题,一招轻松解这道小学几何题,我们一起来看。已知直角三角形斜边为十,周长二十四,求它的面积。 直角三角形的面积是底乘高除以二两条直角边就是天然的底和高。 已知斜边时周长二十四,可直接算出两条直角边的和是二十四,减十等于十四,但只知道边的和,没法直接求乘积,这时候借助古代的前途就能轻松突破。找来四个完全相同的直角三角形拼成弦图。 四个全等的直角三角形拼接后,斜边围成中间的图形。因为直角三角形的两个锐角和为九十度且斜边相等,所以中间是边长为十的正方形,而两条直角边的和十四正是拼接后外侧大正方形的边长。 接下来计算面积,先算大正方形面积,十乘十四等于幺九六,再减去中间小正方形面积,十乘十等于幺零零,得到了九十六。 这四个直角三角形的面积和最后用九十六除以四等于二十四,就是这个直角三角形的面积了。
262数学殖民火星 06:12查看AI文稿AI文稿
06:12查看AI文稿AI文稿好的,这么这节课呢,进入第四章的学习啊,几何图形,初步啊,这个主要是看大家这个平面内或者空间内的图形想象能力啊。嗯,没什么好讲的,就大家咱们去过一下啊,书上有哪些知识点吧。好的,咱看一下四点一几何图形, 一起来看一下。那么几何图形呢?他其实就是立体图形和平面图形的组合,立体图形和平面图形,那平面就是大家,呃,正在看的这个手机啊,比如说电脑啊,这个他这个表面吧,这个就是个平面对面,然后里面画个图形,就这个就是平面 图形。那立体图形的话,就是比如说你拿起,随便拿起一本书,他是有厚度的吧?那么他整体呢?就是一个立体的,他是立体的,对吧?那他就是立体图形, 很简单。好的,那么看一下图上给的这个,这个书上给的这个几何图形,他是什么定义啊?就看这些啊,长方点、圆柱啊,你看点线段,这些都是几何图形啊,以及这些三角形、四角形,呃,三角形、四边形啊,这些都是几何图形。 好,那么看完几何图形呢,咱们看一下他这个部分的这个立体图形,首先看一下立体,立体图形图上给的是什么定义呢啊?很好理解的,你看这是一个平面,这个是一个平面内啊,很好理解的。你看这是一个平面,这个是一个平面, 这部分不在同一个同一个面,这个图形他就是立体的啊,这个茶叶盒子上有,有一个,有个上面有一个,上面还有一个针对咱们这个面,对吧? 好,这个就是立体图形,没什么好说的啊,看一下平面图形,平面图形的话就更简单,平面图形就是这个立体图形的这些啊,他这是一个面吧啊,这是一个面吧,他可以是三角形,可以正方形,对吧? 三角形啊,长方形啊,圆这些啊,角他也是线段和角,需要注意的线段,角他也是平面图形啊,线段和角他也是平面图形啊,这些图形。好的, 好。那么咱们看完了几何图形以及他的两个组成部分,立体图形和平面图形之后呢,咱们再来看一下这个,嗯,第四个重点,第四个重点就是这个,嗯, 你要学会从嗯头上他给和一个每个都是应该是正方形,正方形的这个积木吧搭起来的这种图形,大家要知道他从他从正面看什么样子啊?从正面看,从上面看啊,也就是从侧面,从侧面 看他是什么样子的,这个需要他这个空间想象的,两个在可以同时拿这个正方形的窟窿啊,这个练习一下,学习一下啊,都可以的。 那么咱们简单看一下这个图形吧,这个图形是非常简单的,相当于三个正方体搭一下啊,也不一定是正方体啊,他可能是其他可能是其他的形状的啊,大家都一样,都一样啊,归根结底原理都一样。然后呢,大家看一下他从正面看的话,是不是只能看到这一部分,这个就是你看 从正面看就是这样,从左面看就是侧面看,左边看只能看到这个面和这个面,对吧?那也就是上下两个面,从上面看当然只能看到正面和正面,这个面,这个面两个面,对吧?再看你看这两个是不一样的,对吧?他说明他这个图形, 哎,好的,哎,这是小细节,这是小细节。我们再来看一下我们展开图啊,那么什么是展开图呢?就是啊,有些立体图形啊,它可以,它是有一些,有一些这个平面图形的围成的,然后将它的表面适当展开呢?可以展开平面图形啊,你比如说这个啊,随便画一个正方体吧,随便画一个正方体, 然后的话最简单的展开图就是什么呢?就是,嗯,这个啊,可能这幅画的不太标准啊。好的,那么最简单这个展开图就是这样子了,对不对?你看这这这个这个四个相当于他的这个四个这个侧面吧,对吧?然后这个相当于一个底面,这个相当 于一个底面,他就是他这个最简单的展开图,但是他不止这一种啊,啊,就是打开图就是这个意思啊 啊,对应图形的这个展开图,把它展示在平面里面。好的,我们再来看一下。六啊点线面体,我相信这一些大家都不陌生,对吧?你比如说点,就是你在平面里面随便点个点线的话,就是随便画条直线,不管是直的和斜的也好啊, 这些都是线,对吧?都是线。然后我们再看面的话面,你比如说这个面,这个面吧,我们再画一个这个正方形和这个三角形,他们都能代表一个面啊,他们所在的都都是一个面,对吧?那么面呢?他其实有有平的面和曲的面,你比如说这个 啊,湖水,对吧?湖水它的表面如果有分的话,它会不会形成波浪一种曲面,对吧?当然咱们接触更多的还是那个平面,对吧?接触更多的还是平面,还有最后呢?什么是体呢?按咱们刚才之前说的,就是这个各部分它不在同一个平面的呀,你看这个在这个平面,这个在 这个正面,对吧?它不在同一个平面啊,这就是体啊。 嗯,好的,然后我们最后呢看一下这个什么是点动成线啊?什么是点动成线?线动成面,面动成体啊?你比如说我一个图形,对不对?然后如果我这里点一个点,然后他左左右动,他会形成一条线的啊?这就是点动成线啊, 点动成线呢?线动成面,就是如果说他上下动的话,会不会有很多直线这些残影啊?他整体就会构成一个面对面,整体就会 面,那么这个就是线都成面了。你比如说这个面啊,这个面的话他上下动,哎,在这个范围内上下动的话,他就会形成这个这个正方形呢,在这个范围内上下动的话,他就会形成这个正方体,对不对?那这个就是面动成体啊,非常容易 理解。那么什么是面面相交形成线呢?你比如说我这个面,这个面啊,这个正面和这个上面啊,这两个面相交,他就会形成这条线了,你看他 他们中间就形成一条线,对吧?好的,那么又什么是线线相交形成点呢啊?你比如说这条直线和这条直线啊,他俩相交就会形成这个点,对不对?好的,那么这个就是面面相交形成线,线线相交会形成点啊, 这个就是点线面体这个四点之间的关系啊。好的,那么这节课呢,咱们整体过了一下四点一,他书上的内容有哪些?好,那么以上呢?就是这节课的全部内容。

