安徽九上几何压轴题
好,各位同学们,大家好啊,今天何老师来给大家分享一道我们四十八中九上期末的选择压轴题, 这道题的话,能拿到分的同学证明你平时学的真的比较扎实,对于动点的理解非常的清晰。在这个题中,同学们他告诉我们,在三角形中, ab 等于六, bc 等于八,那在这里 bc 等于直角, d 呢?在 bc 边上的一点,在边上连接 a d 过点 d 做 d, e 和 a d 的 垂线啊,垂直,而且 d e 等于 a d。 在 这里朋友们他做了一个类似于等腰直角,虽然没有连对吧,但是这个 a d, e 肯定是一个等腰直角三角形, 那连接 c e, 求 c e 最长最小时 b, d 的 长为多少?那这个题应该怎么分析呢?它的核心的难点在于 c e 的 长最小,我们应该怎么分析这个 c e 啊?朋友们, 很明显 c 点是一个定点,是吧?这个三角形是不动的, c 点是个定点,那 c e 的 最小,我们对 e 点是息息相关的,是吧?所以我要搞清楚 e 点他在怎么动, 他是不是在乱动,所以我们的核心点就知道了,我们的核心是 c e 最小值,我们 c 是 定点,我们要分析 e 点这个动点的轨迹。那怎么去理解这个 e 点呢? 他有什么特殊的吗?在这里同学们还可以用何老师教给你的底层逻辑就是多画几个,说实话,朋友们,如果你多画几个,朋友们,你甚至能够发现他的轨迹啊。在初中阶段,那在这里比较扎实的同学已经发现了。在这个题中,我们可以用什么去理解呢?利用 刮豆原理去理解这道题是吧?为什么呢?因为在这个题中,同学们你会发现 d 点和 e 点, e 点啊,它为什么特殊?它就永远满足 a, d 等于 d, e 永远会有一个等腰直角三角形的存在。那怎么去利用这个理解这个等腰直角呢?就可以利用咱们的刮豆原理, 我们刮豆原理的特征是我们有两动,一定两个动点,一个定点是定值 角度呢?夹角呢?是定角是吧?所以在这里你会发现他们,因为三角形 a, d, e 啊,它永远是一个等腰直角三角形,永远是一个等腰直角三角形。 所以的话,同学们在这里啊,你会发现我们的 a 点是一个定点, d 点是一个动点,你会发现 a, d 和 a e 在 这里它的夹角永远都是四十五度,而且这个比值永远是一比一比二的关系。 所以在这里我们就发现了你的满足 a, d 比上 a, e 是 等于一比根号二的,而且这个角 d, a, e 的, 它永远都是四十五度这样的一个特征,那我们就是这是一个瓜豆原理的题目啊,在这里地点我们把称之为主动点, e 点称之为从动点,那从 d 点到 e 点,我们可以看作这绕着 a, 我 们利用几何变换的视野去看待它绕着 a 进行一个逆时针的旋转, 逆时针的旋转,旋转四十五度,而且在旋转同时呢,我把这个放大了根号二倍, 放大了根号二倍。所以同学们我们想要发现 e 点的轨迹,只需要清楚 d 点的轨迹是什么,主动点的轨迹非常清楚,就是线段 bc 是 吧?那从动点的轨迹呢?按照一样的操作就行了,因为同学们还是那一个老师讲过的,我们每一个点再怎么动,那这个轨迹的整体也就怎么动,因为轨迹就是有无数个点组成的, 所以咱们就把这个线段 bc 啊,也是一样,绕着 a 去旋转,四十五度在旋转,同时放大根号二倍,所以他们你会发现 b 点,对吧?你把这个线段线段不就有两个端点组成的吗?这个 bc 不 就有两个端点组成的吗?咱也是这样去操作就行了,所以我把 ab 朋友们也去给他进行一个旋转,四十五度,再放大根号二倍,那其实也是做一个等腰直角三角形出来了,所以 b 的 对应点应该在哪? b 的 对应点应该是构造一个等腰直角三角形,这边咱们把不妨把它记为 b 撇点,在 这里满足 b, b 撇也是六六六,这六倍根号就满足这个了,是吧?那这就是我们线段的起始点, b 撇 c 的 话也是一样的,朋友们也是一样的,我们去构建一个等腰直角三角形, a c c 撇, 构建一个等腰直角三角形即可啊,在这里我们把记为 c 撇连接 a c 撇, 所以同学们我们知道 e 的 轨迹就是线段 b 撇, c 撇连接 b 撇, c 撇就是我们动点的轨迹啊,动点的轨迹, 所以这 b c 撇是 b 撇, c 撇是我们线段的轨迹。那什么时候最短呢?就一目了然了,那应该是 c 点是一个定点, 我们的异点呢,是在 b 撇 c 撇这条线上动,那所以最短距离就应该是垂线段最短,所以我们过点 c 向 b 撇 c 撇做垂直即可,这个就是咱们要找的真正的异点好吧,但是人家问的是你找到了,人家问的是 b、 d 的 长,这怎么办啊? 在这里朋友们,这种旋转的感觉是吧,我们已经发现了,它其实就是一个手拉手的相似,我们此时连接这个 a、 e 就 可以了。连接 a e, 那 第一点的话,朋友们,就是它做一个等腰直角的位置啊,做个等腰直角的位置 啊,这个可能稍微有点难画啊,这个有点难看出来啊。呃,你可以,你可以在图中他们重新画一下,把此时的地点找到啊。此时的地点找到,你会发现,因为这种旋转的感觉,我们永远会有三角形 a、 b、 d, 他 应该是相似于三角形 a、 b 撇 e 的, 这个相似是永远全立的,是吧?因为发现啊,利用这个一比根号,再加一比根号,还有中间的公共角模型,永远都会有这种手拉手的相似, 所以的话,我们的 b、 d 和咱们的这个 b 撇 e 的 比值就应该等于一比根号二,而 b 撇 e 能不能求呢?完全可以,这里边同学们大家看看怎么求呢?你的总长是八, 这边是六,所以剩下的应该为二,是这样的吧,四十五度,这个呢,同学们,因为手拉手的相是直角,所以这边也是四十五度,那所以我就搞清楚了,这是一个等腰直角三角形,而且斜边为二,所以 b 撇 e 的 长就应该为根号二啊。 b 撇 e 的 长应该为根号二, 那 b 撇 e 为根号二,那你的 b、 d 的 长就应该为一。所以这个题同学们,单选 a 啊。我们利用刮豆原理分析一点的轨迹,我们利用垂线段最短找到最短的这个 c e 是 吧?然后怎么去求出此时的 b d 长呢?因为这种旋转 永远都会有手拉手的相似,这个相似比呢是一比根号二,我们就进而去求出此时 b d 长这道题。同学们大家好好的去总结一下这种刮豆原理。
粉丝457获赞1686
相关视频
 04:27查看AI文稿AI文稿
04:27查看AI文稿AI文稿好朋友们,我们来看看这个包口区九上期末考试的第十四题,这道填空压轴题啊,我们来一起读读题。这里告诉我们,在三角形 a, b, c 中, a, b 等于四 啊, b, c 等于二。做好标记,线在 a、 c 上去一点, d 使得角,使得 d, b 等于 b, c, d, b 等于 b, c。 这个咱也标二 角, d, b, c 等于角, b, a, c 奥特曼。那这个标记之后,同学们厉害,同学已经发现了,在这里已经存在反 a 了,公共角在这个位置是吧,异侧角相等,所以我会知道三角形 c, b, d 应该是相似于三角形 c, a、 b 的。 具体怎么用呢?我们先稍事休息一下,看看他等会在干嘛啊。题读完,然后的话, p 呢,是 b, c 边上延长线上的一点过点 p 做 p, q 垂直于 bp, 做了个垂直标。好了,那在这里他进行一个延长,使得 cp 设为 x, d, q 呢,是为 y。 问你 y 关于 x 的 函数解析式,像这种题,很多同学一读完就开始害怕了啊,袁老师,他的函数关系式我也不知道啊,你要这样理解,同学们,我们知道函数解析式还有个名字叫函数 关系式,我们的核心是发现 y 与 x 的 关系,那根据这里边图形,大家来看 y 和 x 有 什么样的关系呢? 其实他们从图形来看的话,他就做了一个直角,能够把 x、 y 联系起来,所以我想到是他们是利用三角函数能够建立起 x 的 和 y 的 关系,所以在这里他们把目光放在这个角。阿尔法老师设的阿尔法上,你会发现 cosine, 阿尔法 啊,这个 cosine 啊,是零比斜,他就等于二加 x 比上二加 y 啊,这就是 x 与 y 的 关系啊,利用这个 cosine alpha 实现。所以这个题同学们我只需要把 cosine alpha 求出来就行了。那 cosine alpha 怎么求呢?题目中最开始的相似应该怎么用呢?我们分两步去解决这个问题。首先同学们,我们先想一想 这个相似怎么用,这个相似的话,同学们大家来看啊。在这里这个相似我们知道,大的小的三角形是一个等腰三角形,那大的很明显也是一个等腰三角形,是吧?而且的话,同学们,在这里, b、 d 和 ab 它刚好是一组相似的对应边, 这个 b、 d 和 ab 啊,它刚好是相似的对应边就是一比二的关系。所以利用这个对应边的话,同学们你在标记时候效率就很高了。相似比是一比二,所以 c、 d 就 应该为一,然后呢, bc 是 二,那 ac 总共应该也为四, 那所以 a、 d 的 话就应该为三,就是咱的标记啊,标短不标长,所以咱把短的先擦掉。然后的话,朋友们,这个相似用完之后,那既然我要想求 cosine alpha, 那 我就要把 alpha 放到直角三角形中,是这样的吧, 那那肯定我就不用这个本身的这个了。朋友们,我们用上面这个不等量代换吗?这不也是咱的 alpha 吗?是吧?所以我想把它放在直角三角形中,我直接做一个垂直就完事了。那过哪个点去做比较方便呢? 这里边需要试一下。同学们,我们只需要过点 b 向 c、 d 做一组垂线就可以了。假设交点我们记为 e 点, 那做完垂直之后,因为等腰三角形会带来三线合一,所以 d e 和 c e 的 长,同学们,刚才是一,咱标个零点五就可以了, 是这样吧,那标记好之后, cosine 法就已经出来了。 cosine 法的话,我们知道是等于零比斜,零边是 a, e 斜边是 ab, 所以 应该等于三点五, 比上四完乘以二,应该等于七比八,是吧?而七比八朋友们,就是我们刚才这个二加 x 比上二加 y 的 关系,所以我们进行一个交叉相乘,关系就出来了。所以十四加七 y 应该就等于十六加八 x 一项算一下,七 y 的 话就等于二加八 x, 所以 y 就 应该等于七分之二,再加上七分之八 x, 那 这个就是我们 x y 的 关系式。所以这个题总结一下,老师要告诉两个东西,同学们,函数关系式不要着急,不要直接陷入一次二次, 一次函数,二次函数这样的害怕的过程中,你要找到 x y 的 关系联系在哪个地方?这道题是利用这个 cosine alpha 实现的。其次,同学们在题目中给的条件我应该如何去正推使用,你要把这个条件给它用好, 是吧?另外的话就是对于三角函数的求解,想求三角函数,我就要把这个角放在直角三角形中啊。然后呢,我们去,呃,利用这个线段长,利用一些几何特征,把这个线段长给它求出来。好,这个题我们就讲解到这。
 07:39查看AI文稿AI文稿
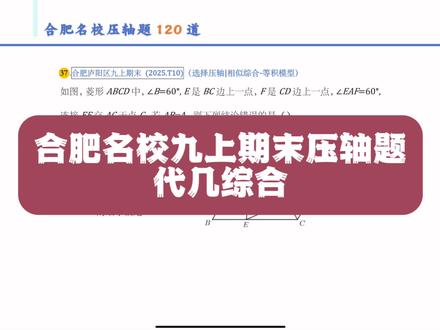
07:39查看AI文稿AI文稿好题都是一道顶十道的,这道题是合肥名校压轴题一百二十道的第三十七题。这道题综合了菱形、等边三角形、叠角模型、一线三角斜八字模型 以及最重要的这道题我们可以用代数的方法去求解动点最值问题,也即是代几综合。我们来看一下这道优秀的压轴题,它的解法, 它给的条件是,菱形 a、 b、 c、 d 中角 b 是 六十度。菱形它本身就是特殊的平行四边形了,如果有一个角是六十度,那么它就更特殊了。特殊在什么地方?特殊在如果我们连接一百二十度的 这样的两个顶点,那么就会把这个菱形分成两个等边三角形,也即是三角形 a、 b、 c 和 a、 c、 d 是 两个等边三角形,并且这两个等边三角形,它的边长是四, 又告诉我 f 点是 c、 d 边上的一点,这一点呢,是可以运动的。 并且角 e、 a、 f 这个角是六十度,由于角 b、 a、 c 是 六十度,而 e、 a、 f 又是六十度,那么这两个六十度的角是不是就重合在一起?这就是典型的叠角模型。 来背一下口诀,叠角必有等角。那么在这里我们能推出角 b、 a、 e 和角 f、 a、 c 是 相等的,那么围绕着这两个相等的角,必然会产生两个要么全等,要么相似的三角形。这两个三角形,我们发现 它有两组角是相等的,角 b 等于角 a、 c、 f, 角 b、 a、 e 等于角 f、 a、 c 再加上 ab 等于 ac, 所以 它俩是全等的。 全等之后,我们能推出 a、 e 是 等于 af 的, 也就是这个三角形 ef, 它是一个等边三角形,因为有一个角是六十度的等腰三角形,就是等边三角形。到此为止,我们把这个题目中的信息已经挖掘的差不多了。好,这里是三个 等边三角形,它们共顶点。来看下。第一问,他让我求 ef 的 最小值, e、 f 的 最小值,我们可以转化成求 a、 e, 那 么肯定是垂线段最短,所以从 a 点往 b、 c 做垂线,假设垂足为 h 的 话,那么 a、 h 就是 a、 e 的 最小值,也即是 e、 f 的 最小值。而这个 a、 h 很 明显,它是在一个特殊的三十、六十、九十度的直角三角形当中。好,这是四, b、 h 是 二,所以 a、 h 是 等于 e, f 的 最小值,是等于二倍的根三,也即是 a 选项是正确的。好,那把 a 选项求出来,同学是比较多的,但是 b、 c、 d 能够算出的同学是比较少的。 b 选项让我们求 c、 g 的 最大值, c、 g 是。 在这个地方来看一下老师的解法,老师储备的模型以及对模型是非常熟悉的,所以我就从我的工具箱里面拿出了一线三等角,这样一个模型是非常熟悉的,所以我就从我的工具箱里面拿出了一个六十,这个角是不是六十, 这个角是不是六十?这是不是典型的一线三角?一线三角。在这种情况下,三角形 a、 b、 e 和 g、 e、 c 是 相似的,那么直接利用相似带来的结论,也即是 a, b 乘以 g, c 是 等于 b, e 乘以 e, c, 很 明显, a、 b 是 等于四的, g, c 是 让我们求的。我不妨设 b、 e 这一段为 x, 那 么 e、 c 的 话,是不是就四减 x? 到这里的话,你已经看出来老师是在用代数的方法了,所以我们得出了四倍的 g c 等于 x 倍的四减 x, 这是不是一个方程? 我们稍作整理,发现 g c 等于四分之一 x 倍的四减 x, 很 明显,这是一个二次函数的形式,当 x 等于二时, g c 取得最大值,最大值是四分之一乘以二,再乘以二等于一,也即是 b 选项,正确的 c 选项。让我们求三角形 cf 面积的最大值,我们是不是首先要把三角形 ecf 它的面积表示出来?如果以 ec 为底的话,是不是要从 f 点往 bc 做垂线? 那这样 fh 是 不是就在一个特殊的三十、六十、九十的直角三角形 fhc 当中,这是一百二, 这是六十,这是三十,这是垂直的。所以来看一下 f c, 我 们前面是不是已经正过了?这两个三角形 a, b, e 和 a f, c 是 全等的,由于 b e 是 x, 那 么 f c 是 不是也是 x? 那 c h 是 不是二分之一 x, f h 是 不是二分之根三 x? ok, 好, ec 乘以 f h 乘二分之一。好,二分之一倍的 四减 x 乘以二分之根三 x。 好, 整理一下,发现仍然是一个二次函数的形式,所以还是在 x 等于二十取得最大值,这个最大值代入之后发现是二乘以二四 四,再乘以四分之根三,那就是根三。发现 c 依然是正确的,那这道题肯定是选 d 了,但是 d eg 乘以 g f 的 最小值,为什么是三?我们也可以通过代几综合,也就是代数的方法把它算出来。来看一下老师的解法, eg 乘以 g f。 来找一下 eg, g f, eg 是 不是在这里, g f 是 不是在这里? 老师的解法还是用模型?因为老师储备的工具比较多,我在这里又看到了一个斜八字的模型,因为在这里是不是六十度,这个角是不是依然是六十度,所以这就是一个斜八字的模型。而 e g g f 就是 在这个斜八字模型里面。 我们直接利用斜八字模型的结论,那就是 e g 乘以 g c 的 jc, 也就是 b 选项的这个 jc, 它是有最大值一的。我不妨设 jc, 它的长度为 t, 那 么我们就把这样一个乘积, eg 乘 jf 表示成了 t, 因为 j c 是 t 啊。那么 ag 的 话,是不是用 a c 减去 t, ac 的 话,是不是就等于 ab 是 等于四的?那就是四减 t, t 乘以四减 t 很 明显是一个二次函数的形式,它与 x 轴两个交点,一个是零,一个是四,开口向下,所以 应该是在 x 等于二的时候取得最大值。但是注意一下,此时 t 是 不是有最大值, t 的 最大值是不是呃一,所以呢, t 注意一下它的范围其实是大于等于零,小于等于一的 好。 t 等于零的时候,也记着这个 f 点运动到 c 点的时候,这点的话呢,也跑到 c 点了。好,这是一个运动的一个过程。 好,因此 e g 乘以 g f, 它的最大值就是在 t 等于一处取得。好。这个最大值我们代入之后也可以算一下,那就是一乘以 四减一等于三。好,最大值是三,最小值是多少?最小值是在 t 等于零处取得,也即是最小值其实是等于零的。这是合肥名下压轴题一百二十道这本书里面的一道典型的关于动点最值的压轴题。这道题典型在什么地方?就是 他的 b、 c、 d 三个选项。我们是用代数的方法去求解的啊,这种方法是很多同学不重视的,或者说不熟悉的。 好在这里的话呢,就是给大家拿出来这道题,想引起大家的重视,因为我们初中,因为我们安徽中考是非常重视代数推理能力的,所以呢,代数的解法看起来好像没有几何那么的巧妙,但是呢,他是你以后学习高中的一个基础,好,他也非常的重要。
183任老师讲中考压轴题 16:46查看AI文稿AI文稿
16:46查看AI文稿AI文稿这个视频我们来讲九上期末考的压轴题,这个题整体难度会比较大,那我们来看题目,它首先告诉我们是正方形 a、 b、 c、 d 的 面积是三十六, 但是正方形的面积知道对应我们是不是也就知道它的边长其实是会等于六?一是动点, f 是 bc 上的中点,那这一条线段等于这条线段,并且它们多等于三, 那像现在告诉我们是设 c e 为 m, 三角形 b e、 f 的 面积是 s, 求 s 以 m 的 函数关系,那在我们体系当中看到的是面积,你建立自己的体知识体系, 那看到面积你对应了你要想到什么?第一,你可能要想到的是关于公式法,也就是说比如我要求三角形的面积,那就是我用底层以高。 第二,我们可能关系到面积,我们会往胳膊的方向去考虑,那很简单,这一题他已经告诉我们要求的相关的三角形的面积底知道了,高也知道了,所以我们可以直接用公式法。那我们在这一个地方 s 的 面积会等于什么呢? 二分之一底是多少?底是 b, f 等于三,那高数是 c 一, c 一 就等于 m, 所以 s 它会等于二分之三的 m, 这是关于第一小问相对比较简单,那我们来看第二小问,它告诉的话 句式上面 c 一 上面的一个动点,也就是这里面屏幕的背景是这两个点都是关于一个动点,那在这一个地方他又告诉我们的 b m 这个等于九十,等于九十度, 并且他告诉我们这一个角会等于这一个角的三倍,那像这种情况,我们可以先再涂两个,这一个角等于 r, 那 这个角是会等于三 r, 这是你可以在题目看到背角,这样去标注,可能会更清晰,并且你在像这一种背角关系,你看到这个你要想要什么,你要对应的去考虑说可能会潜在你要做题过程当中可能会使用到你会把大的角通过什么或平通过, 这样比如说这是三倍角,那你可能会做这样子是阿法,这个是阿法创造角度的相同的这样关系。另外你可能会什么假设这一个是阿法,那么你可能就是补两个角,那他等于阿法建立出角的等量关系,这是可能看到倍角关系你要去想到的, 那他第二个信息又告诉我们了,吞整的这一个角会等于左边的这一个线段的比例关系,那是我们要先想到首先三角函数里面的吞整, 他首先都是建立在什么的样子的一个填集条件,你必须要想他必须要在直角三角形里面建立关系,也就是说只 在三角形里面,他能鉴定说线段之间的关系,所以你一定要看到三角函数里面的相关信息,一定要想着去构造直角三角形。 第二还有这一个地方, b e 减 e f, 那 b e 减 e f, 那 像这种线段,这是不是关于线段的和差关系?那线段的和差关系你就要联想到什么截长补短。好,那第一想问他要求的是吞整 b h c 的 值, 也就是求这一个角的值,那这个角题目是不是告诉我们这一个它有线段之间的这样子的一个等量关系, 那我们首先看到要求吞针的这一个角,那我们第一反应是不是向这边说要在直角三角形里面,并且这个地方确实也给我们提供了一个直角三角形,因为这一个垂直这一个,那这边垂直的这两条线段垂直这个角是不是九十度? 那我们如果求,如果能知道这一条线段和这一条线段的长度,是不是就可以求出来相对是比较直观的这样子的一个方式。 但是题目当中告诉我们的条件里面关于线段的值是除了正方形的边长是六,还有这边是三,这边是三,除了就没有说在这一个范围里面去提供相应的一个线段值。像这一种我们一般不会去考虑这这一边的一个解析的一个方式, 那我们接下来就需要去考虑说要怎么来解,那像在我们现在所有的题目当中一定要去有合理的使用,说所有的一个条件都不需要去用到,那这个题目当中只告诉我们说除了这边垂直这一个,这三个之间的一个关系, 那这一边的关这一些关系我们说我们要怎么去入手?从这一边得到的一个暗示,我们刚才也分在提议里面,关键信息分析的时候我们有说过,第一我们会去什么去把角度进行一个平分, 这边截长补短,那其实从这两个条件你一结合,你可能就会去想着说,那我先来处理这一个,如处理这一边通过补短截长不断的方式,那是不是就可以构造线段的一个相等,那在这一个我们先考虑就是截长, 那截长我们会在什么?会在 b e 线上截取一个点是 i, 那 使得 e i 会等于 ef, 我们这样子来做这,那我们通过这样子的截长补短,那我们截长补短完以后,这一边做这个什么? e i 会等于 e f, 那 e i 等于 e f, 那 我们现在是不是得到这一个三角形?它是什么?等腰三角形,对不对?所以我们就可以得出, 那这一边它是一个等腰三角形。那等腰三角形,我们是不是就会想着说,那我这个角知道,这个角也知道,那这一边的这个角是不是可以求出来?那这个角求出来,这两个角是不是对应也会知道?那我们来看一下,这又会有什么这样的一个关系? 我们设这一个角等于角一,那这边的角一是不是会等于什么?等于一百八十度减去四倍的一个算法, 那四倍的四倍的算法,顶角的角,因为我们知道,那我们把这一个角角,这个角为角二,这个角为角三,那我们是不是可以求出角二等于角三,会等于二分之一的一百八十度减去角一,那这个求出来它会等于两倍的算法,发现了没有? 角 b f d 等于三倍算法,那角三等于什么?两倍的算法,那现在你是不是就可以知道角 i f b 知道了什么?等也等于 alpha, 它会等于三 alpha 减去二, alpha 也会等于二,等于 alpha, 那 你现在有没有发现, 也就是说现在的角 d 角 e b f 等于角 i e f, 那 这两个角相等,是不是就得到了 b i 会等于 i f, 也就是 三角形 i b i f, 它是一个等腰三角形,好,那这一个它是一个等腰三角形,它等腰三角形你会想到什么?因为现在我们要求的是这一个,但是我们知道一些,这一个角会等于什么?会等于 这一条边通过我们现在算完,那是不是等这一条边比上这一条边,就等于这一个这一个角的吞整角? 那或者是这一个表等于这比上这一条边,对不对?那我们现在这一个是一个等腰三角形,那等腰三角形,你一定要联想到什么?等腰三角形?你一定要敏感的联想到什么一线三线合一,所以我们这时候我们可以过什么? 过 i 做 b f 的 一个垂线,假设这一个四 k, 那 这一边你做垂线以后,那你是不是刚才我们知道什么?那我们现在是不是就可以有什么 b k 会等于什么?二分之一的 b f, 那 b f 等于多少?等于三,所以等于二分之三,对不对?那这一个地方等于二分之三,那这时候我们再来看一下,我们刚好 这一个是一个什么直角三角形,那这一个也是一个直角三角形,并且它什么共顶点,这是不是是 a 锥模型?那如果是这样这两个三角形相似,那你是不是就可以求出这一条线段比上这一整条线段的一个比值,对不对? 并且 b i, 你 是不是也可以求出 b i 或等于 b e 的 这一个比值?对,所以我们可以易得到什么三角形 b k i 会相似于三角形 b c e, 那这两个三角形相似,你就可以得到 b k 比上 bc 会等于 b i 比上 b e, 那 它会等于什么?会等 b k 是 等于二分之三,对不对?那 b c b c 等于六,那它会等于四分之一,那这我们已经求出这一边它等于四分之一。那四分之一。四分之一,所以我们就可以得出什么,所以我们就可以知道 b e 会等于四倍的 b i, 那 b i 知道你是不是可以去除 e i e i 是 不是等于 b e 减去 b i, 也就会它会等于三倍的 b i 的 值,并且 e i 我 们前面已经知道 e i 会等于 e f, 那 他也是 b f 也会等于三倍的 b i, 那 这边我们可以叫吞着角 b h c, 他 会等于 b e 减 e f, 那 他是等什么? 等于 b i, 那 ef 是 等于三倍的 b i, 两个 b i 相约,那就会等于三分之一,所以我们第一问就除出了 t 正的角 b h c 的 值是三分之一。好,这是第二第二问的第一小问, 接下来我们来看一下第三小问,我们来看第三问,求 c n 的 值。在这一个有这一个条件和这一个条件,在我们在解决 解决第一想问的时候已经使用过了,那在这一个条件是不是我们到目前的话还没有去使用?这是我们可以重点去引起来关注的, 现在的数学当中,特别是几何题当中,所有条件都是需要去使用到,如果你某个条件没有使用过,你可能这时候你要引起注意,是不是有哪里算错?这是现在的一个压轴题普遍的一个特征,那是不是在这一个地方其实还有一个隐藏的一个条件是什么?呃,是不是 这一个你也是想到的,这一个三角形的面积等于多少?这一个三角形的面积是不是等于底?是六,高也是六,所以这个三角形的面积是不是等于十八?这也就是从这个题目当中 引含的这个条件,你也需要去把它挖掘出来。那如果是这样子,那你是不是如在这一边我是不是可以去过 c 点做 b h 的 一个高?那如果做这一个高,你是不是?如果我再知道这一个,那是,或者是我只要去知道这一条跟这一条叉之间是不是会赚建立一定关系,这两条相乘的二分之一 等于十八,对不对?因为这一个看成是底,这一个看成是高,那如果你做了这样子的一条高,这个是不是直角?那现在是不是又通过我们刚才除了这一个吞整角又建立的这样子的关系? 也就这一条比这一条会有一定的成比例的关系,也就这一条比这条是三分之一的这样子的一个关系,对不对?这 做了也就我们做这一条高,是可以达到什么?我们做辅助线的原则,一举多得的这样子的一个目标,对不对?所以我们过 c 点做他的一个垂线,假设这一点为,这一点为 p, 那这一点为屁,那我们再来看,如果这一点是为屁,那在这一个地方我们还会看到什么?在这里面你可以去注意这一个角会等于这个角,对不对?那这一个角等于这一个角,那这一个角加这一个角等于九十度, 并且这一个角加这一个角也等于九十度,那你现在是不是就可以得出这两个角其实它是相等的,对不对? 那相等这一个地方又是九十度,这一个地方又是九十度,那你是不是可以得出这一个三角形和这一个三角形相似?其实里面是存在很多的这样子的一个相似的一个关系。那我们现在是得到了什么? 那你现在就可以去得到了它对应边乘比例的这样子的一个关系,那我现在我们就可以去得到什么?我们这一个又可以推出什么? p c, 它会等于什么? p c, 我 们把这一些具体的 b c 等于六,还有什么?还有 a b 也等于六,那我们 p c 就 可以转换回,它会等于三十六除以 b h, p b 会等于等于六, a h 除以 b h, 对 不对?好,那我们现在是不是就求出了 p c p c 这一段的关系?还有这一段,那我们又知道 p c 跟 p h 的 话是三一比三分之一的这样子的关系,也就 p c, 它会等于 p h, 会等于三倍的 p c, 那 这一边是不是等于三?乘以 b h 乘以三分之六,也就是等于 b h 分 之一百零八? p h 也求出了,我们现在求出了 v p 和 p h 的 一个式子, 那我们 b h 是 不是把这两填线段相加就可以得出 b h, 那 所以我们 b h 是 不是会等于什么?会等于 p v 加上 p h, 那 b p 会, b h 会等于 p v 会等于六?乘以 a h 除以 b h, 加上一百零八除以 b h, 那 b h 这一个式子里面它的都含有分母 b h, 那 我们是不是可以去分母?把式子两边同时乘以 b h, 所以 我们就可以推出 b h 的 平方会等于什么?会等于六,乘以 a h 加上一百零八,那这时候你有没有发现 b h 会等于什么? b h 的 平方,它是不是是这一个直角三角形 a b h 的 斜边对不对? 那它的斜边的平方是不等 a b 的 平方,加上 a h 的 平方等于三十六,所以它等于三十六。加上 a h 的 平方等于六倍的 a h 加上一百平方,发现了没有?这一个式子相当于是一个关于 a h 的 一元二次方程, 那我们接下来再来整理一下。好,那我们现在把式子整理成这样子,那整理成这一个式子,接下来我们是不是可以去求减 a h 的 值? 那我们这时候可以用什么?用十字相乘法,那这一边的话相当于 a h 减去十二,乘以 a h 加上六等于零, 那我们可以解得 a h 等于十二或 a h 等于什么?等于负六,那负六肯定是舍去的对不对?因为线段的长度不可能是负数,所以我们就求出了什么,我们就求得的 a h 的 长度,这一条的长度是等于十二, 那我们要去的是这一个,那是不是接下来我们再来看这一个是等于九十度,对不对?那这一个也是九十度,那这一个角加这样,这个角等于什么?等于九十度,那这一个角加上这一个角也等于九十度,所以我们现在就得到这一个角等于这一个角, 并且这一个等于九十度,这一个等于九十度。所以是不是就可以正得三角形 a、 b h 跟三角形的吗?三角形 d、 c、 n 这两个三角形相似,那是不是就可以来求出 c n 的 值? 所以三角形 a、 b、 h 相似于三角形 d、 c、 n, 那 这两个相似的话,所以我们就可以得到什么 a b b, c, n 会等于 a h 比上 c d, 所以 cn 的 值会等于 a b, a b 等于六,乘以 c d 也等于六,除以 a h, a h 刚才算出来等于十二,所以求得等于三,所以最后求得的 c, n 的 值会等于三。其实这一个题目相对于对于各位同学来说要求比较高是什么?是你要充分的去挖掘题目里面的条件,也就是要把题目里面的 条件挖掘出来,并且把挖掘的条件对应说在你知识体系当中对应的一些相关的一个知识点,这一个关联和体系的搭建是比较重要的。
118初中数学戴老师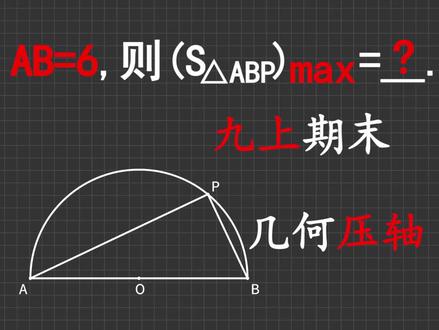 04:15查看AI文稿AI文稿
04:15查看AI文稿AI文稿快来看这道题,你需要几分钟?今天这道题是一道九上期末考试的几何压轴大题。我们先来看第一问啊, 题目给了我们一个四边形 a、 b、 c、 d, 其中 a、 d 和 b、 c 是 平行的,他说若三角形 a、 b、 c 的 面积是九,让我们求三角形 d、 b、 c 的 面积,那这个是不是直接写啊?因为它的面积也是九, 因为平行线之间的距离是处处相等的,所以这两个三角形的高是相等的,而又因为它们俩共用一个底边,所以它们的面积自然也是相等的。 好,再来看第二问,题目给了我们一个半圆,他的直径 a、 b 是 等于六的,然后 p 点是圆上的一个动点,让我们求三角形 a、 b、 p 面积的最大值,那由于他的底边是一个定值,所以我们只需要研究他的高就行了。 显而易见,当 c p 最大的时候,三角形 abp 的 面积会有最大值。接下来我们连接 o p, 那 它的长度是等于三的。 不难看出,在直角三角形 cop 中,直角边 cp 是 小于等于斜边 o p 的, 所以说 cp 的 最大值是三,那三角形 abp 面积的最大值就是九了。 好,我们继续来看第三问,题目给了我们一个直角三角形 abc, 其中 ab 的 长度等于二角 abc 等于六十度,然后 p 点是平面内的一个动点,并且角 cpb 是 等于四十五度的。 题目问,若 aq 和 cp 平行,让我们求这个四边形 aq cp 的 最大值。 好,读完题目之后,如果你又是一头雾水,不知道该从哪下手的话,那我建议你回头好好分析一下前两问存在的意义。 我们都知道几何压轴题永远没有无缘无故的第一问,那根据他的提示,我们可以知道他这是在告诉我们平行线之间等底的两个三角形面积是相等的,而这第三问刚好也有一组平行线, 所以说我们肯定要进行一个面积的转换。好再来看第二问的提示啊,他是在告诉我们,在一个固定的圆中,如果弦长为定值的时候,那么圆上动点和这条弦构成的这个三角形,它的面积是有最大值的, 也就是说我们可能要把这个四边形转化成一个圆内的三角形,虽然来说 p 点确实是一个圆上的动点,但是显然这个三角形 a、 q、 p 的 面积和三角形 b、 c、 q 的 面积不是相等的, 所以不要想着说去用三角形 bcp 的 面积来解决问题,这条路肯定是走不通的。那照这么分析下来的话,我们就只能把 a、 c 当做这条定弦来看了。 这里我们可以把四边形 a、 q、 c 的 面积拆成三角形 a、 q、 c 的 面积加上三角形 a、 c、 p 的 面积, 而其中三角形 a、 q、 c 的 面积又等于三角形 a、 q、 p 的 面积,那如果我们延长 c p, 并且令 d p 等于 a、 q, 然后再连接 a、 d 的 话,那这个四边形就是一个平行四边形了, 这个时候三角形 a、 q、 p 的 面积就等于三角形 a、 d、 p 的 面积了。现在你们再看 三角形 a、 d、 p 的 面积加上三角形 a、 c、 p 的 面积,它刚好是等于三角形 a、 c、 d 的 面积的,并且这个角 a、 d、 c 还是一个定四十五度。 所以说现在问题是不是就变成了跟第二问是一样的了?那后面的计算我就不讲了,你们自己慢慢去算去吧。最后算下来这个四边形面积的最大值应该是三加三倍根二,你学会了吗?
629五星几何兔 12:35查看AI文稿AI文稿
12:35查看AI文稿AI文稿讲一下最新的五中稀缺的这个期末考试的第十题啊,我们来看一下题目。首先审题, c 呢等于 c, b 等于二。标一下二二角 a, c、 b 呢等于九十度,所以这样能得到一个等腰直角三角形 a、 c、 b, 因此 a、 b 呢等于二倍。根号二 点 d 呢,在 b、 c 上运动, d 是 动点 d。 在 运动的过程中呢,以 a、 d 为边,做一个正方形, 做一个正方形,过点 f, 再做 f, g 呢,垂直于 c 的 延长线,交它呢于点 g, 然后把 f、 b 呢给它连起来啊,交这个 d, e 呢于点 m, 这个 d, e 呢又跟这个 a、 b 呢交于点 n。 问,下列说法错误的是, 那这一题很显然它是一个怎么样反照这个二五年咱们的这个中考题出的一道这个压轴,对吧?我们这二五年的那个背景的话是一个刮豆模型,那这题依然还是一个呃,刮豆模型。所以这一题的话,就需要大家对刮豆模型呢有一个非常熟练的一个了解。 好,我们来看一下啊,这个刮动模型呢,我们就先不在这里面介绍了,有兴趣的同学。嗯,可以看我以前录的这个视频。我们来看一下这个刮动模型的话。呃,很显然这个点 d 呢是主动点, 点 e 呢是从动点好光度模型满足什么呢?就是主动点到定点的距离跟从动点到定点的距离比是一个定值。那这题很显然, a、 e 比上 a、 d, 就 这有个距离比, 这个距离比很显然等于根号二是一个定值。还有一个就是夹角的这个夹角,比如说主动点 和定点的连线,从动点和定点的连线,你看,以定点为顶点组成的这样的一个夹角,那这个夹角呢?也得是一个定角,那这题很显然它是一个四十五度,有了这两个条件,它才符合我们的这个刮动模型。 那刮动模型的话,熟悉的同学应该知道,就是主动点的轨迹它是一致的。现在主动点的轨迹呢, 是在一条直线啊,或者说他这是直线上面的一条线段,那么我点 e 呢?他应该也是直线上的一条线段,对吧?那么所以这样的话,我们就可以把从动点的轨迹给他,干嘛给他确定,我们要确定这个从动点的轨迹, 那从动点的轨迹呢?如何去确定呢?方法呢?有很多。那这题比较特殊,我们可以通过主动点的特殊位置去找从动点的特殊位置。 大家来看一下 d 点在特殊的位置时候,能推 e 点的这个特殊的位置,我们就把 d 放在哪个特殊位置,你比如说 d 可以 在 这个 c 的 时候,对吧?那如果 d 跟 c 重合,此时 a d 是, 是这个对不对?那很显然,那我的这个 d e 呢?是不是就呃等于这个 c b, 所以 这个当地在 c 的 时候,那 e 呢?是不是在这个地方?这帮我可以标个 e, 对 吧?好,那这时候我们再找 d 的 一个特殊位置, 那显然我们可以找当 d 在 b 点的时候,你是不是以 a d 为边?是不是再向外面再做一个?等腰直角三角形的时候,或者在外面再做一个这个,呃,正方形的时候,给它擦一下,那此时这个正方形画出来了,那刚好 应该是长这个样子啊,那刚好应该是长这个样子啊,那差不多呢,嗯, 在这啊,这个地方我图就不要画的特别准了啊,那很显然,那这是一几啊?这是一二,你看这三个点刚好在一条线上面,一一一二一三,我们刚才知道这个从动点的轨迹是一条直线,对吧?其实我只要找这条直线上面的两个特殊的点,就能把这条直线给它,缺什么给它基本确定了啊。 好,那这样的话,我们的一点的轨迹呢,就全部怎么样解决了?把这个图给它擦掉,五官的图都给它擦掉啊, 那这个一二的这个点的坐标呢,也比较特殊,也比较特殊,那我们来看一下啊,因为这个角是四十五度,这个角呢也是这个,呃,四十五度,所以这个三角形,这个三角形相当于就是一个等腰直角,是吗?三角形啊, ok, 那 我们现在把这条线呢再给它延长一点点,那整个 e 呢?就在这条直线上面干嘛动啊?这上面动。 好,嗯,我们来看一下啊, a 选项,他是说了当这个点 d 在 直线 bc 上面运动的时候,也就是说 a 选项有一个关键词,他把地点的这个运动的一个范围,从刚开始的这个边上面运动扩展到了这个直线上面运动, 所以现在这个 e 点的轨迹也是在整个直线上面动,而 a 选项让我们求 a e 加 c e 的 最小值,那很显然 a 选项求的是 a e 加上 c e, a e 加上 c e 的 话,它的一个是线段之和的最什么值?最小值,因此的话,那 a 选项很显然是一个将军印什么印码,而且是两定一动, 你看啊, a e 加上 c e 的 这个最小值,那很想我是不是做一下对称就可以了啊?那我就把 c 点关于它对称一下,我们把图给它标一下。 好,咱们把这个 c 呢给它对称过来,用个绿色的吧,对称过来,好,对称到这个地方,这边标一个 c e 撇, 那此时的话,我们的这个 c e 是 不是就变成了 c 撇 e, 然后直接连上 a c e 撇是不就可以了?也就是说,此时 a e 加上 c e 的 最小值,是不就等于 a c e 撇, a e 加上 c e 的 最小值,等于 a c e 撇,我们怎么去计算?那很显然我们还是要去。呃,添加辅助线,把它构造成一个直角三角形,我可以过 c 呢,往这边再做一条垂线啊, 这方我标个点 m 点 q 吧。 ok, 那 么现在我们开始一个计算,呃,咱们知道这个角呢,可能说是四十五度,那这个角呢,也是四十五度,所以 三角形这个地方呢,这个三角形它是一个等腰直角三角形,这条边呢是二,因此的话,那这个,呃,这条边的长度呢,就等于根号二。对称过来,这个长度也是根号二,这个方是垂直的,所以我们的 c c 一 撇呢,等于二倍根号二,是不等于二倍根号二, 而这个角呢等于四十五度,这个角呢也等于四十五度,所以我们的 c 一 撇 q, c 呢,它是一个等腰直角三角形,因此这条边呢, c 一 撇 q 等于二, c q 呢也等于二,所以我们再用勾股定顶,就能把它长度呢给它算出来了啊。那此时很简单,等于根号下, 应该是二的平方,再加上四的平方,所以答案呢,应该等于二倍杠五,所以这题的最小值呢,应该等于二倍杠五,并不是等于二倍根号二加二。如果你选了这个答案,你是估计没有看到这个关键词,它是在直线上面运动。好,这是 a 选项,所以当然呢,这题呢,就直接选 a 就 可以了。 这个和我们二五年的那个安徽中考题,他的那个第十题的压轴题的答案呢,也是 a 选项,如此一个类,一个意思啊,一个意思,但是他也是,呃,有一个审题的一个关键点。好,那这样的话,我们 a 选项呢,就不在这方继续讲了,继续我们看 b 选项, b 选项的话,它点 d 在 边 bc 上运动的时候,问我们正方形 a、 d, e、 f 面积的最大值,那 b 选项很简单, 这个正方形是不是等于 a d 的 平方,所以 a d 最大的时候呢,它整个面积就最大。那很想这个 a、 d 是 不是有一个直线形的距离,就是一个线段,那它距离最大的时候,肯定到 a b 的 时候是最大,所以那个 b 选项它是对的啊,所以这个 s 的 最大值呢,刚好等于二倍根号二括号的平方等于八。 c 呢?我们再看 c, c 是 点 d 在 这条边上运动的时候, b m 的 这个最大值是二分之一,我们知道这个地方是个垂直,所以这个图里面会形成一个一线三等角, 这有个一线三等角,这种题目在做一线三等角的题目的时候应该接触过,对吧?我要求一下 b m 的 这个最大值,那这个地方呢,我们就可以几何转代数啊,几何转代数, 那这条边呢,是二,我们可以设个圆就可以了。设这条边是 x, 那 这条边呢,等于二减 x, 把 b m 呢设成 y, 我 们知道这方有一个一线三角的相似,那熟知一线三角相似的乘积式的结论的同学,这方就可以直接写了啊, 或者你把比例式列出来,那我们直接写乘积式,应该两个 y 等于 x 乘上二减 x, 那 这方把 y 呢写出来,应该等于二分之一, 这个负的二分之一 x 的 平方再加上 x 配方就可以了。那就是负的二分之一 x 的 这个平方再减二, x 再加一,再减一,等于负的二分之一 x 减一,括号的平方再加上二分之一。所以 当这个 x 等于几时?等于一时,它的最大值呢?等于二分之一一,刚好呢,在这个取值范围上面,对吧?好,所以 c 答案呢,也是对的啊。这题比较难的是这个 d 选项啊,像有很多同学当时呢可能没有办法很好的处理这个 d 选项, d 选项呢,是一个模型, 这模型大家可以学一学啊,就是目前像咱们安徽的话,考的不是那么多啊,不是那么多,它是一个斜大于直的模型。斜大于等于直来讲一下啊,那 这个三角形是一个直角三角形,那这种题目呢,因为我们要求 a n, a n 刚好是这个直角三角形的斜边,对吧?我们遇到直角三角形的斜边,我们可以考虑取一下 a n 的 中点,取 a n 中点 o, 我 们取一下它的中点 o。 啊,这个地方的话,嗯,图不一定很准啊,就差不多这是点 o。 好, 这是它的中点,那显然的话, o d 是 不就是这个?呃, o n 的 这个 a n 的 一半,所以它是等于二分之一 a n。 好, 那这时候我们可以设个圆,把 o d 呢设成 x, 把 o a 呢也设成这个 x, 那么我这时候我再过 o, 那 向这再做一条垂线,在这再做一条垂线,把垂足呢标为点 h。 很 显然,此时我是不是形成了一个直角三角形 o d o h。 现在的话, o d 在 这里面是不是作为它的这个斜边,而 o h 呢,是作为它的这个什么边,这个直角边,显然这个 o d 的 话,它一定是大于这个 o h 的。 那什么时候能等于 o h? 就是 当这个地点和这个 o 点,就是这个 h 点和这个地点刚好重合了,那此时 它的这个斜边呢,刚好肯定是等于这个 o h 的。 有时候这方有一个取等的过程,有一个取等的这个这个过程。好,那这时候我们就把这个 o d 和 o h 用我刚才射源的这个量给它表示进去啊,所以 x 呢,就大于等于。我们看一下, o h 等于呢,我们射的这条边是 x, 因此这个 o b 这条边呢,它应该等于二倍根号二,再减 x, 而这个地方 o h b 始终是一个等腰直角三角形,所以我的 o h 应该等于这条边,再除以根号二,所以它就大于等于 根号二分之二,再减多少减 x, 然后把这不等式解出来,那就根号二 x 大 于等于二倍根号二,再减 x, 把不等式解一下啊,那就根号二,加一倍的 x 大 于等于二倍,根号 x 应该大于等于二倍根号,除以根号加一分母由里化, 那又变成的是根号乘以这个根号,再怎么样减一啊?减一这括号打不下去了,那应该等于多少?所以的话应该是 x 大 于等于这个四减二倍根号,而我刚才说了这个 o d 呢,它是等于 a n 的 这个一半,因此 a n 的 话就应该大于等于八减四倍根号,所以 d 答案呢,它也是对的啊。所以这题大家重点学习一下 d 的 这个模型的一个处理的方法。
76数学戴老师 07:04查看AI文稿AI文稿
07:04查看AI文稿AI文稿哈喽,小伙伴们大家好,我们是九上期末的一个复盘,我们一天一套期末卷,那么接下来一天一套期末卷,今天我们这套卷子是合肥的一套期末考试卷,大家都知道安徽的卷子在中考当中全省统考一套,也是我们接下来近几年的一个趋势,你像 什么?河南、陕西、安徽、江西、海南,包括云南、广东好多地方现在都开始是全省套圈了,这样我们出题也比较统一,出题包括我们去准备的时候,也相对来说比较统一。一点来看,今天的内容 也同样是选择的,是选择压轴、填空压轴以及最后两道压轴题。但是选择题当中,除了选择最后一道题,那选择题的倒数第二道题我觉得也很有意思,值得来给大家去说一说,我们一起来看。首先这道题他给我们交代了一个背景环境, 这个背景环境呢,很多同学应该是没有听过的,叫三角形 a b c 当中若 o 为 b c 边的中点, 那么就会满足这样的一个公式,这个公式很多同学没有见过,他叫什么,他叫中线长公式。我们来简单先理解一下这个公式,我们有一个三角形,比如说叫做 abc, 好 吧,在这个三角形任意一条边上,我取一个中点,比如说我取 这个,就按照他这个要求,我们就取 b c 边的中点,比如说我们叫做 e 点,好吧,连接 a e 之后,我们知道 a e 就是 中线,那么在这个图里边,它满足一个什么样的关系?就是 a c 方加 ab 方, ab 方加 ac 方,等于这个中线长 a e 方,再加上 这个中点所在的这条边的一半的平方啊,就是比如说你写 b e 也好,写 c e 也好,都可以,然后他的两倍,好吧,这就是我们中线长公式。其实他这道题呢,就以这条中线长公式做了一个背景,让出题老师不经意间秀了一下肌肉。但实际上 对于这个东西,我们出征阶段不需要证明,也不需要记住,就不用管他,你在这道题他出出来你就你会用就 ok 了,行不行?这个就给大家说到这了,接下来我们就来看这道题目当中,我们是从哪开始,其实是从这开始说,在这个矩形当中告诉我们, d e 等于十二, e, f 等于八 m 呢?在以 d 为圆心,四为半径的圆上,让我们求 m f 的 平方加 mg 平方的最大值,又是一道最值的问题,求 m f 方加 mg 方。我们先来找一下这两条线段, m f 的 平方加 mg 的 平方, 那很显然,那我要想求这个问题,那一定是借用前边的中线长公式, 那按照我们前面的要求,你会发现 ab 方加 ac 方其实是一个三角形的,两条边的平方等于什么? 等于第三条边上的中线和第三条边的一半的平方和的两倍。其实就是把这个公式在这道题里面去用一下,比如说这就相当于我们的 ab 方, ac 方, 这就相当于我们的 a o 方,这个就是我们的 b o 方,对吧?它俩的两倍。所以那么做题的时候,我们第一步肯定是套公式了,把这个公式先套进去, m f 的 平方加 m g 的 平方等于两个 m o 的 平方,再加上两个 f o 的 平方,或者你也可以写 c o 的 平方,是不是这样子, 那我要求它的最大值,那不就是求它的最大值吗?那你会发现这个 f o 我 们是知道的,是等于六的六的平方三十六,再乘以二七七十二,所以就是二倍的 m o 的 平方加七十二, 所以我要求他的最大值,其实就是求 m o 的 最大值。那么接下来剩下的我们要想求 m o 最大,圆中的最值都跟谁有关?都跟圆心有关,你不管是找最值还是求最值,都跟圆心有关。 来复习一下圆中的最值,我们叫一句话,叫连圆心够直线,看最大与最小,还记不记得?比如说这是我们的圆心 o 是 吧?有一个动点 q, 在 这个圆上运动,来回跑 圆外有一个定点 p, 要求这个定点 p 到圆上,这个动点 q, 这 p q 这条线段的最大值和最小值等求一定跟圆心相关。连接点 p 和圆心构成一条直线,这叫连圆心构直线。 那么这条直线跟我们这个圆产生的两个焦点,一个叫 q 一, 一个叫 q 二, 那这个时候离得远的 p q 一 就是我们的最大值,离得近的 p q 二就是我们的最小值,这就是我们圆中求最值问题的心。这个说完了之后,接下来我们就来看这道题,那我要求 m o 的 最大值,你会发现 o 其实是一个定点,是 g f 的 终点, m 是 圆上的一个动点,是不是就跟我们刚才一样?那我什么时候 o m 最大呢?连圆心勾直线,看最大与最小,连接 o 和圆心 b, 因为是最大,所以我就知道那个 m 运动到这个位置的时候,那这个时候就是我们的 m o 最大 圆中的最值,接下来我们继续来看,那我要这个 m o 最大,这个最大是几,好不好?求,现在就好求了,对不对?那求 m o, 那 我就是一个半径,再加上一个 o d 是 不就可以了? 半径是四, o d 是 几,这个是八,它告诉了我们这个是一半是六,所以我们的 o d 就是 十,没问题,所以这个 m o 最大就是十四。 那剩下的是不就简单了,它的最大值把这个 m o 等于十四,带进去那两个 m o 的 平方再加七十二,那是不就求出来最后的结果了? 这就是我们今天没错,一箭穿心语文中的最值,大家可以自己去算一算。今天也给大家准备了一份这个学习资料,是我之前整理的,叫做初三期末复习宝典,虽然有些同学已经期末复习结束了, 这个期末考试结束了,但是我们的期末复习没有结束,因为你还有也就是五个月左右的时间,你就要参加中考了,所以这个寒假千万不能放松,大家领到这个资料之后,可以自己去做一做, 它包含了我们初三上下册两本书全部章节的内容,一共汇总了十二大专题, 好吧,从知识讲解到这个例题,有基础题,也有压轴题,含答案电子版,好吧,想要这份资料的同学,大家可以在公屏上扣一,好吧,我们的小助理就会联系你。
33数学赵蒙蒙老师 07:51查看AI文稿AI文稿
07:51查看AI文稿AI文稿好,同学们,好啊,那临近期末,那个我们一起来看一看几何题啊。那题目跟我们讲了啊,在正方形 a、 b、 c、 d 中, e 点呢,是 b、 c 靠近 b 点的这个三等分点, 那然后呢,将 a、 b 啊,绕着 a 点逆时针旋转,得到线段 a、 f, 那 逆时针旋转以后, a、 b 必然等于 f, 然后三角形 a、 b、 e 和三角形 a、 f、 e 又都是直角三角形,是不是?那还有 a、 e 是 公共边,那必然这两个三角形也就全等了,他还跟我们讲使得角 b、 a、 e 等于角 f、 a、 e 啊,那这里 三角形首先全等,我们是不是把它放在我们的口袋里面了?是不是 a、 b、 e 全等于 三角形?直角三角形啊, a、 f、 e 是 吧?怎么证明全等的呢?是我的 h、 l 是 吧?搞定。然后呢,现在跟我们讲啊, pa 等于 r f 对 吧?那 b、 e 角 pa 等于 r f 是 不是意味着这边的角也是等于 r f 对 吧?那所以啊,我们把它写一下,角 b、 e、 a 也就等于角什么 a、 e、 f 等于 r、 f 是 吧? 好,它等于 r 法以后我们能还知道什么呢?是不是推导出什么角 c、 e、 f 等于什么?等于我的一百八十度减去 r r 法,因为去掉两个角以后,剩下的平角是不是我的角 c、 e、 f 这样一件事情 致辞后面呢?后面的脚表达是不是就进入困难了?我的脚 e、 f、 c 我 不知道怎么表达,如果我知道怎么表达的话,游戏就结束了,是不是因为知道他,那这个脚也有了,这个脚也有了,以后我的脚 f、 c、 d 不 就找到了吗? 关键就是这里的脚我们不知道怎么去表达,那是不是意味着我得怎么样? 得想一想辅助线的事情了是不是?那好,那这里的图形呢?我们就一起来看看辅助线该怎么做。 那首先角 f c d 一定是要放到直角,放到三角形里面去看的,是不是?那目前来讲,我们这个垂直是不是还有啊?那目前我们看到了这三条边是相等的,那我延长 ef 以后啊, 那这里假设交的交 c d 于 g 点,那你看一下,我们这里垂直有,垂直有,那这边 af 是 等于 ad 的, 那 ag 作为斜边,它又是一个什么公共边?那对于我来讲是 可就相当于又一个直角三角形全等出现啦。三角形 af g 也就全等于什么?全等于直角三角形啊,我们把这个删掉一下啊。 afg 全等于哪个三角形?是不是全等于我的 a d g 啊?是吧?是不是还是我的 h l? 那 这个全等以后了,我们会得到什么?得到 f g 等于 d g 这样一件事情, 那是不是我仍然没有办法去写下面的东西啊?那这里角 c e f 啊, c e f 我 们已经表达出来了,那目前来讲,在 r t 三角形什么 ecg 中,我是不是可以表达我的角 egc 了? egc 等于什么?是不是等于九十度 减去什么?我的角 cef, 也就是我们照写 rf 减去九十度就是我的角 egc 啊, egc 这个角已经知 知道可以用 r 法表达了,那唯一的 f c d 我 们想一想怎么表达?那这里是不是涉及到这个 f g 跟 c g 的 问题啊?我画的图形看上去像是等腰三角形啊?那但是呢,我们得去证明啊,那这个时候怎么证呢?那不就想到我们的勾股定律了吗? 我设 b e 为 x, 那 ef 是 不是也是 x 啊?那么这边写啊, b e 等于 ef 等于 x, 可以 吧?那这里 f g 呢? f g 是 不知道的,那我们就设 y 呗, 那 f g 一定等于 d, g 这边也是 y, 是 吧?那它是三等分点,并且是靠近 b 点的,所以 c e 是 r x, 可以吧?那这里 c d 等于多少? c d 可就三 x 啊,那 c g 等于多少?是不是很明确了? c g 也就是我的三 x 减 y, 那至此我该表达的这个式子是不是都有了?那所以这里的 eg 的 平方是不是等于 ec 的 平方?加上什么?加上我 c g 的 平方。那 eg 的 平方是多少? x 加 y 括的平方? e c 呢? e c 平方是四 x 平方,再加上什么 c g 的 平方,也就是三 x 减 y 括的平方。那这里计算,我们把它走一下啊, x 平方加上 加上什么? r x y 再加 y 平方等于什么?等于我这边的 四 x 平方,加上九 x 平方,然后呢?减去减去六 x y 再加 y 平方,那 y 平方是不是都约掉了?约掉以后啊,我们就剩 x 平方跟 y 了, 那这里我们把它抵一下,是不是四 x 平方?这边移过来,都移过来啊,那这里是我什么?我的十二 x 平方,减去八 x, y 等于零,提出 x, 十二 x 减八 y 等于零, 是吧?那这里 y 等于多少? y 是 不是等于我的二分之三 x 啊?这里我们就把 y 求出来了啊?八分之十二嘛,通出四,对吧?二分之三,那 y 既然等于二分之三 x, 那 整个 c d 是 等于什么?三 x 的? 那 y 等于二分之三 x, 那 是不是意味着 g 为 c d 的 中点啊,是吧,那既然既为 c d 的 中点,我们就好解决这个问题了啊,那既为 c d 的 中点以后,那我这里的 f g 可就等于 d g 啊,也就等于 g c 啊,所以我们就推出 f c 等于 c g, 那这里的角 egc 是 等于二 r 法减去九十度的,那我的角 fcd 就 等于什么?是不是等于一百八十度减去我的角 egc 啊,也就是二 r 法减九十度啊,然后再除以二,是不是就搞定了?二百七除以二 就是我的一百三十五度,然后呢,减去 r r 除以 r 减 r 法,最终呢,这一题我们选 b 啊,是不是这里呢,我们运用了很多的知识去解决啊, 当然一定是看出了辅助线的做法才能解决我们这一题啊,那辅助线是怎么做的呢?一定是通过我们可以看到未来的全等,最终呢, 找到边长的数量关系,是不是通通过这个勾股定律啊,最终解决我们的问题啊,非常有 深度的一道题目啊,建议大家如果不会的话啊,再多看一看啊,好,那这一题呢,我们就分析到这里啊,这节课我们就讲到这里啊,好,下课。
30中考数学老赵 03:55查看AI文稿AI文稿
03:55查看AI文稿AI文稿第三题说通过调节 c 大 角,让你去求一下灯泡 l 的 实际功率的范围,哎,那我们首先要考虑一下实际的功率该怎么求电,功率的公式是哪些?我们一起来回顾一下。我们说了,这个灯泡相当于是一个纯电阻吧,所以 p 十首先等于 u 乘一个 i 还可以,等于什么呢? i 平方啊 啊,还有呢?用 u 平方比上一个啊,那这三个公式我们用哪一个呢?那要抓住这个电路中谁是不变的量,他要让你求小灯泡实际的电功率。我们说了,这个小灯泡在此种情况下,什么是固定不变的?哎,非常好电阻,所以那我们就抓住哪一个跟电阻有关的公式。那你用电压还是用电流呢? 肯定还是要用电流,为什么?因为电流会受到 r m p 这个电阻的影响,电阻越大,电流会越小,所以呢,电流越小,电阻就越大。再反过来再想一下,电阻不变的情况下,电流越大,那功率是不是就越大? 所以那这题的核心的关键就是要求在这个电路中通过调节 c 踏脚电流的最大值和最小值。 那我们来看一看,既然都已经说到了 r m p 随着 theta 的 变化而变化,而且它们成正比, theta 越大, theta 越大,电阻越大,电流就越小。所以那我们要分两种情况去讨论。第一种情况就是当这个 theta 角等于零度的时候,什么情况? 这个圆弧形电阻有没有?没有?所以此时 r m p 是 不是就等于零欧姆,相当于没有电阻吧。那此时整个电路中是不是就剩小灯泡了呀?那我们已经知道了,电源电压是六伏,那小灯泡两段的电压是不就正好等于电源电压?那此时 ul 应该就等于 u 总等于六伏。 六伏是什么?小灯泡的额定电压,那此时整个电路中的功率是不就是小灯泡的额定功率?所以此时的 p 十 g 功率 也就是等于 p l 也就等于三瓦,那这个三瓦是最大还是最小呢?那我们刚才已经说了,阻值越大,电流越小,那阻值越小,电流最大,电流最大对应的是最大的电功率,所以此时求出来这个电功率应该是最大的。那我们可以再写一下 p 十 max 最大三瓦,这是我们第一种情况,最大的是三瓦,我们先写在这上面,那他左边最小的时候呢?我们一样的第二种情况是不是就可以讨论出来了?第二个,那是不是就当 c 大 角等于最大的度数一百八的时候,那 r m p 是 不是最大了呀?那此时电流最小对应的功率也是最小的。 那你说这一百八十度对应的阻值,我不知道呀,但是我们第二题是不是求了一个九十度的呀?九十度是一百八十度的什么啊? 终点吧。那九十度对应的是六欧姆,那你说一百八十度对应多少?哎,非常好,对应十二欧姆正好是它的两倍,那此时 r m p 接入的电阻是十二欧姆,小灯泡的电阻是十二欧姆,那整个电路的 总电阻等于多少?是不是就是两个加在一起?十二欧姆加十二欧姆应该等于二十四欧姆。那此时电路中的电流呢? 电流应该就等于 u 总比上一个 r 总等于六伏,比上一个二十四欧姆,那快速的算一算,它的电流应该等于 四分之一,也就是零点二五安培,那这个电流是不是就是最小电流?那此时对应的电功率是不是也是最小的呀?所以 p 十,那最小,我们根据电功率的公式,应该等于 i 最小电流的平方乘以一个 r l, 那 我们说了代入,也就是零点二五安培的平方乘以一个,此时 l 多少还是十二欧姆, 那算一算,它的结果应该是零点七五瓦,所以整个电路中的最小的电功率应该是零点七五瓦,最大的电功率应该是三瓦,所以呢,整个这个小灯泡的实际功率的范围应该在零点七五到 三瓦之间。那这就是我们这一道题的所有的一个题目的一个求解过程,这也是我们期末考试必考的电学综合应用题,希望同学们课后呢可以好好的把这题给整理一下,记得点赞关注哦!
猜你喜欢
最新视频
- 1.2万嘉~嘉







