佛山一模数学圆锥曲线比例调整

这个佛山一模的这个题出的太，这计算量太变态了。正常算，把 r 点坐标算出来，反正我是让我硬算，我很难算出来啊，但是我知道答案，答案怎么去看的呢？就是说这个 a 点是三啊，是二三， b 点是二一。 呃，能够发现啊， ab 是 关于这个双曲线的公和点，公和点，那么这有个屁有个屁 pa 加于 d 点啊，加于 q 点，题目说的加于 q 点，然后 pb 加于 r 点，那么这个 q r 呢，一定是过 ab 这条直线所对应的几点啊？几点就是二分之一啊，两个乘起来等于 a 方就行了嘛。双曲线是 x 方减 y 方的一， 而且这个点呢，这个点其实是 a 点的极限， b 点的极限的角点呢？正好也是啊，以正常算，我反正算不出来啊。我承认了，好变态，这数 不想算看，我觉得答案解析应该就是另外等于零，或者说证明一个三点共线。对，但是这个点怎么来的，就需要一点背景。

你们说我这个三角带框群里，有没有百分之八十以上的人能够秒杀佛山一模这道圆锥曲线压轴呢？不管如何，今天叶老师再次讲一下这道题目。在讲这道题之前，叶老师先要问大家一个问题， 就是做圆锥曲线是会背景重要还是表达条件重要？在我看来，我觉得表达条件更加重要， 因为我们说你无论用连利还是不连利，我们最重要的一点就是要搞清坐标间的一个相互关系。比如说你用连利伟达出来的 x 一 加 x 二 与 k 之间的一个关系，它也算是坐标间的关系，对不对？再比如我用三角代换，我三角代换里面有 t 一、 t 二、 t 三、 t 四， 然后我利用三点共线创造出 t 一、 t 二、 t 三 t 的 关系，他也是坐标间的相互关系。所以我觉得说真的表达条件比会背景要更加重要。好了，那我们现在开始吧。首先这个题我明确是使用三角代换，所以说我前面的步骤就直接写出来了， 前面必要的设点设线，大家可以看一看。写完了这些条件之后，我们要讲这道题关键的地方就是如何算出参数间的关系。 今天我们一开始要把这个 a 点带入 p q， 因为 a p q 它是共线的，这时候我得到了这样一种关系下去呢？再把 b 点带入 p q 点带入 p r， 说错了，你带入 p r 的 话，我又得到一组关系，你得到这两组关系之后，接下去由于我这个要求的是 q r 横过定点 挂固定点，他核心是要搞清 t 二、 t 三的关系，对吧？你要如何求出 t 二 t 三的关系？那我采取的方法是消元法，是一式，这是二式。我先通过一把 t 一， 用 t 二表示一下， 那就是 t 一 等于三倍的 t 二减一，除以三倍的 t 二减三。这个大家应该没有问题啊，直接把这个 t 一 当成主元嘛。 哦，我把他带入二中的话，那我得到这样一串的式子，可能一开始比较难算，我给大家演示出来。知道这样一组看起来很不好看的一个关系，但其实很多人会说，哎呦，我说这个怎么算啊，希望了。其实很简单，就两个字，通风关，有着相同的分母。对，那你就同乘以三倍的 t 二减三吗？ 大，于是我应该能够得到这样一种关系，指三倍的 t 三乘上三倍的 t 二减一这一串，然后后面以此类推开就好了吧。你会得到一个很漂亮的是 t 二乘 t 三的三分之一。 那这样我 q r 方程写出来就特别清爽，你就可以把 t 二加 t 三看成一个整体，对不对？一定整体，这个等于零，那 y 就 等于零， x 就是 二分之一，所以 q r 过二分之一都零。这道题前前后后不会超过三分钟，如果熟悉三角代换的话，谢谢各位。

我岳云鹏用不算常规的方法解决二零二六届佛山一模的圆锥曲线大题。第一问，这里根据渐近线条件推出 b 等于啊，再根据弦长条件求出啊，进而求出 c 方程。 第二问，第一小问设 p 求坐标，根据 p 求，在 c 上得到一和二式，根据另一个向量条件可表出 d 坐标。 接下来就是关键的定比点差，一是减拉姆达的二次方倍，二式刚好可以代入三和四式。再整理一下，可以验证点 d 在 二 x 减三 y 等于一上。 第二问，第二小问，这里我可以验证 p q， 而坐标可以这样设，这样 p q p b q 方程可以这样写，在形式上还算是令人舒适。 我要验证 t 二过定点。第一想法就是寻找仅关于 t 二和 t 三的等量关系，此时点 a 在 p 角上，这样， t 一 可用 t 二表示，也就是五式。点 b 在 p b 上，这样 t 一 一也可用 t 三表示，也就是六式。 根据五和六式可以消去 t y， 整理一下可得此等式，进而验证 t 二确实过定点。

新鲜出炉的广东佛山一模又是一份重量级高三一模数学卷，难度和思维量都在线导数压轴题出的很优质，圆锥曲线压轴题计算量很恶心人。视频最后有解析，单选后四题都不是送分。基础题多，选择题都不错，前两题都不是常规题。 第十一题是小题中最棒的，虽然以往考的较多，但 a 选项有迷惑性，多少同学仔在 a 选项填空。第十四题比较重视对几何思维的考察。 解答题的前三道非压轴题中，第十六题和第十七题都非常不错，尤其第十七题比较唬人。第十八题是本卷最好的一道题，第一问计算量就较大，分类讨论多，题目中暗含中零点对称。第十九题计算量太大，杂揉的东西太多，考场上能计算完的估计没几人。

佛山的高三家长注意了，今年的佛一模，今天下午试卷已经出来了，晚上呢，曹老师完整的将试卷做了一遍。今年一模的题，最明显的就是前三道大题呢，比去年要常规一点，但是亚洲题的计算量呢，极其不讲武德。比如说啊，第十八题的导数题， 前两问呢，非常中规中矩。第一问呢，考单调性的分类讨论。第二问呢，集字典的相关计算，这个都没什么太大问题。 但是第三问呢，他开始玩抽象了，大部分的学生呢，只能表达出切线，后续的计算方案呢，是不好想出来的。最后一题，十九题，圆锥曲线呢？第二问，定直线啊，要利用定笔点叉法。 这个呢，我们经常给学生讲的啊，是我们圆锥曲线里面的老演员了，大部分学生应该是没有问题的啊。最后一问呢，这个计算啊，真的是一言难尽。 此题和二二年的五行二调的题比较类似，当时二调考的是抛物线的模型啊，今年考的是双曲线，尽管印刷不出答案呢，但是呢，我们可以用极点，极线啊，可以把答案给它秒出来。

此题不会清北劝退玉哥教你在一分钟之内秒掉这道高考气息浓重的佛山倒数。如果你想考一百五，务必要听完。 第一问，讨论单调性，我直接就是一个求导，一不小心发现是导后二次型，又不小心分为 dota 的 两种情况讨论， 秒掉 over。 第二问，让我联想到 g x， 于是我不小心用了夏维达定律，又不小心写出了 f x 分 之一，发现相加正好为零，秒掉， over。 第三问，根据我多年的经验，肯定是要用二的结论，于是我闭眼默写，顺手写出了 l 一 的方程，又不小心发现把 t 换成 t 分 之一，得到的就是 l 二， 我又闲着没事，连累了一下，发现想要相等 x 必须等于零，这样三也秒掉 over。 如果你也想像玉哥一样秒提，在评论区评论一个秒杀，玉哥会保佑你的。

圆锥曲线的角度问题，面积问题，一个视频给你指引方向，所谓的倒角公式，不过就是两角和与差的正切而已，所谓的四边形的面积，不过就是割补法而已。一道看上去很复杂的压轴题，其实一点也不简单，你看到题目就挺吓人，这道题呢，特别是这一问，非常的复杂啊， 网上很多倒角公式啊，什么阵的，我总觉他们不是很严谨，我来教你们一些方法啊。所有同学，你看到这句话想到了什么公式？ q 一 加 q n 乘以 q 一 减 q n 等于零，想到什么公式？当我说出平方差的时候，我的政治选跟我说，勇哥，平方差在向量里面也能用啊。 我说可以啊，完全平方式平方差都可以用的，不是那么极端的平方差嘛。所以就说明 q e 的 平方减去 q n 的 平方 就等于零，也就是 q 一 等于 q n 好， q 点是动点， n 点是固定的， e 点呢？我们假设它是固定的，那么 q 点在什么地方？各位，如果说 e 点跟 n 点是固定的， q 一 的模 等于 q n 的 模，也就一个动点， q 点到 e n 两点的距离相等。各位回答一下这个，嗯，以负根三零四 为圆心的圆上运动好， m 点在这 n 点呢？在这我们看一下啊，这个 e 点是这个圆上一个动点。 其实你们以前呐，一定做过这样的题目，只不过他这个东西呢，换了个样子，你们就感觉到有点吓人了，这个 e 点在这 e n 对 吧？ e 点是圆上动点， q 点就在他的垂直平分线上。扎心了老铁啊， q 点在这个垂直平分线上，而且题目还说了， q m e 三点共线，把它翻译成人化。什么意思？把它翻译成人化是不是就说 q 点在垂直平分线上，在 e 的 垂直平分线上， q 点也在 e m 上，所以 q 点就是 e m 和这个垂直平分线的交点， 这就是一个很常规的，只不过它搞的挺复杂啊，换了各种各样的说法，什么三点攻陷，说个人话，不就是 q 点就是 e m 和 e n 的 垂直平面的交点吗？看到垂直平面想了什么东西？各位老铁看到垂直平面想了什么？垂直平面线上点到线段，两端点的距离相等一年， 所以我们就用 q m 加上 q n， q m 我 们不变， q n 就 等于 q e， 这两个加起来就等于 e m， e m 是 啥东西？ e m 是 不是半径对不对？半径等于几啊？半径等于四，也就是动点 q 到两定点，负根三零和根三零的距离之和等于四，这不就是椭圆吗？第一问，三分或者四分到手， x 方除以四加上 y 的 平方 等于？一听懂了以后，懂了我就插图了，因为这个题要花大量的地方，这是我就把这个图插掉了啊。 l 零与这个曲线，尤其是一个共点。好，这个曲线我们已经知道了，就这个方程， l 零是什么？ 根据我们的极点极限，把 x 的 平方就要换成 x 零 x， y 的 平方就要换成 y 零 y， 二倍的 x 就 要换成 x 零加 x， 所以 x 零 x 除以四加上 y 零 y 等于一。请证明这两个只有一个焦点怎么办？用因解定律得了啊，根据我们的因解定律，判别式等价于什么呢？等价于 a 方， a 方加上 b 方， b 方减去 c 方等于零，其中这个 a， 这个 b， 这个 c 就是 x 加 b， y 加 c 里面的东西。 ok， 其中这个 a 呢，就是椭圆里面的， b 呢，就椭圆里面的判别式，就等于这个东西。 ok， 告诉大家理解题里面东西啊，攀比等加这个东西，所以呢， a 方就是四乘以 a 方四分之 x 零 括号的平方加上 b 方是一乘以 b 方就是 y 零平方减去 c 方，这个一就是拿过来负 c 嘛，一拿过去做负一负一就是 c， 看等于多少，就等于四分之 x 零平方加上 y 零平方减一， 而这个 x 的 外零是椭圆上的点，所以四 x 加外零的平方不就等于一吗？它等于零，所以稍微偷个懒啊，判别等于判别等于，所以有一个焦点或者一个共点结束啊，这是我们的第一问做完了， ok， 第一问的第一小问，第二小问就真的超复杂啦，真的是这个我偷了个懒，交给你们自己做啊，其实过程相当的复杂，怎么复杂呢？把这个跟这个年龄分成组，得到一个 x 的 方程，然后把判别式解出来，最后判别式等于多少倍的他，然后这个等于零结束。 好了，我们来看一下第二问，第二问就已经往死里整，来吧，先把图给画出来啊，压力非常大的啊。这个这个题的第二问还是很狂野的， 给你们分享一下，当然我还是比较自信的，因为我已经讲过了，给我们的学生啊，屁点在这个地方，屁一撇在这个地方，关于圆点对称啊，一看到圆点就感觉啊，就是那个呃，椭圆上任何点到 圆点对称的两点斜率之积为定值负立方 b 方 n 点在这， n 点在这，然后过这个 p 点有个切线，好，有个切线，这就是 l 零，这是 l 零， p 一 撇 n 与它。你们看一下怎么做的，我跟答案的方法不一样，我自己现场做的啊，教育 h 点，然后要你求 n h p 角比上 h p n 这个角。所有同学啊，你们买过彩票，现在给你们买个彩票的结果，你们说这个答案猜一下，猜个解，忙猜个一啊，就在这这这两个角度相等，然后呢，这个题需要大量的空白的地方，我需要重新来张纸，这些全部删掉， 不要了啊，我只要留下这两个东西就可以了。道教公司，我看到网上各种各样的说法，我总觉得其实道教公司有个有个缺点，就有的时候到底加不加绝对值啊什么的，各种各样的问题，我用今天我我本来是准备在网上想去学习的啊，但我发现，哎，算了， 学啥呀，求人不如求己，还不如自己把它研究研究，我自己觉得我决定呢，是这么整，宁这个角为阿尔法，这个角是贝塔，这个大的角是伽马，没问题吧？所以各位看我写一下啊，我们就给说，看你的角， h p n 就等于碳你这个角，三角形的这个角等于两个不相连的，这个加这个是不连贝塔等于外角，贝塔减伽马没毛病吧？ ok， 就 等于碳你的贝塔减去碳你特伽马， 我看能不能把它做出来啊，一加上碳，你特贝塔乘以碳你特伽马，好，其中碳你的贝塔就是 l 零的斜率 k k l 零就等于负的 b 分 之 a， 四倍的 y 分 之 x 零，这探点被它好探点的阿尔法又等于什么东西呢？这个阿尔法呢？其中 p 点的坐标是 x 零， y 屁的坐标负 x 零， y 点的坐标是一个根三零探点的阿尔法就是 np 的 斜率， np 的 斜率呢？少了个负号，是不是 np 的 斜率？零减负外零， 零减方就是 y 零，然后根三减去负 x 零，根三加上 x 零。好，这是探点二法。 ok？ 还有个探点伽马啊，探点伽马等于什么？就这个角度，那是不是这个直线的轻？这个探点它的 kpn 就 等于 kpn？ 算了，我跟他写的清楚一点点啊，免得你们总是看的不太懂。它是 kpn 就 等于这个， 这个呢，就是 p n， p n 减去根号三 好了。叹你阿法，叹你贝塔，叹你伽马，于是分别往这里面直接带做这种题目，我觉得真的好需要耐心和那种信心啊。 y 再除以 x 零，减去根号三，看我能不能一次性做。对啊，然后呢，叹你的贝塔乘以叹你的伽马，就是加号就得变减号了，因为这里面有个符号啊， 于是呢，就是 x 零，除以四倍的外零，再乘以外零，除以 x 零，减去根号三。好了。接怎么做呢？分子分母同乘这个啊，同乘这个上面就等于负 x 零乘以 x 零减去根号三，再减去一个四倍的外力和它约掉，那么就四倍的外力，四倍的外力的平方，下面呢，就是四倍的外力乘以 x 零减去根号三，再减去 x 零外力， 那么就等于什么东西呢？继续你把括号打开，上面呢，就是负的 x 零的平方，再减去 四倍的外零平方，加上根号三倍的 x 零，下面呢是四倍的 x 零外零减去外零就是三倍的 x 零外零，再减去四倍的根三外零好了。因为 x 零外零它刚好是这个椭圆上的一个点，所以换个颜色，好吧，所以就有 x 零的平方加上 四倍的外零，平方就等于四，也就是负的这个等于几呢？那就等于负四，所以它的分子就等于一个根三倍的 x 零，再减一个四，没毛病吧，把根三倍的外零 提出来，还剩下根三倍的 x 零，再减一个四，该约掉的约掉，所以它就等于根三外零分之一好了。这个题目占的 p p g 太大部分了，这 位置写的太小了啊，接着再求什么呢？再把这个都擦掉啊，再求下一个喽。刚刚是 h p n 对 吧？再来一个，顺便我问一下直播间的朋友们，特别同行朋友，我如果不记什么，到家公司我就用这个方法，能不能搞定，这不也 ok 啊，你们看一下，碳级的 n h p 是 这个， 探险这个跟这个是互为相反数的，对不对？是互为相反数的，探险这个跟探险这个互为相反数啊。所以呢，就等于加个符号啊，那么就是要求探险这个角这个角是贝塔减二法啊，于是就是我就把步骤省一步了啊， 就是探险贝塔减去探险二法，所以一加上探险贝塔 乘以它减二十，我们得到这个了，我们看也能不能把这个化解一下啊。碳杯塔标准答案放好，是做辅助线，然后用角平面定力去证明的。怎么角平面定力好像是连接了 o p 吧，还是怎么回事？我记得，但是我觉得直接倒角公式更加的直观一些啊， y 零除以 x 零，加上 根号三，一减去 x 零除以四 y 零，所以 y 零 x 零加上根号三。看你的 beta， 看你的 alpha， 搞定分子分母同时乘以这个东西啊，就是负的负 x 零乘以 x 零加上根号三，然后四外零，再减去四外零的平方，没毛病吧？这边就等于四倍的外零乘以 x 零加上根号三， 再减去 x 零外零好了，那么就等于一个我们这个符号，我们看把把符号放到分子里面去，就等于 x 零的平方加上四倍的外零，平方加上 根号三倍的 x 零，再除以四倍的 x 零外零减去它呢，就是三倍的 x 零外零，再加上四倍的根三倍的外零， 然后 x 零四倍的外零又刚好等于四，所以上面就是根三 x 加上四，再除以这个，下面呢就是根三倍的外零。提出来还有根三倍的 x 零加上四，该约掉的约掉，所以 打完收工听懂没有？这根三万分之一，根三万分之一，所以我们就能得到什么东西，角 n h p 等于角 h p n， 所以 这个值等于一 来，可以鼓掌了啊，可以鼓掌了啊。第三，我们来看一下啊，他说的过点 p m， n 呢，分别是交点，过点 p 做斜率为负一的一条直线，斜率为负，一条直线交另外一个 k 点交它为 k 点，这个 k 点的重坐标要大于零，一定，那么就是在低向线外力也要大于零， 对不对？也要大于零，所以一定要在上方啊，一定要在上方 x 上方，要你证明 p k n m。 第四道题 要证明它的面积小于五分之九， n 点是焦点。对，这没问题啊，这个四面形的面积怎么表示啊？各位，我告诉你一个方法啊，割就可以补嘛，既然有割就可以补嘛，大家有没有思路，要么把它分割，要么把它补一下。延长，哎，对，延长啊，屁， k 延长 r， 所以 这个四边形面积就是这个三角形的面积，再减去这个小三角形面积。所以同学们，我们现在就要尽可能把 p 点和 k 点的横坐标还是纵坐标给留下来。你们说横还是纵？这个三角面积二分之一底乘以高， 这个三角面积二分之底乘以高，是不是重坐标，对不对？是重坐标。既然重坐标，那么呢，我们用什么方法比较好一点呢？我们留下 y 反射啊，反着就是就是那个 p， k， x 等于负 y 加上 m， 它都是有原理的，我们要搞 y， 懂不懂？搞 y 就 把 x 消掉，好，把 x 带进去，这个地方就是 x 方，加上四倍的 y 方等于四。 所以呢，就是 m 减去 y 的 平方加上四，外方等于四，所以呢，就是五倍的外方减去二 m， y 再加上 m 方减去四等于零。最后它的面积肯定是 y 一 加上 y 二等于负的一分之 b 就 等于五分之二 m， y 一 乘以 y 等于分之 c 就 等于五分之 m， 平方减四。所有同学，最后的面积是不是肯定要用 m 去表示出来？这面积怎么表示呢？我来写到旁边啊， s 就 等于 s， 三角形 p， m， r， 哦，那个 r 点的坐标还表出来啊？ r 点坐标我们写了这得了。好吧，他的重坐标等于零，横坐标点多少呢？ x 等于 m， m 等于再减去 s 三角形 k， m， r。 好， 那么呢，就等于二分之一 m r 的 距离就是 m 加上根号三，这就底高呢，我们 p 点的坐标就设为 y 一， 好吧，然后减去二分之一 m， 减去根号三，这个高呢，我们就设为 m 二 k 点的重坐标。 所以呢，我们把这个观察一下，二分之二分之几，我们把二分之 m 提取公因式，是不是 y 一 减去 y 二的，然后呢，再加上二分之根三倍的 y 一， 后面二分之根三倍的 y 二，那是不就可以了？ 其中 y 一 加 y 二。哎，这个也没啥问题，这个地方再怎么处理？第二个三角形面积表示错了吗？有个字母错误啊，问题不大啊，问题不大，字母表错了，是不是？这个应该是 k n， r， 于是二分之 m 这个地方就要写成 y 一 加 y 的 平方，五分之二 m 括号的平方 减去四倍的五分之 m 方减去四，再加上二分之根三 y 一 加 y 二，就再乘以五分之二倍的 m。 好 了，写成这个样子了以后呢，我们来继续看一下啊。其实一直有个 有个事情还没有做，你们说什么事情你们知道吗？根号下二十五分之四，我们把它通分成二十五得了。二十五分之四 m 的 平方，再减去二十 m 的 平方，然后呢，再加上四除以十六十六乘以五八十，再加上五分之 根号三倍的 m， 上面四减二十，有个负六，所以我们可以把二分之 m 提出来，五可以提出来，还可以提个四出来，再乘以根号下八十八，这个 五减去 m 方，再加上五分之根三 m， 然后再来就等于五分之二 m 乘以根号下五，减去 m 平方，加上五分之根三 m， 那 么怎么证明 这个值小于五分之九？我们还有个事情没有做啊，还有个什么事情没有做，你们知道吗？ m 的 取值范围啊，判别式，负二， m 的 平方减去四 a， c 要大于零，而且是两个正数，五分之二 m 要大于零，这听说要大正数，然后五分之 m 的 平方减去四，要大零，懂不懂？要帮你们算一下啊。好了，这个地方呢，我们看同时约掉个四，说是 m 方减五 m 方，就等同约个四，这是 m 方减去后面五 m 方，就等于 m 方角负四 m 的 平方，再加上二十要大于零， 也就是 m 放要小于根号五到根号五之间，下面这个呢， m 要大于零，这个呢， m 要小于负二，或者 m 要大于二，这既然都大于零了，所以小于负二的就不要要了。最后我们算出来 m 的 取值范围要大于二， 小于根号五，现在就剩下一步了，距离高考考满分一百五就剩下一步了。接着怎么处理，怎么样证明这个是小于五分之九？我是这么做的啊， 你看到根号下五减 m 的 平方，有没有什么方法？根号下五减 m 平方，令 m 等于根号五倍的 上减 c 塔，三角换原。所以呢，原式就等于五分之二乘以根号五倍的上减 c 塔，然后五减去五倍的上减平方，就是再乘一个 根号五倍的扩散 c 塔。我们就不妨啊，令这个 c 塔是递向线的啊，递向线的，反正大致确定一个东西啊， 再加上五分之根号三，再乘以根号五倍的上 c 塔，根号五，根号和五一约掉，所以就是二倍的上 c 塔扩展 c 塔就原四就等于什么东西呢？原四就等于上二， c 塔加上五分之根号十五倍的 上一 c 塔五分到 c 塔肯定小于几，肯定小于一，对吧？虽然它小于一，加上五分之根号十五。然后我现在要证明的 就是一加上五分之根号十五。其实这个还是很好做的啊，它很好放松，证明它小于它两边头减个一。是不是要证明五分之根号十五 要小于五分之四？根号十五肯定比根号十六还要小啊。结束高考满分到手啦。跟着永哥跑数学一定好。

同学们呐，塑形结合思想一定要掌握啊，因为塑形结合思想做这种题，那纯粹就是天敌克制般的关系啊， 非常的简单。这种题你用代数方法怎么做吗？也做不了，但是你用塑形结合思想，你会发现，就是画画图数一下，焦点就一清二楚了。 好，首先他说呢，是与曲线 y 等于 x 立方减三， x 交点个数最多的是，那首先我们就要画吗？ y 等于 x 立方减三， x 画这种函数图像怎么画？先通过因式分解，找到它的零点， 然后再通过导函数找到它的什么，找到它的单调性和极致点，不就可以了吗？所以呢，通过这样的话，我们可以得到 它的零点是零，正负根号三，而它的极值点，是啊，极值点是 x 减一，乘上 x 加一，那不就是正负一吗？所以对于这样的一个三次函数，我们就可以轻松的把它给画出来了，把点标一下， 那么这假设就是负的根号三，那这就是负一，然后呢，这是一啊，它是一个奇函数啊，这个还是很好看，很好判断的。那这是一，这是根号三， 根号三。那么很显然，根据这个导函数，它的什么负无穷，到负一的时候呢？是单调递增的，负无穷的时候，显然是趋于负无穷，所以呢，这个时候它的方式就是这样，然后往上增增增增，增到几呢？增到二啊，注意，这是二哈， 这里所对应的是二啊，你代入进去嘛，可以算出来它是二，然后呢，从负一到一呢？是减函数，就这样减减减，减到几呢？ 减到负二，当然可能画的不是完全的，那么标准哈，大家能理解就行。然后呢，再一到正无穷又是真呗，真真真真，真到正无穷了，大致就是这样的一个函数图像， 那就是这样的一个函数图像啊，这就是我们 x 立方减去三 x 的 函数图像。好，接下来我们再来看一下 a、 b、 c、 d 四个选项的函数图像怎么画。首先，第一个应该是最简单的，我们先画简单的好不好？第一个是最简单的， y 等于负二 x， y 等于负二， x 不 就是啊，注意啊， 这是负一，这是一，这是对的负二，所以它的就是一个斜率为负二的这样的一次函数呗， 是不是？那他的焦点我们是不是就数清楚了？这里一个，零点一个，还有这里一个，所以对于 a 选项，他总共是三个焦点啊，写在这里， a 选项是三个不算多。好，接下来我们再来看一下，我们先先画好画的好不好？好画的，你先画了，然后再画不好画的。 c 选项也好画呀。 y 平方等于四，那么 y 平方等于四，不就对应着 y 等于正负二吗？是不是 y 等于正负二，正负二，那就是一个平行 x 的 直线呢？这是正二呗，是不是？这是正二，然后画的可能不是那么的， 这是正二，这是负二，那它的焦点不也数得清楚吗？这里一个，这里一个，这里一个，这里一个，所以它是四个啊。对于我的 c 选项，它是四个，刚才 a 选项我们算出来是三个，那无论如何呢， a 选项是肯定不能选的，因为已经有比它领先的了 啊，这是我们刚刚算出来的，它是三个，它是四个啊，你至少 a 选项是不能选的，三个里面蒙一个是吧？接下来我们再看 b 选项和 d 选项怎么画好。首先我们来看一下这个 d 选项怎么画好不好，因为 b 选项好像是最难的，我们先留在那里， d 选项我们 y 等于 x 平方，你会画吧？ y 等于 x 平方， y 等于 x 平方的话，那它的图像大致就是这样呗，因为它等负一的时候是一，所以它的图像大致就是这样子， 是不是就是这样子？然后这边的话，因为它的多少，它的导函数是这个， 他的导函数是这个，而对于他的导函数是二 x， 很 显然我们这个三次函数的增长率更快，所以这里肯定还有一个焦点， 是不是？而 y 的 绝对值代表什么？ y 的 绝对值就是我 y 取相同的正数和相同的负数是都可以啊，得到这个 x 平方的，所以这个图像其实他还要关于我们的 x 轴对称下来，也就是这样子 啊，这样才是它最终的形式，这就是加绝对值的意义，能理解了吧？因为我的 y 值，无论取正值取负值都能够等到这个 x 平方，所以我画了 y 等于 x 平方的时候，我只需要在关于 x 轴对称一下，那么这就是它最终的形式。 因为你会发现呢，无论是我在上方还是在下方，我最终都能够得到 y 的 绝对值等于 x 平方。那接下来数一下焦点呗，这里一个， 这里一个，这里一个，这里一个，还有一个零点，零点两个曲线都交了，但是呢，他只能算一个啊，注意。所以呢，对于 d 选项总共是几个？总共是五个， 能理解了吧？对于 d 选项呢，总共是五个啊，把 d 选项也标上， d 选项总共是五个， 所以在这里面呢，我们可能最终就是在 b、 d 里面打 pk 了，因为 a 和 c， 三个和四个都排出来了嘛， b d 里面打 pk， d 是 五个，那 b 是 几个呢？同样 b， 这个图像应该怎么画呀？大家思考一下。还是一样的，我先把 y 和 x 做下分离， y 的 绝对值等于二减 x 的 绝对值， 二减 x 的 绝对值，大家应该会画吧。首先你不要看那么多，你先看 y 等于二减 x 的 绝对值，这个肯定会画，因为 x 的 绝对值呢，是一个什么？ x 的 绝对值是这样的一个 v 字形，是不是 这是 x 的 绝对值啊？一个 v 字形，那么加个符号是不是就倒过来了？加个符号呢，就变成向下的 v 字形吗？ 因为我的函数值变成负的了，这样向下的一个位置写，然后再加个二，加个二不就向上平移两个单位吗？啊，所以它是向上平移两个单位， 向上平移两个单位就在这里了呗。然后注意它的零点啊，它的零点是 x 等于正负二，所以呢，它的零点是在这个三次函数的左右， 这就是 y 等于二减 x 的 绝对值，这就是它的函数图像。但是现在要注意了，注意什么呢？注意 y 的 绝对值等于它。首先绝对值是大于等于零的，所以二减 x 的 绝对值是大于等于零的，要大于等于零的话，那负数部分就没有了，所以它的实际图像只能怎么样？ 只能到与 x 轴相交，所以呢，对于它来说，它只能是这样子，这边这样 对，所以它实际呢？因为它大于等于零，我们刚说了它只能是这样子，然后同时呢，因为加了个绝对值。根据第四问，我们刚才已经研究了，加绝对值其实就是同等的 y 啊，有正负心，有正负心的话我只需要怎么样关于它对称一下就好了。是不是对称一下就好了？ 对称一下，那对称了之后，接下来再数一下几个焦点呗。一个、两个，三个对称，下面还有三个一、二、三，所以总共是几个？对于 b 选项总共是六个，那么最终答案就应该是 b。 好 了，本次篇到这里就结束了。

二零二六年的佛山异模新鲜出炉，官方答案没出来解析，咱们配上了，大家可以对对答案了。一般质量都较高，几乎每届必做佛山异模。这份数学卷思维量及计算量均爆棚，尤其是压轴圆锥曲线的计算，能让人在考场上直接崩溃。

我从未反对过连力。回答，我从来没有反对过连力，我反对的永远是类似表达的这种连力，因为他出现了非常多奇丑无比的式子，影响我们的运算。 ok， 今天叶老师借用连力的手法来处理一下 这个佛山一模的圆锥曲线大体，让那些连力与不连力的挑拨者彻底闭嘴。好话不多说，我们开整。首先呢，一开始我们先射点，对不对？你射完点之后，但重要的一句话，因为这个 a c， 它会等于两倍的 c b 相量， 所以说，我能得出的条件，利用相似三角形也不要用项量坐标了，对吧？简单一点，那是不是就可以得到 y 一等于负五的两倍的 y 二，对不对？然后呢，因为 s a o b 利用这种项量差成，是吧？那它就是二分之一的 x 二 y 一减去 x 一 y 二，是吧？这大家应该没有任何问题哦。 然后这个时候我们说又因为这个 a b c 贡献，那这样子，我的这个 x 二 y 一减去 x 一 y 二，它就等于 y 二减 y 一嘛，是吧？那这样一转换，我的面积表达式是不是就特别简单？它就是负的二分之三 y 二，对不对？你利用这两个式子一转换一下，那肯定是比标达的那样简单嘛。 当你转化完之后，我们就要求这个外二就好了，那怎么去求呢？这个时候我们连力，那我们的连力肯定是非常简单的呀，因为我这个外二要求，那怎么连力呢？我们把这条直线设成 x 等于 m y 减一， 然后椭圆方程就是 x 方除以 a 方，加上四 y 方除以 a 方，正好等于一出来的这个方程，它也比标答的要好看许多，大家 也可以欣赏一下，是不是要好看特别多呢？那这个时候我只需解说外一加外二就好了，也不要像标答那样写外一层外二，那也就是外一加外二，这个时候就是二 m 除以 m 方加四嘛， 然后它这里不是有一层关系吗？对不对？所以也就是得到负的 y 二正好是多少啊？正好是二 m 除以 m 方加四。那这样直接结束了嘞， s、 l、 b 它会等于多少？负的二分之三 y 二，那就是 三 m 除以 m 方加四，然后基本不等式搞一下，先把它同除 m 变成三除以 m 加上 m 分之四，那这样的话它就小于等于四分之三。 当 m 正好等于多少啊？等于二的时候取等。所以此时的话，我的 y 一就等于一，那这样的 a 点坐标就是一，一带入椭圆，那 a 方就等于五。这题搞定好，谢谢各位。

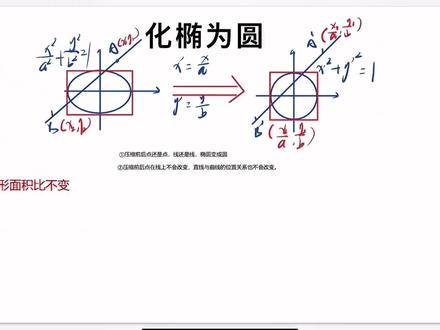
大家好，我们今天来讲到圆锥曲线里面的一种技巧，画椭为圆。什么叫画椭为圆？有的时候我们在研究椭圆的时候啊，由于椭圆我们比较复杂吗？对不对？他的两个分母不一样，又带有平方，那么此时呢，我们可以通过一些替换，把它变成一个圆的形式。 怎么替换呢？我们椭圆的方程呢？ a 方分之 x 方，加上 b 方分之 y 方，我们令 x 一 撇，它等于 a 分 之 x， 然后呢， y 一 撇等于 b 分 之 y， 所以 它就变成了 x 一 撇方，加上 y 一 撇，方等于一， 那么此时这个方程它就是一个圆的方程。那我们经过变换之后，原来的一些点，它又开始产生什么变化？如图，我们开始里面有两个点， a 点以及 b 点。 a 点我们开始写成 x 一， y 一， b 点呢？ x 二， y 二。好，它对应的点分别是 a 一 撇， b 一 撇。我们来推导一下， 我们的 a 撇应该是直接写成我们的，呃， x 一 一撇以及 y 一 撇，它对应过来的吗？对不对？然后呢，我们开始有，呃，它是怎么过来的呀？ x 一 撇，它是直接令它等于 a 分 之 x， 对 不对？所以这里 x 一 一撇呢，它应该可以写成我们的 a 分 之 x 一 一撇。好，那么我们的 y 一 撇，它是变成了 y 一 撇，它是变成了 b 分 之 y 吧，所以我们这里的 y 一 一撇，它应该就是 b 分 之 y 一。 所以呢，我们最后 a 一 撇，它这个点的坐标可以写成 a 分 之 x 一， 然后 b 分 之 y 一。 同样， b 点，它也可以变过来，变成 b 一 撇的时候，写成 a 分 之 x 二以及 b 分 之 y 二。同学们可以把这个点自己再去尝试一下，这是我们的点经过变换之后它的写法，那我们对应笔的面积它又怎么样？ 对应图形的面积比不变。我们来看到这个椭圆，它的外接，我们算矩形吗？外接矩形， 然后呢？这个圆的外接正方形，他们两个应该是怎么样对应的图形？开始这个矩形的面积多少？我们写一下，我们就用 s 一 来表示好了，它应该是等于二， a 乘以二， b 等于四倍的 ab， 没问题吧？我们的 s 二的正方形呢？ 它的半径是一，对不对？所以这里是一，然后这里是一，所以变成了二乘二吧。等于二乘以二等于四，所以我们的 s 一 啊，比上 s 二，它等于 ab， 所以他们的面积之比其实就等于什么？等于我们 ab， 这个同学们自己记住了，记不住也没关系，我们自己再推导一遍就可以了，其实很好推导吧。还有一个就是我们的直线的斜率之比，他又怎么样？我们来把第一个直线求出来，第一个直线的斜率 k a b， 它应该等于我们的 y 一 减去 x 一 比上 y 二减 x 二，没问题吧？我们的 k a 撇 b 撇呢？等于我们的 b 分 之 y 一 减去 b 分 之 y 二 比上 a 分 之 x 一 减去 a 分 之 x 二。好，它最后就变成了 b 分 之一倍的 y 一 减 y 二 比上 a 分 之一倍的 x 一 减 x 二。我们用 k a b 比上一个 k， a 一 撇 b 一 撇， 我们这个 y 减完，它都有的吧，就是公共的，对不对？你这样一比，你会发现它等于 a 分 之 b， 我 们把它写过来，也就是 k， 它等于 a 分 之 一个 k 一 撇， k 一 撇呢，就是我们变换之后，圆他那个直线所在的斜率。当然你也可以写成什么 k 一 撇的等于 b 分 之 a 倍的 k， 为什么我要把它写成这种形式，那不多此一举吗？ 因为有的时候啊，我们椭圆里面的直线的斜率是 k 是 已知的，你经过变换之后，你这个 k 一 撇往往才是要求的吧，所以我们记这个啊，还是会稍微的比较好一点，其实记不记都没有关系，同学们一定要会推倒就可以了。 还有一个就是什么呀，我们直线它与曲线的位置关系又该怎么去判断？我们来一个例题来讲解一下。首先我们令 x 一 撇等于 a 分 之 x， 还有呢？ y 一 撇等于 b 分 之 y， 那 么此时我们的椭圆它就变成了圆吧，变成了我们的 x 一 撇的平方，加上 y 一 撇的平方等于一，对不对？那我们的直线是不是也可以用 x 一 撇以及 y 一 撇来表示啊？我们现在 x 一 撇，它是等于我们的 a 分 之 x， 所以呢，我们能把 x 与 y 去分解出来吧， x 等于 a 倍的 x 一 撇， 还有就是我们的 y 等于 b 倍的 y 一 撇，那么我们的直线此时就变成了小 a 大 a 倍的 x 一 撇，再加上小 b 大 b 倍的 y 一 撇，加上 c 等于零。它判断这条直线与这个椭圆的关系， 其实就是判断这条直线怎么样与这个圆的位置关系吧，我们只要看到 d 与 r 的 位置关系就可以了，对不对？好，我们来看一下 d 与 r， d 表示什么呀？ d 就是 我们的圆心到直线的距离，我们的圆心它是零，零到直线的距离，我们来算一下， 我们的 d 它是等于零，零带进去绝对值 c 比上一个根号，我们的 a 方大 a 方加上 b 方小 b 方，对不对？ 它这个就是对于我们的 d， 我 们要跟什么去比较？跟我们的半径去比较吧。第一种情况，如果我们的 d 等于 r， 也就是绝对值 c 啊，比上一个根号 a 方大 a 方加上 b 方 大 b 方 d 的 时候，意味着我们怎么样相切？我们把它整理一下移过去，然后两边同时平方，再整理下，会得到一个什么？ 能得到我们的大 a 方小 a 方，再加上大 b 方小 b 方减去 c 方等于零，此时呢我们就相切对不对？然后第二种就是我们的第二种，写下我们此时如果 d 它小于 r 的 话， 绝对是 c 比上一个 a 方大 a 方加上 b 方大 b 方，那此时它应该怎么样？它应该小于一， 我们自己去整理一下，能得到我们的 a 方小 a 方加上 b 方小 b 方减去 c 方，它是大于零的， 那此时我们是怎么样的？我们是相交的对不对？这两种其实我们才是考的最常见的吧。还有第三种是什么呀？我们的相离， 第三种的相邻就是我们的 d 大 于 r 啊，这里我就不写了，因为位置有限，能推到什么？我们的大 a 方小 a 方加上大 b 方小 b 方减去 c 方，它应该是小于零的吧？ 我们不管是相交啊，相切，还有以及最后一种相离，它其实都能通过得它来推断对不对？第一种它是得它等于零，第二种呢？得它大于零，第三种得它小于零。我们还记得前面讲的因解定律吗？它是不是我们求得它的一部分呢？ 我们用之前用英姐定律求得它是什么样的？得它等于四倍的 a 方 b 方括号，我们的这一项减去 c 的 平方吧，这一项什么？这一项不就是分母吗？分母减去 c 的 平方， c 就是 常数，对不对？你看看 三母减 c 的 平方，是不是能决定这个得它的正负问题啊？因为我们前面的四倍的 a 方 b 方，它一定是大于零的嘛，所以这一项它其实才是真正决定我们判别式的正负号的问题。所以说呢，我们的得它的正负决定式，那其实真正的是什么？ 我们的这一项对不对？它与前面的四倍的 a 方 b 方其实没有什么关系吧，对不对？好，我们下面呢一个具体的例题， 看到他让我们判断这两个的位置关系很好判断，我们怎么办？直接把它带公式就可以了吧。看到这个公式， 你看看这些公式哈，他这个 a 方啊，以及 a 小 a 方，大 b 方，小 b 方减 c 方，他都与 x 一 撇与 y 一 撇与 x 与 y 都没有关系吧， 就我们直接把对应的位置带进去就可以了，对不对？带公式就可以了，公式我们一定要记住哈，大 a 方小 a 方加上大 b 方小 b 方 减去 c 方，这个呢，是我们的得它的决定式，正负号的决定式。你如果前面你要写一个四 a 方 b a 方啊，也没有关系，我们只用这个公式代入吧，它应该就直接等于我们大 a 方就是 x， 前面的 三平方就是九乘以四，再加上我们的四乘以五，然后再减去二十五，对不对？这里三十六，再加上二十减二十五， 最后算出来等于三十一，他是大于零的吧，所以呢，他们两个肯定就相交了，对不对？话妥为圆呢？除了可以判断我们的直线与椭圆的位置关系，还可以用来解决一些面积的最值问题，而且用起来是非常的舒服。下面有看到一些有关于这类的例题， 椭圆给了我们，他说上面有两个不同的点， a b。 关于某条直线对称，第一问让我们求实数 m 的 曲值范围，第一问我就不讲了，看到第二问，他让我们求三角形 a o b 面积的最大值，三角形 a o b， a o b 这个面积最大值吧，如果我们在椭圆里面算，我们怎么样？我们就是底层高，对不对？或者说你用二分之一的 a、 b、 c 的 都可以，但是不管怎么样，肯定是稍稍的有一些计算量，或者说有一点点麻烦吧。 我们看到用我们今天讲的方法，先把椭圆，然后呢变成圆的形式，此时我们的三角形 a o b 变成了什么？ a 一 撇， o 一 啊， o b 一 撇，对不对？变成这个三角形，那这个三角形有什么好处？你看看这个三角形呢，它 o a 一 撇， o b 一 撇，它都是等于半径的吧，这个半径肯定又是一了呀，对不对？那我们这个面积的最大值 就与这个假角有关了吗？只要这个假角，我们写一下吧，二分之一的 r 乘以 r， 再乘以 sine theta， 对 不对？你看看这里都是固定的吧，你要求这个面积最大值，你不就是 sine theta 的 最大值吗？ 三因 c， 它的最大值是多少？三因 c 的 最大值，它不就是等于一吗？所以算出来呢，它就等于二分之一的 r 方，就是它的什么最大值？注意，你这个最大值算出来的呀，只是这个圆里面的面积大小对不对？你要算这个三角形的最大值， 你记住了，它们是有一个比例关系吧，我们的 s 比上 s 一 撇，还记得吗？等于 a b 啊，这个不要漏掉。那我们接下来来写一下第一步怎么样？第一步，我们同样还是令 x 一 撇等于 a 分 之 x 吧，这里的 a， 它是根号二分之 x， 对 不对？然后我们的 y 一 撇等于 b 分 之 y， 这里 b 是 一，所以呢，它直接等于 y 就 可以了。所以我们的椭圆，它此时就变成了什么？变成了我们的 x 一 撇的平方，然后再加上 y 一 撇的平方，等于一。所以呢，此时我们要求的三角形 oab 的 面颊不就变成了 o a 一 撇， b 一 撇，这个三角形的最大值就可以了吗？我们下面去求一下我们的 s 三角形，我们的 o a 一 撇， b 一 撇，它是等于二分之一。 o a 一 撇乘以 o b 一 撇，然后撒引 c t， 我 们把这个 c t 角去标出来， 它就等于我们的二分之一乘以 r， 再乘以 r 乘以 sine theta 吧，因为我们的 sine theta， 它是小于等于一的，对不对？当我们的 theta 等于二分之 pi 时，我们等号 可以取到，可取啊，这里写一下。所以呢，我们的 s 三角形 o a 一 撇， b 一 撇，它的最大值啊，它就等于我们的二分之一乘以一，再乘以一，再乘以一吧，就等于我们的二分之一。 最后呢，我们还知道，我们原来的 s 三角形 o a、 b， 它比上我们的 s 三角形 o a 撇 b 撇等于 a b， 对 不对？这里的 a 它是根号二， b 它是一嘛，就没有了。 所以呢，我们 s 三角形 o、 a、 b 的 最大值，它就等于根号二倍的 s 三角形 o a 撇 b 撇就等于我们二分之一，乘以根号二，等于二分之根号二。那么这个题目呢，我们就做完了，我相信做刚刚那个题目，同学们并没有过瘾，我们就看到再来一个题目吧， 已知点 a 啊，给了我们，他说椭圆 e 的 离心率给了我们 f 是 什么？右焦点，直线 a f 的 斜率，这个其实都是第一个的条件。第一个让我们求椭圆 e 的 方程，我这里不求了，直接写出来四分之 x 方加上 y 方等于一。我们主要看到第二问， 设过点 a 的 直线 l 与椭圆 e 相交于 p q 两点，那我们就求三角形 o、 p、 q 的 面积的最大值。 我们画一个草图吧。针对于这个第二问，你有一个椭圆对不对？好，我画一个椭圆，然后呢，你有一个过哪个点 a 点 a 点，它告诉我们是零负二嘛，那么零负二在这个地方对不对？然后呢，它与 椭圆有两个交点 p 点，然后呢？ q 点，让我们去求 o p q 这个面积的最大值吧， 我经过变换之后，把这个椭圆变成了圆，我们再来看看我们是怎么去写的。好。第二问，我们第一步还是干嘛令 x 一 撇等于 a 分 之 x， 这里的 a， 它就是二了。二分之 x， 然后 y 一 撇等于我们的 y， 哎，这个写到旁边去了，不好意思， y 一 撇就等于 y， 对 不对？然后此时我们的椭圆变成了什么呀？变成了我们的 x 一 撇的平方，加上 y 一 撇的平方等于一，那么这个圆呢？我这里已经把它 画出来了，那这个 a 点怎么办？我们原来的 a 点，它是原来的 a 点，它是零负二，对不对？我们要经过变换，变成我们的 a 一 撇吧。 你的 x 是 怎么变的呀？ x 它变成了 x 一 撇，无论怎么变，你这里是零嘛，对不对？所以你仍然还是零了。然后你的 y 呢？ y 你 有没有？呃，你又没有变，所以你的 y 还是负二吧。所以你这里 a 点变完之后，你的 a 一 撇仍然是零负二，所以 a 一 撇我也标出来了， 它与它就相交为两个点， p q p 一 撇 q 一 撇，这里对应的点对不对？然后呢？现在我们求的是什么呀？那我们求的是三角形 o p 一 撇 q 一 撇面积的最大值吧，就可以了。好，我们画个草图。那我们现在要求的是 s 三角形 o p 一 撇 q 一 撇的最大值。我们先把它的式子写出来，等于二分之一倍的 o p 一 撇乘以 o q 一 撇，再乘以 c 它吗？那同样这个角，它是 c， 等于二分之一 r 平方，再乘以 c 它吧。那么 c 它什么时候取最大值？取九十度的时候吗？这里我就不再重复的啰嗦了，等于我们的二分之一乘以一，再乘以一，它就等于二分之一。 这个面积是什么？是我们这个三角形的面积吧。我们原来的 s 三角形 o p q， 比上我们现在的 s 三角形 o p 撇 q 一 撇，他应该等于我们的 ab， 这里的 a 是 二， b 是 一，所以我们 s 三角形 o p q 的 最大值 就等于我们的二分之一乘以二，对不对？就等于一，这里我们取最大值的条件我还是写一下吧，等于九十度吗？对不对？你看看他原来的标准答案，他的最大值的面积是不是等于一啊？我们这里也是一，我们比他来说，相对于来说是不是少了很多计算呢？ 它还要让我们求什么？求直线 l 的 方程，你的 l， 你 这里是什么？我们这里应该是所谓的 l 一 撇，对不对？这里呢才是 l， 我 现在 l 一 撇能不能直接求出来？ 你 l 一 撇求出来没用，但是我能把 l 一 撇它的斜率求出来。如果你求出它的斜率，那么我们 l 的 斜率呢？它也能知道，你知道它的斜率，并且这个 a 点呢？ a 点它是给了我们的吗？它是零负二，那我这条直线的 方程不就写出来，写出来了吗？那我们来看看这条直线 l 一 撇直线的斜率怎么求呢？这里我放大一点，方便同学们看清楚。我们要求这条线的斜率，那我要求斜率，我是不是求出平行的 c， 它也是可以的，没问题吧？ 我们求出假角的正切值也可以。那我这里所谓的假角是哪个角呢？第一个角是不是可以，没问题吧？ 那我们这个角如果为 c 它，那这个角也为 c 它喽？ 那这个角求出来行不行？它应该跟 theta 怎么样？是互余的吧？是二分之 pi 减 theta。 我 这三个角，你随便哪个角的正切值去算出来，我都能算出什么？ 这条直线它的斜率对不对？好，我们来看一看，这三个角哪个比较好算呢？首先我们排除的肯定是这个角了，它都没有在三角形里面相对好算的，是不是这个角， 那这个角怎么办？我们要算它的正切值，这条长度知道吗？这是零零，这个呢？零负二吗？不是已知的吗？这条长度它应该就等于二长度，对不对？那我们这条长度怎么去求？还有这一条长度是要求的吧，你想想看，这条长度我们怎么去求啊？ 并不是很好求，对不对？但是要注意了，它这条直线它是什么情况下的直线呢？是不是我们这个三角形面积最大的时候，我们这个三角形面积什么时候最大？也就说我们的 c， 它等于啊，这里就这个角吧，因为我们都有 c 它了，那这个角为九十度的时候，对不对？那它为九十度的时候， 那么他呢？我们做一条怎么样垂线下来过 o 点，做一条垂线下来的话，你看看，那么此时呢，我们这个角多少度？是不是四十五度？然后呢？这里也是四十五度，对不对？然后这里是个直角，它是一，那么这条边呢？我们记为 o m 好 了， o m 的 长度我们是不是就能求出来了？是不是二分之根二二呀？哎，你会发现一个什么问题，我们撒硬了，这条边知道了，对不对？这条边也知道，当然这条边你也是可以去求出来了吧？那我们， 呃，二分之派减去，我们还是把它念成 c， 它，我们这样已经写了 c 它，虽然它这两个重合了哈，二分之派减 c， 它的正切值是不是可以求出来？ 或者说它的正弦值先求出来也可以，反正都能求出来，对不对？那么我们 c 的 正切值呢，肯定是能求出来，所以我们的 l 的 l 一 撇的斜率当然就能求出来了。好，我们下面来求一求，我们把图中的三角形拿出来吧，图里面实在是太小了， 它是一个怎么样的三角形？这边是一个 o， 然后呢，这边是一个 a 一 撇，还有一个是 m 点，我们刚刚做了，对不对？我们的 o m， 它这条长度我们是求出来了，它是我们的二分之根号二嘛， o a 一 撇呢，它是二，所以 a 一 撇 m 这条边也能求出来吧。我们来用一下勾股定律， 四减去平方就是二分之一，再开根号就是二分之七，开根号嘛，然后就是我们的二分之根号一十四， 所以呢，我们的吞进的二分之派减去 c， 他 就等于，呃，注意这里的 c 他， 我们还是区分一下吧。我们就，呃， 还是写上 c 它吧，我懒得改了，同学们要记住，这个 c， 它表示的是什么？是我们后面这个直线 l 的 倾斜角的 c 的 哈， 那直接等于多少？我们比一下，就是二分之根号二，比上我们刚刚求的二分之根号是四吧，二分之根号二乘以根号是四分之二，那么最后呢，就是 开根号七分之一开根号嘛，那么就是我们的七分之根号七，所以呢，我们根据的 c 它，它应该是就等于根号七了吧，这个根号七呢，也就是我们这条 l， 它这条 l 一 撇的斜率，对不对？ 所以我们原来直线的斜率啊，它跟我们现在的斜率有什么关系呢？如果忘掉了，没有关系，我们的 k 它是等于什么的？同学们记得到这个斜率公式肯定是不会忘的嘛，对不对？我们的 k 它是等于 y 比 x 的 吧？或者说德泰 y 比德泰 x 无所谓，你写上德泰 x 就 更严谨一些。那么我们的 k 一 撇呢？它是等于我们的德泰 y 一 撇比上德泰 x 一 撇，对不对？ 然后我们的 y 一 撇，它是等于什么？是不是等于我们的？呃，我们前面 y 是 怎么换的？ y 一 撇跟 y 是 一样的，对不对？ 所以呢，我们的 y 一 撇，它就等于 y 是 一样的。然后我们的 x 一 撇，你看看这里， x 一 撇，它是等于二分之 x 吧，所以下面应该是等于得它我们的二分之 x， 所以 它应该等于啊，这个二拿到前面的是两倍的，得它 y 比上得它 x 吧，就等于二，对不对？二倍的 k 嘛， 所以我们就能求出来了。你现在 k 一 撇已经知道了，你现在 k 一 撇知道了，你现在要求 k 把二除过去就可以了。 所以我们的 k 呢，它就等于我们的二分之根号七，就求出来了。写到这里，同学们不要天真就以为写完了， 我们是个圆，对不对？它具有什么对称性吧？你既然能在右边画出这样一个图，那我左边呢，自然也能画出一个一模一样的图形了，对不对？ 所以我们的呃， q 一 撇在这里， p 一 撇在这里是没有任何关系的，对不对？所以我们其实前面的 k 一 撇啊， k l 一 撇，他其实有两个答案，一个正负根号七吧。那我们这边的 k 呢？他是不是有两个 正负二分之根号七？所以最后的直线我们带进去之后有两条，你看看他传统的方法做出来确实是有两条，对不对？一个是斜率为二分之根号七，一个斜率呢？ 为负二分之，刚好起好。这就是我们今天要讲的什么化土为圆的一些常见的知识点。希望这节课对同学们能够有所收获。感谢收听，再见！

如果今年高考倒数考，这个题，你能不能十七分全部拿下？主播教你图像法秒杀倒数大题，聪明机灵的视角，教你一秒直接秒杀出最终答案， ok， 那 么本期视频带各位深度解析一下这个佛山一模考的这道倒数大题啊，就是，还是这样的答案，就还是直接秒， ok 啊， 但凡你看我之前的那个大年双击啊，或者说，呃，大年双击之后，其实还讲了个导数，这个，其实这题的话，反复就考那几个点啊。其实 张姐啊，这题的话，一看就懂了，你还有没有印象，就说之前那道题目的话，是不是有一个 low 啊，对不对？有这么一个什么？有这么一个就是这种分式形的对不对？那道题的话是不是带 f， 什么括号 s 乘以等于什么来着？说负的 f 什么什么东西，对不对啊？咱们后面再说啊，有没有点印象， ok， 那 道题的话一定要看，其实非常重要，那么我们一定就是， ok， 那 我们就来说啊，那么第一题的话，它其实考了一个函数讨论啊，函数讨论， 那这个盘算讨论的话，呃，其实是一个高频重点， ok， 那 其实一个真题中的话，经常会考察， ok 啊，所以说各位一定要掌握啊。然后我们来继续来看啊，那就比如说啊，首先看落案，那你骑手就应该有一个什么反应，是不是应该是他的这个定义域啊？ ok 啊， 定义域其实非常，你看应该是达零了啊， ok， 你 肯定是没有见过什么落落案的复数，对不对？你做那么多题了啊， 然后第一个是达令，另外一个是什么呢？另外一个就是说啊，这块他有一个断点型的这么一个定律，就说这这个点取不到啊，对不对啊？所以说一定要注意啊，那么至此，哎，那我们再来看一下，还有没有其他定律啊，其实这个分子就应该是没有什么定律的。 h， 对 对，我再问一下， 你认为这道题的话，这道题的话差点意思啊，你认为这道题的话啊，其实因为不是原题啊，你看着啊，这道题的话，这个这个 a 有 没有什么？这这个应该有没有什么范围啊？那有人说这个 a 什么范围？ a 范围的话，你是不是应该是讨论的时候你再去说啊？ ok， 那 我们我们一会再说啊， ok， 那所以至此啊，我们就有，哎，第一个准备就是说他的定域我们就已经搞到了，搞到手了， ok， 定域啊，定域之后一定要注意啊，其实后面的这个分头你一定是要按照这个定域啊去讨论的， ok， 哎，什么意思？如果说你技术不是很好的话，我们继续来说，一会你就懂了，看着啊，这什么，这是大家看这块， 对啊，那么至此我们就发现啊，那实际上你的这么一个导数呗，对不对？导完之后它就是这么一个东西，那这个导数的话，我们应该很熟悉的，要不然你就是这个分母是正的，要不然你前面成了这么一个正数，对不对？成这么一个 e 的， 什么什么 x 这种形式对不对？然后呢？对不对？ 哎，我给你写一下，我给你写一下， ok 啊，你想其实这种形式你很常见，要么什么 e， x， 对 不对？成这么一个？哎呦我去啊， 乘法一个括号对不对？那这个的话，这块啊，这有你横正部分，你就不用讨论了，对不对？你就讨论这个块里面的这个函数，要不然就是是这种分式形的，对不对？底下给你来个什么？底下给你来个这个正的，对不对？要不然是怎么样？要不然我再给你举个例子，就比如说，哎，其实真这种考核形式，就比如说这要是这么一个动 s 加上， 呃，加什么来着？加上 a 还是什么来着？哎，反正就这么个意思，对不对？有两个括号对不对？然后他俩乘以大零啊，小零啊，对不对？对不对啊？ 这都就感觉应该是直接秒秒刷秒写的，我看非常简单啊，而且他这个题的话，其实有你是个第一问，他并没有给你，对不对？涉及到这么个开口的讨论，我看非常简单，那这个一次性项目应该应该是一个的，他讨论， ok 啊，我们就来看， 所以说呢，对不对？横着不能去掉，按照刚才所说的，横着不能去掉， ok， 那 就剩这么一个，这是应该是啊，就剩这么一个东西啊，是什么？ s 平方加上二倍这么一个东西，加上一个 e， 所以 说我们直接定它为什么漂亮，定它为 g x， 对 不对？讨论它，那它就是一个开口，不是，它就是一个二次方程，二次方程的话是开口讨论呀， ok， 你应该是直接能默写出来的， ok， 那 么刚才其实咱留了一个点，这个 a， 你 到底要怎么讨论呢？对不对？你说要看换以后的这个字它啊， ok， 一定要注意啊，一定要注意啊，其实这个，哎，行了，先不说啊，你想，那这句话 a 啊 a 啊 a， 你 要怎么讨论呢？对不对？你是不是要讨论一个二，讨论一个零啊，对不对？那我们就要分什么？我们是是不是就要分啊？有人说要，如果说，哎，为什么要讨论二和零呢？对不对？哎呀，这个什么，这个根号下标点 c c 嘚，它大零等于零，小零啊，对不对啊？大零小零等于零，对不对？你讨论一个是否跟这个相交啊？对不对？ 相交相切，对不对？然后就没有交点，对不对？那不就是这么一个东西？所以你要讨讨论这个得是大零小零等零， ok， 但是你能就直接讨论大零小零等零，对不对？你实际上是不能直接这么讨论，那为什么呢？这道题的话，你看你一个零啊，一个二，对不对？哎？ 一个零一个二，你要讨论就是小零时候可以小零等于零， ok， 那 大零大零的话，是不是又分那个什么零和二之间的这个大零和大院，就直接纯大院的这个零啊？对不对啊？你而而且这你是不是还有一个等于二 啊？那有人说，哎，有人就看了这么一个解析，那为什么就是这个没有等于零呢？问的好，为什么？因为我们说过了，哎，对不对？这里你猜一下，为什么没有等于零？因为你可以看一下这个原题啊，在这里啊，这题你 a 要是等于零的话，那这题， 那这题就是 f x 等于零， x 让你求这么一个东西，让你讨论这么个，这么一个，就是这个导数啊，这么一个函数啊，所以说这个啊，它这个题目的话是没有 a 等于零的， ok， 这里我们就应该是可以了啊，那我们大家去看一下， 所以说找题的话，你不用去讨论 a 等于零，呃，一般题目的话都会告诉你，这种题目的话 a 是 不等零的， 然后我们继续来看一下，那其实这个这其实就比较简单了，对不对？那这里的话就是，呃，一个小鱼手，这里的话，你讨论之后，你会发现当小鱼的时候，它其实是一个恒量恒大绿灯啊，你往回，你往这个点里一带就 ok， ok 啊，那其实我们主要说这块啊，主要说这块 看一下啊，然后我再墨迹一句啊，你考试的时候一定要不要这么去写，就说德小等于零，然后这个 a 就是 这个德大零就是。你要怎么写呢？你最好就是你要去写的是小零等于大零，你这么去，你要分三，不要去分两，也就是说这个等号你不要随便去加， ok， 因为很多人这个，哎，其实这个题其实技术不是那么好，所以说这个等号的话，你不知道到底要填哪里。 ok， 那 我们继续来说啊， 看一下，那也就说你看我们刚才所说，你是不是要讨论什么？这个 a 小 零零等于零，然后等于二，什么？这个大零，呃，这个二严格大于二，这个时候对不对？那我就来先讨论这种情况，当 a 大 于零的时候对不对？当 a 大 于零的时候对不对啊？我就会发现，你想你 a 大 于零的时候对不对啊？ 先讨论几种情况，你说 a 是 吧？ a 这个大零小于二的时候，那如果说 a 大 零小于二的时候，那么你带回到这么一个什么原式对不对？你想你带回到这个原式的话啊，那等于它呢？ 你你就带个数， ok 了，就比如说你带个一， ok， 你 带个一，你带一的话，这个 d 他 肯定小零的，对不对啊？然后这个 a 你 还不能等于零啊，因为题目的定域的话，就是说这个 a 是 不能等于零了，但是你会发现啊，那我 a 不是， 我不是我 a 的， 那我这个 d 它是很小于零的， ok， 那 当你你应该是能懂我意思，所以说此时啊，此时的话啊，你如果说你的这个 d 它 横小零的，那怎么办？那你这个 g s 应该是大零的，横大零的，那就横成立了呗，对不对？同理啊，其实这个你的归到这种情况， a 等于二的时候，其实也是这个 ok， 又归到这种情况了，那么 同理啊，当你 a 大 于二的时候，当你 a 大 于二的时候，你还是按照我刚才所跟你说的，对不对？往后一带啊，往后一带， ok， 那 其实咱们主要说的是哪里？在这里啊， a 小 于零的时候，你想 a 小 于零啊，如果说你 a 小 于零了啊，那此时呢，你的这个得它肯定是恒大零的，不代表负一，对不对？那你这这这，你看负负是不是得正啊？负一的话是不是负负四，然后呢？乘这么负的负数，对不对啊？ 所以说至此啊，你会发现啊，那如果说你这个 a 小 零的时候，那我的这个嘚儿是横大零的，对不对？然后这里有有个关键点啊，有一个关键点啊，还是那一块，你讨论到这里的话，你就应该，你想你大零的话，是不是应该是有两个焦点，对不对？这块 这俩焦点，那这叫 x 一， 这叫 x 二，那我 x 一 和 x 二还有一个什么关系呢？此时你说要要盯的就是 x 四对不对？那 x 四的话跟这个零有什么关系？ 你还记不记得我的这个定义？你要是大零，所以说你发现 s 一 和 s 二恒大于零， ok， 然后，然后其实如果说你写的比较准确的话，应该是什么呢？你带一个一啊，你带一波一啊，其实你会发现最终的这个 s 一 啊，应该是 s 二大于什么？ s 二大于这个一， 然后那个是大于 x 一 的，所以最终的话你的这个 ok， 就 比如说在这里啊，那你就，呃，这是 x 二对不对？这 x 一， ok， 那 你就会翻一道题，完事了， ok， 你 这其实写的不是很好，对不对？正常话 是什么？什么正负正啊， ok， 所以 说增减增，这这这写的有点哼啊， ok， 就是， 这是这么个意思啊，那至死的话，哎，你就将这个题的这个全写出来了，那形容这个 x 和 x 二就等于这个， ok 啊，那么最终的话一定要注意啊，你分讨论之后，你要总结一波，对不对？所以说综上所述对不对？当 a 大 零的时候对不对？它是这个单调递增的对不对？就是在这个 f s 零一合成一到六九单调递增啊，就在这个定域之内，单调递增到 a 小 零的时候，对不对？ 在什么呀？在这么一个，呃，哎，你就自己自己去看，反正咱们都写出来了，对不对？就在这区域内啊， 是先增加增啊，增加增， ok， 那 这个第一问你就 ok 了，那话这也就是说我为什么说这一题的话跟那个大的双击他其实差不多的，呃，你想就是之前你有没有印象，其实他套了个， 哎，算了，不讲啊，不讲，不讲啊，这个你自己去翻，一定要去翻，那个导出非常之重要。 ok， 那道题的话，它其实是不是通过这么个绝对值去给你配得出的这么一个 x， 一 乘以二等于这个一啊？而这道题的话，你会深思，他其实通过而函数给你配得出的这么一个 x 乘以 x， 而且两根之积啊，对不对？通过这个尾巴给你配出的这么一个一啊，对不对？在这里啊，那所以说这次啊， 来看这里，他俩是不是一的，哎，不是不对，对，他俩一乘是不是一，那漏完一是不是就是零？这你就不用看了，你是不是直接看这一块，那这块的话，你但凡做那道题，你都知道他最后一一就是一顿化简，他肯定全部能约掉的，或者约掉一部分，对不对？那不就这么去考啊， 相当简单，所有质子化来，你看你这 x 一 和 x 二，就跟那道题的话是一样的，你看一顿约，你就直接秒秒掉， ok， 最后都有零 啊，你看第二问的话就直接秒，那第三问的话，他其实问到的一个什么，你说已知啊，他有这么个零点，然后呢？对不对？这个图是不正确的啊，这个图是不正确的，因为我这个确实是画了这么一个图，那个那个图是正确的，那个图就不放上来，然后我们就来看这个，这就很简单了， 你纵坐标一定要翻译一波，它跟圆的曲线其实一样的，你这这这在 y 轴上说明 x 等于零啊，对不对？所以说你思维就是要证明 x 等于零的时候，这两个 y 其实相等的， ok， 那 这这题秒了，说说话对不对？然后还有这么个性质，当， 这就是我一开始铺垫的了。对，当你见到这种形式的时候，你是不是要带 f 就是 x 一， 你要是看一波啊，对不对？你就得到这么个结论，那只要体报你直接秒掉了，那最最终的话，那我们就会发现零点七是这么去对应的。 ok， 然后我们就来看，那当零点钟去对应的话，那你是你想它是不是让你求切线？你是不是要写出这么一个方程，对不对？ y 一 y 等于等于这么个 k 为 s 减 s 零，对不对？这里的那个 s 对 不对？它还是一还是一个零，你最终是不能换出这种形式，那你最终的话， 你可以令它为这么一个对 h x， 那 你最终话，你适合证明它俩相等对不对？你怎么证明？你往里一带不就完事了？所以说这道题的话，哎，不好意思，这道题的话就直接丢掉了。 ok， 你 换出这个，然后 你往后一带，其实正好就是一样的，那这道题的话就证明完毕了。所以你会发现这道题的话，整体思路，其实我再再墨迹一遍， 整体思路的话，其其实并没有什么难的。第一问，第一问一定要分横，他是这么一个大体型的考点，如果说你跟过我们的这么一个，对不对？内部的这个全课程的话，这是已经给你总结的相当到位了。 ok， 基本上就是你见了就是直接秒掉啊，你就可以拿到这么一个程度啊， 基本上你是可以拿到这么一个程度，非常简单啊。我说话那个导出其实并没有那么难啊，那这这这，这就完事了，对不对？所以你会发现整个的话，你会发现 这个三个题啊，全部都是宋文题。 ok， 这并没有那么难，一定要注意啊，你一定要去画图，一定要去画图，你画完图之后你就会发现导数其实又比较清晰了。 ok， 如果今年高考导秀考这个题，你能不能十七分全部拿下？主播教你图像法秒杀导秀大题，聪明逼人的视角，教你一秒直接秒杀出最终答案。

三，嗯，最后我们秒杀一个高考原题啊！最后一题，这个题的特点呢，是计算量超级大啊，这个椭圆方程我直接给出来啊， 九分之 x 方加四分之 y 方等于一。题目是这样的啊，平面内的动点 p， 满足 过 p 的 两条椭圆切线始终垂直，求满足此条件的 p 点轨迹方程啊， 这个题啊，当年学生出考场问我，结果我告诉他， x 方加 y 方等于十三。同学啊，老师，你怎么立刻告诉我你没算，我说我是在头脑中做了这个推测。大家看， 我们先取一些符合提议的动点批再进行研究啊。 我点这四个点，大家都认可其横纵坐标的绝对值分别是三、二啊，这四个点当然满符合提议啊， 我们还可以根据对称性在 x 轴、 y 轴上各找到两点啊，也符合题，现在我们考察的轨迹已经错了，没有螺旋线摆线了啊，可以排除直线吗？哦， 可以，同样可以排除抛线与双曲线啊，因为这点的分布同时在 x 轴和 y 轴上都具有排除这两种曲线，另外这两种曲线也都是开放图形。我们这个问题， 轨迹一定应该感觉到是封闭图形，这样仅剩圆与椭圆了啊， 那么圆和椭圆，我们只要满足条件点做一判断，到对称中心的距离 看是否相等即可啊。这样我们看 y 轴正半轴甚至一点，如果此点满足其，那么过此点做椭圆的切线，假设与 x 轴交于交点交 r 啊， 根据对称性，我们知道此直线与此切线与 x y 轴交角为四十五度， 那么另一端啊，与 x 轴的交点交角也为四十五度，即 y 轴声点若满足其意，则 x 轴声之点也满足其意啊。那么这两段距离是相等的，是 和圆点三点构成一个等腰直角三角形距离，两条直角边距离相等啊，这样我们就确定轨迹不会是椭圆啊。 那么我们再看四个象限内的点，横中坐标分别为三 二啊，那我们就知道此圆圆心是图形的对称中心坐标圆点 o 圆的半径应该是根号下三的平方加二的平方啊，所以当然这个轨迹方程就应该是 x 方加 y 方等于十三啊！完了， 那这个题呢，如果我们正常做，我们应该设 p 点坐标 x 零，要掌控住这个变量，把这个直线方程设为 y 等于 k， 乘括号 x 减 x 零加 y， 这样把直线方程与椭圆方程 连利啊，带入，消掉了 y， 得到关于 x 的 一元二次方程啊。 k x 零， y 零作为系数出现， 那么这条直线是与椭圆相切啊，即有 dx 等于零。大家在分析， dx 等于零里边还含有三个量， k x 零 y 零啊， 那我们把它当做 k 的 一元二次方程来处理哎，为什么老师你能知道一定是 k 的 一元二次方程呢？这个我们在计算中啊，会出现 k 的 四次下，但是你要坚信它一定会消掉啊， 因为过 p 点做椭圆的切线能做两条啊，对应有两个斜率值啊，所以一定是圆 k 的 一二次方程啊，你要用心解啊，一定能消掉。那么关于 k 的 一二次方程 应该有两根之积， k 一 乘 k 二，两条切线互相垂直等于负一。 大家再看看一乘 k 二这个式，式子里边仅含 x 零 y 零，我们也就得到了 x 零 y 零的一个等量关系式，即整理即可啊。迅速是什么过程？但是你真正的解却是很繁杂啊。 我建议啊，如果时间不够的话，我们把推测的是结果在后边中写整理得啊，你时间不够了啊，那呃，得这个最终结果啊。 哎，这样呢，可能不扣分也可能扣一两分啊。你只能不完美中求完美啊。 ok， 就 这样。

大家好，我们来讲解一下苏北四市高三数学一模试卷的第十八题，圆锥曲线压轴。首先我们来看一下题目的意思，虽然说 这一题是关于圆锥曲线抛物线的问题，那么实际上在第二问主要是关于硕列地推的问题，重点考察的是硕列之间的关系，属于硕列和圆锥曲线结合的题目。 那么第一问接起来相对来说比较简单，我们把先把第一问来计算一下。 首先抛物线 的准线方程 为 x 等于负的二分之 p， 将 x 等于负二分之 p 带入圆零的方程，可以得到 四分之 p 的 平方，加上 y 的 平方是等于四的，从而可以求出 y 的 值。 实际上 m n 之间的距离就是 y 绝对值的两倍， 从而可以求出 p 的 值， 就求出来了抛物线的方程， y 的 平方等于二 x， 这是第一问的解答，那么实际上第一问相当于基础送分，做出第一问 可以得到三分，这三分得起来是比较容易的。 那么重点在第二问， 那么在解第二问之前，我们先根据题目的意思先画图， 那我们把这个图先画出来，圆零圆一，圆二与抛物线之间的关系。 那么第二点去找狭裂之间的 硕列之间的递推关系。题目第一小问让我们证明的是 r n， 这个硕列为等差硕列，那我要找到 r n 减 r n 减一， 它等于一个长硕，从而证明出来这个硕列是一个等差硕列。那么要想找 r n 和 r n 减一之间的关系的话， 首先我们需要去设 圆 i n 对 应的圆心坐标。 根据地推关系， i 一 是可以等于二，加上 r 一 的 i 二等于 i 一 加上 r 一， 再加上 r 二 等等等。根据这个递推关系，所以 i n 应该等于 r n 加上 r n 减一，加上 i n 减一。 也就是可以把这个圆 i n 和圆 i n 减一，它对应的圆的方程就可以写出来了。 这时候我圆 i n 和圆 i n 减一，它都是与抛物线是相切的， 那我们可以去连立抛物线和圆的方程。 消去 y 可以 得到关于 x 的 e x 方程。 同样的道理 可以得到 x 和 i n 减一的 u s 方程。 那么由圆 i 与抛物线，它有两个公共点，且我的抛物线为对称性的关于 x 轴对称的图形，这时候相当于 两个 d r t 均应该等于零，也就是上述两个一元二次方程 有两个相等。 施硕根 g 化简之后， u d r 等于零。化简之后可以得到两倍的 i n 等于二， n 的 平方加一。两倍的 i n 减一是等于二， n 减一的平方加一再结合 i n 等于 i n 减一，加上 r n 加上 r n 减一，一二三三个式子结合可以得到。 至此就证出来了， r n 减去， r i 减一是等于二的，等于一个常数，由此可证 r n 为等差数列。 这是第二问的第一小问。那么第二小问 我需要先求出下列 r i n 的 首项 r e 以及 圆 i n 的 半径及圆心坐标。 由提圆一的圆心应为二一加二零，半径为二一，那么圆一的方程 为。 此时去连立圆一的方程和抛物线方程 同样消去 y， 可以 得到关于 x 的 一元次方程。再利用 圆与抛物线相切，德尔塔等于零既， 从而可以求出 r 一， 求出 r 一 是可等于三的。另一个 r 一 等于负一是需要舍去的， 也就是首项缩列 r n 的 首项。 r 一 等于三求出来了， 那么二 n 应该等于三，加上 n 减一乘以二，也就等于二。 n 加一，也就是圆 n 的 半径 为 r n 求出来了，那么再去求 i n， 也就是圆 i n 的 圆心的横坐标。 i n 由 i n 等于 r n 加上 r n 减一，加上 i n 减一， 可得 i n 减 i n 减一，是等于 r n 加上 r n 减一的，那么作为 r， 那么作为 i n 减 i n 减一的形式，我们可以采用理加法计算 i n， 也就是 i n， 它可以等于 i n 减 i n 减一，加上 i n 减一，减 i n 减二，加上 i n 减二，减 i n 减三， 加上等等等。加到 i 三减 i 二加上 i 二减 i 一， 再加上 i 一， 那实际上它就等于二 n 加上二， n 减一，加上二， n 减二加上二， n 减二，加上二， n 减三，加上等等等。一直加到 二，三加二，二加二，二加二，一加二，一加二， 实际上基本上除了 r n 之外，都是两倍的，两倍的，两倍的，两倍的、两倍的，所以它它可以等于两倍的括号。 r 一 加上， r 二加上 等等等，一直加到 r n 去减掉一个 r n， 再加上二， r n 为等差数列，用前 n 项和的公式去求括号里面的就等于 两倍的括号。 m 的 平方加二， m， 括号减去二， m 加一，括号加二，等于两倍的 m 的 平方加上二 m 加一，也就求出来了。 i n 是 等于两倍的 i n 的 平方加上二 n 加一的，也求出了圆 i n 的 横坐标，圆 i n 的 圆心 i n 横坐标， 所以圆 i n 的 圆心为 圆心。求出来了直线 l 的 方程， 继续连立 抛物线方程和直线方程 消去 x， 得到 关于 y 的 y x 方程由伟大定律 可得， y 一 加 y 二等于二， y 乘以 y 二等于负的两倍的， 这时 a b 之间的距离就等于根号二倍的 y 一 减 y 二就等于根号二倍的根号下 y 一 加 y 二，括号的平方减四倍的 y 一 y 二， 将 y 一 加 y 二， y 一 乘以 y 二代入可得， 从而求出 i n 等于九或 i n 等于负十舍去 最终答案， i n 等于九。这题是我们圆锥曲线关于抛物线的 十八题压轴主要考察的实际上是关于掠猎的地推关系。

今年的广东大湾区高三一模数学卷中，压轴大题考了双曲线与数列结合题，是这类题中近期最难、计算量最大的一道，想冲刺幺三五的同学来挑战下。

如果今年高考考到斜坨岩，你能不能五分直接秒到？小恒定律秒杀法，带你直接拿下高考必考斜坨岩的视角，教你一秒直接秒杀出最终答案，这题还是直接秒啊，那么本 期视频呢，给各位带来这么个斜坨岩的秒杀技巧， ok 啊，那么众所周知，这个斜坨岩的话，今年的这个高考真题的话，呃，其实是考过的啊，一个多选五分， ok， 那 么他有没有可能啊？对不对？他其实已经给你暗示了， 就说给你出了这么一个多选，那他有没有可能，对不对？接下来的话，给你出了一个什么情况啊？对不对？给你出，甚至出这么一个大题啊，对不对？都是有可能的。所以说呢，本期视频的话，教你啊， 无论说是这个小题大题啊，还是各种题，对不对？哎，告诉你如何去破解这种缺德啊，而且基本上是可以达到一个秒的这么一个程度，哎，什么意思呢？对不对？我们直接来看， 那么首先我们有这么个意识，对不对？在你碰到这种形式的时候，他就是一个什么呢？他就是这么个斜椭圆， ok， 但是当然其实这么说不太不太准确，因为这个你要看他那个德他，那么我们后面再说啊， 只需记住两个点啊，三步，这题就直接秒杀了，什么意思？你就记住，当你变换完之后的这个斜角线，原来是写的，那么当你变换完之后的这个椭圆，因为你要把它去给我变成正的啊，那么正，有可能水平正的，也有可能是这么一个什么， 也有可能是数值的这么一个正，那有时候什么时候是正呢？就什么时候是这么数值正，什么时候是这么水平正呢？问的非常之好， 这个的话，你就看他那个那个 a b 啊，其实我说说实话对不对？你看题目要求啊，题目会告诉你 a 大 于 b 啊，对不对？大于零子这么一个条件的啊，对不对？或者说如果说题目没有给你要求的话，随意啊，为什么呢？因为我问你啊， 你对于一个椭圆而言的话，你竖着横着，如果说他在这么一个 a b 啊，啊，不变的情况下啊， a b 的 这个不变的情况下，对不对？你竖着和他这个横着啊，其实我问你离心率他有没有差别，他其实是没有差别的， ok， 或说这个，呃，或者这后续碰到题你就知道了，现在也不过都继续竖了， ok 啊，这都无所谓的。看着啊，后面全懂了，看着啊， 那么这里的话，你只记住一个什么东西呢，对不对啊？记住前面的这个系数 abc， ok， 这个 f， 这 f 你 也要记一下，对不对？那么在它变化完之后的话，你想我们是不是就是要去掉这个旋转量啊，对不对？中间就是旋转量啊，所以说你要去掉这个旋转量，那么这个旋转量的话，它其实有两种方法能去掉这个旋转量啊，什么方法呢？对不对？ 第一种就是说将这个椭圆变成这么一个平的，或者说另外一种就是说啊，直接就变成一个圆，哎，悟这个缺什么意思呢？那我们后续再看，对不对？那首首先一定要注意啊，哎，这这这，你不不用懂什么记了，对不对？你就直接这么去记，就是说前面的话， a 和 c 啊，和后边你变化完之后的这个 a 和 c， 它其实相等的， ok 啊，另外一个呢，它判别式，它实际上是呈红的，那么你只需记住一个核和这么一个什么和这么一个乘积就完事了，那这两套全部都是 a 和 c， 这没关系 啊，这还有个 b， 那 么看这两核看着核就是原来的核，那么乘积就是，哎，你有没有发现挪过去时候是不是负的四分之，这个什么嗒嗒 ok 就 在这里，对不对？ 然后呢，这个嘚有什么用呢？这个嘚他就让你去判定啊，你到底是这个椭圆啊，还是这么一个抛线啊，对不对？还是双曲线啊，对不对啊？一般情况下，注意啊，一般情况下的话，你其实就就两个，当然大多数的话，真题其实是考过斜的，还没有考过这种双曲线的， ok， 那 道多选题啊，对不对啊？一会我们也会给你去讲述一下的，然后这个斜的你就基本上嘚小零是这么个斜角圆， ok， 而这个斜角圆我再告诉你， 你题做多了的话，你会发现基本上它都是旋转多少度呢？哎，你一定有这么一个啊，你脑子里一定有这么个想法，你一定知道它基本上它考就考旋转多少度，一会再去说， ok， 那 我们再来看这里话注意哦，对不对？实际上就是，哎，要么是椭圆，要么是双曲线， ok， 那 么我们的做题步骤实际上是什么呢？对不对？你可以啊，第一步啊， abc， 你 先识别出来啊，你先识别出来， ok 啊， 然后呢，这个 b 就是 x y， 就 那那选旋转量前面的这个系数对不对？ a c 对 不对？什么 x y 前面的这个系数啊，对不对啊？应该是 x 平方和 y 平方前面的系数啊，这无所谓啊，就，就是这，就这么意思就可以啊，另外一个就是这么一个得 ok 啊，然后呢，对不对？ 注意啊，做重题的时候，但凡将小圆啊，那什么形式是斜口圆呢，对不对？刚才已经跟你说过了，对不对？然后第一个是和，第二是乘积，和与乘积，对不对？你想你是不是要去算旋转之后的这么一个 希尔元？在这里，在这在这在这，对，对啊，他加这么一个常数，哎，对不对？我再墨迹一句啊，这个 f 的 话，任意啊，添，这也行，添，这也行，对不对？因为实际上最终的话，你是不是要变成这种 s 平方比一个什么东西，对不对？和 y 平方比一个什么东西的这个形式等于一， 对不对啊？这是加是减，看他是那个，到底是那个希尔元还是那个是，就是，你应该懂我什么意思啊，然后呢？哎，看这， 然后啊，这你都不用记，其实你想这都不用记，不用看，不用看，不用看，对不对？然后有人就要问了，那这里啊，我一旦变成这种形式之后，对不对啊？那怎么变呢？对不对？你是不是要求 a 一 和 c 一 啊，对不对？ a 一 c 怎么求？你通过这个求，对不对？两方程两个位数，你一定能求出最终的这个 啊，对不对？这的这个 a 一 啊，它实际上是够用的，对不对？你可以这么一代入啊，对不对？这的这个 a 一 啊，它实际上是够用的，对不对？你可以这么一挪咔一除， 对不对啊？你就变成这种形式不就完事了，对吧？等一，这不就比上一个东西，比上这么一个东西，对不对？就完事，这都不用看，你就看这就完事了，对不对？就不用背啊。 然后我们就来看一下那离心率的话，对不对？你看，其实我，我们刚才已经说了，你无论说是这么一个平的还是这么一个竖的，离心率全部都不变的， ok， 那 面积的话我们都知道啊，对不对？ s 等于什么？拍 ab 啊，对不对？这个之前我的实名也跟你说过对不对？才那么一考点， s 等于 ab， 然后呢？如果说你看哪斜的话，他问你什么呢？如果说是一个斜椭圆的话，他有可能问你对不对？你这个什么，哎，这个，这个，这个最长的这个距离啊， 对不对？那这个最长的距离啊，那实际上是不是有什么？哎，对不对？那实际上是不是就是这一段啊？对不对啊？那最短呢？那是不是就是这这一块？你应该懂我什么意思，对不对啊？ 完事。所以说他其实这个距离啊，范围其实就是什么，就是这么一个什么 b 和 a， 他 就是那个你算上来最终的那个 b a， 我 看， 那我们再去往下来看，对不对？那又说，哎，我去，还要去背一个，对不对？你这里你需不需要背啊？这个其实之前我那个啊，我的这个频道上也发过这种视频，就是告诉你说这个 c 它啊是等于这么个 b b a 减 c 的 啊，但，可是，可，但是你注意啊，实际上你是不需要背的， 你是不需要背的啊，为什么呢？我们一会再说， ok， 看见得了啊。然后最终的话，如果说题目给出一种参数方程怎么办？那你消三呗，消三的话你还是变成这种 x y 呗，其实就是这就是参数方程了， ok， 然后， ok， 那 么我们首先来进行这么一个大总结啊，那么当你碰到这种形式的时候对不对？ a， s， b， s， c， y 方对不对？那个 f 在这种形式的时候对不对？第一步是什么？第一步是不是提取这么个 a、 b、 c 啊？系数你要有对不对？然后之后怎么办呢？第一个是这个，然后第二呢，是不是识别这个得嗨啊，对不对啊？得小零的时候他是这么一坨，还记不记得对不对？ 然后，然后，然后剩下的话，你就那那剩那根就是这个了呗，对不对啊？然后另外一个就说解方程组，解方程组之后对不对？你就就是这个方程了，对不对？最终的话啊，你将这个成功，将这个斜椭圆变成这么一个平的或者说竖的这么团之后，这题就迎刃而解， ok， 我 们继续来看， 那么首先啊，如果说是对不对？给你出你这种形式的话，让去反求这么一个标准方程，你该怎么去求呢？其实已经非常之明显了，刚才已经说过了，是不是？这就是对不对？你是首先来个两根之和，对不对？来两根的这么个乘积，那乘积是不是应该负的四分之的他呀，对不对？在 这里的话，得上你一定是小零的，这不一看就小零这 b 方对不？这二平方减去四倍他俩，那肯定小零，对不对？所以说他一定是这么一个斜椭圆， ok 啊？ 呃，那然后这个你求出这个，求出这么一个啊，新方程，那其实你这一画眼就能求出他原原来对应的这么一个，就是正常的这么个椭圆了啊。那么两个问题看这俩，那么第一个问题就说，那第一个问题就说什么呢？第一个问题看这俩对不对？ 你看对不对？他是不是这块得上了，对不对？一除四是不是就成鸡了？那有人说啊，这个有两根之核啊，然后有两根，哎，我这么去给你写，看着你有两根之核，对不对？有两根之鸡，那怎么去求，对不对？你怎么去求，对不对？你有说双姐，你将它往里带不就完事了，对不对？那就麻烦了 啊。这理发其实就是你看着啊，这理发你直接就能看出来啊，你两个是核啊，是不是负的？你看这块其实就是负的，这个 s 加 s 二，这就是那个什么知识了，以前的这个知识，老铁，这块的话你就直接一写完事了， ok， 你 根本不需要这个存贷。 我都服了，你都回答了，你再反求圆成，那你还你，你再你再往回带出去，那你就对不对啊？那就有点麻烦喽，对不对？那至此一个啊，十字相乘，十字相乘一个球来了，如果说你十字相乘不太好的话，你直接求公式完事了， ok， 直接求公式，万能求公式，对不对啊？人求完之后对不对？ 就这俩，就这俩，这里的话，对不对？就这俩，这里的话，对不对？就这俩了呗，对不对？同出九六啊， 已经得到它了，然后这里我已经说过了，就说，呃，其实这两个都都差不多，说实话都差不多。其实题目会告诉你的，这道题原题应该是会给告诉你这个 a 加 b 的， ok， 那 至此这就是原方程了， ok 啊，不是这个，这这这这个，这原方程 a 加 b 对 不对？ ok， 一 般情况下的话，它都会给你这种形形式的，如果说没有给你的话， 那其实一般情况下的话是选天，那其实都可以啊，你，你去通过这么一个啊，平的，或者说这么一个啊竖的啊，去做它最终的这么一个 a、 b、 c、 d 四个选项， ok 啊， ok， 那 么如果说给出这么一个操作的话，对不对？那这题的话，其实一看就是一个斜椭圆啊，对不对？标点 c、 c， 它一定是小零的，所以它应该是一个斜椭圆，那其实这个题转多少度呢？这题其实一看就应该不是四十五度， 为什么呢？我们后面再一说啊，对，那个公式，这个残疾他一个二，那个那个二 c， 他 你不用去背啊？不用去背，然后我们去继续来看，对不对？那洗手员对不对？德他对不对？那那那，那这不就是一了呗，对不对？ 有没印象？成绩应该是一了，对不对？那他俩值合呢？那他俩值个三呗，对不对？那值三呗，对不对？一个三，一个一，你是不是就可以求求求出圆方程对不对？所以你不用去，这个 怎么办呢？啊？你不用去这个，刚才那个什么那个就是用之前的那个公式， ok， 派币啊，你是不用用的，你直接咔用这个就一样了， ok， 你 就直接求出来了。 但是看这点我还要讲一个方法是什么呢？就是说，呃，实际上你有没有印象，我一开头就给你留了个选念，我就是说啊，实际上你是不是啊？你是不是，怎么办呢？你要消除一个选选项啊，对不对？怎么消？第一种就是对不对？直接让它变成这种平，另外一种就是直接将它变成这么个圆啊？ ok 啊，那这种换圆的方法，你就能直接将它变成圆了，变完圆之后，它其实面积是不变的，这种面积是不变，那怎么去变呢？对不对？一个是 x 减 y， 那 么令它为 y， 你 就能变成出这么一个圆的形式了啊？其实有时候的话，你还要去变成这么一个 s 减 y 和 x 加 y， 就是 这种形式，那你去凑出它的那个圆， ok， 那 么这里问题就来了，我的第一个问题，就说这题他为什么你要这么去令啊？这题为什么你要这么去令？那如果说换成其他的这个形式，那你的这个这个 u v 啊，你到底怎么去令呢？才能去变成这种标准的形式呢？ ok， 这是我留的这个第一个问题，你可以将你的这个 想法写在评论区， ok， 那 么如果说这种形式的话，现在各位应该是比较熟悉，他是不是就是那个真题啊？对不对啊？ 一负一，一对不对？两个之和两个之积啊？那其实这个其实你看你能看来，他应该是一个，是一个二分之一和二分之三， ok， 那 么这其实就是这么一个，你看在这个椭圆的在渐零下，问你这么一个圆的这个，这，这，这非常明显的对不对？就是这块 对不对啊？那所以说，呃，你最终的这个结果居然是这么一个三之二和二，然后这块也是对不对啊？这种注意啊，这你要打一个，最好打一个投影，因为你是斜的呗，对不对？这个图其实画的不是很好， 这么一个意思，这么个意思 ok， 又应该是算出它的这个最终结果了， ok， 那 么我们这里要说的最后一个题目啊，这里其实是非常之重点的，看着 在这里的话，我再给去给各位揭晓这个悬念，对不对？为什么？他说他这个旋卷对不对啊？旋卷就是他旋转的，一定是这个四十五度呢？因为他其实你有没有发现上一个题，或者说其实很多题你看就是一个四十五度，这里直接记啊，你不用记这个什么弹性 r c 的 那个公式啊，就什么比乘谁减谁啊， 直接你记住啊，如果说啊，如果说他的这个 x y 互换不变，就是那个轮换对称的话，但他一定是一个转四十五度，为什么啊？你可以在这个评论区说啊，就是你将你的这个答案打在评论区，这其实一想就能想到， ok， 而且大多数的话他其实都是四十五度的， 那如果说有人说那不是思路，那该怎么办呢？对不对？那么我们在我们的这个题员内部的这么一个课程中啊，是给各位去讲怎么办的， ok， 而且我说实话，刚才刚才根据那道真题啊，他其实还有另外一个协助员的这个延伸考点啊， 那其我感觉是非常之重点的，那这个也放在我们的这么一个全课程中啊，去给大家去进行这么个预测讲解，然后首先来看这题逻辑性，所以说这题直接秒了，那这个 a 呢？放这一来，你将它去给我换成这个对不对？平的不就是完事了呗，对不对？你看它这个这个这个长度呗，对不对？ 音律那 a 分 之 c， 你 变成平之后，这题不直接秒掉对不对？你有这个之后对不对？打打个选项量对不对？你就能 呃完事了，你打个扣弹音就完事了对不对？这其实就是我们之前所说的了，这都没有什么可说对不对？一转过去啊，就完事了对不对啊？最后一道题留给大家，直接秒，将你的答案放在评论区，更多精彩内容尽在题源！反。