人教七上数学第六单元角不会写怎么办

六点三角欢迎来到数字竞技场，同学们，今天我们将踏上冠军之路，一起探索神秘的角的世界。 哇，老师，角的世界会有什么奇妙的挑战呢？别急，让我们一步步来。首先我们要了解什么是角，今天我们将学习这些关于角的重要知识点，他们将帮助你们在接下来的比赛中取得好成绩。 看，这就是一个角，它有两条有公共端点的射线组成，这个公共端点叫做角的顶点，这两条射线叫做角的边。哦，我明白了，就像钟表上的时针和分针形成的角一样。没错，机器人你真聪明， 角的大小可以用度分秒来度量看，这是量角器，我们可以用它来测量角的大小。老师，那一度是多少呢？ 一度就是把一个周角三百六十度分成三百六十等份中的一份。就像我们把一个大蛋糕切成三百六十块，每块就是一度。我们可以像比较线段长短一样，通过移动角的一条边来比较两个角的大小。 那角的运算呢？是不是和加法、减法一样？对角的运算也有加法和减法。比如两个角相加，就是把它们的度数加起来。 看。这条射线，把角分成了两个相等的小角，它叫做这个角的平分线。那如果要分三等分呢？那就需要两条射线，它们分别从顶点出发，把角分成三个相等的小角。 如果两个角的和是九十度，那它们就是余角。如果两个角的和是一百八十度，那它们就是补角。哦，就像两个直角三角形里的两个锐角，它们就是余角吧。 没错，机器人你真是个数学小天才，比如现在时钟上三点整，时针和分针之间的角度是多少呢？嗯，九十度吧， 完全正确，因为三点整时，时针指向三，分针指向十二，它们之间正好是一个直角。 看，这是一个等腰三角形，它的两个底角是相等的，如果我们画出顶角的平分线，它会平分这个顶角，并且垂直于底边。哇，好神奇啊！是的，数学中充满了这样的神奇和美妙。 同学们注意了，量角的时候一定要把量角器的中心对准角的顶点，零刻度线对准角的一条边，不然就会像这样量错哦。哈哈，看来量角也要认真仔细呢。 好了，同学们，今天我们学习了关于角的五个重要知识点，角，角的度量、角的比较与运算、角的平分线与角和补角。希望你们在接下来的比赛中能够灵活运用这些知识， 取得好成绩。谢谢老师，我会加油的，我们下集见。

问你一个问题，这个月期末考试，你觉得咱家孩子遇到这种动脚压轴题，能做到不丢分吗？今天韩老师就用三个步骤带孩子轻松得分，不丢分一定记得保存给孩子 看哦！再把我整理的七上期末复习押题卷，包含了人教、北师、苏科、社教、华师等全国十二大版本，给孩子练习期末考试冲高冲满。我们一起来看这道题。角 a、 o、 b 和 角 c、 o、 d 都等于九十度，角 b、 o、 c 是 二倍的角 a、 o、 d。 现在射线 o、 a 绕着点 o， 以十度每秒的速度顺时针旋转，射线 o、 d 绕着点 o， 以五度每秒的速度逆时针旋转射，旋转时间为 t。 当角 a、 o、 d 等于十五度的时候，问 p 的 值是多少？这是一道非常典型的双射线旋转问题，那要解决这类问题，我们只需要将它转化为数轴动点问题的三个步骤，那在数轴动点问题中，我们有圆点，有正方向， 那在这里我们不妨第一步就去确定一个零度射线和正方向，那在这幅图中，我不妨就确定 o、 b 为零度射线，逆时针旋转为正方向。那么接下来由于这个条件，我是可以将角 a、 o、 d、 角 b、 o、 c 的 大小全部都求出来的，那我不妨就设角 a、 o、 d 为 r 法， 那整个角 b、 o、 c 呢？就是二 r 法度。那么现在角 b、 o、 c 其实是由两个九十度相加，再减去一个 r 法是等于整个角 b、 o、 c 的， 那所以此时 r 法就应该是等于六十度， 那么 r 等于六十度，这个角就是三十度，那么这个角是六十度，这边这个角又是三十度，那所以说每一条射线的度数我都可以给他表示出来。 我们既然逆时针旋转为正，那么我们顺着零度的方向逆时针旋转，那所以 o d 这条射线出使位置就应该是三十度，而 o a 这条射线出使位置是一百二十度，那么接下来我们就要表示动射线的度数了。 注意，在表示动射线度数的时候，我们需要用到一个公式，就是射线在动的过程中，它的度数其实是由它的起始位置 加减旋转的角度，那假设咱们的 o d 现在转到这个位置的时候，那它的表示方法就是用它的起始位置三十度， 它是逆时针旋转，所以加上旋转角度，旋转角度是速度去乘时间，那假设时间为 t， 那 所以它旋转了五 t 度，所以是三十度加上五 t 度，那 o a 是 顺时针旋转，那么假设 o a 转到这个位置的时候， 此时它的起始位置应该是从九十度开始转的，那么它顺时针旋转，就要减去它旋转的角度，它的速度为十，那时间为 t， 它旋转了十 t 度，所以是九十度。减去十 t 度，那此时表示出两条射线的度数以后， 咱们要的是旋转之后的角 a o d 为十五度，那就是表示两条射线夹角的度数，那它其实对应的就是咱们数轴动点中表示两点之间的距离， 那我们在表示两点之间的距离的时候，已知两点谁大谁小，用大数减小数不知道两点谁大谁小的时候，我们用两个点做叉加绝对值，那同样我们这两条射线在旋转的时候， 它的位置关系也是不确定的，所以它的度数也是不确定谁大谁小的。那这个时候咱们的角 a o d 就 表示为 o a， 这条射线九十度减去十七度，再减去咱们 o d， 这条射线是三十度加上五 t 度这个整体，然后去加一个绝对值，那么这里我们化简一下，它应该就是等于六十度减去十五 t 度的绝对值， 那对于角 a o d 等于十五度，那我们就直接进入到第三步列关系式，就是让六十度减去十五 t 度的绝对值等于十五度。那不难解出咱们 t 有 两个值，第一个 t 应该是等于三，第二个 t 是 应该等于五， 那么最后我们只需要检查一下，咱们的 t 是 在这个零到八的范围内，所以综上所述，这道题有两个答案，那么这种方法你学会了吗？

同学们好，我是刘老师，今天我们一起来学习我们数学线衣上色第六张几何图形，初步六点三点二角的比较与匀算。我们来看一下我们这节课的一个学习目标，首先呢，我们要掌握一个角的大小与比较，然后理解我们角平分线以及我们 角的和差辈分问题，能用几何语言来进行表述。第二个呢，会涉及一些度分秒的一个角度的预算，这是我们这节课的一个学习目标，我们来看一下，我们先来复习一下我们上节课所学的线段的比较，那我们知道我们线段的比较有两种，第一种呢就是从我们的数的 从数出发，也就是说量出来，当我们量出我们线段的大小的时候呢，就可以就可以比较了。 第二种呢，就是从形出发，利用我们的线段叠合法，然后把它放到一块，那就很容易观察了，比如说我们下面 ab 和 ac 很 明显啊， ac 是 不是小于 ab 啊？ 同样的，那我们来看第二种，那 ab 和 ac 应该是相等的，那最后一个呢， ab 应该是小于 ac 的， 所以说我们可以测量和我们叠合，那我们来看一下，那我们知道啊，我们类比一下我们线段的一个比较方法，能不能把两个角也进行这样的一个度量呢？我们先来看一下第一个， 我们是不是能用两角去去把两个角量出来，比如说这个角明显是五十多度，这个角明显不到四十度，那很明显，是不是说我的黑的第一个大于第二个，对吧？ 再来看一下我们第二种能不能把它俩放在一块，你会发现啊，我的脚这个黑色的应该大于蓝色的，对吧？所以说我们度量法和叠合法呢，在我们脚中同样的适用。 好，当我们知道这两种办法呢，我们能不能用几何语言来表示呢？比如说我们来看一下啊， 我们来看一下第一个角 b o a， 那 我们来看和我们的角 a 撇 o 撇 b 哪个大呢？很明显，红色所标的这个 o 撇角 a 撇 o 撇 b 撇大， 那我是不是就是角 a o b 小 于角 a o b 撇 b 类似的，那当它俩相等的时候，是不是就是等于号，当它俩当我的角 a o b 比它大，对吧？ 是不是我们用我们的几何语言也能说明我两角之间的关系啊？好，再来看，如果说我把角 a 的 两边都延长了，那你想一下角 a 的 大小改变吗？ 我们来看一下，当我把角 a 两边延长之后，它的大小是不变的，对吧？我们知道啊，我们角 a 两边是射线，可以无限延伸，所以说无论你延伸多少，它角的大小都 不会发生改变，只与我的开口开口大小，也就是说只与我的开口大小这里有关，其他的都是不变的啊。 好，再来看线段的和差问题，我们知道啊，我们下面 ab 是 不是也能写成 ac 加 cb， 同样的 ac 是 不是能写成 ab 减 cb， 那 我们来看一下，所以说那 bc 呢，是不是也能写成 ab 减 ac 啊？ 那我们线段有和差，再来看一下，线段也有终点，若 c 是 线段 ab 的 终点呢？是不是我们知道 a c 等于 bc 等于二分之一倍的 ab， 反过来也能写成 ab 等于二倍的 ac 加上二倍的 bc， 这是我们线段的终点，类似于像我们的什么呀？ 线段，那我们来看角是否存在这样的问题呢？看一下图中有三个角，第一个 a、 o、 c 也是我们最大的角，以及我们的 a、 o、 b， 这个角和我们的 b、 o、 c 三个角，那他们三个角之间是不是也存在我们刚刚类似的关系？比如说我们来看一下 a、 o、 c 是 不是就等于 a、 o、 b 加上我的 b、 o、 c， 那 再来看是不是我的 a、 o、 b， 那 a、 o、 b 也能写成 a、 o、 c 减 b o、 c。 最后类似的 a、 o、 c 减我的 b o、 c 是 不是就等于 a b o c a o c 减 a o、 b 是 不是都等于 b、 o、 c 啊？ 那我们角之间和我们角与角之间也是啊，和我们现在之间可以用我们的和差来计算。 好，我们来填一下空。第一个角 d、 a、 b， 我 们来看下 d、 a、 b 等于谁？等于这个加这个，对吧？第二个角 a、 c、 b a、 c、 b 等于谁？等于角 d、 c、 b、 d、 c、 b 减这个是吧？所以说我们可以很明显的把这两个填上来， 没问题吧？角之间的预算大家要能看出来，再来填一个。第一个角 abc， 来我们来看一下角 abc 是 哪一个呢？是不是这个呀？等于角 a、 b、 d 和我们的角 c、 b、 d。 什么呀？他俩相加 角 b、 d、 c， 也就是说我们的这个角等于角 abc 和我们角怎么 b、 d、 a 啊？是不是把这个减掉就等于它呀？所以说这里应该没有问题。再来看 角 a、 o、 c 是 哪两个角合呢？我们来找一下角 a、 o、 c 是 不是很明显角 a、 o、 c 是 我的角 a、 b、 o 和我的角 b、 o、 c 合呀？所以说第一道题应该就是 等于角 a o b 加角 b o c。 同样的角 a o b 是 哪两个角之差呢？角 a o b 是 哪一个呢？ 是不是角 a o b 是 这个，那是两哪两个角之差呢？是不是我可以用角 a o c 把我的角 b o c 剪掉，那同样的可以用 a o d 把我的 b o d 剪掉，两种写法都可以，大家应该能明白啊。 好，再来看一下。角 a o b 等于我的角 b o。 角 a o b 来， a o b 和我的 c o d 相等， c o d 相等，那我们看 a o c 和 b o d 就是 a o c 和 b o d， 当它俩相等的时候，你会发现它俩加它俩， 当他俩相等之后，这两个角是不是就是他俩加了同样的角啊？那是不是也是相等的呀？所以说我们的角 a o c 等于角 b o d。 要会表示我们角与角之间的关系。 当我们借助我们三角尺的时候，如何来画出我们十五度和七十五度呢？比如说我们第一个七十五度，把我们的四十五度和三十度放到一块，就能画成七十五度， 三十度放在我们四十五度之上面，也是能画出十五度的，这是不是就是我们角与角之间的和，和，角与角之间的差呀？那我们借助三角板可以画出其他的度数，对吧？大家可以试试画一画。 好，再来看一下。当我们角为 aoc 为五十三度十七分时，那我们求我们角 boc 的 位置，那你知道啊，我的角 boc 是 不是就是一百八十度？把这个剪掉就可以了。之前我们学过我们的和差辈分问题。 呃，之前我们学过我们的角的角度制，我们来看 aob 是 平角，那我们知道啊，角 aob 就 等于角 aoc 加角 boc， 同样的我们的角 b o c 就 等于角 a o b 减角 a o c。 好， 那就是一百八十度减五十三度。我们知道啊，如何来计算呢？我们来看一下，是不是它后面没有 分呀？好，当没有分的时候，我们可以把它借一个，也就是把它借成五十，一百七十九度六十分，那这样的话就可以进行运算了，我们度减度分，减分就可以了，这种做法大家要会啊，这种做法大家要会。好，最后算完一百二十六度，四十三分。 好，那我们再来针对一下训练下。第一个角 aoc 等于三十五度，角 boc 等于四十度， aoc 三十五度，然后呢？ boc 等于四十度。问你，角 aob 很 简单，加起来就可以，是吧？ 好，这是第一个。第二个，我们来看一下角 aob 六十度，也就是整个等于六十度，然后问你，他那很明显六十度减四十度，是不是就等于二十度呀？ 再来看一下，角 a o b 等于六十度，角 a o c 等于三十度，那是不是就是说我们换一个六十度的角，角 o b 等于三， a o b 对， 等于六十度，然后呢？角 a o c 等于三十度。哎，那你说这个 a o c 是 在这里还是在这里？ 那是不是有两种情况，一种是在这里，那我的脚 b o c 就 等于三十度，那如果在这里的话呢？是不是就等于多少度呢？等于九十度了，所以说此时啊，此时有两种情况，对吧？所以说我们要分情况来讨论，那一个是三十度，一个是或者是九十度， 所以说我们角度啊，它存在多种情况。好，我们来看一下，那角的平分线是什么意思呢？就是说，当我把一个透明纸在我脚上画，在我的一个纸上画上一个 a、 o、 b， 当我刚好画出一个呃线段的时，哦，射线的时候， oc 刚好是它俩的一个终点，也就是说 b、 o、 c 也就它和它相等，当它俩相等之后，你会发现，是不是我的角 oc 就是 它的一个平分线， 例如我们的中线中点是不是是一样的呀？当他弄他的时候，那是不是角 aob 就 等于二倍的角 aoc 啊？所以说我们的角平分线大家要会啊，当我们把这样的角呢，就叫做角平分，这样的线段呢，这样的射线呢，就叫做角平分线。 好，那应用格式呢？就是说，因为 a、 o、 c 是 我的角 a、 o、 b 的 角平分线，所以 a、 o、 c 等于 b o c 等于二分之一倍的 a、 o、 b， 同样的，反过来也就等于 a、 o b 等于二倍的角 b、 o、 d 等于二倍的角 a、 o、 c。 好， 当我们知道这个的时候，我们角的三等分线是不是一样的呀？也就是说它等于 a、 o、 d 三倍的 c o d 三倍的 a、 o、 c 是 一样的啊？ 好，当我们知道角平分线的概念的时候呢，我们就能做题了，你看一下， o、 b 是 a、 o、 c 的 角平分线，也就是这个等于这个 同样的 o、 d 是 它两个平分线，这个等于这个 a、 o、 c 呢？等于多少度呢？ a、 o、 c 呢？等于八十度，那 b、 o、 c 等于多少呢？应该是比较简单的是吧？就等于它的一半，也就等于四十度。 好，再来看，如果说我 a o b 等于四十度， a o b 等于四十度， d o e 等于三十度， d o e 等于三十度。问你 b o d 那 是不是把它俩刚好是，我们刚刚说了它是角平分线，是不是把它俩加起来也，最后呢就等于多少呢？七十度没问题。 再来看， a o e 等于六十度也 a o e 等于一百四，整体等于一百四， c o d 等于三十度， c o d 等于三十，那这个是不是也等于三十？那一百四，把这两个，把这两个减掉，是不是 就剩下它俩了？除以二。然后呢，我的 a o b 的 度数是不是也就能求出来最后等于四十度，对吧？所以说我们的角平分线在我们的期末考试里面是不是也就能求出来最后等于四十度，对吧？所以说我们的角平分线我们的概念弄清楚要会写 好，我们来总结一下，我们涉及到角度运算时呢长，除了常规的和差辈分问题，我们还有去分，嗯，用我们的方程思想和我们的分类讨论思想来解决问题，我们来巩固一下。来第一道题， oc 呢，是我 aob 的 角平分线，那就是我这个和这个角相等的，然后呢， o d 呢？是它的角平分线，有这个和这个有相等的，所以下列格式正确的是选哪个呢？大家可以看一下 是不是选 a 呀？我们知道啊， c o d 就 等于二分之一倍的角， a o c， 因为它俩，因为为啥呢？因为我知道 c o d 等于二分之一的，它等于二分之一的，它，是不是这个 b o c 和 a o c 是 相等的，所以 最后也能写成这样的关系，对吧？好，这是我们的第一道题，其他都是错的，大家可以验证一下。再来看一下我们第二道题，来填空第一个角 a o b， 也就是我的角，它加上我的角 b o c， 很 明显，是不是角 a o c 啊？ 那角 a o c 加上 cod 呢？是不是就是我们整个大角的角 a o d， 同样的，它减，它就等于 b o c a o d 减，谁减？我的 b o d 就 等于角 a o b。 这几个角要会填好， 那我们知道啊，如图，当我的 a o b 也就等于 b o c 等于我的 c o d 的 时候，是不是 o b 是 我 a o c 的 角平分线？那角 a o c 是 不是就等于角 b o d， 同样的，它等于三分之一倍的 a o d， 就是 我们的三等分线，对吧？ 好，来再看一下，因为 a d 是 它的角平分线，是不是说我就知道了，既然你是人家角平分线，是不是你剩下的两个角就相等了呀？所以说这个角等于这个角角平分线的 e， 同样的，因为它等于它，所以它是它的平分线，那就是反过来也要会用，对吧？ 角平分线的意义，所以说角平分线呢，是我们必考的。再来看来，角 aob 等于它等于九十度，那就是这个角和我们的哪个角呢？ codd， 这个角等于九十度， aod 等于多少呢？这整个角等于一百四十。 呃， a a o d 啊，这个角等于一百四十六度。问你啊，角 b o c， 角 b o c， 那 是不是根据我们的什么呀？九角最后就能算出来，减去，减完之后就等于三十四度，没有三百六十度，把它来减去就可以了啊。 好，再来看一下来，已知 aob 等于三十八度， boc 等于四十五度 aoc 的 度数，那是不是就是有两种情况， aob， 那 我的 boc 是 不是？呃， boc 可能在这里，也可能在这里，所以说有两种情况，那就有两个答案，大家可以算一下。 好，那我们来总结一下我们角的比较吧。第一个我们学了角角的度量法和叠合法，是不是能进行我们角的比较呀？那角的运算呢？就是角的和差辈分问题，以及我们角的角平分线问题。最后呢是我们角的计算问题。 其中我们角什么呀？角的平分线是最喜欢考的啊，这个是在我们考试里面最喜欢最喜欢考的，大家要清楚。好，那我们这节课呢，就上到这里，我们下节课再见。

风暴太猛烈了，右前的灯火已经熄灭，我们正在失去与主船队的联系。 哪怕看不见星辰，只要电海罗盘还在，我们就能找到路。可是罗盘呢？糟糕，罗盘被震坏了，时针脱落，核心受损，没有它指引方向，全船的兄弟都会触交。沉默不，不能放弃！朕和大人说过， 万物皆有规矩，只要运用几何的智慧，我就能重构罗盘的秩序。各位年轻的领航员，现在只有你们能帮我，快随我一起进入几何的世界。修好罗盘，带大家回家！ 先修骨架，看这根磁针和底盘上的指向线，必须汇聚在中间这个固定的点上，才能展开成一个图形。 在几何图谱里，这个固定的点和这两条延伸的线分别叫什么名字？快告诉我！答对了股价才能立住！ 太棒了！股价已经稳固，磁针感应到了地脉的召唤，它要开始动了。看，磁针绕着中心点 o 从 a 转到了 b， 这转动留下的痕迹就是我们要找的角。可是盘面上方位线这么多，如果我只喊角 o， 舵手肯定会搞错方向。第二项挑战，为了精准指挥，我该用哪三个字母来表示？刚才转出的这个角 横向必须分秒不差。海图显示，我们偏离航线，虽然只有零点三五度，但在茫茫大海上，这点误差足以让我们偏离几十里。舵手的操作盘只能调分零点三五度到底等于多少分？快帮我算出来！这是避开暗礁的最后机会。 别慌，角度和时间一样，都是六十进制，一度等于六十分，一分等于六十秒。有了这个口诀，就能精准修正航向 成功了，我们找回了顶点与边，学会了角的命名，更算准了度与分。罗盘终于恢复了神，力 保船队正在归航。只要掌握了几何的规矩，就没有到不了的彼岸。不过要准确描述那座海岛是在北， 需要用到更厉害的方位。角知识小船员们，期待我们下一次的冒险，再见！ 航海秘籍描述方向时，先说南或北，再说偏东或偏西。

好，接下来我们看到动角问题当中的角平分线的应用啊，我们的思路就是用这个竖轴的思路来解决这个角度的旋转啊，用点的移动这种思维来解决角度的旋转的问题。好吧， 好，我们看到这个例题，入图一，角 c、 o、 d 呢？等于二十度， 角 b、 o c 等于八十度啊，这个等于八十度，那剩下的 a、 o、 b 呢？就等于一百八十度，减八十度，减二十度，这个也是八十度，然后 o m 平分 a、 o b， 那 么所以这个角等于四十度，这个角等于四十度， o n 呢？平分 b o d， b o d 是 一百度，那所以说这个是五十度，那下面的也是五十度，所以这个是三十度，所以我们先把它们每一个小角先给它求出来。 所以第一问，如图一角， a、 o、 m 等于多少啊？ a， o m 等于四十度。角 d、 o、 n 呢？等于五十度 啊，第一问就完了。好，如图二，将射线 o、 d， 将射线 o、 d 以六度每秒的速度旋转一周啊， 顺时针旋转一周，同时呢角 b、 c、 d 啊，这两个角，这个角有两条射线，它都在动，是吧？ 都是以四度每秒的速度呢，也是顺时针旋转啊，这两个都是以四度每秒的速度在旋转啊，这里相当于说有三条线在动了，对吧？ 他说当色性 o c 与色性 o a 重合的时候，角 b、 o、 c 就 不动了啊，就停止运动了，色色性 o、 d 的 运动时间为 t。 问， 因为当 t 为和值时， o b 啊，这个 o、 b 平分 a o n， o b 平分 a、 o n。 我 们讲了，我们说像这种旋转的问题的话，我们先把每条射线的位置给它标出来，比如说 o a 就是 零，对吧？ o m 呢，它就是四十， o b 呢，就是八十度所在的位置，八十加五十，这个是一百三十度所在的位置，这个呢是 一百七十度所在的位置，是吧？ o d 呢，是一百八十度所在的位置啊，这是一百六。好，完了之后它开始旋转，那么旋转，首先 o b 在 旋转，对吧？ o b 在 旋转，它原来是八十，然后呢，顺时针旋转，减去一个四 t， 那同理， o c 呢？也在旋转，以前是一百六，减去四 t， 同时呢， o d 呢，也在旋转，它以前是一百八，一百八减六 t。 好， 你看，第一步，把它旋转的位置给它，位置给它标出来，然后第二问， o m 的 平分 a， o b 那 根角平分线啊？用刻度的角平分线，你看这这两个相加除以二，八十减四， t 加零除以二，那这个就是四十减二 t 啊，它的位置，这个 o m 所在的位置就标出来了。 o n 平分角 b o d。 那 就把 o b 和 o d 所在的位置加起来，除以二一百八，加上八十二百六，除以二减五 t。 好，你们看，这，那这个位置都标出来了。第一问，他问， o b 什么时候平分 a o n 啊？ o b 什么时候平分 a o n， 那 怎么，怎么时候平分啊？那就是 o b 是 a， o a 的 角平分线嘛，我就不写过程了啊，对不对？那就是我的 o b 平分角 a o n 的 话，那就是 o b 是 你的角平分线嘛，那就根据我们的总点公式，那就是 o b 是 八十减四， t 就 等于 o a 加 o n， 对 吧？ 再除以二就行了嘛。我们把这个方程解出来，是吧？解的呢？ t 等于十， 看就完了啊，就完了，不需要求谁是谁的，这个角度是多少，那个角度是多少，不需要表示。你看这如果他考我们角平分线考终点，我们直接用终点公式就可以解决了，对吧？秒杀，对吧？ 第三位也是一样的，虽然说他旋转的信端很多哈，但是你们不需要考虑那么多对不对？他问题是是否存在某一时刻使得角 m o n 等于三十五度， 若存在，请求出 t 的 位置，那就是角度旋转当中的角度表示嘛，那你看，你把 o m 也表示出来了， o n 也表示出来了，对吧？那有的同学在做这个题的时候啊，这个角度是多少，那个角度啊，又是多少表示出来？不要这个样子，你直接就表示角 m o n， 嘛 叫 m o n， 是 不是用 o n 所在的刻度减去 o m 所在的刻度啊？一百三十减五 t 对 吧？减去四十减二 t， 然后加一个绝对值， 对吧？有可能 o n， 因为 o n 要转动的快一点， o n 的 速度为五，对不对？ o m 的 速度人为二，那么 o m 有 可能会超过 o n， 看到没有，所以说我们这里要加绝对值啊，它等于三十五，然后我们求解这个方程，你看这九十减三 t 的 绝对值 等于三十五，那么就是九十减三 t， 要么等于三十五，要么等于负三十五，是不是？所以我们求的 t 等于三分之五十五，或者是 t 等于三分之 一百二十五啊，所以你看这两个 t 值就求出来了，对吧？当然呢，我们做的很简单， 同学们大家考虑一点啊，就是说因为我的 o b 啊，我的 o b 旋转到哪里就结束了啊？当 o c 旋转到 o c 的 时候，就 o a 的 时候就旋转了，比如说一百六按四度旋转，它最多旋转四十秒钟，对吧？它最多旋转四十秒钟， 那我的 o d 呢？那同学们就要考虑一个问题啊，就是说，呃，有没有超过三百呃，这个一百八十度的情况啊？有没有超过一百八十度的情况？ 那你看这里的 o d 最多转一周嘛，最多转到这里来。当你的 o d 转到这里来的时候，我的 o m 呢？你看这你要转六十秒钟，但我的 o b 转六十秒钟的时候，我还在这里，看到没有，它是没有超过一百八十度的啊，所以答案呢，就只有两个， 所以呢，我们给大家归类一下啊，给大家归类一下，第一个解决动角问题，用动点问题的思维啊，把每一个射线的刻度给它表示出来啊。看到没有？射线的刻度先表示出来， 表示出来以后，然后它是怎么旋转呢？顺时针旋转就为减，角度在变小，逆时针旋转刻度在变大。 只要你把每条刻度表示出来以后，然后你表任表示任意的一个角度，它都可以啊，对不对？如果，比如说你表示角 c o n， 那 你就用 o c 减去 o n， 如果你不知道谁在上面，谁在下面，那你就加绝对值 啊，看到没有是非常简单的一个问题，还有就是你看这个题，有的同学一看到就被吓到了，说，哎呀， 这里有三条线在动，你看这，这里有角度在动，这里有色性在动，你们不要考虑这么多啊，把注意力都放在色性刻度的表示上面，好吧。

这个视频说一下几何图形的初步认识。先提一个问题，就是一个正方体如果随便切一刀的话，截面积能截出什么形状 就算是一个很有意思的小问题。首先看一下立体图形，立体图形就是各部分部都在同一平面的几何图形。围成面最小的应该是四面体， 小学都学过的柱体、棱柱和圆柱、锥体、棱锥和圆锥以及球体都是立体图形，通过这些可以组合成各种立体图形。平面图形就是各部分都在同一平面的图形，包括线、角以及一些常见的三角形、四边形等等。 三系图就是立体图形在正面、左面和下面观察到的平面图形。正面的是正系图，能看清立体图形的长和高。左面看的是侧系图，能看清立体图形的高和宽。从下面看是图形的俯视图，能看清立体图形的长和宽。 展开图就是将围成立方体的各个面一般沿棱或者曲面的一条线剪开所得到的图形。当然不同的剪开方式形状是不同的。 所谓的题就是由面围成，有长度、宽度和厚度的。我们所求的三维空间可以理解成是无限的，可以用各种面随便在里面截取出任意一个立体图形，也可以理解成体是通过面运动轨迹形成的，也就是所谓的面动形。体 包裹着体的就是面，它是有长度有宽度的，但是没有厚度。二维的平面是无限延伸的平面图形，可以理解成在这个无限延伸的平面上，右线为出的一个图形，也可以理解为面，是由无数条线段组成，也就是线动成面， 面与面相交的地方会形成线，它可以有长度，但是没有宽度，没有厚度。线由无数个点组成，这就是点动成线。 线与线相交的地方会出现点，点只能表示一个位置，没有大小，也没有形状。点的很特殊，它既不属于平面图形，也不属于立体图形，它是构成一切图形的最基本的元素。立体空间里有无秀个点，二维平面里有无秀个点 一维的现象，也有无秀个点。数学几何数写表示点，一般用大写的英文字母，比如点 a、 点 b。 直线是由一个点向两段无限延伸所形成的图形，一般用小写字母或极限向任意两点表示， 比如下面这两种表示方式。由于一个点可以向四面八方无限延伸，形成无数多条线，想要确定一条线，还需要这条线向另外一个点才能确定，这就引出了一条公里两点确定一条直线。 有理数学的数角就是一条直线。解析规定了正方向、圆点和单位长度。直线是没有端点，也就是没有中点，因此他们无法测量，也没有长短。直线上有无求点，比如数角上有无限多个有理数经过一点，有无数条直线。 无论在平面还是空间内，点以线的位置，幺幺点在直线上，幺幺点在直线外线以线的位置。现在只考虑同一平面内只有相交和平线两种情况。 射线是极限的一部分，就是从极限向的一点出发，向一个方向无限延伸的部分。表示极限的方法是以端点和射线向的另外一点表示。端点的字母必须写在前面， 因为射线有方向性，射线有一个端点，剩下的特点和直线一样。怎样识别多条射线是不是同一条射线？先看端点，如果端点不同的话，肯定不是同一条。 如果端点相同的话，再看一看射线的方向是不是一样的，如果方向也一样，那么就是同一条射线。如果方向不一样，那就不是。 线段是极限的一部分，它是极限向两个点之间的部分，一般用小写字母或线段。两个端点的大写字母表示。两点之间所有的连线中线段最短， 所以线段有个公里，就是两点之间线段最短。连接两点线段的长度叫做两点之间的距离。与极限和射线相比，线段是可以度量的有长度的 线段运算中，如果线段 a、 c 等于 ab 加 bc， 那 么 ab 与 bc 首尾相连，在同一条直线上的长度就是新线段 a、 c 的 长度。 后续如果遇到这种线段运算相加的证明情况，尽量将相加的几条线段归到同一条直线上，容易作比较。线段相结，可以认定为在比较长的线段上截取一段， 所剩下的就是另一段线段。两线段相乘是求面积，在这里一般是倍速关系或者分速关系。线段的几倍可以理解为延长自线长度的几倍，所得到的新线段 倍速系延长几倍。等分就是等分几份，取其中一份有个特例就是中点将线段等分两份的点， 当然还有三分点、四分点等。二分点所分成的线段是原线段的二分之一。三分点分成的线段，每一份是原线段的三分之一 角，可以理解为拥有公共点的两条射线所组成的图形，也可以理解为一条射线要将它的端点旋转所形成的图形。射线的公共端点叫做角的顶点，两条射线分别叫做角的两条边， 角的大小仅与两条射线之间的张开幅度有关，与射线的长度无关。角的表示方法有很多，可以用数字或者小写的希腊字母表示单独的一个角， 如果顶点处只有一个角，可以用顶点的字母表示。还有就是自由度比较高的，用两条边向的点的字母和顶点字母表示任意一个角。在画一个角的时候，我们可以看到， 其实它是将平面分割成的两部分。两条射线之间的比较小的区域，一般在零到一八零度之间所组成的角叫做裂角。初中几何中如无特殊说明都是几的这一类。还有就是另外一边比较大的区域，一八零到三六零度之间的角叫做优角， 这个区域虽然不涉及，但还是要有这个意识，因为很多时候考虑优角的时候，问题会变得很简单，这是角的一些性质。角可以度量比较，可以运算 角的度量，一般用度数计将一个研究平均分成三六零等份，每一份对应一度，一度等于六十角分，一角分等于六十角秒。还有弧度计，它是弧长与半径的比值对应的圆心角。弧度计消除了单位只是一个数字，是一个比值， 初中一般不涉及弧度记，另外还有密位记、 y 分 度记等等。角的加法可以理解为将两个角的顶点重合，另一边也重合的情况下向外进行拼接所组成的新角减法可以理解为向内拼接截取后剩余角就是两角的差 倍数，可以理解为沿自己的顶点旋转几倍所组成的新角。能分就系将一个角平均分成几份， 其中角平分线就是将一个角平均分成两份的射线平均度数可以将角分为几个，特殊的有周角、平角和极角，分别对应三六零度、一百八十度和九十度。 普通的角大于九十度，小于一八零度的角叫做钝角，大于零度小于九十度的叫做锐角。 两个角的和如果等于九十度，那么这两个角互为一角。互为一角的两个角都系是锐角。同样的可以推出来，同一个角的与角都相等， 相等角的与角也相等。同样的，如果两个角的和等于一八零度，那么这两个角互为补角。互为补角的两个角一般是锐角和钝角。比较特殊的是两极角 和前面类似，同一个角的所有补角都相等，相等角的补角也相等。看一下角的画法，首先准备集齐和两角器，先画一条射线作为角的一条边， 再将两角器的中心对准射线的端点，两角器的零刻度线对准射线，在两角器的刻度向角到要画角的度数地方点一个点，最后将这个点与射线端点连接，这个角就是要画度数的角。

有些数学题实在学不会，咱们该放弃的就放弃吧。有初一的家长和小朋友跟我说，动点动脚问题太难了，学不懂。甚至有家长跟我说，他们家小朋友畏难情绪很重，考试遇到这类题型就直接放弃了。 动点和动脚是初一的一个难点。动点问题，它是从有理数到线段和角度，再到一元一次方程，初一上册最重要的三个单元都有涉及，可以说是从开学贯穿到期末。 如果小朋友还是学不会做题，很抗拒，那就放弃吧，不要再逼着小朋友去学了。动 点和动脚这个难点，只有初一上册他会考，初二、初三乃至中考都不，都不会再有初一的动点和动脚的这一类题型，所以该放弃的就放弃。这很多小朋友，他不是一笔不会动，他是第三问的。折返问题、变速问题、 折线问题、装线段和双线段或者双角在动的问题，确实比较有难度，所以实在攻克不下来，咱们就放弃了。 学习是有策略的，一定要学会取舍。考试它本身就是在筛选，特别是中考和高考一张完整的试卷，它是有百分之六十的基础，百分之三十的中档题和百分之十的难题。 与其与其去纠结这百分之十的难题，不如稳扎稳打，把另外的百分之九十的分数拿下来， 根据自己的小朋友的情况划定一个锚点。考试不用面面俱到，也不用把每个题的分儿都拿到手，保证基础不出错，计算不丢分儿。中档题尽量少扣分， 就已经超过了大部分的同学了。学会取舍，是更高级的学习智慧，家长们放下焦虑，更重要的是帮自己孩子找到合适的节奏。

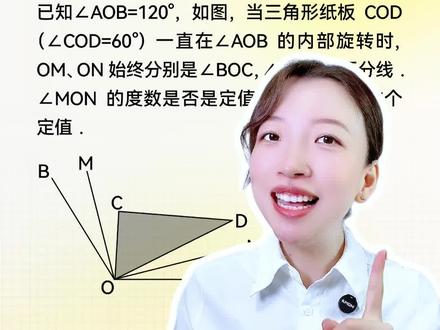
挑战每天一道压轴题，期末多考二十分！今天要讲的是冻脚问题，双脚平分线模型。冻脚问题是除以期末压轴题的必考点，百分之九十九的孩子不知道解题方法，得不到满分。想要彻底搞定期末考试，一定听完这个视频，再把我整理的七上期末考试复习押题卷， 包含了全国十二大版本，给孩子练习期末考试冲高冲满。这道题是一道非常典型的三角板旋转的问题，当三角板 c、 o、 d 在 角 a、 o、 b 内部旋转的时候，问角 m、 o、 n 的 值是否是一个定值？那想要解决这类问题，我们 就要学会表示动角，用未知数将动角表示出来，最终我们算出来的值中含有未知数，就不是定值，如果不含有未知数，就是定值。那么接下来呢？我们来读一下具体的题目。已知角 a、 o、 b 是 一百二十度，整个大角是一百二十度。 当三角形直角，角 c、 o、 d 等于六十度。在我们的角 a、 o、 b 内部旋转的时候， o、 m 是 一条角平分线， 它平分角 b、 o、 c， 也就意味着这两个角相等，那我都用未知数 r 法来表示。 o、 n 又是另外一条角平分线，它平分角 a、 o、 d， 那 于是这两个角也相等，那我们用另外一个未知数背它来表示。现在问角 m、 o、 n 的 度数是否为定值，那接下来我们就要找等量关系了， 会发现题目已知整个大角是一百二十度，那其实我们可以列出两个 r 法加上中间的六十度，再加上两个 贝塔，角是等于一百二十度的，那于是不难解出 r 法加二贝塔是等于六十度，所以 r 法加上贝塔是等于三十度的，那我们已经找到了 r 法和贝塔的关系，那接下来呢？我们角 m o n 用 r 法和贝塔表示出来， 发现角 m o n 在 这个位置，它其实表示为而法加六十度加贝塔，所以是而法加贝塔加 六十度，那由于而法加贝塔我们已经求出来了等于三十度，那所以就代入三十度加六十度等于九十度，那所以角 m o n 的 值为一个定值，并且为九十度。那其实这道题呢，也是一道非常典型的双角平分线模型问题， 它的结论就是两条角平分线之间的夹角，角 m o n 就 等于整个大角 a o b 加上中间的角 c o d 的 和的一 半，那你将咱们的角 a o b 和角 c o d 的 度数带进去以后，发现算出来依然是九十度，你听懂了吗？

伤元之夜，长安如昼，万民都在等待此时的烟火，但这掌管全程报时的金凤机关此刻却陷入了死寂。 核心基建天宫伞意外卡死，若不修复，盛典将成至暗时刻。 图纸显示，只有解开三道关于角度的谜题，才能让天宫伞重开。各位学徒，时间紧迫，这第一道难关还请助我一臂之力！ 想要修复天宫伞，必须先看懂这张由于年代久远而模糊的机关图纸。这第一道难关便是辨别零件的大小， 这两根散股的张口看似一模一样，但只要差之毫厘，机关就会卡死。各位，除了用眼睛箍，你们有什么法子能帮我精准比出他俩谁大谁小？ 一剪能不能凑出这个数来？ 机关修复必须分毫不差度，分秒的计算是六十进至满六十，进一不够。简介一档六十，切记， 究竟该画在哪里？ 是你们的智慧修正了毫厘之差，今夜长安的盛世光景，有你们一份功劳，各位学徒出师了！

大家好，我们今天继续学习速刻版新年级上学期第六单元平面图形的初步认识，我们今天开始学习第二节的内容角， 我们来看一下这几节。第一个，七十度十九分三十秒，这个是要让我们把它换成是多少度的，那这样的怎么换呢？有分有秒啊，对不对？先把秒换成分， 多少秒是一是一分呢？六十秒是一分，对不对？所以三十秒是等于零点五分，对不对？好，那十九分加上零点五分就是十九点五分了，一多少分是等于一秒呢？ 六十分等于一秒，对不对啊？再求出来，他是有零点三二五度，所以这个是多少度啊？就是七十四点三二五度下面的计算啊， 把他们都给换成啊，看看这些加起来啊。先把这样怎么算呢？先把分分加起来啊，度度加起来，分分加起来，秒秒加起来，对吗？好，看看。 哎，度度加起来，分分加起来，秒秒加起来是等于多少度了？等于一百七十九度 五十九分七十秒。那这样写可以吗？因为这边还可以进一的，是不是啊？六十度是一秒，对吗？嗯，六十秒是一分，六十分是一度，对不对 啊？这边进进一就变成了一百七十九度六十分十秒啊，这边是不是又可以再再往前进一了？那就是一百八十度十秒。 好，那这样的呢？哎，加减乘除混合就完了，对不对？哎，乘以三了，先把它们分别乘以三 分度分秒，先分别乘以三，那就是四十五度，一百二十三分八十七秒，对吗？然后再往前进，这边呢？哎， 八十七秒往前进一，是不是变成了一百二十四分二十七二十七秒了，对不对？那这个呢，是不是可以再往前进二了呀？那就是九十度减去四十七度四分二十七秒，对吗？然后，哎，这边 再把八十九度，这边九十度换成八十九度，五十九分六十秒，这样的话，因为这边有分有秒，我们这样换了之后才好去减，那么就是四十二度五十五分三十三秒。 第三个给出下句说法，哎，正确的。是啊，要看清楚题目，正确的是有两条射线组成的图形，叫做角。哎，是吗？哎，我这个是一条射线，是不是这边也是一个射线？哎，那他们组成的是一个角吗？ 哎，不是一个角，对不对？所以这一个是错的啊。角的大小与边的长短无关，只与两条边张开的幅度有关，这一个是对的，对吗？ 角的两边是两条射线，这个对不对啊？这就我们的定义，对，他这是对的。把一个角放到一个放大十倍的放大镜下观察，角的度数也扩大十倍，这一个对不对啊？这一个是错的，那么我们小学的时候就已经知道了，所以正确的有几个？正确的是有两个， 第四个，哎，如图一，将一副直角三角尺的直角顶点重合在点 o 处，第一个角 a o b 和角 b、 c、 b o c 相等吗？哎，说明理由。 a o c 和 b o d 实际上是什么关系？也说明理由啊。第一个， 先说结论啊，它们是相等的，为什么呢？啊？ a o b、 c、 o d， 它们都是三角板的， 哎，直角边的点对吗？好，再减九十度。角 i o d。 是 不是问 i o d 和 b o c 是 不是相等？那 i o d 等于什么？ i o d 是 等于 i o b 加上 b o d， 对 不对？好，那角 b o c 呢？ b o c 呢？是等于角 c o d 加上角 b o d 了，对不对？哎，所以 a o d 和 b o c 相等的，因为 a o b 等于 c o d， 对 不对？又加上一个相同的角，所以它们 a o d 和 b o c 是 相等的。 那么 a o c 和 b o d 是 什么关系呢？啊？先说结论，他们是加起来是一百八十度，那为什么呢？ a o b 等于 c o d 等于九十度，对不对啊？那么 a o c 加上角 a o c 加上角 a o b b o d c o d， 这不一个周角的呀，等于三百六十度，对不对啊？ i o c 和 b o d 是 一百八， i o c 和 b o d 是 一百八十度，对吗？ i o c b o d 是 一百八十度，那么嗯， i i o b 和 c o d 是 一百八十度， 所以 i o c 加上 b o d， 也就是一百八十度了，对不对啊？ i o b 是 九十， c o d 也是九十，这两个九十就是一百八，那么 i o c 加上 b o d 也是一百八十度 啊！第二条问，将三角式如图二摆放啊，三角式的顶点重合，那么 i o d 和 b o c 还相等吗？ 啊，先说结论，还是相等的。为什么呢？ a o b 和 c o d 是 九十度，对不对？那么 a o d 呢？ 哎，我们问 a o d 和 b o c 对 不对？ a o d 和 b o c 啊？ a o d 等于 a o d 减去 b o d， b o c 呢？是 c o d 减去 b o d， 对 不对？哎，都是减了一个 b o d， 对 不对？那么 a o b 和 c o d 还是相等的，都是九十度， 所以 i o d 和 b o c 也是相等的。第二问，它上述关系成立了吗？还是成立的，对不对？好？为什么呢？因为 i o b 等于 c o d 等于九十度，所以 i o c。 嗯，看看 i o c 加上 b o d 加上什么？加上 b o d， 是 不是就等于 i o b 加上 b o c 加上 c o d， 再减去一个 b o c， 哎，是不是？哎，一加一减啊，对吗？哎，加一个 b o c， 减一个 b o c， 对 不对？哎，看看，那这个是什么呢？ 就等于 a o b 加上 c o d 了，对吗？就等于一百八十度，所以 a o c 和 b o d 的 和还是一百八十度 好。第五题，已知角二法和角白塔都是钝角，假如你四人计算六分之一角二法加上角白塔的结果为，五十度、二十九度、七十二度、九十度，如果其中有正确的结果，那么其计算正确的是哪一个呢？ 啊？角二角的角都是钝角，对不对啊？那么二角是不是在九十到一百八之间呀？角白菜是不是也是在九十到一百八之间呀？对吗？那么二角的白菜呢？是不是 之和是不是大于一百八十度就小于三百六十度了呀，对不对？好，那六分之一个二号加白塔的和呢？那就是三十度到六十度之间，对不对？好，那这几个数哪一个是在三十到六十之间的呢？ 哎，就只有五十度这一个，是的，对不对？所以计算正确的是假。 第六个钟表时针和分针如同兄弟两个赛跑形成的。丰富的数学知识啊！一个如，初一上午八点十分的时候，时针与分针与时针所夹的角度为多少？哎，是不是这一个度啊？这一个呀，是多少度啊？是一百二十度，对不对？因为，哎， 时针的一格，这边的一格是三十度，对不对？所以他是一百二十度。第二个，在图二中大致画出八点二十的这个时刻的位置， 并思考回答。从八点十分到八点二十，时针的时针转转过的角度，还有他的十分钟那个时针所转过的角度。 好，八点二十是大概是这样的一个位置，对不对啊？好，分针转转过的角度。 分针每分钟转多少度啊？分针转一圈，哎，三百六十度就一个小时呀，那么平均每分钟呢？那就是转六度，对不对？好，那时针呢？每分钟转多少度呢？时针转一圈是不是十二小时 对不对？哎，十二个小时转了三百六十度，对吗？好，那么他每分钟是转多少度呢？ 十二个小时对不对？每个小时是六十分，对吗？所以每分钟转多少度啊？每分钟是转零点五度 啊。那我们来看看二十分钟分针转多少度啊？那就是二十来乘以六度就是一百二十度，那么时针呢？那就是二十来乘以零点五，就等于十度，对不对 啊？第三个，元旦的一天，城西某中学青年级部分学生上午八点多集中在学校门口，准备步行去啊，去步行街进公益服务 领出发。使足了，看了一下手表，时针与分针正好重合。下午晨有时候回到学校，进门时，手表的时针与分针方向相反，正好在一条直线上。 那你知道他们外出了多长时间吗？通过计算来加以说明，哎，看看，八点多的时候来，我们把这图画出来啊，八点多的时候，哎，八点多，哎，时针是在这边了，对不对？ 然后看来手表分针与时针重合，那怎么办？我们还不知道对不对？我们就先设是 x 分 出发的，那么 x 分 出发的时候，时针是在一个什么角度上面呢？ 如果是八点的时候，是在多少度啊？哎，从这边转，转到这边是不是转多少度啊？转到二百四十度，是不是再经过 x 分 呢？ 啊？那是不是就是零点五加上二百四十度了，对不对？那么再等于六 x 是 不是等于？哎？分针所转的角度， 是吗？分针所转的角度对不对？一分钟是转六度，那么 x 分 呢？那就是转了六 x 度，是不是这样？是不是可以求出来 x 了？ x 是 等于十一分之四百八十，约等于四十四分啊，那么他们回来的时候呢？ 回来的时候啊，时针与分针的方向相反，正好在一条直线上，那么是什么时候啊？两点多对不对啊？两点多 时针是在这边对吗？分针呢？在它的相反的方向，对不对？那好，我们还是设未知数，设下午两点外分回到了学校 好吗？好，那么这个是什么呀？六 x 减去一百八十是什么 啊？六 x 对 不对啊？是分针所转的角度，减去一百八十就就就是时针所指的角度了，对吗？等于六十加上零点五 x 两点多的时候， 时间是不是已经止到了二这边了，对吗？这就已经是六十度了，对不对？再加上零点五 x， 就 说这啊，零点五 y 啊， 零点五 y 是 不是 y 所转的角度啊？对吗？这样解得 y 是 等于解这个方程， y 等于十一分之四百八十，约等于四十四分。 所以他们是下午几点钟回来的？是下午两点四十四分回来的。他们一共是外出了六个小时，是上午八点四十四分出发，到下午的两点四十四分回到的学校。

同学们好，今天我们来学习第四章几何图形。初步，本章所涉及到的知识点包括几何图形的认识，直线、射线、线段、角的认识。 大家有没有听说过这样一句话，点动成线，线动成面，面动成体。有点线面所组成的像正方形、长方形、圆柱体、长方体、圆点，这些就叫做几何图形。 有些几何图形，它的各个部分不都在同一平面内，我们称之为立体图形。如长方体，有些几何图形，它的各个部分在同一平面内，我们称之为平面图形，如三角形。 也就是说，几何图形可以分为立体图形和平面图形两大类。接下来我们回顾一下直线、射线线段的定义。 直线没有端点，可以向两边无限延伸，线段有两个端点无法延伸， 而且经过两点，尤其只有一条直线，也就是两点确定一条直线。当两条直线产生公共点，我们称这两条直线相交，公共点叫做它们的焦点。如果有一点 m， 把线段 a、 b 分 成相等的两条线段，那么点 m 就 叫做线段 a、 b 的 终点。 同理，我们还可以找到线段的三等分点，四等分点。连接两点间的线段的长度叫做这两点的距离。两点间的所有连线中，线段最短，也就是两点之间线段最短。在小学，我们用度来衡量角的大小，今天我们要在学两个角的度数的单位。一个周角是三百六十度， 我们把它分成三百六十份，每一份叫做一分的角，把一分的角六十等分，每一份叫做一秒的角， 也就是说角的度分秒是六十静止，这和时间计量的时分秒是一样的，他们叫做角的角度制。把一个角平均分成两个大小相同的角的射线，叫做这个角的角平分线，类似的还有角的三等分线等。最后 我们再来学习一下与角和补角。一与角，若两个角的和为九十度，则这两个角的和为一百八十度，则这两个角互为补角，简称互补。 它们有以下性质，一同角或等角的与角相等。二同角或等角的补角相等。