什么是均值不等式

我们接着来看不等式的第四节，均值不等式。先来看知识书里第一条是均值不等式。提起变形公式，第一个 左边是二分之 a 加 b 大于等于个号 ab， 这是君子不等式的公式。左边是算数平均数，右边是几颗平均数。这里的条件要求 a 和 b 都是而正当且仅当 a 和 b 相等的时候取等号。 但实际上啊，实际上这里头的 a 和 b 都大于等于零，实际上就可以满足了，可以满足了，只不过是君子不能是给公式的时候限定了一个 a 和 b 都是正的，但实际上可以是零，懂吗？我把这个也申一下，如果是三个数， 左边是算数平均数，那么他也大于等于他的几颗平均数，当其紧当 abc 相当的 时候，成的等号成立。好吧，这就是均值，不能试。那第二个，第二个简单，就是由第一个左右都乘一个二就行了，还是当且仅当 a 等于 b 的时候启动第三个。第三个你可以理解成做个叉就是完全平放式了，对吧？ 很简单，但是第三个，你注意这里的 a 和 b 可以是负的了吧，所以 a 和 b 属于二，对吧？ 第四个，第四个，实际上呢，是由前三个推倒出来的一个，但是第四个是第七个里的一部分，所以咱们一会通过第七个就统一说一下，这里第四个咱们就不证明了先。好吧，来看第五个。 第五个 a 加 a 分之一大于零，二 a 大于零，如果 a 大于零， a 加 a 分之一，是不是就均值啊？ 是不是等于二，对不对？那 a 大于零什么时候去等呢？这两部分相等的时候，也就是解出来 a 等于一，这就是取等条件，是不是？ 实际上他跟对号函数是不是一个东西啊？这不就对号函数吗？只不过对号函数里面的 x 范围是 x， 不能等于零。你这里用均值的话，得要求 a 大于零，对不对？ 好了，第六个，第六个， a 分之 b 加呃， b 分之 a 加 a 分之 b， 大女儿还是直接均值呗。 但是你注意，我用均值的话，用要求 a 和 b 都是正的吗？用不着，他只需要满足这两个数大于大于零就行了吧。这两个数大于零，也就是 a 乘 b 大于零呗。所以他俩先加大于等于 二倍高下， a 分之 b 乘以 b 分之 a， 是不是等于二？什么时候去等啊？是不是就是 a 分之 b 等于 ba， db 分之 a 的时候，也就是 a 等于 b 的时候去等，是不是？然后第七个？第七个实际上，呃，第七个出来，第四个就出来了。所以咱们就第四个就没说，直接说第七个。 很多学生以为君子不能试，知道这么个东西就行了。这个东西是什么？是和和鸡的一个大小关系对不对？和和鸡的一个大小关系。但实际上你要想做好君子不能试的题，你除了和和鸡之外，还需要知道 平方盒还有到处盒他们的一个关系懂不懂？那这相当于这里有四部分，这四部分是有名字的，第一个叫做家全平， 第一个叫做加全平均数，第二个叫做呃，算数平均数， 第三个叫做几何平均数，第四个叫做条和平均数。这些名字无所谓， 重点你得把公式给我背下来，他们怎么挣呢？中间俩直接是公式的，剩下的实际上你都可以用平方呀，或者是做差呀，都可以挣，咱们就不细争了好不好？然后既然他们都是平均数的话，你要知道如果 a 和 b a 大于等于 b 大于零的话，那既然是拼语数，他们这四个肯定都得在 a 和 b 的中间，那所以 a 在最前面， b 在最后面，好吧？然后这一部分， 这一部分我可以把它变一个形式，分子分母都乘以一个二 ab 下面是不就是 a 加 b， 所以有的时候他给的是这个形式，你也得知道他表示的是调和平均数啊，这些不能是都是当且紧当 a 等于 b 的时候去等。哎，你注意，我这里头没写 科系不能试和全方合不能试。为什么呢？因为正常的这两个公式，他不是咱们高中需要掌握的内容， 对吧？而且你很多题，有的学生说，哎，很多题我用科技不能适合，全方和不能是，呃，可以做，对吧？但是你要知道，用我正常的方法，用咱们正常高中学过的方法，他也不复杂，所以有能力的学生呢，你可以背背 刚才我说的那两个科西和全方盒。那正常的学生，正常的学生，其实，呃，没有什么太大的必要啊，你用正常的方法就可以做了，好吧， 好，那接下来我们看第二条叫做均值不等式的使用条件。均值不等式的使用条件写了一正二定三相等。你注意均值不等式是指最上面这个对不对？ a 和 b 是不是要保证 a 和 b 都是大于零，这叫一正二定，什么意思呢？我举一个简单的例子，比如说， 比如说啊， x， 当 x 大于零的时候， x 加上 x 的平方，我用均值是不是大于等于二倍？个号下 x 乘以 x 的平方等于，那就是二 x 个号 x 呗，是不是这样的？我问你这个式子对不对？这个式 对不对？这个式子是对的，我用了均值是对的，但是有一个问题，你要知道你用均值是为了什么？咱们均值用均值不能是是为了求一个代数税的最大值或者最小值，那你说 这个东西是它的最小值吗？当然不是，为什么呢？因为这是一个变量，也就是虽然我均值不等是公式，我用的没有问题，但是没得到咱们想要的东西，咱们想要的东西是一个一个定值，但是这是一个变量，所以得要求 和式定值，或者是机式定值的时候，咱们才用均值，不能是这叫二定的意思，懂不懂？什么是三相等呢？举个例子，当 x 大于零的时候， x 加上 x 分之一，是大于等于二的用均值，对吧？什么时候去等 x 等于 x 分之一，也就是 是 x 等于一十取等，那也就是 x 和 x 加 x 分之一，最小值是二。但是我写一个 x 大于等于二的时候， x 加上 x 分之一大于等于二，他的最小值还是二吗？就不对了， 为什么呢？因为此时是 x 等于一的时候取等，但是明显此时 x 不能等于一，那你取不了等，取不了等，你就不能用均值，也就是此时态的最小值不是二，那是多少？咱们可以利用分那个叫对号函数 去结合对号函数的图像去求，懂吧？后面有对应的题，对应的题去做，所以俊职不能试的使用条件就是一正二定，赛前等我就解释清楚了。好吧， 那接下来那均值不等式的作用是什么？是解决合机平方合，还有到处合 这四者的相互转化以及求最值问题。相互转化以及求最值问题。嗯，那想过呃，深入的了解他，使用他。那咱们就通过 题呃后面的题型，一个题型一个题型的去练啊。好吧，那这个知识书里部分我们就讲到这里啊。

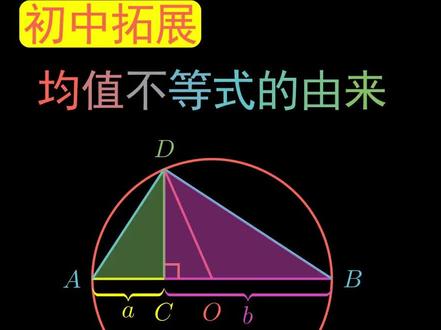
意图证明二元形式的均值不等式。证明条和不等式小于等于几何平均数小于等于算数平均数小于等于平方平均数。 先画一个长度为 a 加 b 的线段，再画一个直径为 a 加 b 的圆过点 b 做垂线 pb。 分别将三条线段连接起来。可以根据相似三角形 a 比 pb 等于 pb 比 b 算出 pb 等于根号， a 乘 bpa 为圆的半径， pa 等于 a 加 b 除以二。 只有当 b 点运动到 a 点时， p a 才等于 p b。 因此 p a 大于等于 p b， a 等于 b 时，等号成立。 所以算数平均数大于等于几和平均数。我们对图形进行改造，做垂线 a、 c 和 b， d 连接 b、 c。 根据相似三角形 p d 比 p b 等于 p， b 比 p a 算出 p d， a、 b 等于圆的半径减去 a， 再根据勾股定理算出 b c。 当 b 点运动到 a 点时，四条线段重合，因此 a 等于 b 时，四条线段才相等。所以 p d 小于等于 p， b 小于等于 p， a 小于等于 b c。 二元形式的均值不等式链就成立了。当 a 等于 b 时，等号成立。

该蒙格记，书学不弃，书学不辍和蒙格学。大家好，我是爱讲高中数学脱口秀的孟老师。今天呢，我们来看一个比较基础，但是也比较好用的一个结论，就是我们高一上学期学过的基本不等式， 由基本不等式可以推出一个非常长的式子叫均值不等式。那均值不等式列 好，那有的同学呢，可能还没有听说过，说我在高一上学期只学习过基本不等式。那有的同学呢，可能对这一方面比较了解的比较多，但是每次记忆呢，也都会啊，总是忘记。 那今天呢，孟老师就用一个小技巧，帮助我们没有听过的，或者是每次记忆都记忆不牢的同学来对这个东西记得更加牢固。 那首先我们先说一下什么是基本不等式，那基本不等式大家应该背的比较熟了，就是根号下 ab 小 于等于二分之 a 加 b。 当然呢，嗯，这个形式我们可以变化，比如说变成 a 加 b 大 于等于二分之大于等于二 b 的 根号下 ab。 那 这个形式呢，其实它包含了两个平均数啊，像左边这一个呢，我们叫它几何平均数， 右边的这个呢，是我们比较常见的一个平均数哈，这个我们叫它算数平均数。 那我们的均值不等式啊，也就是我们的平均数不等式呢，那在这个两个的基础上面，增加了额外的两个平均数，一个叫我们的调和平均数，这个叫调和平均数。 调和平行数其实在我们的生活当中运用的也是比较广泛的哈，比如说我们的物理当中啊，有这样两种题，会经常用到我们的调和平行数，第一个，两个电阻并列啊，有学物理的同学可以啊，仔细的观察一下哈， 二一，二二，那我们如果把它俩并列起来，它的总电阻是多少呢？就是我们的二一分之一加上二分之一分之一。 还有啊，如果有一段路啊，我们前半段啊，这是终点，前半段我们用 v 一 去走，后半段用 v 二去走，那这时候我们的平均速度是谁呢？是 v 一 分之一加上 v 二分之一分之一， 当然大家理解即可，因为不是所有的同学都要学物理，是不是？那重点还是我们的数学上这个不等式的记忆和运用，那前面这个呢，叫平数，后面呢，我们加了一个叫平方平数， 那就是把两个数的平方取个平均数，然后再开根号，这个叫平方平均数， 这个不等式列呢，虽然只有四个部分，但是记起来其实比较难记，因为他又有 a， 又有 b， 又有加又有减，还有开根号。所以今天呢，孟老师用一个小技巧帮大家记忆牢固。 首先呢，啊，中间这个东西其实没有什么特别好记的方法，因为它是我们的基本不能失，我们需要把它记得非常的牢，即使没有任何的方法，也要把它记牢。但是呢，左边这个啊，我们不常见的这个调和平素，它的开头字母呢，是 t 啊，那我们就用 t 来代表右边这个呢，平方平运数 啊，我们取谁呢？我们不取屁啊，我们取 f 啊，为什么不取屁呢？其实很多同学在这里啊，如果对我们的追星比较感兴趣的话，其实已经出现端倪了，是吧，那我们凑齐了 t， 又凑齐了 f， 那 接下来是不是就可以跟我左手右手一个慢动作了？ 也就是说，哎，我们的基本不等式在两侧加上我们的 tfboys， 就 构成了我们的均值不等式，所以大家可以再默写一下，基本不等式是谁呀？是我们的根号下 ab 小 于等于二分之 a 加 b， 那 在两侧加上我们的 tfboys， 那 左侧是我们的调和频域数啊，是我们的小 t， 右边呢，是我们的平方平均数啊， f 啊，这样就我们就比较容易把它记下来了。当然啊，有喜欢 tfboys 的 同学们不要啊，对老师有什么意见啊，我也是想利用我们的公众人物帮助我们把数学公式记得更牢啊，不要小气啊，借我用一下你们的偶像啊。 好的，那这个均值不等式呢？如果只有这么简单，那老师也没有必要单独给大家去说了，那其实他 好就好在他其实可以进行一个比较大的拓展，那这个只有 a 和 b 两个变量是不是？那如果那同学们对于我们书上的基本不等式有所了解或者比较熟悉的话，那在这里我们知道基本不等式它可以进行一个多变量的一个变化， 哎，这是我们的基本不等式的一个多变量的变化。那其实呢，在这里我们仍然也可以把前面也加上，后面呢，也可以加上啊，所以就变成了我们的三元的 均值不等式，那甚至我们也可以什么呢？也可以，哎，这里 a 分 之一加 b 分 之一加 c 分 之一，哎，有多少加多少，一直加到 n 分 之一，后面呢，哎，就是 n 次根号下，我们假设啊，在这里啊，这是 n 个数号， 那后面就是 n 次根号下， abc 一 直一直一直乘到 n， 这里也是 n 个数哈啊，因为这里啊， a 到 n 并不是 n 个数，是吧？那我们直接假设哈，后面呢，就是 n 分 之一啊，这是我们的平均数的计算方法， 那这里也是 n 个数哈， 后面呢，哎，就小于等于十一啊，我们的 n 分 之 a 方加 b 方加 c 方这些这些加一直加到 n 方，然后最后开个更好啊，这是我们的平方平数。所以大家啊，如果想要简单记忆的话，就可以记住，我们的基本步骤是两侧加上 tfboys 啊，如果想要继续深化的话，我们也可以记住它可以从两个变量变成任意的变量，只需要在相应的二的基础上变成 n 就 可以。所以啊，也感谢 tfboys 为我们提供这样一个良好的记忆口诀，大家能记住吗？

今天我们来证明一道不等式， abc 大于零， a 的三次方加 b 的三次方加七的三次方大于等于三倍的 abc， 这是三元均值不等式，我们可以转化成二元均值。 利用这个式子，我们考虑建一个 abc， 这样就可以两两凑对，转化成二面镜，是吧？ 又变成了两个数相加，再用一次二元禁止， 这边每个字母都是四次方，以后又开了四次方，所以最终是四倍的 abc 消掉一个 abc 就完成了证明。如果还不会二元禁止，我们还有一个方法， 用左边剪右边 把它硬分解成， 然后配个方， 他是大于等于零的，所以左边大于等于右边。想知道这个英语春节怎么来的，可以给我留言，关注贾哥数学，体会更多数学思想。

好，今天我们一口气讲透君子的本是，首先看第一种类型，已知了，然后数的积，然后求他们和的最小值。其实这种题的话，就可以直接的去用到我们的 呃，均值不等式， a 加 b 大 于等于二倍，根号下 ab， 当然前提是 a 大 于零， b 大 于零，不要忘了，那我们本题就可以直接用了，因为这个是大于零，这个也是大于零，所以我它就可以直接 写成大于等于二倍的根号下六， x 方 y 方，对不对？那么我们这个地方就可以直接写 二倍的根号六，乘以根号下 x 方 y 方，那么 x y 它乘起来等于一，所以说我们这个地方就可以直接开出来，它就等于 二倍根号六，所以这里就很简单啊，这种就是可以直接去套公适用的。然后我们再看第二个，第二个， a 分 之一， b 分 之二等于一，求 ab 的 最小值，那 这个话也是一样的，我们还是用到了均值不等式，因为它们俩都是正数，所以 a 分 之一和 b 分 之二都是正数，可以直接套公式换着颜色，那就是 a 分 之一加上 b 分 之二，是不是大于等于什么呀？大于等于二倍的根号下 ab 分 之二，对吧？然后不要忘它等于一，我们把一写在这，它等于 一。好，那这这一块的话，没用，我们就不要了，你就把它删掉了，不要了，我们就留下了一大于等于二倍的根号下 ab 分 之二，然后你把这简单做了处理，它就是根号 ab 分 之二倍，根号二 小于等于一，是不是？好，我们现在呢，我们看下怎么办？那把 ab 是 不是可以直接乘过去，因为 ab 它是大于零的数字，所以我们把根号 ab 乘过去，就是根号 ab 啊，这样大家看的舒服一点，就这样吧。然后我们两边平方一下，那就是 八小于等于 ab。 好， 所以 ab 是 大于等于八的，所以它最小值就是八，看懂了吗？这两个的话都是可以直接套用公式的。 ok， 好，我们把它删一下吧。好，继续往下看第三题，第三题的话他是跟第二题差不多。嗯，我们还是可以直接用，因为他说他们俩都是实数啊，是实数，然后 a 分之一加 b 分 之二等于根号下 a b， 求 a b 最小值。我们来看一下怎么做呢？我觉得题目中可以改一下，应该是这个地方应该是他们两个和是正的，那不能保证他们 都是正的，但是他们如果是一正一负的话，这个 ab 也不能放在底下，所以说这个地方其实保证他们俩都是正数了，已经是也是正数啊。好，所以我们可以直接用大于等于二倍的根号下 ab 分 之二。然后呢，我们继续还是用刚才的方法把它简单整理一下。根号下 ab， 二倍的根号二， 小于，这边不是等于根号 a b 吗？然后把这个就消掉了，那这边就是小于等于根号 a b。 好， 然后我们因为根号 a b 大 于零，所以我们把乘过去，就是二倍的根号二小于等于 a b， 所以 a b 就 大于等于二倍根号二。就这样做简单啦。这是前三道题都差不多 学会了吗？就可以直接套公式的那种类型。直接套公式是可以直接套公式的类型。公式我们还写在这 a 加 b 大 于等于二倍的横号 a a d a 大 于零， b 大 于零的情况。好，这过程也删了啊，如果需要看的话，可以从回头去看，这个是等于 好，我们看下第四题。第四题这种类型呢，他也是比较简单，因为他告诉我们 x 是 大于零的，那么我们也是可以直接套公式的， 这边的 a 加 b 就 相当于等于二， x 这边的这边已经符合 a 加 b， 所以 我们直接套啊，就是二 x 加上 x 分 之一大于等于二倍的分号下，二 x 乘以 x 等于二倍的根号二，所以他是大于等于二倍根号二，也就是二倍根号二是他的最小值。然后这个第五题和第四题是差不多的，但是需要发，我们会发现他们两个下面是不一样的，所以我们需要给他来一个拼凑法，把它凑出来。 这边是 x 减一，所以我们这也把它配成 x 减一，那就是二倍的 x 减一，加上 x 减一分之一， 这边相当于多减了一个二，随便随便加一个二就行了。然后这两项可以用均值不等式去做，大于等于二倍的根号下，它们俩乘起来等于二，所以大于等于二倍根号二，再加上二的话，那就是 二为根号二加上二。但前提要注意啊，这个地方有一个 x 大 于一，也就是我们要保证他们的每一项，我们在用军军事等式的这个不等式的时候，这两项都是大于零的时候才能用。需要特别提醒的啊，我们这个视频先到这，下面我们再讲下面的内容。