遵义九下锐角三角函数经典例题
一个视频教会你特殊角的锐角、三角函数值。
粉丝1.4万获赞6.6万
相关视频
 22:36查看AI文稿AI文稿
22:36查看AI文稿AI文稿同学们好,我是来自南京市第十三中索金分校的周成成老师。今天我们学习的课题是七点六,用锐角三角函数解决问题。三、 同学们,今天我们再和小明一起坐一坐热气球呢,看看热气球又会带来哪些新的有趣的问题呢?先看问题一, 小明在游乐场某处利用侧角仪观测热气球的仰角为二十七度,然后他沿着正对气球的方向前进了五十米, 此时观测气球的仰角为四十度。如果侧角仪的高度为一米,那么气球的高度是多少呢? 我们还是先来抽象图形,请同学们在学习单上跟着老师一起画一画。根据实际情景,我们来发挥一下自己的想象力。 我们可以把地面抽象为一条直线,在直线上任取一点作为某处,再画出热气球的位置及点 c 的 位置。这里有一个新名词,羊角。我们来认识一下 仰角的定义,从低处观测高处目标时,视线与水平线所呈的夹角。 相对的还有俯角的定义,从高处观测低处目标时,视线与水平线所呈的锐角。我们来看左面这幅图,可以清楚地明白什么是仰角和俯角。 那么在这个问题中,我们需要画出水平线和视线,从而标注出仰角。 沿着正对气球的方向前进了五十米,到达了 f b 处,我们还是要再画出此时的仰角, 那么要求的是什么呢?气球的高度?我们来一起看一下这个数学问题。 先来梳理题目中的已知和未知,为了方便表达,我们可以过点 a 做 a h 垂直 c d 垂足为 h, 由题意可知点 b 也在 a h 上面, 那么这个时候仰角我们就可以表示为角 c a、 b 等于二十七度,另一个仰角 c、 b、 h 等于四十度。还有 ab 等于 e, f 等于 d, h 都等于一米,要求的是 c d 的 长。 同学们思考一下,这个已知和未知之间有什么样的联系呢? 同学们有想法了吗?这个图形看上去没有那么简单哦, 我们在分析这个问题之前,不妨先思考这两个问题呢。第一个问题, c d 需要转化吗?如何转化?观察图形 c d 等于 c h 加 h d, 而 d h 就 等于一米,那么问题就转变成只要求 c h 就 可以了。 那么随之第二个思考就出现了, c h 与哪些已知量有关呢?请同学们观察图形。先想一想, 我们不难发现 c h 同时存在于两个直角三角形当中,可惜的是,这两个直角的角形都只是已知一个角,我们无法直接解除 c h。 但是我们可以根据已知角的三角函数得到三边关系。例如,在直角三角形 c、 b、 h 中,我们可以根据已知角 c b h 得到 c h 的 关系。 同样在直角三角形 c h 中,我们可以根据已知角 c h 的 三角函数得到 c h 与 a h 的 关系。 那么这里为什么我们要选择 c h 与 b h 以及 a h 的 关系呢?请大家观察图形, 我们看出 a h 和 b h 与已知量之间联系紧密,我们可以找到它们与 ab 之间的数量关系。带着这两个思考,我们再来分析也许就清楚多了。 先从三角形 a h 出发,利用 tangent 二十七度等于 c h 比 a h, 从而得到用 c h 来表示 a h。 同样,在直角三角形 c b h 中,利用 tangent 四十度等于 c h 比 b h, 从而得到用 c h 来表示 b h, 而 a h 减掉 b h 等于 ab。 这里我们只要设 c h 为 x, 即可得到一个方程,从而求解出 c h。 在 这个思路过程中,我们是从已知条件出发,不断地推向未知。像这样的思维方法是在由因导果 解决这个问题之后,我们不妨再回顾一下整个分析过程。在这个问题,图形中出现了两个直角三角形,而且都无法直接解出, 但是两者之间有一个公共边,这时候我们可以选择设这条公共边为 x, 再利用已知角的三角函数找到边与边之间的关系,即可用 x 表示出其他未知边。最后再利用图形存在的线段之间的等量关系建立方程求解。 当然,这道题也有其他的解法,我们选择的未知数不同,建立的方程也就不同,同学们课后可以尝试下,然后再互相交流对比下,看看谁建的方程更方便解答呢? 下面我们一起来看一下这个方法的具体解答。首先描述辅助线,交代已知条件,并设出未知数。然后利用三角函数分别用 x 表示出其他的未知边。 接着再根据数量关系建立方程,大致分为三段,选择合适的未知数,利用三角函数表示其他的未知量。根据线段的数量关系建立方程求解。 小明神奇地发现,原来用测阳角的方式就能得到热气球的高度了。于是他登上热气球之后,又尝试了用同样的方式去测量大楼的高度,请看便事。 小明乘坐热气球到达一百米高处时,从热气球探测器显示,从热气球看一栋高楼顶部的阳角为四十五度,看这栋楼底部的俯角为三十度。求这个高楼的高度。 我们同样要先抽象图形,相信这个时候同学们已经可以画的很快了。 点 a, 即小明到达一百米高速时,从热气球显示看一栋高楼的顶部仰角为四十五度,即从点 a 处看点地的仰角为四十五度, 看这栋楼底部的俯角为三十度,即从点 a 看点 c 的 俯角为三十度。求这个高楼的高度及 c d 的 长。同学们先思考一会儿, 我们发现 c d 在 一个一般三角形里,根据之前所学的解一般三角形的经验,你会怎么做呢? 对,我们可以画斜为直,将一般三角形转化为直角三角形, 我们可以过点 a 做 a h 垂直, cd 垂足为 h, 这时候 cd 就 可以分解成 c h 和 h d 了, 而 c h 就 等于 ab 等于一百米。那么问题就转变成如何去求 d h。 我们发现 d h 在 直角三角形 a d h 中,我们可以根据 tangent 四十五度等于 d h 比 ah, 从而得到 d h 就 等于 a h 乘以 tangent 四十五度, 那么我们就需要把 a h 的 值找到就可以了。进一步观察, a h 在 直角三角形 a h c 中,而 a h c 中我们已知一角和一边,那么即可解出 a h。 我 们可以利用 tangent 三十度等于 c h 比 a h, 从而解得 a h, 得到 d h, 进而得到 c d 的 长, 这样我们的路线就打通了。在这个思路过程中,我们是从带球的结论出发,逐步靠拢已知条件。像这样的思维方法,我们是在执裹索因,下面我们来看一下具体解答。 在这个问题中,我们不需要建立方程,可以直接的过程,最后精确到一米。 小明的测高实验再次成功了。可见在我们生活中测量高大的建筑物本来是很困难的事,但是有了三角函数的帮忙,一切都变得简单了。数学知识就是如此的奇妙, 我们可以用锐角三角函数知识解决测高问题。接下来我们来看。第一, 如图,在以笔直的海岸线上,有 a、 b 两个观测站, a 在 b 的 正西方向, a b 等于两千米。 从 a 测得船 c 在 北偏东五十六度的方向,从 b 测得船 c 在 北偏西二十度的方向,求船 c 离海岸线的距离。 这里出现了方位角,我们来认识清楚。 如图,绿色的线表示北偏西三十五度方向,红色线方向我们可以称之为南偏东六十四度。 也就是说方位角我们一般都是从南北偏东西,不从东西偏南北。理解了方位角之后,请同学们在图中标注出方位角。 下面我们一起来看这个问题如何解决。要求船 c 离海岸线的距离可以过点 c 做 c h 垂直 a b 即求 c h 的 长。那么该怎么求呢? 我们先来梳理已知和未知。这个题目中已知的两个方位角并不在三角形中,我们可以找出它们的余角转化成三角形的条件, 即角 c a、 h 等于三十四度,角 c b a 等于七十度。当然还有 ab 等于两千米,我们要求 c h, 请同学们先自己找一找已知和未知的联系, 同学们,找好了吗?我们发现这个图形中虽然有两个直角三角形,却依然不满足可解条件。根据之前测热气球高度的问题,同学们有什么启发呢?两个问题有相似之处吗? 我们发现这两个问题中都有一条公共边, c h 是 两个直角三角形的公共边, 那么我们可以在直角三角形 c h 中利用已知角 c h 的 正弦表示出 a h, 再在直角三角形 c、 b h 中,同样利用已知角 c b a 的 正切 表示出 b h 的 长。而观察图形,我们可以找到 a h、 b h 与已知线段 a b 之间的数量关系,即 a h 加 b h 就是 ab 的 长, 从而我们可以设出 c h 等于 x 米。建立方程求解 这个思路,过程依然是在由因导果。接下来我们来看一下具体的解答。 整个过程依然分为三段,选择合适的未知数。在两个直角三角形中,分别根据已知角的三角函数值,从而用 x 来表示出其他的未知量。在寻求线段之间的数量关系,建立方程求解。 有这个问题,我们发现锐角三角函数不仅可以解决测高问题,同样还可以解决测质问题呢。接下来我们一起来挑战一下。立二 大海中某小岛周围的十千米范围内有暗礁。一海轮在该岛的南偏西五十五度的方向某处,由西向东行驶二十千米后,到达该岛的南偏西二十五度方向的另一处。 如果该海轮继续向东行驶,会有触礁的危险吗? 这个问题是要发挥同学们的想象力,首先在脑海里面想象一下海伦行驶的情景,并根据提议把你抽象的图形在学习单上画出来。可以先按暂停键, 同学们画好了吗?有一定难度吧,我们一起来交流一下呢!大海中某小岛, 我们用点 a 表示周围的十千米,用圆 a 来表示,半径为十千米。 一海轮在该岛的南偏西五十五度的方向的某处,我们画出方位角,得到点 b 处。由西向东二十千米后到达该岛的南偏西五十二十五度的方向,我们可以向东行驶, 直到方位角在南偏西二十五度的方向得到点 c。 如果该海轮继续行驶,会有触礁的危险吗? 请同学们想一想,我们可以通过什么依据来判断是否促交呢? 我们先画出轮船继续向东行驶的路线,即延长 b c。 这时候所谓促交即可理解为这条延长线与圆 a 是 否有公共点,也就是要判断直线与圆的位置关系。 同学们的思考方向清晰了吗?我们可以过点 a 做 a h 垂直, b c 的 延长线垂足为 h, 那 我们只要把 a h 的 长求出来即可。该如何求呢? 我们依然可以延续前几个问题的思路。我们发现 a h 也在两个直角三角形当中, 可以在 a h、 b 中利用 tangent 五十五度等于 b h 比 h, 从而我们可以用 a h 来表示 b h。 同样在三角形 a h、 c 中,我们可以根据 tangent 二十五度等于 c h 比 h, 从而实现用 a h 来表示 c h。 而由图中可以看出, b h 减 c h 等于 bc, 而 bc 是 已知的,从而我们只需要设公共边, a h 为 x 即可。建立方程求解 决这个问题之后,我们把今天的几个问题联系在一起回味和对比呢。请大家观察今天的四个问题的图形结构, 你有什么看法呢? 不难发现,这四个图形中都有两个直角三角形, 并且都含有一条公共的直角边,我们可以归纳为有公共边的双直角三角形模型。 那么这四个图中又有什么区别呢?你又会怎么将它们分组呢? 像这样两个直角三角形,在公共边的同侧的,我们称之为同侧母子形。像这样两个直角三角形,在公共边的翼侧,我们称之为翼侧背靠背形。 这两种模型在我们解直角三角形的问题中比较常见,通常我们都是设公共边为 x, 在 寻求线段之间的等量关系,建立方程求解。 我们归纳模型并不代表我们在解析时都需要去寻找模型,模型带给我们的是亲切感和熟悉感,这样可以帮我们更快的找到解析思路哦。 现在我们进行本节课的小节,通过这几节课的几个问题解决,我们进一步认识了锐角三角函数知识对我们生活的影响。 同学们现在可以总结用锐角三角函数解决实际问题的方法了吗? 我们首先需要将实际问题转化为数学问题,再利用三角函数结合见方程解直角三角形。 当然,我们可能遇到的是直角三角形,也可能是一般三角形,那么我们就需要添加辅助线转化为直角三角形的问题,再解直角三角形,从而得到实际问题的答案。 那么这个方法我们又是如何找到的呢?经历这几节课解决问题的过程,我们更重要的是领悟了很多数学思想,例如 转化思想、方程思想、模型思想、塑形结合思想等等, 而这些数学思想指引着我们如何思考问题,并找到解决问题的正确方法。希望同学们在以后的学习中可以获得更多的数学思想和方法,从而解决生活中更多的问题。 今天的课就送到这里,谢谢观看,同学们再见!
 02:28查看AI文稿AI文稿
02:28查看AI文稿AI文稿这是九年级锐角三角函数一张特别有趣的一道题。在四乘四的正方形网格中, a、 b、 c、 d 为网格,格点连接 a、 b、 c、 d 相交于 o, 求 cosine 角 b、 o、 c 的 值。 锐角三角函数是在直角三角形当中定义的,首先需把角 b、 o、 c 放到直角三角形当中。 通过观察我们发现三角形 d、 b、 c 是 个等腰直角三角形,因此连接 b、 e 一 只角 o, e、 b 是九十度,所以 cosine 角 b、 o、 c 的 值就在直角三角形 o、 e、 b 当中, 等于 o、 e 比上 o, b, o, e、 d、 e 的 部分 o, b、 a、 b 的 部分 d、 e、 a、 b。 观察发现 a、 e、 d、 b 相等且平行,所以四边形 a、 e、 b、 d、 e 组对边平行且相等是平行四边形,而平行四边形的对角线 互相平分,因此 o、 e 等于二分之一, d, e、 o、 b 二分之一 a、 b、 d、 e、 a、 b 分 不有理化。今天的题稍微有丢丢丢,小难度,一遍听不明白请听两遍。 亲爱的们,今天你听明白了吗?咱们下期再见!
20果老师初中数学 20:48查看AI文稿AI文稿
20:48查看AI文稿AI文稿同学们好,我是来自南京市第十三中锁心分校的周晨晨老师。今天我们学习的课题是七点六用锐角三角函数解决问题。一 同学们在前几节课中,我们已经掌握了锐角三角函数的相关知识, 也学会了如何解直角三角形。而数学知识源于生活又服务于生活,那么用锐角三角函数又能解决哪些生活中的问题呢? 今天我们就跟着小明一起去游乐场吧,看看这一路上是如何邂逅三角函数的呢?请同学们看第一个问题。 小明从家出发,路过一个横截面为等腰梯形的过街天桥,已知天桥的高为五米,鞋面的坡角为三十七度,求斜坡 a、 b 的 长度。 这是一个实际问题,我们可以从数学的角度出发,将其转化为数学问题。那么首先就需要在实际情境中抽象出几何图形,画出一个等腰梯形。 接着将提议中的条件和问题数学化,条件是天桥的高为五米,即等腰梯形的高为五米, 鞋面的坡角为三十七度。这里出现一个新名词,坡角。我们来认识一下坡角的定义, 坡面与水平面的夹角叫做坡角,那么在本题中, 我们任选一个斜坡 a、 b、 a、 d 的 夹角角 a 即为斜坡, a、 b 的 坡角为三十七度。最后提出的问题是求 a、 b 的 长, 这样我们就成功转化成了一个数学问题。这个问题又该如何解决呢?一起来思考。 面对一个几何问题,我们首先要分清题目中的已知和未知,为了便于分析,请同学们在图形上标注出已知条件和要求的是什么? 梯形的高为五米,可以过点 b 做 b, e 垂直 a, d 垂足为 e, 即 pe 为五米角 a 为三十七度, 要求的是 a、 b。 打个问号,梳理完已知和未知之后,现在我们就要寻找已知与未知之间的关系了。 be 角 a 还有 a、 b。 观察图形,相信同学们很快发现这三个元素在同一个直角三角形里,这时我们就很容易联想到三角函数。 在直角三角形 a、 b、 e 中,我们已知边 b、 e 和角 a。 在 前面的解直角三角形的学习中,我们已经明确知道已知一边一角即可以解出所有的元素。 那么现在该选择哪种三角函数来求解 a、 b 呢?根据这三个元素边角之间的位置关系, 我们的选择应当是角 a 的 正弦。答题思路已经清晰了,下面还需要一起来规范的解答。 首先要描述辅助线,并根据提议将已知的条件用数学符号语言表述出来, 再选择适当的三角函数。本题我们选择正弦值,用解直角三角形的规范过程求出未知量。最后还要回归到实际问题的答案,也就是别忘记答。 就这样,我们解决了这个实际问题。回顾求解过程,同学们有什么收获呢? 我们不难发现,根据已知与未知的数量关系,找出或构造直角三角形,即可利用锐角三角函数知识解决问题啦。 那么在这个问题情景中,我们还能进一步提出哪些新的问题呢?同学们先自己想一想, 老师想了两个新问题,会和你们想的一样吗?问题一,你还能求出哪些线段的长呢? 很显然, c、 d 和 a e 的 长根据等腰梯形溢得 c d 等于 ab, 那么 a e 呢?我们发现 a e 也在直角三角形 a b e 中,那么只需要换一个三角函数的选择,把 sin a 换成什么呢?换成 tangent a 即可解除 a e。 问题二,若要知道桥底 a d 的 宽度,还需要添加什么条件呢?这也是我们常见的提问方式哦,根据要知道的结论,倒推需要给出的条件,请同学们思考一会, 相信同学们已经有答案了。 a、 d 是 梯形的底边,并不在一个直角三角形里,是无法直接解出的。 那么这个时候,一个重要的数学思想转化思想就会指引我们思考,我们可以将 a、 d 转化,如何转化呢?不妨再过点 c 做 c f 垂直 a d, 这样 a d 就 可以转化成 a, e, d f 还有 e f 这三者之合。 接下来只要逐一求出这三条线段即可由等腰梯形、异正三角形 c、 d f 和 b a e 全等,所以 d f 就 等于 a e, 现在就只剩下 e f 了。在这个图形中,除了两个直角三角形,我们还可以得到一个矩形 e f cb, 从而 e f 就 等于 b c。 那 么要知道 e f 就是 要知道 c b 的 长。同学们有答案了吗?回归实际,我们需要添加桥面的宽度, 接下来我们再把这个问题的条件变一变呢, 红色字体就是变化的部分,我们由坡脚变成了坡度,因为在我们生活中,除了坡脚,坡度也是可以刻画斜坡的陡峭程度的。那么什么是坡度呢?我们来认识一下 坡面的铅垂高度与水平宽度的比叫做坡度或漂坡比,记作 i i 等于 tangent 的 而法,而法为坡角。 这里坡面的铅垂宽度我们任选。坡面 a b 即 b e, 水平宽度即 a e, 那 么坡度就是 b e 与 a e 的 比, 即角 a 的 正切。这样我们就可以得到一个新的数学问题。我们数学问题中,如果条件发生了变化,那么之前的思路过程会发生变化吗?首先,没了坡角就不能自由的选择三角函数了, 我们只能从坡度正切出发,有角 a 的 正切,我们可以得到 a、 e 的 长,再结合勾股定力, 我们就可以得到 ab 的 长了。由此启发,在解直角三角形的问题中,我们常常还需要联合勾股定力一起解决哦。 在经历了和三角函数的天桥相会后,带着刚刚的收获,我们再一起来看看利一。 如图,水坝的横截面是梯形 a、 b、 c、 d。 引水坡 bc 的 坡角为三十度。背水坡 a、 d 的 坡度 i 为一比一点二,坝顶 d、 c 等于二点五米,坝高四点五米。 求一背水 a、 d 的 坡角二坝底 ab 的 长度。这是一个实际问题,我们同样需要转化成一个数学问题。我们先看题目中给出的抽象图形,一个梯形 a、 b、 c、 d, 我 们可以把条件和问题数学化,并标注在图上。 盈水坡 b、 c 的 坡角为三十度,即角 b 为三十度。背水坡 a、 d 的 坡度 i 为一比一点二,即 tangent a 等于一比一点二, 坝顶 dc 等于二点五米。梯形的上底为二点五米,坝高四点五米,我们可以过点 c 做 c, e 垂直, ab 垂足为 e, 则 c、 e 即为梯形的高四点五米。 要求的是什么呢?背水 a d 的 坡角,即角 a 的 度数。把底 a、 b 的 长。我们来一起分析这样的一个数学问题。 先看第一小问,要求角 a 的 度数。 在这个问题中,已知角 b 的 度数为三十七度,可是我们能由角 b 来得角 a 的 度数吗?显然是不行的。那么我们还可以从哪一条路来获得角 a 的 度数呢? 我们之前已经知道锐角三角函数值随着锐角的大小的确定而唯一确定,因此我们是可以由锐角三角函数值借助于计算机来求得对应锐角的大小的。 因此,在这个问题中,我们可以由角 a 的 正切来得到角 a 的 大小。规范解答,由于角 a 不是 特殊角,我们需要用计算机计算角 a 等于三十九点八度。 接下来我们再来分析第二小问,这里要求 a、 b 的 长 同学们有似曾相识的感觉吗?对,不就是之前天桥的底的问题吗?仿照思路,我们依然是要将 a、 b 转化。 在本图中, a、 b 可以 转化为 be 加 a e, 但是 a、 e 依然不在一个直角三角形中。我们可以尝试过点 d 再做 d, f 垂直 a、 b, 从而将 a、 b 转化成三条线段, b, e, e, f 还有 af。 而 af 在 直角三角形 a、 d、 f 中,我们可以根据 tangent a 得到, 而 b e 在 直角三角形 b、 e、 c 中,我们可以由 tangent b 得到。最后我们再看一下 e、 f 在 矩形 c, e, f d 中,从而 e、 f 就 等于 c d, 这样我们就逐一求出了这三条线段,即可得到了 ab 的 长。 解析思路一下子就清晰了,我们不妨再回味一下这道题和天桥问题如此相近,它们有什么共同之处呢? 一定有同学发现了,我们常常可以添加辅助线,构建直角三角形加矩形的模型, 这样可以分解线段,从而逐步解决问题。希望同学们以后看到这个模型会有亲切感,能更快速的找到思路哦! 下面请同学们结合图形和分析思路,在学习单上写出自己的解答过程。可以先按暂停键, 同学们写好了吗?我们一起来核对一下。首先仍然是要描述辅助线和将已知条件用符号语言表达。 然后在直角三角形 a、 d、 f 中,我们用角 a 的 正切,即坡度等于 tangent a 等于一比一点二,从而可以计算出 af 等于五点四米。 再在直角三角形 c、 b、 e 中用角 b 的 正切三十度等于 c, e 比上 b, e, 从而得到 b, e 等于四点五比 tangent 三十。这里我们可以暂时不用带入 tangent 三十的数据。 接着我们再由矩形得到 e, f 等于 d, c 等于二点五米。所以 ab 就 等于 a, f 加 e, f 加 e, b 等于五点四加二点五加四点五比 tangent 三十度。 我们可以在这里代进 tangent 三十的径四值,从而计算出 a、 b 的 径四值,精确到零点一,约等于十五点七米。最后别忘记了要答哦,两个小问都要答, 接下来我们再一起来挑战一下列二呢?如图,小明从点 a 出发,沿着坡角为十度的坡道向上走了一百二十米到达点 b。 再沿着坡角为十五度的坡道向上走了一百六十米,到达点 c。 请问小明沿垂直方向升高了多少呢?精确到零点一米, 请同学们按暂停键独立思考五分钟。 同学们想好了吗?我们一起来交流一下。 这道题已经给出了图形,并在图形上标注了条件, 这时候我们只需要找出要求的线段,小明从点 a 走到了点 c, 那 么小明沿垂直方向升高的高度即 cd 的 长。 那么我们该如何求 cd 呢? 也用之前的思路。首先, c、 d 能直接求解吗?显然不能,它并不在一个直角三角形中。 那么我们又是怎样添加辅助线实现转化呢? 同学们,你们是怎么做的呢? 这里我们可以利用化身为直的思想做两个垂直,过点 b 做 b, e 垂直 a、 d 垂足为 e, 再过点 b 做 b f 垂直 c、 d 垂足为 f, 从而构造出了两个直角三角形加一个矩形的模型,这样 c、 d 边就可以转化为 c f 加 f d, 而由矩形一只 f、 d 就 等于 b、 e 的 长。那么我们只需要求出 c、 f 和 b e 就 可以得到 c、 d 了, 而 b、 e 可以 在直角三角形中已知 a、 b 和角 b、 a、 e 要求 b、 e。 根据这三个元素的边角关系,我们可以选择角 b、 a、 e 的 正弦值, c、 f 可以 在直角三角形 c、 b、 f 中已知 bc 等于一百六十米,角 c、 b、 f 等于十度, 我们同样可以选择正弦值解出 c、 f, 这样就可以得到 c、 d 的 长了。 同学们思路清楚了吗?请课后把这道题的完整解答写出来。 现在我们进行本节课的小节。这节课我们用锐角三角函数解决了一些实际问题,具体的步骤是怎样的呢? 一、将实际问题抽象为数学问题 画出平面图形,转化为解直角三角形的问题。 二、根据条件的特点,适当选用锐角、三角函数等去解直角三角形。那我们怎么样正确的选用呢?可以根据已知和未知元素之间的边角位置关系。 三、得到数学问题的答案。答案最后别忘了还要回归到实际问题,得到实际问题的答案。 小明和三角函数的故事还未完结,下一节课再续哦!今天的课就上到这里,谢谢观看,同学们再见!
 23:55查看AI文稿AI文稿
23:55查看AI文稿AI文稿同学们好,我是来自南京市高城区第一中学的杭香香老师。今天我们所学习的课题是五点三,锐角三角函数。第二课时, 上一节课我们已经复习了锐角三角函数的定义。这节课我们利用锐角三角函数来解决问题。 第一题,如图,在 r、 t 三角形 a、 b、 c 中,角 c 等于九十度,角 b 等于三十度, bc 等于六,则 a、 b 为结果,保留根号。 根据图中 bc 为角, b 的 邻边, ab 是 斜边,我们选择角 b 的 余弦 cosine, b 等于 bc 比 ab 变行为 ab 等于 bc, 除以 cosine, b 等于六,除以二分之根号三等于四根号三。求解 第二题,在 r、 t 三角形 a、 b、 c 中,角 c 等于九十度, a、 c 等于根号六, b、 c 等于三根号二。解这个三角形。 这里的解这个三角形就是要把三角形 a、 b、 c 中除了已知的两边和一角外,其余的剩下的两角以及一边全部求出来才叫解这个三角形。 根据 a、 c 是 角 a 的 邻边, bc 是 角 a 的 对边。我们选择贪婪的 a 等于 bc, 比 a、 c 等于三根号二,比根号六,化简为根号三。 记忆角 a 就 等于六十度。然后根据直角三角形的两个锐角互余求出角 b 等于九十度。减角 a 等于三十度。求 a、 b 方法很多,可 也可以选择角 a、 角 b 的 任何一个三角函数值。 这里选择的是三十度角所对的边等于斜边的一半,所以选择了一个最容易的办法, a、 b 等于两倍的 a、 c 等于二根号六。 上面解直角三角形的过程总结为就是确定直角三角形除直角外的条件,也就是判断直角三角形全等的条件。 我们只需要在已知除直角外的两个元素,就可以求出剩下的三个元素,这就是借直角三角形的过程。 在已知的两个元素中,至少必须有一边,因为三个角相等是不能判断两个直角三角形全等的,所以还分为已知 一边一角求另外两边和一角的过程,以及两边求第三边和两角的过程。这个过程当中所利用的知识有 三边之间的关系,就是勾股定律,两个锐角之间互与的关系以及边角之间的关系,就是两个角的六个三角函数值的选择。 例二,在三角形 a、 b、 c 中, a、 c 等于八角, b 等于四十五度角, a 等于三十度求 a、 b 的 值。 这个三角形不是直角三角形,我们可以把它称为叫斜三角形。如何来利用三十度角和四十五度角,我们需要天垂线 过 c 做 c、 d 垂直 ab 垂足为 d, 这样原来的三角形就可以分成左右两个直角三角形来分别求解。 在 r、 t 三角形 a、 c、 d 中,已知一个锐角一条边,我们就可以求解这个直角三角形。这里需要求的边有 a、 d 和 c、 d, 所以 选择口上以 a 等于零边比斜边, 所以 a、 d 就 等于 a、 c 乘 cos 等于 a 等于八,乘二分之根号三等于四根号三。 还有 c、 d, 我 们选择的是最简单的等于 a、 c 的 一半等于四, 这个 c、 d, 它属于两个直角三角形,是两个直角三角形的公共边,是两个直角三角形联系的桥梁。 在 r、 t 三角形 b、 c、 d 中,已知 cd 一 边角 b 四十五度,我们又可以去求解这个直角三角形,这里所需要求的边是 b、 d。 根据弹性的 b 等于 c、 d 比 b、 d 等于一,我们可以求出 b、 d 等于 c、 d 乘弹性的 b 等于四,乘一等于四。当然这里你也可以选择特殊的等角对等边来解决 b、 d 的 长度。 最后 a、 b 的 长就等于 a、 d 加 b、 d 等于四根号三加四。第二题,在三角形 a、 b、 c 中, a、 c 等于六角 b。 三十度角 c。 十五度求 a、 b 的 长,结果保留根号。这道题目 最初的想法很容易过 a 做 b、 c 的 垂线把斜三角形分割成两个直角三角形, 但是有一个直角三角形,还有的是十五度,这个角我们是非特殊角, 我们一般情况下是不知道十五度角的三角函数值的,所以这个办法应该来讲是走不通的。 我们选择过 c 做 c、 d。 垂直 ab。 垂直为 d。 根据三角形中角度的位置,我们可以求出角 c、 a、 d 等于 角 c 就是 角 a、 c、 b 加角 b 等于四十五度。四十五度又是我们常见的特殊角,这样我们就找到两个还有特殊角的直角三角形, 一个是 a、 c、 d, 一个是 b、 c、 d。 在 a、 c、 d 中已知斜边等于六角 c、 a、 d 等于四十五度。选择 cosine 角 c、 a、 d 等于 a、 d、 b、 a、 c 转化为 a、 d 等于 a、 c 乘以 cosine 角 c, a、 d 等于六乘 cosine 四十五度等于六乘二分之根号二等于三根号二。 同样 c、 d 我 们也可以求出来等于三根号二,或者用 c、 d 等于 a、 d 求出来等于三根号二。 这个 c、 d 它同时属于两个直角三角形,所以它的位置非常的重要,是两个直角三角形的公共边。 在 r、 t 三角形 b、 c、 d 中,又一只 c、 d, 一 边还有一角角 b 等于三十度。 我们可以选择贪婪的 b 等于 c、 d、 b、 b、 d 转化为 b, d 等于 c、 d 除以贪婪的 b 等于三根号二,除以三分之根号三等于三根号六。 求出了 b、 d, 求出了 a、 d, 我 们就可以得出 a、 b 等于 b、 d 减 a、 d 等于三根号六,减三根号二。 这个题目也是把一个三角形分割成两个直角三角形,但是这个分割是通过做一条外面的勾来分割的。 总结一下,确定两个三角形全等的条件,我们知道要三个条件,这三个条件当中 已知就可以确定求出未知的三个元素。我们也可以类似的把这个过程称为叫解斜三角形。解三斜三角形其实就是转化为解直角三角形。 转化的方法一般有下面两类,在三角形的内部添一条勾,或者在三角形的外部添一条勾, 这条勾我们称为叫两个直角三角形的公共边,起着非常重要的作用。那么分为已知两边加角, 求另外两角一边或者以至两角集齐一组等角的对边或者以至三边来求三角的过程, 这就是解斜三角形的过程。一般的题目中没有出现解斜三角形的这个词,但是它会求出一部分的大,比如说它只要求某一条边或者某一个角。 好,下面我们看例三。如图,为了测量建筑物 c、 d 的 高度, 小明在 e 点分别测出建筑物 a、 b 的 顶端的阳角, a、 e、 b 这个标在图上等于三十度,还有一个阳角 c、 e、 d 等于四十五度,这个我在图上没有标出来。在 f 点 分别测出建筑物 ab 的 顶端的阳角是 a、 f、 b 等于四十五度, c、 f、 d 等于七十度, 已知 ab 的 高度等于十四。求 cd 的 高度。答案要求精确到零点,一,并提供了三个参考数据, 这也是我们每年中考常见的三角函数的一个类型。在这个图形当中比较复杂,它一共有四个直角三角形 a、 b、 e、 a、 b、 f 还有 c、 d、 e。 其中 a、 b、 e 是 已知一边十四,一角三十是可解的, a、 f、 b 同样已知一边十四,一角四十五度也是可解的。 三角形 c、 d、 e 中没有一条变异值,三角形 c、 d、 f 中也没有一条变异值,所以这个题目的难度就加大了。 但是我们可以看出来,三角形 c、 d、 e 和三角形 c、 d、 f 他们有一条公共的边, c、 d 还有他们的边 c、 e 和 c、 f 之间相差的那个 e、 f 是渴求的。所以此类题目我们要把这两个三角形关联起来求,也就是需要借助于设 未知数的方法来列方程或者方程组解决问题。设 c、 d 的 长为 x。 好,我们先把能求的求出来。在 r、 t。 三角形 a、 b、 e 中,角 a、 b 等于三十度, a、 b 等于十四。 选择贪婪的角, a、 e、 b 等于 a、 b、 b, a、 e 转化为 a, e 等于 a、 b。 除以贪婪的三十度等于十四根号三、 在 r、 t。 三角形 a、 b、 f 中, ab 等于十四角, a、 f、 b 等于四十五度,很容易求出来, a、 f 等于 ab 等于十四。 所以 e、 f 的 长就等于 a、 e 加 a、 f 的 长等于十四根二三加十四。 接下来我们在三角形 c、 d、 e 中和三角形 c、 d、 f 中 都找不到一条一致的边,但是通过假设的未知数 x, 我 们可以用 x 来表示其余的边 c、 d、 e 当中角 c、 d、 e 等于四十五度。很显然, c、 d 等于 x, 那 么 c、 e 就 等于 c、 d 等于 x, 这个应该是特别好计算的一个量。 那么在 r、 t 三角形 c、 d、 f 中,角 c、 f、 d 等于七十度, c、 d 是 它的对边,还有一条 c、 f。 其实我们已经可以借助已知的量和设的未知数表示出 c、 f 的 长, c、 f 是 七十度角的邻边,所以我们选择贪婪的七十度,贪婪的角 c、 f、 d 等于对边 b 邻边, 也就是 x b, x 减去十四加十四,根二三等于二点七五。 这个方程解出来 x 等于六十点一。 完整的作答。 我们经常在碰到解直角三角形的时候,无法直接 用边来表示,那么我们的另一个手段,也就是设未知数,然后通过设的未知数来表示另外的线段构造方程来解决问题,这其实也是一种模型的思想。 好,我们再看。第四。如图,在横线 l 的 两侧分别有观测点 a 和 b。 点 a 到横线 l 的 距离为两公里,点 b 位于点 a 的 北偏东六十度 方向,且与点 a 相距十公里处。这个题目的题干就要求理解 ab 的 长度就是十。 现有一艘轮船从位于点 b 南偏西七十六度的方向的 c 处,就是图中的 abc 等于七十六度, 正沿自西向东的方向途中自西向东,也就是 c、 d 的 方向航行五分钟后到了 d 处。 这个题目对方位角的理解以及对方向题目意思,对应的线段的要求比较高。 第一个问题,求 b 到航线的距离,也就是图中虚线 b 一、 这条垂线段的长度。第二个问题,求轮船航行的速度,提供的参考数据 可以供你选择,答案要求精确到零点一千米每小时。 那么这个题目中我们首先要找到要求的是哪些量,它比前面一个题目难在,就说你要需要求什么量,审题的要求就提高了。 这个题目我们需要找出相应的条件以及相应的三角形。设 a、 b 与 l 相交于点 o, 在 rt 三角形 a、 o、 d 中,已知角 o, a、 d 等于六十度, a、 d 等于二,我们可以选择相应的三角函数, tan 等于 o d, b, a、 d 等于 a d, b 上 o, a 求出 o、 d 的 长和 o, a 的 长。 根据 a、 b 等于十,我们可以解出 o, b 等于 a, b 减 o, a 等于六。 在 r t 三角形 o、 b、 e 中,我们还需要知道角 o、 b、 e 的 度数 等于角 o、 a、 d 的 度数等于六十度。然后选择相应的三角函数,同样的办法求出 o、 e 和 b, e 的 长,这样第一题的答案就得到求解。 第二题为了求 cd 的 长度, 在 r t 三角形 b、 c、 e 中,角 c, b, e 等于七十六度, b, e 等于三。选择 tan 角 c, b, e 等于 c, e 比上 b, e 变成 c, e 等于 b, e 乘 tan 角 c b, e 带入相应的数字,求出 c、 e 的 长度。 又因为前面的答案已经求得 d 一 等于 o, d 加 o 一 等于五倍的根号。三、 带入相应的数据等于八点六五,这样我们就可以用减法求出 c、 d 的 长度等于 c 一 减 d 等于 十二点零,三减八点六等于三点三八。题目中五分钟我们把它化成十二分之一小时, 求的轮船的速度为路程除以时间约等于四十点六。然后完整的写出题目的解答过程。 总结一下,我们通过直角三角形的边角关系,总结出了锐角三角函数的定义, 那么在具体的问题当中,我们需要去找到相应的直角三角形来解这个直角三角形,从而解决实际问题的答案。 今天的课就上到这里,谢谢观看,同学们再见!
 01:44查看AI文稿AI文稿
01:44查看AI文稿AI文稿今天我们一起来学习九年级下册三角函数章节,比较喜欢考察的解这样三角形的问题。如图,在三角形 a、 b、 c 中抛三, b 等于五分之四,它的 a、 c 等于根号三,然后 a、 b 的 长等于五,按求 a、 c 的 长。同学们在做题的过程中一定要来注意,咱们学的叫锐角三角函数, 必须在直角三角形中才能去应用,所以说这里面它给了个三角形 a、 b、 c, 并没有说它是一个直角三角形,所以第一步根据这个特点 a、 d 点的又是五,然后给了角 b 和角 c 的 三角函数,那我一定要构造直角三角形才能用, 那考虑观察我们过 d 点如何做垂线构造出来的两个,这样三角形中既能包含这两个角的三角函数,还能包含 a、 d 这条边,也便于我们在复序解三角形中去应用。我们过 a 点做 b、 c 的 垂线,推入 o、 d, 这时候我们看他说 cosine, cosine b 是 在三角形 a、 t、 d 中应该等于 邻边比斜边,邻边就是 b, d 比上斜边是 a、 d, 也就等于 b, d 比上五,等于五分之四,所以说我就能解成 b、 d 等于四,然后这条边是四,当然它是四的话,我又不一定谁能解出来 a、 d, 那三、四、五咱们常见的勾出。其次你再看探探 d, c, 在 a、 d、 c 当中可以用探探 d, c 是 应该等于对边比邻边求 a, d 比 c、 d, 那 就等于三,比上 c 零,它就等于根号三, c、 d 是 不是等于根号三?其次他要让我求 a、 c 求 ac 的 话,我就可以用勾股定律了吧,三方加上根号三方,这里就是二倍 cos, 当然了,很多同学可以观察出来它在底 c 的 根号三,说明这个角等于六十度,那我可以再用六十度的正弦或者六六余弦都可以求 ac, 最终切开 ac 和二倍 cos 三,这就是咱们解这个方程里面的一些常见用法,有什么问题在评论区给我留言。
16数学思维杨老师 23:06查看AI文稿AI文稿
23:06查看AI文稿AI文稿今天和大家分享苏格版九年级数学下册期中复习期锐角三角函数自我平移。第一角 c 为九十度 a, c 是 二倍的 bc, 这是 x, 这就是二 s, 这就是根号五 x 啊。要求 cos 大 于 b 就是 五分之 根号五啊。 第二题,某人也斜坡前进了三十米,上升了十五米,那这个十五倍根号三,那么坡比就是一比,根号三 接一题,角 a, 角 c 九十度三 a 二比三, 二得四,根号五,问扣撒于三分之根号五,选择 c。 下一题,这个铁塔离铁塔一百米处 a, 所以 我们这题把这个水平线跟铁塔垂直 假设是一点啊,我们 a, d 是 一点四,这边是一点四,这边是一百,这是一百餐厅 阿尔法等于 b e 比一百来一百乘以它点,阿尔法再加一点四,所以选 b。 第五题,是吧?这个又,我们这样把 b、 c 连起来, 发现这两个三极全等全等,正负值是等于二直角三极,所以三角 b, a、 c 是 三个四十五度二分之根号二。 第六题,角 a c b 四十五角 p 二 p 二, q 是 一八二五 b c 边上的高为 h e, 这是等腰直角 h e 等于啊,二分之五倍,根号五 二二,那么五倍二除以二是吧,那这个呢? 是吧,这 q 二边上高是,这是吧,这个是 五十五度是吧?这个好,我们可以这样做,这是 h 一 等于五乘三 a 四十五 h 二 等于五乘三 a 五十五,三 a 随着角度增大而增大,所以 h 二大 注意选择 b。 第七题, 这个北偏东六十度啊,这就是六十度,这是三十度,相距五百米处有一个铁塔, 那么是个水塔,水塔所在位置与公路 a、 b 的 距离啊,这就是啊,这是二倍五十。选择 a 这一题,角 a 三十, a e a e、 b, 这是四比一,那这边也是四比一, 我们要求 c f c f b 求这个角,我们设这个为 x, 设这为四 x, 这整体就是五 x, 对 吧?五 x 除以 根号三啊,就得到这个用探听了是吧?除以根号三的差,然后再用勾股定力求 b、 f 还有没有空位探听它,就拿它比,它就已经出来了啊。 所以选择 c 三分之五倍根号三啊,利用一次相似平行转换啊,两个垂直平行就相似,就这面成比例,不叫相似,这面成比例啊。下面一个角, c 为九十度 b, c 为一 a, c 为三,三三点九,根号十,那扣撒于 a 就是 十分之三倍,根号十 啊。 a、 b 是 三,我错了,错了错了,我怎么看着我在写上 a, c 是 三, a, b 是 三啊, 所以看错已知就一定错,三就二倍根号二啊,三分之二倍根号啊,口才啊。第十题啊, c 三, a 六十度, a, 角 a 等于六十度,角 b 等于四十五度一百零五七十五度。 第十一题,黑点坐标三四四三,黑点坐标与圆点连接, 这个与 s 轴加交为二八三四五,是吧,扣上五分之差。 十二题,幺是一,底是根号三,幺是一, 要求底角的正切做垂线,这是二分之根号三, 这是一,那,那这购物定率就二分之一,那正切值实际上就出来了啊,三分之二,三 啊。 第十三题,如果一个正九边形的半径是二,那么它的边长九边形,正九边形 啊,边长还有一个九,它就是四十度。四九三十六,三百六米有四十度,你做垂线, 这是二,这是二十度啊,它的变长,我们用二乘以三英二十度再乘以二,是吧? 零边长一和根号三是吧?斜边就是二,这都是一,这就是等边三角形啊,矩形两条对角线夹角就是六十度, 正等边就可以了啊。方法比较多,下面角 a、 b、 c 六十度, c 六十度, a, b 为八, a, c 为七, c 一 c 二,这都是七。做垂线 加上 a、 d, 这是四,这是四倍根号三,这是七,七七四十九减去四十八,再等于一 啊。所以一个四减一,一个四加一,一个三,一个五,底,一个三,一个五,然后二分之一乘以 三乘以四倍根号三,二分之一乘以四倍根号三,得到面积六倍根号三,一个是十倍根号三,我们来弄情况, 最后写答案。第十六题,在三角 a、 b、 c 当中,角 a 三十度,探听 b 也给你了,所以做垂线就可以了, 是吧? a、 c 二等于根号三,那这就是根号三,那这就是三,那个探听 探听 b, 那 这就是二。加起来,然后这是更好起, b、 c 更好起啊。 第十七题,这个,这肯定要给这弄过来,是吧? 嗯, c、 m 破比一,比刚,一比三,一比三,这个在 c 处测的旗杆仰角三十度在 m 处, 现在一样料子啊。 c、 d 是 二,这是二,这就是六,那这就是二,是吧?这个 要求其杆高度是吧?我们就要设啊,我们可以设什么呢?呃,你可以设 b m, 假设是 x, 这就是 x 加六,是吧?这就是根号三 x, 根号三, x 减二啊。根号三 x 减二,这就探顶三十度 等于根号三, x 减二,除以 s 加六,探顶三十度等于三分之根号三,从而求出 x, 求出 x 以后啊, a、 b 就是杠三, x 就 结束了啊,我们看它是怎么看,这是二啊,它设的就是 bm 五 x, 哎,跟我思思路一样,这是六,这是二啊 啊。最后 a 方程解出来,最后约等于啊,实际高度是三加三倍杠三,它要约等于,你再去约等于就行了。第十八题,卡尔法减倍,它为九十度,乘这样的三角形为准直角三角形 啊。若三角形是准直角三角形,角 c 是 大于九十度,角 a 等于七十度啊,这个,这个大于九十度,是吧?所以 角 a, 角 c 加角 b 啊,角 c 加角 b, 就 该一百一十度,对吧?角 c 减 啊,角 a 等于九十度, 是吧?角 c 减七十度等于九十度,求出来一个啊,再角 c 减角 b 啊,再出来一个,我们两种都去检验啊, 是吧?这个求出来, 角 c 等于一百六,那就不不符合题,那剩下一个,角 c 加角 b 一 百一,角 c 减角 b 等于九十啊,这种应该成立啊,两种有一个成立,有一个不成立。 好,下面第二题,这是一个外接圆, ab 是 直径,那这就是九十度, ab 为十啊。 d 是 这长一减,且探听 b, 探听 b 等于四比三,那就是六,这就是八 啊。若 cd 为二分之九啊。判断 a、 b、 d、 a、 b、 d 是 不是准直角三角形,是吧。也就说我们要求这个角尖某一个角大于九十度,是吧,并说明理由啊, 这个是不是我们一开始不知道,我们只有慢慢推理是吧?好,我们刚才已经推理到 c、 d 为二分之九啊, 不对, 好,我们已经算出这是六,这是,这是六,这是八啊, 这是二分之九啊!餐厅角 c、 a、 d, 我 们算,这是直角,算出来也是四分之三啊,那就是说这是四分之三,这是四分之三,那这两个角就相等啊,而这个角 等于九十度,加它,那它减,它就等于是准直角三角就对了啊。 下面第三题啊, ab 是 直径, e 在 啊, ab 下方, ab 为十,这半径就是五啊。探听角 abc, 那 就是六,这是八啊。若 a、 c、 e 是 准直角,算进去,准直角算进去啊。这个 求 c 一 长是吧?它是准直角三角形,我们刚才已经求出来,这是六,这是八, e 在 下边,要是又在 ab 上,要是准直角三角形,这个 c a、 e、 c、 a、 e 一定是大于九,这个角大于九啊,这个 c、 a、 e、 c、 a 都小于九十度,这两个都是小角,且角 c、 a 跟这个角相等, 是吧?好,那当就要分类讨论呢。当这个角 c、 a、 e 等于九十度加角 c、 e、 a 时 啊,则角 c、 e 都等于九十度加角 a、 b、 c 代入逆算,等于一倍八十度减角 c、 a、 b。 就是 分类讨论啊。四边形内角和三倍六,两个九十,这两个九十,是吧?所以这个角等于一倍八减 c、 b、 e 等于一百八减角 c、 a、 e 对 不对?也就等于角 c、 a、 b。 所以 角 c a、 b, c、 a、 b。 等于角 c、 c、 a、 b。 这个点又相等,这是它们一开始相等,所以角 c、 b、 e、 c、 b、 e 和角 c、 e、 b 相等 啊,因为这是八,这也是八,这是六。我们要求是要求的,是 要求什么来要求 c、 e 长啊? 啊?第一种,这 c、 e 长已经求出来,再来讨论。第二种,当角 c、 a、 e 等于九十度加角啊, e、 c、 a 是 加这角,是啊,等于九十度加这角是对吧? 角 c a, e 等于九十五加角 e c a e c a 就 等于这个角啊,等于角 a b e 啊,然后就等于一百八十度,再用内角和减角 b, a, e 啊 啊,也就一百八十度,先减去角 c b。 等量代换也算出 c e, 算出了 c, e 等于 b 啊,这是八,这是六,是吧?那我们要求的是啊, 给它平角 a, b, e 是 四分之三, a b c 四分之三,那 c 角 c a b c a, b 就是 三分之四,对吧, 是吧?因为这两个角等,所以角 c e, b, c, e, b 的 摊平值也是三分之四。那怎么办呢?下边就要做直角三角形, 做垂线,做垂线啊, c m, 因为这是刚才挣出这两段等了,它是等腰一做垂线,三线合一,这都是四, 对吧? e h 这刚才不是四比三吗?啊,设它为 三 s, 则它为四 s 啊,然后勾股定离,这就是五 x 啊,五 x, 那 这就是五 x, 然后根据等面积法再来求高三 s 四 s 五 s 四四,对吧?利用等面积法求出 e m e m 表达式出来,最后勾股定力代进计算啊,把五 s 平方看成一个整体,求出。最后啊, 上至可表为啊,这用泛元的解二次方程求出来, t 等于八十二十,不合题再去检验,不是舍去 八十, c, e 就 等于根号八十,也就等于四倍根号,所以增上,所以特别第二位,非常之繁琐啊,这就是我们这节课学习的内容啊。
1毅力数学 07:42查看AI文稿AI文稿
07:42查看AI文稿AI文稿同学们大家好,本节课我们将学习第七章、第六节用锐角三角函数解决问题。 你们看锐角三角函数解释了直角三角形的边与角的关系。在许多实际问题中,我们可以根据其中的数量关系或位置关系,找出一个直角三角函数的相关知识解决问题。 我们来看几道例题啊。例题一,如图,水坝的横截面是梯形 a、 b、 c、 d 迎水面 bc 的 坡角阿法为三十度,背水坡 a、 d 的 坡度 i 为一比一点二,坝顶 dc 等于二点五米,坝高四点五米。求一 背水坡 a、 d 的 托脚北塔二坝底 ab 的 长。 我们分析一下,要做梯形 abcd 的 高 c、 e、 d、 f。 根据题意,在直角三角形 a、 f、 d 和直角三角形 b、 e、 c 中可以分别求出 f 与 b、 e 的 长,从而可以求得把底 a、 b 的 长 作 c、 e 垂直于 a、 b、 d、 f 垂直于 a、 b, 垂足分别为 e 和 f。 看第一小问, 背水坡 a、 d 的 坡度 i 等于 tan 的 贝塔等于一比一点二,等于六分之五。用计算机 计算可以得到,贝塔等于约等于三十九点八度。 看二,在直角三角形 bc 中,阿法等于三十度,角, bc 等于九十度减三十度等于六十度, e、 b 等于 c, e 乘以它的角, bc 等于四点五,乘以它的六十度。 在直角三角形 a、 f、 d 中,因为 d、 f 比上 f 等于一比一点二, 所以 f 就 等于一点二。 d、 f 等于一点二,乘以四点五,等于五点四。 又 f、 e 等于 dc 等于二点五,所以 ab 就 等于 f 加上 fe 加上 e, b 等于五点四,加二点五,加上四点五,乘以它的六十度, 约等于十五点七。答,背水坡 a、 d 的 坡角约为三十九点八度,坝底 ab 的 长约为十五点七米。 看例题二说游乐场的大型摩天轮的半径为二十米,旋转一周需要十二分钟。小明从摩天轮的底部 大约与地面相距零点三米出发,开始观光。两分钟后小明离地面多高? 我们分析啊!如图,用圆 o 的 用圆 o 表示摩天轮。小明从底部点 a 出发,经过两分钟后到达点 b。 有提议可求的角 b、 o、 i 的 大小。如果做 dc 垂直于 o, i 垂直为 c, 在 直角三角形 o、 c、 b 中,可以根据 o、 b 及角 b、 o、 i 的 大小求得 o、 c, 那么就可以知道此时小明离地面的高度了。看解如图,用圆 o 表示摩天轮, a、 b 分 别表示小明的出发点和两分钟后的到达点。 有提议可知, o、 b 等于二十角, b, o、 i 等于三百六十度。除以六等于六十度 作 bc 垂直于 o, i 垂直为 c。 在 直角三角形 o、 c、 b 中, o、 c 等于 o, b 乘以考三英角 b, o、 c 等于二十,乘以考三英。六十度等于二十,乘以二分之一等于十, 那么 i、 c 就 等于 i o 减 c, o 等于二十减十等于十。因为摩天轮底部与地面相距零点三米,所以小明离地面的高度为十点三米。 当两分钟后,小明离地面也十,离地面十点三米。再来看例题三, 郭晓明在某处利用侧角仪观测气球的仰角为二十七度,然后他沿着正对气球方向前进五十米,此时观测气球的仰角为四十度。 如果侧角仪高度为一米,那么气球的高度为多少米为多少呢? 我们再分析下看如图,小明分别从点 a、 b 处观测气球 c 则 cd 表示气球与小明观测气球时的水平视线的距离。有提议可知,角 c、 i、 d 和角 c、 b、 d 分 别为二十七度和四十度, a、 b 等于五十米。要计算 c、 d。 可分别在直角三角形 a、 c、 d 和直角三角形 b、 c、 d 中寻求 c、 d 与已知量的关系式,再计算 c、 d。 看解如图和点 a、 b、 c 分 别表示小明两次观测点及气球的位置有提议之。角 c、 i、 d。 等于二十七度。角 c、 b、 d。 等于四十度 c、 d。 垂直于 a、 d、 a、 b 等于五十米。设 a、 c、 d 等于 x 米。在直角三角形 b、 d、 c 中有 tan 的 四十度,等于 c、 d。 除以 b、 d 得到 b、 d 等于 x, 除以 tan 的 四十度。在直角三角形 a、 d、 c 中有 tan 的 二十七度,等于 c、 d。 比上 a、 d 得到 a、 d 等于 x, 除以 tan 的 二十七度。 因为 a、 d 减 b、 d 等于五十,所以 x 除以 tan 的 二十七度,减去 x 除以 tan 的 四十度,就等于五十,所以 x 就 等于五十。乘以 tan 的 二十七度, 再乘以 tan 的 四十度,除以 tan 的 四十度,减去 tan 的 二十七度。有计算器记得 x 约等于六十四点九有。由于侧角移的高度为一米,因此气球的高度约是六十五点九米, 打气球的高度约为六十五点九米。好!今天的课就到这里布置一下课后作业。课后完成课本第一百一十七页习题,七点六的第一题和第二题。好,同学们再见!
10李老师教你学数学 01:45查看AI文稿AI文稿
01:45查看AI文稿AI文稿这是九年级锐角三角函数一张一道必考题,已知锐角的一个三角函数值,求其他两个三角函数值必考! 锐角三角函数是在直角三角形当中定义的,所以画图根据一个锐角的正弦等于它的零边比上斜边, 所以不妨设每份是 k, 则 由勾股定律已知。 所以 a c a b b c 那 么 sign a 等于角, a 的 对边比上斜边。 tangent a 等于角, a 的 对边比上邻边。 亲爱的们,今天这道必考题你听懂了吗?咱们下期再见!
16果老师初中数学 04:43查看AI文稿AI文稿
04:43查看AI文稿AI文稿今天我们来教大家如何记忆特殊的三角函数值啊, 以这个三十度为例,咱们就把这个三十度啊放在这个直角三角形里边去啊,好, 把这个地方怎么样当做这个三十度,那么根据三角形的内角和这里是九十度,所以上边就是六十度,对不对啊?上面就是六十度,那么我们要找一些特殊的数据,比如一呀,这些对不对啊?把三十度的这个对边这地方 看成一,那么我们知道在直角三角形里边三十度所对的边是斜边的一半,那么你这边是一,你这个斜边就是几啊,斜边就是二,对不对?那么根据勾股定律,咱们就知道这个另一个直角边就是 根号下二的平方减去一的平方就是四,减一等于多少?等于根号三,对不对?好,我们来看啊, 那么这个散音三十度散音指的什么?指的是对边比上斜边对不对?那么现在这个三十度对的是哪个?这是一,对边是一,对不对?斜边是二,所以就是多少?就是二分之一啊,就是二分之一,好,那么再看这个 与弦, cosine 啊, cosine 是 哪边比哪边? cosine 是 这个邻边比上斜边,那么邻边是根号三,斜边是二,那么就是多少?就是二分之根号 三,对不对?好,再来看这个贪心的正确啊,贪心的三十度,那么贪心的指的是什么?指的是这个对边比上零边,那么对边是多少?对边是一,零边是根号三,然后化成这个什么?这个 最简二次根式对不对啊?分子分母同时乘以根号三,那么就变成三分之根号三啊,就说这个的值就是三分之根号三啊,然后这个六十度啊,这里这个地方啊,也是一样的啊,那么 这个角散移正切值啊,它的六十度等于什么?等于对边比上斜边对不对啊?对边是根号三,斜边是二,所以说 就是二分之根号三啊,二分之根号三好。然后是 cosine 六十度,就是 鱼弦。 cosine 六十度,它是等于零边比上斜边,零边是一,斜边是二,那么就是一比二就是二分之一啊,二分之一好,然后贪心的六十度,贪心贪心的等于什么?等于这个对边比上 零边对不对?那么对边是根号三,零边是一,就是根号三比上一,那么这个一怎么样?可以省略不写,就是根号三啊,所以这个贪镜的六十度就是根号三好,然后还差多少度啊?差这个四十五度, 所以咱们把这个四十五度放在这个直角三角形里边来,那么让这个角等于四十五度,根据三角形的内角和,那么上边这个角怎么样?他也是四十五度,所以这是一个等腰直角三角形,咱们把这个腰怎么样?看左一,根据勾股定律的话,那么这个斜边就是多少, 斜边就是根号二,对不对?好,然后再来看啊,心算三引正切啊,三引四,四十五度就是这个角的正切值,正弦值对不对?那么这个 角的正弦值怎么样?等于对边比上斜边就是一比上根号二啊,等于一比上根号二,然后化成最减二次根式分子分母同时乘以根号二,就是二分之根号二,对不对啊?就说这个三引四十五度是二分之根号二啊,同理这个, 嗯,余弦啊,这个 cosine, cosine 四十五度,它一样的啊,等于什么?等于它的零边比上斜边,也就是一比上那个比上根号二,一样的,画成最减二根 四就是二分之根号二啊,这个是二分之根号二。好,再来看这个正切摊近的啊,摊近的四十五度, 正切值怎么样?等于什么?等于对边比上一就是几啊?等于 一啊,等于一啊,当然哈,如果说你能够把这个表啊,把它怎么把它这个背下来也可以,只是说我教的这个方法就是如果你在这个做题或者说考试的时候,突然忘记某一个特殊的三角函数值等于多少的时候,你可以用这些特殊的三角形啊,再 带入这些特殊的这个数据啊去推导。好,那么今天这个内容啊,咱们就讲完了,大家听懂了吗?
40中考数学每日一题 07:00查看AI文稿AI文稿
07:00查看AI文稿AI文稿我们今天再来看一道九年级下册锐角三角函数的一个典型问题,请同学们一定要关注解析思路的分析过程。 如图,已知直角三角形 a、 b c。 中角 i c b 等于九十度 c、 d 是 斜边 a、 b 上的中线点 a 过点 a 作 a e 垂直 cd c e a e 分 别与 c d、 c、 b 相交于点 h e i h 等于两倍的 c h。 一、 求证, i h 乘以 i b 等于 i c 乘以 bc。 那 么当同学们看到这种相乘的表达的时候,首先我们要想到要用到什么, 要用到相似问题,要用到相似问题,那么这个表达式我们给它列成比例式就比较好看了。 i h 乘以 i b, 我 们可以写成 i h 比上 i c, i h 比上 i c 等于 b c 比上 i b。 那我们看一看这四条边分别位于哪两个三角形当中? i h i c。 我 们看一下 i h i c 是 这个直角三角形 i c、 h 的 长直角边和斜边 b c i b b c 和 a b 是 大三角形的长直角边和斜边,所以要想证明它两人 成比例,我只要证明三角形 i c、 h 相似于 b i c 就 可以了。 那么我们看一看三角形 a、 c、 h 和 b i c。 它有哪些相等的角? 这个角是直角,这个角也是直角垂直吗?直角直角,有一个角相等了,那么我们再找一个角相等就可以了。朋友们,那哪个角呢? a、 c、 d 是 等于这个角 d i c 的。 为什么?为什么?因为 c、 d 是 斜边上的中线,我们根据直角三角形斜边上的中线等于斜边的一半,我们可以得到 a、 d 是 等于 c d 的, 那 a、 d 等于 c、 d 就 可以得到角 b i c 等于角 i c h, 然后再配上九十度的角,等于九十度的角,直角等于直角, 那我们就会正数这两个三角形相似,那么这两个三角形呢?乘比例,再把这个比例写成相乘的形式,那这道题就解出来了, 不知道同学们听懂了没有?如果没有听懂,请同学们多多看几遍。那么有了第一问,第二问,让我们求三 a b, 那 么三 a b 这个角正弦值, 那么因为这两个三角形相似,所以角 b 是 等于角 c i h 的, 所以 三 a b 就 等于三 a b 就 等于三 a c i h 相等的角,三角函数是相等的,所以三 a、 b 就 可以转化为求三 a 角 c i h 三 a 角 c h, 那 么三 a 角 c i h 等于什么呢?在小直角形当中,三 a 角 c i h 应该等于对边 c h 比上斜边 a c, 那么我们只要取出来 c h 比上 i c 就 可以了。那么我们还有一个重要的条件没有用在这,那么因为 i h 等于两倍的 c h, i h 等于两倍 c h, 那 么我假设 i h 是 x 的 话,那么 i h 是 r x 啊 r x 这样,那么 c h 是 x, 那么 i h 是 r x, c h 是 x, 我 们很容易用勾股定理得到, i c 应该等于根号下 x 的 平方, 加上 r x 的 平方也等于根号五 x, 那 么就等于 c h。 我 们设的是 x, 那么 a c 就是 根号五 x x 和 x 约分约掉,最后结果应该等于五分之根号五,那么三根角 c i h 是 五分之根号五,那三根 b 也就是 五分之根号五。这道题第一问是证明相似,第二问是利用相等的角 像,还有如下的来解答这个问题,同学们听懂了没有?好,本节课我们讲到这里,同学们再见。
11一起玩转初中数学 02:10查看AI文稿AI文稿
02:10查看AI文稿AI文稿今天我们一起来学习九年级下册三角函数章节,比较喜欢考察的一类三角函数构造函数。如图,在 r、 t 三角形 a、 b、 c 中,角 c 等于九十度, b、 c 等于勾号点, d 是 a、 c 上的一点连接 b、 d, 然后它内 a 等于二分之一, 它的一角 a、 b、 d 等于三分之一,然后求这个 c、 d 的 长。其实咱们知道三角函数必须在直角三角形中应用,那在这里面的话当然也可以用,我发现这个角 b 的 正弦值呢,就是对边比邻边就 d, c 比 a、 c, 随后是可以把这个 a、 c 求出来,然后这边这个角 a、 b、 d 它就没有,在这样三角形中,那我们肯定要构造一些垂直才行,对吧?然后建议这个角 a 和角 b, 它都需要利用正弦,这是我两个角的正弦,之后我都可以用的。上过 d 点垂直于 a, b 垂直于 b, 那 就是 d, e 比上 a, e 是 一比二, d, e 比上 e, b 是 一比三。那在这里的话,我们第一步可以先把 a、 c 取出来,在 r、 t 三角形 ab 四 c 值,它那点 a 应该等于 b, c 比上 a、 c 就 等于根号五比 a、 c 就 等于二分之一,所以说 a、 c 就 等于二根根号。 下面我们再想到的是,如果我能把 a、 d 求出来也行,那这时候还有一个 a、 b、 d 的 正切值三分之一还没有用 d、 e 加都是公共变量,我如果把它设成 x 的 话, 那 a、 b 就是 二 x, 那 e、 b 它就说三来 x 了,那我是说如果把 x 求出来的话,那我 a、 d 也是能求出来。哎,其实我要这样算的话,我发现这个 a、 c 会有平方差二倍,根号五,那这个三角形 它不是满足勾股定律吗? a b, c, 所以 a、 b 就 等于根号下二倍根号五的平方加二根号五的平方就等于五。 a, b 等于五, x 不 就等于一呢? x 等于一, 这是一,这是二。 a、 d 的 根号,那 a、 c 是 二的根号,我们检查一下 c、 d 的 根号,这边就成了 c、 d 的 差。那在运用三角函数的时候,如果没有现场的这样的函数形,一定要自己去构造这样的函数形,才能去用一般的三角形是不满足咱们这个三角函数的关系。有什么问题的在评论区给我留言。
35数学思维杨老师 24:51
24:51 18:49查看AI文稿AI文稿
18:49查看AI文稿AI文稿今天和大家分享速读版九年级下册第七章锐角三角函数的复习课。 这一章学习了锐角三角、锐角三角函数。锐角三角函数包括三种正弦、余弦、正切自主角的三角函数,且直角三角当中利用三边关系、勾股定三角关系、三个三角函数 以及实际运用两角方位角、括对括角、辅角等问题。锐角还在三角函数直角三角形当中。啊 角锐角 a 的 正圆等于它的对边比,斜边与弦等于它的邻边比邻边正确等于它对边比邻边。啊, 三英三十度二分之一啊,扣三十六度也二分之一,三英四十度和扣三十四度都二分之高二、三十六度和扣三英三十度都是二分之高。三 餐厅三十度三分之高三餐厅四十五度一餐厅六十度高三好 解,直角三角形是吧,三边扣股定底三角两锐角互余是吧?边角关系啊三角函数是吧, 三角 a 等于三 a 除以 q 三 a 啊,找出它们之间关系。 直角三角形可解的定义和解法解,直角三角形吃到其中两个元素要至少有一边,就可求出其他三个位置元素。 解法,一边一锐角,先用两个锐角互余,求出另一个锐角支斜边,用正弦或余弦求另两边支直角边,用正弦求另一直角边, 再用正弦或勾股定力,求斜边至两边,先用勾股定力,求第三边用,再用边角关系求锐角。 斜三角形问题可通过添加适当的辅助线转化为解决这三角形问题。啊 锐角函数的正弦和正切角度越大,弦数越大,弦角度越大,函数值越小。 解直角三角应用啊,仰弧角,首先概念考究啊,方位角啊, 解直角三角的应用,抠角过度这概念要抠懂啊。 坡度啊,是坡面的铅直高度与水平宽度的比,要坡度,坡角是坡面与水平方向的夹角。要高度啊,坡面与水平方向夹角叫坡角,坡角弹力二法就等于坡度啊。 坡度通常写成一比 m 形式,由于正截值增大,正截值的增减关系可知,坡度越大,坡脚就越大,坡面就越陡。 好,那像这题是吧。哎,这题没有图,我们把图画出来,角 c 九十度, 角 c 九十度,摊平 a twenty a 等于二,那就是设它为一,它就是二啊, 那它就是根号五,所以 q 三 a 一 比,根号五,所以等于五分之根号五。这个啊, 这个确确定热影长度定热影长度的仪器称为啊。来,我们看一看,立柱 a c 为 a。 冬至时,此时北京正午, 日光入射角约为 a b c 二十六二十六点五度,则立柱根部与 微表的东至线的距离,即 b c 长,求 b c 长,我们看一看,这是什么? d 比邻是正切是吧,所以选择 b 啊, 这是第一个考点,求三角函数值啊。再看这题,怎么求呢?我们注意这点啊,这点你看,都是对角线, 而我们要求这个角的三角值要放在直角三角形,所以我们取这个焦点,假设 d 连接 c d 就 出来一个直角, 两个四五度加减直角。好,那这为根号二,这为三,根号十,所以等于根号十除以根号二,那等于啊, 对不对? 三三减九,根号十吧。 clear 啊,写到了根号二除以根号十,或者怎么得,所以等于根号五分之一,等于五分之根号五,哎, 三对笔斜,是吧?所以啊,好,这一题呢,就用拿玄玄,我们当时还没学,是吧?这个用,拿一个同符所对的圆周角相等,就是这个角,就等于这个角啊,这是十五, 这是九啊,这是十二,是吧?求角 a、 d、 c 的 摊平值,并且这是直角,这直径所求摊平值等于九比十二啊, 六分啊。这题等学过圆,你再回头再来看好下面这一题,这个落到这跟,这是直角 a、 e 是 五倍,根号五,五倍根号五,那这题我们看看,这是直角,这是直角 啊,那它加它九十度,这是九,这是九度一百八,那所以它加它九度,所以它等于它,所以左右两个三角形相似,关系相似。 好用贪心 e、 f、 c 等于三比四,那可以设它为三 x, 则它为四 x, 设它为五 x, 勾股定律,则这也是五 x, 这就是八 x, 八 x 跟它相似,是二比一,所以这点是十 x。 然后再用勾股定律啊,十 x 括号平方加五 x 括号平方,等于五倍,根号五的平方,对吧? 哎,从而求出 x 值,是吧?再求出,这就是六 x, 最后十 x 把周长求出来,就出来了。这题便是 a, b 为十, b, c 为八,这是十。翻过去,这是十,那这是六。要求这个角摊平值,我们刚才已经证明了,这个角就是这个角摊平,那就是四分之三 啊,或者怎么办呢?还可以怎么办呢?你设这为啊,这是六了,那这节就是四, 那设置为 x, 这也为 x, 这就为八。减 x, 利用勾股定力,再求出这个探针值。好,所以本题可能用第二种方法更快一些啊。 第一种方法,呃,第一开始说的就是这方法二更快一些。这种方法可能慢一点啊, 再看又是翻折,求正相似。我刚才正过了啊, 翻过来,这是九十度,它加它九十度,这是直角,这是直角,它加它九十度,所以这个两个三角形相似。这题问题,第二个餐厅三角 d e, d f e, d f e 啊,三一比三设它为 x, 设它为三 x 啊,再为三 x 则为四 x 啊,这个,这是三 x。 再利用相似 这个啊,三 s s 三三点九啊,八二倍根号二 x。 好 利用相似 在求出它要求探听角 e, b, c, e, b c, 这个角就是这个角啊,那它就等于探听角 e、 b、 f, 那 求着就是它跟它之比 啊,算出来,我们用来比比看啊。这个 a b f 比上二 x 等于 等于什么?四 s 比二倍根号 x 啊,那 b f 乘 就能求出来了啊, b f 出来了, f 也能求出来,对吧? i f b x 把大家求出来,带进去就出来了啊。自己做我就不再拖拖写了啊。 最后等于二分之二十七点,这个点呢,你就代入百二乘二分之一加二分之一 减贪心六十度根号三,这是三分之二,三也是根号三分之一,再加二分之二括号的平方,最后把它算出来 啊,这个呢,二分之一一加二分之,根号三加上一,贪心三十度三分之 根号三,对吧?你再化简一下是吧? 同乘以二,二加根号三分之一,再加啊,根号三, 对吧。然后二加根号三分之一加二倍,根号三加三等于四加二倍根号三,二加根号三就等于二, 这个是吧?这个绝对值大于等于零,平方大于等于零,所以它的 a 减一等于零,构成以 b 减二分之一等于零,所以它的 a 等于二分之一。 角 a 就 等于啊,等于一二十一,等于四十五度,扣三根 b 等于二十一啊, 扣三根多少度啊,对吧? 角 b 是 多少度啊? 三十三十度等于 cos 六十度,是吧?所以角 b 是 六十度, 所以角 c 是 七十五度。好, 再看这个是吧?要变式是吧?这就是根号三。餐厅六十度,也是根号三加上一啊,二倍根号三加一, 这个训练根号二,这是啊,二分之高,二分之一 啊,就这也是根号,这个是倒数啊。二分之根号二的负一,则也就是根号二减去二分之一啊,乘以 啊,二分之一加上负一,再加一,这两个没有了,这是二减四分之一,等于,是吧,也有四分之三啊, 这个要求,这个等高 c, a 等于 c, b 扣三 a, c 扣三 a, c 要首先要做高, 好做高扣三音 c, 你 看,这是四扣三音,那这是一,那这就是三,这就是根号十五,这是根号十五,这是 根号二十四,那就是二倍根号六。好要求。三 a b 就 等于根号十五比二倍根号六啊,二倍根号二,比根号五,就等于四分之根号十。好,发现出来, 这个是吧?要把这个角标上,这是四十五度啊,把坐标系方位角啊,这是三十度, 这是六十度,那这也三十度,那这个也三十度,好要求啊。 b m 长要做直角三角形, 对吧?好,我们看一看。这个,这是九十啊,一个半小时,这九十,我们设这个 b c 为 x, 这就为二 s 啊。第一个九十加 x 等于根号三 x, 也就是根号三减一,括号 x 等于九十, x 就 等于四十五乘以根号三加一, 那 b c 长就是四十五。括号根号三加一,那 p c 等于 md 等于 p c 就 同乘以根号三,就等于三加根号三乘以。 好,这个是四十五,这个是四十五, 乘以三加根号三。嗯,这个角有三十度要求啊。 b m 长给它乘以二 乘以二,那就是九十,括号三加括号三,再除以这个速度六十好化解就能得到。啊。这个 啊, c 为底是吧? a c 为三,这个六十度, 那这就是根号三,这就是二倍根号三,这就是四倍根号三,是吧?嗯,这就是 a b 把 a b 再算出来,就等于三的平方加五倍根号三的平方再开方。 九加七十五,等于根号二十四。啊,等于二倍,根号二十一, 对吧?然后这个周长就等于三加五倍,根号三加二倍,根号二十一。啊,这,这一个内容。
7毅力数学 01:10查看AI文稿AI文稿
01:10查看AI文稿AI文稿那么接下来我们来看第二个定义,叫做余弦。那么余弦前提也是在一个什么三角形中,直角三角形中依然是拿出来一个角 a, 比如说这一个角他是不是有一个零边,那么他的余弦值就是这个角的。什么边?零边,跟哪个边的比, 哎,跟斜边的比,那比如说来告诉我,哎,角 a 的 余弦应该是哪条线段比哪条线段 ac 比上 ab, 那 么对于鱼弦,它有自己的符号是 cos, 都是小写的,那 cos 读作 cosine, 那 所以 cosine 角 a 我 们就可以写作来告诉我哪两条线段的比 a c 比上 ab, 那 依然是邻边比斜边,分母依然是什么边,斜边那斜边依然比直角边干嘛大,所以 cosine 鱼弦值也一定是什么一的 i, cosine 值也一定是小于一的,依然是什么零 i 大 于零的,明白了吧?这就是正弦和余弦,那我们在记的时候怎么去记呢?你就记住,不管是正弦也好还是余弦也好,你会发现它的分母都是谁, 这不都是跟斜边去比的,对不对?都是跟斜边去比的,一个是对着的,哎,对边比斜边就是正弦值,邻边比斜边,那就是余弦值。
 20:25查看AI文稿AI文稿
20:25查看AI文稿AI文稿同学们好,我是来自南京市洪山初级中学的吴涛老师。今天我们学习的课题是七点五,解直角三角形。一 经过前几节课的学习,我们学习了锐角的正弦、余弦、正切的概念,会求特殊角的三角函数值,由三角函数值求锐角。 今天我们一起来利用所学知识,进一步研究解直角三角形这一问题。首先我们来学习一下,什么叫做解直角三角形呢? 一般的直角三角形中,除直角外共有五个元素,即三条边和两个锐角。 由直角三角形中的已知元素求出其余各元素的过程,叫做解直角三角形。 那么在直角三角形中,除直角外的五个元素之间有怎样的关系呢?请同学们思考一下这个问题。 除直角外,还有两个锐角,两条直角边和一条斜边。从边上看,根据勾股定律,有 a 方加 b 方等于 c 方。 从角上看,根据直角三角形,两个锐角互余有角, a 加角 b 等于九十度。 从边角之间的关系上来看,根据三角函数的定义,有 sine a 等于 c 分 之 a, tangent a 等于 b 分 之 a。 sine b 等于 c 分 之 a b。 cosine b 等于 c 分 之 a, tangent b 等于 a 分 之 b。 那么首先就要请同学们思考一下,知道这个五个元素中的几个就可以求其余元素呢? 我们不妨从一个元素出发,也就是如果已知一个锐角或一条边,可以求其余元素吗?请同学们尝试着做做看。 相信同学们都有了自己的思考,我们一起来分析一下。如果仅仅知道一个锐角,此时缺少边的条件是无法求出各边长度的, 根据动画展示,我们可以更加直观的感受到直角三角形的大小,不能确定,自然不可求解。那如果只知道一边呢? 比如已知 b、 c 边的长度,此时缺少角的条件,无法求出其余各边和两个锐角的大小,此时直角三角形仍然不可解。 已知一个元素我们已经讨论完了,发现不行,那么如果已知两个元素可不可以呢?我们再尝试着做做看。 让我们一起来分析一下。已知两个元素就会出现多种情况,我们不妨对这个问题进行分类讨论。分为已知两角、 已知两边和已知一角一边。如果已知两角,我们发现就等价于已知一个锐角的大小。这个问题我们已经讨论过了,发现不行。 如果已知两边,需要我们进一步分类,分为已知两直角边和已知一直角边一斜边。我们先来分析一下已知两直角边的情况。 利用勾股定力,首先我们可以求解出斜边 c 的 长度, c 等于根号下 a 方加 b 方, 再利用正切可以求得角 a 和角 b 的 度数,即 tangent a 等于 b 分 之 a 分 之 b。 类似的,如果已知一直角边一斜边,我们可以根据勾股定律求得另一条直角边长 b 等于根号下 c 方减 a 方,再利用角 a 的 正弦值和角 b 的 余弦值求得角 a 角 b 的 度数。 sign a 等于 c, 分 之 a 和 sign b 等于 c 分 之 a。 我 们再来一起分析一下已知一角一边的情况。已知一角一边可以分为已知一角一直角边和一角一斜边两种情况, 其中已知一角一直角边。根据直角三角形中锐角与直角边之间的位置关系,又可以分为下面两种情况,我们来具体研究看看。 我们先来看第一种情况,如果已知角 b 的 大小和边 bc 的 长度,利用直角三角形两个锐角互余,我们可以求得角 a 的 度数。 记,角 a 等于九十度,减角 b。 已知角 b 的 零值角边和角 b 的 大小,利用三角函数的定义求出 b c 长度记 c 等于 cosine b 等于 a 乘以 tangent b。 类似的,如果已知角 b 和角 b 的 对边,我们也可以求出角 a 和斜边 c 以及另一条直角边 a 的 长度,即角 a 等于九十度,减角 b, c 等于 sine b 分 之 b。 最后,我们来看已知一角一斜边的情况。如果已知角 b 的 度数和斜边 c, 同样也可以利用直角三角形的两个锐角互余求得角 a 的 度数, 再利用角 b 的 正弦和余弦值求得 a b 的 长度,即 a 等于 c 乘以 cosine b, b 等于 c 乘以 sine b。 综上,如果一个直角三角形可解,可以分为以上四种情况。这四种情况其实就是判断两直角三角形全等的条件。 也就是说,一个直角三角形可由五个元素中的两个,其中至少有一个是边来唯一确定,此时直角三角形是可解的。 下面我们一起来看几个例题。例一,在直角三角形 a、 b、 c 中,角 c 等于九十度。根据下列条件解,直角三角形 一角 a 等于三十度, a 等于五二, a 等于一百零四, b 等于二十点四九、结果,保留小数点后两位 请同学们思考一下这个问题, 我们一起来分析一下。例一的第一小题,我们可以看到本道题是没有配图的,为了方便我们理解题意,我们先可以根据题意画出草图。 由题可知,角 a 等于三十度, a 等于五,这是已知一角和一直角边的情况。 通过前面的分析,我们知道此时直角三角形是可解的,那么要解这个直角三角形,就要求出角 b 的 度数和边 bc 的 长度。 利用直角三角形两个锐角互余,我们很容易得到角 b 的 度数。 再通过观察条件,我们可以发现已知角 a 的 对边要求角 a 的 零值,角边可以利用正切进行求解。 解,角 b 等于九十度减,角 a 等于九十度减三十度等于六十度。 因为 tangent a 等于 b 分 之 a, 所以 b 等于 tangent a 分 之 a 等于三分之根号三分之五等于五倍根号三。 又已知角 a 的 对边要求斜边,我们可以利用正弦进行求解, 即因为 sin a 等于 c 分 之 a, 所以 c 等于 sin a 分 之 a 等于二分之一,分之五等于十。 那么请同学们再思考看看你还有哪些方法可以求出斜边 c 的 长度呢? 相信同学们一定想到了很多种方法,那么老师这里呈现一种方法。 通过前面的求解,我们知道了两直角边的长度,那么我们就可以利用勾股定律求出斜边 c 的 长度。 记在直角三角形 a、 b、 c 中,根据勾股定律得 c 等于根号下 a 方加 b 方等于根号下五的平方加五倍,根号三的平方等于十。 让我们回顾一下本小题。首先我们需要根据题意画出草图帮助我们理解。 要解直角三角形,需要我们综合利用直角三角形中各元素之间的关系。在利用三角函数进行求解时,要关注锐角与直角边之间的位置关系,选择正确的函数关系来列式, 我们再来分析一下第二小问。根据上题的经验,我们知道先要画出草图标记数据, 因为此时已知两只角边长,我们可以先利用勾股定律求解出斜边 c 的 长度, 即结在直角三角形 a、 b、 c 中。根据勾股定律得 c 等于根号下 a 方加 b 方等于根号下一百零四的平方加二十点四九的平方。 用计算器计算得 c 约等于一百零六点零零。 然后因为已知角 a 的 对边和零值,角边可以求得角 a 的 三角函数值,通过三角函数值求出角 a 的 度数。 这里可能会有同学想到用斜边来参与求解角 a 的 度数,那么我们还要注意结果的精度,尽可能用原始数据进行求解。记 尤体一只 tangent, a 等于 b 分 之 a 等于二十点四九分之一百零四。用计算器计算得角 a 约等于七十八点八五度, 所以角 b 等于九十度减七十八点八五度等于十一点一五度。 下面我们再来看例二这道题。如图,圆 o 的 半径为十,如何求圆 o 的 内接正五边形 a、 b、 c、 d、 e 的 边长呢?结果保留一位小数, 请同学们思考一下本道题, 我们一起来分析一下。三角形 a、 o、 a、 b 是 等腰三角形,我们可以通过做等腰三角形的高,将等腰三角形转化为直角三角形,借助直角三角形来解决问题, 我们一起来看解。因为五边形 abcd 是 正五边形, 所以角 a、 o、 b 等于五分之三百六十度,等于七十二度。 过点 o 做 o, h 垂直于 ab, 垂足为 h。 在 直角三角形 a、 h、 o 中,因为角 a、 h、 o 等于九十度,角 a、 o、 h 等于二分之一角 a、 o、 b 等于三十六度, o, a 等于十。此时我们可以发现,直角三角形 o、 a、 h 是 可解的, 所以 a、 h 等于 o, a 乘以 sin 三十六度,所以正五边形 a、 b、 c、 d、 e 的 边长 a、 b 等于两倍的 h 等于二乘以 十乘以 sin 三十六度,约等于十一点八。 最后,请大家用五分钟完成本道题,作为我们今天课堂内容的小结。 好,我们一起来看一下这道题。 第一小题,已知角 a, 则角 b 等于九十度减角 a。 因为已知的是直角边, a 要求另一条直角边和斜边,所以要关注锐角与直角边之间的位置关系,选择正确的函数关系来列式, 分别求出斜边和另一条直角边长,所以得 角 b 等于九十度减角 a。 因为 tangent a 等于 b 分 之 a, 所以 b 等于 tangent a 分 之 a。 因为 sine a 等于 c 分 之 a, 所以 c 等于 sine a 分 之 a。 第二小题的思路与第一小题大致相同,不同的是三角函数的选择, 因为已知的是一个锐角和一斜边,所以只能选择使用正弦或余弦进行计算,分别求出两只角边 解。角 b 等于九十度减角 a。 因为 sign a 等于 c 分 之 a, 所以 a 等于 c 乘以 sign a。 因为 cosine a 等于 c 分 之 b, 所以 b 等于 c 乘以 cosine a。 第三小题是已知两直角边,先根据勾股定律求出斜边。记在直角三角形 a、 b, c 中,根据勾股定律得 c 等于根号下 a 方加 b 方, 这时三边都已知,可以根据三角函数值求出锐角的度数。这里我们只展现了其中的一种解法。 通过这三小问,我们就对解直角三角形做了比较全面的总结。 今天的课就上到这里,谢谢观看,同学们再见!
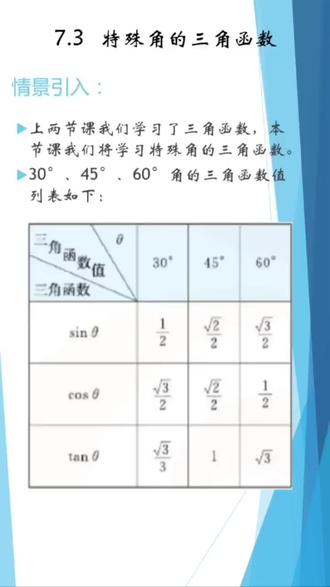 03:29查看AI文稿AI文稿
03:29查看AI文稿AI文稿同学们,大家好,本节课我们将学习第七章第三节特殊角的三角函数。 我们看上两节课,我们学习了三角函数,本节课我们将学习一些特殊角的三角函数。 我们看三十度、四十五度和六十度的角的函数值是多少呢?我们看三英三十度等于二分之一。三英四十度四十五度等于二分之根号二。三英六十度等于二分之根号三。 考三英三十度等于二分之根号三。考三英四十五度等于二分之根号二。考三英六十度等于二分之一。 tan 的 三十度等于三分之根号三, tan 的 四十五度等于一。 tan 的 六十度等于根号三。 哎,我们看几道例题,例题一说,求下列各式的值。第一个,二倍的三英三十度减去考三英四十五度二、三英六十度乘以考三英六十度 三,它的三十度加上考三英三十度。我们看一说二倍的三英三十度减去考三英四十五度等于二,乘以二分之一,减去二分之根号二,等于二分之二减根号二。 看考三英六十度乘以考三英六十等于二分之根号三。乘以二分之一等于四分之根号三。它呢,三十度大加上考三英三十度等于三分之根号三,加上二分之根号三,就等于六分之五倍根号三。 再看例题二,求下列等式中的锐角阿尔法一、二倍的三 a 阿尔法等于减根号二等于零。二根号三,它的阿尔法减一等于零。 看一,有已知可以得到 sine alpha 就 等于二分之根号二,所以 alpha 就 等于四十五度。第二,有已知可以知道 tan 的 alpha 等于三分之根号三,所以 alpha 等于三十度。 通过这节课的学习,同学们要掌握课本第一百零五页特殊角的三角函数值。看三角函数值。三英阿尔法 三英三十度等于二分之一三英四十五度,它等于二分之根号二。三英六十度等于二分之根号三。 看考三英三十度等于二分之根号三。考三英四十五度等于二分之根号二。考三英六十度等于 三分之根号三。他宁四十五度等于一,他宁的六十度等于根号三。通过今天的学习,同学们有什么收获?会正确的运用所学的知识吗? 好,今天的课就到这里布置一下课后作业,课后完成课本第一百零六页习题七点三的第一题和第二题。好,同学们再见!
猜你喜欢
- 350信承



