八上数学画图怎么画45度角
粉丝4.4万获赞25.5万
相关视频
 08:20
08:20 05:47查看AI文稿AI文稿
05:47查看AI文稿AI文稿大家好,我是小老弟,爱发明圆管,四十五度角的洁面怎么画?今天我就教大家,这是直径一百毫米的圆管, 画一个圆, 找出圆的垂直线, 将圆分成十二等份, 画出垂直线, 找出鞋边长度的一半 画圆, 然后量出圆管直径的一半, 找出圆的垂直线, 将元分成十二等份, 将他们连接中心点, 这样就画好了。现在开始标上字母, 这样就标好了,现在开始下一步。 横的就画好了,现在开始画垂直线, 现在找出香蕉点, 加上数字, 现在用光滑的曲线把这些数字连起来, 我加深一点颜色, 这样就画好了。学会的老铁给个关注,谢谢。
73小老弟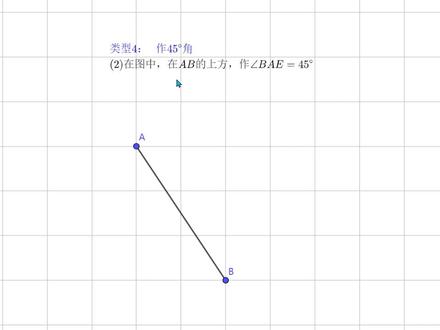 08:16查看AI文稿AI文稿
08:16查看AI文稿AI文稿第二道例题还是做四十五度角,在图中,那要求在 ab 的上方做 bae, 那等于四十五度。想法还是一样啊,怎么找这个 使它成为正方形的对角线,或者说等腰直角三角形,对吧?等腰直角三角形的斜边。 嗯,其实呢,数学这个东西呢,都是要有敏感性,对吧?通过大量的训练呢,得到敏感性, 然后呢,也有人的话天生就有敏感性啊。其实呢,还有一句话叫什么大胆假设,小心求证,是吧?我们先看一看啊,就是这个四十五度,那大概方向应该在哪里?是不是应该在这个方向,对吧?是不是应该在这个方向?为什么呢?看时间,看这个角,这个角他肯定是小 于四十五度的,对吧?因为如果是等于四十五度的话呢,应该是这样的一个对角,正方形吗?是吧?这样一个对角应该是四十五度,那么这个角肯定小于四十五度,那么这个角肯定大于四十五度。嘛意思要得出一个四十五度呢?那画一条线的话,是不是应该在这个方向, 对吧?应该在这个方向。那如果在这个方向,我们先大胆假设的话,在这个方向的话,有什么特殊的点能够让我们给他连起来?你想要从这里找,这里 没有什么特殊点,对吧?从那里点呀?为什么?那这里呢?也没什么特殊点,那这里有没有什么特殊点呢?那你看大概在这个方向,这有什么特殊点?这里是不是有一个什么有一个这个小正方形,他的 什么对角线的焦点啊?是吧?那行,我们看连接对角线的焦点,是不是就是我们想要的,是吧?这只叫 是吧?大灯假设吗?啊?我们先利用就是说这个敏感性啊,是吧?或者叫直觉,我们先试一下。 呃,一会的话我再介绍一种,我们比如说如果想用确定用算数的办法来算出来他那应该是怎么弄?我们先看直觉,那是不是可能是这个点,对吧?我们先把这个点弄出来,比如说我们先把这个对角的点啊,连线 对角点点出来,然后连线,行,这样呢我们就得到什么呢?得到了这个焦点,对吧?得到了这个焦点,我们连接一下,我们连接一下,现在一 连接一下线段 a e 啊,看一下这个线段 a e, 然后呢如果说再连接线段什么 b e, 是吧?这个是不是 是一个等加直角三角形呢?那我们看看他是不是一个等加直角三角形呢?啊?其实的话呢,如果说我们从一点往这里做一个垂足 啊,往这里做一个垂足,那这里是不是形成了一个小的直角三角形啊?对吧?然后一点的话呢,往这里做一个垂足,那这里呢也是形成了个小的直角三角形,对吧?也就是说这 通过一点做一条垂线啊,上半部分呢就是给他的,下一部分呢就是给他的,是不是这两个三角形刚好是什么? 刚好是一个完全相等的一个三角形啊?你看他的宽都是二分之一,对吧?他们的高是不是都是二有二分之一,对吧?这里也是他的这个宽是 二分之一,高呢?是二又二分之一,对吧?然后呢九十度,九十度是不是完全相同三角形?因此的什么呀?因此的话,这个小角加这边的若做了一条垂线啊,那我们可以看一下啊,假如说这里通过他做了一条垂线, 嗯,这有点乱了,假如说通过他做了一条垂线的话,要稍微有这样一条线啊, 这些不直,是吧?看着可别扭, 是吧?如果是这样的话,看这个三角形 a h e 和这个三角形,比如 b e, 嗯,随便一个点,比如 m, 是吧?那是不是一个弯线等三角形,因此的话,这个小角加这个角九十度,所以的话这个就是九十度,对吧?那这个是九十度,所以的话呢, 完相等三角形吧,所以 b e 呢,也是等于 a e 的,那么就说明这个三角形 a e b 是不是就是一个什么等腰直角三角形啊?是吧?因此呢,我们可以知道,行,这个角 b a e 就是四十五度,是吧?这是什么?这是通过这个一个直觉的方式,对吧?然后得到的。 那我们在想的话呢,那能不能通过就是刚才说的能不能通过这个计算的方式呢?其实也是可以的,其实呢,我们在第一问里边是说过的,是吧?然后呢,我们看 看看啊,我把这个写在这里了,我们也是观察一下, a b a b 的话,是不是和这边刚好组成个直角三角形,因此的话呢, a b 的平方是不是等于什么?这三吗?三的平方加二的平方,是吧? 加起来就等于十三,对吧?那么如果说他是一条等腰直角三角形的斜边,那我们假设等腰直角形的 直角边,比如说是 ac 啊,这里是 ae 吗?假如说是这个 ac 的话,那么是不是就意味着 ab 的平方就等于二倍的 ac 的平方,对吧?那么 ac 的平方呢?就等于二分之十三, 那么 a c 的平方等于二十四三,因为我们想什么呢?就是我们想找它的一个,它呢是这个呃的 直角边,同时呢他呢又是我们要找的另外一个,就是利用正,利用什么?利用正方形的边组成的直角三角形的什么?他的一个斜边, 所以的话,那,那他是斜边,那他得二分之十三,那就意味着什么?是不是意味着另外两条直角边他就不可能是完整的一组成的了呀?就不是一的倍数了,对吧? 那不是一的倍数了,那是不是我们还可以得到?我们之前晒低利的时候我们就讲过,就是说除了可以得到一之外,还可以得到二分之一,那是不是可以想到他是可以等于二分之一的, 那我们把它上下都乘以二,所以二分之三等于四分之二十六,又可以拆分成四分之二十五加四分之一,也就是可以拆分成二分之五的平方加二分之一的平方,也就是意味着这个这 这个边,这个 ae 这个边的话呢,它是由什么?是一个边长是二分之一,另外一个边长是二分之五的直角三角形组成的,因此的话呢,也可以得到这个点,对不对?也就是说,哎,我们应该找一二 二,有二分之一就二分之五,然后呢这边呢?是找二分之一,是不是想的是,哎,对,他应该是这个点, 这就是什么?就是说既可以通过这个直觉,我们,哎,往这边应该是走,大概往这瞄一下,是吧?因,可这有个特殊点,是吧?直觉同时呢,这不大胆假设,然后再去小心求证啊。 另外一方面就是呢,我们是不是可以可以通过这种方式理论的方式来算出来算的啊?我们应该找一个边长是二分之五,然后这边边长是二分之一的这样一个直角三角形,是吧?然后他的一个斜角边, 对吧?这就叫构成的啊,构成法,至于大家喜欢用哪种办法是吧?那就用哪种办法, 同时呢,其实呢这种就是基础题,基础题呢是告诉我们呢,就是我们要把它形成一种直觉,就是以后我们再看这类的就直接找他是吧?而不是说再去这个不断的去求证了, 因为到时候等综合的时候是要把这些基础的话呢,是把它综合起来的啊,那个时候呢,你再去这个去求证啊,啊,去论证啊,那时候这个花的时间又太多了,真的在考试中的话,往往是没有这么多的时间的, 所以我们在下面就应该先把这些模型的话呢,把它内化吸收好。
50松塔聊数学














