椭圆零定义
粉丝43获赞120
相关视频
 15:14查看AI文稿AI文稿
15:14查看AI文稿AI文稿椭圆是许多高中生的梦魇,因其题型多变、推倒复杂而成为高中数学的一大难点。教科书上椭圆的第一定义是这样写的,到两定点,距离之和为定值的点,它的轨迹视为椭圆。 然而,距离公式中有根号的存在,距离和并不是一个好处理的对象。从定义推导出解析式要一页纸还很易,错也不好理解。可是大家有没有想过,椭圆其实首先可以是一个圆呢? 名字里有圆,长得像圆,方程也和圆很像。有没有可能从圆出发来理解和定义椭圆呢?毕竟圆是一种更和蔼的数学对象,理解起来更简单,推倒也更方便。 在这期视频中,我将向大家展示一种从圆出发来理解和定义椭圆的方法,然后我还会带大家了解如何用这一方法来解决具体问题。 对于一个横截距为 a, 纵截距为 b 的椭圆,观察他的方程可以发现,他比单位圆只差了分母上的 a 的平方和 b 平方。 怎么从一个圆得到它呢?其实很简单,把单位圆在 x 轴方向拉伸 a 倍,在 y 轴方向拉伸 b 倍,我们就能得到想要的椭圆了。 这里我可以给一个简要证明,对单位源上的任意点 x y 设经过拉伸变换之后得到的点为 x 撇 y 撇。那么我们就有 x 撇等于 a, x, y 撇等于 b, y 稍稍变形之后就是 a 分之 x 撇等于 x, b 分之 y 撇等于 y。 我们再把这个关系是带回单位元,满足的方程就有 a 分之 x 撇的平方加上 b 分之 y 撇的平方等于一。聪明的同学肯定已经看出来了,这就是直角坐标上椭圆的方程,只不过换了变量名而已。 对曲线的方程来说,变量名是无关紧要的。我们可以把 x 撇和 y 撇替换回 x y, 这样我们就完全的得到了椭圆的方程,这就是每个椭圆内隐藏的圆。 因为我们出发于更基本的圆,试图用更简单的圆来定义椭圆,因此我称之为椭圆的第零定义。与教科书上的第一和第二定义相对。这一变换,我称之为椭圆的单位圆变换,因为他把高矮胖瘦各不相同的 椭圆统一变换成了整齐划一的单位圆。一般来说,圆比椭圆更好分析,也更容易计算。因此,如果能把一个椭圆问题变换到圆上面来求解问题往往就会简单许多。 下面我们来讨论一些基本量的变换关系,例如面积、斜率、长度这些基本量在变换前后,他们的关系是怎么样的。得到了变换关系,我们就能在单位源上把问题求解出来,然后在硬社会椭圆,从而解决对应的椭圆问题。 首先,我们先来考虑面积的变换关系,再从圆到椭圆的拉伸变换下,面积会变为原来的 a b 倍。为什么呢?我们首先来考虑最简单的三角形。 对任意一个三角形,我们可以将其分割为两个底边平行于 x 轴的小三角形。在拉伸变换下,一个小三角形的底边平行于 x 轴,底边就变成了原来的 a 倍。高垂直于 x 轴,平行于 y 轴,就变成了原来的 b 倍。 根据三角形面积公式, s 等于二分之一,底乘以高。每个小三角形的面积都变成了原来的 a 乘以 b 倍 大,三角形面积因此也做了同样的变换。那对更一般的图形呢?我们不能用三角形公式计算面积了, 但我们可以追随先前的脚步,换一种思路来处理。我们可以在图形上画很多细密的网格,把图形分成很多小的部分,每个部分都充分小,以至于几乎不会和边界相交,从而可以当做矩形来 来处理。在拉伸变换下,每个小矩形的长都变成了原来的 a 倍,宽则变成了原来的 b 倍,面积就变成了原来的 a 乘以 b 倍。而整个图形是由无数个小矩形所组成的,因此整个图形的总面积也乘以了 a、 b 倍。 事实上,思考到了这里,我们已经可以给出一个严谨的微积分证明了,有兴趣的同学可以暂停观看。你会发现,有了前面的思考作为铺垫,做这样的证明就变得容易多了。 这有什么用呢?下面我给大家举两个简单的例子。首先,我们已经知道单位尾的面积是 pa 乘以 are 的平方就等于 pa, 于是我们立马可以得到通过拉伸变换得到的椭圆面积, 就会是派乘以 a b。 什么?你觉得这题太简单了?那我们不妨来看一道更有挑战性的题目。第二个例子是一道经典的高中椭圆题。一个椭圆长半轴在 x 轴上, 横轴上有一点 p 过 p 的直线,交椭圆于 a、 b 两点。请问三角形 o、 a、 b 的面积什么时候最大?最大值又是多少? 我试过了,用传统的直取连力方法,要花掉好几页纸推倒颇为复杂,但是在这里我们不妨试一下单位元变换。 把 x 轴方向缩小 a 倍, y 轴方向缩小 b 倍,我们就由椭圆得到了单位圆,原来的三角形也被变换成了弦心三角形。因为变换下,所有图形的面积都均等的变换, 因此现在面积最大的时候就是原来面积最大的时候。注意到直径 o a 和 o b 很等于一,我们可以利用这一点来解决问题。过 o 向 a b 做垂线,垂直为 h, 那么三角形 o a b 就被分成了上下两个部分, oab 的面积就等于三角形 oah 的面积,加上三角形 obh 的面积,也就是 obh 面积的两倍。因此,想要最大化 oab 的面积,只要最大化三角形 obh 的面积就可以了。问题被进一步转化, o b、 h 是一个斜边长为一的直角三角形,而斜边为定长的直角三角形中又属等腰直角三角形,它的面积最大,不信你看。我们把斜边作为底,不难发现,锐角为四十五度, 是斜边上的高最长,而底边的长度又是固定的,因此此时的小直角三角形面积最大。 最后的问题是,我们的问题中还有直线 a b 过 p 点这个约束, o b h 和 o a h 能取到等腰直角三角形吗? 这是个好问题。因为三角形是歪着的,所以直接分析并不是很方便,我们不妨换一种思路,考虑 o h 与 o p 之间的长度关系。 o h 是三角形的直角边,如果它太短,那就取不到等腰直角三角形,而不难发现, o h 是小于 o p 的。因此, o b h 能不能取到想要的形状,其实取决于 o p 的长度,如果 o p 很短, o h 最长的时候也不够长,那就 无法取到等腰直角三角形,也就无法取到面积最大的形状。相反,如果 op 足够长,那 oh 就可以在直线斜率合适的时候取到合适的长度,构成我们想要的等腰直角三角形。 好了,分析到这里,我们已经可以写结论了,如果 o p 很短,短于根号二分之一,那么直线 a b 垂直 x 轴时面积最大,因为此时图形的形状是最接近等腰直角三角形的 g o p 的长度为小 p, 那么根据勾股定理, b p 的长度就是根号下一减去 p 的平方,此时三角形的最大面积就是 p, 乘以根号下一减去 p 方 映射会椭圆,就是 a b 乘以 p, 再乘以根号下一减去 p 的平方。如果 o p 的长度足够长,长于根号二分之一的话,那 那么当直线角度合适的时候,我们就能取到理想的等腰直角三角形。此时 o a、 b 也是一个等腰直角三角形,很容易就能算出它的面积是二分之一。如果映射回椭圆,椭圆中 o a、 b 的最大面积就是二分之一 a b。 至此,本题求解完毕。 好吧,我得承认,这道题用几何方法还是有一点复杂,但这一定程度上是由于题目本身的难度所导致的。而且更重要的是,分类讨论的几何图像很清晰很好的解释了为什么会有两种情况,这是代数推导所做不到的。 好让我们回到主线刚刚讲完的面积,接下来让我们来看一看斜率的变换规律。 假设我们有一条直线在横轴距离 detail x 内,纵轴距离上升的 detail y, 即斜 为 k, 那么 k 就等于 delta y。 除以 delta x, 在拉伸变换下斜率 k 会怎么变化呢?我们注意到,在变换下,横向距离被拉伸了 a 倍,变为了 a delta x, 而纵向距离被拉伸的 b 倍就变为了 b delta y, 即变换后的斜率为 k 撇,那么新的斜率 k 撇就等于 a 得到 x 分之 b 得到 y, 提取出 detail x 分之 detail y, 这就是原来的斜率。因此新的斜率就等于 a 分之 b 乘以原来的斜率 k。 这意味着在单位元变换或者逆变换下,所有直线的斜率都会同比例的变化。 好,讲完了理论,接下来我们来看一道经典例题。对一个椭圆过椭圆上的一点梯做一条切线, 即为 l。 一连接圆点和切点,就又有了一条直线,即为 l。 二、求证两条直线斜率的乘积是一个固定的长数,负的 a 平方,分之 b 平方。 用传统方法做,需要把直线和曲线的方程连力展开,然后根据判别式等于零,再推出直线的斜率,推到相当复杂, 但是在椭圆的地灵定义下,这却是一道可以被秒杀的题目。把椭圆变换回单位圆, 椭圆的切线问题就变成了圆的切线问题。显然,圆心到切点的连线与切线是垂直的,因此两条直线斜率现在的成绩就是负一。然后我们把结果变换回椭圆。一条直线变换时,斜率要乘以 a 分之 b, 那么两条直线斜率的 乘积就需要乘以 a 方,分之 b 方。因此我们最后得到的结果就是负的 a 平方分之 b 平方正 b。 在这里我们还可以证明一个有用的推论, 即切点的坐标为 x 零 y 零。那么我们就可以证明切线的解析式是, a 平方分之 x 零 x 加上 b 平方分之 y 零 y 等于一。有兴趣的同学可以自己证明一下。我会把参考答案放在视频的最后。 然而,在解决长度问题上,单位源变换却不怎么奏效。同样考虑一段斜例为 k 的线段, 假设横向距离为 dette x, 纵向距离为 dette y, 那么线段的长度 l 就等于根号下 dette x 的平方加上 dette y 的平方。因为 dette y 等于 k, dette x, 所以代入展开之后,可以把 delete x 的平方这个公因子提取出来,整个长度的关系是就变成了根号下 k 的平方,加一再乘以 delete x。 拉伸变换之后,横向距离变为了原来的 a 倍,纵向距离变为了原来的 b 倍,那么新的长度 l 撇就等于根号下 a, d, t, x 的平方加上 b 的 t, y 的平方, 同样带入 deta y 等于 k。 detax 展开再提取公因子, deta x, j 的长度就变成了根号下 a 的平方,加上 b 的平方,乘以 k 的平方,最后再乘以 detax。 你发现了吗?如果把变换前后的长度做比较,二九的比值会是一个与 k 有关的数值,而且也无法通过推导消去 k。 这意味着椭圆框架 中不同斜率的长度会以不同的比率进行变换,这个比率是和斜率有关的。变换之后得到的形式往往还是很复杂,问题不能得到简化。因此,有关线段长度和角度的问题,我不推荐用单位元变换或者说椭圆的地灵定义来处理。 为了说明这一点,我们再举一个例子,椭圆的周长。椭圆的面积公式是相当简单的,甚至可以说是原面积公式的简单推广。但是椭圆的周长计算却相当复杂。椭圆的周长可以由许多贴合边界的短线段来近似。 当线段足够多,分的足够细的时候,所有短线段的长度和就可以看作对椭圆周长的很好的近似。而我们刚刚讨论过,斜率不统一的线段长度是一个不好处 处理的量。数学家们前赴后继的研究了几百年,也没有能为椭圆周长找到一个初等的表达式。 事实上,椭圆的周长是无法用出等函数表达的,只能写成积分的形式。最后,数学家们不得不妥协,专门为他定义了椭圆积分,这还是一个重要的非出等函数。 好让我们总结一下。椭圆的第零定义对很多高中题目都很有效,我自己就使用过很多次,都没有被扣过分。 不过我还是更多的建议在填空和选择中使用它。如果想在大气中使用的话,需要把椭圆到圆的变换过程说清楚。除此之外,他对理解椭圆的基本性质也是很有帮助的。唯一的缺点在于他在长度问题和双曲线问题 上不太好用。最后,在视频结束之前,我还想提一句变换在数学中的作用。除了将单位元变换应用于椭圆,你还可以在数学的许多其他领域看到类似的变换。例如矩阵的对角化, 就是通过坐标系变换让线性变换只作用在坐标轴上,从而简化对他的计算和分析。又例如,在一些微分方程中,我们可以把需要求解的定义域映射成更规则的区域,从而简化后续的求解, 把复杂的变成简单的,把陌生的变成熟悉的,这是数学中基本的思想,也是数学永恒的追求。好了,这期视频就到这里,我们下期见。
4.5万科普宇宙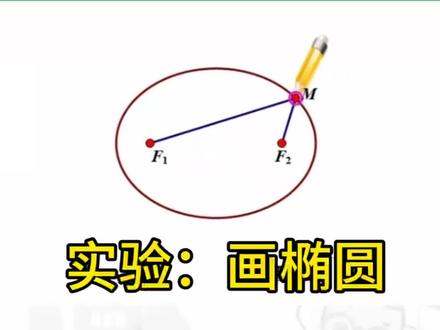 01:04查看AI文稿AI文稿
01:04查看AI文稿AI文稿公元一六零九年,德国天文学家开普勒就发现,许多天体的运行轨道都是椭圆。椭圆在我们的日常生活中也很常见,比如一些摆件、饰品、钟表,一些汽车标志、广告标志,也喜欢设计成椭圆形的。那么到底怎样才能准确画出椭圆呢?不妨和我一起来做试验。 取一条定长的细绳,把它的两端都固定在纸板的同一点处,套上笔,拉紧绳子,移动笔尖,这时笔尖画出来轨迹是什么?曲线 是一个圆。如果我把绳子的两端拉开一段距离,固定在纸板的不同的两个点处,仿照刚才的画法,套上笔,拉紧绳子,移动笔尖,这时笔尖画出来的轨迹又是什么?曲线 好画完了,是一个椭圆。试验中绳子两端固定的两点,以及笔尖基围 点 f 一、 f 二及减 m。 请思考,在此过程中,哪些量是变化的,哪些量是不变的?你能不能以归纳一下椭圆的定义?
100孜孜不倦百花争妍
猜你喜欢
最新视频
- 1210小涵













