一元一次解方程式的解法和技巧书
粉丝5.0万获赞4.8万
相关视频
 04:18查看AI文稿AI文稿
04:18查看AI文稿AI文稿方程你早见过了,就是含有未知数的等式,啥意思呢?首先方程含有未知数,比如 xyz。 其次,方程还得是等式,所以得有等号。考考你这几个是不是方程呢? 一个一个看吧, s 加三有位置数,没等号不是方程。五减七等于负。二有等号,没有位置数也不是。第三个有位置数,有等号是方程。第四个有位置数,也有等号,还是方程。所以说是方程必须满足俩条件,一是要有位置数,二是要有等号。 在古代,人们把位置数叫做圆,于是有几位置数就有几个圆。比如第一个方程有俩位置数, x 和 y, 就是二元方程啦。第二个方程只有一个位置数,那就是一元方程呗。除了圆以外,方程还有一个重要的概念,次数。 比如这个方程,第一项 x 的次数是二, y 的次数是一,加在一起就是三了。 第二项是一次,第三项是二次,其中最高次是三次,那么这个方程就是三次方程。发现没找方程次数和找多项式的次数是一样的,都是找最高次。那类似的。看第二个方程,对于两项都是一次,所以就是一次方程啦。 刚才我讲过方程的圆和次数,现在把圆和次数合起来,给方程们起个全名吧。回想一下,第一个方程是二元方程,也是三次方程,所以是二元三次方程。 第二个是一元方程,也是一次方程,所以叫一元一次方程。注意了,一元一次方程是最基本的方程,先概括一下他的特点吧,一元说明只有一个问 数,一次说明方程最高四项的次数是一,也就是说 x 最多只能是一次。既然说到次数,那就必须是整式。也就是说,分母中不能含有未知数,但分子中可以有。比如 x 分之三等于四,就不是一元一次方程,但三分之 x 等于四,就是个一元一次方程。 总的来说,一元一次方程有三要求,未知数只有一个,次数必须是一,且分母中没有未知数。讲完了一元一次方程,来实战一下吧。下面这几个式子是不是一元一次方程呢? 第一个连等号都没有,压根不是方程,更甭说一元一次方程了。第二个有等号,但有两位置数,所以是二元的,不是一元一次。第三个只有一个位置数,但外跑到了分母上,不是整事,所以也不对。 第四个虽然有分母,但分母是五和三,不是未知数。未知数在哪呢?一个在分子中没问题,一个就是这个 y 也没问题,再加上他俩的次数都是一,所以是一元一次方程。 第五个只有一个未知数,次数也是一,也是一元一次方程。除了要能判断一元一次方程以外,你还得会用他的概念来计算。比如这个题 听不说,这个方程是一个关于 x 的一元一次方程,那 x 的次数 m 方就必须等于一,也就是说 m 等于正负一,所以最后答案就是正负一了呗。 错了,如果 m 是一的话,系数就是零,那 x 就被干掉了,所以 m 不能是一,只能是负一。以后你要再看到关于 x 的一元一次方程,除了要让 x 的次数等于一外, 一定要注意它的系数绝对不能等于零。在方程中还有一个词会经常出现,就是方程的解,比如这个方程的解就是 x 等于十五, 我是咋知道的呢?很简单,把十五回带到方程中,先看左边,三分之一乘十五得五,五分之一乘十五得三,五减三等于二,右边也是二。呦西, 这个等号是成立的,所以判断方程姐的最好的办法就是把他回带回去,如果等号成立,那就是他了。 好了,就讲这么多,总结一下,第一,先说方程有俩要求,还有未知数和等号。第二,一元一次方程有四个要求,未知数只能是一个,次数,必须是一切,未知数不能在分母中。另外, x 的系数绝对不能是零,否则 x 就消失了。 第三,要判断方程的解,最好的法子就是把它回带回去,看看等号成不成立。听懂了吧,赶紧刷题爽爽吧!
3.3万漫画初中数学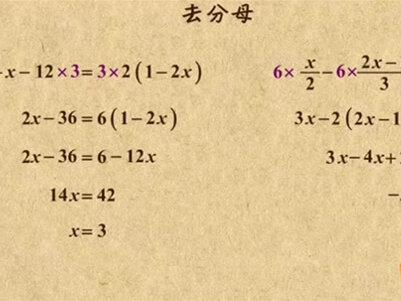 03:59查看AI文稿AI文稿
03:59查看AI文稿AI文稿这个视频我要讲讲解方程的另一个重要步骤,去分母。先看看这道题,三分之二 x 减十二,等于二倍的一减二 x 系数变分数了有没有?计算变麻烦了有没有?别着急,如果能化去分母三,把系数变成整数就好算了, 把等式的左右两边都乘上三,那每一项也得乘三三乘三分之二 x, 约掉三后得二 x。 负十二乘三得负三十六,三乘二,再乘一减二 x, 得六乘一减二 x, 这样就干掉了分母下来该咋办呢? 对了,去括号呗,把六乘进去,六乘一得六,六乘负二 x 得负十二 x, 这样就把括号去掉了。接着一项吧,负十二 x 移过来变成十二 x, 负三十六移过去变成三十六,二 x 与十二 x 合并为十四 x, 六与三十六合并为四十二。得到了这样的式子,接着就好办了,把十四除过去, x 就等于三。 你看,系数是分数也没有关系,只要对每一项成分母三就行。那要是俩系数都变成分数咋办呢?看看这道题, 二分之 x 减三分之二 x 减一等于一。这回出现了俩分母二和三,也想一举单调这俩分母啊。在同时乘二和三的最小公倍数,六 对,每项都乘六。六乘二分之 x, 约去二后得三 x, 六乘三分之二 x 减一,也许三后就是二乘二 x 减一了。咦,等等,好像哪里不对呀?这个二应该乘的是整个分子二 x 减一,而不是仅仅乘在二 x 的前面。咋办呢?加个 括号不就完了?千万注意了,区分母时,如果分子不是一个数,而是一坨数,一定要记得加括号。 好了,分母去完了,方程变成了三 x 减去二乘二, x 减一等于一。慢着,好像哪里又不对劲了,刚才左边每项都成了六,那右边这个一也不能例外啊,也得乘六才行。哎呀妈,又是个天坑有没有一定要注意了!区分母时,每项都得乘上分母的最小公倍数, 像一这样孤零零的一个数也不例外。搞定了分母,接着去括号吧。把负二乘进去,负二乘二, x 得负四, x 负二乘负一得二,这样又干掉了括号。 再往后就是一项合并了,二一过去变成负二,三 x 与负四 x 合并为负 x, 六减二得四,最后把负一除过去得 x 等于负四。 像刚才这道题冒出来俩分数,这对每一项都呈上分母的最小公倍数,尤其不要忘了,一这样的整数也不例外。同时,如果分子不是单独的一个数,比如二 x 减一,那你去分母的时候还得加个括号缓冲一下。掌握了这些,你就可以挑战大 boss 了。 看看这道题,二分之 x 减三,加上三分之二, x 减一,等于二 x 减一,这个方程仍然有俩分数,还是先去分母,每一项都乘上二与三的最小公倍数。六 六乘二,分之 x 减三,也许二得三,乘 x 减三,注意填括号。六乘三分之二 x 减一,也许三后得二乘二 x 减一,也得填括号。六乘二, x 减一,还得填括号。现在分母算是去完了,接着该轮到去括号了,三乘进去得三, x 减九,二乘进去 得四, x 减二,六乘进去得十二 x 减六。算到这,接下来就是最后的一项合并了,十二 x 一过来变成负十二 x 负九,负二移过去变成九和二等号。左边三 x、 四 x 与负十二 x 合并为负五 x 等号,右边负六加上九再加二等于五,也就是负五 x 等于五,那把负五除过去, x 就等于负一了,妥妥的。 好了,趣分母就讲这么多,总结一下就两点,首先,每一项都要成分母的最小公倍数,不能漏成。其次,如果分子不是一个数,而是一坨数,要对分子加括号。怎么样,听懂了吧,赶紧去刷题爽爽吧!
1913大成老师教育圈 00:35
00:35 05:20查看AI文稿AI文稿
05:20查看AI文稿AI文稿一起来解一下这道方程题,这是一道一元一次的方程,对于一元一次方程,解题步骤我们必须清楚,今天我要利用这道题,将一元一次方程所有的步骤全部罗列出来。好,首先看下题目, 方程是一个等式,解方程之前必须先写上解字。 第一步骤,第二步骤,我们看下整个结果,发现整个方程里面具有小数,不方便减。所以第一步我们需要将小数全部变为整数,使得它形成整数方面的一元一次方程。 如何形成整数?我们可以利用分数的基本性质。什么叫做分数的基本性质?分数的基本性质指的是分子和分母同时乘以一个非的因素,它的结果 是不会变的。所以先看下第一个数字我们应该怎么变。可以分子分母同时放大十倍,这样就可以使得所有的小数变为整数。而第二个我们发现都是两位小数,因此分子分母同时乘以一百,可 都让所有小数变成整数。最后一个不用变,所以也不用动,因此第一步过程称之为整数化比较整理 啊,这第一步整理,我们看一下这个分子分母都是一个小数,所以呢,分子、分母同时乘以十,变成五分之四 x 加上九。第二个式子可以变成乘以一百,变成三分之三,加上二 x。 最后一个不要动。 对,分子分母同时乘以一个非零数,结果不变,他是分数的基本性质,他跟其他分数之间是没有关系的,只跟自己有关系而已,因此这个不要动。第二步去分母, 因为有分母在,我并不好算,所以呢,我们需要将分母五三二同时去掉,如何去掉呢?可以利用等式的基本性质。等式的基本性质指的是等式的左边和右边同时乘以一个数,他的结果是不会变的,因此我需要找到一个数 去乘以左边所有的项,然后呢,也乘以右边的所有项,这样的话这个等式依然成立,可同时也能够使得分母消失。那我们看一下如何使得分母五三二消失呢?可以 寻找五三二的最小公倍数,这样的话就可以将五三二同时约掉。好,五三二的最小公倍数是几三十,对不对?所以呢,这里的话,左右两边应该同时乘以三十来,将整个分母去掉,左边乘以三十, 右边也乘以三十。 好,我们把这个下一步我们需要把三十乘进去,也称之为序括号 来,三十乘进去,五六三十约掉,还剩下六,得到是六倍的四 x 加九。这边呢,减进去得到是十倍的 三,加二 x, 得到的是十五倍的 x, 减五。好,现在可以慢慢的去括号了啊,四六二十四,得到二十四 x 六九五十四,减掉三十,注意外面是负号,所以要变号。减二十 x 等于十五来,开始减掉十五乘五,也就是七十五。下一步是什么?下一步叫做一下, 好,我们移下,移下下,将所有的位置,位置处的下全部移到左边,长处下全部移到右边, 得到二十四来开始减掉二十来。开始。记得一下的时候一定要注意编号好,等于负七十五, 先超自己再移这五十次,你不来减五十次加三十。好,我们看左边,这个时候下一步我们需要把合起来,也称之为合并同内向 左边二十四 x 减二十, x 减十五, x 相当于等于二十四减二十得到十四,四减十五得负十一 x 负七十五减五十四加三十,相当于得到的是负九十九。好,最后一步称之为位数的系数化为一, 画为一个步骤,最简单就是要把副 十一变成一,那说明左边需要除以副十一吧。根据等式的基本性质,左边除了副十一,要使得等式仍然成立,那么右边必须得除以副十一,所 相当于是左右两边同时除以负十一,得到系数为一,也就是 x 等于九。
1.1万大尧有数 02:35
02:35














