一个等比一个等差什么意思
粉丝2.7万获赞5.4万
相关视频
 03:37查看AI文稿AI文稿
03:37查看AI文稿AI文稿做一题之前题,今天我们来聊一聊什么呢?聊一聊等差和等比,你知道吗?如果连续三项既等差又等比,不用多想,他们三个就是相等的,是不是很神奇? 来,下面我们来看一道题,你看这个题是不是特别特别长,甚至于说都不是特别乐于读了。但是这时候你没有发现一件关键的话,叫做第七八九名的平均成绩既构成等差又构成等比。 如果我们知道刚才的小技巧,那其实代表着就是第七名,就和第八名和第九名的平均成绩就是一模一样的。 那我们继续再来看一下这个题吧。说张龙位列第十位,并且与第九名差一分,是平均成绩差一分,对吧?那么也就是说第七八九名减 去那一分之后,其实就是张龙的分数了,对吧?他说张龙的英语成绩是一百二十一分,但是老师啊,登记成了一百一十二分,登记错了,是不是少了九分,对吧? 一科少了九分,不要忘了我们排名的时候排的是什么?是三科的平均成绩成等差数列,对不对?那既然少了九分,平均到三科上,也就说他的平均成绩应该是少了九除以三,也就是啊,三分呗。那他本来应该位列第几呢? 我现在位列的是第十,加一分之后,我是不是就变成了第九名?变成第九名其实就是第八名和第七名吗?对不对?我再加一分。他们说了,之前前七名平均成绩不都是构成公差唯一的等差数列吗?所以说加一分 是不就变成第六名了?再加一分是不就变成第五名了?所以说我本来应该排在第五名,答案直接选择二 b 选项就可以了。 那你看,如果我们知道这个前提条件的话,这个题虽然长,但是做起来是不是一点都不复杂,甚至于说不用特别大算特算,直接口算,哎,加个三我们结果就出来了。 所以说小伙伴们做一题值千题,知道我们这节课要学的技术知识了吗?是什么?记着,连续的三项,如果既为等差,又为等比,不用多想,就是这三项完全一样,也就是 a 等于 b 等于 c。 如果特别想知道他是如何推倒出来的话,那下面给大家简单推倒一下。如果 abc 成为等差的话,那么 有中间的一项的两倍,是等于前后两项之和的。如果 abc 成为等比的话,那么就中间向的平方是等于两边向的之机的。 那根据这两个式子,我们一式是不可以推出 b 是等于二分之 a 加 c 的,对不对?带入到我们的二式当中,既有二分之 a 加 c 扩起来的平方是等于 ac 的, 其实化解一下就是 a 加 c 的平方是等于四 ac 的,把四 ac 移到左边来,其实最后又是一个平方,叉功是 a 减 c 的平方是等于零的, 一个数的平方等于零,只能是这个数为零,那也就是说 a 等于 c, 那 a 等于 c 了, e 不也等于 ac 吗?对不对?所以说 a 和 b 和 c 就是相等的。当然推倒过程大家无需关注,只要记住这个结论就可以了。连续的三项,如果既为等差,又为等比,那就是这三项完全一样。再把刚才的题砸磨砸磨吧,小伙伴们记住了吗?
29公考小魔女 02:07
02:07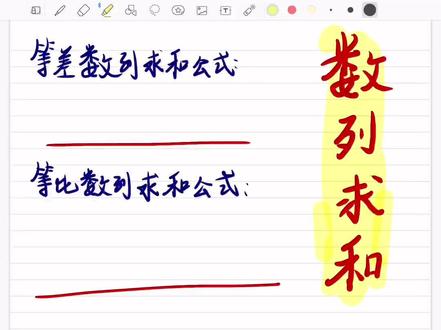 02:50等差数列,等比数列的求和公式你记住了吗❣️等差数列求和公式有两个,等比数列求和公式也是有两个,但是等比数列是分情况,有两种情况,而等差数列是任何等差数列都能用这两个的#数列前n项和#等比数列#等差数列查看AI文稿AI文稿
02:50等差数列,等比数列的求和公式你记住了吗❣️等差数列求和公式有两个,等比数列求和公式也是有两个,但是等比数列是分情况,有两种情况,而等差数列是任何等差数列都能用这两个的#数列前n项和#等比数列#等差数列查看AI文稿AI文稿我们这个视频,大家来一起记忆两个求和公式吧。等差数列和等比数列的求和公式是我们太长太长,用了就你基本上有了,给你一个数列是等差,你有了他的手相,有了公差,你就能够求前恩相合,对不对? 然后给了你等比数列的首相和功比,你就能够求前想和。即便是不给你功比,给了你第一项,或是给了你第 n 项、第 m 项、第 n 项、第三项、第五项、第七项、第几项。只要他说明了是个等差数列,或者是个等比数列,咱们都能够把相应的弓叉和 工笔求出来,然后进而去求他的钱。想和就很简单了,你只需要套用这个公式就好了。普通的等差数列和等比数列,不用去想什么错位相减法、分组求和法、列向相销法等等那些方法啊,咱们就给他用最常规的求和公式。 昂贵的求和公式,如果你都没有记住的话,你想想你能把题目给做对吗?对不对?等差数列的求和公式我们一起来背一下,嗯, s n 一起默写一下。嗯,我们经常会说,等于二分之首相加尾相括起来乘以项数。哎, 首先加尾上乘以项数除以二。还有一个,一共是两个,另外一个是 n 倍的 a 一加上二分之 n 倍的 n 减一乘以 d, 对不对?这两个式子其实是可以互相推的,你怎么推这个 a n 的话,你可以把它写出 a n 的一个通向公式来, a n 在 等差数列,应该是通向公式,是 a 一加上 n 减一倍的 d 等比数列。 a n 等于什么呀? a n 等于 a 乘以 q 的 n 减一次方, ok, 你把这个 an 的柿子带到这个 an 这来就能够退出,后面这个柿子我不再对他。对,跟着大家,不再带着大家去退了,大家拿那个草稿纸自己退一下哈,很简单的,然后等比数列球和公式也是有两个,但是他那两个是分开的, 记住他是分开的就好。就是公比等于一的时候,你想想公比等于一的时候,第一项是首相 a 一,第二项还是 a 一,第三项 a 一,第四项 a 一,第五项 a 一。你哪一项不都是 a 一吗?前恩相合的话就是有 n 个 a 一就好了。所以 q 等于一的时候是 na 一, q 不等于一的时候是一减 q 分之 a 一倍的一减 q 的一减 q 的 n 次方再括起来。这样 你看如果啊 q 等于一的时候,他分母不就为零了吗?所以咱们用这个公式默默认的就是 q 不等于零,公比不为零,公比不为零。大家看到这个求和公式了吗? ok, 那我们这个你默写对,默写对了吗?这个视频就到这里了,拜拜。
384十万八千梦yiyi 02:34查看AI文稿AI文稿
02:34查看AI文稿AI文稿关注张老师学数学就是玩,再来砍一道尖子生上的一道题啊!再来回顾一下咱们的错位相减法计算,一加二加二的平方,加二的三次方,加二的四次方,一直加加加加到二的二零二零和二的二零二一次方。 那看这些数,一二二的二次方,二的三次方,是不是?这每一项都是前一项乘以二, 所以说这些数本身放在一块都是一些等比数列,对不对?比值相等啊?都是在前一项的基础上乘以二,对不对?所以这种题是不是用我们的错位相减法就很好做呀?是 啊,这个一加二加二的二次方,加二的三次方,加二的四次方。咱们设咱们原来这个式子,他等于 m, 那刚才 咱说了,他是不是乘以二得到他,他乘以二得到他,他乘以二得到他,所以咱们这个 m 也乘以二,所以说二乘以 m, 二乘以 m 等于多少?他是不是变成了二? 他是变成了二的二次方,他是二的三次方,一次类推二的四次方,二的五次方,一直加加加加到他变成二的二零二一次方。最后一项是二的二零二二次方, 对不对?所以二 m 减去 m 等于什么?这个数减这个数来,二减二,没了, 他没了,他没了,他没了,一直没了,这个也没了,最后剩什么?是不是剩这个的尾相?二的二零二二次发减去这个手相减一, 二 m 减 m, 是不是就是 m, 是不是就是这个式的?所以这个式的最后等于多少?二的二零二二次方减一, 这就是我们常用的什么错位相减法。一看他是一个等比数列,他的公比是几?公比是二,那咱们设他为 m 的话,咱们乘以他的公比,乘以他的公比,目的是什么?那原来的第二项就成了这个新式子的 一项,那第一项跟之前的第二项一抵消,一抵消,全部抵消没了之后只剩下尾项和首项啊,就简化成了二到二零二二次 啊,这是我们非常常见的错位相减法啊,不会的同学,通过这个题咱们再掌握一下啊!掌握一下。好,这个题咱们今天先讲到这啊,关注张老师学数学就是玩下课。
364战老师开课了 10:07
10:07 00:18
00:18
猜你喜欢
- 22.5万C位壹姐












