粉丝9460获赞5.2万
相关视频
 03:53查看AI文稿AI文稿
03:53查看AI文稿AI文稿上回说到分式的基本性质,也就是分式的分子和分母成或处以同一个整式,分式的直不变,利用它咱就可以给分式进行变形了。 举个例子来说,二 xy 分之外放,不难看出,分子分母当中都有 y 这个供应室,那咱就可以把它约掉,得到二 x 分之 y, 这个过程就叫做分式的约分。而约分之后得到的 rx 分之 y, 他的分子和分母就没有供应式了,这种分式就叫最简分式。 学会了约分,那咱就来看一个更复杂一点的分式, x 方加 x 减二,分之 x 方减一,那这个分式能不能约分呢?现在这个分式,他的分子和分母都只是多项式,要想约分,得先因是分解才行。先来看看分子 x 方减一,这不就是个平 方插共式吗?分解一下就是 x 加一乘 x 减一,分子搞定了,接下来再看看分母,这个式子,咱利用十字相乘法就可以很轻松的分解成 x 加二乘 x 减一。都分解完了,就来观察一下, 很明显,分子分母当中都含有 x 减一这个因式,把它约去,分子就剩下 x 加一,分母就剩下 x 加二,这就是最终的结果了。 和分数计算类似分式这除了约分,还可以进行通分,比如 a 分之一和 b 分之一这俩式子, 要想把他们的分母变相同,那第一个分式分子分母就得同成 b, 变成 ab 分之 b, 而第二个给分子分母同成 a, 变成 ab 分之 a, 现在这俩分式的分母就相同了,这个相同的分母就叫公分母,而这个过程 就叫做分式的通分。怎么样,很简单吧,再来试试看二 a 方 b 分之一和 ab 方分之 c, 这俩分式该咋通分呢?由于他俩的分母比较复杂,那咱就得先来观察一下。要想确定公分母,那就得让他包含这俩分母当中所有的仪式才行。 先来看看系数,这有二,这没有,因此公分母就得有二。接下来就是字母,这 a 是两次,这 a 是一次,那公分母就得是 a 方,这 b 是一次,这 b 是两次,那公分母就得是 b 方。搞定 最后的公分母就是二倍的 a 方成 b 方。和第一个分式的分母对比一下, b 方和 b 差一个 b, 那这个分母就得成 b, 相应的分子也要成 b, 变成二 a 方 b 方分之 b。 再来对比一下第二个分式的分母, 技术差个二,那分母就得成个二, a 方和 a 差一个 a, 那分母也得成 a, 也就是说,分母得成个二 a, 相应的分子也得成个二 a, 最后就变成二 a 方 b 方分之二 ac。 像刚才这样,为了确定公分母,咱就把这俩分母当中每一个因式的最高次密取出来,盛在一起就可以了,这种公分母就叫做最简公分母。学会了咋找最简公分母,那咱就来挑战一下这俩分式的最简公分母是个啥呢? 首先还是来应试分解第一个分母,提取个 x 就行,得到 x 乘 x 加一。接下来再看第二个, 利用十字相乘,分母就被分解成了 x 加一乘 x 加二。都分解完了,接下来就可以找最简公分母了。先来看第一个,这儿有个 x 和 x 加一那公分母,当然也要有这俩因式。 再看第二个,除了已经有的 x 加一,还有个 x 加二,那公分母也要有他。到此,这俩分式的最简公分母就是 x 乘 x 加一,乘 x 加二了。 好了,已经说了不少了,总结两点,第一,约分就是要把分式、分子分母的工艺式约去,而且一定要约到最简分式才行。 第二,公分就是要把几个分母不同的分式换成同分母的分式。一般咱把这些分母通成最简公分母就成。怎么样,听懂了吧,赶紧动手试试吧!
1.4万乐乐课堂天天练-初中数学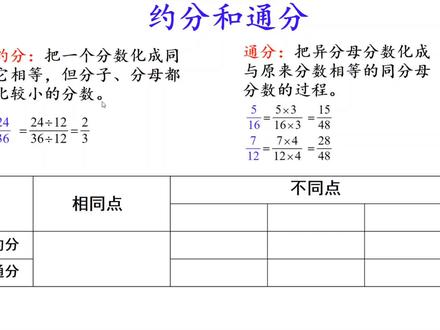 03:00查看AI文稿AI文稿
03:00查看AI文稿AI文稿约分和通分是两个非常重要的知识点,也是比较容易混小的,我们这节课就一起来梳理一下约分和通分的联系和区别。 首先看他们的意义,约分是把一个分数化成同他相等,但分子、分母都比较小的分数, 而通分是把一分母分数化成与原来分数相等的同分母分数的过程。我们可以发现他们的定义当中都有一个关键词,就是相懂, 这是他们非常重要的一个联系,或者说是相同点,就是说约分和通分都要划成从原来相等的分数,也就是 说每个分数在转化的过程当中,分子、分母都会发生变化,但是分数值是保持不变的。 那么怎样才能保持分数的大小不变呢?这就需要用到分数的基本性质,把分子、分母同时乘或者除以相同的数。 好,他们的相同点就是都利用分数基本性质,分数值保持不变。那么不同点是什么呢?不同点主要有三方面,第一是对象的数量不同, 约分是针对一个分数而言,而通分至少是针对两个分数,因为通分是要将一分母分数转化成同 分不分数,所以至少要有两个分数。第二个不同就是方法不同。约分要用除法,分子和分母要除以相同的数,因为我们是要把分子分母都变小, 所以要除以相同的数,那么这个相同的数就是他们的公因数,而通分要用乘法乘相同的数。 第三个不同就是结果不同。约分通常要约成最简分数,如果分的分不都除以他们的最大公因数,那么得到的结果就是最简分数, 而通分最终的结果是要画成同分母分数,这个同分母就是原来两个分数的公分 分母我们一般用最小公倍数做公分母,可以看出,约分我们要用到公因数或者是最大公因数,而通分我们要用到公倍数或者是最小公倍数。 好,这就是约分和通分的联系和区别。约分和通分是我们进行分数大小比较和计算的基础,同学们要熟练掌握。
418杜 老师 11:16查看AI文稿AI文稿
11:16查看AI文稿AI文稿大家好,这节课我们来学习约分,那什么是约分呢?首先我们看约分的概念, 关于约分的概率,利用分式的基本性,约去分式分子和分母中的公因式, 不改变分式的值,这样的分式变形就叫做分式的约分。 好,我们来解释一下这个相关的概念。我们说分式的约分,我们说实际上本质上就是一个分式的变形过程,他其实是一个横等变形,因为我们要求他不改 变分式的值,注意是不改变分式的值。那么怎样进行这个约分呢?我们说是约去分式分子和分母中的公因式, 其实就告诉你了,怎样进行约分,就是约去分式分子分母中的公因式的理论依据就是分式的基本性质。 好,这是关于分式约分的概念,我们对他进行了一个强调和说明, 那么用式子表示一下,就是这样, b 乘以 c 分之 a 乘以 c, 很显然这是一个分式的形式, c 呢,我们可以看着是公因式,那么我们分子分母同时约掉这个公音公因式 c, 这样以来我们说就等于 b 分之 a, 那么这个过程呢,就叫做约分。 不妨我们举个例子来说明,大家看 a, b 分之 a 方 b c, 显然这是一个分式,那么我们说 ab 不动,我们把分子进行整理,写成 ab 乘以 a c, 很明显这里有 ab, 这里也有 ab, 那么 ab 呢,就是公音式,那么很显然整理一下,结果就是 ac, 那换句话说,我们已经有分式 变没了。 当然这是一个约分的过程,下面得二十四 a 方 b 的立方 d 分之负,三十二 a 的立方 b 的平方 c, 一样道理,我们来看一看他们的公音式。我们说二十四, a 方 b 的立方 d 呢,可以写成八 a 方, b 方乘以三 b、 d 分子也是一样写成八 a 方, b 方乘以负四倍的 a、 c。 很明显,八倍的 a 方 b 方属于分子分母的公因式,那么约掉公因式以后,结果就是父 三 b d 分支四 a、 c, 那么我们就把这个分式达到了一个约分化解的目的。 好了,下面我们来说一说约分的法则,就说我们怎样进行约分呢?怎样来找相应的供应室呢?我们可以按如下的方法进行操作。一、如果分子和分母都是单向式的话, 那么约去分子和分母中相同因式的最低次密, 注意是约去分子分母中相同字母的最低次密。分子与分母的细数,约去他们的最大 公约事,就说细数,我们要找他约去他们的最大公约事。 如果分子式的分子分母式多项式,如果是多项式怎么办呢?注意,要先分解因式,然后约分。分解因式完了以后,我们就容易找到相同的因式,然后我们进行约分即可。 注意,我们一定要注意找到他们相应的方法,如果是单向式,我们要找到相同因式的最低次率 细数,要找到他们的最大公约数。然后呢,如果是多项式,一定要注意分解因式。 好,我们来看这个式子,八 a 的立方 b, c 的平方分之六, a 的平方 b 的立方 c。 很明显,如果我们整理一下的话,六八他们的最大公约数显然就是二, 剩下除以二的话,显然就是三和四对应起来,然后 a 方这里有 a 的立方,那么我们说找到最低次密就是 a 的平方了,所以 a 的平方削掉以后,这剩一个 a, 然后 b 的立方这里有 b, 最低四米就是 b 了一次方了,所以这剩下 b 的平方这里边有 c 和 c 的平方,那么把 c 的一次方就是 c 去掉以后,这剩下一个 c, 这一来我们就找到了约分的法则。 下面大家看 是一个多项式,那么对于这个多项式来说, x 方减 x 减二,分之 x 方减一。注意,多项式的首先要注意进行分解因式, 那么分解仪式的话就是 x 加一乘以 x 减一,就是平方差,然后下面是 x 方减 x 减二,我们可以用十字相乘,乘开的话就是 x 加一乘以 x 减二,注意看 x 减一和 x 减一同时出现了,并且他的次数最低就是一次,这样一来两个消掉以后就是 x 减二分之 x。 好,这就是关于约分的法则以及相关的举例说明。下面我们来说第三个问题,就是最简分式。 我们约分的目的其实就是想化成最简分事,那么什么是最简分事呢?就是说一个分事的分子与分母没有公因式的时候,就叫做最简分事。 我们说约分一般就是将一个分式化为最简分式,当然我们说约分所的结果有时可能是一个整事, 除了最简分式以外,还可能会出现整饰这种情况。举例说明,大家看 a 分之三, a 方减 a, 很明显我们可以前面提供因式进行因式分解,就是 a 背的三 a 减一,那么分子分母同时有 a, 约掉公因是 a 以后,结果就是三 a 减一,很明显三 a 减一是一个展示。 好了,下面我们来看相关的题目。第一个,十二, a 的四次方, c 乘以括号里边外减 x 分之八 a, b 乘以口号里边 x 减 y 第一个,然后 e、 c、 c, 第二个,第三个和第四个,我们逐一进行说明。 对于第一个来说,我们来看,这里边有 x 减 y, 这有 y 减 x, x 减 y 和 y 减 x, 很明显他们相差一个符号, 下面一个负号,这样一来,我们两事相消以后,前面多出来一个负号,变成了负的十二 二 a 的四次方, c 分之八 ab。 很明显,下面我们需要处理的就是细数,细数的最大公约数为四,所以对应的就是二和三,然后 a 和 a 的力四次方对应起来,那么除以 a 的话,就是 a 的立方, b 呢?没有跟着走就可以了, c 没有对应的下,这样就可以,所以结果是负的三 a 的立方, c 分之二 b。 第一个表达式的约分,那么对于第二个来看, i a 减 b 乘以 x 的二 n 次方, 这是 b 减 a 刻起来乘以 x 的三 x 吧。很明显, a 减 b 和 b 减 a 相差一个负号,我们约分以后,同时约分以后,就是负的 x 的三 x 方分之 x 的二 n 次方,那么我们说他的最低次密就是 x 的二 n 次方。约掉以后,就是负的 x 的 n 次方分之一,因为 x 的三 n 次方,我们可以写成 x 的二 n 次方,再乘以 x 的 n 次方。 好,这是第一个和第二个简约分。我们来看第三个, a 方减 a, b 减二, b 方分之 a 的四四方减 a 方, b 方。很明显分子分母均为多项式。 多项式的约分的话,首先要进行因式分解,所以就是 a 加 b 乘以 a 减二, b 分之 a 方乘以 a 加 b 乘以 a 减 b, 就是先提供因式,然后利用 平方插公式。很明显,这里边有 a 加 b, a 加 b, 这有 a 加 b, 以后两式相消掉以后,就是 a 方乘以 a 减 b, 可起来 b 上 a 减二 b, a 减二 b, 最终的结果。 好,我们来看第四个,第四个式子也是一样,这是一个多项式。很明显,首先分子分母均为多项式的话,就需要因时分解, 就是 a 的二 n 次密,统一括号里边 b 的二 n 次密减去 a 的平方,合起来,然后下面是 a 的二 n 减一次密, 括号里边的是 b 的二人次密减去 a 的平方,合起来来看,这两个式子是相同的,同时遇到以后,结果就是 a 的二 n 减一次蜜,分之 a 的二 n 次蜜,我们说相同的话,找最低次蜜,遇到以后,结果呢等于 a, 当然结果实际上是一个展示。好,这个题目呢,我们就讲到这里。 好,本节课就到这里。
58佐管家 14:23查看AI文稿AI文稿
14:23查看AI文稿AI文稿约分与通分。 哈哈,累坏了吧,我这正好还有半个西瓜。哇,有西瓜吃了。这份西瓜咱们四人平分,一人一块。 叔叔,一人一块太少了吧。好,哈哈,那就一人两块。 一人两块也有点少。好,那就一人四块, 干脆一人一百块得了。好,那就一人一百块。你们慢慢吃,我做饭去了, 这是一块西瓜, 你们看,我用这个圆形表示一个西瓜,我问你们这个西瓜平均分成四份,我们四人每人可以分得几分之几啊? 四分之一,那平分分成八分,每人可分得几分之 八分之二?平均分成十六分,每人分得几分之几?十六分之四, 他的四分之一。八分之二。十六分之四 表示的大小是一样的。没错,这样可以很清楚的看出这个西瓜的四分之一和他的八分之二以及他的十六分之四是相等的。 其实他们的分子分母是按照一定的规律变化的, 四分之一的分子分母同时乘二就得到了八分之二。 八分之二的分子分母同时乘二就得到了十六分之四。也可以这样看,十六分之四的分子分母同时除以二就得到了八分之二。 八分之二的分子分母同时除以二,就得到了四分之一。 这其实就是分数的基本性质,分数的分子和分母同时乘或者除以相同的数零除外,分数的大小不变。 哦,原来只是把西瓜切成了更多的快速,每个人分得的西瓜的量还是一样的。 阿嚏。 哎,好多作业啊,赶紧开始吧。小瑞文雅,你们的作业完成的怎么样了? 我一共有十二页,已经完成八页了。我完成的比你多,我共有十五页,已经完成十页了。麻豆,你有多少作业?我只有一道题。哇,你们老师太善良了,什么题? 抄写课文九十九遍啊,我已经写了六十六遍了。我们的进度是一样的。 怎么会呢?我完成了全部作业的十二分之八。温雅完成了全部作业的十五分之十。麻豆完成了全部作业的九十九分之六、十六。 这几个数经过约分之后是相等的约分?什么是约分? 我先问你们,八和十二的音数有哪些呀?八的音数有一、二、四八, 十二的因数有一、二、三四六、十二、 一、二、四是八和十二。公有的因数 叫做他们的公因数。几个数的公因数里最大的那个数叫做他们的最大公因数。 所以,八和十二的最大供应数就是四。也可以用分解质因数的方法来找最大供应数八分解质因数是二乘二乘二, 十二,分解智音数是二乘二乘三。 找出他们共有的至因数,把这些至因数相乘,就可以得到他们的最大供应数。公有的至因数是二和二,所以八和 十二的最大公因数就是二乘二。等于四十二分之八的分子、分母同时处以他们的最大公因数四,十二分之八就化成了三分之二。 三分之二的分子和分母只有公因数一,这样的分数叫做最简分数。 我发现约分使一个分数的分子和分母都变小了。 是的,把一个分数化成和他相等,但分子和分母都比较小的分数,叫做约分。一般情况下,要把分数约分成最简 分数。我的进度是十五分之十,十分解之因数是二乘五十五,分解之因数是三乘五 十和十五。公有的制因数是五,所以十和十五的最大公因数是五,因此十五分之十月分后就是三分之二。 还可以这样约分,比如九十九分之六十六,分子分母先同时除以三, 在分子分母同时处理十一,这样九十九分之六十六就化成了三分之二了。 文雅,我们的进度都是三分之二,所以我们的进度的确是一样的。 这种方法有问题,我明明就比小瑞哥哥多做了两页嘛。人家麻豆他都没意见,你就接受吧。好了好了,不要吵了,再吵今天就做不完作业了, 哎,今天又布置了十八页作业。我的有三十页呢。我的作业只有一题, 这是什么作文?快乐的童年字数两千字。快乐的童年,我怎么没 感觉到呀?麻豆,你们老师真幽默,不跟你们说了,我得抓紧做作业了。 同志们,进展如何呀?我已经完成十四页了。我已经完成二十四页了,我写了一千五百字了。 我们的进度分别是十八分之十四、三十分之二、十四,两千分之一千五百。 把他们画成最减分数就是九分之七、五分之四、四分之三。 这次我们三个人的进度谁快呢?九分之七,五分之 四、四分之三。这三个分数的分母都不一样,怎么比较大小呀?要比较这三个数的大小啊,得先通分,通分又得先学会求最小公倍数。 怎么求最小公倍数啊?比如要求二和三的最小公倍数,可以分别先求出二和三的倍数, 二的倍数有二、四、六、八、十、十二等等, 三的倍数有三、六、九、十二等等。六和十二是二 和三公有的倍数叫做他们的公倍数。几个数的公倍数里最小的那个数叫做他们的最小公倍数,所以二和三的最小公倍数是六。 是的,也可以用分解至因数的方法来求最小公倍数。比如求四和六的最小公倍数,先将他们分解至因数,四分解至因数就是二乘二。 六分解至因数就是二乘三。用公有的至因数去成他们的独有至因数, 就可以得到最小公倍数。所以四和六的最小公倍数为二乘二乘三等于十二。 用这个方法可以求出九分之七、五分之四、四分之三这三个数。分母的最小公倍数为一百八十。 再利用分数的基本性质,九分之七的分子分母同时乘二十,得到一百八十分之一百四十 五。分之四可以画成一百八十分之一百四十四,四分之三可以画成一百 百八十分之一百三十五。 像这样,把一分母分数分别化成和原来分数相等的同分母分数叫做通分。 通分是非常重要的,不仅在比较分数大小中要用到,在一分母分数加减法中也要用到。 分母相同时,分子大的分数就大,所以我的进度最快, 我的进度不是最慢的,我不跟你们闲聊了,不然就完不成作业了。 分数的基本性质, 分数的分子和分母同时乘,或者除以相同的数零除外,分数的大小不变。 最大公因数几个数公有的因数叫做他们的公因数。几个数的公因数里最大的那个数叫做他们的最大公因数。约分, 把一个分数化成和他相等但分子和分母都比较小的分数叫做约分。通常采 采用的方法是分数的分子、分母同时处以他们的最大公因数。 最小公倍数。几个数公有的倍数叫做他们的公倍数。几个数的公倍数里最小的那个数叫做他们的最小公倍数。 通分,把一亿分母分数分别化成和原来分数相等的同分母分数叫做通分。一般把一亿分母都转化成他们的最小公倍数。 还有什么要补充的吗?有,老师们,请把快乐还给学习,把快乐还给孩子吧!
252菏泽家教上门辅导 01:48
01:48 04:53查看AI文稿AI文稿
04:53查看AI文稿AI文稿这节课我们讲一讲约分,最近有不少家长反映孩子在这个方面掌握的不好,我们来讲解一下。首先看约分的定义,把一个分数化成同他相等,但分子、分母都比较小的分数,叫做约分, 关键词是相同,也就是说这个分数在转化的过程当中,分子、分母都变小了,但是分数值是不变的。 约分的方法,分子、分母同时除以他们的公因数。约分是通常要约成最简分数。什么是最简分数呢?就是分子和分母只有公因数一的 分数,也就是分子和分母是互质数。接下来我们具体看两个例子,三十六分之二十四, 我们一般不要在原市上月份,所以我们抄下来,首先要找到三十六和二十四的公因数。三十六和二十四的公因数有很多,我们可以一个一个的去除, 我们可以先除以二,二十四除以二等于十二,我们把二十四划掉, 然后将结果写在他的上面。三十六呢,也要同时除以二,划掉结果写在下面, 注意不要往左右写好。现在分数变成了十八分之十,二十八分之十二不是最减分数,我们还可以继续约分,再除以二 十二,除以二等于六,还是往上写十八除以二等于九, 那么九分之六也不是最简分数。分子、分母还有公因数三,所以我们继续除除以三等于二,分母除以三等于三。 好,这样得到的是三分之二,就是一个最简分数,这就可以了。 那么这个分数我们是经过三次月分,最终变成了最简分数。在月份的过程当中,我们可以发现分子分母都发生了变化,但分数值是不变的, 三分之二和三十六分之二十四的大小是一样的,因为我们是依据分数的基本性质,把三十六分之二十四的分子和分母同时除以相同的数, 所以最后分数的大小是不变的。那么除了像这样逐次约分,我们也可以一次约分。要想一次约分,我们就需要找到分子和分母的 最大公因数。三十六和二十四的最大公因数是多少呢?应该是十二,我们用二十四除以十二等于二,三十六除以十二等于三, 这样我们就一次约分,得到了最减分数三分之二,一步到位。 那么这两种方法同学们可以根据情况灵活的选择, 不要强求一次月份,因为有的时候找最大供应数不是很容易找的。好,接下来我们再看第二个,七十五分之四十五。首先找七十五和四十五的供应数,我们看各位都是 五,所以他们的供应数肯定有五,四十五除以五等于九,七十五除以五等于十五。然后十五分之九还可以继续同时除以三,九除以三等于三十五除以三等于五, 最后等于五分之三。这个我们是进行了两次月份,当然我们也可以 直接除以他们的最大更音数十五,那样一次就可以了。好,接下来我们做个练习。
142杜 老师 03:35查看AI文稿AI文稿
03:35查看AI文稿AI文稿一个视频给大家讲清楚约分和通分的问题。在讲约分和通分之前,我们先来看这三个分数。我们把这个圆不妨看成是一个月饼,那这里阴影部分是一个月饼的二分之一,这里是一个月饼的四分之二,这个呢是一个月饼的八分之四。 通过观察我们可以发现三个图形中阴影部分都占了这个月饼的一半,所以我们可以把这三个分数画上等号。 二分之一等于四分之二等于八分之四。二分之一,我们分子和分母都去同时给他乘以二,你会发现分子就成了二,分母就成了四,这也就是分数的基本性质。刚才是分子和分母都同时成了同一个数, 分数的大小不变,那这里八分之四,我们也可以把它的分子和分母都同时除以 一个数。四除以二等于二,八除以二等于四,所以他通过分子、分母同时除以一个相同的数,也可以画成和他相等的四分之二,也就是分数的大小不变。 熟悉分数的性质,我们来看一下约分。约分是把一个分数化成与他相等,且分子和分母都比原来小的数的一个过程。比如这个分数六十分之七十五,谁要想给他约分,需要化成和他相等的一个数,那根据分数的性质,分子和分母就要同时除以一个相同的数, 分子和分母就需要同时除以七十五和六十的公因数。第一个方法,那这里是尾数,是五,这里是尾数,是零,他们两个应该都是五的倍数,所以我们先给他约个五,六十除以五是十二,七十五除以五是十五,现在化成了十二 分之十五。我们再来看十二和十五,他们两个还有共同的因数,三三四一十二、三五一十五,所以我们可以给他画成四分之五,有没有更简单的约分方法呢?我们用这两个数中啊,比较大的这个数去减去比较小的数,七十五减去六十等于十五。 我们来观察一下,十五正好是七十五和六十的最大公因数,我们直接用十五去约,七十五除以十五等于五,六十除以十五等于。 所以呢,我们直接给他约成四分之五,把几个分母不同的分数分别化成和原来分数相等,并且分母相同的分数的过程。比如说八分之七和六分之五。因为我们经常要比较两个分母不同的分数的大小,为了方便比较,我们就把他们 变成分母相同的分数,这样只比较分子的大小就可以了。这里八分之七和六分之五,他们两个的分母是不同的, 那我们想要把它画成分母相同的,就要用短除法,原来的两个分母分别是八和六,我们就写在这里,先用他们的最小的公因数去约,八除以二等于四,六除以二等于三, 那四和三除了一之外,再也没有共同的因素了,短除法就除完了,那我们再用这里的二去 乘四,再乘三,可以得到他们的最小公倍数是二十四。最小公倍数作为他们新的分母,八分之七变成二十四,分之多少,那分子和分母都同时给他乘个三就可以了。六分之五变的时候, 这里二十四是六的四倍,所以六乘四,那五呢?也要去给他乘个四,所以是二十四分之二十。通过比较这两个数的大小,我们就可以知道,八分之七是大约六分之五的。
223杨老师逻辑思维












