黎曼和定积分公式
粉丝1830获赞2.1万
相关视频
 01:11查看AI文稿AI文稿
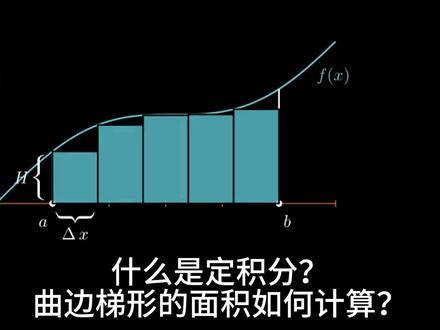
01:11查看AI文稿AI文稿什么是定积分?区边梯形的面积如何计算?设函数 y 等于 fx 在区间的闭上恢复连续由函数 y 等于 fx, 直线 x 等于 a, 直线 x 等于 bgx 轴所围成的图形称为区边梯形。那么区边梯形的面积该如何计算呢? 我们知道矩形的面积等于矩形的长乘以矩形的宽。我们试着用一个矩形填充替代曲边梯形计算面积 显然会产生较大的计算误差。那么我们试着将矩形的个数增加,用五个等宽矩形填充曲边梯形,则曲边梯形的面积 近四为五个矩形的面积和,但仍然存在误差。将前面的推倒过程进行整理,可以得到按个等宽矩形面积的计算通视。显然,当按的取值较大时, 计算误差会缩小。当链区域无穷大时,区边梯形的面积等于无穷个等宽矩形的面积之和。这就是函数 fx 在区间 a 倒 b 上的定积分。 that man we can!
554公考笔记![什么是定积分[高等数学24] #大学数学 #高等数学 #定积分 #定积分定义 #微积分](https://p3-pc-sign.douyinpic.com/image-cut-tos-priv/7c65ecb0c7fb2d9467d8eaed17f6e43c~tplv-dy-resize-origshort-autoq-75:330.jpeg?lk3s=138a59ce&x-expires=2079547200&x-signature=eK9HvTYEZl9mOH3Nv%2FeW1lZ3FQE%3D&from=327834062&s=PackSourceEnum_AWEME_DETAIL&se=false&sc=cover&biz_tag=pcweb_cover&l=202511270440319AE295900E58692D8A48) 21:43查看AI文稿AI文稿
21:43查看AI文稿AI文稿大家好,今天我们就来讲一下高等数学的定积分,也叫黎曼积分。为什么叫黎曼积分呢?因为本来咱们这节课讲的定积分的定义就是由黎曼首先提出来的,他主要分三步,走哪三步呢?一会你就知道了, 这节课我们分三部分内容啊,第一部分的话就是讲一下这个区分梯形的面积,还有这个定积分的实际应用的一些一个题目。 然后呢,第二个就是定计分,定义了由区编梯形的面积引出定计分的定义,然后第三部分就是定计分的几个亿,那咱们来看吧。第一部分啊,区编梯形的面积。什么叫区编梯形呢?人家说定义了 如图这部分,你一定要仔细好好读一下啊。嗯,假设平面图形是由什么组成的呢?你注意,人家分成了四部分,第一部分是这这条曲线,这条曲线呢,就是 y 等于 fx 的这个函数了啊,这条曲线。 第二部分的话是 x 等于 a 这条线啊,然后第三部分的话是 x 等于 b 这条直线。 好,然后第四部分的话是 x 轴啊,这四部分然后围成了一个什么,你看这两条边, x 等于 a 和 x 等于 b, 这就是 x 等于 b 这条线啊,然后左边这一条的话是 x 等于 a, x 等于 a 和 x 等于 b。 肯定是要互相平行的吧,有一组边平行的四边形叫什么?叫 t 型, 那么我们这个图的话特殊一些,虽然 x 轴是水平的,但是 wifx 一般是有弧度的吧, 所以这个梯形叫做什么呢?这类图形都叫做曲边梯形,理解了吧,曲边梯形啊,那接下来我们就是要求这样一个曲边梯形的面积了,这个曲边梯形的面积呢,我们记为大写的 a 吧,这个知道就可以。那怎么求呢?分三步走,记住啊,三步, 第一步分割。怎么分割呢?因为你是区别,你不是说一条直线,如果一条直线的话,我们直接利用什么?如果你是普通的梯形,我们直接利用梯形的面积公式,上底加下底,乘客除二就行。但是这个不是啊,这个是区别梯形。第一步分割啊, 怎么分割呢?我们在区间 a 到 b 上插入若干个分点,一共有多少个呢?一共有 x 零,注意啊, x 一是第一个分点, x 二第二个分点,那接下来肯定是 x 三,一直往后,一直往后啊, 然后一直到哪呢?一直到 xn。 所以啊,一共插入几个分点啊?有同学说,老师啊,你一共分成了几部分呢?一共分成了 n 部分,所以插入了 n 个点。呵呵,插入了 x 一,一直到 xn 减,一共是 n 减一个点啊,你想想啊, n 个人排 排队,其实中间只有几个空,只有 n 减一个空,所以一共插入了几个分点,一共插入了 n 减一个分点啊,那继续往后。那接下来这个你就懂了啊,将区间 a 到 b 分成什么?分成 n 个小区间。 那每一个区间都怎么来定义呢?每一个区间的话,我们就写成了,你看, x 零到 x 一,这是第一个区间吧, 然后呢,这个 x 一到 x 二,这是第二个区间吧,省略号。那最后一个区间应该怎么写?那肯定是 xn 减一,一直到 xn 了,就这样一回事,那么每一部分所对应的区间长度可能相当于可能不相等的啊。那这个区间长度的话,因为你分成了 n 部分, 所以我说我们这个区间长度就分成什么,我们这个区间呢,就分成了 xi 键, xi 键 理解了吧?一共有 n 个,有可能相同,也有可能不同的区间长度,那么这样分的话有什么好处呢? 看看这一部分啊。嗯,我们把把刚才谁呢?把这个 x 等于 a 改成什么?改成 x 等于 x 零这条直线和 x 等于 x 一这条直线。看我画的红色的部分,然后 y 等于 fx, 还有谁?还有 x 轴这四部分围成的这样一部分。他叫什么?说啦,他的名字叫曲变梯形。那不就是分成了若干个几个 n 个小的曲变梯形吗? 那你最重要求的是大的总的面积。那我们接下来要干嘛?你分割以后要求和对不对?哥不发哥不发,先分割再加起来嘛。第二步要求和了啊,这求和的话,我们只能暂时先 球这个近似的和。为什么?就是因为你是有弧度的。这个 fx 对不对?他不一定是一条直线任取科赛,这科赛的话一定是在哪之间呢?你比如说科赛一,他肯定是在 x 零到 x 一之间。 你比如说你取的这个横坐标科赛二,那他肯定是在谁呢?那肯定是在 x 一到 x 二之间了。就这么一回事,那以此类推,那这个科赛 n 的话,肯定你也能看出来吗?他就是在 xn 减一到 xn 这两个数字之间了。 然后我们用谁来代替这个曲边梯形小的曲边梯形的面积呢?我们就用矩形来代替,来近似的代替这样曲边梯形小的曲边梯形的面积。你比如说第一个看好了啊,刚才因为是曲边梯形,我们确实没法求,但是现在 举行举行的面积你还不会求啊?看长和宽就行了吗?比如说这个宽是达尔塔 x 一,对吧?那这个长是多少?这个长不就是 f 科赛一吗?这个理解了吧?那以此类推,都加起来 f, 我写上科赛一, 乘达尔特一,再加上 f 开赛二,再乘达尔特二,一直加到最后一个团,那肯定是 f 克赛恩,再成达尔特 xn 了。你想写成这样一个耒核的形式,不就写出来了吗?懂了吧?那 第二步,做完这个近似和之后的话,我们发现有一个地方不太好,哪部分呢?你约等于我们这道题是要求你要求这个面积的精确值,你现在约等于我不满意怎么办?近似吗?什么叫近似?最后一步啊?要去极限了。 曲吉祥的意思呢?比如说第一个矩形原来还是挺大的吧,然后我把让它变小一点,然后再让第一个矩形再变,每一个矩形都变得特别特别小。那每一个矩形都变得特别小的情况下,那实际上每一个矩形就变。 变成什么了?就变成了一条线呀,一条长短不一样,长短会变化的线段。第一条线啊,第二条线,第三条线,第四条线,第五条线,一直扫过去,你说是不是就是阴影部分,也就是说整个区别提醒的面积了?为什么?其实你在初中的时候肯定见过这句话。 线动点,动成线我就不写了啊。线动成什么?线动成面,现在我们求的不就是这个面面积的意思吗?理解了吧?好,懂了。这样一个极限过程之后,那接下来看当栏目的区域,栏目的区域零,实际上就是让谁啊?让每 一部分这样一个宽度打二塔 x 都屈均于零,就越来越细,越来越细。原来你这个矩形呢,还是有宽度的,后来一直细,就趋行于一条线了,线等成面,就这个意思。当这个区间宽度屈均于零的时候呢? 以上这个合适哪个合适啊?就这个右边的形式,他的极限。刚才我也说了,线动成面,就求出精确的面积来了, 最终的话,我们就可以这样来记面积。他是等于看啊,等于黎明,他这个能不能取决于零,他实际的含义你也能够看出来, 你想啊,最大的区间宽度打扰他,他都已经是非常小区间于零了,那就别说最小的其他的情况了,对吧?实际上他这个人们的区间于零的含义就是让每一个区间宽度都趋均于零,其实也就是让什么让每一个矩形都几乎变成一条线了,线弄成 场面就求出面积来了。就这个含义一定要多理解,多自己看看。那继续往后接下来的话,他是这么个意思, 已知一辆小车沿直线运动,行速度呢?画了一个媒体图像嘛。然后呢?用以上方法。用什么方法啊?用以上我写和的这种方法来表示一下小车从这个 t 一运动到 t 二的路程,怎么表示呢?好说,第一步干嘛? 分割呗,这个把 t 一到 t 二分成多少部分啊?把 t 一到 t 二分成若干个部分,分成 n 个部分,这个没问题吧?然后比如说第一部分的话,我们就写成什么,就写成 t 一到 t 一,小 t 一啊。然后第二部分的话就是 题到题二,第三部分,嗯,题二到题三,就这样一直去写,然后第二部分的话就是什么 就进四合了,一共分成最后一部分的话,我们就写成 tn 减一,一直到 t 二吧,其实这个 t 二其实就相当于什么呢?就相当于这个 tn, 你知道是怎么回事就行。 那最终的话我们怎么来写?写呗。第二步干嘛写这个?近似河吧,也就是说面积,面积,路程不就是这个面积吗?就是阴影部分的面积。那就写呗,刚才讲的区别的地形,这一部分写的是 fx 八。那现在的话我们要换成什么?我们就换成这个微了啊, 知道就行,这个是 xi, 然后再成这样的区间宽度,打出他的 ti 就可以了,这理解了吧?那这就表示完了, 继续来看啊。我们接下来的话有一个非常特殊的运动,上边这个的话是变加速之前运动,就是速度在变化,那下边这个的话就是语音加速之前运动。关于这个语音加速之前运动的话,比如说图中这个点啊,这个点的话点 a 吧,它的坐标 我们写成 t 零 v 零。凡是学过这个高中物理的同学,他都知道这一部分的面积从哪啊?从零时刻一直到 t 零,这个时刻 整个经过的路程是多少?肯定是二分之一多少啊?二分之一 v 零 t 就可以了。那怎么求出来呢?不就是这一部分的面积吗?其实他你也可以分割成无限的部分,最后呢,求出来还是等于二分之一 v 零 t 的,你自己可以尝试一下用分割近似和曲迹性的方法来求一下。 那第二部分的话,就就是这个定积分的概念了,定积分的概念一定要好好读一下。定积分概念这一讲的话,我当时在大学学的时候呢,整整花了两个小时的时间才完全理解啊。 来看吧,定级分的定义,他是这么说的,假设函数 fx 在 a 到 b, 他有定义,然后对 a 到 b 这样一个 b 学呢,做任意的分割,就是说你不一定每一部分他这个打扰他 x 都相等啊,这个宽度不一定相等。做任意分割, 然后将什么呢?将这样一个 b 区圈分成了 n 个小区间啊,没有问题,然后任取什么?任取可赛, 他在爱在对应的这样一个区间内部,其实跟刚才都是一样的。第一步干嘛呀?分割第二步干嘛呢?第二步其实就是求这样一个核,第三步干嘛?第三步就是极限,你也能得好好读一下,然后现在干嘛呢?从这开始仔细读了啊, 且这个极限爱,极限爱是个什么东西啊?且极限爱于区间 a 到 b 的分割方法啊,他这个极限首先是存在的,而且这个极限呢,跟这个 a 到 b 这样一个 b 选的分割方法是没有关系的,你可以 一就是这 n 等分没有问题,也可以每一部分他这个宽度,但是他矮这个 xi 呢,都不相等都是可以的啊, 然后干嘛呀?继续往后读,以及他这样一个取法也没有关系,也就是什么意思呢?你这样一个变量,看在爱可以取最左边的,也可以取最右边的 xi 也可以,取 xi 减一和 xi 中间的某一个数值都可以,但是最后取出来的极限就是一样的, 此时我们就成函数, fx 在区间 a 到 b 上是客机,客机就是可以积分的意思啊, 然后呢,极限 i 就成为 fx 在 b 选上的定积分。然后怎么记呢?就这样来记,还是挺熟悉的话,我们之前是学过了不定积分,不定积分是没有这个 ab 的,这叫不定积分。那定积分的话就指的是 a 和 b, 已经告诉你 这个范围了吧,其中小 a 叫什么?小 a 叫做积分下线。哎,那这个小 b 叫做什么呀? 他这样一个整体里头,这个小 b 呢,叫做积分上线,然后 a 到 b 叫积分区间 fx, 当然还叫背积函数,然后 x 成为这个积分变量。哎,那你说这个 fx 乘 dx 这样一个整体叫什么呢?叫背积表达是,其实跟这个不定积分的名字是一样的。 后边呢,有这样一个写法,应该理解了吧,他这个人的曲均于零的意思就是每一部分不管你怎么分你每一部分,他这个宽度啊,就是这个达尔塔 x 都是曲均于零的。 那这种情况下,他的极限呢,就是定积分,我们以后就用后边这样一个专门的写法了。那现在来看了啊,现在我想说的是定积分他也成为里面积分,为什么?因为这种定义就 是由黎曼首先提出来的,那这种情况他这个求和的形式叫什么?就叫黎曼和,当然也叫积分和。那么我们规定什么呀? 你想啊, a 到 a, 你看这个图像吗?如果说他左边这个端点 x 等于 a 和右边这个端点 x 等于 b, 成何啦? a 和 b 相等,你说中间还有面积吗?那就没有,面积就是一条线,线哪来的面积?所以实际上还是从定义里头出来的,他其实并不完全是规定出来, 数学上零的阶层等于一,这个就是规定出来的,因为他更加方便计算了很多时候。但是其实这两条规定都是可以由定义推出来的。 接下来我们就要看第二点了。第二点就是可击的充分条件。什么函数一定可以积分呢?是这样的,假设 fx 在 a 到 b b 圈上连续,或者说 只有有限的第一类间断点,第一类间断点就是左右,什么左右极限都存在的间断点,叫做第一类间断点啊。 那此时则 fx 在 a 到 b 上是可击的。哦,这个意思啊,如果函数连续在 b 线上连续,或者是是有有限个第一类阶段点,就一定是可以用来定积分的。 那现在的话,我们判断一下吧,你说在一到二上可以定几分吗?可以。为什么?首先看 y 等于 f x 基本冲等函数吧,然后 y 等于 lon x 基本冲等函数吧。那 y 等于 x 乘 lon x, 这叫初等函数吧。 古董函数,你在定义率一到二上肯定是连续的吧?你既然连续的话,根据刚才我们说的这样一个条件,这其实就是一个定理,要记住的啊,所以说他在 一到二上是存在的,也就是说一到二的定计分咱写上吧, xl x 它是存在的,直接写就行了。 来看第二道啊,第二道的话其实有难度,有同学刚看到这个第二题啊,就马上想到了用牛顿来布尼斯公式来,我们现在还没有讲这个公式,你先不要用它啊,如果你要用这个公式的话,比如说咱就相当于第一种方法把它求一下,可以的啊, 这个元函数的话是谁?元函数是三分之一 x 三次方,那元数当然是三分之一 x 三次方,来一个零到一,对吧?那最后的话,当然就是把一带入多少三分之一,把零带入减零,最后就是三分之一就求出来了。但是你仔细读题了吗?人家题目是怎么说的? 让你用定计分,刚刚讲完的定计分定义来求,并没有让你套用那个公式,那现在确实有难度了, 分三步走,第一步干嘛?分割?分割成几段来着?分割成 n 段对吧?啊?第一步,先分割,然后每一段的话,也就是说零到一,分割成了 n 段啊,第一段的话,我们就继承什么了?就继承 x, 其实 x 零就是零啊, x 零到 x 一, 然后第二部分呢,就是 x 一到 x 二,第三部分一直往后写,最后一部分当然就是 xn 减一,一直到 xn, 当然这个 xn 的话其实就是一,这个你知道就行。那切下来干嘛?第一部分这个科赛一肯定在他之间,然后这个科赛二肯定在他之间,最后一直往后边写,那科赛 n 肯定就是这样取了 近似和,因为咱们要求的就是这一部分的面积,这一部分的定计分嘛,接下来怎么写啊?请告诉我。第二步,写这个近似和的时候,我们应该这么写啊,分割完了,第二步取近四呢?根据刚才的定义 也已经写完了。第三步要干嘛?第三步要取极限吧。极限指的是什么呀?指的是每一段他这个区间宽度都趋均于零啦,线动成面,最后就求出来精确的面积了。就这个含义,按照定义的话,我们很快可以得出来吗?第一步的话干嘛?分割呗?第二步的话干嘛?第二步的话取近似河,第三步就是取极限了。 对,这个栏目的代表什么含义呢?栏目的实际上代表的是最宽的那样一个区间宽度,他都是曲均零。第三步的话,要稍微注意一下这个栏目的他指的是什么?指的是最大的宽度。 当你这个最大的宽度都曲均于零的时候,那你每一部分不就都无限的曲均于零了吗?也就是曲线宽度,曲线宽度,曲径于零,那线就变成线了,原来都是矩形,对吧?线东成面,最后就求出来的是实际的等于号这样一个面积,这就是定积分了。那写到这之后的话,人家老说,老师你写到这没用啊,不会算。 确实不会算,但是要注意,定计分他跟这个区间的分割方法有关系吗?没有关系,你说怎样分割能够最容易去计算啊? 我们分割的时候分成了 n 份,我们所向分割的时候直接来一个什么?直接来一个 n 等分。 n 等分的话,你原来这个区间宽度是一吧? n 等分的话,每一部分他这个区间宽度实际上都横等于多少?都横等于 n 分之一,相当于零到一分成了 n 份,这个你知道就行。 n 等分。 那第二步,第二步的话,刚才他也说这个定计分他不仅跟这个分割的方式没有关系,他还跟这个科赛的取值没有关系。也就是说科赛你可以取 x 零 x 一,也就是左右短点,还有中间的值都可以。那既然如此的话,为了方便计算我这个科赛爱,你知道我要怎么取吗?我这个科赛爱 锁镜都取这个右侧的端点,右侧的端点的话,每一个区间右侧 n 等分。第一部分是不是有个 n 分之一啊? 什么意思呢?比如说这,这有个 n 分之一吧,第二部分是不是有个 n 分之二啊?我都取这个区间右侧的短点, 也就是说卡萨艾特分别对了,就是恩分之爱啊。那既然如此,接下来就简单了,我们只需要把什么把, 把这样一个打扰他 x 区间宽度等于 n 分之一带入,然后把这个 case 等于他也带入解决室里头,最终就可以写出这样一个表达式来了。现在你看出来了吧,这个就是那个区间宽度 n 分之一,然后这个就是带入表达室以后的结果。为什么?因为你这个 fx 本来就是等于这个 x 的平方的嘛。带入以后, 那带到这之后的话,有一个细节我希望大家注意,这个人们的曲俊玲不就相当于 n 曲俊于无穷的意思吗?因为你是无穷当分了是不是?那 再往后边写,其实就好计算了,你说从一的平方,二的平方一直加到 n 的平方,这个高中你应该就知道吧,平方和的求和这个公式等于多少啊?它是等于我直接写吧,六分之 n 乘 n 加一,再乘二, n 加一,就这个结果。当然前头的话人家还有一个什么呢?还有一个 n 的三次方分之一,你别忘了抄。 好。那写成这个样子之后的话,好说啊,我第一个 n 跟他比一下,消掉一个 n 吧。然后后边的话,我把六分之一这个长数提出来啊,那等于多少?我稍微整理一下,其实就变成这个结果了。 你看这个括号,再跟 n 比一下,那不就变成了一加上 n 分之一吗?但是还有一个 n 啊,二 n 加一这个整体再跟 n 比一下,那就是二加上 n 分之一。请你算一下,当这个 n 屈均无穷的时候,这是不是零,这个部分是不是也是零,所以最终就变成了多少呢?我这 个箭头写上来没有地方了啊,实际上也就是等于多少呢?他就等于六分之一,再乘二,那不就是三分之一吗?同学们, 原来无论你用牛顿来不及是公式,还是用定积分的定义,最终算出来,他都是精确的三分之一,这就是定积分定义一定要掌握了,三步走分割、近似和曲极线。好了,现在我们来看第三部分最后一部分,这个比较简单啊,但是你得掌握 定计分的几合一。什么意思?如果你这个函数都是大于等于零,也就是说函数图像他是在 x 轴上方,那你求的明显就是区别题型的面积,我们定义就是这么来的,这就没有什么可讲的。 但是,但是,但是,如果你这个函数图像是在 x 轴下方的话,也就是说函数值小于等于零,那么此时这个定计分表达的并不是区别 的面积,而是这个面积的相反数。哎,那为什么会有这样一个结果呢?好说,从定义来的嘛,根据黎曼和根据积分和这样一个表达,是你每一部分, 因为你这个 f 是不是负数啊?我其实乘这个高的话,我这个达尔塔 x 肯定是正数,对吧?但是我乘这个高,我是不是应该加上一个负的 fx i 啊?所以每一个部分前头都有一个富豪,每一部分都有富豪呢?最终我们把总的富豪都提出来就可以了。所以说一定要记住了, 如果说你的函数图像是在 s 轴以下的,你的面积并不是定积分,面积的相满数才是那个定积分,也就是说定积分他也是小于零的,记住这一条就够了。那有了这一条以后,接下来我就来一个小小的例题,请你写出来吧。这个好说,我们完全可以分成三部分嘛,比如说这个 横坐标 a 到 b 之间啊,我写成 c 这个点的话,写成 d, 那根据定计分,他这样一个算法,那就变成了 a 到 b, 那就先写了一个 a 到 c 呗,这个没有问题,然后再写一个什么,再写一个 c 到 d 呗。好, 然后再写一个什么,再写一个 d 到 b, 写成这三部分。写上这三部分以后的话,不用多说什么,因为第一部分的话, a 到四一之间,函数图像在 x 轴以上吧,然后第三部分也在 x 轴以上吧,所以说第一个圈的话,我们直接写成这个 s 一就行了。 然后第三个圈的话,我们直接写成什么?直接写成 s 三就可以,但是中间这个写什么,那当然是写加上负的 s 二,实际减 s 二就可以了, 懂了吧?用面积 s 一、 s 二、 s 三来表示的话,那就是 s 一加 s 三,再减 s 二才是他总的定。计分,分享他的知识,感受数学之美。我是杨帆老师,下节课再见。
3053会放羊的教书匠 05:11查看AI文稿AI文稿
05:11查看AI文稿AI文稿呃,如果说是 a 到 b 的 b 区间上单调,他就在这个区间上一定可及。呃,比如对任意的一个分法, 假设我这里把它分成了啊这样的三个部分, 然后我实际上就是还是使用这个定理一,就是可以证明这些小的常规的面积的和小于认给的这个 epc 的,那这三个面积的和,我就可以考虑把它 实际上就是这这这些这部分,那我就可以把它都平移到这个还等于 a 这条,把这条边平移到这个位置,平移完了,那这个呢? 这最左边这不用动,其他的我都可以往这边平移。那现在呢?这里边呢?这个是这一段是最短的,比如我是如果说这段是最长的,那他就是 b t, 现在呢,我可以呢让这些这个三个面积的和,就是这个三个长方形的面积的和,也就是他, 它呢就一定会小于这个。现在我就以这个,如果说这段是 d t, 我就以这个 d t 为宽,那长呢?长就是它,这个呢,就是因为如果线上递增的,那这个长度 从这到这显然就是 f b 减去 f a, 所以它就是它呢,就小于等于它。 然后他为什么就能满足定理一呢?我可以这样来做一个解释,可以这样看,就是说 f b 啊,如果我就让他小 e b c 呢?现在 f b 呢?假设他不等于 f a, 因为如果 f b 等于 f a 啊,它这是单调的, f b 就等于 f a, 所以它就是一长数函数。对于长数函数来说,就可以理解成就是这样的,所有的小的长方形的面积的和一定是零,所以它一定是零。 那如果 fb 不等于 fa, 那我就把它可以挪过来,那我只需要这个,就是这个最大的这个去,比如说我这里边就是这个这第二个这个小的区间,它是 dt, 我让它小于它, 那于是呢,这个成这个,呃,成绩的和就一定小于认给的一个 u c 呢? 我找到 d t, 那这证明就结束了,所以呢啊,这个就在 a 到 b 的 b 圈可击了啊。接着用一点时间把定力三里边这个 epset 撇儿 怎么设定的图式啊?我想做一个解释,就是这里呢,他首先是把我认给的 ebc 的平均分成两部分,其中的一部分呢,就是以 b 减 a 为 长啊,这个高呢,就是二分之一八 c 的,呃,除以比较 a, 所以这个面积就是二分之一八 c 的。然后从这到这,他一定是连续的,因为间断点只有一个,所以一定会找到这样的,嗯, deartee, 呃,当这个 d t, 当在在这个区域里边儿的这个 d t 小于这个 der 的一的时候,这些小的长方形的面积和一定小于这个长方形的面积。同样道理,这个区域域上它也是连续啊,所以它,呃一定可以找到一个 der 的二, 嗯,使得 d t 小于 der 的二的时候,对于所有的分法,它的这些长方形的面积和一定就小于这个长方形的面积。 然后就是这个关于 epc 的撇儿的设定,实际上它就是这个是二分之 epc 的,这长方形的面积是二分之 epc 的,剩下的它还有二分之 epc 的,它同样用了一个长方形,那这个长方形我就用了这个,它的这条边如果是长的话, 呃,应该是这个函数值的上确界减去下确界。呃,然后呢?这边呢?这边它是四倍的 epc 的平, 那我可以看一下,就是这两边都乘成四,那他呢?就等于他,然后我用这个相乘正好就是二分之一的,也就是说这个面积 就是二分之一的 c。 然后我从这条虚线到这条黑色虚线中间呢?我做出的根据分法都特别小, 长方形的面积的和一定被他囊括在里面,而且一定是严格的小于他啊,这样就是我对这个 epc 他撇他定力三里的做了一个解释。
5新西望 01:18
01:18


![黎曼积分_计算抛物线下面积(x²的不定积分)[manim]自学14天原创Python编程动画日常练习#微积分 #可视化 #黎曼积分 #Python #编程](https://p3-pc-sign.douyinpic.com/image-cut-tos-priv/b7e5535abcc7865ad9e93a84fe57109b~tplv-dy-resize-origshort-autoq-75:330.jpeg?lk3s=138a59ce&x-expires=2079547200&x-signature=1sn8Ykwk4r%2B%2FsaFqldcd0KYG4bc%3D&from=327834062&s=PackSourceEnum_AWEME_DETAIL&se=false&sc=cover&biz_tag=pcweb_cover&l=202511270440319AE295900E58692D8A48)











