大毛他爸买了四根一模一样的原木罐,为了拿着方便,他用橡皮筋把他们捆成了这个样子。如果这些圆的半径都是一,你能求出橡皮筋有多长吗? 仔细观察一下这根皮筋,不难发现,他既有直线部分,又有曲线部分。如果要求他的程度,必须把曲直分开来取, 那曲线和直线的分界点在哪呢?咱把这个局部放大来观察一下。如果让一个点先沿着橡皮尖的曲线部分移动,那它就是绕着圆心转到圆形的距离始终都是半径一。可一旦当它移动到直线,就不再是绕着圆心转了,到圆心的距离就会变得越来越大。像图中这个样子, 那这两种运动状态的分界点在哪呢?不难看出,就在半径与直线垂直的那一刹那,从这个状态起动,点与圆形的连线就开始拉长了。所以,这就是你要寻找的曲直分界点, 他恰好是半径与直线在垂直状态下的焦点。同理,你可以把其他曲直分解点也都画出来。在右上角就是这个点和这个点,在右下角就是这个点和这个点,在左下角就是这个点和这个点,在左上角还差这个点。 这样,橡皮筋就被这八个点分成了四段圆弧与四条线段。你只要分别求出他们的长,就有总长了。 先看曲线吧。每条曲线都是半径为一的九十度圆弧,如果把他们都拼到一起,恰好就是一个半径为一的整圆。所以弧长就是二派乘一得二派。 至于直线嘛,每条线段都恰好等于两条半径相加,所以长度都是一加一得二,那四条线段就得是二四得八,曲线和直线都有了,再相加就是总成。 所以答案就是二派加霸。除了能球总长面积,其实你也能球了。看出来没有的。取值分界点,你能很自然的把整个图形分为四个扇形、四个长方以及一个正方,把它们分别求出面积,再相加,就可以得到整个图形的面积了。 由此可见,取值分界点是解决所有问题的关键。所以我得把分界点的画法再跟你强调一遍,就是半径与直线在垂直状态下的焦点。 用这个思路,你还可以解决更复杂的问题。比方说这幅图类似一个六边形,你把这个局部放大,找一下曲折分解点吧。 根据刚才所说,必须是半径与直线在垂直状态下的焦点。所以取值分界点不是这个,而得是这个。用同样的法子,你还可以画出其他取值分界点,最终会画出十二个分界点。利用这十二 第二个分点,你就可以精准的对边界进行分段求解了。好了,关于捆原的周长与面积,我就简单讲到这,只要你知道怎么寻找取值分界点,剩下的事都好办。怎么样,明白了吗?如果明白,就自个动手试试吧。
粉丝3196获赞1.5万
相关视频
 01:32
01:32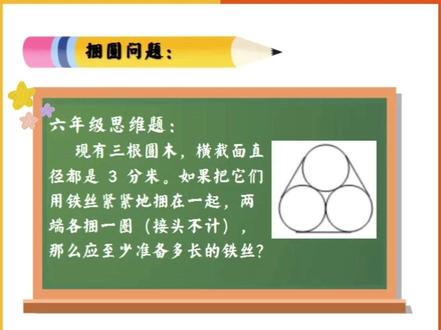 01:50查看AI文稿AI文稿
01:50查看AI文稿AI文稿如何求捆原的奏仓?首先咱们来思考一下这样一个问题,将两根直径二十厘米的竹竿捆到一起,需要一根多长的铁丝?咱们做图分析一下。分别过圆心做铁丝的垂线,将铁丝分成四段,连接两个圆心,会发现 上下两段的长度刚好等于两条半径之和,也就是直径顶左右。两个半圆弧合在一起,刚好是一个圆,所以捆两个圆铁丝长度等于两个直径,加一个圆周长。 咱们再看款三个月应该准备多长的铁丝,用同样的办法,分别过原星座铁丝的垂线,将铁丝分成六段 连接圆心,发现这三个线段跟圆心之间的连线一样长,都等于直径。 三段圆弧合在一起,刚好等于一个圆周长。咱们可以找圆心角来验证一下。这两个角都是九十度,中间是一个等边三角形,这个角是六十度, 所以圆心角等于三百六十度。减括号,九十度加六十度加九十度等于一百二十度。所以三段圆弧合起来,正好等于一个圆周长。即捆三个圆的铁丝,等于三个直径加一个圆周长,直径是三分米, 所以铁丝等于三乘三加三点一,四乘三等于十八点八四分米。直到题捆两圈,所以还要乘以二十八点八四乘二,等于三十六点八四分米, 所以至少要准备三十六点八四分米的铁丝。小结捆原问题,外圈有几个圆,就是几个直径地加一个圆周长。
103黄老师 00:17
00:17 05:40查看AI文稿AI文稿
05:40查看AI文稿AI文稿大家好,我是钟老师,我们来一起看到圆的周长的一个拓展题,我们把它称之为捆圆, 有四根底面直径是零点五米的圆柱形管子,被一根铁丝紧紧的捆在一起,求铁丝的长度, 打结处呢?用铁石的长度呢?我们把它忽略不计,那我们看到这是有四个直径是零点五米的圆柱形的这个管子,我把它捆在一起, 那用力捆完之后呢,他会把四个圆牢牢在一块,也就是求整个最外围这一根绳子的铁丝的这个长度。那这类题型我们应该怎么去做呢?我们可以去成 找规律的方法来进行,也就是从少到多,我们先看到一个圆,如果来进行捆的话呢,那么他的周长 整个就是圆的长度,所以他应该是直接是太低。那如果是两个圆捆在一起,我们这个题也做的比较多, 那他就是有两根直线,这两根直线分别是这里是半径、半径,所以这是一条直径,这也是一条直径加上两步 两个圆弧的部分,所以这两个部分上起来正好就是一个圆,所以呢它的整个周长其实就是用派的一个圆的周长加上两条直径,也就是加上奥迪好 那两个圆捆起来,他是派 d 加二 d。 那我们现在来看看三个圆的,如果三个圆把它捆在一起,我们也发现通过分解,那么这部分三个直线的部分, 那么正好是这里是一条半径,这里半径加起来这是一条直径,这是一条直径,这也是一条直径。那么同样的道理,这三个圆弧的部分 把他们拼合成一块,他正好就可以拼成一整个圆的周长,所以他是由一个圆的周长加上一二三三个直径,所以是派地加上三地。 那这里面我们其实可以发现一个规律了,那从两个圆到三个圆,再到四个圆, 四个圆是不是也是一样的呢?我们来分析一下,这一段到这一段他正好是一个直径,这一段到这里他正好也是一条直径,那么左边呢也有一条直径, 下面呢也有一条直径,而正好这四分之一的圆弧长度算下来正好就是一整个半径, 而一整个圆的周长,所以我们就可以发现他的周长其实就是太低,去加上四条直径,所以是太低加上四低,那我们也就能够通过计算了。 那么整个直径是零点五,所以呢它的周长会等于太低加上四的。用三点一四乘以零点五,算出来是一点 点五七加上四条直径,四乘以零点五,所以算出来是一点五七加上二会等于三点五七米。 好,这个题我们虽然解决了,但是我们能不能通过这个题来探讨一下关于捆原的这个公式的推倒, 那一个圆呢?就是一个圆的周长,从两个圆,三个圆到四个圆,我们发现两个圆是派的加上二的 好,三个圆捆在一起呢是派滴加上三滴,四个圆捆在一起呢是派滴加上四滴。所以我们如果无限的去加圆进去,所以我们发现如果说五个圆捆在一起,那正好融化出五条直径,那么圆形的部分刚好就是 一整个圆了,所以呢我们来把这公式推倒一下啊,那如果像这一个的话呢,我们这里画出来一二三四五六七个圆,那七个圆是不是派的加上七的呢?其实我们要发现这里是一个、两个、 三个、四个、五个、六个,所以这里只有六个直径,而六个弧形的部分刚好拼在一起,他就是一个圆的周长,所以他是用什么呢?太低去加上六滴, 这并不是这里面捆了几个圆就加几条纸巾,而应该看什么呢?看外面的这个周围的圆有多少,所以我们就把这个公式呢提炼一下,所以就把它看成是太低加 上安迪最这个安表是什么?这个安表是我们捆圆的最外这一圈有几个圆? 薛同生们记住了,捆原的公司呢,是派 d 加上 nd, 那么这个 n 表示的就是最外面这一圈有几个月,外面这一圈有六个月,所以加上六条直径,如果有八个月呢,就加上八条直径 好了。同学们,如果接下来遇到这种困员的知识,你能够快速的进行计算吗?
 00:56查看AI文稿AI文稿
00:56查看AI文稿AI文稿圆柱圆锥常考题型七、捆出来的问题,这样的一个蛋糕盒用绳子捆起来,需要绳子多长?我们看一下绳子的长度分布是这一段, 这一段的长度很明显是圆柱的直径,还有这一段很明显他也是圆柱的直径,上面有两条,下面肯定有两条,所以说直径相当于有四条五乘四。 那么这个是什么?圆柱的高,这里也有,那后面也有这样的高,也有四条三乘四, 再加上打结处需要六分米,那它加在一起等于二十加十二、三十二、三十八分米。
846董老师数学思维













