等价无穷小替换技巧
当你看到这道题目的时候,是不是觉得很简单,等价无穷小替换,把分子当中摊积的 x 替换成 x, 三 e x 也替换成 x, 比上一个什么呢?三 e x 的三次方啊,或者你把分母也可以替换成三次方都可以。那么这个时候大家会发现 x 减 x 等于几呢?零,所以很多人说,嗯,这个题目答案是等于零的秒了,显然不是, 这里面出现了一个我们等价无穷小在使用的时候一个经典的错误,等价无穷小在替换的时候不能在加减的位置上替换,要在因子的位置上进行替换,何为因子呢?就是一个因式或者乘数乘式的位置上才能够进行一个替换。好,那我们来看一下这道题的正确减法,我们还是把零带入以后,零减零比上零,那么判定出他是一个零比零型。 零比零型最常用的确定也是等价,从小会先考虑,但是由于分子呈现了一个减号的形式,我们在解题当中往往会采用先变形的方法,把它写成三 a x, 把它变成参见的 x 乘上扣三 a x。 好了,那么接下来我们看分母可以先替换出来了。 分子当中呢,我们继续阴式的这一步,把它写成摊进的 x 乘上一减扣三 x 比上 x 的三次方。接下来我们把分子当中做一个替换,变成 x 乘上二分之一 x 的平方比上 x 的三次方,那么同时摊进的 x 增加不少,替换成 x 一减扣三, x 替换成二分之一 x 的平方,那么二分之下三次方比上三次方,最后这个结果等于 二分之一,这才是等价无穷小的正确替换方式,一定要在城市的位置,大家一定要注意,也就是因子的位置才能够进行有效的替换。这道题你学会了吗?关注我,让数学变简单!
粉丝6616获赞10.6万
相关视频
 01:05查看AI文稿AI文稿
01:05查看AI文稿AI文稿公式,看着多,找到规律分分钟就能记住。我们分成三组,有三对正反三个拓展和三组相似, 三 x t x e 得 x。 四帮减一法函数分别是 f 三 x x t t x 加一 在 x 区径于零时,都等价于 x。 第三组稍长,也有技巧把 x 看成零,来倍易的零,次方减一等于零,那零加一等于零, 咱再拓展一组。如果把 e 换成 a 时,那么右边乘以浪 a al a 换成 love you a, 右边则除以浪 a。 高中被拐求倒。公式,有一组很相似,请记住出现 a 的 x 四方形式 乘以浪 a 出现闹个 a 是除以浪 a。 再拓展一组 x 加一的 a, 次方减一等价于 ax 四,把 a 换成 n 分之一,就有了上面的公式。
3068高数帮帮忙 03:35查看AI文稿AI文稿
03:35查看AI文稿AI文稿每天一节高数课,期末考试不挂科,今天我们来分享一个等价无穷小替换的一个原则,这虽然是一个比较小的知识点,但是很多人在做题的时候对这个点非常的困惑,我们来看一下什么时候可以无穷小替换,什么时候不行。 课本上写的很清楚,就只有对所求极限中相乘或相除的因式,才能用等价无穷效量来替换,而对极限中的相加或相减的部分则不能随意替换。 好,那我们来看一下这个关键的就是相乘或相除的因式。什么叫因式?我们初中都学过因式分解,你比如说 a 方减去 b 方,那我们可以把它分解成 a 加 b 乘以 a 减 b, 那这个 a 加 加 b 这个整体和这个 a 减 b 这个整体就是他的音式,这个就叫音式分解,你一定要对音式这俩字 去理解。好,那我们来通过一个例题来看一下,利用等价无穷小量来代换来求极限,他这个分子是一个坍塌, x 减三 x, 那很多同学做的时候,你就比如说像下面这个去做了, 他上来的话,直接等价无穷小替换,把弹台 x 用 x 换掉,三叶 x 用 x 换掉,分子是 x 减 x 等于零,那这样去换的话就错了,因为我们这样说的很清楚,对极限适中的相加或相减的部分是不能随意替换的, 只能替换的是相乘或相除的因式。那好,那这个题如果正确的去做的话,那第一步弹腿换成三,引出考三应,把考三应给他 题下来,分子变成了这个样子,那变成了这个样子后,我们再去看这个题,那就变成了三应乘以一减考三应这个整体,那一减考三应这个整体,他就可以成为一个因式了,就 相乘或相处的因式。那这个时候我们把三用 x 换掉,一减靠三用二分之 x 方换掉,三 e x 三次方用 x 三次方换掉,然后 x 屈进于零的时候去求极限啊,那答案出来就是二分之一。好,下面的话给大家写了一些 x 去进零的时候,一些常见的这个无穷小替换的一些结论,这个结论的话我们在下节课会去推倒啊,这个结论的话,其实你只要抓住一个关键点就行了,就这个 x 三 exxxxx 一加 x e 的 x 方,这个一定要保持一致向啊。这个很多老师包括我上次说了,他都喜欢拿狗来讲,那就狗啊,这边就是三应狗, 那同样的 x 三英狗,那你也可以一直往下写,把所有的 x 看作一个整体,或者看成一个方块,方块 三,一方块啊,这样都是可以的,把它整体换掉就可以了。好,那我们再看这个例题,这个例题的话,那我们就说了可以直接替换了,因为他没有加减的部分,就是我们这个概念里的相乘或相除的因式啊。那这块的话直接换就可以了。 阿尔克坦坦 x 用 x 换掉,三 e 四 x 用 cx 换掉,我们就说了这个是一个整体,这是那条狗,那这也是那条狗 啊,这是那个狗,这也是那个狗啊,那这样的话他就可以直接换成他了,那答案就是四分之一了。好了,我们下节课来分享一下这个的证明,今天我们就分享到这里。
2200骑哈雷的数学老师 02:07
02:07 03:08查看AI文稿AI文稿
03:08查看AI文稿AI文稿我说一遍啊,各位同学,加法什么时候等 t? 两种情况,第一,你对我们常见的替换公式你熟不熟悉?如果不熟悉,加减就别替换,你就只记得乘法可替换就可以了,这个也能解决大部分问题, 够六了。你再想加减替换的问题,加减什么时候可替换?有两种情况是可以替换的,第一是低阶加高阶,他直接等价于低阶。我们举个例子, x 确定于零的时候, x 加上 flow 扣三 x, 前面写个三 x 吧,这个你就不用考虑了,你看就直接等价于 x, 因为前面这个三 x, 它是等价 x 的,后面这个 lon cos x, 它是 lon 一,加上 cos x 减一,它等价于 cos x 减一, cos x 减一等价于负的二分之一 x 的地方。这两者什么关系?后面是前面的高阶低阶加高阶,直接等价于低阶。如果你对替换 公式不是很熟练,我跟你讲,这个玩意一点用没有,你看你什么情况?第二个法则,同阶的相加,并且只要系数和不为零, 则可替换。相加的时候系数不能互为相反数,相减的时候系数不能一样。这你就记得啊,同接相加,因为减也是加嘛。所以我就总结这一句话,同接相加,并且系数和部位里则可替换。 举个例子,怎么替换?首先我给他中间减个一,再加个一 cosinex 减一,等价于负的二分之一 x 方,一减去 e 的 x 方次方,这个等价于负。 这两个不是同接的吗?那你一看系数和是不为零的,那么就可以替换等价于负的二分之一 x 方减 x 方,也就是负的二分之三 x 方加法,就这两种情况可替换,那什么时候不能替换?那就是同接相加,并且 系数和也为零,比如说 x 区零, cosine x 减去 e 的负二分之一 x 方, 你要么呢?可以落,被打也可以,他能展开吗?我找到下一节不就完了吗?对他实现降为打击。你看这个例子,我如果给他减个一,再加个一,这就不行了,因为系数和是零啊,你这个扣三 ex 减一等价于负的二分之一 x 方。后面呢?等价于二分之一 x 方的除以和是零,这个就不等值的等级了, 攒到下一节就行。一减去二分之一 x 方,加上四的接长分之 x 的四次方,再加小 ox 的四次方。 e 的 x 次方等于一加 x 加上二的阶长分之 x 方,再加小 ox 方。一减去二分之一 x 方,再加上 二的阶长分支。负二分之 x 方,加小 ox 的四次方,这就行了,括号打开二十四分之 x 的四次方,加上小 ox 的四次方, 减去八分之一 x 的四次方,再减小 ox 的次次方,等于负的十二分之 x 次次方,再加小 ox 的次次方等加于负十二分之 x 的次次方。 好,这个就完事了。第三种情况,如果同阶相加,系数和也为零,那你就他的展开展到下一节就可以了,也可以有更简单的处理方式,都展开就行。做题他就是这样子啊,你要不想动脑子,你就算的慢一些。
2110李擂讲考研数学 01:06查看AI文稿AI文稿
01:06查看AI文稿AI文稿使用等价无从小代换的时候一定要记住一个原则,只适用于乘除,不适用于加减。本题中首先把 x 趋向于零,带入原式,发现分子、分母 限值都是零,是个零比零型,于是转入第二步化点,发现没有可以化减的项。来到第三步,等价代换。因为分母是相乘形式, 直接把 ex 减一,换成 x 把,所以分母直接代换成 x 的立方分子部分是两式相减,不可以代换。原样抄下来,在这个式子当中,既没有代换的,也没有化减的。来到最后一步,洛必达法则 上下同时求导,下面求导是三 x 平方,上面求导是 second 方减一。此时利用三角公式把分子换 成潘金的完全平方,除以三 x 方。再次按照求极限的四部曲,此时潘金的完全平方带换成 x 方,除以三 x 方,最后结果是三分之一。
534利哥谈升本 00:49查看AI文稿AI文稿
00:49查看AI文稿AI文稿当你看到这道题目的时候,是不是很开心?这不就是等价无穷小替换吗?直接秒的一亿到这里。恭喜你,你做错了,这个是大家在使用等价无穷小的时候容易犯的经典错误。无穷小指的是当 x 区域 x 零时, f x 也要趋于零,并不是 x 区于零的任何式子都是无穷小。因此提到无穷小,要说明自变量的趋势,比较两个无穷小是否为等价无穷小,也要在同一自变量趋势下。正确的做法是 think 分之一。虽然在 x 区于零时 期限不足,但他是一个有界函数,所以这道题是无穷小乘以有界。这道题的灵,你学会了吗?快按你专升本的朋友来学习!
2582圣泊老师教数学(专升本) 16:37查看AI文稿AI文稿
16:37查看AI文稿AI文稿这个视频中呢,我们将会讨论一个非常重要的问题,等价无穷小到底什么时候可以用? 很多同学在做题的这个过程中啊,他用等加无穷小,然后就容易出错,那出错的根本原因在哪?他其实不在我们本身,而是在等加无穷小这个方法。 因为等价无穷小他并非真正的完全相等。比如说撒引 x 和 x 是等价无穷小,但是你用 x 去替换撒引 x, 就有可能出错。因为我们的撒引 x 和 x 并不是真正的相等,他俩只是近似相等。 所以就是说你这个替换以后可能会出错,因为你横等变形的话,他永远不会出错。那我们怎么才能是做到横等变形呢?你用 type 公式就可以做到这个横等变形 泰勒公式呢?它是非常精确的一个表达,但实际上我们要展开到足够高阶的话,那你这个泰勒公式也相当复杂。 所以说泰勒公式他其实也只需要展开到前几阶他就够用了,只要足够精确他就可以,并不是说一定要完全精确, 能明白我意思吧?那这样的话,等价文胸小和泰勒公式两者,你到底啥时候用等价文胸小,啥时候用泰勒公式呢?你用等价文胸小怕出错,你用泰勒公式,你又怕太麻烦,展开的次数太高了,对吧?有一个基本的判断原则, 如果说你使用等价无胸小,那你就考虑他会不会丢掉高阶无胸小。如果说你使用他的公式,那你就考虑会不会产生不必要的高阶无胸小,这样的话,你就能把它区分开了。 好,我们现在来看几个例子啊。先看第一个例子,第一个例子求极限啊。这个分母 x 很简单,分子 r x 减去 c x, c x 能用等加我们选 x 直接去替换吗?可以。为什么可以? r x 减去 x, 它是得到的是 x, 它并非是零,这个时候就可以。如果说减法的话,如果说减去你得到的是一个零,那你这个时候你要考虑你是不是把高界无穷小丢掉了。 再看这个分母,分母其实也是一次方,从泰勒公式的角度来展开的话,那你这个分子只需要我每一项每一部分都展开到一次方是不是就够了?那你撒,一 x 展开到一次方,实际上就是我们的等价文,胸小 等价无穷小,只不过是拿了我们泰勒公式的最前面的一小部分,能明白我意思吧?假如说我们就不要用这个等价无穷小,我就要展开啊,我把它展开到足够高阶,那你看行不行? 我二 x 减去三一 x, 三一 x 加 x 加开始多少 x 减去六分之一 x 的立方,对吧?然后它比上 x, 那这样的话,分子就变成了 x 加上六分之一 x 的地方比上 x, 对吧? 这个时候是不是抓大头就行了?你抓大头后面,这是高阶无胸小,因为我们的 x 是趋近于零的嘛, x 塞槽是更比 x 更高阶的无胸小,那你直接去掉是不是只剩下它了?这个时候跟我们的等价无胸小使用是不是一模一样的?所以说这个时候你用等价无胸小就没有问题 啊,你直接用啊,这就是第一个。那我们再来看第二个。第二个题目, x 减于零的时候分母足够简单,没有问题吧?看分子,分子是两项相乘, 这个时候你考虑左边这个 x 加上 san x, san x 可以使用等价无胸小吗? 可以。那右边的这个三 a x 可以使用等价无穷小吗?不可以,不可以。看左边的这个 x 加上三 a x, 它如果说用等价无穷小得到的就是二 x, 对吧? 右边的这一部分 x 减去三一 x, 如果使用等加五小,它就会出现零。出现零的时候,你要考虑到这个不对,你要反应过来这个不对,所以说立马把它展开到泰勒公式 展开到三次方,用它的公式把它展开,懂我意思吧?所以这个题目呢,你就可以这么做, 它呢就等于 limit x 区间于零的时候, x 加上 x 乘以 x 减去三 x 展开,是 x 减去六分之一 x 的立方,对吧?这个样子,然后再比上 x 的四次方,对吧? 你看前面这个,这个是不是二 x 接接下来往往下继续啊?化解一下,二 x 乘以后面这是六分之一 x 的地方, 再比上 x 四次方,得到大概是多少?三分之一啊?同样的,如果说我们从太大公式的角度来考虑, 那前面这个我说的刚才上面说的每一项,实际上就是加减号把它隔开的,这样的每一项你每一项都要展开到足够高阶, 就是跟分母的次数是一样的,那你看下面这个分母次数是四次方,因为它俩是相乘的,这个其实你要当做一个整体来开的呢,不要把它隔开,懂我意思吧? 如果说 x 加三 x, 你用它的公式展开的话,那就是 x 加上 x 减去六分之一 x 的立方,对吧? 那左边这个得到的就是二 x 减去六分之一 x 的立方,也就说这一部分是六。二 x 减去六分之一 x 的立方 就是这个。你用 r x 减去六分之一 x 的立方来替换的话, r x x 和六分 d x 立方相乘得到是不是 x 四次方?那你后面这个 x x 方和 x x x 方相乘,是不是得到六次方?六次方是比我们的四次方更高阶的无穷小。这个时候你说他需要吗?他不需要,他不需要。 实际上如果说啊,前面一个是 x, 一个是 x 的三次方,后面这是个 x 的三次方,你就可以当做这样,我们把系数全部去掉,就可以当做这样来处理,对吧?这样来看的话,这项和它相乘, 也就说这两项相乘得到的是 x 的四次方,这两项相乘得到的一定是比 x 的四方更高阶的无胸小,因为我们的 x 三次方是 x 的更高阶的无胸小。所以说这一项你就不用考虑了,你不要再展开到 塞接了,这个就不需要了,能明白我意思吧?这是我们的第二,然后我们来看这个第三啊,第三说求这个极限 靠三 x 减去 e 的负二分之 x 的平方,我把它复制粘贴一下 放到下面。 对于他来说啊,很多同学这个办法是有的啊,他就说 limit x 区间于零,我分子减一个加一个考三, x 呢?我减谁?减一嘛?然后再加上一减去一的 负二分之 x 的平方次方,然后比上 x 的四次方,对吧?那这个时候是加。 其实我们的加减法要慎用等价无穷小,而不是不要用,他可以考虑用,但是我们的乘除法通常来说你可以正常的使用,就没有啥问题。 懂我意思吧?乘乘除法用等加五小基本没有啥问题,但是其实也有注意的点啊,我们这个例题讲完再说, 对于他来说啊,你看这个分母是四次方,那你这个直接用等价问小,得到的是负大分之一 x 的平方, 对吧?后面这个直接应用等价五小时二分之一 x 的平方,第一个方面它这次数一定是不够的,它的每一项如果说这个开做一个整体,这个开做一个整体,每一项你等价 五角以后得到的是二次方,那你看分母是几次方?四次方。所以说你使用等价五角的时候,同时你要观察这个分母呢,要跟分母的次数要保持一致呢, 就是你得达到达到这个四阶才行,四阶往后的五阶你是不是不需要了?六阶是不是也不需要了?你不要管他,但是四阶你一定要达到了。 另一方面还有个问题,就是说你这个二一二分之一 x 的平方,减去二分之一 x 的平方,就是他俩相当于相加嘛,就会出现这样的情况,这两个最终得到的是零。也就是说不管加法还是减法, 你使用等价无穷小以后,你出现得到零的情况,那你这个时候就要考虑你是不是把高阶无穷小丢掉了,也就是说我前面这个这句话怎么说的? 使用能加无穷小,你要考虑会不会丢掉高阶无穷小,你一定要考虑这个问题,然后使用他的公式会不会产生不必要的高阶无穷小,也就说泰勒公式,你更高阶的你展开没有任何意义,因为他展开以后依然相当于是更高阶的无穷小,他会削掉你抓大头就能把他直接抓掉。 那这个题我们只能是用 tele 公式把它展开以后就很方便做了啊。那这样的话,我们展开一下它呢?就等于 limit x 区间于零 x 的四次方分支。 考三 x 减一嘛。考三 x 我们直接展开啊,这个态度公式一定要非常熟悉。一减去二分之一 x 的平方,再加上四的阶成分之 x 的四方,四方是不是就 就够了?用我们的分母,最高次方就是四次方,再加上小欧 x 四次方,这足以。然后再说后面这个一的 x 方啊。我们先说一的 x 方展开这个公式一定要熟记, 一加上 x 加上二的结成分之 x 的平方,这是不是就够了?我为什么再没往上展?因为我知道它的指数是负大分之 x 的平方,我展开到这个 x 的平方以后,这个这个平方会得到一个四次方,这就够了,对吧? 那前面这个相当于是负的二分之一 x 的平方,然后再加上这是多少四的阶程?四六二十四嘛。二十四分之 x 的四次方 没有问题吧。然后一减去一的负二分之 x 的平方, e 的负二分之 x 的平方,次方也给他展开啊。呃,考场上你要足够熟练,直接写他,懂我意思吧,直接写他 一减去二分之 x 的平方,然后再加上二的阶层分之四分之 x 的平方,那也是八分之 x 的四次方,然后再加上小 o x 的四次方,然后这应该是平方啊,这个地方小 o x 平方啊,这是平方。 那现在把它带进来啊,一减去它,那就是二分之一 x 的平方, 然后再减去八分之 x 的四次方,没有问题吧?这个消掉,这个也消掉,那最后我们就得到 limit x 区间于零 x 的四次方分之 负的二十四分之二嘛,负的十二分之一嘛,是不是他得到是负的十二分之一啊?这个答案就对了。 那接下来我们说这个事情,乘除, 原则上来说,你可以使用等价 win 小,可以随意使用等价 win 小, 但其实他也有一定的条件啊,一会给你举个例子,加减呢,要慎用 加减法将。刚刚应该说的比较多了啊,那我们现在说这个乘除乘除有个例子,哎,你看这个能不能用 limit x 区间无穷手 e 的 x 平方乘以烙印一加 x 分之一比上是比上一的 x 方。那你说这样能不能直接用等价无胸小?不可以,不可以。虽然这个看似是一个乘法, 但实际上啊,你仔细观察,这其实是个无穷,这个是个无穷,嗯,这是个无穷,这个相当于是趋近于零的,对吧?这是个无穷小酿,对吧? 我们要使用等价无胸小啊。乘除里面使用等价无小说的是 a 乘以 b, 这两个都趋近于零的时候,他俩使用等价无穷小。并不是说任意的乘除啊,任意的乘除不行啊,任意的乘除不行,他俩必须同时趋近于零的时候。 这是第一个地方啊。第一个地方还有一个要点,我举个例子,写个 t 立 limit x 区间于零的时候, x 的 size 方分之 x 乘以烙印一加 x, 然后再减去 x 的平方,然后再加上 x 的 size 方。那你说这样的烙印一加 x 能直接用等加无穷小去替换吗?你看前面这一部分,这是无穷小亮吧,后面烙印加 x 也是无穷小亮吧。两个无穷小相乘。哎,刚说了乘除你是不是可以任意用, 但实际上它不是这么回事,它其实也有一定的要求,也就是说 如果他是一个能当做一个整体的话,整个分子上他都是 a 乘以 b 的话,那你使用是没有问题的。但是说他如果说是仅仅是极限中的一小部分, 后面又有加减号的时候,这个时候你又要考虑了,他到底能不能用,实际上他不能用。如果说用的话,那这个答案就是 x 平方减去 x 平方,加上 x 的三次方,然后比上 x 三次方,他俩销掉得到的极限是一对吧。但是你仔细观察我们的分母是三次方啊。那你这一项你用等价文学展开以后,实际上只到了哪只到了二次方?你还有三次方,是不是没有展开到位? 所以说它还是不能用啊,你用等下无效。不行,应该这么做, limit, x 区间于零, x 三次方分之 x 乘以它泰罗公式展开展开到几次方够?二次方就够,因为我前面已经有了一次方了,一加二得到的是三,懂我意思吧, x 减去二分之一 x 的平方, 后面不用写了,再减去 x 平方,再加上 x size 方,对吧?现在呢?我们是不是得到 这个极限,应该是得到的是二分之一,对了吧?这样的话就对了啊。所以说我们纵观下来要考虑问题啊,并不是说简简单单的 说用什么别人教你的什么方法来判断啊,你应该用我最基本的这个原则 啊,用我这个原则能明白我意思吧?极限它相当于是一个整体,不要拿一部分去做一些貌似可行的处理,能明白我意思吧? 嗯,现在大家应该比较清楚了吧,如果还有其他的疑问在评论区留言啊,然后我会录制视频给大家解答。好,这节课就到这。
5065考研数学清沐 08:20查看AI文稿AI文稿
08:20查看AI文稿AI文稿在上一期的视频当中,我们对下边这一个求极限的问题给出了一种做法,其中有百分之四十多的同学认为这种做法是错误的,但实际上这种做法是正确的, 他们认为错误,错误的理由是什么呢?错的理由是我们在这个地方利用了等价无穷小的替换,他不敢保证这种替换是正确的, 因为他在课堂上上课的时候,老师曾讲过一句话,说等价无穷小的替换在乘法或除法当中可以随意用, 但是在加减法当中不能够随意用,那么他用词说在加法减法当中不能随意用,不是说不能用, 而是在满足了一定的条件之后,加法和减法当中仍然是可以使用的,而且使用的时候 过程会变得更加的简单。你比如说这一个题是不两步就做出来了,当然这个题有人也提出来说我用诺贝达法则,很快,也有人提出来说我用胎了,公式也可以。 当然大家的想法都很对,但是如果你会用等价无从小的替换,是不是更加的简单一些?那么下边我们就来讲一讲等价无从小的替换,在加法或者减法当中,什么情况下能够使用? 好?我们假设有一个无穷少量,阿法是一个无穷少量,说明他是区域零的,贝塔也是 区零的,也就是说阿法和贝塔都是什么东西嘞?都是无穷小量,简称无穷小。然后我们再假设阿法和贝塔这两个无穷小啊都已经找好了他的替身,假设他的替身是他, 然后再假设他的替身是他。那么我们前边已知的就是说第一种,如果是阿法和贝塔是成的形式 乘的求极限的形式好求极限,那么他就等价于什么呢?直接让他们两个的替身上场去求,或者第二种情况,求极限,他们两个是相除的形式,就等价于直接让他们两个的 替身上场。但是在除法当中要注意,分母是不能为零的,分母不能为零好,此时要注意分母是必须不能等于零才能用它。 但是我们在题目当中碰到的第三种情况就是求极限是加法的时候 能不能直接让他们俩的替身上场,也就是说能不能直接变成他的替身,加上他的替身上场之后再求期限呢?那么此时必须要满足条件,那么条件什么呢?条件就是我给这两个 将要做替换的这两个无穷小做笔直求极限,如果极限不 等于负一,那么此时我就可以在加法当中任意的去变换好。那么第四种情况,如果是在减法当中呢? 什么时候能够让他们的 t 神上场嘞?那么也有条件,条件就是 我给这两个做笔直求极限,如果极限值不等于一,那么他们两个就可以在减法当中换成他们相应的替身来计算极限。那么这个十字我们再把它看一看,能不能再总结出一些更加好记的结论, 比如说第三点,我们来看第三点,第三点最后的解冻什么呢?说是阿尔法跟贝塔作笔直求集 线不能等于负一,如果等于负一就怎么办?如果等于负一,我要是换进去,是不是这个地方就等于零了? 哎,如果这里等于一是不这个地方放进去也就等于零了,所以我们把它说的再简单一点。在加法和减法当中,能够让替身上场的条件就是,当我把他们换成替身之后,加法 他加上他不等于零,和他减去他不等于零, 如果加起来不等于零,那么在减法当中就能换,如果减完之后不等于零,那么在减法当中就能换。所以第三点和第四点我们可以简计成下边的这个结论。下面我们再来 看一道例子。假设求极限 x 去于零,上边是 ttent, x 减去三 ex, 下边是 x 的三次方,那么这个题目能不能用等价无穷小的替换?我们先来判断判断一下, x 区域零的时候,摊正的 x 替身是 x, 商议 x 的替身也是 x。 好,这个替身和这个替身这个地方是做的减法,替身相减之后怎么样等于零呢? 替身相减等于零。回到刚刚的结论,在减法当中,如果替身相减不等于零才能替换,那么现在 等于零了,等于零就说明不能替换, 替身不能上场说明减法此时换了就错了。但是我没有想到在乘法和除法当中可以任意换,所以我把这个题目能不能想方设法把这个减法改写成乘法或者除法的形式? 好,我来改写 x 区域零。好, tangent x 不变 song x 等于什么嘞?我们知道 tangent x 是等于 sunny 除以 cosine 的,那么也就是说桑 in 就等于 constant 乘以 cosine, 我把它换掉就等于 constant 乘以 cosine x 的三次方。再继续分子,此时有公因式 tangent x 会把它提出来,提完之后剩下一减去 cos i x, x 的三次方下边我们仔细观察,仔细观察,发现我可以此时把分子当成两项,前边的贪整的是一项,后边的一减 cosine x 是一项, 变成了两部分的乘法,而两部分的乘法是我们可以用等价了。 tangent x, tangent 狗等价于狗, 一减 cosine x 等价于谁?是不等价于二分之一 x 的平方是不继续利用等价狗,此时就可以换掉了,换掉之后,结果最终等于 x 取零, x 乘以二分之一 x 三次方下边是三次方,好,这里是平方,该约的约掉,最终结果等于多少?等于二分之一, 好,所以这个题目是不能随便用。我们再回到我们上一期的视频当中这个题目来,这个题目前边的替身是三 x, 后边的替身是五 x, 三 x 减去五 x 是不等于负二 x 不等于零,他不是零, 不是数字零,所以它是可以做替换的。那么这一类型的题目,如果你在专升本考试当中懂得懂得了这个条件,对于某些题目来说还是比较快的。这一类型的题目你会了吗?
342贾哥专升本高数 00:31查看AI文稿AI文稿
00:31查看AI文稿AI文稿当你看到这个题目的时候是不是很开心,这不就是等价无穷小替换吗?只需要代入,轻轻松松秒的零到这里。恭喜你,你成功的做错了,这个是等价无穷小替换使用的一个经典错误,就是等价无穷小替换要在因此就是乘法的位置上, 不能发生在减法里,正确的做法是先变形得到这样再使用等价无穷小替换,这样才是正确的答案。快艾特你的朋友来学习!
4396圣泊老师教数学(专升本) 07:36查看AI文稿AI文稿
07:36查看AI文稿AI文稿为什么在极限的计算中,一用等价无穷小就很容易错?为什么有些老师会告诉你,在加减法中一定要慎用等价无穷小? 想弄明白这个问题,你就要先搞清楚泰勒公式和等价无穷小之间的关系。简单的来说,等价无穷小就是泰勒公式的一个简化的版本, 因为它是简化的版本,所以呢,它的这个应用的范围也受到了限制,它主要是应用在这个乘除法中,加减法一定要慎用,或者说你就不用,你用 tal 公式就可以,也不会很很麻烦的。 那他是怎么简化的呢?他用的就是极限加减法中的吸收性。 你比如说啊,对于 san x 来讲,它的这个泰勒展开式是这样的,它实际上有无穷多项,只不过我们把这种更高阶的无穷小通通写成了这样的形形式啊,比 x 的三次方更高阶的 无穷小,我们都给他写到一个像里边了。那如果我们用吸收性啊,什么是吸收性呢?就是我们只留下那个最高级的东西。什么是最高级的?我们根据这个表来看, 左边就是高级的,右边就是低级的 x 在 x 区零的这个前提条件下,它是一个低一阶的无穷小,因为它是一次方嘛,剩下的这些相对于它来讲都是高级的,所以说通通舍去,最后就变成这样, x 等价乘 x, 那这个等价无穷小和泰勒公式在这个具体的计算中到底应该怎么用呢?啊?我先给大家讲一个这个最一般的规律啊,任何一个式子,当我们拿到它的时候, 都可以给他进行一个划分啊,分块分成就怎么分呢?你把它分成若干的几个部分,而这些部分之间呢,都是乘法点成或者这种除法的关系。 这个括号内部啊,有可能加减乘除都有,但是这个括号之间啊,他们都是乘除法的关系,任何一个式子,你经过变形啊,都可以化成这样一种形式。这个时候你就要注意了,在这个括号内, 我们进行计算的时候,我们一定一定要慎用等价无穷小,尽量用泰勒公式去算,因为呢,这个括号内部啊,他们是加减法是存在的啊, 而且我们用泰罗公式的时候,尽量要往后多展两,多展几项啊,省的有一些我们需要用到的项数啊,被省略了。一般来说呢,展到三项就够了, 然后再通过我们之前提提到的这个啊,吸收性,把每个括号中啊,最大的那一项,最高级的那一项找出来。 你比如说像这这道题三个括号,那就有找出三个项啊, a, b、 c, 最后把它们进行一个计算,最后再带入我们前提条件, 比如说 x 区域零啊,你看两个具体的例子啊,第一道题啊, limit x 区域零,三 x 比比上 x, 那这道题我们如果分块分成两块,而且我们发现这个, 呃,这个括号内部,他没有加减法的,那我们其实在括号内部进行计算的时候啊,是可以用等价无穷小的,他不会出错。如果我们用等价无穷小这道题怎么算? 把三 x 等价乘 xx 比 x 等于一好,这道题就很轻松就做对了。那我们看第二道题,第二道题我们也给他进行一个划分,划分成两块好,我们就发现分子啊里边是有一个减法, 那如果这个时候我们再去强行用等价无穷小去算,很容易就出错。你比如说呀, limit x 区域零 三 x 等价乘 x x 减 x 比上 x 三次方,那是零比 x 三次方等于零啊,这就是一个很经典的错误。那正确应该怎么做呢?正确,碰到加减法要用泰勒公式的, 要用泰勒公式。用泰勒公式的目的是什么?目的是把它之后的后续的那些项写出来,而后续的那些项就是解题我们需要用到的关键的项。你比如说等于 limit x 区零 san x 的泰勒展开式,我们刚才背过了,是这样的, 然后减去 x 比上 x 的三次方啊,经过化解是这样一个形式, 那在这一步中,这个分子啊,我们已经给他化点好了,但是呢,你会发现, 呃, x 的三次方相对于这个部分来说啊,这一部分的含义就是说,呃,比 x 三次方更高阶的无穷小,那它实际上呃是要被舍去的,因为吸收性嘛,它的等级会更低啊,它就没有了。最后的答案就等于 负的三的阶层分制, x 的三次方比上 x 三的方等于负六分之一啊,这就这才是一个正确的答案啊。所以呢,呃大, 大家通过这样一个例子很清晰的就看出来,为什么等价无胸小。有的时候你用它,尤其在加减法中是错误的,因为它省略了 本来应该用泰勒公式出现的后续的那些项,而这些项在加减法中是有可能被用到了,因为在这里你看 x 和 x 是抵消掉了,那它就不能代表这个,呃,它就不能代表这个是这一部分的最高最高级了,那它的最高级就得接着再往下找,你在这接着再往下找,你就必须要用脑 tele 公式。 那大家在之后做题的过程中啊,自己去多多尝试啊,看哪些情况下用等价无穷小可能会更便捷,哪些情况下用太 公式才能做出准确的答案啊?一个非常重要的关键点就在这,你一定要把这个谁是高阶的,谁是啊?谁是高级的,谁是低级的,这个关系一定要理顺啊。无穷大是大于非灵长寿的, 是大于无穷小的,是大于零的,那无穷小中低一阶的无穷小是比高一阶的无穷小要更高级的,在无穷大中是相反的,高一阶的无穷大是大于低一阶的啊,这个应该很好理解吧,因为 它本身 x 区域零,那你 x 的平方,那肯定你这个是没有 x 的一次方要大的,因为次数越高相当于它的值越小嘛。 好,那就希望大家在做题的过程中,不要再因为呃不够理解等价无穷小的这么一个本质,而呃用它导致你做做错题了。
937加减乘除WarmMath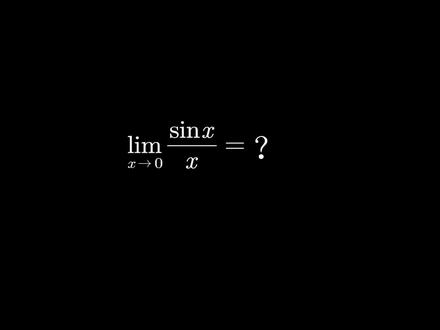 01:59查看AI文稿AI文稿
01:59查看AI文稿AI文稿上期说到这个极限,极限中没有很明显可以直接约分掉的因式,不过我们可以用逐渐逼近的方法来计算,我们这里让 x 的取值不断逼近零。直观的看一下 x 分之三 x 变化趋势,我们分别代入一、 零点八、零点六、零点五,看到 x 分之三 x 接近一的趋势,我们再带入更小的数,零点四、零点三、零点二、零点一,可以看出 x 接近零, x 分之三 x 接近一,这样我们就知道 x 分之三 x 在 x 区域零时的极限是一。 现在我们知道了,在计算极限时遇到三 x 除以 x 的情况时,我们就可以用类似前一级的方法把它们直接约分掉。比如这个极限约分掉 x 和三 x 之后,再代入 x 等于零。但是如果极限表达式中只有三 x 没有 x, 又 该如何应对呢?我们可以先分子和分母同时乘 x, 构造出类似前一题可约分的局面,然后再约调三 x 和 x。 当然每次这样乘除约分也很麻烦。 我们可以发现之前的操作其实和直接把三 x 替换成 x 效果是一样的,所以熟练之后我们见到三 x 直接把它替换成 x 就行了。虽然这个题还没有解出来, 但是我们已经向前迈了一大步了。类似三 x 这样的函数还有很多,他们趋近于零的时候都可以直接当做 x 来处理。以下列出来的函数,遇到之后都可以像三 x 一样直接替换成 x, 我们把这些函数取个名字叫做 x 的等价无穷小。大家注意了, 这里是极限计算的一个门槛,就好像小学计算八乘七的时候,我们直接背下来等于五十六,而不是真的把八个七加起来算一样。计算极限 的时候,我们也不能每次都列表格,真的让 x 一点一点趋近于零。所以要想熟练的计算极限,等价无穷小,必须像乘法口诀一样烂熟于心才行。那么学到这里这道题你知道应该等于多少吗?
2165考研数学李老师
猜你喜欢
- 1.9万韦奈奈এ








