毕达哥拉斯勾股定理图怎么画
粉丝625获赞2047
相关视频
 00:53查看AI文稿AI文稿
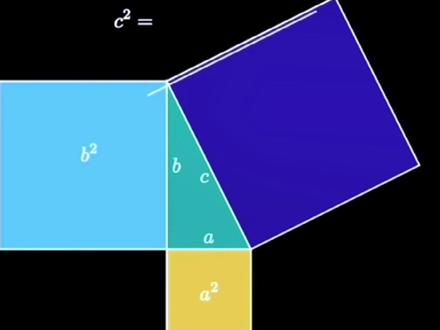
00:53查看AI文稿AI文稿为了证明必达格拉斯定理,以边长为和 b 斜边长度为 c 的三角形为例,现在在边长上分别画正方形,面积分别为的平方和 b 的平方,然后在斜边上画一个面积为 c 的平方的正方形。以下是一个证明,证明了 c 乘以 c 的正方形中包含的面积等于其他两个正方形的面积之和。 想象一下长度,维 c 的这两条线穿过 b 乘以 b 正方形的中心,然后他们将 b 乘以 b 正方形的边长切割成了 b, 加上除以二和 b, 减去除以二的长度。然后我们可以将得到的四个部分移动到 c 乘以 c 的正方形上,像这样,剩下的中间部分也是一个正方形,你可以验证其边长位, 因此我们可以将一乘以的正方形移到内部。因此我们已经证明了 c 的平方等于 b 的平方加上的平方。其中为何 b 是直角三角形的两条腿的长度,而 c 是斜边的长度?这就是必达哥拉斯定论,由亨利杜登尼证明。从开始。
1.3万科普宇宙 00:59查看AI文稿AI文稿
00:59查看AI文稿AI文稿你肯定知道勾股定理,但是你可能不知道他是怎么被发现的,历史上第一个发现并证明勾股定理的人呢,是必达格拉斯。这个数学大佬,有一天在参加聚会的时候,注意到了地上的地砖,由于这个聚会比较的无聊, 就选择了一块地砖,以这个地砖的对角线呢为边换了一个正方形,他发现这个正方形的面积恰好等于两块地砖的面积之和, 这个就成功的引起了我们这位天才的好奇心,于是呢,他又更换了一些不同大小的地砖,发现这个结论都是成立的。他就开始大胆的假设,任何直角三角形,其斜边的平方恰好等于两边的平方之和,这个就是我们著名的勾股地理了。 可惜呢,贝达哥拉斯的这个证明的过程已经失传了,但是有一样东西流传了下来,就是他还根据这个勾股定理啊,画出了一个可以无限重复的图形,这个图形在重复足够多次之后呢,会变得非常像一棵树,这个就是勾股书了。
128917赫兹 02:46
02:46 02:53查看AI文稿AI文稿
02:53查看AI文稿AI文稿用 scratch 编程画分型几何图形系列之九,必达哥拉斯树必达哥拉斯树是由必达哥拉斯根据勾股定理所画出来的一个可以无限重复的分型图形。又因为重复数次后的形状好似一棵树,所以被称为必达哥拉斯树,也叫勾股树。 勾股定理,直角三角形,两个直角边平方的和等于斜边的平方。故此,两个相邻的小正方形面积的和等于相邻的一个大正方形的面积。而同一次数的所有小正方形面积之和等于最大正方形的面积。三个正方形之间的三角形, 其面积小于等于大正方形面积的四分之一,大于等于一个最小正方形面积的二分之一。根据所做的三角形的形状不同,重复做这种三 角形的必达哥拉丝树的枝干茂密程度就不同。必达哥拉丝树的生成机制是从一个大正方形开始的。在该正方形的上方建立两个较小正方形, 三个正方形的相邻便构成一个锐角为 sata 的直角三角形。不左正方形的边长为大正方形边长的 cosita。 用正方形的边长为大正方形边长的 ccta 对这两个较小的正方形重复,这一过程,得到四个更小的正方形。如此继续下去,生成机制如下图, 先建立画实心正方形和未知存取的子程序,便于地规子程序调用。再来设计地规程序,最初停止地规 n 零。按上述规则,先画本级正方形。在地规化本级的另外两 两个较小正方形主程序设置好一些初始值,比如地规的层级、初始正方形的长度和初始位置和方向等等。由于 set 值的变化,勾股数在较小角那边占用宽度大, 而且又是从第一个正方形的左下角起笔,因此这个起点位置要根据 c 特值适当动态设置,有兴趣的读者动手试一试。 必达格拉斯树的一个变种是改变正方形之间的夹角,比如第一步时,让两个较小的正方形和大正方形之间的夹角为六十度,三个正方形之间的三角形成为等边三角形, 这导致组成数的每一个正方形的边长都相等。这一变种到了第四步开始就会发生重叠,最后形成了全等的正方形组成的一个大六边形。 你会编写这个地规程序吗?提示,每一集的长度规模不变。第三个小正方形的位置和方向要注意正确找到。 根据地规的深度适当设置边长 r 的值。根据 sata 的变化做一个动画程序,演示各种状态的必达格拉斯数。正方形是空心石又如何?
22刘汉杰 01:02查看AI文稿AI文稿
01:02查看AI文稿AI文稿必答克拉斯数。我们看下这道题,如图,所有正方形的面积和是六十,这些正方形和是六十。求最大正方形的面积,怎么办呢?我们看一下最大正方形,他的边长正好等于这个直角三角形的斜边,我们把它标成 c, 那么这个直角三角形的两条直角边,我们分别写成 a 和 b, 根据勾股定律,我们就能得出 a 的平方加 b 的平方 等于 c 的平方,那么这个 c 的平方正好等于这个最大正方形的面积。那么我们就能理解最大正方形的面积,每一次向外扩张就增加与他面积相等的面积,那么第一次扩张增加了与他 面积相等的面积,第二次过账又增加了与他面积相等的面积,一共增加了几 几个?最大的正方形增加了两个,加上它本身一共是三个,三个一共是六十,每个就是六十,除以三等于二十。你学会了吗?关注我,每天学数学!
492大超数学课堂 01:03
01:03 08:10
08:10 00:47查看AI文稿AI文稿
00:47查看AI文稿AI文稿如图,已知大正面积是十平方厘米, 图形中所有的三角形都是直角三角形,求所有正方形的面积之和。 上个视频中我们讲到两个蓝颜色的面积恰好等于什么呀?黄颜色的面积。那么同样的道理,两个绿颜色的面积等于一个蓝色的面积,那就四个绿色的合到一起也等于一个大正方形这个蓝色的面积。 那整个图形我可以看出是五层,每层都是一个大正方形的面积。我们来看一下。 哎。所以说,那这道题答案就是多少呢?五十你听懂了吗?











