三角函数初三
粉丝9735获赞2.7万
相关视频
 11:45查看AI文稿AI文稿
11:45查看AI文稿AI文稿去年山东青岛的这道题,然后这道题他也是属于多边形结构,因为你自己观察一下什么叫多边形结构啊?就是这个现在你应该能理解我们前面所说的什么叫多边形结构问题,就是他里边会涉及到很多的结构形式,对吧?你像江苏盐城的这个 一个多边形结构,再到山东青岛这个是不是也是一个多边形结构?再到下面辽宁鞍山这个是不是也是多边形结构,对吧?就只要这种,他的解题技巧都是固定的。我们来看一下山东青岛这道题啊,他说准备测量一栋大楼 bc 的高度,那是不是就我已经知道了我们现在的目标是不是就去求这个 bc? 这个线段长,对吧? 现在给了我们观景平台斜坡第一的长度,也就这节长度,给了我们是二十米,是这一节长,又给了坡脚是三十七度。那你说我们之前是不是一直说他给的这个角度,如果参考数据里面又正好有这个角,那说明这个角你铁定会用到,而且你不会不用往后去看, 你自己都能猜到这个角你会怎么去用,肯定是把它放到直角三角形那边去用,对吧?你怎么样把这个角放到直角三角形,放到哪一个直角三角形啊?这个第一长都给了你是二十,这个角是三十七度,你是不是想都不用想,我都知道我要延长这个 a e, 对吧?或者说过点 e, 像这里做垂线段,假设焦点是 f, 你是不是放到这个直角三角形里面去?为什么?因为这个是二十,这个角是三十七度,我是不是就可以利用三人三人三十七度和可三人三十七度,我是不就可以把这个 e f 和 d f 的长度是不是可以直接给他算出来了,对吧?然后我们三人三十七度是不是就等于这个 e f 比上它的斜边 d e? 而 e f 是不是我们现在要去求的 d e 的长度提干是不是给了是二十?那三零三十七度是不是约等于五五分之三,对吧?也就说它约等于五分之三,这样的话,我们是不是可以直接算出来这个 e f 的长度是多少?是不是二十乘以五分之三嘛?是不是就是十二米,对吧?那 e f 长度 算的是十二,然后接下来是不是同样的 cosine 三十三十七度是不是可以把这个 d f 长度算出来?应该是约等于十六米, 对吧?是不是哦,它会约等于十六,因为 crazy 三十七度是不是就等于这里的 d f 比上 d e 嘛?对吧?那你是这里是不是 crazine 三十七度是不是就五分之四?所以你 d f 是不是就二十乘以五分之四算出来应该是约等于十六,对,对吧?所以我们后面的条件不看,你只看到这里的二十和三十七度,我们都能猜到辅助线是不是就给我点一下这里做垂线段? 然后接下来他是不是又说斜坡 d e 的底部 d 距大楼底端 c 的距离 c d 是七十四,那就代表告诉我们这一节长度是七十四吗?那你说这一节是七十四,这一节是十六,是不是就告诉我们整个 c f 的长度是不是就知道了? 是不是七十八十在九十,是不是七十四加十六,是不是?整个 cf 的长度是不是就九十,对吧?然后他又说与地面 cd 垂直的路灯 ae 高度 是三,然后又给了我们这一节长度是三,然后而且他都说了于地面 cd 垂直,那他的意思是不是就是刚才你把 a 延长 aef 整个三点一条线,而且跟 cd 垂直,对吧?那这一节是三,这一节是十二,是不是得到了整个 af 的长度是不是十五?现在说从顶楼 b 测得路灯 a、 z 的顶端 a 的浮角是四十二点六度,让我们去求这个大楼 b、 c 的高度,然后这个地方你自己注意一下题干给的这四十二点六度在他的参考数据里面有没有出现,如果他出现了,那说明这个奖励铁定了会用到,而且你会怎么用? 我问一下同学,你会怎么用?是不是直接过点 a 向 b、 c 做一个垂线段,或者你过点 a 向这里做一个垂线段也是一样的,对吧?也就是你们把这个 e、 a 这条线我们给它延长,然后交这个点,我们假设基围这个这个 m 点可以吧?这里是不是就是垂直的?这个我们肯定是要把这个参考数据连着四十二点六度放到直角三角形里边,那是不是就放到了这个直角三角形里边?那你怎么去解这个直角三角形呀? 现在只有这个角度是四十二点六度,然后这个 b、 m 的长度知不知道 b、 m 的长度是不是就等于这里的 c、 f 的长度呀?因为这里正好是一个矩形嘛, 对吧?那 c、 f 的长度我们刚是不是算出来了?七十四加十六是不是就是九十?那这样的话,这个是四十二点六度,我们要去求 b c 的长度, b c 是不是等于这里的 m f? 看你这个 a e e f 全都知道了,我只要把 m a 只要截出来了,是不是 b c 就直接求出来了?那 m a 怎么来求啊?就直接放在这个直角三角形里边嘛,是不就是 penite? 四十二点六度是不是等于这个 m a 比上这个 b m, 也就是 m a 比上九十,而 tony 的四十二点六度体感给的是多少?约等于十分之九, 那么是不是可以直接把这个 m a 的长度是不是就可以直接算出来了?是不就是约等于多少?是不是就直接把这个九十乘过来吗?是不是就九十乘以十分之九?是不是直接约等于八十一米?那你 m a 的长度只要算出来了是八十一, 他再加上三,再加上十二,是不是八十一,再加上十五,最后算出来是不是这个大楼 bc 的高度是多少呀?是不是直接就是九十六米, 对吧?你最终算出来 bc 的高度应该是九十六米。所以这道题也是一样的,就是我们应该要对题干里面的这个角度特别的敏感,如果他题干给的这个角在参考数据里面正好又出现了,那这个角是铁定的要放到直角三角形里面了,就想都不用想的。然后这个是山东青岛的这道题,我们最后再来看一下辽宁鞍山的这道题,也是一模一样的 说小明和小华约定一同去公园游玩,公园有南北两个门,北门 a, 哎,那就是代表这是一个, 对吧?在南门 b 说明这个是一个门, b 也是一个门,对吧?这是北门,这个是南门,然后他是不是说北门 a 在南门 b 的正北方向,我前面是不是说只要体验里面说到什么正北、正东、正西,他给你这句话是什么意思?就是在提醒你真的有直角,就是在提醒你有直角,对吧?然后说小明 自北门 a 出发,也就说这个地方是小明出发的位置,然后他先沿南偏东三十度的方向前往游乐场地,比如往这个方向上走,而小华呢,是从南门出发,也就是小华是在这个地方,对吧? 然后他是怎么样呢?他先沿正东方向走了一百五十米到达 c 处,也就是说这一节长度是一百五十,我们给他标一下,对吧?是不是先到达了 c 处,然后干嘛呢?再沿北偏东二十二点六度前往地处 处与小小明汇合,对吧?也就是大家最最后都是在这个点地处汇合,这节是一百五,然后到点地,而小明是不是从 a 直接到点地?现在说两人所走的路程相同是什么意思?这个条件给我们是什么意思?是不是就告诉我 ad 这个?这句话出题人给我是不是已经告诉我一个等式了,也就是 a、 d 这个线段长等于 b、 c 加上 c、 d 是不就告诉我这个?而 a、 d 我们现在还不知道, b、 c 长给了是一百五, c、 d 长现在也不知道。所以接下来我是不是就知道,我肯定是要结合题干里面给的这些角的角度,把 a、 d 长度表示出来, 把 cd 长度给他表示出来,一个等式减一个未知数吗?对吧?这肯定是我们通过这个来建立等式,然后他现在是不是让我们求的是什么?求的是不就是 ab 这两个南门之间的距离?那我们怎么样去求这个距离呢?我们是不是说你一定要从体干所给的这个角度上下手?一个是三十度三, 我们肯定是要把它放到直角三角形里面去进行研究的,对吧?哪个直角三角形不用我提醒,你应该也得也知道,我肯定是过点 d 向 a、 b 做垂线段,假设垂足点交为点一, 对吧?肯定是像他做垂线段,然后呢,这个二还有一个二十二点六度,而二十二点六度在参考数据里面有没有?你一定要记住哦,题干给的这个角不一定是一定会用到的,但是如果这个角在参考数据里面出现了,那说明这个角铁定会用到,而且这个角你会怎么去用?一定是把它放到直角三角形里面去用,那你这个角怎么样?放到直角三角形里面 肯定是过点 c 像 d、 e 做垂线段,假设焦点是 f, 对吧?所以接下来我们肯定是在这个直角三角形用一次,在这个直角三角形里面再再用一次,然后在这个地方去建立等式,对吧?那有没有发现?哎,感觉怎么这个直角三角形,这个 d、 e 长度, d、 f 长度不知道,这个 c、 f 长 长度也不知道,这个 d、 d、 c 的长度也不知道,没有任何一个长度是知道的。然后这个直角三角形呢?这个 d、 a 长度是不是也不知道?题干也没给 a, e 长度也不知道,然后只有这个 e、 f 和这个 b、 c 长度相等是等于一百五,其他所有的东西全都不知道,那这种我们怎么办? 你是不是必须要去设未知数了,对吧?因为他现在未知的东西实在太多了,我们这个怎么办?我们可以把这个 df 假设成 x, 可以吧? 如果 d、 f 是 x, 哎,那整个 d、 e 的长度是多少呀? d、 e 的长度是不就是一百加 x? 因为 d、 e 是不是就是 e f 加 x 加 d f 嘛?也就是这个 b、 c 加上 x, 而这里应该是一百五,不是一百, 对吧?应该是一百五十。因为这个 b、 c 长度是一百五十吗?是不是一百五十加 x, 是不是这个第一长?哎?那第一长是一百五十加 x, 这个角是三十度,在上面这个直角三角形,我们独立的一个一个三角形去看啊, 在这个直角三角形里面,这个角是三十度,这是一百五加 x, 那我们要求的这个 a、 d 长是不是直接就出来了?那三十度所对的直角边是斜边的一半,所以 a、 d 是不是就是等于二倍的 d、 e 也就是三百加二 x, 对吧?你 a、 d 的长度是不是就表示出来了?那接下两步是不是还要再把这个 c、 d 的长度求出来吗?那 c、 d 怎么来求?是不是放到这个直角三角形里边去, 对吧?我们要去求 c、 d, 这个是 x, 是不是 x 比上 c、 d, 正好是这个角的三因值,是不是就是三因?二十二点六度, 它是等于 d f 比上 d c, 也就是 x 比上这个 d、 c, 那这样的话,我们是不是可以求出来这个 d、 c 的长度是不是就是 x 除以三以二十二点六度,也就是 x 除以十三分之五? 因为三二十二点六度约等于十三十三分之五吗?所以 d、 c 是不是就约等于五分之十三 x, 对吧?取一个倒数 d, c 是五分之十 三 x, b, c 是一百五十加。我们是不是可以直接把 a、 d, 把 d、 c 全都带入到这个等式里边来? a、 d 是不是就是三百加二 x 等于一百五十,加上 c、 d 是多少?是不是五分之十三 x? 你接下来是不是直接去解这个一元一次方程,说可以直接把 x 值解出来了,对吧?我们把它移向移一下嘛,这个二 x 挪到右边来,五分之十三 x 减二 x 是多少?是不是就是五分之三 x, 再把这个一百五挪到这边来,三百减一百五是不是等于一百五? 那你不是可以直接把这个 x 解出来了?应该是等于多少?是不是一百五十乘以五,再除以三三和一百五约了是不是?五十五十乘以五是多少?二百五十 是不是直接算出来?然后一定要看清楚这里是不是让我们最后结果要取整?我之前说了,你一定要注意题干这里说的到底是什么,对吧?是不是取整这个 x? 我们最后约算出来的结果约等于是这个,我们刚说是二百五十米,对吧? 但是你算出来的这个只是这个 x 的值,他最后要求的东西是这个 x 吗?不是啊,他问的是从 a 到 b 的距离,你这个 x 解出来了之后,他是一二百五十,那说明整个第一的长度是不是就知道了?是不是一百五加二百五是多少?是不是四百? 那它是四百。我们是不是可以把 a e 的长度是不是可以直接解出来了? a e 的长度在这个直角三角形里面吗?这个边是四百,这个角三十,你是不是可以直接把 a e 求出来了? a e 只要求出来了,然后下面这个这个边 x 是二百五十,这个是二十二点六度,你是不是可以把这个 c f 解出来了?在这个直角三角形里面再把 c f 求出来, cf 知道了, a 也知道了,你把他们俩一相加,整个 a b 是不是就直接出来了?我们最终后面这一步交给你自己去算了。我们最终算出来这个 a b 应该是约等于一二九三米,约等于一二九三米,你可以自己动笔去算一下,看一下最终的结果对不对?因为你必须要自己从头到尾做一遍, 你才能梳理清楚这道题的整个解题逻辑是什么样子啊。所以我们发现多边形解构问题看似很难,对吧?但他其实跟我们前面所讲的几种类型基本上还是一模一样的,对吧?不管是胁迫问题,还是我们前面所讲的是两个三角形有一个重叠边,这种情况就是做解直角三角形这种解答题,他的技巧就是 是什么?就是他题干所给的这个角度是我们的突破口,如果这个角在参考数据里面出现了,那这个角就铁定了会用到。 如果他这个角在参考数据里面没有出现,那这是我们要干嘛?你要去分析这个角和参考数据里面这个角,这两角之间的关系是什么?是他们俩之和等于一百八,还是他们俩之差等于九十度?你要去做做一下拆解, 对吧?那以上就是我们解直角三角形,整个这一张去年所有的这些真题我们已经全都讲完了,然后你自己一定要去详详细细的再去分析一下这三个大热门题型,他的解题技巧和解题方法。哦,那这个视频我们就讲到这里了,我们下一个专题再见哦,拜拜。
522二师兄讲数学(非直播号)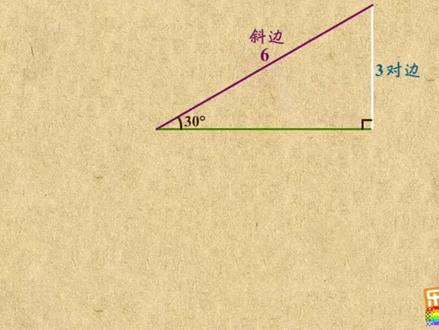 03:25查看AI文稿AI文稿
03:25查看AI文稿AI文稿这是一个三十度角,咱以他为内角做一个直角。三角形就是一块你已经很熟悉的三角板,其中这条边叫做三十度角的对边, 这条边叫做三十度角的斜边,这条边叫做三十度角的鳞边。根据之前所学的知识,如果我告诉你对边的长是一,那你一定知道斜边的长就是二。如果我告诉你对边的长是三,那你也一定能推出斜边的长就是六。 换句话讲,不管三十度角的对边与鞋边具体长度是几,只要三十度角这个角的大小不变,那对边与鞋边的比始终都等于一比二。 这说明对边与斜边的笔直,其实是由三十度角所决定的,与三角形大小无关。与之类似的还有对边与鳞边的比,以及鳞边与斜边的比, 他们都与三角形大小无关。你像三十度角的林边比上三十度角的斜边,就等于根号三比二。而三十度角的对边比上三十度角的林边就等于一比根号三。 这一系列笔直都只与三十度角有关,而与三角形的具体大小无关。所以,数学家给他们起了一个统一的名字,叫做三十度角的三角函数。 为了把这些三角函数互相之间区分开来,他们又起了三个不同的名字,把对边与斜边的笔叫做三十度角的正弦击做三,三十度。把林边与斜边的笔叫做三十度角的余弦记做扣三三十度。 把对边与林边的比叫做三十度角的正,切记做 thantan 的三十度。根据刚才的结论,三、三十度就等于二分之一,扣三三十度就等于二分 根号三探探的三十度就等于根号三分之一及三分之根号三三十度角的正弦、鱼弦和正切。你已经明白怎么回事了,那别的角的这三个三角函数你会求吗? 比如咱来算算四十五度的三角函数值,你同样以四十五度为内角做一个直角三角形,显然三边的比为一比一,比根号二。根据定义,正弦是对边比斜边,那它就等于一比根号二,化解后就是二分之根号二。 而余弦是林边笔,斜边这两边的笔显然也等于一比根号二,画奖后就是二分之根号二。至于正确,他是对边与林边的笔,结果就等于一比一得一。其实,对于任意一个锐角,你都可以像刚才这样借助直角三角形来计算他 三角函数。比如这个角 a 要求他的三角函数,你就以 a 为内角做一个直角三角形,把对边比斜边的笔直记做散 a, 鳞边比斜边的笔直记做扣散 a, 对边比邻边的笔直记做 tentana。 进一步的,如果我告诉你这个直角三角形恰好就是三四五,那三 a 就是三比五得五分之三,扣三 a 就是四比五得五分之四。弹弹的 a 就是三比四得四分之三。 以上就是三个常用三角函数的定义。关键就一点,牢记这三个三角函数的算法。对于任意一个锐角 a 而言,以他为内角做一个直角三角形,角 a 的正弦散 a 就是对边比斜边角 a 的余弦扣散 a 就是邻边比斜边 交易的正切探探的 a 就是对边比邻边。怎么样,记住了吗?如果记住,就快快去刷题试试吧!
5351高斯竞赛数学-G 07:01查看AI文稿AI文稿
07:01查看AI文稿AI文稿现实生活中测量物体的高度, 特别像旗杆、高楼、大厦、塔等较高的不可到达的物体的高度,需要我们自己去测量,自己去制作仪器,获得数据,然后利用所学的数学知识来解决问题。 那会利用到什么样的仪器和怎样利用三角函数的方法来测高的?我们一起来了解下吧。 第一步,测量阳角或辅角首先,我们需要先自制一个侧脚仪,它由肚盘、纤垂和枝干组成。是这样的,制作是需要注意枝干的中心线、纤垂线和肚盘的零度刻度线重合,否则测出的角 角度就不准确喽。肚盘的顶线、 pq 与枝干的中心线、千垂线、零度刻度线要互相垂直,并且肚盘有一个旋转中心,是千垂线与 pq 的焦点。当肚盘转动时,千垂线始终垂直向下。 侧脚仪准备好了之后,把侧脚仪的枝干竖直插入地面,使枝干的中心线、牵垂线和肚盘的零度刻度线重合, 这是肚盘的顶线。 pq 在水平位置上,接着转到肚盘,使肚盘的直径对准较高目标 m, 记下此时铅垂线所指的度数及角 bca, 那么这个角 bca 的度数就是较高目标的阳角。根据这个图形,我们不难发现,角 bca 加角 bc b 等于九十度,角 mce 加角 ecb 等于九十度。角 bca 和角 mce 都是角 ecb 的余角,根据同角的余角相等,因此角 bca 等于角 mce, 那么我们只要读出角 bca 的度数,也就能读出羊角 mce 的度数了。这里角 bca 等于三十度,因此角 mce 也就等于三十度。 测量浮角和测量仰角的步骤是一样的,只不过测量浮角时转动肚盘的直径是对准低处的目标的 转动结束后记下此时铅垂线所指的度数。同样,根据同角的与角相等的原理,铅垂线所指的度数就是低处的浮角了。第二步,测出底部 可以到达的物体的高度。底部可以到达就是在地面上可以无障碍的直接侧的侧点与背侧物体底部之间的距离, 比如这里 na 这段线段就是底部可以到达的距离。要测的物体 mn 的高度,首先在测点 a 处安置侧脚仪,根据第一步测得 m 的阳角, nce 等于三十度,接着测 a 到物体底部 n 的水平距离, an 等于一百二十米, 量出侧角移的高度, ac 等于两米。根据这些信息就能求出物体 mn 的高度了。 在 rt 三角形 m e, c 中叫 m c, e 等于三十度, a, n 等于 e, c 等于一百二十米,所以 tendon 叫 m c, e 等于 m e。 除以 e c, 其 m e 等于 tendon 角 mc 一乘一, c 等于一百二十乘三分之。根号三等于四十倍,根号三米。 又因为 n 一等于 a, c 等于两米,所以 m n 等于 m 一加 e, n 等于四十倍,根号三加二米。这就是测出底部可以到达的物体高度的原理。那如何测量底部不可以到达的物体高度呢? 所谓底部不可以到达,就是在地面上不可直接侧的侧点与背侧物体的底部之间的距离的。 比如测量一个高峰的高度,中间的距离层层阻碍,没有办法直接测出侧脚仪与山峰之间的距离。同样在侧点 a 处安置侧脚仪,侧得 m 的阳角角, mce 等于阿尔法。接着在侧点 a 与物体 之间的 b 处也安置一个测脚仪, ab 与 n 都在同一直线上,也测到 m 的阳角角。 md 一等于贝塔。角度测完了,测长度, ac 等于 bd 等于 a, 侧点 ab 之间的距离是 b。 根据直角三角形的边角关系,在 r t 三角形 m, e, c 中角 m c, e 等于 arfa, 则 tangent arfa 等于 m e 除以 e, c, e, c 等于 m, e 除以 tangent arfa。 在 rt 三角形 m, e, d 中角 m d, e 等于贝塔,则 tendrin 贝塔等于 m, e 除以 e, d, e, d 等于 m, e 除以 tangent 贝塔。根据 c, d 等于 a, b 等于 b, 且 c d 等于 e, c 减 e, d 等于 b, 所以 m e 除以 tangerine r 法减去 m, e 除以 贝塔等于 b, m e 等于 b 除以 tangent arf。 分之一减贪准贝塔分之一的差等于 b 乘 tangent arfa 乘单准贝塔除以 tanger 贝塔减 tangerine arf 的叉。最后用 m e 加 e n 的距离就是 m n 的高度了, 这就是利用三角函数侧高的方法。步骤总结下,首先需要准备侧脚仪,通过侧脚仪测出倾斜角的度数,接着分为底部可以到达的物体和底部不可以到达的物体的高度,来测量底部可以到达的物体,利用一个侧脚仪即可。 底部不可以到达的物体的高度则需要通过两个侧脚仪测出的羊角,再通过三角函数的知识来把高计算出来。 来看一道题目吧。在一次活动中,阿道 站在距离旗杆底部 b 处六米的 d 处,仰望旗杆顶端 a 侧的羊角为六十度,眼睛离地面的距离一低为一点五米。同学们能帮阿道求出旗杆 ab 的高度吗?结果精确到零点一米,根号三约等于一点七三二。 先来分析一下题目,根据题目中的意思可知,四边形 b、 c、 e、 d 是矩形,所以 b、 c 等于 d、 e。 然后在 r、 t 三角形 a、 c、 e 中,根据 tendon 角 a, e, c 等于 a、 c 除以 e、 c, 这样就可以求出 a、 c 的长了。 因此,因为 b、 d 等于 c 一等于六米,角 a、 e、 c 等于六十度,所以 a、 c 等于 c 一乘 tend 六十度等于六乘,根号三约等于六乘一点七三二约等于十点四米。最后求得 ab 等于 ac 加第一等于十点四,加一点五等于十一点九米,因此阿道仰望的这根旗杆的高度约为十一点九米。 好了,同学们,我们本节课堂到这里就结束了,利用三角函数侧高,大家都学会了吗?观看完整版课程,关注花花老师!
838花花老师动画乐学园
猜你喜欢
- 70.1万40629537633












