平面解析几何直线
粉丝564获赞2610
相关视频
 03:55查看AI文稿AI文稿
03:55查看AI文稿AI文稿一条视频教会你线面角。今天我们学习如何利用空间向量研究空间中直线和平面所形成的角, 类似于研究空间中直线和直线所成的角。首先我们要明确范围,空间中直线和平面所成夹角的取之范围为,大于等于零度,小于等于九十度。那么在空间中直线 l 和平面 pi 是 相交的关系, 平面 pi 呢,有 n 一 向量和 n 二向量代表的两类向量来表示。直线 l 呢,有 n 三向量和 n 四向量两类 方向向量来表示。那么如何利用方向向量和法向量来研究空间中直线和平面所形成的角呢?我们做一个结面图给大家直观的展现,这是我们的平面 pi, 这个是我们的直线 l。 我 们可以发现平面 pi 的 法向量有 n 一 向量和 n 二向量,而直线 l 的 方向向量呢,有 n 三向量和 n 四向量两类,此处形成了两类四个角度,也就是 r 法和 v 塔。那么我们如何通过平面的 法向量和直线的方向向量来将真正的直线与平面所成夹角转化成为方向向量与法向量间的角呢?我们一起来看。 在阿尔法和贝塔处,类似于空间中直线和直线所成的夹角。阿尔法可以用 n 一 向量、 n 四向量、 n 三向量二向量的夹角来度量,得到这样的关系式。而贝塔呢,可以用 n 二向量、 n 四向量、 n 三向量和 n 一 向量所形成的夹角来度量,也就是得到了这样的关系式。 同理,在这里可以看到 alpha 和 beta 一定是互补的,那么我们就有关系, alpha 就 等于 pi 减 beta, 我 们给它套上余弦函数的模子就是 cosine alpha 等于 cosine pi 减 beta。 此处又用到了诱导公式,我们可以得到 cosine alpha 等于负的 cosine beta, 于是就有了这样的结论, cosine alpha 可以 通过 n 一 向量、 n 四向量、 n 四向量、 n 二向量、 n 二向量、 n 三向量和 n 三向量和 n 一 向量的夹角与弦值的绝对值来表示。这个地方如果忘记了,我们可以复习一下空间中直线和直线所成夹角的这个视频,那么我们知道了 法向量和方向向量锁成夹角阿尔法,或者说锁成锐角阿尔法如何度量?那么这个阿尔法和真正的线面夹角之间有什么关系呢?我们进一步探索。在直角三角形当中,我们会发现 c 塔和阿尔法是互余的,那么阿尔法和 c 塔相加就应该是二分之派。通过一项我们就会发现 ar alpha 是 等于二分之 pi 减 theta 的, 我们给它套上 cosine 的 模子,那么就是 cosine 二分之 pi 减 theta 等于 cosine alpha。 此处又用到了什么?对诱导公式,我们就会发现 cosine 二分之 pi 减 theta 根据诱导公式可以化简成为 sine theta, 那 么 cosine theta 照抄就得到了 sine theta 等于 cosine alpha。 那 么此处注意,这里的 theta 是 真正的空间中直线和平面所形成的角,而 alpha 呢,是 平面的法向量与直线的方向向量所成夹角之一。从微观上讲,此处的 c t 和阿尔法不仅角度不同,而且形成的类型和原理也是不一样的,只是 c t 的 正弦值和阿尔法的余弦值或者阿尔法余弦值的绝对值,从宏观上看,二者的数值是相等的, 所以我们就得到了空间中直线与平面所成夹角的度量方式,也就是三 c, 它等于 n 一 向量和二向量夹角余弦值的绝对值,其中 c 它 是直线与平面所形成的夹角,而 n 一 向量呢,是直线 l 的 任意非零方向向量。 n 二向量呢,为平面派的任意非零法向量。此处记住,要用这公式一定别忘了绝对值。那么我们也要注意这个 theta 和此处的 n 一 向量和二向量 加角,它们从微观上讲不是同一个角,角度不一样,形成的原理也不一样,只是我们线面角的正弦值和两个向量余弦值的绝对值在数值上是相等的,也就是角度不同,量值相等,你学会了吗?
17悟空数学工作室 02:03查看AI文稿AI文稿
02:03查看AI文稿AI文稿同学们好,今天我们来学习高中数学中的重要内容,空间直线与平面的平行关系。 首先我们来看直线与平面平行的定义和判定方法。如果一条直线和一个平面没有公共点,我们就说这条直线与平面 alpha 没有任何交点,我们记作 l 平行于 alpha。 直线与平面平行的判定定理是,如果平面外一条直线与平面内一条直线平行,那么这条直线与平面平行。我们来看图示,直线 b 在 平面 alpha 内,直线 a 在 平面外。 如果直线 a 与直线 b 平行,那么我们可以得出直线 a 与平面 alpha 平行。 接下来我们学习两个平面平行的判定方法,如果两个平面没有公共点,我们就说这两个平面平行,记作 alpha 平行于 beta 平面与平面平行的判定定理式,如果一个平面内有两条相交直线分别平行于另一个平面,那么这两个平面平行。 在平面 alpha 内有两条相交直线 a 和 b。 如果这两条直线都平行于平面 beta, 那 么平面 alpha 与平面 beta 平行。 最后让我们总结今天学习的内容,直线与平面平行的判定通过证明平面外直线与平面内直线平行来实现。 平面与平面平行的判定通过证明一个平面内两条相交直线分别平行于另一个平面来实现。解析的关键是找到平行线,然后利用判定定理证明平行关系。 希望同学们通过本节课的学习,能够熟练掌握空间直线与平面平行的判定方法,谢谢观看!
22知象视界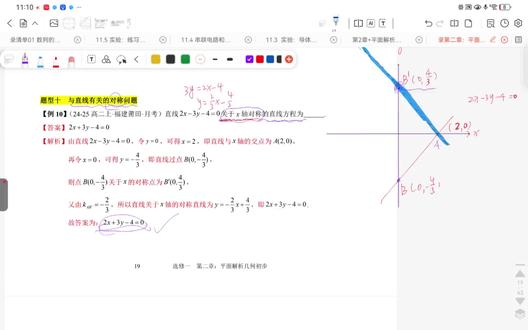 04:00查看AI文稿AI文稿
04:00查看AI文稿AI文稿题型时与直线有关的对称问题,他看到右边这个图像,我们很容易算出 a 点的坐标是二零 b 点坐标是零负三分之四。 题目中告知我们这条直线关于 x 轴对称,那么我们现在看到 ab 片这条直线,它的关于 x 轴对称的点 b 片就是零三分之四。 在此时我们知道 ab 撇的两个点,这两个点我们可以用两点求出斜率, 负三分之二斜率啊,那我们再随便找一个点,此时直线方向就写出来了点到直线的距离公式。第十一题目,套公式就行了啊,这个也没有任何难度。第十二题, 这个是两条平行线之间的距离公式还是套公式?放大一点,大家看一下,公式我写出来了,画圈里面就是了,然后算出来,答案是它,答案选 d。 与距离有关的最值问题, 这是我们初中时候学的叫将军一马的类似的一种题目。他问我们 p a, p b 最小, p a 加 p b 最小,那我们这里面像照镜子一样,这个 l 直线就是镜子。然后寻找关于 l 这条直线对称的点, a 撇,这很容易算出来, a 撇的坐标是四二, 不会算的同学可以看这个地方,这两个方程就出来了一二二,然后知道这两个点两点之间距离公式,就算出来是十。他问说表示一个曲线, 表示的曲线是一个圆,我们现在对这个进行推导,就我们初中的完全平方公式, 那推导完之后,这个是不是就是圆的,它半径的平方,那半径就等于它, 我们知道根号里面肯定必须大于零的,不能等于等于零,圆就不存在了,所以解出来之后就这个值,所以答案选二 b。 第十五题,圆的标准方程和一般方程。 这个题目他告诉我们焦点是 m, 我 们把 m 点这个很容易算,然后他说是圆心,圆心那就是它, 然后他告诉半截是它。送分题答案选 r, b 啊,直线告诉我们圆,告诉我们它们的位置关系,让我们看一下圆心到直线,它的根据距离公式算出来是它, 他是小于半径的,说明他们一定是相交,是气体。圆的切线问题,他问这一条切线 我们明明叫 l, 这个 l 他的方程是多少?我们知道他过的这个点是二负二,我们现在还缺斜率, 那我们知道 ac 的 这个点是 a 点啊,我们知道 ac 的 斜率很容易求出来两点坐标嘛,都知道 c 的 它的坐标是多少,圆心就是一负一, 那么 a, c 的 斜率不就出来了吗?那么切线的斜率就出来了,因为两条直线垂直斜率相乘等于负一的,那么直线方向也就很容易写出来。
18老王维修数学 09:13查看AI文稿AI文稿
09:13查看AI文稿AI文稿本期视频呢,我们来说一下节气几何中关于直线的一个倾角与斜率的关系,以及它们的一个推导证明过程。 而我们大家都知道呢,如果一条直线,它的倾斜角如果是 sine, 那 它斜率就等于 tan d sine, 是吧?好,下面我们来说一下关于两条直线,两条直线它的一个倾角以及斜率之间的对应关系。好,我们先说结论啊,我们先说这几个常见的结论,第一种, 都为你的 c 大 角啊,两条直线如果相等的话,剪切角相等的话,你可以推出这两个斜率呢,一定是相等的。然后第二种,如果两个倾斜角呢,它是互余的关系, 那可以推出什么?可以推出你的斜率之积呢?等于正一啊。第三种,如果呢,你的 c 大 二减 c 大 一,如果等于九十度了啊,存在这个关系,那可以推出来什么? 推出来你的两个之积呢?是等于负一的啊。第四种, 那我们如果你 c 大 一加 c 大 二等于一百八十度互补的关系,你可以推出什么?推出 k 一 呢?是等于不得 k 二相反数的关系 啊,这个我相信第三个,这个常见的,大家肯定知道,这是垂直的关系是吧?那这个是什么?连道之间是平行的关系啊,像第二个和第四个, 嗯,大家可能会有那么常见是吧?啊,这,当然,这这这两边都是可以互推的啊,是互推的,一般情况下都是可以互推的,你只要留意那些 并给脚等于零度啊,或者是其力不存在啊,你要注意这些特殊的情况就可以,正常的情况下,这是可以互推的啊。 好,下面我们来说一下它的一个退套方法啊,它的一个方法,首先我们看第一种是把 c 态一等于 c 态二的时候,为什么它的弹力极绿洲看到了, 试探一下。 c 打一艾鲁一吧。 c 打二,那鲁二,好,那这个很简单,说你 k 一 就等于汤底, c 打一,你 k 二就等于汤底。 c 打二, 那那 c 那 c 加一等于 c 加二,那肯定 k 一 就等于 k 二了,那这肯定就是个平行线啊,这个很好说,我们看第二度, c 加一呢,加 c 加二,它说等于了九十度。说好, 然后我们看一下,哇,重来, z 加 e 加 c 加二,如果等于九十度是什么意思呢?比如这 c 加 e 在 l e, 你 另外以道线的, 哎,它是 c 加 r 嘛,两个加起来等于九十度,那这个叫 l r。 那现在看 k 一 等于什么? k 一 等于 tan t c 大 一, p 二等于什么? p 二等于 tan t c 大 二。好,那我们把这个 c 大 二呢换一下啊, k 二等于 tan t x 点二等于九十度,就是二分之 pi 去减 c 叉一了,是吧?我们用一下那个呃,三角函数中的关系啊,二分之 pi 减一个 c 叉到了第一象限是吧? 第一项键的话都是正的,那就是口三 d 喽。哦,单 t c 大 一,好,大家知道口三 d c 大 一跟单 t c 大 一是什么关系?是不是互为倒数的关系?所以你 d 一 等于 g 二啊,等于正义啊,这是这么推来 的是吧?在几何上面啊,你要注意,像这种情况的, 他们会关于,他们会关于呢,这条线是对称的,在几何上的关系,这条线呢,永远他的斜率是等于一的,这个可以通过出中的一个角平分线的一个 几何知识,你可以去证一下。这个角呢,肯定是等于四十五度的啊,永远是等于四十五度的,无论你平移在哪里,这条线的斜率,它的对称轴一定是四十五度。好,那我们再看第三种啊, c 大 一加 m 一 单轴是哪一个? 我们说的 c 大 二减 c 大 一等于九十度这种关系的时候,那我们来看一下, 比如说这是 c 特一, 这是 c 特二啊,艾鲁一,穆德鲁二是吧,就是说这个角度呢,就等于,嗯,特 c 特一加九十度。哦,那这了,那就说明这是九十度, 这是其实就是垂直的关系。撞死。嗯,这个只是一个三角形的外角,那以它加上达普相连两个内角和,我们也写一下啊。啊, k 一 等于什么? k 一 等于碳体色大一, k 二等于碳体色大二。 那我们把那个 c 打二换掉吧, k 二就等于什么? tan t 幺分之 pi 加上 c 打二。那我们特别也是用一下啊,三角函数的知识,是不是这等于负的或单调 d c 一, 那我们知道了它和它什么关系,是不是 k 乘 k 二等于负一啊?哦,对于你经常用的这个节数呢,是这么来的 啊, k 二等于负一,它们这两条线就会垂直,是吧?啊,那我们再看第四种,如果 c 带一加 c 带二等于一百八十度。好,这种情况我们画一下 啊,这是 c 带一,哎呀,这就是 这个大角呢,就 shift 二是吧,那是 l 二 l 一, 那我们来看一下啊, l 一 啊,会说 k 一 吧, k 一 就等于 tanty 四大一, k 二就等于 tanty 四大二, 那我们也是把这个 shift 二换一下, shift 二换成一百八呢,就是派派减派大一 啊。这位也用一下三幺函数的值等于什么?是不等于一个负的 tan 四加一 是吧?好,那看一下此时的 k 二 k 什么关系,是不是 k 一 就等于负则 k 二,因为你是 tan 四加一,你是负则 tan 四加二,这明显是相反数的关系啊,所以它俩互补的时候呢,它就是一个相反数的关系啊。 我们再看哦,肖寒若这种,我们看他的这个,利用他这初衷的一个几何的关系也不能看出啊,他这个,这肯定是他的顿震轴,横转这一圈呢,也会是他顿震轴啊。 好,那我们这个常见的这四个已经说了啊,一定要注意倾斜角和斜率啊,关于这两条直线的一个关系,是吧?其实这个方法呢,可以推倒你,你见的那些,呃,倾点角跟斜力的关系啊,都可以推倒。比如我给大家最后留一个座位, 统统,这是 l e。 好, 我们那我们说一下 l e, 都说 y 等于 t e 加 k, s 加 b 吧, 那它呢?把 l e, 呃,我看一下这个方向旋转吧。呃,这叫逆时针,它属于逆时针, 逆时针旋转四十五度啊,逆时针旋转四十五度, 到这吧,这是从这旋转到了四十五度,变成 l 二, 嗯,得到 l 二。那么你来求一下 l 二中的斜率 t 二与 t 一 的关系 啊,这个大家可以用我上面那些方法呢来推一下。
16樂知樂言 05:43查看AI文稿AI文稿
05:43查看AI文稿AI文稿探索直线平行的条件一、首先请你回忆同一平面内两直线的位置关系。位置关系有两种,一相交,二平行。 同一平面内不相交的两条直线叫做平行线。现在来做一个实验,如图,有三根木条相交成角一、角二。 黄色的两个木条是固定的,绿色的木条可以转动。现在转动 a, 观察角一和角二的关系,以及直线 a、 b 的 位置关系。请你注意观察, 转过去,再转过去。好,第一种情况,当角一大于角二时,直线 a 与 b 不 平行。第二种情况,当角一等于角二时, 直线 a 平行于直线 b。 第三种情况,当角一小于角二时,这两条直线也不平行。请你再看一遍转动过程。当角一等于角二时,直线 a 平行于直线 b。 具有角一、角二这样的位置关系的角称为同位角。 像这三个图中的角一与角二都是同位角,那你能说出同位角的特征吗? 好,来看这三个图。角一和角二都是在直线 a、 b 的 右侧,又是在直线 c 的 上方,所以两直线被第三条直线所截。位于两直线同一侧的两个角叫做同位角。 如果图形较复杂,或者涉及到的角比较多的时候,那么该如何找同位角呢?这个时候就需要把复杂的图形分解成简单图形,比如 右上分解出来,左上分解出来,左下 右下好。从这些简单图形中容易识别。数字标出来的每一对角都是同位角,你发现它们形成一个很有趣的形状,同位角是 f 形状。 很显然,角一和角二不是同位角。虽然角一和角二是指在直线 a 和 b 的 上方,但是它们不是在第三条直线 c 的 同一侧。该图中的角一和角二应该是同位角, 因为他们在直线 a 和 b 的 右侧,同时又在直线 c 的 上方。还记得如何画平行线吗?一放二靠三推四划角一、角二。 想一下角一和角二具有什么样的数量关系?当然是相等的。那么直线 a 和直线 b 是 什么位置关系呢?平行能得到一个判定两直线平行的方法了吗? 如果角一等于角二,那么 a 平行于 b, 由此我们得到两条直线被第三条直线所截。如果同位角相等,那么这两条直线平行, 简称同位角相等。两直线平行。写法,因为角一等于角二,所以 a、 b 平行于 c、 d, 理由是同位角相等,两直线平行。如图,哪两个角相等能判定直线 a、 b 平行于 c、 d。 角三和角四相等,因为同位角相等,两直线平行。图中有四条直线,如果角一等于角二,你能判定哪两条直线平行?对啦,直线 a、 b 平行于 c、 d, 那 改成角三等于角四呢?直线 ef 平行于 g、 h, 角二等于角五呢?能判定哪两条直线平行? e、 f 平行以 g、 h。 如图,角一等于角二等于五十五度。角三等于多少度?直线 a、 b 与 c、 d 平行吗?说明你的理由。角三与角二是一对对顶角,所以很快能求出角三的度数, 这是已知条件。由于角三等于角二,理由是对顶角相等,所以角三应该也是五十五度,它和角一相等都是五十五度。 角三和角一又是同位角,同位角相等,就能得出 ab 平行与 cd。 理由是同位角相等,两只线平行 怎么样,你听懂了吗?好,来吧,本堂课小节一下。首先,如何判断同位角? a 两角在两线的同一方, b 两角位于第三线的同侧,这样两个角就是同位角 小节啊。判定两直线的平行方法一, a 找出同位角, b 同位角相等,那么这两条直线就平行。
5以微课堂 03:13查看AI文稿AI文稿
03:13查看AI文稿AI文稿hello, 亲爱的同学,大家好,欢迎来到希望杯系列,我是小赵啊,今天我们来研究一个直线图形,但是它的解法特别特别的有趣,我们赶紧来看一下说甲乙丙三个梯形,它们的高支笔一二三,上底支笔六九四,下底支笔十二十五十。 条件这么多,我们通常是不建议大家用眼睛去记的,一定要列出表格来。高支笔一二三,但我们不能直接写一二三,为什么? 因为如果一道题只给了你笔,你是完全可以直接设数的,但是这道题除了笔以外,还给了你一个实实在在的面积, 所以你就不能只是设为设高一二三底是六九四,不行,你得设未知数了。 并且它们三个比对应的一份量是不一样的,所以你不能设 x, 二 x 三 x 六 x 九 x。 不 行,你得分开设,你的高应该设成 h 二 h 三 h, 上底是六 a、 九 a 和四 a, 下底是十二 b, 十五 b 和十 b。 只能这么说,别嫌麻烦,也别给我整什么特指法,在这种问题上,你越省事,你的结果就越难受,万一你的结果跟这个三是对不上,你真的是, 我就不说那个严重后果了,就属于时间也花了,这个呃,功夫也下了,但是结果是铁是不对的啊。所以我们一定要记得三个比且有一个具体的面积,你只能设不同的一份量,设不同的结果。 好,然后把这个三十表示一下啊,梯形的面积,上底加下底的横乘高除以二,记得化简。结果是三十,说明我接下来这个一饼两个梯形的面积之合呀。你一定是既求不出 a, 也求不出 b, 也求不出 h, 但是你可以把它 化成这个样子的倍数,大概率是这样的,不信我们试一试。那乙丙两个题型的面积,对于乙来说,上底加下底的和乘高除以二,丙也是上底加下底的和乘高除以二。简单化简之后得到了,哎,分别相乘啊,九 a h, 十五 b h, 六 a h 和十五 b h, 然后再分别合并得到的是十五 a h 和三十 b h。 哎,这个和这个有什么关系啊?你会发现它刚好 a 和 b 啊,它刚好是一个两倍的关系,所以我从里面只要掏出三 a h, 那 么它是三 h 的 五倍, 这个是六 b h, 你 看这俩六 b h, 发现它也是六 b h 的 五倍,所以你能得到它是五倍的这个整体,而这个整体它刚好是三十,所以就是一百五,这个答案就是一百五 啊。我希望各位同学通过这个问题学会的一定是首先第一步设数,第二步 一定一定不要着急,我们不需要求出每一个一份量的己,我们是可以通过整体代换设而不求来求出最后的结果的。好,线上学不够,线下来找我。希望今天的分享对你来说有帮助,咱们下次再见,拜拜!
 02:39查看AI文稿AI文稿
02:39查看AI文稿AI文稿好,同学们,咱们这条视频呢,接着讲解是几何题型啊?来,我们先做题,直线这个方程与直线这个方程的距离,为什么?对吧?题目给出来是两条直线,让我们求它距离。来,我们先来观察一下第一条直线,它前面两个东西跟后面这条直线前面两个东西是不是长得一模一样? 那前面两个东西都长得一模一样的话,那说明这两条直线是平行的嘛,平行才有这个性质啊,就是两条直线前面这两块东西是一样的,一模一样啊。好嘞,我们知道它是平行了, 好,那我们想算的距离的话,那就是用两直线平行的距离公式就是他啦。啊,来,那我们想用这个公式的话,那就得把这些东西,对吧?得找出来呗。那 c 跟 c 二,还有 a 跟 b 是 什么呀?来,我们先把这个两条直线把它画成原始公式啊, 就是 a x 加 b, y 加 c 等于零,对吧?那这个是第一条直线的,所以说我们把它字母都记作是一啊,都记作是一, 都记作是一啊。好,把这里查一下,加上 c。 好, 这,这个是第二条直线,对吧?所以说我们把它记成是第二条直线的啊,就是 a 二 加好, a 二乘 x 加 b, 二乘 y 加 c 二等于零,对不对?好,来观察一下,那这里的 c 对 应的就是负一,对不对?好,套进去呗。 c 对 应就负一,负一减去减什么 c 二, c 二对应的就是什么数呀?就是二,对不对?好,二, 好,下面就是 a 的 平方加 b 的 平方, a 是 什么呀? a 跟这个 a 他 对应的数字都是一样,对吧?都是 x, 前面数都是一,对不对?好,就一的平方加上 b 是 什么呀? b 跟他的 b 同样的,对应的就是 y 前面的数字,对不对?就是同样都是负一吗?啊?负一好,平方等于什么呀?来算一下。答案就是等于下面啊。下面算出来就是根号二,上面就是 绝对值的负三。那绝对值开出来就等于正数吗?就三呗。好,下面就是根号二。那分母啊,记得分母不能有根号,所以说再乘一个根号二,所以说下面就是 二,对不对?那下面乘以根号二,上面要跟着乘以根号二啊。所以说最终答案就是二分之三倍根号二,答案就是 b 选项。好,这条视频就讲完了,你有没有听懂呢?最后为了检验同学们到底有没有听懂啊,老规矩,出来到同类型题型,同学们可以回去做一下,有做的时候把答案写在评论区里。好,拜拜。
326中职数学大雄老师












