风筝模型公式推导过程动画小学奥数
粉丝5028获赞1.8万
相关视频
 04:37查看AI文稿AI文稿
04:37查看AI文稿AI文稿今天我们讲一个小升初奥数风筝模型,它是小升初必备模型,任意一个四边形 a、 b、 c、 d, 然后呢连接 a、 c、 b、 d 相交于点 o。 那么风筝模型在推倒过程中,我们主要运用以下知识,一、三角形面积公式,人教版五年级上册的知识。二、比例三、比例的基本性质都是六年级人教版六下的知识。接下去啊,我们先来看一个任意的三角形 a、 b、 c, bc 上任意取一点 d, 然后连接 ad, 再过 a 点做 bc 的垂线,垂足为一,并标上垂直符号,我们就可以得到三角形 abd 的面积比,三角形 bacd 的面积,他就等于 a, a、 b、 d 的面积就是 d, b、 d 乘上高 a 一,再除以二,三角形 a、 c、 d 的面积。第一是 c、 d 乘上高 a 一,再除以二,然后呢,我们对乘 a 一除以二进行约分,就得到 b、 d 比 c、 d, 所以我们就可以得到在高相等的情况下,两个三角形的面积比等于底边长的比。这句话我们等会要用到的非常重要的一句话。 我们来看一下这个任意的四边形,为了讲解方便,我们分别标赏一号、二号、三号和四号,然后呢,过点地做 ac 的垂线, 我们就可以得到一号面积比,二号面积等于的是 aoboc, 这个是怎么来的呢?就是下面那句话,在高相等的情况下,两个三角形的面积比等于底边长的比。 同样道理,过 b 点做 ac 的垂线,我们也可以得到三号面积比,四号面积也等于 aoboc, 同样道理,就是下面这句话。那么在这个地方啊,我们看一下,大家都是等于 aoboc, 所以一号面积比二号面积等于三号面积比四号面积。 接下去根据比例基本性质,我们看这个红色的这个比例对角相乘以后,就可以得到一号面积乘四号面积等于二号面积乘三号面积。所以我们得到的第一个结论是 得出任意一个四边形对角线相连,相对的三角形乘积相等,这跟我们五年级的梯形蝴蝶模型是否很相似,对吧?但是呢,梯形蝴蝶模型呢,是五年级的知识,但这个风筝模型必须是在六 年起才能够学习,因为他涉及到的知识,书本的知识都是六下的。接下去我们继续看这个绿色虚线框框起来的这一部分,根据比例的性质,前向之和与后向之和的比,与圆比相等。 那么我们来看一下,一号面积比二号面积,他就等于一号加三号面积和,比二号加四号的面积和,可能有些小朋友这个地方他听不懂,我们来用数字简单的举个例子, 二比三是等于四比六的,然后呢,二比三等于的是二加四的和,比三加六的和等于六比九等。月份好以后是二比三,所以我们得到的是这一块是正确的。 然后我们继续看啊,一比二,一号面积比二号面积等于十,看一号加三号,我们看看这里,一号加三号就是三角 a、 b、 d 的面积,二号加四号的面积就是三角形 b、 c、 d 的面积,那么也就是蓝色面积比红色面积。所以我们得到第二个结论, a、 o、 b、 o、 c 等于的是 ao 是绿色的,红, oc 是红色的,绿色的线段比红色的线段等于的是一号三角形面积,比二号三角形面积在这块地方是有的,对吧?那么一号三角形面积比二号三角形面积又等于的是蓝色 abd 的面积和红色三角形 bcd 的面积。 同样道理,我们 aoboc 它也等于三号比四号等于三角形 abd 面积。 b, 三角形 bcd 的面积。我们继续往下看,我们来看 dobobdo 是蓝色, ob 是紫色,这两天线灯笔的话,它就等于是 一号面积,比三号面积同样等于这块蓝色的是三角形 acd 的面积比红色的三角形 abc 面积。 继续研究 do b o b 它同样还是能够等于二号面积,比四号面积,它也等于三角形 acd 蓝色部分面积。 b, 三角形 abc 红色部分的面积。这个就是我们说的风筝模型。好了,今天我们就讲到这里,希望对你有帮助,谢谢。
8708哈弗课堂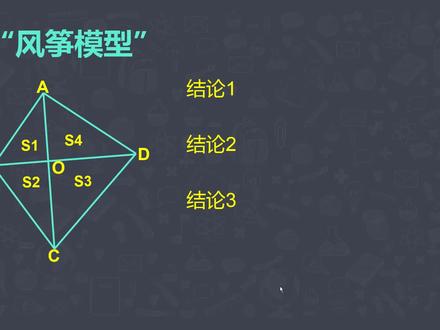 05:11查看AI文稿AI文稿
05:11查看AI文稿AI文稿大家好,本期视频我们来共同学习风筝模型的三个结论啊,以及对于结论的一个简单的一个推导过程啊,我们一起来学习一下啊! 在一个任意四边形 a、 b、 c、 d 当中,两条对角线将这个四边形呢分成了四个三角形,我们用 s 一, s 二, s 三和 s 四分别对这四个三角形进行标注啊。 我们首先来看结论一, s 一乘上 s 三等于 s 二乘 s 四啊,这是结论一,结论二, s 一加 s 四, bs 二加上 s 三等于 aobco。 结论三, s 一加 s 二比 s 四加 s 三等于 b o 比 d o 啊,这是三个结论。接下来我们来看简单的一个推导过程啊。我们首先来看结论一, s 一, s 一乘 s 三等于 s 二乘 s 四。那么有关于结论一的推导过程呢?我们可以利用等高模型, 在三角形 a、 b、 c 当中, s 一和 s 二这两个三角形呢?等高, 那么面积的比就等于对应的底边的比啊,等于 aobco。 同理,在三角形 a、 d、 c 当中, s 四与 s 三这两个三角形呢,依然是登高面积比等于对应的底边的比也等于 ao 比上 co, 那么就有 s 一与 s 二的面积比就等于 s 四与 s 三的面积比。 最后一步交叉相乘,得到结论一啊, s 一乘 s 三等于 s 二乘 s 四啊, 这是有关于结论一的,利用等高模型来推导出的这个结论啊,我们来看结论二, s 一加 s 四, bs 二加 s 三等于 ao bco。 有关于结账二的推导,我们需要简单了解一下等比定理。 等比定理简单描述一下啊,若 a 比 b 等于 c 比 d, 其中 b 和 d 呢,均不为零, 那么就有 a 加 c 的和 b, b 加 d 的和就等于 a, b 也等于 c b, d 啊。简单描述一下等 b 定理, 那么接下来呢,我们来看一看,对于等比定里还有接龙二,我们该如何去理解啊?我们举个例子,我们假设 s 十一等于二, s 二等于四, s 三等于十二, s 四呢,等于六, 那么 s 一与 s 二的比经过化减一比二, s 四与 s 三的面积比经过化减也等于一比二啊。 a 比 b 等于 cbd, 那么 s 一与 s 二的面积比就等于 s 四与 s 三的面积比都等于 a o 比 c o 啊,都等于一比二。 那么我们来看结论啊, s 一加 s 四比 s 二加上 s 三,我们将 s 一 s 二 s 三, s 四的 面积带进来啊, s 一等于二,二加上 s 四,六啊,二加六比 s 二加 s 三, s 二十四, s 三呢?十二啊,四加十二, 分母是十六,分子是八,化减之后得到一比上二。 所以说 s 一与 s 四的面积和比, s 二与 s 三的面积的和就等于 ao bco。 那么也就是说,三角形 a、 b, d 啊,与三角形 b、 c、 d 这两个三角形的面积比就等于 a a o, b 上 c o 结论三的推导过程呢?与结论二呢类四?
616明明爸爸爱数学 01:31
01:31 05:24
05:24 02:18查看AI文稿AI文稿
02:18查看AI文稿AI文稿今天我们来复习一下风筝模型。什么是风筝模型?比如说随便一个四边形,那么连接他的两条对角线,上边的三角形和下边的三角形,他们的面积之比就是他们两条斜线的笔。那为什么有这样的这个结论呢?我们可以来证明一下, 假设 a 一比一, c 是三比二,那么我们只要证明三角形 abd 比上三角形 bcd 等于三比二,就能证明他们的面积之笔是两这两条前面的这个笔了。那先标记一下,这里是三,这里是二。 先把目光锁定在左半部,观察一下, abe 和 bce 两个人是等高三角形,他们的头呢共用的是 b, 脚底板都是 ac 这条线上的,所以他们是等高三角形,那也就是说他们的面积 一支笔可以是三比二,那我可以将 abe 设为面积为三, x 对应的 bce 的面积就是二 x, 那么以此类推,我可以把左边也遮住,观察一下右半部分, ab 可以设为三外, ecd 可以设为二外,那么我可以把 abd 改成是三 x 加上三 y, bcd 呢?可以把它用二外加二 x 来代替。 这个时候我们再提取公因数,把三提出来 x 加 y, 再把二提出来 x 加 y, 那么两边同时进行 啊,约掉 x 加 y, 这个操作就可以变成三比二,那么就证明完毕了。如果能学会风筝模型的话呢,做很多这个几何形的时候还是蛮 很方便的。这个风筝模型也叫做烤串模型,我们有一个比较形象化的记忆方法啊。先来说第一个,就是两个三角形的面积之比呢,为甲高之比,因为它是斜线,不是垂直地面的,所以它是假的高。第二个叫做两片肉的面积之比,为穿过的天的长度之比, 把这两个造型给画个圈,那就很像是一个烤串了,所以我们可以用这个烤串的方法去记忆肉的面积之笔,就是穿过的签字的笔。 ok 了,如果能听懂的朋友呢,请记得点个赞,收藏关注我,学习更多数学小方法。
39比老师会数学
猜你喜欢
- 26.6万是剧剧呀












