二次函数分之一的不定积分
粉丝4086获赞3.3万
相关视频
 04:27查看AI文稿AI文稿
04:27查看AI文稿AI文稿大学数学救命课第八期,今天我们来说一下相对复杂一点点的这个不定积分的处理办法。 我们上一期说了,这个不定积分说白了就是找元函数,但是真正考试的时候啊,他未必有那么善良啊,就比如说我们面前的例题一和例题二这个样子,你很难一眼看出元函数啊。就换句话说,这种分式类型的,我们应该怎么处理?核心的核心就是一句话,就是老师圈起来的这堆东西, 我们一定要把分式相乘的东西,把它变成分式相加或相减的东西。好吧,哎,这个东西其实本质上它只是一个变形的技巧,并不难,算是一个大学的一个新知识,但是我们大家积累一下这个技巧,对我们考试做题会很有帮助。好吧,哎,所以 为什么要这样呢?因为你相乘的东西很难找到元函数,但是如果要把它变成相加的东西,那这个函数一定是会被化简的。那这样的话,我分开找元函数,这个结果说不定就会变得很简单很简单。比如说我们也看了一下例题一。好,我们按照这个公式啊,把它拆成这个样子, ok 啊,核心的核心啊,就是我们一定要求出这个 a 和 b 来,其实就是某种意义上的待定系数法啊。好,那我们先处理这个函数,再回头处理这个不定积分。 好,那意思就是 x 分 之大 a 加上 x 加二分之大 b, 得等于那个原式呗。哎,我们把它强行通分一下,就是这个样子, a 倍的 x 加二加上 b 倍的 x, 而这一堆分子 肯定得跟 x 加一对应相等。好,我们把这个蓝色的圈圈给它打开,也就是 a 加 b 倍的 x 加上二 a, 好, 那这样的话,我们说你 a 加 b, 一定得跟 x 前面的系数对应相等, 然后这个二 a 一定得跟那个常数项一对应相等,那这样的话,我们就非常容易求得, a 等于二分之一, b 也等于二分之一,非常非常简单,所以说这个积分这就变成二分之一,这就变成二分之一就 ok 了。好,我们就想 x 分 之一的原函数,那是不是 long x 的 绝对值啊,所以非常简单直接,一步到位就给它求出来了,就是这个样子, 最后别忘了加常数 c, 好 吧,嗯,这个 x 加二啊,虽说是个负函数,但是你求完倒了之后,它没有任何附加的系数,所以说原函数依然是绕你这一堆啊,大家放心求就行了。 第二个题也是一样的,我们还是利用一下这个,把分式相乘变成分式相加,哎,也就是把这一堆函数先变成这个样子, x 减一分之大 a 加上 x 加二分之大 b, 然后给它强行通分一下,就是这个样子, a 倍的 x 加二,我老师直接展开,加上 b 倍的 x 加一,老师也直接展开。好,简单处理一下,分子就是 a 加 b 倍的 x 加上二, a 减 b, 分 母跟原式保持一致, 所以核心的核心,我这个变形完了之后,那在这一堆一定跟分子那个三对应相等,所以说,哎, 既然这样, a 加 b, 你 x 那 一项不能有,就等于零二, a 减 b, 这一堆东西就等于三好,那解得 a 等于一, b 等于负一好,那这样的话就非常简单了,对不对?哎,我只需要求这个这个函数的原函数以及这个函数的原函数是不就得了?哎,我们简单写写过程啊,也就是这个样子。 好,那这一堆的元函数肯定还是跟 long 看齐嘛,对吧?也就是这个样子, 后面那个也是要跟 long 看齐,最后别忘了加上常数 c。 所以 说大家在考试当中如果遇到分式相乘不好找元函数的,我们一定要利用这个公式把它拆成分式相加,然后分别找元函数,这样就会相对简单一些。
1308芒果街上的咖啡厅2 02:17查看AI文稿AI文稿
02:17查看AI文稿AI文稿大家好,我是一分钟讲数学,接下来我们学习不定积分。不定积分额其实非常好理解,它本质上就是求导的逆运算,比如 x 求导等于一,那么一的不定积分就等于 x, 再加上常数 c。 再比如三 x 求导等于 cosine, 那 么 cosine 的 不定积分就等于 c, x 再加上常数 c。 为什么要加常数 c 呢?因为不只是 x 的 导数等于一, x 减一, x 加二, x 加一方等等,它们的导数都等于一,所以我们要在后边加上常数 c 来覆盖所有情况。 同理,不只是 sine x 的 导数等于 cosinex, sine x 加任意常数的导数都等于 cosinex, 所以 我们也要在后边加上常数 c。 总之就一句话,不定积分的结果要加 c。 好,现在你已经掌握了第一种求不定积分的方法,只要能知道谁求倒等于背记函数,那么背记函数的不定积分就等于谁加 c。 其实对于这种非常简单的不定积分,教材已经帮我们整理好了一张基本积分表, 乍一看内容很多很难记,但其实你只要熟练掌握了前面学过的求导公式与法则这些就不用围外记忆了,因为表中的结果,求导之后都能很容易的得到。背记函数 最后不定积分还有两个非常简单的性质需要大家记住,第一个是俩函数先相加,再求不定积分等于它俩先分别求不定积分,再相加相减也一样,就不多说了。 第二个是当被记函数为非零常数倍的某函数时,该非零常数可以提到前面。
164一分钟讲数学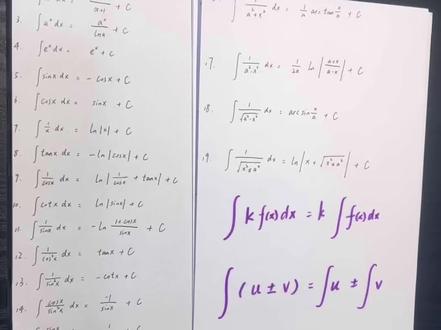 04:08查看AI文稿AI文稿
04:08查看AI文稿AI文稿开始大学数学救命课第七期,今天我们正式来说一下不定积分。不定积分是什么东西呢?哎,核心的核心,就我们面前的这一堆啊,我用一根像撬棍一样的东西,再加上一个函数,再加上一个 d x, 得到了它的原函数。 啥叫原函数呢?原函数取完倒了之后叫倒函数,那倒函数的上一级就叫原函数。比如说,哎,整个从第一条一直到第十九条,等号的右边都是原函数, 然后呢,等号六边取完倒了之后,哎,就得到了左边带 d x 那 一堆就是他们的导函数。说白了,不定积分干啥事呢?不定积分就是找元函数啊,就这么简单。好吧,来 第一条,一直到第十九条,大家一定要把它背下来,虽然说这个过程可能稍微有一点困难,大家大家一定要克服困难,把这个东西给它背起来,好吧,嗯,然后紫色线的这两条是不定积分的系数,拿到这个翘棍前面,结论依然是一样的。 然后呢,再一个,不论积分是具有加法的和减法的性质的,就是我在内部加减法,跟在外面分别算完不定积分,再进行加减法,是一模一样的。好吧,大家对这个简单有些印象,来,我们看一些奇题,看一下例题一,呃,根据不论积分的性质,首先我可以对它进行这么一个操作, 好,核心的核心,谁的原函数啊?这个口塞四 x 的 原函数是谁?塞二 x 的 原函数是谁?那口塞的原函数肯定是塞嘛,对不对?因为塞求导是口塞嘛,所以说那一定是这个样子。 由于负函数的求导,我们说了,哎,正常这个家伙,求导会前面多个四,那我这来个四分之一不就得了吗?对不对?哎,这个东西正常原函数应该是负的口塞 x, 因为负的口塞 x, 求导是 sine x, 也就是这个样子。 好,为了保证这个负函数,求导跟这个,呃,这个系数要跟原来保持一致,所以这前面上一个二分之一, 然后这前面符号,然后这自己又有个符号,负负得正,哎,来最终结果,别忘了加上一个常数 c 就 ok 了。好,再看下例题二,还是啊,根据性质先对它进行这么一个操作。 好,然后前面的这个,这算啥呀,这是不是 x 的 负二四方啊?我们应该想起哪个公式啊?我们是不是应该找到这个元函数的公式啊?一加二发分之 x 的 一加二发四方,是不是,哎,把二发等于负二往里头带,对吧,那就是 负三分之一乘上这个负一分之 x 的 负一次方,这就找到了它的原函数。然后后面这个东西的原函数是谁呀?哎,我们之前背过求导公式吧, r 个弹进来 x 吧。 ok, 最后别忘了加常数 c, 前面这个东西,对它简单整理一下就是最终答案。再看下例题三,这是二的 x 方,乘一的 x 方,我们可以先对它进行这么一个处理。二,一,括号 y 的 x 次方。那我们想起哪个圆函数公式啊?这个吧, a 的 x 次方的圆函数的公式是这个, 好,那我们就这样,就是把 a 等于二一往里头带,就这个样子。 最后别忘了加常数 c, 非常非常简单啊。再看一下例题四,还是利用性质把它进行一个简单的操作, 三次根号下 x, 那 是 x 的 三分之一次方。二次根号下 x, 那 是 x 的 二分之一次方。无论是哪个,我们都代入这个 x 的 r 法次方往回找原函数就行了。这个 r 法等于三分之一,这个 r 法等于二分之一,来二的原函数自然就是二 x 减去。哎,往这个 alpha 等于三分之一,往里带就这个样子。 alpha 等于二分之一,往这里带就这个样子。 ok 啊,对这个函数对做一个简单的处理,最后别忘了加常数 c, 最终就是正确答案。好吧,所以说核心的核心,大家一定要记住原函数的公式。
2312芒果街上的咖啡厅2 41:54查看AI文稿AI文稿
41:54查看AI文稿AI文稿今天主播带你们学不定积分, 好,我们来看这个,是啊,不定积分,不定积分的定式就是这个式子,这相当于说是这个,这个是这个的元函数,一个元函数 原函数的话,它就是因为比如说 y 等于三, x 的 横方加上一,为什么要加 c 呢?因为这个求出来,求出来它的导函数导出 x, 加平方出来,为什么要加 c? 因为常数求求导成整数里必须要加个 c 啊。 然后我们来看看求五点七分,这个,这个这个数字啊,这个数字啊,我们老师讲的是入中心变量啊,他说另这个 另一个 u 等于三,加上二 x, 那 么我们这个另一等于三加 x 的 话啊,那么我们就来求这个 d u d u, 就是 对这个求微分,求微分的话,这个就是就要对这个求到 三,加上二 x, 求到六,求到二,然后求微分的话再加 d x, 所以 就等于二 d x, 那 么我们再把这个 d x, 再把这个 d x 算出来,这个 d x 就是 等于二分之一的 du 啊, d x 有 了,然后 d, 这个是 d u, 是 等于这个,那么我们的这个圆圆数字,圆数字,这个三加 x 就 用 u 代替,然后啊这个 d u 呢? 啊,这个 d x d x 用二分之一的 d u 来太晚 t 晚,那么二分之一停在前面,那就变成了这个数字,这个数字,那么这个 u 分 之一,我们很容易想到的零 n x 等于 x 分 之一的这个符号是 x 分 之一,那么 u 分 之一的话,应该就是零 n u 零 n u, 零 n u 的 绝对值,因为我们知道 u 是 大于零,因为零 n 嘛是这个数, 它是要,它是要大于零的,这个就是比如说这个 x x 是 要大于零的,所以我们这里要加个绝对值,加个绝对值加 c, 那 么 u u, 我 们是第一个乘三加 x, 那 么我们再把这个 u 把它替换成三加 x, 再加 c, 所以 说,所以这个不定积分三加 x 等于 e x 求它的它的原函数就是二分之一 n 三加 x 的 求幺加 c。 但是呢,刚刚刚刚那个老师讲的那个我感觉有点麻烦啊,就是丢到脊柱中间丢,然后再丢那啥有点有点麻烦。我现在来讲一下我的这个,我的这个就是移步出来的 啊,你看我们这个是我们现在的这个是三加 x 分 之一 d x, 然后我们还能想到这个幺 a x 等于 x 分 之一,是不是幺 x 等于呃,幺 x 这个求导,求导等于 x 分 之一,那么幺 a 三加上 r x 的 绝对值,它这个它这个求导是不是也等于三加上 r x 分 之一呢?你看 是求导数等于这个分之一吗?是不是?然后因为这是一个复合函数,因为它有 a 是 一个函数,然后三加到 x 又是一个函数,所以我们又要再对内函数再求次导,再加上 x 求导,求导,求导求到二,那么说所以我们这里是要乘以一个二的 后面尾巴这里乘以个二,那么这个三加二 x 分 之一乘以二,就比这个三加 x 分 之 d x 比这个少多了,多了一个二,多了一个二的话,就是就是说这个这个求求出来的 这个求导,求出来的这个路来个 r, 那 么我们要怎么办才能说?我们要怎么办呢?要怎么办才能说明这个是这个的原函数,是不是我们再乘以一个二分之一,把这个 r 消掉出来,所以我们就在这里这个 l n l n 三加上 r 四的前面加上个二分之一, 你看这个加出来二分之一,然后对这个内函数求导的时候,把求出来的二这个二分之一约掉了。所以呢,它的这个,它的这个圆函数,你看它这个圆函数原式减一次,就直接等于 原式,就直接等于幺 n 三加上 r x 等绝对数加 c 加 c, 然后再乘一个,再乘一个二分之一,前面再乘一个二分之一倍的幺 n 三加 x。 你 看你现在,你现在对这个求导,看看 这个求导,这个求导就等于三加上二 x 分 之一,再乘一个二,你看再乘一个二,因为这边还是求导吗?二 x 求导求到二,常数求到零,所以还要乘一个二,你看前面有二分之一,就跟这个二丢掉了, 就可以按一个,所以我们求你看,所以再加上 d s。 我 们的这个式子,我们对这个式子求微分,求微分的时候就跟上面这个一样,所以,所以就是我们证明你求的这个圆函数是对的, 减一是等于。你看这个,这个我们知道这个 cycle x 的 平方是等于 time x 的 平方加一嘛。那么 time x 的 平方就等于括号 cycles x 的 平方减一 d x, 那 么 cycle cycle x 的 平方,呃,那个它兼且 x 求导数等于 cycle x 的 平方嘛,所以这个就直接,这个就直接是, 这个就直接是它,兼且 x 加一和减一减一 d x, 好不对?不对?不对,这我们把它分出来,我们把它分出来这个样子,这个 cycle x, 然后 d x 加上,错了,是减求导还是这个还是 d x 嘛?你看还是 d x。 我 们这个这个的原函数,这个原函数的话就是它间的 x, 因为它间的 x 是 等于 塞口 x 的 平方嘛,然后这个 e 导数 x x 的 导零 c, 所以 这里再加上一个 x, 然后因为原函数这个求原函数要加 c, 加个 c, 所以它的这个 case x 的 平方 d x 的 等那个元函数就是 case x 加 case x 加 x 加 c 啊,这个 case x d x 也是等于,然后这个 case x case x, 我 们知道就等于散影 x 除以多散影 x 乘以多散影 x 乘以 d x, 那 么就等于散。然后这个我们把它又括括,散影 x 分 之一,再乘以散影 x, 再乘一个 d x, 你看,那么这个这个散引 x d s, 它的这个元函数是不是就是负的多散引 x, 你 看,因为多散引,多散引求老是等于负的散引 x 嘛,那么加个符号是不是就等于就变成了散引 x, 如果求它的微分的话,那这个 d s 就 低了。所以呢,我们最后我们先把它之后,我们先给它放了,然后呢,那个 它的这个扩散 x 分 之一啊,还是那个幺幺幺 a x 等于 x 分 之一,幺幺 x 乘以 x 分 之一,那么幺 a 的 幺 a 的 扩散 x 的 绝对值 求导了,也是等于扩散 x 分 之一嘛。但是呢,还要在对面还是求一次导,这个求一次导,这个求一次导的话,就是扩散 x, 求导就就成一个负的散影 x。 你看我们原来我们那个不定积分里面,你看括号 x 分 之一这里有了,然后散 x 有 了,所以呢,我这里是个有了一个符号,有了个符号的话,我们我们再在前面加个符号,你看加个符号,那么你看就直接就等于负的 n, 括号 x 加 c, 你 看括号 x, 呃, n 括号 x, 你看你这个求导破三元 x 分 之一,然后呢还要再给破三元,再求一次导,破三元求导求的负的三元 x, 负的三元 x, 再跟前面的这个符号负负抵消,就变成了这个三元 x, 然后 求微分,再乘个 d s, 所以 你这个原函数了,负的 n 或者 x, 就是 将 c 就是 这个它的 x d s 的 原函数就直接就可以出来了。 这个的话我们看一下,我们看这个,我们看如果说他,他是这个样子,他是波散引 x d x 的 话,你很容易就能看出它的余函数,它的余函数就是等于,因为因为散引求导数等于波散引嘛,就等于 z x 加上一个 c 就 就完了,但是呢,他这里是 x x 的 话,我们这里 那么散影 x 这个求导是不是等于,是不是等于铺散影 x, 然后铺散影 x 跟那个是一样的,但是呢,因为这是个复合函数,里面还有个 x x, 在 这个 x 求导的话,多出来个 r, 多出来个 r 的 话,我们要在这个前面加个二分之一, 所以呢它的这个,它的这个就直接是就等于原式,就直接等于这个 o 散影 r x d x, 这里面是这样,就直接等于等于二分之一的散影 r x 加 x c, 你 看 三以 x 求导或三以 x 有 了,然后呢,因为它这个函数还要再对 x 求导,又要求出来个二,所以前面要乘个二分之一,所以它这个求导求出来就跟这个一样,这个求为 零,然后沿式等于 你看我们把这个,我们把这个三心提到外面 x, 这个,然后这个这个写成那个指数形式写成 e 减去 x 平方,然后这里是二分之一乘以 x, 把 x 提到后面变成一个 d x, 那 么我们就,我们现在就来看啊,我们就看这个,我们就来看这个,这个是哪个求导求出来的这个因为因为你看他是啊,你看这个 一减去 x 的 平方啊,这个要多少次密?求导球的一减去 x 的 平方的二分之一次密,因为我们知道这个球老是要在这里减一吗?所以我们要在圆的这里加上一,那么这里就是二,二分之三次,二分之三次的话,你看二分之三次,然后呢? 他的这个二分之三次,那么这个这个球导对这个球导就是,就是你看这个二分之二分之三 括号一减去 x 平方,然后这个二分之一次密码,还有这里还要再去内含去求次导,这个求导还要再乘以一个负的大 s, 你 看 原本原本我们的只是这个样子,我们的只是这个二分之一,二分之一,二分之一有了,然后多出来的二分之三,所以我们要在,我们要在它圆形的前面乘一个 二分之三,我们要在圆心乘一个三分之二,乘一个三分之二的话,就相当于要在这里乘一个三分之二,你看啊,就写着写着你看 三,然后这里三分之二的,你看已经减去 x 的 平方,这里说的二分之三是密,然后你看, 你看就选对了吗?然后这里,你看这个里求出来又多了一个什么,多了一个负二,多了一个负二,你看 x 有 吗? x 在 这里多了一个负二,我们还要再乘一个二分之一,所以我们还要再在这里再乘一个二分之一,再 乘个二分之一,然后这个二分之一把它挪到这来,就是二分之三,你看,然后整体再乘进去,就乘以三分之二,你看,然后, 哦,这里是个乘以一个负二二分之一,因为这里是正的, x 是 正的,那里是负的,所以这里是负的,这里啊,这里是负的二分之三,乘以三分之二,然后括号一减去 x 的 平方, 再等二分之三次密,再加 x, c, 你 看,现在这里这两个一定要去掉,所以它的整体就直接就变成了一个等于 e, 减去 x 的 平方二分之三次密,再加一个 c, 哦,这是负的负的 e 减 x 的 平方,二分之三次密加一个 c, 你 不信,你对这个再求求导,你看这个求导,你看你这个求导,是这样, 这个求导求出来就跟我们原函数是一样的了。好,我们再看这个,这个你看,如果你按老师的,按老师的那个思维来的话,你看三 x 的, 你换成一一的 x 的 三次密,你看你怎么找中间变量,中间变量不好找, 你在那里,在考场上想半天,那中间变量,哎,这个中间变量到底是多少?时间过去了,时间不等人,所以我们来先,我们来一个简单的方法,也是等于 你说等于,你先不要把这个,你先不要把前面这个数字,你先来看后面这个,后面这个我们知道,我们知道 e x, e x 求导还是 e x 本身吗?是不是 e x 的 e x 的 三次密求导呢?是不是也是等于 e x 的 三次密?然后呢?这个是个符号函数,这个还要再对 x 的 三次再求次导。 x 的 三次求导你们会用吗?等于三 x 的 平方,再乘以三 x 的 平方,你看这个 e x 的 三次幂乘以三 x 的 平方,是不是跟这个这个一模一样?所以,所以它这个就直接就等于 e x 的 三次幂加 x c, 对 就完了。 我们先把它沿四等于,那怎么做?我们先把它分开来写嘛?我们把它分开写三引根号 x, 再乘一个根号 x 乘以 d s, 啊,是吧? d s, 然后呢? 然后我们来想这个,我们来想这个这个的原函数是多少?这个这个的原函数是波散影的根号 x, 是 吧?波散影的根号负的,因为散散影 x 求导是负的 x 嘛?负的 x 求导是负的散影 x, 那 么加个括号就变成正的,那么 就说明它的这个散影还散影 x 的 原函数是负的,波散影 x 的 话,原函数,我们 我们对它的这个元数求到。元数求到求得多少?求得三根号 x, 是 吧?三根号 x, 跟这里一样的,然后呢? 然后呢?这个元数求到,还要再根号 x 求到根号 x, 根号 x 是 等于 x 的 二分之一次密码 x x 的 二分之二分之二分之一次方,那么这个求到,这个求到就求到二分之一。 x 的 负二分之一次方,那么这个 x 的 负二分之次方就就等于根号 x 了。 这边,呃, f 的 话就括号 x 分 之一了吗?括号 x 分 之一,并且这里也有了,但是这里多出来个二分之一,多出来个二分之一的话,我们这里就要圆函数的这里多出来,那里多出来个二分之一。我们圆函数就肯定要再加个 r, 再加个 r, 再加个 r, 然后再加个 c, 所以 圆函数就等于等于这个样子, 等一等。好,我们再来一遍, 我们再来一遍,把圆长数等于多少?我不写了,这里你看我们把它拆开来。三根号三乙,根号 x 乘以根号 x 分 之一 d s, 他们两个人在一起肯定有某种关系啊,你不要去想这个中心变量,那中心变量很难找你就,你就想着你就想这个,这个又有散减 x, 又有变化 x, 那 么又散减 x, x 又有变化 x, 肯定他他的函数求导肯定要多出来某个东西,你这样想,那么这个的函数是多少?这个函数是不是就是负的负 的波三 e, 根号 s, 是 不是啊?因为函数的符号就变成了这个的三 e x, 你看对这个求导啊,我们判断了这个三 x 等于负的后弦根号 x, 然后我们就把求导看一下能不能测出来这个。你看我们一条求导 就等于负负的正码负的三 x, 负的正六点散影根号 x, 然后这是个负函数,还要在根号 x 求导根号 x 的 二分之一侧方求导的话,就要乘一个二分之一,然后再乘一个 x 的 负二分之四方, x 的 负二分之四方呢? 就是根号下根根号 x 分 之几了吧?是不是根号 x 分 之,根号 x 分 之几了?这里多出来的二分之一,就是说这个球到球的球出来的时候多出来的二分之一,那么我们要,我们就要要在它的原函数的前面加个二,来给这个大分之一,二的二分之一丢掉,所以说我们这里的原函数就等于 负的二分,负的二倍公分乘以根号 x, 就 这个样子了。 ok, 我 们再看这题好写, 原式等于原式,等于我们把它拆开来写,我们把它拆开这个,这个就写成这个样子,一加上二,这个幺 n x 就是 一,再乘一个 x 就是 一,再乘一个 e x, 我 们这样来写,那么你看,这里,这里有多数项啊,这里有多数项, 那我们就可以想到,我们就可以想到这个喽喽 a, 我 们也没想到,我们也没想到是什么喽? a x 求导数的 x 分 之一,最小是求 x 分 之一,那么什么求导数的一加上二倍的等于 x 分 之一呢?是不是也是这个喽? a, 一 加上 二倍的等于 x, 是 不是这个求导这个求导是不是也是求的一加的 x 二倍的等于 x 分 之一,但是呢, 这个求到得到一加上二倍的 n x 分 之一,但是呢,这个是个负函数,这个负函数的外就是读了这个里面,读了这个里面,要再对这个里面求到这个里面求到一,求到求得零,然后二二倍的二倍的 n x 求到, 就求了多少 x 分 之一了,是吧?哦,嗯,求得前倒后不倒,前倒零,前不倒后倒 o 是 求得 x 分 之二, x 分 之二就相当于是 x 分 之一再乘以一个二嘛。你看,所以它这个写法,就这个写法就求得还要再乘以一个 x 分 之一,或者乘以一个二。 那么我们元数,你看我们元数啊,我们的这个不定积分,你看不定积分有一个一,加上二倍的 x 分 之一乘以 x 分 之一 d x, 你 看这个我们假想出来的,我们假想出来的,这个求的求到求的一,加上二倍的 x 分 之一乘以 d x 和乘以 x x 分 之一再乘以二,是不是多出来的二比我们的这个是不是多出来的二,多出来一个二出来 是不是做出来的啊?那么我们就要在它的这个圆长形前面就是它的圆长形前面加个二分之一,加个二分之一啊,要在它圆长形前面加个二分之一,这就直接就等于二分之一的六 n 一 加上二分之六 n x 的 绝对值,再加上一个 c, 看 这个求导,这个求导,这个求导,因为因为我们要求的是圆函数,圆函数啊,就是说圆函数求导要求要等于它的这个不定积分,要等于它的不定积分。你看这个圆函数求导出来是求的这个样子多来个 r, 比不定积分里面多来个 r, 所以 要在这个圆函数前面剩下二分之一把它的 r 消掉,所以它,所以它本身原来的样子是这个样子的。再加 x, 不要去管这个样子啊,这个这个这个一定有,这个前面的这个里面求导一定能求,能,一定能知道这个,所以不用管。你看,如果你按老师的来评你一个中间变量,你想中间变量是什么?这个样子,这个中间变量是啥?你是想到中间是什么样子了? 我们来看这题,把减圆式圆式等于这个这个样子,这个这个分子,我们把它,我们把它分,我们把它放松一下,把它写成这个样子, a 加 s, 然后 a 减 s, 然后 分之一,再减个 d s, 减个 d s, 那 么我们这步这步,我们再把它分开来,我们再把分开来,我们又要再减一点,这个样子,这个样子啊, a 加 s 分 之一,加上 a 减 s 分 之一,这样子变成 d s, 你 看,但是呢,我们这步这步到这步,这步到这步也是不是一样啊?是不是一样的话,我们要对这个通分,这通分 a 加 s 啊, a 减 s, 那 么这里乘以 a x, 那 么分子乘以它乘以 a x, 然后然后再加上这里 a x 通分,那么它是乘以 a x 乘以 a 加 x, 乘以 a x, 那 么你看 x 跟 x 又掉了,多来二 x 嘛,多来二 x, 我 们这一步,这一步到这一步多来二 x, 所以 我们要在这个前面, 我们要在这个前面加上二, a 分 之一要在前面加二, a 分 之一,跟这里的二 e 就 掉,跟二 e 就 掉, 那现在我们就来,我们就来算,我们就来算这个,我们就来算这个,这个这个小变化就等于二 a 加分之一,这个的圆函数已经知道了这个圆数,这圆数就是等于 a 加 这个 a 加 x 嘛?那绝对值要因为 a 求到零,然后 x 求到这个,这个转角求到 a, a 加 x 分 之一,等于一,就一样,然后这个是负函数, a 求到零, x 就 到一,没有变化,所以再然后再加, 再加上,再加上这个 a, 这个也是一样, a 减 x, 但是这里稍稍有变化,这里你看这里 a 的 a x 求到是求的 a 减 x 分 之一,然后再乘以它的负函数,求到这个 x 的 点下负 x, x 求到负一啊,这里这里乘一个负一,那么这里就要变符号了,这里, 但是这里的加号要变成减号,减号、减号,慢慢,你看现在就来嘛,然后再加上一个反手 c, 那 么我们把这个这个五点七分的圆数就变成什么样子,把这个这个还是一样造型啊,零分之一,然后这个这个减这个我们知道他们相处是他们的指数相减出来,所以我们这个变成的 n 绝对是 a 加 x 的。 注意 a 减 x 绝对是加 c, 因为这个因为的 n a 减 b 的 n, a 减去的 n b 嘛,啊,一样的,所以就变成这个样子啊,它原数是二百分之一的 n 这个样子,然后再加上一个常数 c, ok, 前面我们讲的全都是第一类用法啊,现在我们来讲第二类用法, 第二类用法呢是要要进的第二类用法。看这个题,我们,我们来,我们,我们这样,这样等于, 嗯,根号下 x 减二分之七,乘 x 等于 d s 啊,我们定一个,我们定根号下 x 减二等于七,那么推出来 x 等于多少, x 等于多少呢?我们这里这里我们两个同时平方, x 减二就等于七方,那么 x 就是 七方加二, s 就 推出来是七方加二, s 推出来是 t 方加二二,嗯, s 推出来是 t 方加二,那么那么我们我们把这个 d d s 再求一下 e s, d s 是 不是对,嗯, x 求微分,对吧?求微分嘛?对 x 求微分,那么这个求微分就要求到,求到,这个求到就形成 r t r t r t, 然后对它求到了 对 r t, 然后 d d s 就是 对 x, 就 说对 x 求倒了,再乘一个,它的力量现在变成 d t 了,变成 d t 了, 然后呢?然后我们就把它写一下,写一下,写一下它的这个,那么原式就等于 原式,就等于原式,就等于。你看这里,这里的根号,根号加 x 减二,已经变成了,这里,就变成了 t, 然后 t 乘以 x 乘以 t 方,加到那里的 x 乘以 t 方加二,然后 d x 乘以 t, 你 看二 t 乘以 t, 嗯,大 t 是 d g, 然后呢,我们把这个,把这个 r 写到这个前面来,传输,传输,我们把它写到前面,写到这里, 写到这里,那以后呢?我们就,嗯,你看这里有个 t, 这有个 t, t 跟 t 就 对了, t 跟 t 就 对了,所以它的整个就又变成这个 r 变成这个样子, t 方加上 r, 然后 d t 看 t 方加上 r 跟 t, 所以 我们只需要对这个,这个,我们只需要把这个的那个啥,那个整数求出来, 你还是求出来吗?我们看下 t 方加二,然后 d t, 我 们求整数,什么?什么函数?什么函数求的是 t 方,这个是三分之一的 t 的 三四方。 因为你看你对这个球打分,三根三要垂在前面,再减去 t 就 变成 t 方了,然后三根三分之一又掉垂是 t, 所以 t 方,所以 t 方的原函数是三分之 t 方啊,三分之一 t 方,然后二 t 呢?求导数等于二十分, 现在你把这个 t 看成 x, 你 不要说,哎, t 不是 未知数吗? t 现在变成这样,变成 x 了,所以呢,它的这个元数就可以写成什么样子,它的这个元数就就变成了,它的这个元数就变成了,就等于等于二倍的, 你看二倍,二倍的三分之一 t, 三三分之一,然后 t 的 三四三,然后加上二四四倍的 t, 然后再加上,再加上 c, 嗯,就变成这个样子了,对,现在是就是三分之二七点三四三,然后再加上四 t 加 c, 然后呢?这个 t t 啊? t 呢? t 呢?我们是令根号下 x 减二等于 t 啊,所以你现在再把这里的所有的 t 换成根号下 x 减二就可以了。 我们一样的留意另一个另一根方向, e x 减加 e 等于 t 等于 t, 那 么我们就这个 e x 加上 e 等于 t 方减 e, 那 么 x 就 等于多少, x 就 等于多少。高中数学就等于零 n 七方减 e 等于多少,七方减 e 就 等于零了,零 n 七方减 e 就 等于十二, 然后呢,我们把这个前面的这个减原式就等于原式,就等于。你看这个,我们定这个点七啊,对不对?直接是, 呃,直接变成七,然后,然后呢?直接变成七了,然后我们我们现在知道 s 了啊, d s, 我 们写成 d s, d s, 就是 对这个球倒再求,再求过一份啊,这个球倒,这个球倒减一啊,积分减一分之七,这个球倒还要再减到二 t, 那 还是减到二 t, 所以 我们这个这里的 d s, 我 们用这个记号就乘以,再乘以,再乘一个 r t, 再乘以一个 t 方,再乘一个 t 方减一乘七 这个样子,然后,然后就这里,这里还差个 d t, 然后呢?这个你看这里,这里的,这里有个 r r 出来,然后这里 t 乘 t, t 方啊, t 方,然后 t 方减一, t 方减一, t 方减一 t 提方减去 t t 啊,然后呢?你看我们这个,我们这个讲到这里啊,讲到这里的话就就要讲到一个,呃,老师讲到的那个无中生有啊,无中生有。我们 这里,你看我们这里 t 方减一,你看这个分子没有了,这个分子没有,所以我们要再减去一个一,然后再加个一嘛,这个一加就没变,所以你看这里这里就变成了什么样子了啊?变成这个,你看 t 方减一, t 方减一,就直接写成一嘛,一,然后再加上一个 t 方减一, 一,然后一 t 剪成这个样子啊,剪成这个样子,剪成这个样子了以后呢?剪成这个样子以后呢?我们就现在就分别对这个里面,这个里面好求了,现在就这里面求这个规范,求求求圆数,一的一的圆数肯定是 t 吗? t 求搞求的 e 吗? x 求的 e, 现在的边缘变成 t 了 t 啊,所以 t 的 话就是元数是 t, 这个元数呢?这个元数肯定是的,分 t 方减 t 嘛,你看,因为这个这个写的 t 方减一分之一嘛,然后还这个,还有这个什么,这个只是这个样子啊,但是这个图出来分成一个,这个图出来二 t 啊,所以,所以要在他前面乘一个二 t 分 之一,要在前面乘一个二 t 分 之一啊, 要在他前面乘一个二 t 分 之一,嗯,所以他的这个元数变成什么样子?元数,元数,元数,元数 怎么写啊?圆数,把这个擦掉,圆数就变成第一个就等于二倍的符号,然后一就是 t 的 啊,一就是 t, 然后这个就是加上的 n, t 方 减一啊,减一的这个值,然后再加个 c, 但是呢,这个这个求出来是多来的,跟我们说是多来的二 t 啊,所以这里,这里的前面,这里的前面要乘一个,嗯,这里的前面要乘一个二七分之七,二七 r 七分之一,这里要乘以 r 七分之一,然后再把 r 乘进去,就是 r 七,然后再加上 r 跟你看,然后 r 七,然后这里 r 跟 r 掉了,然后就变成 t 分 之一,等分 t, 然后 t 绝对是加上 c 平方数就变成了幺二七,加上七分之一的 a, t 翻起绝对是加 c 平方数就变成这个样子了,这个平方数就出来就是这个样子, ok, 不 定积分的第一类幻用法跟第二类幻用法都给你们讲了,不知道你们还没懂啊。我,我也感觉我有点不懂啊,不知道你们能 不能解答。好,现在我们来, 我来。嗯,我来给你们梳理一下。期末考可能可能会考到这个重点。重点是啥?我只是我个人的意见啊,个人的意见啊,两个重要极限。可能会考两个重要极限,第一 个重要极限呢,就是厘米 x 距离零的时候,三 x 等于一,这是第一个重要极限啊。然后第二个呢,是厘米厘米 x 距离也读清的时候,这个一加上 一加上 s 分 之一的 s 四,这个等于一,这个是阿拉伯数字一个字母一。然后呢?他会怎么讨论这个?来个例子,来个例子, 一米 x 乘以零,然后这个三米三 x 除以 x, 你 们说等于多少?这里是 x x 啊,但是这个是 x x, 这个是 x x, 你 在这里配个三 x x, 那 你后面乘个三 x x x, 那 么前面的整个是七啊,所以一乘三等于三啊,所以这个可能会这种形式来考,或者说是他出现在那些, 嗯,就是我们在那些求求那种极限里面啊,可能会会遇到这种,这种,所以这个两个重要极限,你要记住了,就是让它求极限求出来, 那么这个这个这个它会怎么求呢?这个比如说 mini s 求求的时候,它的这个 一减去 x 分 之一的 s 次,你看这个是加,这个是加,这加 s, 这里是,这里是减去的,你看这里呢?这幅画,这里是这个是正的,这个是正,但这个绝对是正的啊,所以我们要给它变一下,它等于一 x 去进行正无穷,然后这里 这里你看这里积,我们把这个加号一加的,那么负的,那我们就把它写成分子上分之一,然后然后我们要把它凑成,我们凑出这个来,凑出这个来,因为这里是正的,这里是正的,这里也是负的,这里也是负的。负的 x, 那 么题目上它是正的啊,题目上它是正的,所以这里还要再乘一个负一,把它还原掉,然后就等于, 就等于,就等于说呢你,你然后 s 确定你的情的时候,那好就直接等啊。这个这个这个前面这个这个前面这个就等于多少就等于一嘛,一嘛。 因为这里是一的时候,等于一的时候,这是这个这个时候他是他是这样的一嘛,然后这里有个负极,所以这个分数加个负极就可以了,就是这个类型的分数嘛。 好,那么下面就是可能会考到切线还有法线啊,切线还有法线, 切线,法线,那么那我们几个例子, y 等于 x 的 三四方,那么这个切线我再再这个点击,点击在这个点,这个已经点击的这个切切线啊,那么切线的方法不要调捣乱,所以调到这个三 x 的 零方,然后,然后 k, k 就 等于 k 啊,这个是 k d 嘛? k d 就 等于把这个 x 的 值再加上就变成了三,所以 k 就 等于三,所以它的切线,它的切线就等于 y 减 y 嘛。 y 减 y 减 x 等于 x 减一, y 减 y 减 x 减 x 减 x 减一,然后这个你放出来就行。那发线,发线是 法线,法线的法线的斜对的斜对相乘以负一啊,我就为什么写 k 一 k 一 k 一, 它乘 k 二乘以负一,那么我们把 k 二乘出来, k 二就等于负三分之一,负三分之一还是一样的。 y 减 y 减 x 减 s 减 s 减 x 减 x 减 t, 这个就是切切线,这个就是法线。嗯,就切线就切线就取完了啊, 切线法线就取完了啊。 复合函数求导,比如说你看这个 y 等于散引 x 的 三次方,叫你求它的一阶导,叫求它的二阶导,那么一阶导它就是 y, 等于这个求导。散引 x 求导,就是变成 o 散引 x 三次方了,然后 x 三次方又是一个函数,因为它是复合函数,所以要在对散引 x x 的 x 的 三次方求导,所以就有 x x 的 三次方求导,要求三 x x 的 平方, 这个是他的一阶导,那么按阶导,按阶导,就是在一阶导呢基础上再再导啊,所以这个这个,这个就是乘乘,乘的话就是前导都会倒,加上前导会倒,前导呢?这个扩散 x 的 三次方导就是负的三 e x 的 三次方,然后再对住 x 再求几道啊,一样的 x 三次方,还要再乘一个三 x 的 平方,然后 前倒后不倒啊,前倒后倒,然后再乘以 s 的 次,哎,三乘以 s 一 方加上前不倒波三 s 一 s 三次后倒加上乘以后倒后倒后倒,则变成是第二次,所以它的方向就是这样子。 那复合函数求导完了以后呢?就,嗯,复合函数求导完了以后就是,嗯嗯,看一下, 然后就是可能就是不求微分啊,叫你求微分, 你求微分。微分的话,比如说是 y 等于三点 x, 那 叫你叫你求 d y d y 就是 求微分啊,微分就等于这个求到啊,我们求微分好,求这个求到,就这个求到是负三点 x, 然后再选择 d x 啊,微分就好,求一点就是, 然后就把罗汉中轴定义啊,罗汉中轴定义啊,罗汉中轴定义罗汉中轴是怎么说呢?他说是一个函数在 a、 b 上一起接上连续,然后连续,然后开启接上和导内导上内导,然后,然后那么就有一个,就有一个什么呢? 就有 f a 等于 f b 啊, f a 等于 f b, 这三个是条件,条件。然后呢就说他就说那么 a、 b 内 a、 b 内存在 存在,存在一个这个存在一个这个,使得这个这个导数等于零,把这个带进去导数等于零,那么他的这个他的这个是什么个意思呢?他这个是什么意思呢? 比如说他可以用 y 等于 x 的 平方减 x 减,然后我们说 x 属于负二到三,负二到三,那么他说 x 属于负二到三,那么他说 x 属于负二到三,那么如果说是符合的话,把这个,把它的这个 这个这个求出来,这个求出来,这个这个 a、 b、 c、 d 是 怎么求出来?那么符不符合,我们就要看它在 a、 b 内是 a、 b、 b 曲线 a、 b 上是不是连续的。那么它的这个我们看它的定义域,定义域呢?这个二次函数啊,那个二次函数,二次函数,它的定数 r、 r, 然后在这个上面也是连续的,是吧?然后呢? r 的 话,在这个你看 a、 b 内肯定也是可导的, 可导的,你看你不知道它的 x, 那 么 x 现在的 x 也是 r, 所以 说在这个上面也是可导的。 嗯,可导就是你做之前你要换换,他符合条件,那么现在还有,你看这个 f 跟 f 一 不一样,你把 y 等于,然后 x 等于负二带进去, x 等于负二带进去四,然后加大减等于多少,七等于二,这里等于九,然后 y, 这个 x 等于三,带进去, x 等于三,这就是九九减,三减和减是等于七,所以所以 f a 是 等于 f、 b 的 三个条件满足,三个条件都满足, 然后呢?三个条件的满足,那么就已经存在,这个干嘛?还是怎么说?我不知道,所以就把这个放下来,然后一定存在,这个一定存在,这个等于零,那么就说是 就把它带进去嘛,那就说二根嘛就等于零嘛,是吧?二根嘛就等于零,二根嘛就等于零,二分之一,你看二分之一在不在画到三上在吗?所以一直在这个,那这个等于零,所以我们定这个等于零,我们定他的零,然后把干进去,把干进去二分之一, 然后卢旺夫,然后那个男的相对就到了,那个男的中指点啊,那个中指点是 a b 也是在 a b 上连续,然后 a b 内个,然后也是在 a b 内存在一个点,在这个点,然后他的不一样是让他的后面的这个,这个是等于 f b 减减 f a, 然后 b 减 a 啊,后面后面是这个样子,一样的啊,一样的,你判断如果大概二分之一,你看到了这几个都满足条件了以后呢?你把这个球倒出来,然后再进去,然后然后这个剪出来,然后再剪出来就行了, 然后下面下面可能就到了单调性的判断,单调性的判断,单调性的判断,然后就是单调性的话,就是有一个函数 y 等于三四三减去三四啊, 这个样子,那么我们要看到啊,要结束的单调区间,那么要求一一一节导,一节导,然后另另一节导大于零,另一节导大于零,另一节导小于零,然后结束的那个区间就是它的单调间增幅单调减, 然后呢就收到了,然后下一个就下一个可能就收到了凹凹,还有凹凸区,角凹凸区间,凹凸区间,凹凸线,凹凸线,凹凸线,要求他的阿吉岛啊,求阿吉岛,然后他就答应那个就是这里是也有个小朋友装的小凸啊,小凸、大凹,小凸,大凹,小凸的凹是阿吉岛小,一定是凸,阿吉岛大的就是凹, 然后下面就到了,咱们下面就会考到的,就是就说进阶线,进阶线,进阶线的话有三个,有三个水平的,然后牵直的, 然后还有一个是斜的,斜的水平的话,你就比如说是这样子水平的话,比如说这个这个函数,这个函数的进阶线水平的话, 他就说这个样子,他这个如果说这个函数就是他的进阶线,就是 y 零, y 零, 那么牵扯呢?牵扯的,就比如说这样子牵扯,牵扯的话,你就这样子,这里是反方向,这里是负的方向,然后这个图像是平行于 x 的 图像。当比如说你看 b 的 s 平行于方程的时候,你看平行于 x, 曲线一不平衡,你看它的 x, 曲线一不平衡,它的 x 曲线一不平衡,它的 x 等于无穷无穷无穷,无穷无穷,就是当一个函数具体某个数的时候,它就也无穷,它就也无穷。所以这个 x x 等于二分之二和 x 等于负,二分之二就是它的牵制极限线, 就是它的牵制极限线,然后一个斜可以,这个斜极限线呢?斜极限线就是要求求,就是 y 等于 a, x 加 b, 要把 a 和 b 求出来, a 和 b 怎么求呢? a 和 b 的 情况,比如说,呃,还是 y 等于三, x 的 平方加上加上,呃加上三,那么它的这个 d m x 接近无穷了之后,接近无穷的时候,它的这个 a 啊 a 就 等于这个三 x 的 平方加三除以 s, 这个如果求出来是一个常数,常数的话就证明它的斜的存在,如果不是,如果求出来能证明它斜的存在,这个求出来 a 点完以后再求 b, 就 等于 d, m x 除以无穷,然后 三 x 的 立方加三,减去 a x 啊,减去 a x, 必须这样算啊, ok, 那 么还有一个,还有最主要,最主要的,高中时候最主要的问题,比如说呢, y 等于 x 的 四次减去二, s 的 立方加五, 嗯,两个函数属于负二倒八,负二倒八,那么我们要求垂直的话,就把它的极值也求出来,极值就是一阶导,求一阶导完以后,另一阶导等于零,然后求出啊,就是一阶导等于零的那两个点啊,那两个点或者不存在的点呢?把它求出来,然后再跟极值做对比,再跟极值做对比,再跟极值做对比就可以了。 然后后面就是我们要学到的不定积分,就是我刚才讲的那个不定积分。 哦,它如果是一个平方函数,它就说 f x 等于一的负 x 的 平方分之一,然后这个是等于 a, 然后这个 x 等于这个 x 等于再 x 等于除连续的话,则 a 等于多少?连续的话就说是连续的,它的方法就是极限,极限是 极限值等于函数值,就是等于 x, 零极限值等于函数值,极限值,极限值,那么我们求这个极限,我们求下 a 等于 x 虚线零的时候,这个极限一的负 x 的 平方分之一,那么这个我们把它写成一分之一的这个八,那么这个极限, 这个极限要等于这个函数值啊,函数值就等于 f 零就等于 f 零数,那么 f 零是大于等于 f 零等于 a 啊,就等于 a, 那 么我们要把这个极限这个极限求出来,等于 a 的 话啊,这极限求出来,那么极限值等于 a 的 话,这个极限值等于多少呢?这个 a 就 等于什么?那么这个极限值,这极限值的话,你看这个 这个 x 区间点的时候,这里是这里,这个指数是无穷小的,是吧?指数无穷小, 无穷小,无穷小是无穷大,这里一分之一是,呃,比如说你看,比如说这无穷小一 分之一乘以一分之一乘以一分之一,比如说它是这个次面,它旋转下去,那么分分子是分子,是无限大的分子,分子不变,分子无限大,所以它的这个就等于零啊,就等于零,等于零的话就就就等于零,然后这个极限等于零,那么那么函数出来,你要等 a 的 话,这个 a 一 点就等于零了。 哦。还有一个就是它,比如说它这个样子, f x 等于 f, x 减三等于二,再减 s 等于三。 是 f x 等于什么?等于什么?是连起的呢?还是不连起的呢?还是说是跳跃的,还是说是无穷的? 就是这个就是啊,就是要考察间隔点啊,间隔点的话就是这连续的还是不连续的,还是跳跃的,还是无穷的,那么那么 等于三的话,我们就求第一个 x 去进三,去进三,那么 x x 减三,那么你看他去进三的时候,他不能等于三,因为分母不能为零吗?分母不能为零,他去进三的时候,分母不能为零,所以他不能等于三,所以函数在 x 等于三的三数没有定义啊,没有定义的话,嗯,没有定义的话,他肯定是不连续了,不连续他就不连续了,不连续这个不连续就要排出来啊。 你看我们距离三的时候,我们求它的极限,你看呃,它的这个,我们求它的极限。极限,你看距离三距离三的时候越来越接近三,是不是这个是不是无穷小?是不是无穷小? 无穷小吗?越来越小,然后分子不变,分子越来越小,越来越小,那么它就是,它就是极限这种无穷大、无穷大、无穷的,所以 x 等于三,除以六,它是无穷无穷劲道点呢?
218啊福 04:36查看AI文稿AI文稿
04:36查看AI文稿AI文稿通过这道题,找到凑为分的核心诀窍,顺便拆穿出题人的出题套路,挑战期末不挂科一百题之第十三题,来看这道不定积分的题目。我们这个题目呢,采取的是第一还原法,也就是凑为分法。 大家知道凑为分法有个非常关键的步骤,就是将背记函数将其拆解成一个符合函数乘以这个符合函数内函数导数的样子。 将 f x 拆成这个样子,那么你拆成的这个样子啊,它里面有一对关系,有一个 f x 和 f x 的 导数,就是它会存在一个求求导的一个关系,所以我们在做不定积分的题目。如果你看到了这种明显的 导数关系,比如说举个例子, cosine t 分 之 sine t, 那 我们就可以尝试去使用 d 还原法了。你像这里的 cosine t 的 导数是负的 sine t, 你 可以去给它添一个符号,它就变成 cosine t 分 之 d 口算题,然后就好记了,他就看成是一个 u 分 之一 d u 的 这样一个不定积分,这个是好记的,对吧?但是我们今天要做的这个问题呢,这个题目的背记函数没有明显的一个函数和一个函数导数的关系, 这种问题我们怎么办?大家去观察,去观察你的背及函数里面的这些个结构啊,它的因子都有什么?比如说这里面我观察到肯定有 x 这样一项,嗯,还有 x 乘以 e 的 x 是 m, 还有 x 加一,那你就去找 那个较为复杂的,那这里较为复杂的是谁呢?是 x 乘以 e 的 x 次密。我们去找这个较为复杂因子去求它的导数。它的导数应该等于前导后不倒,加上后导前不倒,你去做一个整理, e 的 x 次密提出来就剩下了一加 x。 所以看这个背记函数当中啊,虽然没有很明显的出现 x 乘以 e 的 x 次幂的导数,那我们是不是看到它的一部分就是一加 x, 那 你可以去给它凑一个它的导数出来,我可以在这个分子和分母上同时乘以个 e 的 x 次幂, 那这样分子这一部分分子就是 x 乘以 e 的 x 私密的导数。这里就出现了明显的一个负 x 和负 x 导数的样子, 把这个分子凑到微分里面去, 就变成了 d x e x。 那 接下来我们为了清楚一点啊,这里令 t 等于 x 乘以 e 的 x 次幂,那么这个不定积分就是 t 乘以一加上 t 分 之一 d t 这个不定积分是一个我们比较熟悉的不定积分,它是怎么做的?把背记函数写成 t 分 之一,减去一加 t 分 之一,拆成两项,拆成两项之后,它就好积了。然后第一项积分应该是 lo n t 的 绝对值减去 lo n, 一 加 t 的 绝对值,再加上一个常数 c。 接下来呢,我们将 替换回来,那就变成了 lo n x 乘以 e 的 x 次幂的绝对值,再减去 lo n。 哎, e 加上 e 加上 x 乘以 e 的 x 次幂的绝对值,再加上一个常数 c。 我 们可以给它做一个整理,把这两个 lo n 合在一起,那就应该是 e 加上 x 乘以 e 的 x 次幂分之 x 乘以 e 的 绝对值,再加上一个常数 c。 所以这类问题啊,做这类问题的诀窍就是你去观察它的背记函数的里面的结构,去找那个较为复杂的因子,把它的导数求出来,然后你再去看这个背记函数的其他部分能不能够向,向哪里靠拢呢?向你找的这个复杂因子以及这个复杂因子的导数去靠拢, 去给它凑出来。那我们这个题目其实也可以观察到出题人的他的出发点实际上是利用 这个我们较为熟悉的不定积分的一个结构去把这个 t 做了一个替换,换成了一个较为复杂的 x 乘以 e 的 x 私密的样子,然后给我们设计了这个题目, 所以我们掌握了出题人的这个小心思啊,有些题目你拿过来之后呢,你一下就能辨别出来他想考你什么。
103大米讲数分/高数 30:34查看AI文稿AI文稿
30:34查看AI文稿AI文稿好,同学们好,我们今天来复习一下这个不定积分,顺便呢,呃,给大家呃,讲几道不定积分的作业题。 首先,什么是不定积分啊?大家应该都知道,不定积分它就是倒数的逆运算, 什么意思呢?比如说啊,大 f x, 它如果对 x 求导是小 f x, 那 么小 f x 对 x 积分,你一定它能得到一个大 f x, 当然积分不为一,对吧,它加上任何一个常数 求导都是大 f x 求导的结果,所以说最后要加一个常数 c, 那 我更具体一点,比如说 x 的 平方,它求导是 二 x, 对 吧?那么二 x 的 积分,谁对 x 求导是二 x x 的 平方啊,最后加个 c 就 行了。所以说啊, 不定积分很简单,只要你能找到谁求导以后得到 这个背集函数,那么谁就是他的结果。最后加个 c, 那 么我们导数为什么会算?因为最基础的我们知道一个导数的表,对吧?啊,所有的基本初等函数 求导是什么,我们都是背下来的,没有同学用定义法去算吧?啊,不需要算这个的话呢,老师上课带大家算过一遍,但事实上,我们求解的时候,只需要去背下来这个导数表就行了。比如说, 我们基本出的函数有哪一些呀?长函数啊,还有那个什么密律函数啊,啊,反比例函数啊等等。那你比如说啊,像这 这几个公式我们肯定都知道的嘛,对吧?比如说我对 k 进行一个积分啊,对一个长函数进行积分,谁对 x 求导是 k 呢? 很明显 k x, 对 不对?你反过来试试看。那如果它是一个密律函数,求积分,哎,那我们来看密律函数求导 x 的 妞,我说妞加一次方吧,它求导是不是妞加一乘以 x 的 妞次方 啊?那 x 的 溜次方事实上是不是相当于是溜加一分之一 x 的 溜加一次方的求导, 对不对?有这个式子是不是能得这个式子?所以说 x 的 溜次方,它积分以后得什么啊?这里要加个 c r, 它积分以后是不是这个呀? 啊?妞加一分之一 x 的 妞加一次方, ok, 你 如果是正常的一个负密率,那他世上是不是也应该满足这个式子呀?你无非就是把妞是负的给他带进去, 对吧?那么他是不是就变成了负妞加一分之一乘以 x 的 一减 u 次方啊,对不对?你就把它带进去就行了。但是如果说像反比例函数就比较特殊,反比例函数这个 u 是 不是取一啊? 如果你这么写的话,这个分母是不是零了呀?啊?它就不对了,对不对?所以说啊, x 的 负一次方积分就是 x 分 之一积分,我们做一个特殊的来写,它等于零, x 绝对值加 c, 为什么这么写?老师上课讲过了啊,如果说你不记得了,没事你把它背下来 这个绝对值符号的话呢?还有个别的同学啊,他可能会漏写,注意不要漏写绝对值。除了密率函数,当密率里面包括了正比例啊,反比例,对吧等等, 还有些什么呢?还有我们讲三角函数,三角函数你能求倒,那能不能积分呢?很明显能,比如说我们的 cosine x dx, 谁对 x 求导是 cos x, 那 我们随便想要都知道是塞 x 嘛,对不对?那反过来,谁对 x 求导是塞 x, 那 就是负的 cos x 嘛, 就加上去就行了,对吧?因为我们还知道 tangent x 求导是 c x 平方。 cotangent x 求导是负 c s c 啊,平方。 所以说,如果说我直接问到你 c 方 x d x 是 什么,你也应该想到应该是 tangent x 加 c。 同样,如果说我问到你 c s c 平方 x d x 啊,这个积分是什么,你也应该想到是负的 for tangent x, 对 吧? 除了三角函数,还有我们新学的反三角函数,那反三角函数 我们知道阿克塞 x 或者 cosine x 啊,它求导是根号一减 x 方分之一啊,如果这里是阿克 cosine x, 就是 加个负号,对不对?嗯, 以及阿克宪进 x 求导是什么?是一加 x 方分之一, 如果是口填进,那就加个负号,因为我们知道了这个,所以说,当我们问到你啊,根号一减 x 方分之一 d x, 这个积分等于什么?谁对 x 求导等于它? 很明显阿克塞 x 呢?所以说啊,碰到这个积分,那它等于阿克塞 x 加 c 加 c 啊,都加 c 啊。同样的道理,我碰到一加 x 方分之一 d x, 那 么我们就应该得到 ak 整数 x, 如果加负就是阿克刻 ten, 这个我们就都懂了,对不对?那么除了三角函数怎么样啊?指数对不对啊? e 的 x 四方, 它因为它求导还是 e 的 x 方,所以说的话呢, e 的 x 方积分是 e 的 x 方,然后结果呢? a 的 x 方求导是论 a 乘以 a 的 x 方,所以 a 的 x 方积分就是论 a 分 之 a 的 x 方,对吧? ok, 那么这个表现在我又给你们重申一遍了,你们要怎么样啊?一定要记下来,不然的话呢,你连记积分表这种基本触感函数的积分表你都没有记下来的话,你 你积分将会变得非常非常困难啊,因为我们后面讲的所有积分的方法,我用任何的方法你这个表你记不住,我得到一个很容易得答案的一个积分你都不知道,那,那这个很难做了。 所以说啊,基于不定积分,他是导数的逆运算这一点,呃,对于一些啊,基本出的函数求导所得到的结果,对,他积分,我们能对应得到一个基本出的函数, 对吧?这个东西非常的重要,那我们有了这些表以后,你看啊,这些的话,我称为,呃,我就称他为基本积分表吧。好吧, 这个积分表里面这些公式如果有,你可以直接积分得到,如果没有,他无非是通过这 这些被积函数加减乘的运算或者复合而形成的,我类似于我们的初等函数一样啊, 那你看啊,这些积分表上的函数,我假设它为 f x, 那 么我有可能让你积分的函数是 f x 加 g x, 对 不对?那也很好办呢,你比如说啊,我们知道了根号一减 x 方分之一的积分,我们知道了 x 的 积分, 对不对?那么如果我们给到这一个积分啊,那我们应该也会做,对吧,因为加减以后的积分等于积分以后再加减,所以说他可以写成,同学们也要会写成这样的两个积分相加, 那你这个积分你可能看的有点懵,但是如果你拆成两个,你就会算了,对不对?根号一减 x 方分之一,呃,谁对 x 求导是根号一减 x 方分之一, 那就阿克萨尔 x, 对 不对?那这里面的话呢,他俩人约掉谁对 x 求导是 x, 那 很明显是二分之一 x 方,对吧? 那就这样就算出来了,最后加 c, 不要忘了写。那如果啊,我的结果是 f x 乘以 g x 啊,它是两个相乘的,两个基本处的函数相乘的一个形式,我的这个原函数,那要怎么办呢? 啊?我们知道基本初的函数,你让它让它们两个相乘油,再求导它是等于 f 一 撇记加上 f 记一撇的,对不对?啊?那么写是基于这个,我们就得到了一个积分方法,叫做分布积分法。 你是这些简单的函数,那我们直接通过积分表得到,是这些函数的加减组合,我们通过这种方法把它拆开,能够求解。如果你的原函数是一个乘除的组合,那么你就需要用到分布积分法了。 分布积分法用到什么特征?同学们,你会发现啊,他这样的,我就是有个 u, 有 个 v, 然后 d x, 对 吧? 你两个相乘的元函数求导,你能得到其中一个部分,他也一定是两个不相关的式子相乘, 那这两个式子一般他满足什么规律呢?我们讲了,上课都给大家讲了,分成三档函数,对不对?第一档啊,我优先级最高的,嗯,中的低的三档,这是设为优的优先级。 他一共就五类函数,一类是密律函数,一类是指数函数啊,对吧? 三角函数啊,对不对?另一类还还有两类的是什么?一个是他们的函数啊,一个是对数函数啊啊,或者是反三角函数啊 等等,一共就是这五类函数,优先级最高的就是,什么情况要分布积分呢?你碰到这些函数,它们相乘,比如说密律函数,包括 x 对 不对?包括 x 的 平方, 你 x 方 e 的 x 次方碰到一起分布积分对不对啊?你 x 那 x 碰到一起分布积分对不对?就有这五类函数,碰到一起的,你就用分布积分,然后分布积分公式,我们讲是这样子的,它是不是可以写成 u d v, 我 们就记住这个公式啊, 这个是指 u d v 等于 u, v 减去 v d u 积分, 就这个式子就行了。然后这句话呢,我们第一步就是找 u 啊,令谁是 u 呢?谁越高级谁是 u, 比如说 x 方跟 e x 次方碰到一起, 密率比它更高级啊,密率是中级,它是低级的对不对?我们就令 u 等于 x 方,如果说 x 跟对数放在一起啊,对数更高级啊,那么我们就令 u 等于 non x, 然后解的话呢,我们分别把 v 求出来,有 u 有 v, 带一根式子里面就可以求解了,对不对?好,那么接下来的话呢,看几道例题, 那么我们就举个例子,比如说作业题第一题啊,积分变量是 t 对 不对? ok, 就 谁对 t, 球岛等于这个东西呗,我们要理解它是这样的,那么好,这里面的话呢,可不可以用分布积分? 很明显可以,因为它是一个密律,跟一个指数放在一起,对不对啊?有密律有指数,那就分布积分,令谁为优啊?谁高级令谁为优,很明显令密律函数为优,所以说啊,令 u 等于 t, 那 么 d v 是 不是就等于剩下这部分 e 的 负二 t d t 对 吧?等于 d 什么啊?又到微分了, e 的 负二 t d t 等于 d 什么东西?那你看这个东,这个 e 的 负二 t 是 不是它的导数的结果啊?所以谁导数是 e 的 负二 t? 嗯,是不是负二分之一 e 的 负二 t 啊?好, 这个东西是不是就是这个东西?所以说 v 就是 负二分之一 e 的 负二 t u 是 什么呢啊? d u 是 什么呢?是不是 u 一 撇 d t 啊?那就等于 d t。 有 了这些以后,原式就等于。那我们讲 u v 减去 v, d u 积分,对不对?那是不是负二分之一 t, e 的 负二 t 次方 减去啊? v d u 积分来啦, v 是 什么? v 是 这个东西负二分之一 e 的 负二 t d t 积分。好,那在下一步再往下写, 负二分之一 t e 负二 t 负负得正二分之一可以提出来啊, e 的 负二 t d t 老样子,谁对 t 求导?是 e 的 负二 t 次方 负二分之一 e 的 负二 t 啊?嗯,所以这道题的话呢,他就应该是负二分之一 t e 的 负二 t 次方啊,减去二分之一乘以二分之一,对不对?减去四分之一, 然后是 e 的 负二 t 次方加 c。 所以 说这道题选什么?有两个符号的,那就只有 a 了嘛,就选 a 啊。 然后我们再来看下第二道题啊,第二道题可不可以用分布积分呢?有密律,有三角函数, 那就可以用分布积分。那分布积分令谁为 u? 令密律为 u? ok, 那 么我们就这直接写啊,直接写,讲个简单的写法,那就是令 u 等于这个密律 x 方 d v 的 话呢,等于 cosine x dx 等于 d 什么?等于 cosine x? 那 sine x 嘛,对不对啊? 那么 v 就 等于什么? v 就 等于三 x, 那 u 等于它 d u 等于什么?等于二 x d x 对 吧?那么这道题结啊,直接原式等于,你看 u 乘以 v 减去 v d u 积分, u 乘以 v 是 x 方,三 x 减去啊 vdo, 那 就是 r x sin x d x 对 不对?那碰到这一步 还是一个什么格式啊?密律乘以三角函数的格式,那我们就再进行一次分布积分,是这个意思吧啊, 它还是两个式子相乘,并且这两个式子又符合呃分布积分的这个规律,对不对?那么因此的话呢,它还要做一次分布积分,我们才能得到结果,那还是老样子密律先啊, 设为 x, 然后 d v 是 塞 x, d x 对 不对?那等于 d 什么 啊?谁求导数赛 x 负 cos x, 所以 v 就 等于什么啊?负 cos x, 很多同学容易漏写符号,这里的话呢,你要注意一下,那那么 d u 就 等于 d x 又是代公式, u v 减去 v d u 对 不对? u v 那 就是负 x, 等会啊, x 方 sine x 减去二,我们先用括号括一下对不对?为了避免我们的这一个呃,符号啊,写错对吧?那 u v 负 x cosine x 减去 v d u v 是 负 cosine x 啊, d u 是 d x 得到这个对不对?那么就 x 方塞 x 减去两倍的, 你看负 x cosine x, 这里面有个负负得正啊,对不对?加 cosine x d x cosine x dx 等于什么?我们同学们都很清楚对不对?谁对 x 求导,等于 cosine x sine x, 所以说这一项就可以写成三 x, 这里面就是三 x 减去 x 扣三 x 嘛,对不对?所以说这个时候我们把括号可以给它去开啦,减去两倍的三 x, 减去两倍的负 x cos 啊,减负负得正就变成加上两倍的 x cos x, 最后加个 c, 那 么来看答案都有些什么呀?答案也都是三项,对不对? x 方塞 x 都正的。第二项,二 x cos x, 二 x 扣三 x 前面也是正的啊,那就加答案就直接扔掉 b c 了对不对?那二三 x 是 减的,所以答案就是 a 啊,是不是很简单? ok, 我 们再来看一下作业题第三题, x 方阿克弹紧 x dx, 那 这个时候的话呢,有密律,有反三角函数, 有这两项东西可不可以分步计算?可以,谁的是优先级更高?反三角函数的优先级更高。所以这个时候的话呢,我们就不设密律为 u 了,我们要设这个反三角函数为 u 了 啊,同学们,这个老师给你们汇总的这个表呢啊,记住啊,记住啊,这个地方反三个函数对不对是最高的?所以说有他优先,设他为优啊,你设其他的不对的, 你说其他的,你是做不出来的, ok, 那 么解解这道题,我们也是先令, u 等于 ak tangent x ak tangent x, 那 么 d v 等于什么?是不是等于 x 方 d x, 那好, ok, 等于啊, x 方 d s 等于 d 什么?谁求导?等于 x 方三分之一 x 的 三次方,所以说 v 等于什么? v 就 等于这个三分之一 x 的 三次方 u 等于它 d u 等于什么啊?它求导 d x 对 不对?那就是一加 x 方分之一 d x u v d u 都找出来了,那么我们就直接代公式啊,减原式等于 啊, u 乘以 v 三分之一 x 三次方,阿克特减 x 减去 v d u 积分, 那那就是它乘以它嘛,对不对?那就是一加 x 方分之啊, x 三次方,当然前面有个三分之一啊, d x, 这个就要要用到这个就要用到这个换元法的知识了。如果你会换元积分法,那你很自然地知道,这个积分它等于 二分之一 x 方,减去乱啊,一加 x 方,呃,这里因为横为正数,所以说有没有绝对值都可以啊。前面呢,有一个什么呀?有一个三分之一哦 啊,我们把前面照写下来,三分之一 x 三次方, ark tangent x 啊,减去三分之一乘以二分之一,这个东西最后再加 c, 那 我们要不要化简呢? 我看选项对不对,答案就选啊 a。 那 么来看第四题啊,第四题让我们求解这个, 那这个我们要正常解啊,就正常解就行了。然后我看这 x 加一,一加 x, 我 看到他很不爽啊,明明都长得一样的,为什么换个圆呢?嗯,那我们先换一下吧,如果我看到他,我实在难受,当然是让你换不换都行 啊。我另一个 t 等于 x 加一,那么原式就等于 什么呀?这个是 t 了啊,这个是什么?乱 t 了啊,那 d x 跟 t 有 什么关系? d t 等于 d x 的 吗?那么好,它长这个样子的话,密率对数, 密律乘以对数,那就是分布积分法,对不对啊?谁应该先设为 u 啊?啊,对数更高级,我们设对数为 u, 事实上就是我们讲的一道例题了,对不对?所以这个这个我就写快一点嘛,不懂的其实你也可以去翻 ppt。 我 令 u 等于啊,乱踢 d v 等于 t, d t 啊 t d t 等于 d 什么?谁对,踢球党是 t, 那 是二分之一 t 方, 所以说 v 等于什么?这个跟这个对不对? v 等于二分之一 t 方,而这个呢啊, u 等于它 d u 等于 t 分 之一 d t 啊,你有了这些以后啊,原式就等于 u v 减去 v d u, 那 就是令 t 乘以二分之一 t 方,减去 v d u 积分对不对?减去那就是二分之一 t 方,乘以 t 分 之一 d t, 二分之一 t 方,令 t 减去 t 跟 t 会约掉嘛?那不是二分之一 t d t 嘛,这个是不是很好求啊? 二分之一 t 方,所以说这道题答案是二分之一 t 方乱 t 减去四分之一 t 方加 c t, 我 们给它带回去的话, t 是 x 加一啊,所以说就是二分之一啊, x 加一的平方乱 x 加一 啊,减去四分之一 x 加一的平方加 c 啊,我们看一下有没有这个答案啊,他 d 选项是不是二分之一 x 加一方?给他提出来第一项剩一个 on 一 加 x, 第二项是不是剩一个二分之一啊?啊,对,所以说答案就选 d 啊。 那么最后一道题计算题啊,我这个答案在这里写的非常的详细了啊,并且的话呢,呃,每一步甚至连分值都给你了。这里面的话呢,主要是他,你你要能想到他是 你把它写成两个三角函数相乘,两个三角函数相乘求肯定是可以用分布积分来求的,而且这种类型你是一定能够通过分布积分来得到一个跟原式相等的像的, 然后接着的话呢,你把它看成一个整体去求解就行了。那么这一道题的话呢,主要是啊, 得分点就是我主要考察你分布积分,所以说你但凡你能用分布积分写这个式子出来,我就给你一半分了。那有的同学的话呢啊,只是说令 u 等于什么, v 等于什么,但是没有下一步式子,那这个我很难给到你分呐,我都不知道你记没记下来分布积分的公式 对不对啊?哪怕你翻书把这公式抄,你要给我抄出来啊?有的同学没有抄,那这个,哈哈哈,很难评啊,你说不懂我能理解啊,你很诚实,你没有抄作业,这我也能理解,但是我希望你的话呢,你要通过这道题来 主动的去复习这个知识点啊,这是一点,那你看啊,你用了一次分布积分以后,这里面的话呢,你还要用到一个这个公式的,这公式的话呢,我也说这公式非常的重要,那这里面话,你但凡你能用到这个公式,你又有五分, 对不对?那这里面的话呢,在下一步,在下一步。呃,这个地方呢?老师,这个,这个弄错了,不,不是,不是在用分布积分啊,这里写错了,就是说 你的这个三个 x、 dx, 这个我们是也是背过的吗?你,你会求这个积分,那么你就又得三分啊。最后你看这一项的话呢,跟这一项一样的,那我们把它移过去两倍的,这个我们要求的式子等于 这一堆,对吧?那意思就是我拿这一堆除以二,最后加个 c 就是 结果了。你,这个你不会的,你就看这个答案就行了,这个过程很详细,我这里面就不细说了啊。
22【有晴人】安柒. 01:05查看AI文稿AI文稿
01:05查看AI文稿AI文稿来做一道不定积分,对于 x 乘以 tan 的 x, 乘以 tan 的 x 四次方做不定积分 第一步就是一个凑位分,把这里的 tan 的 x 乘以 tan 的 四次方 x 变成 tan 的 x 乘以 tan 的 x, 再乘以 tan 的 三次,所以前面留下 tan 的 三次,后面凑过去。 这一步的凑位分不能直接像之前那样子。这里有 sine 四次,所以选两个凑过去也许能做,但是可能比这个麻烦。接下来以 sine x 为整体,把它也凑过去。 这个式子我之前推过一个递推公式,但是其实没有必要用,因为我们这里可以直接凑过去,系数又不是很高。 sine 的 方再换成 sine 的 方加一。
140小阿文数学 02:19查看AI文稿AI文稿
02:19查看AI文稿AI文稿接着我们学习不定积分的第二课,第一类换元法。当我们遇到的题目不能直接使用上节课的公式时,我们会优先考虑该方法。 比如这道题,虽然我们知道 e 的 x 次方的不定积分公式,但这里给出的是二 x 多了个二,这样就没法直接套这个公式了。 那怎么办呢?很简单,换元位我们设 u 等于二 x, 那 这个被积函数就变成了 e 的 u 次方, 但只变这部分还不够,后边还有个 d x 呢, d x 咋变? 既然我们知道了 u 等于二 x 四,那么 u 对 x 求导等于什么?很明显,等于二。根据这个式子,我们很容易就可以得出 d x 等于二分之一倍的底油,这样我们就可以用这个结果来替换 d x。 上节课讲过被极寒数理的常数因子可以提到前面。好,现在这个积分你应该会求了吧,直接套公式就可以了。 注意这里的括号要去掉,不去掉就会出现二分之一倍的 c。 这里写二分之一倍的 c 和直接写 c 本质上是一个意思,都表示任意常数,所以不如直接去掉括号,这样省不周。 最后千万不要忘记把 u 再换回二 x 四。 好,这就是第一类换原法的解析流程。是不是挺简单的,我们来总结一下解析技巧啊。要想用第一类换原法,我们要先观察背机函数,看看哪部分让我们比较难受,大概率把这部分设为 u 就 能做出来了。 如果还是做不出来,说明 u 设的不对,或者这道题不能用第一类换原法来做。 下节课我们找几道题给大家具体讲讲如何设这个 u 吧。
185一分钟讲数学 02:15
02:15 05:34查看AI文稿AI文稿
05:34查看AI文稿AI文稿这道题目的背记函数啊,看上去不是一个我们常规的样子,那我们可以想办法把它写成我们比较熟悉的样子,这里呢,设 这个背记函数为小 f x。 背记函数是取了三个数值的最大值,很明显这个最大值和 x 的 范围是有关系的, 当 x 小 于负一的时候,它最大值就是 x 平方。 x 大 于等于负一,小于等于一的时候,最大值是一。当 x 大 于一的时候,最大值是 x 的 三次方。那么同学们有没有想过这样一个未知函数,它的原函数一定存在吗?也就是说这个不定积分写出来是有意义的吗? 我们有一个定律是这样说的,连续函数,它的原函数一定是存在的,所以我们只需要去看一下这个小 f x 呀,它是不是连续的? 它是个分段函数,它在每段上都是一个初等函数的样子,那它在这段上一定是连续的,所以我们只需要去关注在那些断开点的位置是否是连续的就可以了啊。我们来看一下在负一这点,判断一个函数它在这一点是否是连续的,我们可以通过 它在这一点的极限是否等于它的函数值来判断。那在负一这点,它的极限和右极限,因为在这一点,它的左右两侧分成了两个函数,对吧?先来看一下 x 去负一时,从左侧去进,它的极限是什么?从左侧去进,带的是第一段函数,很显然是一。从右侧去进, 带的是第二段函数。第二段函数是长值,就是一,它的极限也为一,因此左右极限都为一。那么在这一点的极限 f x 在 这点的极限就是一,就是一啊。 再来看它的在这一点的这个函数值, f 负一对应的函数值就是一,很显然它在这一点是连续的,同理,在一那点也是连续的,所以这个小 f x 啊,它在负无穷到 正无穷,显然小 f x 在 负无穷到正无穷上是连续函数, 所以,所以它的在小 f x 在 负无穷到正无穷上是存在原函数的。 这里我们设大 f x 是 小 f x 的 原函数,小 f x 是 个分段函数,我们找下原函数,我们先一段一段来看, 在第一段, x 小 于负一时,它的原函数应该是三分之一 x 的 三次方加上一个常数。我用 c 一 来表示,当 x 大 于等于负一,小于等于一, 它的原函数应该是 x, 加上 c 二,当 x 大 于一,它的原函数是四分之一 x 的 四次方加上 c 三。那我们直接把这个大 f x 写在这里,可以吗?是最终答案吗?不是 因为大 f x 啊,它这里面现在有三个常数,这三个常数之间呢,其实是有一定关系的啊,我们要把它们关系找出来,然后用一个常数来表示, 大 f x, 它是小 f x 原函数。我们知道大 f x 它的导数就是小 f x, 其实大 f x, 它是它的原函数,它就一定是连续的。所以这里我们用大 f x 的 连续性来找出这些常数之间的关系。 大 f x 既然是连续的,它在负一这点以及在一这点就应该是连续的,那既然是连续的,它在这一点的极限就应该是存在的。也就是说在这点的左右极限呢,都存在,并且相等。第一个,当 x 从左侧趋近于负一的时候,大 f x, 我们应该带大 f x 哪段函数啊?第一段函数从左侧去进负一的时候呢?应该是三分之一 x 的 三次方加上 c 一, 这个极限应该等于在这一点的右极限从右侧去进负一,带的是第二段函数,就是 x 加上 c 二。 那通过这个关系,我们是可以列出一个式子, x 去负一的时候,第一个极限它就应该等于负的三分之一加上 c 一。 第二个呢,应该等于负一,加上 c 二。再来看在一这一点,在一这一点, x 从左侧去一的时候,带的是第二段函数 x 加 c 二, x 从右侧去一的时候,带的是第三段函数四分之一 x 四次方,加上 c 三,我们同样可以列出一个等式啊。这个极限可以得到, 一加上 c 二,等于四分之一,加上 c 三。那再由这两个等式可以得到 c 一。 我们都用 c 二来表示吧, c 一 就等于把它移过去,是负的三分之二加上 c 二, c 三就等于四分之三加上 c 二。哎,这样的话,我们就把 c 一、 c 二、 c 三之间的关系找到了。然后我们可以把这个 c 二换成 c, 用 c 来表示 c 二。所以最终的这个圆函数大 f x, 它就应该等于 把这些地方都换成 c 即可。我们刚刚记这个 c 二为 c 啊。
31大米讲数分/高数 01:51查看AI文稿AI文稿
01:51查看AI文稿AI文稿三秒钟时间看一下这个题结果这样写对不对,答案是不对的,标准的零分。好,有同学说,那我把这个 c 写成 c 一 c 二之后,能不能对呢?答案是错误的,没有抓住这个题的精髓。这是一个求不定积分的问题, 补定积分就是在找元函数啊。什么叫元函数呢?大 f x 求导之后等于小 f x, 我 们就称大 f x 是 小 f x 的 一个元函数。所以这个元函数首先要满足的条件就是可导 而可导必连续。所以作为元函数,它还必须得是连续的。 那你写成 c 一 c 二也不一定保证他连续啊。所以接下来啊,我们得保证啊,你求的原函数是连续的,那对于分段函数来说,就保证分段点处的连续性啊,就得求一处的左极限右极限,让他们相等,并且呢,也函数值 liamy, 它 x 去一负,带第一个表达式二分之一 s 方,加上 c 一 等于右极限, x 去一一正,带第二个表达式三分之一 s 的 三次加上 c 二,等于一处的函数值,但一处的函数值就是 右极限值,是三分之一,加上 c 二啊,第一个极限求出来是二分之一,加上 c 一, 这样我们就得到了 c 一 和 c 二之间的这个关系。 c 二等于六分之一,加上 c 一, 那如果我们令 c 一 等于 c 的 话,那我们的最终结果等于的是二分之一。 s 方加 c x 小 于一时, 下边是三分之一 x 三次加,注意,这有一个六分之一,然后加 c, 就是 x 大 于等于一时的情况,所以它会多出来一个六分之一,这个六分之一体现出来的就是这个原函数的连续性。
65漫话数学 04:13查看AI文稿AI文稿
04:13查看AI文稿AI文稿这道题长得很吓人,其实都是出题人家的伪装,教你一招撕掉伪装,直接秒解。我们来看这道不定积分的问题,有了上一题的经验呢,我们在面对这样的问题,我们就有了技巧, 怎么做这样的问题呢?我们可以去分析这个背记函数的结构,去看一下这个背记函数里都有哪些因子。那像这个题目当中呢,有口算方,口算方减三 x, 口算 x 以及这一部分,那我们找哪一项呢?我们去找那个较为复杂的那个因子, 初步预判这个较为复杂的因子应该是它。我们去求这个较为复杂因子的导数, e 的 三 x 幂乘以口三 x, 它的导数写出来前导 再乘以个 cosine x, 再乘以它本身的 cosine x, 这变成平方,再减去,加上后面岛是负的 cosine x, 所以 减去减去 cosine x, 乘以 e 的 sine x 自密。我们这里可以提出一个 sine x 自密,就剩下了 cosine 方 x 减去 sine x。 所以我们发现背记函数的分子恰好就是这个复杂因子的导数的一个部分。虽然差了一块儿,差了一块儿,但我们可以把这个导数给它凑出来,通过分子分母同时乘以乘以 e 的 sine x 次幂, 分母也乘 e 的 sine x 次幂。 那么现在我们就可以把分子和这个 d x 凑为分了。 先把分母写上, e 的 sin x 是 me, 乘以 cosine x, e 加上 e, sin x 乘以 cosine x, 分 子和 d x 凑在一起就是 d e sin x 乘以 cosine x。 我们为了方便这个看啊,我们把 e 乘以 e 散 x, 密乘以口散 x。 换元一下,令 t 等于 e 的 散 x, 次密乘以口散 x, 那 这个不定积分就变成了 t 乘以 e 加上 t 分 之一, d, t 又变成了我们较为熟悉的这个结构。 哎,上一道题目我们是凑成了 t 乘以一加 t, 那 这里是一加 t, 一 加 t 也很好处理,对吧? 你把它写成是 t 分 之一,减去减去一加 t 分 之一,它俩减完之后呢,分子上会出现一个 e, 所以 在外面要乘一个 e 分 之一,然后抵 t。 接下来我们对它进行不定积分,这个是比较好。积分的 第一项应该是 loon t 的 绝对值,再减去 loon e 加 t 的 绝对值,再加上常数 c, 最后一步是要把这个 t 带回来一分之一,这两个 loon 是 可以合在一项的,就是一分之一倍的 loon。 上面是 t, e 的 sine x 乘以 cosine x, 下面应该是 e 加上 e 的 sine x, 再乘以 cosine x 的 绝对值。最后别忘了加上常数 c。 同学们可以去,如果你没有看上一个视频,你可以将上一个视频和这个视频呢?你综合起来看,它其实就是利用了一个我们 哎比较简单的一个不定积分的结构,利用它去把里面的这个 t 啊,把里面 t 换成了一个复杂一点的因子。我们这里是换成了 e 的 塞沿 x 乘以口塞 x, 然后利用这个简单的结构把 t 换成这个样子,去出了这道题目。所以当我们掌握了出题人的这个出题规律的时候,他即使把 t 换成了多么复杂的样子,我们也是能够解决这道问题的。 它的思路是将一个简单的不定积分的结构给它加复杂因子,变成一个复杂的题目,那我们的思路呢?就是在这个不定积分的背记函数里面,把那个最复杂的结构给它找出来,然后去进行求导,把它破解了。
322大米讲数分/高数 02:05查看AI文稿AI文稿
02:05查看AI文稿AI文稿三角函数我们固然是喜欢偶数次,但是如果是奇数次,我们也不怕,分子是三次减一次,分母是一加上二次加四次, 分子是奇次,咱们就把它变成偶次,所以提出一个 cosine 放到后面去, 剩下的是 cosine x 方减二,而分母的是 cosine, 所以 显然我们要把它以 cosine 为整体,而且提过去了以后, d 后面也是 cosine, 很 明显的一个呃,提示啊,告诉我们以 cosine 为整体,那 cosine x 方减二可以变成什么关系? cosine 的 呀, 是不是负的一个整体一加上 cosine x 方。 此时这个是我们之前见过的题型,不知道大家有没有印象啊?有点像我们之前推那个一加 x 的 四次方分之一的一个前置积分, 这是一个前置知识,剩下都除以三 x 方,就是这样子的一个式子, 大家看到有没有感觉?应该是有的,就是如果那种推过一加 x 的 四次方分之一的同学应该是有感觉的,它是一个导数, sine x 减去 sine x 分 之一的导数,是不是啊?对,就注意符号啊,这地方一定要注意符号,那分母就给它凑成这个形似呗。 这个三呢,就是 a 方,所以这里的 a 应该是根号三,是吧?那 f 母就应该是根三,所以负的, 嗯,根三分之一乘以二,可 tangent sine x 减去 cosine x, 比上根号三加 c, 嗯。
85小阿文数学






