粉丝347获赞1549
相关视频
 03:43查看AI文稿AI文稿
03:43查看AI文稿AI文稿今天总结一下初中数学五种尺规作图的考点。第一个就是角平分线,如图,角 a、 o、 b 的角平分线。我们首先以点 o 为圆心,以任意长为半径画弧, 将 o、 a、 o、 b 与点 d、 e 分别以 d、 e 为圆心,以大于二分之一 d、 e 的长为半径画弧。因为如果你不大于二分之一,这两个弧是没有焦点的。 两弧交于一点 c, 我们连接 o、 c, 那么 o、 c 就是角 a、 o、 b 的角平分线。其实我们把这个 c、 d、 c、 e 连接起来,你会发现三角形 o、 d、 c 和三角形 o、 e、 c 全等,边边边三角形全等,所以我们可以得到这个角等于这个角,所以 oc 就是角 aob 的角平分线。第二个就是做相等的角。首先我们先画一条射线, o 撇、 b 撇, 那么接下来我们以点 o 为圆心,以任意长为半径画弧,交 o、 a、 o、 b 于点 d、 e。 这个时候我们保持圆规不动,移到我们星座的图形上,以点 o 片为圆心,继续做弧 o 撇、 b 撇与点 e 撇。然后我们在原来的角上用这个圆规量出弧第一的长度,保持圆规不变,移到 e 撇上画弧。弧交于 点 d 撇,连接 o 撇、 d 撇,那我们就得到了角 a 撇、 o 撇、 b 撇,它就是跟角 a、 o、 b 相等的角。第三个就是最常考的做这个线段的垂直平分线。如图 a、 b 是一个线段,我们 先分别以 a、 b 为圆心,以大于二分之一 a、 b 的长为半径画弧。 这个时候在线段 a、 b 的上下是有两个相交的点,分别为 c、 d, 我们连接 cd, 就得到了线段 a、 b 的垂直平分线,那这个作图的依据是线段的垂直平分,线上的点到线段两端的距离相等。也就是说 c a 等于 c b, d a 等于 d b。 接下来第四个是过直线上的一点做直线的垂线。如图, p 一点在直线 a b 上。首先我们以 p 为圆心,以任意长为半径画弧, 交 a b 于两点 m n。 然后呢,我们再分别以 m n 为圆心,以大于 m p 的距离为半径做弧 胡交于点 q, 连接 p q, 那么 p q 就是这个线段 a b 的垂线。这个就是过直线外一点做直线 a b 的垂线。 我们首先以点 p 为圆心,以点 p, 以点 p 大于 a b 的距离为半径画弧 a b 于 m n 两点。接着我们以 m n 为圆形,以大于二分之一 m n 的长为半径画弧, 交于点 q, 连接 p q, 就得到了这条直线的垂线。那其实用圆规作图,无非就是圆规的特点,它就是做出的弧啊,或者圆啊,上面的点到圆形的距离相等好。
1.5万中考数学老师 06:32
06:32 07:39
07:39 23:02查看AI文稿AI文稿
23:02查看AI文稿AI文稿同学们大家好,欢迎来到胡成云课堂,这节课我们要学习的是三角形的齿规作图。我们可以先回忆一下在我们七年级的时候学过的齿规作图有什么? 有两个,一个是做一条线段等于已知线段,做一个角等于已知角。那么这一节课呢,我们来学习一下,利用齿规作图做一个三角形。 先看这节课的学习目标,学习目标有三个,一、了解指规作图的概念,会用指规作图法做线段和角。二、 熟悉指规作图的步骤,并能熟练运用作图语言。三、以三角形全等的判定方法为基础,利用指规做三角形,这也是这节课的重点内容。 我们先来看一个思考题,豆豆书上的三角形被墨迹污染了一部分, 你能帮他在作业本上画出一个与书上完全一样的三角形吗?如何做一个三角形与已有的三角形一样呢? 带着这个问题进入我们今天的学习。用齿规作图,它的定 意识只用直尺,没有刻度的直尺和圆规也可以画出一些图形。这些画图方法被称为尺规作图, 由三角形全等判定。可以知道,每一种判定两个三角形全等的条件都只能做出唯一的三角形。 由此我们来回忆一下,判定两个三角形全等的条件有什么呢? 有边边边、边角、边角、边角以及角角边。带着这四个判定三角形全等的条 进入我们今天真正的利用齿规做三角形。先了解一些齿规所图的知识点。 用直尺和圆规作图是一种具有特殊要求的作图方法,这种作图方法不必用具体数据,只是按给定图形进行作图,这也是他与画图的区别所在。 画图的时候,我们就是按照样子去画出来,而按照给定图形做图,就要求我们做出的图形与原图形和给定的这个图形是完全一样,完全重合, 也就是全等图形。画图一般不限定工具,既可以用直尺和圆规,也可以用其他的辅助工具,比如两角器、三角板、刻度尺等。 在尺规作图中,直尺的作用只能用来连接两点之间的线段,或过两点画直线和射线。 那么在平时的作图当中,这个直尺的作用还可以干嘛呀?它还可以测量,而在尺规作图里边,只能用来连线,不具有其他的一个功能。 下边我们来步入今天的学习,利用指规做一个三角形。 如图,已知线段 a、 b、 c。 求做三角形 a、 b、 c, 使 a、 b 等于 c, b、 c 等于 a, a、 c 等于 b。 在以前已经学习过利用齿规去做出一条线段等于已知线段,今天就是做三条已知的线段,并且把他们首尾顺次相接在一起,才能够 组成三角形。看看用齿规做三角形的步骤分别是怎样进行的。 先来做一个分析,由做一条线段等于已知线段能够做出边 a、 b, 即 a、 b 两点确定。 做出一条线段等于 a, 那么这个 a 这条线段的两个端点就是 a 和 b, 也就是三角形 a、 b、 c 的一条边 a、 b, 而 b、 c 等于 a, a、 c 等于 b, 故以点 a 为圆心, b 为半径画弧长。以点 b 为圆心, a 为半径画弧,这个时候这两条弧长可以有一个焦点,这个焦点就是点 c。 下边看一下具体的做法。 第一步,做线段 a、 b 等于 c, 做一条线段等于 c, 这条线段的两个端点分别是 a 和 b。 第二步,以点 a 为圆心,以 b 为半径画弧长,以 a 为圆心,以 b 为半径去画这个弧长, 做出了一个弧长。具体这个 b 这条线段在哪个位置呀? 暂时还不能确定。第三步,以 b 为圆心,以 a 为半径画弧。这个时候 以 a 为圆心做出的弧长和以 b 为圆心做出的弧长会出现一个焦点,那么这个焦点就是点 c。 第四步,连接 a、 c、 b、 c 即三角形 a、 b、 c 即为所求 把 a、 c 和 b、 c 连接在一起,那么 a、 c 的长度就是线段 b 的长度, b、 c 的长度就是线段 a 的长度,得到了 了三角形 a、 b、 c。 这是知道三角形的三条边,已知三条线段的长度,去做出了三角形 a、 b、 c。 那么已知两边及其夹角,该怎样去做这个图呢?看这个。第一,如图,已知线段 a、 b, 其中 a 大于 b 以及角 alpha, 求做三角形 a、 b、 c, 使得角 a 等于角 a, 法 a、 b 等于 a, b、 c 等于 b。 由此我们可以发现角 a 等于角, 而法 ab 等于 abc 等于 b。 其实知道了什么呀?知道了一个三角形的两条边以及他的夹角, 根据在他的这个角的两边上去去截取 a、 b 和 b、 c 的长度,就可以得到三角形 a、 b、 c。 提示做出符合要求的三角形。关键是根据条件确定三角形三个顶点的位置。 解题时候要根据实际情况判断是否存在多个符合提设条件的三角形 a、 b、 c。 因为有的时候我们在画弧长的时候,他和另一条边可能不只是一个焦点。下边看一下这个题该怎样去做图呢? 做法,第一步,做角 a 等于角 are 做出一个角 a, 使角 a 等于已知角 are 法 第二步,在角 a 的一边上截取 a、 b 这个 a、 b, 我们可以在 上面这条边上截取,也可以在下边这条边上截取。现在我们在上边边上去截取线段 a、 b, 使 a、 b 等于 a 找到了 b 点。 题目当中还告诉了一个 b、 c 的长度,既然是 b、 c 的长度,肯定是和 b 连接在一起,怎样去找 b、 c 的长度?根据刚才在第一种作图方法里边做的 一条边,利用尺规律,用圆规以点臂为圆心,线段臂为半径画弧, 这个时候弧与角 a 的另外一条边出现了两个交点,也就是图中的 c 点和 c 撇儿。点 分别连接 b、 c 和 b、 c 撇儿,此时就得 得到了两个三角形,分别是三角形 a、 b、 c 和三角形 a、 b、 c 撇,它们都是所求做的三角形, 都是可求索索求出做的三角形。那么根据刚才的例一我们来想一下。例二,已知三角形的两角及其夹边怎样去做这个三角形? 如图所示,已知角 alpha、 角 bata 和线段 c 求做三角形 a、 b、 c。 十角 a 等于角 alpha, 角 b 等于角 bata a、 b 的长度就是给出线段 c 的长度。 做法,一,做角 d、 a、 f 等于角 f, 做出一个角等于角 f。 在射线 a、 f 上截取线段 a、 b 等于 c, 以点 b 为顶点 b、 a 为一边做出角 a、 b、 e 等于角 bate d、 e 与 a、 d 交于点 c, 则三角形 a、 b、 c 就是所求做的三角形,同学们可以根据老师讲的这个做法,自己在纸上把这个图形画一下,看一下你们所做出的图形会 会不会完全一样,这是已知两角及其他们的夹边去做三角形。 我们来看一下这节课主要学习了哪些内容。一、做三角形的方法做一个三角形与已知三角形全等, 根据的就是三角形全等的条件,因此做三角形时所给的条件可以是 三条边或两条边及夹角,或两角及夹边或两角及一角的对边。利用的其实就是我们判定三角形全等的四个条件, 边边边边角边角边角角角边。利用这四个条件就可以去做出三角形。 二、做三角形的步骤在寻找做法的时候,一定要根据已知画出草图, 确定作图步骤。也就是说在作图的时候呢,不要直接往纸上去画,不要直接往试卷上去画, 先根据他的已知条件,自己在草稿纸上画出一个草图,确定了真正的一个做题步骤以后, 再把这个做法转移到我们的作业本或者是练习题上。三尺规,做图的基本要求,一、有 图形,画图形,把图形画出来。二、写做法。你这个图是怎样做出来的呀?把做法要写上。三、保留痕迹,尤其是在题目当中一些弧线,这个弧线是一定要保留的。 当然也有些做图题只要求保留痕迹,不用写做法,根据具体问题具体去分析, 如果写了必须有做法和痕迹,都要保留在卷面上。如果说可以不用写做法,那你只需要保留做题痕迹就可以了, 下边我们看一下这节课的一个课堂检测题目。一、指规作图的话, 图工具是什么? 指规作图的画图工具是没有刻度的直尺和圆规,所以这个题选的是 d 选项。 刚才在咱们在介绍指规作图的定义的时候,一直在强调的是直尺括号,没有刻度,即没有刻度的直尺和圆规。 第二个题,利用指规作图,在下列条件中,不能做出唯一直角三角形的是 a, 因为已知两个锐角而边长不确定,所以这样的三角形可做很多,而不是唯一的 b。 符合全等三角形的判定。 aas 能做出唯一直角三角形,知道了一个直角边,一条直角边的长度确定和这一边的对角, 其实还知道谁呀?还知道一个直角,所以利用的判定条件是角角边,因此能够做出唯一的直角三角形。 c 符合全等三角形的判定。 sas 一至两条直角边, 织到两条直角边,织到了两条直角边, 知道这两条直角边了,以及这个角是直角,那么做出来的这个三角形肯定是怎么样的呀?肯定是唯一的 d, 已知一个锐角和斜边,知道其中的一个锐角大小 以及斜边的长度。我们还知道什么呀?还知道一个直角,所以也可以画出唯一的直角三角形,它的依据是 a a s, 所以这个题选的是 a 选项。只知道两个锐角的时候,我们只知道两个锐角, 那么我们画出的什么可以不一样呀?画出三角形边的长度可以是任意的,所以它的两个三角形不是全等的,并不唯一。 第三题,如图所示,三角形 a、 b、 c 是不等边。三角形 d、 e 等于 b、 c 以 d、 e 为两个顶点做位置不同的三角形, 使所做三角形与三角形 a、 b、 c 全等。那么这样的三角形最多可以做出几个呢? 我们可以试着自己去做一下,看一下解析。可以做四个,分别是,以 d 为圆心, a、 b 长为半径做圆,以 e 为圆心, a、 c 长为半径做圆, 两圆相交于两点, d、 e 上下各一个,经过连接后可以得到两个。 然后以 d 为圆心, a、 c 长为半径,以 e 为圆心, a、 b 长为半径做圆,两圆相交于两点, d、 e 上下各一个,经过连接后 可得到两个。所以选的是 b 选项,选的是 b 选项。这个题同学们容易忽略什么呀?容易忽略的是他说了一句话, 他说的一句话是这样说的,以 d、 e 为两个顶点做什么?做位置不同的三角形, 也就是说,只要它的位置不是完全一样就可以了。可以在地点处以 a、 c 为半径去画弧度,那么上边一个弧度,下边一个弧度,也可以以 a、 b 为半径画弧度也是两个弧度,可以这样去画,也可以这样写, 斜着去画都是可以的,所以会出现四个。看一下第四个题,如图所示。已知线段 a, 用尺规做出三角形 a、 b、 c, 使 a、 b 等于 a, b、 c 等于 a, c 等于二 a。 做法一,先做一条线段,等于二, a, 再做一条线段, a、 b、 a、 b 等于几? a、 b 等于 a, 分别以谁为圆心啊?分别以 a 和 b 为圆心,以 b、 c 和 a、 c 的长度,也就是二 a 为半径画弧 量,弧交于 c 点,连接 a、 c、 d、 c, 则 三角形 abc 就是所求的三角形。这个题和咱们刚才讲的第一个例题是一样的,已知三角形的三条边长去做出这个三角形,可以看一下他的解析, 可先做出长二 a 的线段,再做出底边,进而做出两腰的焦点,连接焦点和底边的端点,即刻也就是做出了这个三角形。 第五题,已知线段 b, 角 alpha。 如图所示,求做三角形 a、 b、 c。 使得 b、 c 等于 b, 角 b 等于角, c 等于角 alpha。 做 法,一、做线段 b、 c 等于 b, 标上两个端点 b 和 c。 二、以 b 为顶点,射线 b、 c 为一边做角 m、 b、 c 等于角 a 法 做出一个角来,这个角等于角啊,角 bat 是角 bat 三、以 c 为顶点,射线 c、 b 为一边,在 b、 c 同侧, 在 b、 c 同侧,也就是刚才角 bat 的这一侧做角 n、 c、 b 等于角 bat。 射线 b、 m、 c、 n。 交于点 a, 则 三角形 a、 b、 c。 就是所求做的三角形 a、 b、 c。 这个就是根据两角以及它们的夹边去做出了这个三角形。 这节课就到这里,谢谢大家的听课。
98在线学习初中部 01:41查看AI文稿AI文稿
01:41查看AI文稿AI文稿这个视频我来讲讲。用齿规做角,比如已知一个角 a o b, 只有圆规和没有刻度的直尺,如何做出一个和它相等的角呢? 嘿嘿,要做角,先得有条边,拿直尺画一条边,记做射线 o 一片 a 一片角,有两条边,那还得再来一条。不过这一条就不能这么随意了,咋画呢? 步骤有点多,你可得听仔细喽。首先,在已知角上以 o 为圆心,以任意长为半径,画一段弧,交他于 c, 交他于 d。 接着把圆规挪过来,以 o 一撇为圆心,还是以刚才的长度为半径,再画弧交 o 一撇, a 一撇与 c 撇点,此时 c 一撇就对应这边的 c。 那我只要再找到对应这个地点的 d 撇点, 就能确定另一条边了。接下来,我就教你如何去找这个 d 撇点。用圆规量一下 cd 的距离,保持圆规不要动过来。在这边以 cd 撇为圆心,再画一段弧, 发觉没,第一撇点肯定记在这段弧上,也在这段弧上,那显然这个焦点就是第一撇。把 o 一撇,第一撇连起来做射线 o 一撇, b 一撇,那这个角就等于已知的角 a o b 啦。 好了,再回顾一下刚才的过程,做一个角等于已知角时,一共有三步,首先随便画出角的一条边,接着分别过角的顶点,做两段一样的弧。 最后用圆规亮出焦点距离,再做一段弧,有了这个焦点,就能做出角了。怎么样,明白了吗?明白的话就动手试试吧!
814爱学习 08:00查看AI文稿AI文稿
08:00查看AI文稿AI文稿哈喽,同学们,我是你们的悠悠老师,今天我们一起来学习一下近几年的中考热点之一的指挥作图。指挥作图主要是考察同学们的动手操作能力,那么这九种基本的作图法呢?同学们必须得掌握啊!今天悠悠老师带大家一起来解锁 视频,可能会有点长,全部都是干货,我们接下来从第一个开始指挥做图。一、做一条线段等于已知线段,已知线段 a 求做线段 ab 等于 a, 先做一条射线 ao, 以线段 a 的长度为圆的半径,以 a 点为圆心做壶,壶与 ao 交于 b 点,则线段 ab 就是索求线段 a 的长度,使规做 二做线段的垂直平分线,以至线段 ab 求做 ab 的垂直平分线。以 a 点为圆心,以大于二分之一 ab 的长度为圆的半径做弧, 再以同样的长度为圆的半径,以 b 点为圆心做壶,两壶交于 c 点, d 点连接 cd, 则直线 cd 就是线段 ab 的垂直平分线。 十、规做图三,做角的平分线与直角 aob 求做角 aob 的角平分线,以欧点为圆心,以任意长度为半径做弧,两胡交 oaob 于地点和易点, 在以大于地翼二分之一长度为半径,以地点为圆心做弧,在以同样的长度以一 一点为圆心做壶,两壶交于 c 点,连接 oc, 则射线 oc 就是角 aob 的平分线。指挥作图四、做一个角等于一只角,一只角 aob 求做角 apopeippe 等于角 aob。 先做一条射线 opace, 再以点欧为圆心,以任意长度为半径做壶,两壶交欧。 aob 与地点和一点,以欧一的长度为半径,以欧撇点为圆心做壶,壶交欧 c 与地撇点, 再以 oe 为圆的半径,以 b 撇点为圆心做壶,两壶交于 a 撇点连接 apo 撇,则 apo b 撇就是所求的角 aob。 时规作图五,经过直线,上一点做已知直线的垂线。已知点 p 是直线 ab 上一点求做直线 cd 经过点 p, 且 cd 垂直于 ab, 以 p 点为圆心,以任意长度为半径做壶,两壶交 ab 于 mm, 再以 m 点为圆心,以大于二分之一 mn 的长度为半径,再以同样的长度为半径,以 n 点为圆心做壶, 两壶交于 c 点连接 cp, 则直线 cd 经过点 p 且垂直于 ab, 使规做图六,经过直线弯一点 做已知直线的垂线。已知直线 ab 及直线外易点 p 求奏直线 cd 经过点 p, 且 cd 垂直于 ab, 以 p 点为圆心,以任意长度为半径做弧, 两壶交 ab 于 mn 点,以 m 点为圆心,以大于二分之一 mn 的长度为半径做壶。 再以同样的长度为半径,以 n 点为圆心做壶,两壶交于 f 点连接 pf, 则直线 cd 经过点 p, 且垂直于 ab。 尺规做图七,以至三边做三角形,以至线段 abc, 求做三角形 abc, 使 ab 等于 ac 等于 bbc, 等于 a 做一条射线 ao, 以线段 c 的长度为圆的半径,以 a 点为圆心做弧胡交 ao 于 b 点,则线段 ab 等于 c, 在于线段 b 的长度为圆的半径,以 a 点为圆心 做壶,以线段 a 的长度为半径,以 b 点为圆心做壶,两壶交于 c 点连接 acbc, 则线段 ac 等于 bbc, 等于 a 十、规奏图八,以至两边及加角做三角形。已知线段 ab 和角贝塔求做三角形 abc, 使角 a 等于角贝塔, ab 等于 aac 等于 b。 先做 一条射线 ao, 再以 o 点为圆心,以任意长度为半径做胡。两胡交角的加边与 n, n 点,以 o, n 的长度为半径,以 a 点为圆心做胡。胡交于 ao 与 n 撇点, 再以 m, n 的长度为半径,以 n 撇点为圆心做壶,两壶交于 n 撇, 连接 amp, 则角 a 等于角贝塔。 以线段 b 的长度为半径,以 a 点为圆心做壶,再以线段 a 的长度为半径,以 a 点为圆心做壶。两壶分别 教育 b 点 c 点连接 b, c 得 ab 等于 aac 等于 b。 尺规做图九,以至两角及加边做三角形,以至角二范角北塔。线段 n 求做三角形 abc 十角 a 等于角二范角 b 等于角北塔, ab 等于 m, 先做一条射线 ao, 以线段 m 的长度为半径,以 a 点为圆心做弧 胡椒射线 ao 与 b 点,则线段 ab 等于 m。 以 p 点为圆心,以任意长度为半径做胡。两胡交于 nn, 以 pn 为半径,以 a 点为圆心做壶。壶交 ao 与 n 撇点,再以 n, n 的长度为半径,以 n 撇点为圆心做壶,两壶交于 m, 撇点 连接 am 撇,则角 a 等于角 f, 同样以 q 点为圆心,以任意长度为半径做胡。两胡交于 g, h 点,以 q, h 为半径, 以 b 点为圆心做弧胡交。 ao 于 h 撇点,再以 gh 为半径, 以 h 撇为圆心做壶。两壶交于锯撇点连接 b, 锯撇点至 c 点,则角 b 等于角北塔。 好啦,以上就是持规作读的九种基本作读法,如果不是很熟练同学,语语老师建议反复观看,直到熟练为止好吗?拜拜!
2669悠悠老师讲数学 02:17查看AI文稿AI文稿
02:17查看AI文稿AI文稿这节课我们来学习尺规作图,八年级上册过一点,做一支直线的垂线,点在直线外上一个视频我们已经讲过了,这个视频我们来讲解,点在直线上一共分为四三步, 三步,第一步,以点 c 为圆心,以适适当的长度为半径画胡, 教 ab 与点滴点 e。 第二步, 以分别以分别以 d e 为半径,以大于 d e 的二分之一长为半, 干净画糊, 两胡交易相交于点 f。 第三步,做直线 cf, 直线 cf 就是所求做的的垂线,那么我们要写结论,如图所示, 直线 cf 即为所求。 大家一定要注意,我们在吃亏做吃亏做图题的时候,考试的时候我们都要保留他的弧线, 不要把弧线插没了,一定要把弧线保留下来来,也就是说这些痕迹作图的痕迹, 考试的时候没有让你写做法,但是一定要保留这个作图的痕迹,老师在改卷的时候一定会关注你这个痕迹保留的是否完整。好,那这节课我们就讲到这了。
248小王老师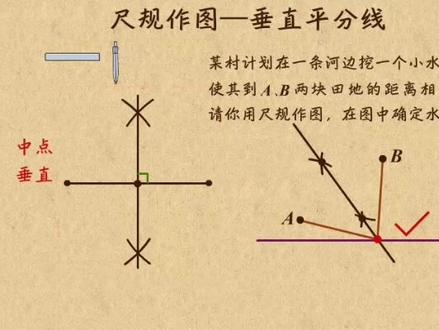 02:46查看AI文稿AI文稿
02:46查看AI文稿AI文稿这个视频咱来讲讲作图,看看怎么用尺规作图,做出线段的垂直平分线。尺规作图自然需要直尺和圆规了,还记得不,这个直尺是没有刻度的,而圆规是用来保证长度一致的。要做线段的垂直平分线,就来想想垂直平分线是怎么判定的呗。 到线段端点距离相等的点,在线段的垂直平分线上,如果找到两个这样的点,两点连线就是垂直平分线了。那么问题来了,怎么通过吃规找这样的点呢? 对了,用圆规,圆规可以保证长度一致,以这个点为圆心,选一个半径,注意这个长度必须大于线段的一半,然后以他为半径,画个小胡,之后,圆心换到另一端,半径不变,再画个小胡。哎,这个焦点不就满足 这两条线段相等吗?那还差个点呀。没关系,你刚才画胡的时候,上面来个小胡,下面也来个小胡,另一个圆心的时候也这样,这个焦点到两端点距离也相等,这不就是俩点了吗?这俩点一连,这条线就是线段的垂直平分线了。 值得一提的是,这条线既垂直又平分,所以找终点和做垂直也用这种方法。选一个长一点的半径,然后这么画个胡,再这样一下, 换个圆心,半径不变,再来两个小胡,连接两点,就是垂直平分线,这是终点,这是垂直。这就是指挥做垂直平分线是不是很简单?那就来个小题目练习一下。说某村计划在一条河边挖一个小水塘,他得到 ab, 两块田地的距离 不等。题目要求你用尺规做图,在图中确定水塘的位置。哎,这个题跟垂直平分线有啥关系呢? 你看这个水塘要到 ab, 两块地距离相等。翻译一下,那就要求这个水塘必须在 ab 的垂直评分线上 做出这条线,以 a 为圆心,选个半径,这么一画,再这么一画,然后以 b 为圆心,半径不变,这么一画,再这么一画,最后把两个焦点连起来,这条线上的任何一个点都满足到 a 和 b 距离相等这个要求。 但是哪个点是水塘呢?水塘总得在河边吧?那垂直平分线跟河的焦点这个点既满足水塘在河边,又满足到 ab 距离相等,就是题目要求的水塘位置了。以上就是垂直平分线的作图问题,画垂直平分线的方法 就是这样画两个胡,再这样画两个胡,连接焦点就可以了。这条线上的任意点到线段端点的距离都一样,用这个性质,你可以解决一些实际问题哦。好了,为师这就讲完了,徒儿们速速刷题去吧!
3024爱上中学物理 02:13查看AI文稿AI文稿
02:13查看AI文稿AI文稿这节课我们来学习尺规作图。八年级上册过一点,做一支直线的垂线。那我们这节课主要 讲的是点在直线外做法一共分为四步,第一步,任意取一点 k, 使得点 k 与点 c 在 ab 的两旁。第二步,以点 c 为圆心, 以 ck 长为半径做弧, 叫 ab 与点地点意三,分别以点地和点意为圆心,以大于二分之一的地意为半径。画胡 两壶相交于点 f。 第四步,做直线 cf, 那直线 cf 就是所求 做的垂线,那我们要写结论,所以如图所示,直线 cf 即为所求。 好,这节课我们先讲点在直线外的做法,就到这里。
410小王老师 02:09查看AI文稿AI文稿
02:09查看AI文稿AI文稿这节课我们学习初中词规作图八年级下册。第一, r、 d 三角形在 r、 d 三角形 a、 b、 c 中,角 a、 b、 c 等于九十度做矩形 a、 b、 c、 d。 第一步,我们测量 b、 c 的长度, 以点 a 为圆心,以 bc 的长度为半径,画弧线好。第二步,测量 ab 的长度, 以点 c 为圆心,以 ab 的长度为半径画弧,两弧交于点 d 连接 ad、 cd。 那么矩形四边形 a、 b、 c、 d 就是我们所做的矩形。那么大家看一下为什么?因为我们刚才做的时候, a、 d 等于 b、 c、 ab 等于 cd。 在四边形中,如果两组对边分别相等,这个四边形就是平行四边形, 再加上这是一个而立三角形,这个角度是九十度,有一个角是直角的平行四边形就是矩形,所以 四边形 abcd 就是矩形。所以如图所示, 四边形 a、 b、 c、 d 极为所求 啊,也可以把它改成矩形 a、 b、 c、 d 极为所求。
51小王老师
猜你喜欢
最新视频
- 13.4万兴趣大王指南针









