粉丝46.6万获赞250.1万
相关视频
 03:33
03:33 13:12查看AI文稿AI文稿
13:12查看AI文稿AI文稿好,今天带大家梳理一下,动点问题当中的胡不归啊。在讲这个模型之前的时候呢,还是先附带一个小故事, 说是从前有一个小伙子呢,他外出务工,突然有一天他得到一个疾报,说是父亲病危啊,然后呢,归家亲戚啊,为了尽快的回家,这个小伙子呢,他就选择了走这条线。 他的选择明眼看上去是对的,因为两点之间线段最短,但是他忽略了一个因素, 走沙地,他走的慢,而这个地方他有一个易道,比较硬,比较直,明显速度要快。结果是走沙地,虽然路程最短,但是回家的时候,他的父亲还是没能够看他最后一眼。 老人在逆流之际,嘴里就一直在叨叨着胡不归,胡不归啊。那么是不是有一种可能,这个小伙子先在易道上走一段,然后再走一条折线, 虽然他的路程变长了,但是这儿速度快。那在这种问题出现的时候,出现这种情况的时候,有没有可能会让他回家的路程最短呢?如果有的话,那么拐点到底在哪才是合适的? 就由这个故事引出了我们的胡不归模型,这个模型长的是这样的, 已知 a 为 l 上以定点, b 为 l, y 以定点, 求 l 上 e 点 t 是 p, d 加上 k 乘以 p a, 其中 k 单名小于一, 就是这个模型好。看一下这个模型的赋态分析,先把这个题目哈稍微补齐一下。 像这一类带系数的折线最值,问题啊,我们通常是把折线段转化成直线段, 利用两点间线段最短,或者是直线外一点与直线上各点的连线当中垂线段最短这么一个结论来进行分解啊, 这个问题的核心算法是什么呢?第一个,它要构建直角三角形,利用三角函数的定义,三角函数定义啊,是九年级上册第二章你们学的啊,转化这个 k 乘以 p a 为另一条线段, 而且这个线段呢,和这个 p b, 它一定在 l 两侧啊,这里边你要注意啊,有小技巧,这个小技巧我给大家写一下啊, 这个 g 还写错了。第一个你要注意啊,这个 p a 它一定是条斜点, 一定是要斜边,谁是斜边,谁旁边就带个 k。 第二个,这个 k 一定是某个角的正字, 嗯,所以一个斜边呢,乘以一个角的正弦,就会转化成另外一条直角边啊。我们通过这几个实力来研究一下这个问题啊,不先处理一下这个小伙子的问题 啊,为了方便解决这个问题啊,这个 k 我 取一个特殊的一个值,比方说这个 k 呢,我取一个二分之杠三, 现在这个大于零小于一,而且大家都知道这个呢,应该是一个顺六十,那么下边我就会以 a p 为一条斜边,构建一个锐角,是六十度的一个直角三角形, 这个是一个六十,然后过 p 去做一个垂线, 然后说垂到点 c 的 位置。好,现在这个 p b 加上二分之根号三 pa 就 变成了 p b 加上 p c, 那现在这个和这个是一个折线,我们说这个折线要变短的话,一定得先把它变成一个直线段,所以这里边呢,你就要把 b c 连起来。 好,那现在这个 p 它是不是应该在这个位置呢? 感觉不大对,是吧?嗯啊,为啥呢?因为缺了一个,除了这个两点间线的最短,我们还有一个和啊,和 直线外一点与直线上各点的连线当中啊,垂线段最短。那你看,现在 l 是 定值,加角六十度定值,所以说 a c 这条直线它就是一个定值,那么点 p 的 位置是固定的,所以说 p 是 不是就直线 a c 外一点? 然后呢,他与这条线上所有点的连线当中,是不是应该是垂线的最短?所以这里边我们知道了,要从这个线上选一个 c 和他的连线上最短,那么这个线和他的这个点和这个点的连线是不是应该是垂直 a c 的? 所以说真正的点 p 的 位置 啊,应该是在这儿啊,而真正的点 c 应该是在这儿。这个题的答案是这个蓝色的 b c 啊, 好,再看一下后边这几个例题哈。理一,在直角三角形 a b c 当中,角 a c b 九十度, p 是 bc 上一个点啊,一个动点,说 a c 等于二啊, bc 等于三, 然后呢,求根号二 a p 加上 b p 的 四小时。哎,这个题不是说那个 k 大 于零小于一吗?这里怎么出现了根二,划一步就能够出现啊?看一下这个东西,把这个根二一提, a p 加上二分之根号二, b p 跟着谁,谁是斜边,现在它跟着 b p, b p 就是 一个斜边,二分之根二是某一个角的正弦值,很明显这个角是四十五度,所以 需要以 b p 为斜边,在 b c 的 e 侧去构建一个等腰直角三角形啊, 然后过 p 做垂线,比方说垂到了点 d 的 位置, 这个角四十五度,那么现在这个二分之根二 b p 就 变成了 p d, 所以 它就等于根号二,乘以 a p 加上 p d, 你 再把这个连起来, 那现在你看这种情况出现的是不是刚才出现的是完全一样的, 这个和这个本身是折线,先连起来,出现了一个直线,直线段,但是我们是要求这个和这上边某一个点的连线当中,是不是要垂线段最短,对吧?所以说它的答案呢,是过这个点 a 哈 做这个 b、 d, 它的垂线啊,真正的点 p 的 位置在这儿啊,点 d 的 位置应该是在这儿,这样的话,这个 a、 d 的 长才是它的最小值。然后这个题最后的答案呢,就是这个蓝色的 a、 d 啊,乘以根二, 再看下边这个题呢,说三角形 abc, 然后 ab 等于 ac 都等于五啊,这是五,这也是五。 以 a、 b 为直径做一个圆 o 交 a, c, b, c 于 d 和 e 连接 d, e、 b、 d, 说 f 是 线段 b、 d 上一个动点 f 在 这儿 说弹他 c、 e、 d 弹他 c、 e、 d, 这就正确。十二、求 c f 加上五分之根号五 b、 f 的 一个最小值。这个题啊,它倒是满足这个格式,但是现在这个问题是个五分之根号五,它并不是你熟悉的三十度、四十五度和六十度的正弦,不是任何一,那么它到底是谁的正弦? 这个直角三角形又得在哪个位置出现?我们的眼光哈,看到这个角 c、 e、 d, 它的正切值等于二, 现在这个 c、 e、 d, 它是这么一个锐角里边的一个角,它不在直角三角形内。 那么怎么去处理这个问题啊?其实这个圆大家学了以后,你能很明显的发现,是吧?这里边这个角和这个角是相等的啊,就是四边形的外角等于内对角, 然后把它变成角 a 以后,你同时又看到了 ab 这条直径所对的这个圆周角呢,它是一个直角, 所以现在我们就把这个角 a 放到了一个直角三角形内部,而且这个角 a 它的正确值等于二,等于二的话,如果我去假设啊,这个最短的边,它的长是一个 m 的 话, 那么现在这个很明显是一个二 m, 根据勾五定律能勾出这个 ab 呢,是一个根号五 m 啊,当然现在人家说了这个 ab 是 五,那么根五 m, 它就等于五,那么 m 呢?就等于五,无所谓啊,我只是看这个比例就行。 当我知道这个以后,我明显的发现了一个什么事,我要求的一个肾,某一个东西, 它要等于五分之根号五,那谁比谁等于五分之根号五,很明显是 a d 比上 ab 啊, m 除以根五 m 就 得这样,那么 a d 比上 ab 是 什么呢?在这里边说的是角 b 啊, 所以这个题它就变成了 c f 加上 b f 乘以乘角 b 啊, b f 乘以乘 b, 那 么这个 b f 是 一个斜边,我们现在呢给它构造一个直角三角形, 这是 e f g, 那 b f 乘以乘 b, 说的是不是就是 f g 啊?对吧? 现在是不是又出现之前的模型了?一个折线首先要变成一个直线段,然后又出现了直线外一点和这条直线上各点的连线当中,是不是垂线到最短的问题? 所以这个垂线段是不是一定是过肺,并且垂直于 ab 的 一条线段?比方说哈,这个点是 h 的 话啊,那么这个题它这个最小值就等于 c h 啊, 学会了吗?
481老李讲理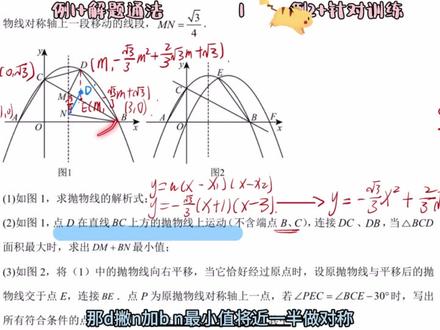 51:54查看AI文稿AI文稿
51:54查看AI文稿AI文稿小宝们,期末压轴题超全大盘点,主包帮你一节课搞定他!最全题型汇总加实战技巧,所有手写笔记和针对性练习主包都放在群里了,完全免费制作不易,麻烦宝子们一键三连,大家的支持是主包最大的动力!哈喽,各位兄弟姐妹们, 今天我们继续讲压轴题,在上一节课我们已经讲过了这个几何的压轴,主要给大家讲解的是类比、拓展、探究这种重要的解题思路。 好,本节课我们主要讲解二函数压轴,在本节课的时候,我会跟向上一节课一样啊,如果说你上节课没听的话,推荐你一定要把上节课听完之后再去听本节课的这个二函数压轴,你学的这样的话更有系统,系统性好吧, 就是这节课的话也是非常重要,非常关键的,我们各种的考试都会牵扯的到,闲话不多说,我们就开始今天的课程。好吧,我在讲这道题之前,你需要明白一件事情,就是二函数最值。 我写到这啊!写到这,你记一下,你记一下, 你记一下, 你记一下,把这句话记记到自己的笔记本上,记到脑子里面,记到脑子里面。不能忘啊,千万不能忘,千万不能忘, 千万不能忘 啊!就是二次函数最值,让求谁的最值,就想办法表示出谁 让求谁的最值,就想办法表示出谁。记完了吧,让求谁的最值,就想办法表示谁。记完了吧, 好,继续听,听好了啊听好了,我现在给你讲的是本质啊,听好了啊,因为题是无穷的,题是无限的,你所遇到的题是无限的,是无穷多的,但是核心是不变的, 就是比如说我在课堂上刚刚讲过了,你会遇到二函数,让你求面积的最值,让你求周长的最值,让你去求利润的最值,那么不管是让你去求谁的最值,你就先把这个二函数给它表示出来,你先把它的面积给它表示出来才行。 而且通过你刚刚讲,我跟你讲那个定轴定区间,定轴动期间,你会发现其实二次函数的最值分析,你发现没有,其实不难,大部分人类听完一听完一遍之后都是可以具体分析的。难在哪里啊?难就难在表示 谁能把这个面积的二次函数给他找到,表示出来,那谁就能往下找到他的最值。 懂我现在说的啥意思吧?难在表示,难在表示出这个二次函数,比如说这道题, 他让我现在求这个面积的最大值, p、 a、 c 的 面积,那么我就第一步,你记住你的核心,你就是把这个 p、 a、 c 的 面积给它表示出来,你表示出来,你用二次函数把它的面积表出来之后,那么它最大值呼之欲出,直接出来,明白吧?你再比如说看下一道题, 这个题他说的是这个 b、 c、 p 的 面积是 s, 然后让你找这个面积的最大值,那么你就要想办法表示出这个 b、 c、 p 的 面积,用二次函数表示出来,表出来这个二次函数之后才能出对折。 你要明白这一类题的核心,你看下一道题,下一道题我让你求利润的最大值,那么好了,那么你就想办法表示出利润,表示用二三数表示利润之后,然后再加上我跟你讲的第一步,求定轴,第二步画草图,然后用这解穷法,然后就可以把它的最大值找到了, 明白了吧?包括我们以后会遇到什么什么周长的最大值,或者什么几个边长之合的最大值,只要是遇到这种求最大值的题,那么难就难在你把它表示出来,不是难在求它的值,而是难在表示出这个函数解析式,明白吧,这是核心,这是实质。 好,我们来看第一题,已知抛物线 y 等于 a, x 方加 b, x 加 c, 与 x 轴交于 a 点坐标负三对零, b 点坐标一对零, c 点坐标零对三。好,告诉我。呃,求解, a 是 用什么?用什么式?一般是顶点式还是焦点式?兄弟们, 一般是顶点式还是焦点式? 对,交点式,是吧?交点式。所以说我们在写第一个的时候, 我们就可以设 y 等于 a 倍的 x 减 x 一 乘以 x 减 x 二, 然后这个交点坐标。啊, a 点坐标是负三对零,然后这个 b 点坐标是一对零,我们带进去啊,把这个负三就带入 x 一 里头,把这个一就带入 x 二里头,我们可以得到 y 等于 a 倍的 x 加三,乘以 x 减一。 完了之后的话,我们再我们再把 c 点坐标带入,把 c 点坐标零度三带入上市。占完焦点之后,然后再带普通点啊, 带普通点的时候,我们把横坐标往 x 里面带入,我们把纵坐标往外里面带入,我们会得到一个三等于 a 乘以零加三,再乘以零减一,算一下,三等于负三, a 是 吧? a 等于负一。 好,所以这个 y 等于负的 x 加三,乘以 x 减一。好,这个解是出来了,我们给它整理成我们的一般式啊,整理一下,那就是负的把它乘开啊,括号给它乘开。负的这个 x 方, 呃,加三 x 再减 x 等于加二 x, 然后再减三,然后给它整理一下负 x 方减二 x 加三。好,负 x 方减二 x 加三,这是我们的第一问,然后接下来我们来看第二个 焦点式。焦点式一般是比较麻烦啊,用焦点式比较快一点,因为这个题的话,给了我两个焦点啊,给了我 a、 b 两个焦点,所以说我们用焦点式。 好,我们来看第二个啊。解析式现在是 y 等于负 x 方,嗯,加,呃,负 x 方减二 x 加三。 然后第二个它说的是设设动点 p 的 横坐标为 t, 它说了这个 t 是 大于负三小于零,然后你这个 a 点坐标是负三都零嘛,对吧?然后你这个 b 点坐标是一都零, 他说这个 p 点坐标大于负三小于零。啥意思呢?他的意思就是说 p 点 p 点就光在这个这个弧 a c 上运动,明白吧?他意思是 p 点就在这个呃弧 a c 上运动啊。他让我们求这个 p a c 的 面积, 他让我们求这个 p a c 的 面积。嗯,关 s 关于 t 的 函数关系式,并说明 t 取和值时面积取到最大值,那么我们接下来只需要表示出这个 p a c 的 面积就行了, 对不对?我们只需要表示出 p a c 的 面积了,而这个 p a c 的 面积也是比较简单的呀,对不对?也比较简单的,我们用那个那个铅垂法,是吧?用铅垂法,因为 c 点坐标是零度零度三啊, c 点坐标是零度三,我们用铅垂法啊,用铅垂法 啊,这个 s 三角形 p a c 就 等于, 哎,对了,还有一个问题啊,这个千锤法有没有同学不会的呀?不会千锤法的扣一波五二零, 不会千锤法的扣一波五二零。 好, ok, 那 我继续了啊。呃,可以求 a c 的 平行线,有时候说的也行,但是咱不用花里胡哨啊,咱就用咱这个,对吧,也就就是用这个比较正统的啊。千锤法, 我们来看下什么是,就是你铅垂法的话,你需要过点 p, 因为 p 点的横坐标是 t, p 点横坐标是 t, 那 么它的纵坐标我们就可以用这个二次函数解析式表示啊,就是负 t 方减二, t 加三, 记住这句话啊,你看你 p 点的横坐标是 t, 那 么 p 点是在这个二次函数上面的,所以说我们就可以用这个二次函数解析式来去表示这个 p 点的纵坐标,记住了吧。然后我们用铅垂法的话,我们需要求 a c 直线 a c, 我们用千捶反的话,我们我们需要求直线 a c, 然后这个 y a c, 对 吧?这是一次函数 y 等于 k, s 加 b 啊, y 等于 k, s 加 b, 然后是 x 加三,你自己求这一次函数,你自己求啊,我直接口算了,这个比这个可以口算,然后求出来之后,那这个一次函数是 y 等于 x, y 等于 x 加三,那么因为这个 p 点坐标你不我们往下做垂线, 比如说我们这个交点 q, 那 么 p 和 q, 它的它的横坐标都是 t, 它的横坐标是相等,都是 t, 那 么它的纵坐标的话就是 t 加三, 所以 q 点的纵坐标我们可以用 t 加三来表示了,明白了吗?所以这样的话我就可以这个 p 点和 q 点,我们就有了 p 点, q 的 线段长度就有了。这个 p q 的 话就是用用 p 点纵坐标,就 y p 减 y q, 用 p 点坐标减去 q 点坐标,用 p 点坐标减去 p 点坐标。我现在在给你讲牵涉法啊,你认真听就行了。这个 p q 就是 p 点坐标减 q 点坐标,我们我们给它整理一下, p 点坐标是负 t 方减二, t 加三, q 点纵坐标是 t 加三,我们给它整理,就是负 t 方减二, t 加三,减 t 减三,给它整理,那就是负 t 方减三 t。 好, 负 t 方减三 t, 这个是 p q, p q 的 距离你就表出来了。那么什么是铅垂法呢?我们现在来给你隐身一下,比如说现在我这里有一个三角形, 我们铅垂法它主要解决的是这种 p a c。 铅垂法,它主要解决的是这种这种斜着的三角形,那么我们的方法就是过点 p 往下做垂直, 做完之后有个 q, 我 们来观察这个 s 三角形 p a c 的 面积,这个这个我们不是要求这个 p a c 的 面积吗?这个总面积,它就等于这个分割出来这两个三角形,对吧? p a q 和 p c q 的 面积。 好,然后我们再来看这个,这个不管是 p a q 还是我们的 p c q, 它是不是都有一个公共的底?我们把 p q 当到底,然后它的高, p a q 的 高是在这儿,对吧? p c q 的 高是在这儿,它们的高啊, 那么它们有一个公共的底,就是 p q, 它们有一个公共的底,就是 p q, 然后你看它们的高,它们的高可以进行合并,它们的高合并之后其实就用 c 点的横坐标减去 a 点的横坐标, 他们的高其实就是用 c 点的横坐标减去 a 点的横坐标,减完之后就是可以减出来这个总高,对不对?所以他们的高就可以用这个 x c 减 x a, 我 这样写能听懂吧?用 c 点横坐标减去 a 点横坐标, 然后他们公共的底是 p q, 他 们的他们的高,高的和和完之后的话,就是 c 点横坐标减去 a 点横坐标,然后再除以二, 那么我们就可以把这个 p a c 的 面积用这个式子来去表示了。而我们的 p q 其实就是用 p 点纵轴标减去 q 点纵轴标,对不对?我们的 p q 其实就是用 p 点纵轴标减去 q 点纵轴标就是 y p 减 y q 它们的高就用 c 点的横轴标减去 a 点的横轴标,就是 x c 减 x a, 然后除以二,这样的话就比较快, 这样画的比较快啊。我,我写这个事,你能看懂吧?下一次你再用牵扯法的话,其实就很简单了,就是意思就是说本质就是这个本质啊,就是 p 点的纵坐标减去 q 点纵坐标就是他们公共的底, c 点横坐标减 a 点横坐标就是他们公共的高。底乘高除以二就出来了, 就这个意思啊,就这个意思。好,明白这个之后,那么我们现在 p q, 你 看是不是 p 点的坐标减 k 点的坐标减出来了,然后接下来这个再用他们公共的高,公共的高就是 c 点的横坐标减去 a 点的横坐标, c 点的横坐标是零, a 点的横坐标是负三,零减负三等于三,所以他们的高是, 对吧?高是三,所以说这个 s 三角形 p、 a、 c 就 等于底 乘高,高是三,然后再除以二,这个它的面积我们就找到了啊。整理一下,那其实就是二分之三乘以这个负 t 方减三 t, 我 们给它整理一下负负二分之三, t 方减去二分之九 t。 好,那么这样的话,我们就把这个 p、 a、 c 的 面积给它表出来了,面积表出来之后,我们呢?你看这个不就是这,你看这是不是这个对伸轴是不是固定的?然后这个区间是负三到零这个区间是不是也固定的?是不定轴定区间,求对值,对不对?求对值。所以说我们这个时候就按照我们的方法,第一步求对伸轴, 求对伸轴, x 等于负二 a 分 之 b, 负的二 a 分 之 b, 然后等于负的这个二分之三求定中,然后接下来我们再画草图,第二步我们就画草图,开口向下, 开口向下,对应轴,给它标出来这个 t 等于负的二分之三啊,这个对应轴不应该是 x, 应该写成 t 哈,因为整个是一个关于 t 的 一个函数, t 等于负二分之三,然后标上去负三到零,负三负三在这,对吧?负三肯定是离这个对称轴是远点,你看负三到这个二,负二分之三是二分之三个单位,零到这个负二分之三也是二分之三个单位,所以零的话就对称的。他俩这两个蓝色点是对称的, 那么我们只看蓝色区域,在蓝色区域内是不是对称轴的时候刚刚取到最大值了,对吧?所以在对称轴取到最大值了啊, 所以这个 s 的 最大值就是 x, 就是 让它的 t 等于让它的 t 等于这个负二分之三, 我剩下我都不算了,你算一下就行了啊,你明白咋算就行了,这就是所谓的就是牵扯法嘛,对吧?没啥难度,没啥难度,你听一遍就懂了啊,还有啊, 嗯,做平行线,这个你,你不用管那么多花里胡哨的东西,兄弟们懂吗?黑猫白猫,抓到耗子就是好猫。为啥这么多老师他去教你牵扯法,那肯定牵扯法正确率是更高的哈, 好,这是我们的第二题,然后我们来看第三题, 我们来看第三题。已知 m 是 直线 a c 上的一个点,动点, m 是 直线 a, c 上一个动点,将 m 绕着点 o 旋转九十度,它旋转它,它也没有说咋旋转,对吧?兄弟们,它也没有说顺时针旋转还是逆时针旋转,所以这个题肯定多个答案,两个答案至少俩答案了吧。 旋转得到点 q, 若点 q 恰好落在二次函数图像上,请写出点点 m 的 坐标啊,就是点 m 绕着点 o 旋转,旋转完之后,点 q 恰好落在二次函数图像上。看这版,看这版, 看见吧,就是这种题,我,我们我,我们来看一下旋转啊,旋转,我们来看一下,就是,首先兄弟们,我先说一句话啊,记好我这句话,考试的时候,在压轴题里头,如果遇到旋转,大概率就是全等, 大概率是全等啊,相似的概率就比较小。再说一遍啊,再说一遍,考试的时候,在压轴题里面,如果遇到旋转,大概率就是全等啊,你要往全等上去想。 好,我们看第一种情况,因为它 m 点不知道嘛,对吧?所以我们点一下, m 是 a c 上,好,比如说 m 在 这, m 在 这,然后我们连接 o m, m 在 a c 上啊,这个提杆,别,别忽略了啊兄弟们。 m 在 a c 上啊,我刚刚就忽略提杆了, 这样子大概啊,好,然后这是 q 啊,思路是不变的啊兄弟们。然后还是这边做垂直,然后这边也是做垂直。 好,做完垂直之后的话,那 m 在 a c 上, a c, 它是 y 等于 x 加三,那这样的话,这个 m 点坐标更好表示了,我们设 m 的 横坐标是 m, 它的纵坐标就等于 m 加三。 好,这个 m 加三,这个 m 是 一个负的, m 本身是个负数,那它的距离就是负 m, 刚刚已经讲过了,同理,这边也是负 m, 这边也是负 m, 然后再来看这个纵坐标是 m 加三, m 加三是一个负数,对不对?那这边是不是也是 q 点?刚好是在负半轴上, q 点的横坐标也是负的,也是这个 m 加三,所以说我们就可以表示出 q 点的纵坐标就是负 m, q 点的横坐标就是 m 加三。 好, q 点有了之后,我们 q 点是不是还在这个二参数上面?我们把这个 q 点坐标带入这个二参数,负 x 方减二, x 加三,我们带进去啊,我们把这个 q 点坐标带进去, 带进去我们会得到一个负 m 等于负的 m 加三的平方减二乘以 m 加三,再加三,就这个啊, 好,明白了吧,然后这个就好解了,对吧?这个完全平方公式,这个解了就好解了,这个解出来两个答案,一个 m 一, 一个 m 二。 好,这是第一种情况,然后接下来我们把第二种情况给它画一下。呃,一会儿我再解答公屏上的问题啊。我们先我们先听,然后把第二种情况给它画一下。 m 在 a c 延长线上啊,啊, 沿着 o 这样九十度, 就刚刚是顺时针,现在我们让它逆时针转, 这边给延长一下啊, 然后交一点 q, 就 这样子啊,好,然后这边也还是做垂直,然后这边的话就 q 往这边做垂直了,对吧?往这边做垂直,做完垂直我们可以得到这两个三角形是全等的, 我们可以再次表示一下啊, m 点坐标还是 m? 逗, m 加三,好,那我们先看这个,这个地方,这个地方是负 m 对 不对?这是负 m, 那 么这个就代表着这个地方是负 m, 而 q 点坐标现在是在负半轴上,在外轴的负半轴上,所以说我们 q 点的纵坐标本身我们就让它是负数, m 本身就已经是负数了,明白了吧?所以我们就 q 点的纵坐标就是 m 了。我们再来看这个横坐标, 这个地方是 m 加三,它是个负数,它是个负数,那么这边我们需要给它变成正数,因为 q 点现在,因为 q 点的话,现在是在横坐标是正的,那 m 加三是一个负数,那它的横坐标想要变成正数的话,就需要在前面加括号,负的 m 加三 等于负 m 减三。这个地方你要注意一下,就是 m 加三本身是一个负数,那么我们在前面 m 加三,这个整体是个负数,我们在前面加个符号,负负得正,那这就变成一个正数了,所以我们表出来 q 点的横坐标 是负 m 减三,然后我们再把这个 q 点坐标就这个,然后再次代入到我们的这个二函数中,我们就可以得到第二个式子了。 m 等于负的负, m 减三的平方减二乘以负, m 减三再加三,然后又可以解出来 m 一 和 m 二,你可以再解出来,总共四个答案,全部保留啊,这个题的话,四个答案是完全保留的。 对,正全等的话,你现在三垂直,这个对你们来讲你们都会啊,我都,我都不说正全等的事了,主要就是你要明白哦,原来它旋转之后,我们要通过设出 m 点坐标,推导出 q 点坐标, 推导出 q 点坐标之后,然后 q 点坐标,它是在二次 m 上面,你表示出来你,你表示出来 q 点坐标之后,你把 q 点坐标带入我们的二次函数,然后我们就可以得到一个 e 二次方程,得到 e 二次方程,然后把 e 二次方程解出来就是答案, 所以你要注意一下啊,然后国二国二同学说的是,呃,老师,咱不应该延长吗?如果要做的话,啊,对,需要把 a c 延长一下是吧?需要把 a c 延长一下,看,我都延长了啊,延长一下能听懂吧?这个题 今天不好意思啊,今天稍微稍微拖了会儿堂,因为这道题的话,我想给大家讲完啊,给大家讲完还有啥疑问没?还有啥疑问没? 我们总结一下今天所讲的啊,今天第一,我给你讲了一个,就是这个我们的二次函数最值范围的通杀的,什么所谓的定轴定区间,定轴动区间,动轴定区间,其实都可以用那个方法解决,你发现没有,这是今天讲那个讲的第一个。第二,我们今天给你讲的就是 我们在进行你的期末考试,月考和我们的第一次模拟考试,第二次模拟考试,第三次模拟考试。我们在遇到这种所谓的最值问题的时候,他不会考定轴动区间,也不会考什么动轴定区间,他只会考定轴定区间,他就只会考这种比较基础的, 明白吧?而你必须要记住一个东西,就是让你求面积的最值,那么你就记住这句话,题干中让我求谁的最值,我就想办法把谁的最值表示出来,表示出之后,答案就呼之欲出了,明白了吧? 好,我们来看这个第三题。第三题先读题,如图,抛物线 y 等于负三分之根三, x 方加 b, x 加 c 与 x 轴交于 a, b 两点点, a 在 点 b 的 左侧, a, b 坐标给我们了,而且是负一度零和三度零, 那么遇到这个题的话,有负一对零和三对零,我们就用交点式了,对吧?交点式,而且这个题里面 a 也有,我们的交点式是 y 等于 a 倍的, x 减 x 一, 乘以 x 减 x 二, 那么现在现在的话,这个 a 是 负三分之三,我们直接带进来了负三分之三,然后 x 一 是负一,那 x 减负等于加一,再乘以 x 减三。我们整理一下这个式子,整理完之后我们的焦点式就有了啊,我们这个 d 一 我就解决了, 整理一下,那就是负三分之三 x 方加三分之二倍根号三, x 再加根号三。好,这个式子还是比较长的,我们来看第二问, 如图一点,得在直线 bc 上方运动,然后连接得 c 和得 b, c 和得 b, 当这个 b c, d 的 面积取得最大值的时候,呃,让我们求得 m 加 b n 等于几?得 m 加 b n 等于几? d m 加 b n, 听里面说了, m n 等于四分之根三啊, m n 是 有的。首先,那,那这个咱们可以用牵垂法,对吧?我们用牵垂法可以快速的表示出这个面积,它让我们面积最大吗?我们就算一算啊,什么时候面积最大?好,第二问, 我们在写的时候用牵垂法的话,那咱肯定现在 需要去求一下这个 bc 的 表达式啊。 b 点坐标,这个 c 点坐标,因为根据这个二三数,我们知道这个 c 就是 就是根号三,所以这个 c 点坐标是零度根三,然后 b 点坐标是这个三度零,我们可以快速求出这个 y bc 啊,设代求写啊,能口算口,但不能口算,用笔慢慢写就行了,算出来是,嗯,负的三分之根号三 x 加根三,好,这是 b c。 然后接下来我们就可以设我们的得点坐标, 设得点得点坐标是 m, 横坐标 m, 那 么中轴标我们就可以用这个二次函数表达出来表示了,就是负三分之根号三 m 方加 三分之二倍根号三, m 再加根号三,那么这个得点坐标我们就表示出来长这个样子。得点坐标有了之后,那么我们就可以 就是往下做垂线,往下做垂线,比如说 abcd, 假如说这是 e 点啊, 那么一点坐标我们就可以表示,表示成为了,因为一点和得点的它的横坐标都是 m, 它是同一条竖线上,然后一点的坐标,我们就可以用这个二函数表,用这个一函数表示一下,就是负的三分之根号三 x m 加 m 加根号三。好,这样的话我们的得益好,我们就简单写一下,设得点坐标是 m 逗号负的三分之根号三 m 方,加三分之二倍根号三 m, 再加根三,则一点坐标是 m 逗,负的三分之根号三 m, 再加根号三。然后呢,这个得 e, 我 们就表示出来了,用上面这个得减去这个 e, 我 们已经给你讲过了,用上减下 得益,那就这个,呃,这个没有人给他减,那所以说还是负的三分之根号三 m 方,然后这个减这个的话负负得正,嗯,那就相当于加上根三 m, 然后根三减根三就没了,所以说我们的得益就有了啊。得益有了之后, 然后我们接下来这个面积 s 三角形这个 b、 c、 d 的 面积,我们就用 b 点的横坐标减去这个 c 点的横坐标,就是他们公共的高,他的底的话就是得 e 好, 那就是负的三分之根号三 m 方,加根号三 m, 然后这是底乘高,高的话是 b 点横坐标是三, c 点横坐标零,那三减零还是三底乘高,然后再除以二,好,整理这个式子,整理这个式子我们算一下,它就等于负的二分之根号三 m 方,加二分之 三倍的根号三 m, 好, 就是这个啊, 送到这之后,然后还有就是你要注意他说了点的是在上方运动,他其实这句话兄弟点的在 b c 上方运动,这句话他其实浅藏的意思就是我们的 m 是 大于零,小于三的,大于 c 的 横坐标小于这个 b 点横坐标。 我,我写一下啊,就是因为点的在直线 bc 上方运动,所以说我们的 m 是 大于零,小于三,因为它说了不含 bc 两点啊,所以说不能有等于号。然后接下来这是不是我们熟悉的二次函数给定区间,对吧?就定轴,定区间,求最值,那就简单了。 然后接下来的话,我们就是换一下草图,开口向下,开口向下,求一下对称轴。所以第一步我们求一下对称轴, 它的 x 等于负的二 a 分 之 b, 二 a 分 之 b, 算一下根三,根三要削掉,你看这个根三,这个根三削掉,然后负负,嗯,也变成正,然后还剩二分之三,所以对准流就是二分之三。呃,然后第二步我们画草图,分析一下开关向下, 然后它的对称轴 m 等于二分之三,这个这个这个地方,这个 x, 我 应该改成 m 啊,因为这个整个题的话,我把字面量已经设成了 m 了,然后它是零到三,哎,你看这个零和三刚好离这个二分之三刚好是对称的,对吧? 这刚好是对称的,所以说我们的最大值其实就是在对称轴的地方取到二分之三的时候取到, 所以最大值 s, 三角形 b, c、 d 的 最大值,那其实就是,呃,当它的等于 m 等于推伸轴的时候,然后把这个二分之三我们代入我们的表达式中,算一下, 再去算一下负的二分之根号三,乘以这个二分之三的平方,再加上二分之三倍根号三,再乘以二分之三。好,我跳一步啊,算出来,算出来之后是八分之九倍根号三。 好,这个面积就有了,这个面积有了之后,那么也就是说当它的面积取得最大值的时候,我们的 m 是 二分之三,我们看我们的 m, 什么?我们的 m 不 就是得点的横坐标吗?对不对?那这样的话,我们把这个二分之三带入得点里头,我们得点是不是就出来了,对吧?得点的横坐标我们是能表示出来的啊。 所以当 m 等于二分之三十,当我的 m 等于二分之三十,这个得点坐标,我跳步啊,就是二分之三。逗,四分之五倍根三, 四分之五倍根三,这个,这个,这个我跳步了啊,你自己带进去算一算哈,得点就有了。得点有了之后,它让我们求的是这个, 呃,得 m 加上这个 b n 的 最小值。呃,这个题里面你要注意啊,得点是在运动的,对吧?得点是在运动的。这,这就相当于我们之前讲过的将军野马嘛,对不对?将军马。所以说,呃,你就做这个得 m, 关于这个,做一个平行线,我们做一个这个得 m, 呃,关于 m n 的 平行线,就这样啊。好,我们做一下, 做完之后,我们可以使得这个得 m 是 平行于这个这个得得片 n, 就这样,这样做一下,就是意思就把这个的点给它平,平行下来,平移下来啊,就这样子。好,你看一下我接下来怎么写,我把这个图稍微放大一下啊,好,然后就这样子做一下。平行, 这个得撇,我们是能表示出来的,对吧?因为这是一个平行四边形嘛,我们其实相当于直接是往下平移了。平移多少呢?那是不是就平移这个四分之根号三,对吧?平行四分四分之根号三。 好,然后平移完之后,这个得撇,找到之后的话,那其实他让我找的是得 m 加上 b n 的 最小值,其实是不就是得撇 n 加 b n 最小值,对吧?那得撇 n 加 b n 最小值,将其码做对称。 b 点刚好是关于 a 点对称的嘛,对吧? b 点关于刚好是关于 a 点是对称的对称,然后我们连接 a 的 撇,那么 a 的 撇就是我们的最小值, 我讲这你能听到吧,对吧?就是意思是把这个得给它平移下来,平移完之后的话,我们本来是让找得 m 加 b n 的 最小值,那么其实就转换成了找得撇 n 加 b n 的 最小值, 然后做完对称之后,那我们只要连接 a, a 得撇, a 得撇就是答案, a 得撇就是答案。好,那么因为你是平移的嘛,你这个得撇坐标是能能找到的啊。得点坐标是二分之三逗,四分之五倍根号三, 二分之三逗,四分之五倍根号三,然后我们是不是往下平移平移了一个四分之根三,四分之五倍根三减四分之根,是不是刚好是根三,对吧?啊?所以说我们这个得撇坐标就是二分之三,逗,这个根三,我们的得撇 得一,撇坐标是二分之三,豆跟三得撇有了之后,然后 a a 的 坐标,我们知道是这个 a 的 坐标是负一豆零,然后有得撇有 a, 然后勾股定律,对吧?我们就可以求这个 a a 得撇了。 好,我给你描一下购物定律,然后接下来在这边就购物定律了啊,购物定律了,所以这个 a 的 撇就等于底,底的话,其实就是的撇的横坐标减去 a 的 横坐标二分之三减负一等于二分之三加一加一等于二分之五, 二分之五的平方高高的话,就是的的纵坐标减去 a 的 纵坐标是根三,那就根三的平方, 然后再开方算一下,算出来是等于这个二分之根号三十七,那么这个最小值我们就搞定了。这是我们的第二问,然后我们来看第三问啊,第三问, 第三问。好,我把图挪一下, 第三问,他说的是如图二,将一中的平行线向右平移,将一中的平行线向右平移,当他恰好过圆点时过圆点,那 a 点本来是负一对零 往右平移一个单位,对吧?左加右减嘛?左加右减,然后过圆点时,设圆抛物线与平行后的抛物线交于点 e 连接 b e 点 p 在 这上面。 如果这个三角形啊,随便点个点撇啊。如果三角形 p e c p e c 这个如果三角形 p e, c 等于 bce, 等于这个 bce 减三十度的时候,就这个角等于这个 bce 减三十度的时候,直接写出所有符合条件的 p 点坐标。 好,那么那么这种这种题的话,那我们写的时候这个有有点难度哈,这个你读着听就感觉有点难度,不好想,不好想。首先我们先把这个平移之后的解析式给它找到,好吧,我们先把平移之后的解析式找到,因为它是左加右减嘛,左加右减 好,往右平一个单位。这个原解析式是 y 等于负的, 原解就是 y 等于负的三分之根号三 x, 方加三分之二,被根号三 x, 再加根三,原解是这个。然后接下来我们把它配成顶点式, 配上顶点式之后,然后我们再次往右平移左右减,对吧?好,顶点式的话,我们之前讲过,我直接,我直接跳步啊,我直接跳步,然后你算完之后,它的现在解式就是 y 等于负的三分之根号三 x 方加三分之四倍根号三 x, 这是我们现在的解式,因为它过圆点吗?所以 c 是 零啊,没有 c 现在解式。这个啊,好,找到现在解式之后, 然后我们来再看这个点 e, 我 们是能求出来,因为点 e 刚好是两个解式的交点,对不对?交点的话我们就连利嘛,对,我们俩连利,我们进来找一点坐标连利啊,让两个解式相等,就这一坨等于这一坨。 负的三分之根号三 x 方加三分之二倍根号三 x 加根三,就等于负的三分之根号三 x 方 加三分之四的根号三 x, 这个刚好这两边都有 x 方 x 方,对吧?负三分之根号三就刚好消掉了,然后这个算也很好算,对,把这个移过来,这个算也很好算啊,算出来我们的 x, 它就等于 二分之三 x 出来之后的话,那你把哎哎这个 x, 你 带入这个第一个节式也行,带入第二个节式也行,都可以算出来,都是答案。这个一点坐标找到了,继续跳步啊,你自己带,带完之后找到一点坐标是二分之三,到这个四分之五倍跟三 好一点,坐标标上去啊,二分之三都四分之五被根号三一点坐标有了之后,我们再来看这个 o c 的 话,等于根号三,因为你这个原解是根号三,对吧?这个 o c, 然后这个地方是三, 你你,你看到这个一比根三比二,你能不能看见,对吧?这是三十度啊,这里面藏着一个三十度的,看到没有?为什么要想三十度?因为它里面有一个减三十度,知道吧?刚好嘛,对吧?根三比上三的话,是不是刚好是一比根三,然后这边一定是二,对不对?所以这是三十度啊?因为 c o 等于根号三, b o 等于三角, c o b 等于九十度,教大家一下垂直, 所以直接推导出来角 c b o 就 等于三十度了。好,然后这边就是三十度,找到三十度之后,然后接下来我们要去找这个这个东西啊,这个 p e c 角 p e c 啊,怎么办呢?我们就 过点 c, 我 们做一个平行线,做一个 cd, 看一下啊,过点 c, 做一个 cd, 平行于 x 轴, 好,左右平行线做完平行线之后,根据内存角相等,对吧?你底下是三十度,那你上面这个这个这个 dcb 也是三十度,内存角相等。好,我们就有一个三十度了。有个三十度之后的话, 那么我们来看啊,现在要求的是这个角 p e c 等于角 b c e 减三十度。你看,我先把这个 p 点坐标给你点一下啊,我们先点一下 角,这是 p p e c, 这个角等于这个等于这个角, b c e b c e, 就 这个角, 这不是三十吗?对吧?这是三十减三十,那说明我们必须得让我们这个 p 跟这边这个角得相等,跟上面相等,所以我就接下来过点 e 做一个平行, 你看我们如果过点一,做一个平行线的话,假如说这是,然后这个这个地方是 p, 因为 p 点在对准手上嘛,对吧? p 点在对准,我们先找到这个点,好,我们找一下角 pe c, 我 们找到 pe c, pe c 找到了吧?就这个很小的 pe c, pe c 等不等于这个角 bc 减三十度,你看,因为你现在做的是平行线往内缩小的,对吧? p e c 是 不是刚好等于这个 ec d, 对 吧?而刚好这个 b c e 减三十,是不是刚好等于这个 ec d 了,对吧?我,我现在给你标一下,相当于标上角一角二吧。 这边是角一,然后这边角二,对吧?角一等于角二,你说角角一等于角二,然后这个角二。兄弟,这个角二是不等于这个 bce 减三十,那是不代表角一也等于 bce, bce 减三十,那是不是推导出来了,对吧? p e c 等于 b c e 减三十,明白吧?所以这个第三问,他就辅助线不好想,他难,其实难的辅助线不好想啊,好,然后他还让我们求此时的 p 点坐标他还让我们求此时的 p 点坐标。 此时的 p 点坐标。嗯, 你想想咋求此时的 p 点坐标,哎,你看这个 p 点跟这个 e 点不是平行的吗?对吧?那 p 点不是在原来这个对称轴上吗?我们可以求一下原函数,求一下这个原函数的对称轴。我们求下原函数对称轴, 它是 x 等于负二分之 b, 负的二分之 b, 负三分之,根号三乘以二,再三分之二倍,根号三负二分之二,算上刚好一,所以 p 点横坐标是一,而 p 点跟一点是不是它是平行的,对吧?那 p 点平行的话, p 点一点的纵坐标相等啊,那 p 点坐标直接出来了。一逗,四分之五倍根号三,对吧?直接出来了, 好,这是第一个答案啊,第二个答案直接出来了,好,这是第一个答案,我们来想,我往下再把图再往下弄一下, 对吧?你听完第一个答案之后,你就大概明白这个题我们需要做平行,对吧?我们看第二个答案, 在第一问题里面我已经求出来一点坐标,一点坐标是我标下二分之三,逗,四分之五倍根号三,好,然后这边是三十度啊,三十度。第二个答案怎么办呢?第二个答案的话,我们是,首先,呃,我们, 我们这个 p e 这边不是做了一个平线吗?对吧?做一个平线啊,然后首先的话我们这样写啊,我们需要就是在直线, 就在这条直线 l e, 我 们现在把这个标成 l e 啊,在直线 l e 上我截取一个点 q, 使得这个 q e 等于 q c。 在这个直线上截取的这个 q 点,它不一定是在抛物线上,这点你要注意一下啊。好,截取一下,使得这个 q, 比如说我们把这个地方命名为 q 啊,我截的是一个 q e 等于 q c 啊。 截取完了之后,然后接下来我们再做一个平行线,我们再做一个平行线, 这样再做一个平行线, 做一个这个 e g, 平行于这个 c q, 啊,做这个平行,因为咱刚不是过点 c, 我 们也做了一个平行嘛,对吧?这个标上去, 好,那就说明这个肯定是就这个点啊,兄弟,兄弟,就这个点,这个点,把它命名为这个 g, 我们来观察,我们来观察这个三,这个四边形,我给它描黑一下啊,兄弟们,就是我们来看这个这个四边形, 首先它上下平行,其次我们是不是做了一个这个 e q, 它是,哎,有 q 了, e g e g 是 平行于这个 c c q 的, 又做了一个左右平行,平行四边,我们是不是还截了一个平面相等,所以是菱形啊?菱形 作 e q, 平行于 c q, 则四边形 c q e g 为菱形,关键我们就用这个菱形,关键啊,关键我们就用这个菱形了啊, 好,然后还有就是我们的 p 在 哪里,对吧?我们 p 在 哪里? 你看这个 p 点,这个 e g 和这个对应轴有一个交点,我们这个 p 就 在这个位置, 就这个焦点这个位置啊,看好了,就这啊,就这,这就是 p。 好, 那么我们来看此时此时的话满不满足?提议啊?此时的话他,他要求的是, 他要求的是这个角角 p e c p e c, 这个角在这呢啊,他要求这个角 p e c, 嗯,等这个角等于这个 bce, bce 减三十,你看这边刚好不是三十度吗?然后 bce 是 不是大角?大角减三十,是不是减出来这个小角, 对吧?这个 ecg, 而 ecg 是 不是肯定等于这个 pec, 因为它是菱形吗?这两个菱相邻,这个角是相等的吗?对不对?所以是符合提议的啊,明白吧? 这个题的第二个辅助线就这样做,不好,不好想,确实不好想,实话实说啊,不好想,好,你想明白之后,然后接下来,我们接下来只需要求这个 p 点坐标就行了,只需要求 p 点坐标,行了,我们我们的这个 q 点坐标和我们的这个 e 点坐标,它的坐标是相等的,对不对?我们可以设 q 点,横坐标是 m, 那 么纵坐标的话就是四分之五倍根号三,我们 q 点坐标是设出来的, q 点坐标设出来之后,那么我标一下啊, 标一下 m 豆四分之五倍根号三。 q 点坐标有了之后,那么我们这个 怎么求? m 是 可以求的勾股定律,你看这个,这个 q e, 对 吧? q e, 我 们能表述出来, q e 刚好是二分之三减 m, 对 吧? q e q e 二分三减 m, 然后 c q c q 的 话,这个地方勾股定律哈, c q, 因为 c 点坐标是, 呃,零度根三,现在这边零度根三,那么这个地方其实就是四分之五倍根三,再减根三等于四分之根号三,就这个地方啊,这个地方是四分之根号三, 然后你,你这个地方是 m, 对 吧?这是 m, 这个边上是 m, 然后勾股定律,所以说我们的 c q 就 等于这个四分之根号三的平方,再加上 m 的 平方,然后它是菱形,菱形的话, q e 是 等于 c q 的, 呃,因为 q e 等于 c q, 所以说这个二分之三减 m, 就 等于四分之根号三的平方加上 m 方,然后我们给它算一算啊,算一下这个,这个其实还是比较好,是一个关于 m 的 一元次方程,我们算出来,我跳一下啊,算出来 m 等于十六分之十一, m 出来之后的话,那么 q 点坐标是不是出来了,所以 q 点坐标就是十六分之十一。逗,四分之五倍根号三,这是 q 点坐标就有了。 q 点坐标有了之后,然后我们再来看, 那 q e 是 不是就有了,对吧?嗯, q e 就 有了, q e 有 了之后,因为这个是因为一点是二分之三,然后这个 m 的 话是十六分之十一,那么 q e 的 话,就是二分之三减去这个十六分之十一,所以这个菱形的边长就出来了啊, 所以 q e 我 们写一下,就用二分之三减去十六分之十一,算出来是我们的十六分之十三。好,那这样的话我们就相当于这个啊,这都,这,这都出来了,是吧?这都出来了, 这都有了,这是 eg, c、 c g 都有了, 好,这都有了,我都给它标一下啊。标完之后,然后接下来就是你要想,你要想一下我们,我们怎么去设这个, 那这个点也有了呀?这个 g 点不也有了吗?对吧?然后我们要求这个屁,对吧?然后我们直接用一函数,我们可以算出来,因为一点坐标也有,然后我们的 g 点坐标,我们 g 点坐标,为什么我说有了?因为,因为这个横坐标是十六分之十三,对吧?横坐标是十六分之十三, 然后纵坐标是根号三,然后这样的话这个 g 点也有, e 点也有,然后这个 e 函数是不是出来了? e 函数出来之后,我们再把这个 p 点是在 x 等于一上吗?对不对?把对称轴这个 x 等于一带进去,我们就可以求出 p 点坐标了。所以接下来就是设 这个 y e g 就 等于 k x 加 b 啊,然后把 e 点这个 g 点这个代入,代入之后的话,我跳过啊,我们算出来这个 e g, 它就等于这个十一分之四倍根号三, x 加上四十四分之三十一倍根号三, 然后我们再把 x 一 代入,算出来这个 y y, 它就等于,嗯,十一分之四倍根号三,加上四十四分之三十一倍根号三。和平一下 算出来是四十四分之四十七倍根号三。好, p 点左边出来了,所以这第二个答案是一豆四十四分之四十七倍根号三,所以说我们的第二个答案就这样出来的, 这个题你会感觉到他对吧?辅助线不好想,其实想明白辅助线之后算,我倒觉得还是比较好算的,对吧?大家一般都能想到,主要就是辅助线难就难的辅助线了啊。 ok, 兄弟姐妹们,我们今天主要讲的是二次函数压轴分成了小题部分和大题部分,小题部分我们主要处理的是这种 abc 的, 这种题也是非常高频非常热门的,认真听,相信你听完之后肯定是有帮助的。然后接下来就是二次函数的大题压轴考最值,求最值! 如果哪里没有听懂啊,推荐你可以再听一遍,或者记记笔记,不会的话随时问。好吧,今天的话我们就先讲到这里,非常感谢大家一直以来的支持, 非常感谢大家,拜拜,兄弟们,拜拜!拜拜!
1710HaiTone海涛 04:15查看AI文稿AI文稿
04:15查看AI文稿AI文稿就是说那刚刚我们第一步是先让它相等的时候,等完了,然后再整条抛物线往左或者往右去平移,因为它只要平移了,它就会跟对称轴之间的距离是会产生改变。 o 不 ok, 它发生改变之后,一个更靠近,一个更远离,那它才会有大小关系的吗?是这个原理吗?对不对?好,所以跟这里也是一样啊,你们这里 第一个开口刚刚往上,现在就要往下了,那开口往下这个就送分的了,二 m 减一就给小于零这个问题哦 o 不 ok? 好, 然后第二步跟他跟你一样,我在对称轴那里先让他相等,也就是当 y 一 等于 y 二的时候,同样的是不是也是对称轴?就是那个一? o 不 ok? 好, 那你们就先把最原始的状态给它画出来,就是当他物线对称轴是一,然后开口往下的时候,他那个图像大致就这样子了。 o 不 ok? 对, 上头抬头往下,然后当 p 在 这等于负五的时候呢?这个就是 p 点的 y 一 嘛,这个就是 q 点的 y 二嘛,现在是不是相等? 好,然后你再让他平移。问题来了,他误线开口往下,我想让这边变小,这边变大,所以往左还是往右?往右?而且其实你这么想开头往上的时候跑左边,开头往上就跑右边,刚好会反过来的吗? o 不 ok, 包包开好,那所以第三步,那现在我要往右移了,问题是移多少?一点点好?移一点点你就一点一点的去移,那他这里我本身是从一开始,你不要说一口气嘣一声跑到那边去,你一点一点分,就是你从那零件点那边来,他下一个零件点是不是三?还记得这个三怎么来的吗? 随便给我?对啊,题目随便给的吗?是不是题目说在这个范围之内他都要最小?所以你不要说一口气把他移到那边很远的地方去,你先让他移到刚刚好,大概是一到三之间的一小段距离就二了。 o 不 o 平移过去一点点,就是我相当于把它的顶点移到这里来而已嘛。好,移过来了之后再看啊。这里第一个要求 p 点,就是这条虚线上面的每一个点都可以是 p 点了吗?现在 p 点的 y 一 是不是比 q 点的 y 二要小, 符合吗?对不对?好,再来,在这一个范围之内,你再看一遍啊,从负五到三这一个范围之内,现在那个 p 点是不是最低点?是啊是啊,要往左移啊。所以啊,你往左移还是最最最小?那你的 y 怎么小的? c 的 最小, 等等我,我往右边移。往右边移是为了让 y 小 于 y 二了,对不对?所以我只能够往右移啊。 ok, 先先往右移,往右移了我就能够满足 y 一 小于 y 二,然后最后一步就是移多远的问题吗?对不对?我刚刚是移了一点点,让他就是这个顶点。对称轴来到一跟三之间,是不是已经可以符合题目的要求了?是啊,对不对?那如果再贪心一点,我再移多一点了,我让他移到三的右边去。假如说 对称轴就是那个顶点跑来这里,我让他移到三的右边去。那条抛物线变成这个样子 o 不 ok? 变成这个样子之后,他现在最高点在这,这个是他的最高点吗?然后在附五到三之间的这一段图像里面,他是不是都是那个最低点?是 o 不 ok? 其实开头往下会比开头往上更好讨论,因为他开头往下的时候,他整个图像只有最高就没有最低,所以我只要保证 p 点跟对称轴更远,是不是他这个就会更小? 而且他都在爬路线,对称轴的左边是不是越往左他就越小?对啊,但是开头往上不一样,开头往上的时候,他那个最低点是由顶点决定的,所以我要保证那个顶点跑到 p 的 这边去,他才不会说在这里成为他的最低点 o 不 ok, 但不是说每个题目都这样,是刚好这个题目条件他就这样,所以你不要说我每次都先考虑这个开头往下不一定的 o 不 ok。 刚刚这一题其实那个一并没有怎么样用上去,但是这一题用上去了,所以我们只要要求那条对称轴在一的右边就行了, ok 吗?啊?所以在在对称轴的 负二 a 分 之 b 在 一的右边,所以就是比一要大,能不能等于一不能?能不能不能等等?先,我刚刚那个一怎么来的? 我刚刚那个等于刚刚我们的一怎么来的?对,当 y 等于 y 二的时候出来的吗?那如果你对称轴等于就就就回去了。 o 不 ok? 所以 这里就是对称轴要比一要大,那然后你负二 m 减一 m 加一,可以跟一带进去,这里两个不等式是可以把它当成了,把那个不等式的范围给它求出来了。 o 不 ok? 所以 你说整个题目,整个题目下来,你说计算量很大吗?也不是他最大,最难的地方就在于画图,然后画完图之后你们反正是想这个点,第一开口往哪里,第二对称轴在哪里?让他跟着抛物线往左往右移移移就 ok 了。移到一个你能够同时符合题目所有要求的地方,然后他的不等式放不出来,计算量很少,这里。
 01:52查看AI文稿AI文稿
01:52查看AI文稿AI文稿停留三分钟,让你学会一个中考考点!今天我们来讲解的是二次函数最值当中将军以马模型相对比较简单的一种题型就是两镜移动模型,它是怎么做的呢? 已知二次函数知道了点 d 是 顶点,那么由图像我们会发现,它与 x 轴交于 ab, 两点与 y 轴交于 c 点,而 p 点是我们 x 轴上的一个动点,让你求 c p 和 d p 的 和的最小值, 那我们会发现其中 p 点是一个动点,而 c 点和 d 点是两个静点,所以我们俗称的是两静一动。那么遇到这种题型,我们统一的做法就是找到其中一个静点, 做动点所在直线的对称点。那对于这个题来说,我不妨把 c 点做关于 x 轴的对称点,我们令它为次 c。 由二次函数的解析式可以轻易得到的是 c 点坐标是零二, 那么我们次 c 点的坐标就是零负二顶点坐标我们也可以简单表示出来, d 点坐标是二四,此时我们连接次 c p 会发现, 那么我们的 pc 长度和 p 次 c 长度是一致的,我们要求的 c p 加上 d p 的 核就可以转化成次 c p 加上 d p 的 核。那我们利用一个三角形三边关系可以知道, 四 c p 加上 d p, 它永远是大于 d c 的。 只有当 p d 四 c 共线时,也就是 p 点是在这个位置上的时候,我们得到的是 四 c p 加上 d p 等于 d 四 c。 而我们通过勾股定律可以得出 d 四 c 的 长度应该等于二减零的平方,加上四减去 负二,也就是四加二的平方,算出的得数就是二倍跟十。好,这道题就是这么简单,以后只要遇到两镜一动,我们就知道找到其中一个镜点做动点所在的轴的对称点,然后连接另一个镜点与对称的点就可以了。
57泡泡数学田老师 13:00
13:00 05:23查看AI文稿AI文稿
05:23查看AI文稿AI文稿今天来讲一下二次函数中比较高频的一个考点,就是面积部分,面积部分如果是求两个等面积,那么它的动点坐标应该怎么来求? 已知它的二次函数是 y 等于负 x 方加二, x 加三啊,当然了,我们已知这二次函数其实 b 和 c 全都能求啊,这里边我们就那个不重点解了啊,老师已经解出来了, b 点是零到三,然后 c 是 三到零, 然后这里边给了你一个对儿,对儿是这个二分之三,对儿四分之十五啊,然后现在这个题会这么样说,说是在这个二三数上取一点 e, 使得这个 s 三角形 b、 c、 e 等于 s 三角形 b、 d、 c, 你 们知道啊,这个 b、 d、 c 是 不是都是定点呢?所以这个三角形 b、 d、 c 的 面积也是能求的啊。那么现在他说要取一点等于这个 b、 c、 e, 当然他这个题也不算是一个难题,我们可以直接用牵扯法就可以把它求出来,这里边老师讲一个比较简单的方法,避免我们 可以不落点,还可以非常非常简单的把它解出来。那么我们知道这个三角形 b 的 c 和 bce, 老师现在画出来这个点是一种情况,它俩现在是共用一个底,是谁啊?共用一个底是不是 b、 c 啊?那三角形 b、 c 的 高是不是这么划过点的向这个 b、 c 做一个垂直,那么我们知道这个 三角形 bc, 一 般它是一个钝角三角形啊,然后我们也可以以 bc 为底,那么高呢?怎么样画高是不是就应该是这么画呀?那我们知道它就应该是它俩的面积应该是相等的话,就应该是一个同底等高的问题,那么高什么时候是等呢?我们肯定是要画平行线,所以现在 我其实是要过点的,过点的画一个 bc 的 平行线,这样的话它会与这个二、三数相交于一点,那么它相交的这点 e 其实就是我们要求的,为什么呢?因为我们现在画完平行线了之后啊,我们能看出来 这个是不是就是 b、 c 上的高,那么我往下来做,如果这个 b、 c 稍微延长一些的话,这个就是 b、 c 上的高,对吧?那么这样的话,它平行线间是不是距离输出是相等的,这样的话我们就能得到这个 b、 c、 e 的 面积和这个 b、 c、 d 的 面积是一样的啊,那么怎么来求它呢?这个点 e 的 坐标怎么来求呢?我们可以求这个 e、 d 的 解析式,然后根据二次函数做一个什么连力啊。那 e、 d 的 解析式怎么来求呢? 我们知道这两条线是平行的啊,平行线它们的 k 值应该是一样的,那这个 y、 b、 c 我 们肯定是可以求了。 y、 b、 c 应该是,呃, y 等于负 x 加三,那这个这个 k、 e、 d, 这个 k 值肯定也是减啊,肯定也是负一啊,因为它俩是平行,这个时候我们就可以设这个 y、 e、 d 的 解析式。为什么啊? 是不是可以为 y 等于负 x 加 b 啊?这 b 肯定是不知道的,但是我们看这个点 d 是 已知的条件,带进去是不就可以求这个 b 了, 对吧?那这样的话,求完这个 y、 e、 d, 我 们就可以进行把这个 y、 e、 d 和谁啊?连立啊,是不是就是 y 等于负 x 方加上二 x 加三,这样的话就可以很轻松的把这个 e 的 值和 d 的 值都给他咋的解出来了啊? e 和 d 都可以解, 那么是不是在下边还有点呢?嗯,没错啊,我们一起来画一下。那下边这个点怎么来找呢?是不是它可能是在这块儿,也可能是在这儿啊?那同理我们肯定是也是要画什么呢?是不是要画平行线,这样的话啊?我们知道这个 这一点,他与二三数交于这一点,这点就应该是一个一二,刚才这个是一一,那么同样我们这块相交这个画的稍微有点短,我往下拉一下,这个时候这点就应该是一三,为什么呢啊?我画一下, 嗯, bce, 哎,他们俩是不是这个三角形,是不是也是以这个 bc 为底?那高是不是就应该是这么画呀?对吧?那我要是画这个等距离的这种平行线的话,所以他这个高肯定也是一样的,那同理这边这个三角形 也是以 b c 为底,那高呢?怎么样画?是不是这么画?那以二是平行线间的距离是出出相等的啊?然后做法还是一样的,我们可以求这个 一二一三的这个什么解析式,对吧?那么它的这个 k 值是不是也是负一啊?所以我就可以设这个 y 一 二一三,它的 k 值就应该等于负 负一,对吧?所以它的解析式依旧是负 x 加 b。 那 这里边有一个问题啊,有一个问题就是这个里边的 b 我是 不知道它不像这个,刚才这个,刚才这个的我们直接是给你的。那你说我现在这个一二一三这条解析式上哪一个点是我们有可能知道的呢?哎,那是不是一定是这块, 那么这个点怎么来求呢?这个点怎么来求呢?刚才我们画的是不是平行线间的距离处处等啊?然后我们就可以,你看啊,那我们现在观察一下这个这个图形,你说它跟它是不是相同的? 嗯?是不是?那我可以这样这样这样做,那你说他是不是四十五度,然后我们做的是平行线,他也是四十五度,垂直垂直平行线间的距离是相等的,是不是就可以正现在画的这两个三角形怎么的呀?全等,对吧?那全等了之后呢?对应竖着的这个是不是就等于他呀? 对吧?没问题吧?那现在就是怎么来求这个呢?哎,那刚才我们这个这个 b 是 不是已经求出来?就是刚才这个 e d 这个解析式对应的那个 b 是 不是就是竖着的这个长了?那它求出来了之后,我们就可以减去这个 b 点的纵坐标,是不是 应该是三?那么现在它就是一个一个已知的条件啊?那它是已知的,这个也知道了,对吧?然后我现在要求这个很简单,是不是就可以用 b 点的纵坐标就是三来减去它就可以求出来了?那现在这一点我给它标一个字母啊,把它交出 q 的 了啊? q 点是已知的,那么就可以代入到这个里边来求这个 b 了, 没问题吧?然后这个一一二求出来了之后咋办呢?一一二求完了之后,是不是就可以也是依旧跟这二三数进做一个什么连力?这样的话是不是就可以求出来这个一二和一三了啊?总体来说这种方法要比牵扯法更简单一些,而且计算起来也相对来说方便,同学们学会了吗?
19关关解数学 06:54查看AI文稿AI文稿
06:54查看AI文稿AI文稿老师,听说学霸都知道那个速算口诀,那我今天毫无保留的告诉你,铅垂法球面积最值,堪称二次函数的隐藏大招! 书上没有,学校老师也没有总结,但是很多学霸呀,早就偷偷学会了,就像这道题,很多孩子压根不知道怎么速算点坐标,别急,老师今天啊,就带着你从源头推导到计算结果,彻底掌握这类二次函数三角形面积对质问题。好,我们来看题, 已知二次函数 y 等于负 x, 方加三, x 加十,上面有个动点 p, 然后这个抛物线呢,是已知的,跟坐标轴交于 ab 两点,现在呢,我把动点和 ab 两点连起来,这是个三角形,问,什么时候 p 点坐标三角形的面积最大? 那么这个题的突破口在哪?是不是三角形面积?那今天呢,给大家介绍个非常重要求最值问题的方法就是牵垂法。 老师为啥要学一个新的方法呢?你给大家去仔细观察啊,这样的一个三角形,如果 a b 去当底的话,你的高是斜着的,没办法直接去求。所以我们遇到不规则三角形面积,有个万能的方法就是千锤法, 这个牵的意思是一个牵重的感觉垂直向下,垂的话就是垂直向下。所以呢,我们的方法就是过动点 p 向下做一条 x 轴的垂线,与固定的 a b 线段相交于一个点,是我们的 q 点。比如 大家去观察一下,现在你的三角形 p a b 的 面积表示成什么了呢?被你这么铅垂线一刀切,改成了 p q a 加上三角形 p q b, 对 吗? 与此同时呢,我们来看一下,第一个面积是等于什么?什么二分之一来 p q, 当我们的公共的底,那 p q 乘以我们第一条高。我来画一下啊,第一条高在这个地方, h 一 好,乘以我们的 h 一, 继续加上二分之一, p q 乘以我们的这个高。我来瞄一下,就是我们这个地方的高 是 h 二,对吧?因为你看啊, p q b 是 个钝角三角形,它的高在行外好,再乘以我们的 h 二。那大家都知道这里该干嘛?提取共音式,所以说它就变成了二分之一, p q 乘以括号 h 一 加 h 二等于二分之一, p q 乘以几。各位告诉我, h 一 加 h 二,把 h 一 平移下来,刚好是 o b 的 长好,请问此时此刻它是不就是我们三角形面积的表达式? 那大家现在思考啊,因为你二次函数是已知的,我把它转换成两根式,就是 y 等于负的 x 方减三, x 减十,然后呢?十字相乘,负的 x 减五, x 加二, 所以我们可以轻松得知。这不是重点啊,我们可以轻松得知这个点的坐标,比如说 c 啊, c 点坐标是几?是不是负二零? b 点坐标呢?是五,逗号零。所以你会发现你这个 o b 长实际上是确定的,也就是五,它就等于乘以五,当然是二分之五倍的 p q。 好,大家现在集中注意力,我要求的是它的最大值,实际上你二分之五是确定的,是不就是 p q 的 最大值, ok 吗?好,我们来展示一下啊。那现在呢,我们的目标就转化了,转化成求 p q 的 最大值。那怎么去求呢?我们这个时候可以设一下啊, p 点的坐标是小 m 轴号,它在抛物线上,那你把横坐标带进去,纵坐标就是负 m 方加三, m 加十, 对不对? q 点是垂下来的,所以 q 点坐标,横坐标也是 m, 纵坐标是什么呢?是不是 q 点在我们的直线 ab 上?你好,你把 ab 直线求一下。 ab 直线怎么求呢?首先是我们通过待定系数法啊, a 点坐标是几呢? a 点坐标是零逗号,你看零逗号与 y 角的交点是零逗号十, 对不对? ab 知道,那么这个斜率就是纵坐标的差,十减零比上横坐标的差,是不是零减五?答案就是负二。好,这是老师,因为另外一个大招啊,我今天就不展开介绍,那就是 负二倍的 x 加十是我们这条直线的解析式,那么由于 q 点在这条直线上,所以说我们的什么 q 点坐标就出来了,是几呢?各位是负二 m 加十, 大家告诉我现在该干嘛了?我们是不是要求一下 p q 的 最大值,我们接下来呢,重点表示一下,那么所以 p q 这个线段是不是纵坐标减,纵坐标它减,它就是 p 的 纵坐标减去 q 的 纵坐标, 它减它是几呢?可以口算一下,是负 m 方,它减,它是加上一个五 m, 然后十减十没了,对不对?那紧接着呢,我们来看一下, 那么得到这么一个式子,请问大家这是个什么?这是一个关于 m 的 一个新的二次函数,是不是开口向下,然后呢它与来提供音式啊,负 m 倍的 m 减五,是不是?所以说它第一个焦点是零,第二个焦点是五,那么什么时候这个式子取到最大值?是当它取到对称轴处的时候,也就是什么零和五,是不是二分之五, 对吗?好,也就是咱们之前所说的负的二, a 分 之 b, 负一分之 b 的 话是五,然后负负得正,所以当然是二分之五。因此我们发现写了,当 m 等于我们的这个横坐标等于二分之五的时候,然后这个时候 p q 有 最大值 是几,大家可以带进去求一下好不好?然后紧接着 p q 有 最大值,那么它乘以二分之五,是不是面积就会有最大值? ok, 就是 这个题,是不是 p 点坐标的话,就是横坐标是几呢?是二分之五,然后纵坐标呢?是不是这里有个式子,把这二分之五带进去就可以了?好,这是我们传统的一个过程啊,从第一步、第二步、第三步求坐标就出来了。当然求面积是不可以直接把 p q 的 最大值带进去,面积的最大值是不是也能求出来? 好,那接下来呢,我再来分享一个口算的方法,就很多同学想问老师,听说学霸都知道那个速算口诀,那我今天毫无保留的告诉你, 大家听好了啊,什么时候这个 p 点在什么位置可以使得三角形 p a、 b 最大的呢?听好了, p 点的横坐标等于 a 和 b 横坐标 和的平均数,也就是它恰横坐标取到 a、 b 横坐标中点的时候,它的面积是最大的。这里呢,有个详细的推导过程,今天不给大家解释了,大家可以把这个结论记住,你可以验证一下,因为 a 点的横坐标是零, b 点的横坐标是几?是不是我们刚才写过是五,你看刚好二分之零加五,请看是不是就咱们刚才的二分之, 各位就甭管是详细的过程牵扯法以及我们这里的最值的讨论,还是大招的小口诀,二次小结论,希望大家今天的二次函数面积最值问题对你有所帮助,各位你学会了吗?
19悟牛郭嘉数学










