月考最后一道几何题。初二
粉丝2.4万获赞11.5万
相关视频
 12:18查看AI文稿AI文稿
12:18查看AI文稿AI文稿各位同学大家好,我们来看一下本次月考的最后一道压轴题啊。嗯,这两天问的人比较多啊,因为我这两天感冒嗓子不舒服,所以讲的稍微晚了一点,那么接下来我们来看这个题。首先原题当中告诉我们,第一问说这个角它等于六十度, 这个大的角 c 等于九十度,那么这个时候我们能够推出角 b, 它是不等于三十度,对吧?接下来的时候 这个 c d 它平分这个角 a c e, 也就说我们能够得出这两个角它各自等于多少?等于四十五度,对吧?角一和角二相等啊,这个图画的已经比较看不清,接下来 他问大家这三个线段之间的数量关系是什么?那我们上课的时候给大家讲过了,但凡出现三个啊,这个线段之间的数量关系,在初二上册的话,就是最长的这个边等于另外两个边,两个边的和,对吧?所以第一问的结论他就是 bc, 他 等于谁?等于 ac 加上 ad 啊?那这个时候如何来进行证明?他第一问当中也给大家了,他说在啊,小明的解析思路是 怎么样在这上面截取啊?截取这两个边的长度线是相等,我们拿蓝颜色进行替换一下啊。首先 a c 他 和 a e 的 长度线是相等,对吧?那么接下来下一步 他说可以证明这两个三角形全等,那全等的理由也非常简单,那这两个边相等,角一它是不是等于角二,加上中间还有一个共边啊?所以这两个角它对应的是不是等于角 a 相等,是不是等于六十度? 那角 b 有, 刚才我们第一问的过程当中说了它等于三十度,那所以根据三角形的外角能够推出角 e、 d、 b, 它是不也等于三十度?那么这个时候我们能够推出什么东西啊? 这个小的三角形,它是一个等腰三角形啊,也就说这两个边的长度,它现在是相等,那整个 d、 e 它是不还和 a、 d 相等,对吧?那这个时候你自己来看一下整个的 bc, 它是由蓝线和红线共同构成的, 那这个时候蓝线和蓝线相等,红线和红线相等啊,当然这个里面的蓝线不包括中间这个公边 c、 d 啊,这是我们刚才 所画的,所以第一个我们非常轻松的能够证明 bc 它是不是等于谁? c, e 加上 b e, 对 吧?那这个时候它是不是可以被转化成 a、 c 加上 a、 d, 所以 第一个我们就证明结束。 那总结起来,第一步就四个字,什么呀?截长补短,对吧?啊?这我们上课讲过的典型例子,截长补短。 那么接下来我们来看第二步。第二步他说在图三的过程当中,点 e 是 整个 b、 c 边的中点啊,这里面点 e 是 个非常特殊的点,是个中点,接下来又有平分产生啊,这里面又有 啊,这个角一它和角二相等,然后这边多了个九十度啊,然后问你解决一下他们三者之间的数量关系,那你大胆猜测一下,这里面的数量关系仍然是最长的 a、 d, 它是不等于 ab 加上 c、 d 吧,对吧?如果我们基础差一点的同学啊,三班或者四班的同学,就你平时考啊七十多甚至七分以下的人,你只要记住我们当时所讲的截长不短的结论,这个 这一步你是能够拿到分数啊,因为可多同学也就证明不了你。像第三题可能学习非常好的一百零几的人,他可能做起来也比较困难,所以我们在这一步就可以和其他人把分数进一步的差距缩小。那接下来我们来看如何来证明?我们先讲 这个截长不短吧,老师当时讲了,截长的话,你尽可能去截长,对吧?那怎么去截呀?我们在最长的边 a d 上来进行截取,比方说现在他是 b 片了,那这个时候我们把谁啊? b e 连接一下,那这个时候这两个三角形它很明显会出现全等,对吧?全等的理由是什么?我刚才说了,我的 ab 它是不等于 ab 片,角一它是不等于角二,再加这块有个共边,所以这两个三角形它会全等。那么全等结束之后, 我们只需要再一次换一下思路,证明这两个三角形全等,它是不就可以了?那么刚才说了, b e 它是什么东西啊? 啊?它和 c e 它是相等,因为点 e 是 终点,对吧? bc 的 终点,所以 b e 的 长度它会和 b 撇 e 的 长度相等,那这个时候它是不是也等于 e c 了?那再加上这个公边啊? d e, 所以 我们只需要凑一个条件,凑哪个条件?凑这个角三,它等于这块的角四,它是不就可以? 那角三为什么等于角四呀?我们来看一下,我们刚才说了,这两个三角形全等的话,这块的角五会和这个角六什么关系?他俩是不会对应相等,对吧?而原来的题当中告诉我们,这个角 a e、 d 它等于九十度,也就是说角三加上角六它等于九十度, 那这个时候还能得出来角五加上角四,它是不也等于九十度,对吧?那这个时候 角五和谁是相等?他和角六是相等,那么角三自然而然就对应的和角四他是不是相等了,这叫什么呀?这叫等角的与角相等。那么这个时候我们来看一下边角边五是不是就可以证明这两个三角形它是不是全等,对吧?啊?那两个三角形我拿荧光笔画一下啊,是不这个三角形它和这个三角形全等, 那么这个时候我们来看一下最长的 a、 d 他 是不是等于这段,对吧?那这段和谁相等?是不和他相等? 那这一段是不和它相等,那这个时候我们就可以证明刚才所猜的结论, a、 d 它就等于这两个边的和,对吧?这是一种办法。那么这个讲完之后我们再来说一下啊,我们当时上课还讲过什么东西,还讲过被长中线啊?因为点 e 它是个终点,这里面就有可能会牵扯到被长中线,那这个时候怎么办?我们来看一下 倍长中线,我们当时说的结论很简单,我只需要把 a e 怎么样延长出来,对吧?到哪里到?比方说我们现在所说的 a e 撇这个位置上,然后连接一下这个 c a e 撇就可以。 那这个时候你自己来看一下这两个边它怎么样?是不是相等?那点 e 作为中点,这两个边它是不是也相等?再加这个对顶角,这两个三角形它是不是就全等?所以整个 这个 ab 的 长啊?我们换个颜色, ab 的 长,它是不是就会等于 c a 撇的长,对吧?那这个时候我们来再来看一下。原题当中还告诉我们,这刚才我们所说的角一等于角二,我说没用到。那刚才三角形全等的时候,角一和这个角三它是不是相等?那这个时候角二就和角三相等, 对吧?那角二和角三相等之后,这一块不是还有个九十度吗?刚才我们是延长 a e 至 a e 撇,那所以这边是不是也有个九十度?那再加上中间这个公共边的话,所以这两个大的三角形它也会产生全等啊,哪个三角形是不?这个蓝颜色的三角形, 对吧?它是不会和背靠背的这个绿颜色的三角形它是不会产生全等。能看明白,那这个时候产生全等之后,我们你看一下 a d 它的长度 他等于谁?他是不等于 d a 撇,那是不等于 c d 加上 c a 撇, c a 撇的长度和 b a 的 长度相等啊。这个时候第二位也可以用这种思路去做啊,这是整个调。 那么接下来我们来看一下难易程度最大的第三位啊,第三位你就记住,这就典型的数学考试题,你前面两份用了接长不短,那这这一份仍然用的是接长不短,那接下来我们来看一下,他告诉大家说 角 a 等于六十啊,各位同学你要好好听啊,这个你就记住,绝大多数人他是做不了的,那你想一想,我做不了的情况下,我怎么能够多拿分,这是最关键。然后这个边的长度他等于一百三啊,这个同学在旁边已经写出来,接下来又告诉你说 这是个角平分,这也是个角平分,对吧?它俩分别是大小 b 和大小 c 的 角平分。那这个时候各位这是不是有我们上课所讲过非常典型的双角平分线模型,也就是说我就不会做,我也能够推出这个角 c p b, 它等于多少?是不是等于一百二十度,对吧?你自己简单的把过程整理一下, 它就能够拿到分数啊,因为其他人都写不了了,你但凡写了,它都会给你分数。那么接下来 他说整个 b m 的 长度等于八十啊,这个边的长度等于八十, c n 的 长度等于十五。接着告诉你说啊,需要,呃弄一个什么步道啊? m n, 并且满足点, p 是 m n 的 重点,那就这两段的长度,它俩是相等,对吧?那这个时候问你说 求 m 的 长度,那求 m 的 长度,我只需要求出其中任意一个不倒的长度,它是不就可以了?那这个时候和刚才一样啊,我们看一下新得出来这个一百二十度怎么用啊?以及刚才我们所说的这些什么一百三呀,十五呀,八十呀,这些东西到底怎么样? 那方法和刚才一样,我们前面用了截长不短,那这块是不是同样用截长不短,那这个时候怎么办?我们在你看 这一块呢,我们把它标作角一吧。啊,这个标作角二,角一和角二它是相等,那中间又有个公边,那和上面一样,我在这上面可以截取个什么东西 啊?这个笔不太好画了啊,因为比较比较小,图比较小,我在整个 bc 上截取一个 c n 撇的长度,它和 c n 的 长度相等,那这个时候我连接一下这个 p n, 那 各位同学,我先问一下你 这个蓝颜色的三角形啊,和这个绿颜色的三角形,他俩会不会出现全等?明显会。为什么这两个边的长度相等是我自己截出来,角一等于角,二是题当中有的,以及这个我们边线有,那么这个时候 这个边和这个边长度是不就相等,对吧?也就说那个十五可以转移到这来啊?那各位同学,这个时候这段的长度它是不就等于十五?那同样道理,底下照猫画虎。再来一遍,我在这个 b c 上再截一个,谁啊?再截一段, 再截一段,这个 b m 撇的长度它和 b m 的 长度相等,再把它连接起来。那各位同学一样的道理, 底下这个绿颜色的三角形,他是不是同样和这个蓝颜色的三角形,他也会产生全等?全等?理由继续啊?这两个边是我们截截出来 这两个角相等是题当中告诉的,这是不是还有个共边,所以这两个三角形也全等,那么这个时候 这段的长度他是不就等于八十了?能看明白,那一百三减,八十减十五,我是不能够得出这段长度,对吧?相当于一百三减个多少啊?九十五,对吧?那么这个时候我们能够得出中间的长度,它等于多少?是不等于三十五? 能听明白,那有的人可能会说,那老师你刚所得到的这个一百二十度咋用?你刚不是说这个大的角它等于一百二十度,那各位,这个时候关键点就来了,你看下,既然证明三角形的全等,那这个时候这个角和谁是相等?是不和这个角它是相等,对吧?或者看这 更厉害一点的办法,这一块的角五它是不会产生相等,那同样道理, 角六它是不等于这块的角七吧,对吧?这个角七指的哪个角啊?可能看不清了,指的是这个角和这个角七它是不相等,那这个数角六加角七,角四加角六,在这个三角形当中,它是不等于一百二十度。那同样道理, 角五加上角七,这两个角是不等于一百二十度,所以这块他会有六十度产生,对吧?那刚才说了这两个边相等,那这两个边他是不是也相等?那再加这个六十度之后,我们现在所新构造的这个三角形,荧光色的三角形,他是不就会是一个等边三角形? 各位同学能听明白,那它既然是个等边函数,这两个变量是不各自等于三十五,那三十五加三十五等于七十,也就是说 m n 的 长度它等于七十。这题就结束了啊,其实非常简单的,截长不等我们就可以解决,这也就是升学考试题当中属于 比较常见的所谓的亚洲题吧。啊,只不过这个时候放在初二,对大家来说难度稍微大一点。 好了,各位同学,这个题我就讲到这啊,总体来说还是稍微带一些难度,但是如果你把我们上课所讲的接长不短啊,背长、中线这些常见的辅助线,有时候听明白,做这些题对你来说也不会特别难。 好了,各位同学,因为嗓子原因啊,你看今天的视频当中,可能听的大家没有那么仔细啊,你结合视频自己多听一听,多看一看。好了,这个题我就讲解到这,各位同学再见。
20桑迪教育 10:38查看AI文稿AI文稿
10:38查看AI文稿AI文稿题有点难,平行四边形 a, b, c, d 的 对角线 a, c 与 b d 相交于 o 点, m 在 d c 上, n 在 ab 上,且 d m 等于 d n, eg, eg 啊, eg 分 别是对角线与 am 与 c m 的 交点, f, h, f, h 是 对角线 a, c 与 d, n 与 b m 的 交点。 第一个要若啊,若 e f 平行于 ad, 它求证 e h 平行于 dc 的, 那我们第一题来正眼去看,它讲了 e f 平行于 ad 啊, e f 平行于 ad, e f 平行于 ad, 那 么 e f 平行于 ad 呢?那么这个三角形跟这个三角形呢,是相似的啊,是相似的,那么所以三角形 o e f o e f 它是相似于三角形 o o d a o d a o d a o d a o d a 那 我们这里要知道。 另外,我们讲 d m 呢,是等于 d n 的, 它又是平行的啊,因为 d m 它平行且等于 b n 的 b n b n 所以 四边形, 四边形 d m b n d m b n 是 平行四边形,平行四边形是平行四边形。那么我们得到所以角 角 h b o h b o h b o 它是等于角 f d o 的 f d o 啊 f d o 等于角 f d o f d o 啊 f d o 实际上这两个角相等啊,这两个角相等,那为什么相等呢?它因为是啊,平行四边形,它是平这两边平行的,这两边平行的内侧角相等。 那么找到这两个角相等,我们所以讲啊,所以三角形 d f o d, f o 它是全等于三角形 b h o 的 b h o b h o 啊 b h o 就 讲这两个三角形,这两个三角形它是全等的, 那么所以 o f o f 啊, o f 它就等于 o h o h。 看 o h, 因为这两个三角形是相似的,所以啊,讲 o h 呢,比上, 所以 o h 比上 o c 比上 o c 啊,比上 o c, 它就等于 o f 比上 o a, o f 比上 o a 的 啊 o l。 因为这个,这,这个长度跟这个长度是相等的啊, o f 比上 o a 呢,又等于?刚刚已经求证了等于 o e 比上 o d 的 o l 啊 o e, o e 比上 o d, o e 比上 o d 比上 o d, 所以 三角形。所以三角形 o h e, o h e, 它是相似于三角形,它是相似于三角形 o h e 啊 啊 o h e, 它相相,相似于三角形 o c d 的 o c, d 的 相似于三角形 o c d o c d o c d 那 么这个相似了以后就是平行了,所以角,所以角 o e h o e h o e h, 它就等于角 o d c o d c o d c o d c 那 么所以这个 e h e h, 它就平行于 d c 平行于 d c。 第二题,若平行四边形 a, b, c d 不 平行,他讲 md 啊, md 等于三分之二 c m c m 加 f e h 是 等于九十度。我们看, 因为三角形 d m e d m e, 它是相似于三角形 b e a 的 b e a b e a。 那 么所以 d e, d e 比上 e b, e b, 它就是等于 d m d m 比上 ab 的 ab, a, b 是 等于 dc 的, 所以 dm 比上 dc, dc, 因为 dm 比 dm 是 等于三分之二的 cm, 所以 dm 比上 dc 呢,它是二比五的关系,二比五等于二比五, d e 和 e b 之比是二比五。那么 e, d, e 的 长度 d, e 的 长度,它是 o d o d 减去 o e 的 减去 o e o e 啊,这个 e b, e b 的 长度呢? e b 的 长度,它是等于 o b 加上 o e, 也就是 o d 加上 o e 啊 o d 加上 o e 的 o e 加上 o e, 这个就是 e b 的 长度啊,也就等于五分之二,五分之二。好,五分之二, 那我们这里交叉相乘,就是二倍 o d 加上二倍 o e, 二倍 o e 啊,它是等于五倍 o d, 五倍 o e, 五倍 o e, 那 么这里就是 八,就是七个 o e, 七 o e 啊,这七 o e 等于等于三 o d 的 等于三 o d。 是 不是三 o d, 所以 这个 o d o d 的 长,它就是等于 三分之七,三分之七 o e, 三分之七 o e, 这个是 o d 的 长, o d 的 长是等于三分之七 o e。 这里我们记下来,记下来, o d 是 等于三分之七 o e, 三分之七 o e 啊,三分之七。那我们接着往下做。同理,同理 这个三角形,这个三角形跟这个三角形是相似的,相似的, 同理三角形啊, c i c m h c m h, 它是相似于三角形 a b h a b h a b h 那 么所以呢?所以这个 c h 比上, 所以 c h 比上 h a h a, 它是等于 mc mc 比上 ab 的 ab, 那 么 mc 是 三分, ab 是 五分,它是等于三比五的三比五。那么 c h 的 长, c h 的 长就是 oc 的 场,就是 o c 减去 o h, o h 减去 o h 啊。 h a h a 呢,是 o c o c 加上 o h o h, 它是等于五分之三。 那么这里三 o c, 三 o c 加上三 o h 等于五 o c o c 减去五 o h o h。 那我们这里要求 o c, 要求 o c 啊,就是二 o c, 二 o c 等于啊,八 o h, 八 o h, 所以 o c 啊,所以 o c, 它是等于四倍 o h 啊,这个 o c 的 长度是等于四倍之 o h, 这是 o c o c 等于四倍 o h 啊,这里我们求得了 o d 的 长, o c 的 长,我们用这两个字比一下啊,看看比值是多少。那我们接着,接着往后分析,接着往后分析啊,接着往后分析,因为这两个三角形,它是 平行四边形,这样是平行四边形,它是平行相等的平行四边形啊,因为 o h 是 等于 啊,因为 o h 啊,它是等于 o f 的, 等于 o f, o f, o f 啊,这里呢,所以这个 o, 所以 o d 啊,是垂直垂直平分啊, o d 垂直平分 f h, f h, f h, 它是垂直,它又相等,所以它是它的垂直平面线。那么所以又,因为啊,又角 f e h, f e h, f e h 等于九十度啊,等于九十度,那么所以呢,角啊, o e h 啊, o e h, 它是等于四十五度的,四十五度啊,那么所以啊,这个 o h, 它是等于 o e 的, 所以 o h, o e 啊,这个相等 o h 等于 o e, 那 么这里 o h 等于 o e 了,所以啊, o c, o c 比上 o d, 它就是等于 o c 比 o d, 它就是四 o h 比上三分之七。 o e 啊, o e 啊, 这里 o h 等于 o e 了,就消掉了。那么就等于呢啊,一,十二比上七啊,所以 o c 比上 o d 等于十二比七,那也就是对角线,也就是啊,所以 这个 a c, a c 比上 d, b, d, b, 它就是等于十二比七啊,比七啊。
22陈老师数理课堂 03:39查看AI文稿AI文稿
03:39查看AI文稿AI文稿好,我们看一下中一中初二的十二月二十三号月考的填空最后一题,他说我有五个完全一样的矩形,如图所示,摆着夹角呢,都是十度啊,这个地方是十度, 告诉你 ab 的 长度是根号三,要求 d、 e 的 一个长度,那观察一下这边长度和角度呢?都有,而且呢角度是不变的,所以我们能想到的是什么呢?就是这个构造一个全等, 因为他这个十度是靠着这个他的这个矩形的这个长啊,所以说我们要去做一个跟这个利用到这个边的啊,啊,所以说我们要构造出一个跟这个三角形是全等的一个三角形,因为你要用到这一个刚好三这个长度, 所以说我们要想办法去构造这个全等,那么你看观察一下它这个矩形到这个矩形的话,它是又斜了一点,但是它这个斜边啊,这个长它是不会发生变化的,所以我们想办法过 c 点做这个矩形的这个长的这个垂线。 d 点也是的,也是做这两个矩形的这个这个两个边的这个垂线,去构造出这样的一个全等三角形。图像是这样,大概是这样子的啊, 我们过 c 点做这个垂线,那么根据这个角角相等,然后呢边也是相等的啊,边也是相等的,然后得到这个还这边要有九十度,所以说很容易能挣出来 a s 啊,能挣出这是全等的这两三也是全等的 和这个啊,全整,那全整的话,那么这个长度跟这个是一样的啊,这个长度是一样的,同理的话这个长度也是的 跟这些长度都是一样的啊,不变,而因为你是做了垂线啊,所以说它这个小的这个四边形呢,它是一个矩形, 它是一个矩形,那矩形呢?你会发现这个长度它是不变的啊,所以说这些长度都不变,那给你的这个 a、 b 的 长度是根号三,那这个部分不变的话, 不变,不变,这些长度都不变,然后这个部分也不变,所以说能得到这个长度,实际上是一个固定的啊,它就是根号三 啊,因为这个角度是可以推过去的啊,这边十度的话,一线三等角,很能得出这个是十度,这个是十度的话,这个九十,这边是十度啊,可以利用这个啊,飞一个经典的一个飞镖的一个模型啊,可以求出这个角度数啊,这个角度数是一个七十,那再反推出这个地方是二十, 二十的话,这边是二十,然后这边是十度,二十,然后再去推啊,再去推,可以得到这个角是六十度,那么他又是九十,所以说又推出他是三十。 三十度的话,因为这两个线是平行的,所以说这个角也是三十度,那么就可以得到对边斜边的一半 啊,所以这三边关系是可以清楚的啊,一比二比根号三啊,一比二比根号三,那我要求的是第一的长度啊,给的这个长度是多少呢?这个长度其实就是啊,之前刚讲的就是这个长度,就是 ab 这个长度啊, 因为这个边都是不变的,都是不变的。刚刚才讲过啊,然后呢,这个边,这个边,这个边都等于这个矩形的这个宽,所以说这个长度就是根号三, 那就因为这是一比二比钢化三,所以很容易得到啊。 d 长度就是二。
297飞镖数学 01:59查看AI文稿AI文稿
01:59查看AI文稿AI文稿这道题呢,是我的学生问我的一道月考选填压轴题,据说啊,班里面百分之九十的孩子都没做出来。已知呢,这里有两个三角板,一个是四十五、四十五九十的,一个是三十六十九十的,而且还知道呢,这个角 a 是四十度, 求什么呢?求角一加角二加角三的和。这道题啊,该怎么去处理呢?首先啊,咱们来看这里的角一和角二啊,其实他俩组合起来有点像我们之前学过的飞镖模型,长成这样的就是一个小飞镖。那飞镖模型的结论呢,是,这三个尖角 加起来等于这个角一,三个臭皮匠顶个诸葛亮可以用外角去正啊,会正的写在评论区。那么我们再看啊,这是一个角一,这是一个角二。如果我想构造出来一个飞镖,我是不可以延长 mf 和 ba 交于一个点,延长 b a 和 m f 之后呢,交一点 q。 这样的话啊,我们把之前的角一、角二、角三设为阿尔法贝塔和伽玛,现在要求他仨的和。咱们发现啊,这个阿尔法加贝塔加角 q 哎, 由飞镖模型可以得到他们仨的盒就等于这个六十度。那现在咱们要找阿尔法贝塔和伽马的盒,我们就要把这个角 q 呢往这个伽马去转化。那咱们来看一下,这个角是伽马,这个角四十五度,那伽马加这个小踮脚是四十五度,所以小踮脚可以表示为四十五度减。伽马 同理啊,对顶角相等,这个小点角也可以表示为四十五度减。嘎嘛,那么我们发现这是四十度,这个小点角加角 q 是不等于四十,所以角 q 其实可以表示为四十度减去四十五度,减嘎 化简一下可以得到角 q 就是伽玛减五度,所以咱们现在可以把角 q 直接替换成伽玛减五度。那这样的话啊,整理一下你会发现阿尔法加贝塔加伽玛就等于六十五度,所以用模型啊,可以帮助我们想出来难题。辅助线的思路你听懂了吗?
2136甜心讲数学 31:54查看AI文稿AI文稿
31:54查看AI文稿AI文稿大家好,我是专治数学压轴的杨玉青,今天给大家带来的是二零二五太原市外国语学校初二月考的十五题。 这道题是一个非常经典的线段计算问题,与中考命题思路极其接近,同时也包含了我们上课所讲到的全部方法,接下来我将以六种方法来对它进行攻破讲解。 首先我们先把题目看一遍,在三角形 a、 b、 c 中, ab 等于 ac 等于四, 给出了等腰三角形,同时 b、 a、 c 是 九十度,这是一个直角点, d 是 bc 上的一点 c、 d 是 小于 b、 d 的 点 d, 它靠近 c 一 点,同时呢,过点 c 做 ad, 呃,做 c、 f 垂直 ad 做了一个垂线,然后与 a、 d 的 延长线交于点 f, 过点 b 做 b, e 平行 c、 f 这里做了一个平行线,那同时肯定也是垂线了。好,就这么多信息, 其实核心我们来整理一下啊,整理一下一个等腰直角三角形 b, 点是斜边上一点,然后同时过 b 和过 c, 分 别向 a、 d 做两条垂线,就这样, 然后给了一个数据, a、 d 等于二分之五倍,根号二, a、 d 的 长是已知的,这个长是二分之五倍根号二。这个数字有点恶心,那没关系,最后求的是 c、 f 的 长, 那我们看到这种题,一般来说它的入手点,它的思路在哪里呢?这个题有个非常特明显的特征,就是等腰直角三角形 三角形 a、 b、 c 是 等腰直角,那他是等腰,所以三线合一就是他一个非常重要的命题思路。所以我们这种题拿到以后,包括我们期中,包括我们中考,看到了等腰三角形的填空题,那么要不自觉的把这个三线合一给做出来, 过 a 点去做 b、 c 的 垂线,好,假设垂足为 m, 得到三线合一以后,我们结合题目来看能得到哪些信息。 等腰直角三角形,那么知道了这边是四,这边是四,所以这边应该是四倍根号二。三线合一切开以后,两个短边各自应该是二倍根号二, 那同时左边这个小三角形也是一个等腰直角,它的三线合一长度也是二倍根号二,那这边也是二倍根号二。这是我们看到的, 在结合题中给了一个 a、 d 是 二分之五倍根号二,所以说我们还可以到这个 a d 的 长好,这个长度就等于二分之五倍根号二, 所以你只需要把这个条件标一标,我们就立马可以发现,通过二分之五倍根号二,通过二倍根号二就可以得到 dm 的 长固定。 所以三线合一这个辅助线一做,基本上这个信息就又会增加, ok 吧? bm 的 糖,那我们来简单算一下啊,一个是二分之五倍根号二,一个是二倍根号二,它作为斜边,它作为直角边,要求第三条直角边, 当然勾股定律的话,就是它平方减去它平方,然后再开方就是第三个直角边。但是我们说这样做的话,计算量会更大一点嘛,所以最好是能同扩倍,同缩倍。会简单一点,你比如说根号二,我可以都提出来, 然后呢再把这个二分之也提出来,如果把二分之根号二提出来的话,那么第一个斜边他就会变成二分之根号二乘五,那第二个呢?就变成了二分之根号二乘四,这样能还原回二倍根号二, 那第三个肯定也是二分之根号二乘一个数,这个数的话,五四,那直角边肯定是三了嘛,就是一个三四五三角形,所以这个直角边的长度是二分之三倍根号二,也就是 dm 的 长, dm 的 长就等于二分之三倍根号二。同时呢,还可以得到 cd 总长度是二倍根号二,左边已经占了二分之三倍根号二了,所以 cd 应该也能求用二倍根号二一减即可, 那 cd 就 等于二倍根号二,减二分之三,也就是乘二分之一倍根号二。这是我们通过 做三线合一得到的一些进一步的结论,而这也是所有的方法解决的一个大前提,你先得把条件去往下推进一步,才能进一步去分析。 我们把这个计算过程擦掉,来看接下来的处理方式。现在的情况就是,我已知了 c、 d 和 dm 的 一个长 题目,求的是 c f。 好 了,接下来我们开始想方法了,想方法了,我们知道啊,在初二阶段遇到线段计算,其实主要着重于两个方法,一个叫勾股方程,一个叫面积法。所以第一个我们可以尝试的就是勾股方程。 法一,可以尝试一下勾股方程这个方法。勾股方程需要在三角形中去设 x, 然后列方程嘛,那你得先选定三角形。现在的情况是,这条 a d 边是已知的,然后呢,这条 a、 c 和 c、 d 也是一致的, 但是呢,这个 c f 未知,同时这个 d、 f 也未知,所以这比较符合勾股方程的。第二种情况回答,有没有这种很强烈的直觉?第二种情况,两个具有共边的直角三角形是可以采用勾股方程的。 两个具有共边的这造型,一个是 r t 三角形 a c f, 一个是 r t 三角形 d c f 这个造型,借助这个直角以及下面这个造型,借助这个直角 的共边就是 c f, 而我一旦把这个 b f 设做 x 的 话呢?好,那剩下的边就可以表示了, d f 是 x 的 话, c f 这个边在 c d f 中, c f 的 边就应该是 dc 方减 x 方嘛,而 dc 我 们刚求出来是二分之根号二,所以来解一下, c f 的 平方就等于二分之根号二的平方,然后减去一个 x 方,这是在下面这个这造型, 你再放到大的三角形 a c f 中,这条 a c 长度等于四,那同时呢,这个 a d 长是二分之五倍根号二,所以也是一样的四的平方,把这个边的长度平方一剪即可, 所以还是 c f 方, c f 方,它就会等于四的平方减去 x, 加上一个二分之五倍根号二的平方, 进而通过 c f 方做桥梁,得到了四方减 x 加二分之五倍根号二的平方,这个结果等于二分之根号二的平方减 x 的 平方。 所以这是一个非常标准的两个共边直角三角形下的巩固方程。其实思路部分只要复习到这里,这个题就结束了, 只是同学们看起来这个题好像计算量稍微有一点点大啊,没关系啊,计算量大的题目一定要耐着性子往下算,不要着急,你去算,一步一步的去写草稿纸上 四四十六,减去一个,展开 x 平方,减五倍根号二, x 再减去一个二分之根号二平方以后是二分之一嘛,五的平方是二十五, 这就是左边,右边的话呢?二分之一减去一个 x 的 平方, 那不出意料,减 x 平方,减 x 平方,可以互相抵消掉,剩下的我们来合并,合并啊,把它放到右边,变成五倍根号二 x, 把二分之一挪过来,变成十六,减二分之二十五,再减去二分之一, 这两个可以先算一下,合起来是二分之二十六,也就是十三。十六减十三,结果是个三,因此三就等于五倍根号二 x, 所以 最终得到 x 等于 三,除以五倍根号二。化简一下,十分之三倍根号二。 ok, 那 我们再看,现在你求到的是 x x, 而我不是要求 x, 我 求的是 c f, 对 吧? c f, 所以 我们只需要在 r t 三角形 c d f 中用一次固定即可。 你的 c d 长度是二分之根号二,然后这个 d f 长度是十分之三倍根号二。 这里还是那句话啊,就是用勾股定律算的时候,遇到数据比较恶心的情况下,不要直接算,而是给他取一个公共的,给他提出来,你的十分之三倍根号二,我可以把十倍根号二提出来乘三,你的二分之根号二,我也可以强行变成十分之 四啊。十分之五倍根号二,十分之五倍根号二,即二分之根号二嘛。所以提出十分之根号二,就变成了五,也就是十分之根号二。乘 五,斜边是五,这个边是三,所以呢,三四五,因此就可以很自然的得到。其实 c f 的 长就等于十分之根号二,乘上一个四,化解就是五分之二倍根号二, 所以这个题就结束了,计算上来讲的话,可能有一点点计算量大,但是你按照我们讲的同扩倍同缩倍的这个思路去做的话,还好,没有那么难算。 以及方法层面的话,三线合一是必备的,但是勾股方程是我们这学期所有十五题的一个首选方法,期末考试同样适用。 这是第一个方法好。第二个,假如我没有想到过股方程,或者说我不想使用过股方程,没关系,因为做这个实物题的时候,第二种思路就是用 面积法来算,但是前提不会变啊,前提一定是三线合一下,已经把这个题的条件进一步做推进了,这个 c d 等于二分之根,号二,这一步已经推进了,才可以继续往下做。所以方法二是面积法。等面积 怎么去做?那你就找三角形呗,因为这个题垂线挺多的,垂线多了自然而然可以想到用底层高做面积了嘛。我们还是把辅助线画出来,这个焦点依然设作 m, 那我只需要盯住这个三角形 a、 c、 d 去思考等面积就行了,也就是 s。 三角形 a、 c d, 它的面积首先能看到底乘高, c d 这个底乘上 am, 这个高就是它的面积, 所以写出来等于二分之一乘 cd, 再乘上一个 am, 同时我换个方向比乘高,我还可以以 a d 为底,那过 c 点做垂线就是这个 c f, 所以 a d 乘 c f 也是它的比乘高,因此它的面积还可以表示乘二分之一,乘 a d 乘 c f, 你要求的是 c f, 所以 我只需要把这三个值代入即可。你看看题中都已知了没,这个二分之一就不用管了。 c、 d、 c、 d 我 们说刚才三线合一推进下已经算出来了嘛, c、 d 是 二分之根号二 am, am 好 求,刚才就求过了,是二倍根号二,然后等于来 ad, ad 是 题中给的二分之五倍根号二 乘 c、 f, 所以 这个方法其实算起来是最简单的。 c、 f 等于把二分之根号二约一下, 它和这边的二分之根号就抵消了嘛,然后这边是二倍根号二,把这个五除过来就行了,所以直接计算量也很小。答案就是五分之二倍根号二, 这是这个题最简单的方法,也不超纲,计算量还小,但是取而代之的是这种思路其实不太好想,我们是硬硬的在想这个等面积,选择了三角形 a、 c、 d 的 面积,实际上的话不太好想啊,真正考场上我觉得没几个同学应该能想到, 那么我们进一步去推进真正的面积法,相对来说思路层面比较好想的就是好想一点的。你是?呃,不是选择这个三角形 a、 c、 d, 而是选这个三角形 a、 b、 d 相对来说好想一点,因为这个 a、 c、 d 作为钝角三角形,它的两条高都在外部,其实我们很难有一个整体性的思考,但是啊,好第三个方法。但是如果我考虑的是这个三角形 a、 b、 d 的 话,那就不一样了。对于这个三角形 a、 b、 d 来讲,它的两条高线已经都爆出来了,一条是 b, 另一条是 am, 所以 对着它用面积法。这个思路相对好想一点,但是好想的代价就是它的计算量也好,它的这个四就是这个转化也好,要稍微麻烦一些。 我们也说一下这个方法啊,法三,法三,这个面积法,它不是纯粹的面积法,它还需要我们看到一个东西叫做一线三垂直, 一线三垂直,因为在等腰直角中,本身我们就比较容易垂三垂直,再加上它这里做了两条垂线,所以它其实这幅图就是一个内三垂的模型。 一线三垂直指的是直角垂直、垂直这条线上的三个垂直,所以三垂直带来的是三角形的全等, 这个三角形和这个三角形这是一对全等三角形,我们解出来三角形 a、 b、 e 全等于三角形 c、 a、 f。 有 了这一对全等以后,能够实现一些线段的转移。我本来求的是 c、 f, 我 求 a、 e 就 可以了, 相对来讲可能会好处理一点,但是 a、 e 也不好直接求呀,没关系,因为你的 a、 b、 四是已知的,只要知道 b、 e 就是 刚才我们说的这个三角形的高,只要知道了 b、 e 勾股定律,即可以求 a、 e。 这是一个方法,那计算量上来讲的话,可能会稍微大一点,因为同样是面积啊,我们求 a 三角形 a、 b、 d 的 面积,它等于二分之一。选 b、 d 为底啊, b、 d 为底的话,二分之一乘 b、 d, 再乘上一个 am, 就 等于二分之一,乘上一个 a、 d, 乘上一个 b、 e。 你看数据往前带二分之一,不用管这里的 b、 d、 b、 d 的 话,刚才我们通过三线合一推进,已经求出来 m、 d 是 二分之三倍根号二,而这里是二倍根号二,所以 b、 d 的 长合起来一共是二分之七倍根号二, b、 d 是 一致的, 乘上 am 还是二倍根号二,然后等于 ad 长,其中是给的二分之五倍根号二, 然后再乘上一个 b 一, 可以看得到这个计算量要比刚才稍微大上一点点了。我们还是把这个二分之根号二,二分之根号二来做一个抵消,所以这里的 b 一 长, b 一 长就应该等于十四倍根号二除以一个。 接下来就是最后的勾股方程。勾股方程勾股定律在三角形 r p 三角形 a、 b、 e 中用 a b 方减 b e 方, a b 的 长度是四, b e 的 长度有点恶心,是个五分之十四倍根号二,不过还是按照同扩倍缩倍的原则,尽量不要吃这种恶心的东西嘛, 对吧?我们写出来四和五分之十四倍根号二,你不喜欢五分之一,你把他五分之一弄走,他就是五分之一乘十四倍根号二,那他如果强行弄走五分之一的话,变成五分之一乘二十, 然后二十和十四,又可以把二提走。所以说五分之二乘上一个 五十,他是五分之二乘上一个七倍根号二。其实你还可以进一步去提,你不喜欢这根号二,你甚至可以把根号二弄走,变成五分之二倍根号二乘七。 而他如果强行提走一个根号二的话,那还剩一个五倍根号二, 所以前面可以变成五分之二倍根号二,再乘上一个五倍根号二,这样的话就基本到极限了,我们只需要拿五倍根号二和七去勾股定律即可,所以结果一定是五分之二倍根号二乘他们两个勾股定律的一个结果。 五倍根号二的平方是一个五十七的平方是个四十九,那五十减四十九刚好等于一了嘛,所以开方还是一,因此的话,结果就是五分之根号二乘一,答案还是五分之根号二。 o 五分之二百根号二,只是这个计算量上稍微大了一点,但相对好想,主要还是因为这是一个锐角三角形,并且两条高相对来说比较明显一点,比刚才的那个钝角三角形要稍微容易考虑一些。 好,这就是第三个方法。那这三个方法不管你选择哪一个,这都是我们初二阶段应该想到的,要么公共方程,要么等面积。 但是如果你提前接触了一点相似的知识以后,那这个题难度立马就降低了,就又变得不一样了,所以适当的超前学习还是有一定帮助的。假如我们学过相似,那这个题就又是别有一番景象来,法四 法四,通过相似的手段来做一下,相似也好,三角函数也好,其实都差不多啊,理解,理解上来讲的话, 区别不大。我们来看这个题还是前面推进,推进到 b d 和 c d 已经求出来了, 已经求出来,这个是大前提啊,大前提。我们在做完三线合一以后,可以发现,这个 am 的 长是二倍根号二, ad 的 长是二分之五倍根号二, md 的 长是二分之三倍根号二。所以这个三角形的三边之比就是一个三比四比五, 也就是我们传说中的三比四比五,三四五三角形。你看这个二倍根号二,它就是二分之四倍根号二。 而三四五的三角形的话,那这个三角形和这个三角形很容易就可以证明成四, 它两个相似,说明这个三角形也是一个三比四比五的三角形。 cdf cdf 它的三边之比 d f 比上 c, f 比上 cd 等于三比四比五。 而 c、 d 是 已知的呀, c、 d 这个长度刚才求出来是二分之根号二, 那至于 d、 f、 c、 f 都能求了, c、 d 会做的是五份吗?那 c、 f 做的是四份,所以一句话, c、 f 就 等于 c、 d 二分之根号二,乘上一个五分之四,答案就是五分之二倍根号二。 学过相似竟然如此的轻松。当然了,嗯,做这个题的时候肯定是没学过的嘛。 包括相似。还有一个操作,就是你结合刚才的三垂直,也能再带一个相似。相似里面有一个比较容易看到的,就是这里的八字相似,这个是很容易发现的 八字相似,所以说法五我们也是结合了相似,但是还把三垂直给它融进来了。三垂直加相似,这个相似是一个八字形的相似。 这两个三角形由于都是垂直,它们两个相似,相似以后,那么对应边成比例, 在我们三线和已经推进的情况下,这个 b、 d 的 长和 c、 d 的 长全部算出来了。 b、 d 是 一个二分之七倍根号二, c、 d 是 二分之根号二,所以整个比例应该是七比一。这个是直白的,我们求得 b、 d、 c、 d, 所以 它俩的比例 b、 d 比 c、 d 等于七比一, 就意味着这个三角形其他边的比例也是七比一。那假设 c、 f 如果是 x 的 话, b、 e 的 长就应该是七 x。 好, 接下来你再看,由于三角形 a、 b、 e 三垂直之下,三角形 a、 b、 e 全等于三角形 c af, 所以你这个边是 x, 那 上面的 a, e 也是 x, 这个地方也是 x, 而 ab 长度是四,所以直接在这个象形中勾股定律即可列勾股方程 r t 三角形 a b e 中 x 的 平方加上七 x 的 平方等于四的平方。好了解出来 x 就 结束, 这个一共是多少呢?四十九 x 平方加上它五十 x 平方等于十六,所以 x 平方等于二十五分之四啊,不是四,二十五分之八,所以开放以后 x 就 等于五分之二倍根号二。 这种方法是融合了相似,融合了三垂直线,又是一个别出心裁的思路。 第五种了,但这两种方法结合的相似的话,都算是超纲了。最后我们再说一个竖形结合的方法,就是传说中的间系法法六 间隙到了初三以后,大家就会口口相传一句话,遇事不决就间隙,不会做了就间隙啊。当然你平面这条坐标系学的足够棒,一次函数学的足够扎实的话,间隙能解决很多很多的问题的。 建立坐标系求 c f, 那 本质上就是求 c 和 f 的 坐标即可。那这个间隙由于是等腰直角,非常的规矩,所以我们就直接以 a 叠所在直线来做一个呃, y 轴, d, c 所在直线做一个 x 轴好了,间隙 就可以了。只是啊,间隙的计算量一般都比较大。在我们知道这个 a, 这里是 o 吧,不要用 m 了, a 点坐标就是零到二倍根号二, 然后知道了这个 o d 的 长是二分之三倍根号二以后,那么 d 点坐标就是二分之三倍根号二到零。 c 点呢,就是二倍根号二到零,其他的暂时用不着, 那 f 点的坐标只要求出来,根据距离公式就可以求 c f 的 长了。那 f 怎么求呢?看它的来源。 f 是 a d 和 c f 的 一个焦点,所以我只需要求 a d 和 c f 的 极值即可。 a、 d 的 话,由于一个点两个点是不都已知了?两个点已知,所以我们可以用代定系数法来求一下。函数解析式,假设 a、 d 是 y 等于 k, x 加 b, 并且 k 等于零,你往前带, 由于这个是零到二倍根号二,所以这个 b 相当于是白给了 b 就是 二倍根号二,那我只要把 二分之三倍根号二到零代入即可。所以零就等于二分之三倍根号二乘 k, 然后再加二倍根号二,那算一下,所以这个 k 值 k, 它应该等于 根号二,根号就抵消了嘛。二分之三 k, k 就 等于负二乘上一个三分之二,所以是负的三分之四啊,计算算算对就好了, 所以结果是负的三分之四。因此 a、 d 的 解析式, y 等于负的三分之四 x 再加上一个二倍根号二,搞定 a d 了, 下一个要搞定 c f, c、 f 的 话,知道一个点是二倍根号二豆离,但是另一个未知了。 我们可以结合斜率的 k 乘 k 等于负一,因为你的 c f 是 和 a、 d 垂直的,所以斜率乘积是负一,现在 a、 d 的 斜率是负的三分之四,所以 c、 f 的 斜率呢,就是正的四分之三,乘积得保证是负一。正的四分之三 x 加上一个 b, 然后把二倍根号二到零代入,再二倍根号二到零,往低一代的话,零就等于四分之三乘二倍根号二,再加 b, 所以 这个 b 其实不难求。 b 等于负的二分之三倍根号二,所以 c f 解析式 y 就 等于四分之三 x 减二分之三倍根号二。 所以你看,算出来解析式这只是第一步,因为 f 的 坐标是两个解析式的焦点,所以还得再算焦点。那这个计算量一看就有一点点恶心了,我帮大家耐着性子算一算啊。 好,接下来连力啊,连力,连力!求 f 的 话,负的三分之四 x 加上二倍根号二,就等于四分之三 x 减去二分之三倍根号二,把它挪过来,把这个挪过去 二分之九 x 加上一个十二分之十六 x, 二倍根号二,加上二分之三倍根号二,合起来二分之七倍根号二,就等于十二分之二十五 x, 好,再去约啊,二和十二约掉剩一个六,所以六乘七四十二倍根号二,除以二十五就等于 x。 天呐,这个计算量是不是吓到了? 还得求外带一个外等于,比如说我们带这个关系式啊,负的三分之四乘上二十五分之四十二倍根号二,再加上一个二倍根号二,算这个结果。这里开始约分 三和四十二,约调是一个十四,四和十四是五十六,也就是二十五分之五十六倍根号二。注意,前面还有个负号,负的二倍根号二就是二十五分之五十倍根号二。 好,负五十六五十,那就是余了个六,负的二十五分之六倍根号二。 终于算完坐标了,所以 f 点的坐标应该是横坐标二十五分之四十二倍根号二,纵坐标负的二十五分之六倍根号二。接下来 c f 的 长只需要用距离公式,哎呀,即可。 距离公式 c 点坐标,二倍根号二。逗,零开始减啊,它二倍根号二减这个东西, 二倍根号二,减二十五分之四十二倍根号二,他的平方再加上零减这个东西,那这个倒好,算二十五分之六倍根号二的平方再开放。 还是那句话,不要傻乎乎的算,你去给他同扩倍同缩倍去啊。先把这个东西算出来,二倍根号二,也就是二十五分之五十倍根号二,再减去二十五分之四十二倍根号二,那么最后会剩下 八倍,也就是这个东西相当于是二十五分之八倍根号二,而这里是二十五分之六倍根号二,有没有很熟悉? 二十五分之八倍根号二,二十五分之六倍根号二。你把二十五分之根号二给他弄出去嘛。八六平方平方相加,所以六八十嘛,所以结果肯定是二十五分之十倍根号二。 你不要那么蛮算嘛,还是那个同扩倍的技巧,二十五二十五分之十,约分一下就是五分之二,所以五分之二倍根号二,结果五分之二倍根号二。 好吧,帮大家算过了,间隙能做,就是这个计算量有点超乎寻常了,我们不是很建议他,除非我其他题全做完了,留的时间还比较充足,那这样做也没什么问题, 间隙所体现的主要还是以数形结合,而且需要你非常扎实的依次函数的功底。因为我们所见的图形线段计算都是直线形的,没有曲边直线形的,那放到坐标系中全部都是依次函数,依次函数过关才能够使用这个方法, 当然看到这个计算量会劝退很多同学的,那我们今天的内容就到此结束。
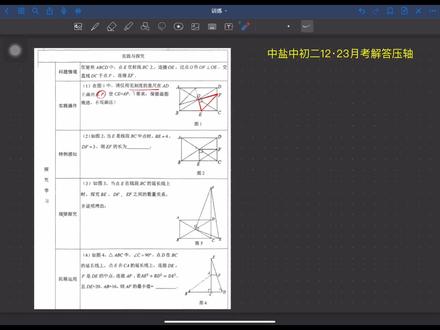 03:51查看AI文稿AI文稿
03:51查看AI文稿AI文稿好,我们看一下中一中初二的十二月二十三号月考的解答。最后一题,在矩形 a、 b、 c、 d 当中, 点 e 呢?是在射线 b c 上面连接 o e, 过点 o 做 o f 垂直, o e 交 dc 于点 f。 第一问是要找到一个 a d 上的一个 p 点,使得 ap 等于 c e, 那 这边利用这个中心对称的性质,连接 o 点,是这个矩形的对称中心,所以连接 e o 就 可以了。交 a d 的 这个点啊,就是 p 点,很简单 啊。第二题,如图二,当点 e 呢,在线段 bc 上面的时候啊,这个地方是中点,那么这边都垂直啊,三线合一啊,矩形的这一个 六角形相等,互相平分,然后三角形中点,所以说三线合一,所以说它垂直,那它就是个矩形啊,矩形那就清楚了啊,这边就是三四,那这边也是四啊,这个地方也是三,所以很能得到 e f 长度是五。 第三题的思路呢,就还是利用这个中心对称的性质啊。第三题,第三题发现这个 e 点跑到了 b c 的 延长线上,但即便 o f 还是垂直的, o f f 是 这个 c d 延长线上,求证这个 c e 啊, b e 和这个 d f 还有 呃 ef 的 这三条边的一个数量关系,那根据这个中心对称的话,所以说我们要把 o e 延长出去, o e 延长交 d a 啊,与点 p, 就是 我们这个第一问当中这个 p 点,那根据这个对称的话,我们是能得到这个 o p 是 等于 o e 的, 而这个量是垂直,所以说它是垂直平分线啊,连接 ef, 连接这个 p f, 所以 说很能得到,这是一个等腰三角形,那就会把 e f 转到这个 p f 这边当中去,那又因为这个中心对称呢?所以说 b e 是 等于这个 p d 的, b e 等于 p d 啊,因为这个地方是这两三角形全等嘛 啊,也就是 p d o 和 b o e 是 全等的,所以说 b e 就 转到 p d 这边,而 d、 f 还在这里,而 e、 f 又转到这个 p f 这当中,所以说三边的关系就出来了啊, 勾股定律啊,也就是 b e 的 平方加上 d f 的 平方等于 ef 的 平方,第三问的话也是第四。最后一问也是建立在第三问基础上啊,他,他会给你这样一个结论啊,所以说我们就围绕这个第三问构造一个跟第三问长得差不多的, 那我们过 b 做垂线,过 a 做垂线啊,构造出这个啊,矩形,然后呢连接对角线, 连接对角线,交点交点,连完之后,那么就得到这个 o e 是 垂直 o d 的 啊,垂直 o d, 那 根据之前的思路,一样的话,根据之前的思路,那所以说我们能求出这个 啊,这个地方是垂直啊,垂直,然后现在给了一个 f 是 d e 的 这个中点, d e 长度不变,是二十,那么中点一半就是十,所以你会发现 o f 的 长度是不变的,用斜边中线去求的话, o f 长度是十, 又给了一个 a, b 是 十六,那么对角线互相平分,所以说 o a 长度是八, o a 的 长度是八, 那它要求的这个 a f 最小值就很明显了,就是当这个 a 点运动到 o f 上面时啊,此时 a f 最小啊,最小,那 a f 长度就是二啊,最小值是二。
100飞镖数学 03:37查看AI文稿AI文稿
03:37查看AI文稿AI文稿来港中和田中八年级这次月考数学试卷的最后一道大题,今天刚考完的,请问你做对了吗?我们一起来看一下啊。第一位呢,说给了这样的一个式子,让我们求 ab 两个点的坐标。 很明显,我们把二 ab 拿到左边来,和 a 方加 b 方构成了一个完全平方式,得到的是 a 减 b 的 平方, 那么它加上它等于零,非负数的和等于零,每一个都等于零,得到了 a 和 b 呢,都等于十三,所以说 a、 b 的 两个点的坐标呀,也就知道了, a 点呢是十三,零, b 点呢是零。逗号十三。好, 那么我们看第二问,第二问呢,给的是 o、 c 等于 dc, 我 们看一下 o、 c 等于 dc, 这是一个等腰三角形, 还给了 b, c 垂直于 o c, 我 们看 b, c 垂直于 o、 c, 这是一个直角三角形,求证的是 b c 等于 c e。 好, 我们要证明两条线段相等,我们首先考虑到的是全等,那么我们仔细看一下啊, b、 c 和 c、 e 所在的三角形,基本上是不可能全等的,那么接下来我们仔细看,那么 b、 c 和 c、 e 在 同一个三角形里面,考虑到角对不对,我们利用角相等,然后得到边相等啊, 那么我们看一下啊,这里既然给了这个 o、 c 等于 dc, 也就得到了这两个底角相等,我们不妨设为二法, 那么这里是九十度,所以说这个小角呢,应该是九十度减二法,接下来 o、 b、 c 也是二法,我们标记一下,这个角呢,也是二法。然后我们看一下角, c、 b、 e 写一写角, c、 b、 e 就 等二 f 减去四十五度。 接下来我们再看这边啊,因为这个 e、 d、 o 是 二 f, 同时又是 e、 a、 d 的 一个外角,那么我们得到了角 d、 e、 a 也就等于二 f 减去四十五度。 看一下啊,这里是阿尔法,是这个三角形的一个外角,这个角呢,是四十五度,所以说这个角是阿尔法减四十五度,因为对顶角 得到了 c、 e、 b, 也是阿尔法减四十五度,所以说我们进而就可以得到角 c、 b, e 等于角 c、 e、 b。 所以 说我们这个结论就得到了证明。 接下来啊,我们看一下第三问,第三问其实比第二问呢要简单一些说, bc 等于五, d, e 等于七,根据第二问的条件,求 a 到 o、 c 的 距离。我们看一下啊,他给了 bc 呢,是个五, 也就是 c, e 是 个五。根据第二问啊, d、 e 是 个七,给的 d, e 是 个七。好,那么我们看一下整个 c、 d, 我写一写就等于五加七十二,那么 c、 o 肯定也等于十二了。 现在让我们求的是 a 到 o、 c 的 距离,我已经做上了啊, a 到 o、 c 的 距离是这个 af 的 长度啊,那么这个 af 的 长度怎么求呢?很明显,三角形 o、 a、 f 和三角形 o、 c、 b 是 全等的, 全等之后要求的这个 a、 f 的 长度自然就等于 o、 c 的 长度,所以说这个 a 到 o、 c 的 距离呢,就是十二,那么你做对了吗?
90大刚数理化
猜你喜欢
- 1575草包1号











