毕老师讲初中数学几何旋转

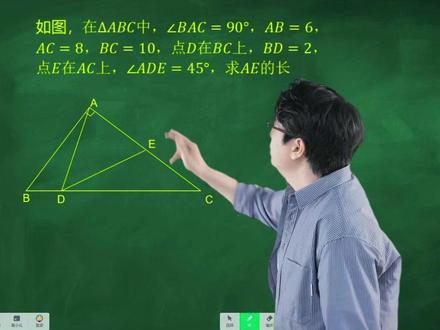
说在一个三角形 a、 b、 c 中角， b a、 c 等于九十度，嗯，这块是九十，紧接着 a、 b 这边得六， a、 c 这边等于八。啊，那根据勾股定律，其实这边已经得十了，对吗？啊，但是人 家怕你勾股定律没学过，给你补充了一个， b、 c 得十，所以这一定是八上咱们这个学期的考题了，对吧？啊，那咱就用八上的知识给它解决掉。好吧，一起来看。说，第一点，在这个线上， 然后 b、 d 这边得二，紧接着又告诉我们这块有一个四十五度，最后问我们 a、 e 这个边长 等于几？首先第一个技巧来了，很多同学为什么看见这题只能看见四十五度呢？然后在四十五度上去寻找突破口呢？是因为你没有一个好的做标记的习惯。毕老师教大家一句话，记下去，好吧，这句话就叫做 同一条直线的线段长，我们标短的，比如说 bc 这条线是不是得十啊？我这小段是不是得二？这十我直接标这上吗？不，我标短的，你是二，整个十，短的这段得几，这一段 就得八。那为什么这么样做标记会好呢？大家来看，你得八，我这是不是也得八呀？哦，所以我这个白色的三角形，它是个啥呀？ 他是个等腰三角形。那作为一个等腰三角形， 我们有一种辅助线的方法，就是已知等腰造对称。哎， 我是个等腰三角形，我本身三线合一为什么这么重要啊？因为三线合一这条线就是对称轴啊，所以你这边有一个什么样的三角形，我对称一下，这边我就可以做一个一模一样的全等。 比如说大家，我这白色的是等腰吧？哦，你这边要求 a e， 你 a e 在 哪啊？ a e 是 不是在这个三角形中啊？那我就给你对称过来，搁这边造一个点 f 啊，我让这个 df 这一段跟你这段相等，可以吗？咱们两个相等啊，公共边也相等，那等腰这两个底角是不是还相等啊？所以啊， s a s s a s 这两个三角形是不是瞬间就全等了啊？ 那要求 a e 的 长，其实就是求 b f 的 长啊。所以这道题关键的辅助线咱就做完了。那接下来再应该怎么解决呢？还是做题的习惯？刚刚毕老师教大家了一个好习惯，叫同一条直线线的长标短的吧。 还有第二个，那就是求边先求角，各位说，我们等腰用来干嘛的？倒角了，四十五度还可以用来干嘛？倒角了吧。所以我这道题我可以倒倒角相等啊。那已知角度求角度，咱就求每个未知呢？咱就设阿尔法贝塔。比如说，各位 说你是四十五度，这个三角形还跟他全等对称的，那我这边这个角就得多少， 那当然得四十五喽，是吧，那你俩都得四十五，这个角就得多少，就得九十呗，是这个道理吧。好，接下来大家来看。 说我让这个角是阿尔法，那你这个角是阿尔法，这角是九十，所以我这个角一是不是就等于九十度减阿尔法呀？根据三角形，全等角一跟角二什么关系？相等吧，所以角二它也得四十五度 减二法，不仅他得四十五度减二法，大家再来给我看，我这个大角得还得九十呢，我还没用呢，大角得九十，这是二法，那这边这个角一样得多少啊？ 九十多减二法吧，你是九十减二法，我也是九十减二法，咱俩相等，等角反过来就对等边，所以要求编程先求角度，一旦知道这个角了，大家，你是六，我这就是六，这小段得二，六减二，剩这问号就得四，所以这道题 瞬间解决了。所以大家记住了，不要见着四十五度就特别激动，一定要照等腰直。你要看看这题还有别的条件没？已知等腰的时候，我还可以照对称，毕老师说清楚了吗？当然，这道题如果你这么做，以它为 哎底角造一个等腰直也是可以的，但是你要知道等腰直的本质是什么？是把这条边旋转过来九十度，那你这边旋转过来九十度，这个边是不是就可以带着一个三角形整个转九十啊？所以在这边截一个六， 六跟六相等。哦，那我这个三角形都能转过来。好吧，那这段得二，这段得二，你再通过倒角倒出来，这段得二也是可以的啊，整个是六，减掉这二依然等于四。但更狠的还有一种思路， 各位，这学期你们是不是都学了一个知识，叫依次函数啊？各位，当一个题我们一点辅助线的思路都没有的时候，毕老师一样能让你得满分。这种方法在这门中考中经常用到，就叫做间隙。各位同学 一起来看，说你这得六，这得八，这得十，那我如果做一个高的话，根据等面积法， 十乘以这个 a h 是 不是等于六乘以八啊？所以它就是五分之二十四，这是五分之二十四。整个这个边长我能不能求 固定里或者等面积是不是肯定能求啊？啊，那这个边长等于几呢？算出来，那就应该等于五分之十八，那我再知道这小段的二，也就是说这小段就是五分之八，各位能看懂吗？那这个时候我们怎么办呢？我让他是 x 轴， 我让他是 y 轴，各位能听懂吗？那么我 a 点的坐标就是零，逗号五分之二十四，他已经知道了， 是吧？啊？ c 点坐标呢？你整个得十，这边是五分之八，那这段知不知道啊？知道吧，知道的话 c 点坐标能不能求啊？能求吧，能求的话，那么我红色的这条直线 两点确定一条直线，这条直线解析式是不是就知道了？哦，那你想求这段长，我 a 点知道，我只要知道 e 点坐标，两点坐标是不是距离就能算出来那 e 点是谁？是这条线跟它的焦点吧。 那你想确定第一这条线只需确定这条直线上的几个点，两个点就行吧。哦，第一个点就是地点本身，是不是啊？地点本身负的五十八，逗号零，我们都知道了，那另外一个点在哪啊？各位回答我还有哪个关键的条件没用上啊？ 嘿，是不是这个四十五度没用上啊？啊？你是四十五度，我怎么用？我是不是可以把它这边做一个四十五，相当于把这个家伙怎么样？ 旋转九十度吧。啊，既然你旋转九十度，那我是不是可以把这个三角形直接转九十过来就得了？所以横向五分之二十四，纵向 五分之八，明白了吗？ a 点向右五分之二十四，向下五分之八个单位，所以这个点坐标是不可求，两点再次确定一条直线，两条直线一连力，这个点坐标就来了 啊。所以这个间隙的方法是这类问题的必杀技，所有的辅助线我们都不会，我们也能把它给做出来。但是 各位，显然第一种方法毕老师教大家做辅助线方法怎么样？巧妙巧妙，计算量就小，但是那种方法你得系统的跟老毕学，你才具备这个思维，因为他比较难想。好吧，那么最后一种方法是人人都能想到，但是他的计算量怎么样？极大，所以两种方法各有 巧妙不同。当然这道题还有更多的方法，也欢迎各位同学在底下评论区刷出来你的辅助线方案。

今年中考压轴题又来了，结果我们定睛一看，哎，毕老师讲过的奔驰模型也叫做三角形。放屁问题 说我一个正方形 a、 b、 c、 d 里边有个点 p p a 得九， p b 得四， p c 得七，对吗？实际上和说等腰直角三角形 a、 b、 c 里面有个点 p 三边长都已知，是不是一模一样啊？那么长成这一种的是不是长得像奔驰车标？哎，我们的奔驰模型，奔驰模型到底怎么做呢？已知等腰直，当然应该再造一个等腰直，所以这题的辅助线，哎，就是这样。接下来我们把边长数据给标上去，首先 它是等腰值， a、 b、 c 连上也是等腰值，那么我们就能得到小的边长相，等，大的边长 相等大角九十度，大角九十度减去公共角角一，还等于角二，也就是说 s、 a、 s 这个红色三角形全等于这个红色三角形，对吗？第二步， 那边长各得几呢？我们来算一下，已知他得四，转过来还得四瞪腰直屁屁撇就是四倍根号二。已知他得九，这边等于七，转出去他依然等于七。 七的平方四十九，四倍高二的平方，那就是三十二，两项加在一起刚好等于八十一，也就是九的平方。说白了， 这个平方等于他们俩平方和对应的这个角就应该是九十度，你得九十度，我底下是一个等腰直啊，所以我这个角就是 四十五度，那么整个大角一百三十五，要想求正方形的面积，其实我只需求边长几个，对吗？边长的平方就的面积。那这道题就转化为一个三角形，已知他的四， 他得七，大角得一百三十五，求第三边得几？这就是经典的三角函数解三角形问题，该怎么做呢？已知特殊角就装到直角三角形里，但是这个特殊角是个钝角的话，我们就谦虚 延长一下，我再做一个垂直，因为钝角的五角就是锐角了，这个角显然等于四十五度啊，它的四，所以这边四除以根号二，也就是二倍根号二。同样这边呢，二倍根号二哦，在大直角三角形 amb 中， mb 这个边长二倍根号二， am 这个边长七加二倍根号二，他们平方的加和是不是就等于 ab 这个斜边的平方啊？ 而 ab 的平方恰好就是正方形的面积。所以这道题不用求复合二次根式，直接把答案算出来即可。快速算一下，二倍杠二平方就是八， 完全平方展开七的平方四十九二倍高二平方又是八，两项乘积二倍，二十八倍根号二，把它们都加在一起，那么最终答案就是六十五加上二十八倍根号二，同学们，你做对了吗？

在二二年和二三年的中考题啊，有一个考点突然间比原来考的密度变大了，这个考点叫什么呢？就叫做对角互补。那么今天毕老师就来一道填空压轴题，带大家一起来分析一下。 说，在直角三角形 a b c 中，哎， a b 还等于 a c， 那摆明了他就是一个什么样等腰直角三角形，对吗？啊？紧接着这个角呢，等于九十度，又告诉我们什么呢？啊？ b e 等于 d e， 也就是我这是一个等腰三角形， 最后 a e 这个边长我们是知道的啊， c d 这个边长我们是知道的。其实整个题读到这啊，毫无头绪，哼，因为 所有这些条件都没有告诉我们接下来该怎么办，哎！比如说有同学有一唯一的一个思路，就是等腰围有一个三线合一，对吗？啊，这个等腰值现在还不知道怎么处理，但接下来灵魂的条件就来了，大家是不是有一个非 非常奇怪的两个角相加等于一百八，也就是对角互补啊？当我们有过对角互补的时候，我们就要想一个事，如果他们两个能够通过位置的改变，让他们拼在一起，那么是不是就会有贡献呢？哎，非常棒！那这个就是咱们今天要讲的条件旋转法。 那么何为条件全乘法呢？他一定要有的条件就是边长相等，比如说在我这里面 ab 等于 bc 好，接下来最好有的条件是角 互补，哎，比如说我这里面这两个角相加得一百八，因为只要互补就贡献，说白了，我只需把这个红色三角形给他旋转九十度，那他是不是就跑这来了呀？啊，那具体来说，你这两个角是相等的，我俩相加得一百八，那咱俩相加得一百八呗，咱们相加 得一百八，那么 dc 一撇是不是就贡献了？并且我这小段是不是得二分之高三呢？并且我这个边长是不是就等于这个边长啊？哦，那大家再来看我这个边长 可以装在蓝色的直角三角形中吧。哦，而你这个边长呢？大家还有等腰，我做一个三线合一，是不是也在一个蓝色的直角三角形中啊？所以两个九十度相等，边长相等。再因为 我原来这个三角形是旋转九十度过来的呀，也就是说 b 一和 b 一撇不仅先等，而且垂直，只要他们垂直，这个角一加上这个角二就得九十，而角二加上角三呢，还得九十，所以同一个角的两个余角是不是就相等啊？哦，角一得 小三，九十度得九路斜边还相等 aas， 两个三角形全等，一旦他全等，那么 b 到 m 的距离是不是就等于 d 到一撇的距离，也就是二分之高二加二分之高三？而我整个是等腰， 也就是三线合一， b d 是 b m 的两倍，所以要求就是他们加和的二倍，即根号二加根号三。这道题毕老师讲清楚了没有？

这两天啊，期末考试一考完，全国各个地区的家长卷又炸锅了，尤其是北京海淀，大家都知道， 全国教育看北京，北京教育看海淀，他一定是改革的前沿，他们今年怎么改的，你们明年就会这么考？那今天老毕就给大家讲一下海淀八年级咱们最后一道大压轴，看看你能不能跟毕老师一样，轻松就把他给做出来。 首先孩子在考试的时候遇见了什么事呢？他们首先先来个二十五题，叫做新定义，很多孩子脑子已经在这道题中爆炸了， 爆炸完以后紧接才是这么样一个东西，几何辅助线，如果你家孩子的辅助线一直以来学的方法都是靠蒙猜凑，不好意思，这道题已经跟你无缘了，因为刚刚脑子已经爆炸了，到现在一点缝都没有了。但 如果你家孩子一直以来每一条辅助线的产生都是基于分析的原理呢？哦，那你这道题可以说 是你史上考过最简单的全能辅助线了，差别就在这。所以提醒一下各位家长，都别看热闹，给你们总结一句话，现在咱们的中考改革是重逻辑， 清计算，毕老师说清楚吗？逻辑不会整个都白费。那说咱这道题到底怎么分析？你来看吧啊，说我这 a d 有 个角平分线，然后呢？然后说我过点 a 做一个 a e， 跟谁呀？跟我画的这个 a d 角平分线， 咱们垂直，并且呢，这条线跟底下这条线，哦，咱们延长以后交于点 d 啊，调整一下。 最后让我们这个角啊， a e a d 这个角等于九度，哎，也就是说 a e 垂直于 a d， 哦，这个图咱就画完整了对吗？好，所以第一个小问一题，补全题型完事。但是大家被老师提醒一下， 很多同学图做出来还会被扣一分，原因在哪？你要答如图，谁谁谁即为所求，这是画图的规矩。那接下来第二个小问说，求证，这两个角相加得一百八，各位， 这题几乎是白给，所以最怕最担心的是啥啊？前边题太难了，最后题你默认不会了，或者没时间去写了，大家哪个题不会，先跳过去先把你会的分得了哦，你要有这个技巧，这套卷你就至少能多得五分，一起来看吧。说，我怎么求这两个角都一百八呀， 咱也没给角度啊，一共就给个九十是这个道理吧。所以未知角度求角度干嘛射阿尔法背他啊！于是乎，第一个小问，你看，多么清晰的逻辑哈，我射这个小角阿尔法可以吧？因为他是九十啊，所以这个角就是九十度减 阿尔法没问题吗？啊，这个角就是 c a e 啊啊， c a e 它就等于九十度减阿尔法，那我再把它给导出来不就得了吗？ 那再看你这垂直啊，大角九十啊，你是九十减阿尔法，所以我隔壁这小角刚好。谁啊？刚好不就是阿尔法吗？咱俩一加不就得九十吗？那我又是角分线，你是阿尔法，我这边还是阿尔法吧。所以最后 b a e 这个大角，哦，它就等于 两个角相加，这边是阿尔法，这边是九十，那就是九十度加阿尔法。最终你再把他们两个加在一起，左边相加，就是咱要求那个答案，是不是好，右边相加，正负阿尔法抵消刚好一百八，所以这分得的是不是超级容易 啊？继续紧接着第二个小问。老师，我就第二个小问被难住了。有什么好难的呀，毕老师教你们辅助线分析的时候有没有讲过呀，在几何上边长的加加减减，那不是随意位置都可行的？ 啥意思？代数上你想实现一加二等于三，你算就行了。但是几何上我想求两个边长能相加，必须让，怎么样啊？必须让它长在一条直线上，只有长在一条直线上的时候，这个边加这个边才等于整个。你但凡不在一条线上，这两边相加得这一边吗？ 强人不得，两边之隔大于第三名啊。是有道理吧。所以几何上想实现边长的加加减减，那就必须让他贡献这种共。这种构造贡献的技巧，我们称之为截长补短。哦，所以听到这有多少人 你的截长补短是死记硬背的呀？你的截长补短啊，是个套路啊。其实是吗？不是，构造共现就是它的本质原理。 会了这个本质，那各位，咱们不就会了吗？说我 a b 想跟两个 a c 加在一起，那我就得让两个 a c 跟 a b 在 一条线上吧。 ok 哦，那在一条线上，要么这边演两个 a c 呗，要么在这边演两个 a c 呗，是道理不？ 那哪边延会比较好呢？这就要跟表老师学一个原理了，叫做条件集中原则。 比如说你往底下延长，延长完以后这两个边跟他还有关系吗？就没有关系了。是这道理吧，但是你往上延长，咱们来试一下。各位，哎，我延长个两个 a c， 他 就长这边了吧，那长这边有什么好处啊？ 大家你要注意咱们条件的延续性啊，前边的结论是不是对后边会有帮助啊？尤其是根据提杆球来的，比如说这个角等于九十减二法八 啊，那大家说我这个角是二法，这个角得九十，而一平角一共一百八，一百八砍掉九十，还剩九十八，再减去这边的二法，所以这边这个角刚好是多少？ 九十多加二发，大家能明白吗？所以你是九十加二发，我也是九十加二发，那反过来，这条线 a e 又是这个大角的什么线？ 角分线，你看条件我就集中在一起了。那当然啊，这个东西被老师插一句啊，如果你初一就跟我学过，初一被老师直接教你们的就是 双角分线，平角的任意一个平角啊。我这个双角分线肯定是什么关系，垂直关系，所以你只要给我垂直的时候，老早我就看出来了， 你应该延长，延长这一个角分线，就会变成两条角分线，到那时候你说是不是就越学越透啊？所以初一那些东西有没有用？有用，哎，你得给孩子讲透了。那接下来，那见着角分线，我又该如何做辅助线呢？各位， 角分线的本质是啥？我这个角是不是搁轴对称图形啊？角分线的本质就是对称轴所在直线呢？是不是这道理？那你整个就是可以对称过来呀。哦，大家这回说我想在 a b a 上延长出来两个 a c， 对吧？啊？然后我还想把它对称过来，那各位，我先在这打一个点，让他俩相等，那我这个 a c 一 一旦等于一个 a c 啊，角分线，角还相等公共边，这还相等？是这道理不？ ok？ 所以 我只要把它连上，这两个三角形什么关系？ 全等吧，这两个三十全等，你是九十度，那我这边就是九十度吧。哦，那接下来我打算把这延长几个 ac 的 两个 ac 吧，那就意味着我这小段还得 ac 啊。啊，你也跟 ac 相等，这还垂直又中点又垂直，什么线？又出来了？ 中垂线吧，中垂线，你还等啥呀？是不是赶紧把它连上啊？哦，因为中垂线点到线段，两端 距离相等。好，接下来结论就来了，说我想让 ab 加两个 ac， 也就是这条白线让他等于 ae， ae 是 这个吧，这个根据中垂线对称过来跑这来了吧。啊，那是不是就让这两个白线相等啊？各位，这两个白线相等，他是什么？三样 等腰三角形吗？等腰三角形，这俩底角当然也就相等了，是不是？最后你问我角角多少度？阿尔法我都设好了，设了一个未知数，那就需要一个等量关系，所以根据等腰给我导个条件出来不就完了吗？是不是 一起来看？首先，你这角分线，咱俩对称，你是阿尔法，我这是阿尔法。其次，你是中垂线，咱俩对称，你这是阿尔法，我又是阿尔法，所以我这边底角 三倍阿尔法啊，那我这边底角显然三倍阿尔法啊。已知，这又是两个阿尔法，再跟一个九十度，咱凑成了一个 三角形吧，这占了九十，这两这两个加和就是多少九十八，所以最后发现五倍的阿尔法刚好等于九十度，一个阿尔法就是十八度。那么要求的咱们这个角 abc 三个阿尔法，最后咱们就是五十四度，毕老师说清楚了没？所以到最后老毕给大家总结两个点，作为考试来说，大家一道有个经验，不一定是后面的题比前面的题难，很有可能前面的题恶心你， 后面题反而很轻松，所以该跳的跳过去，把能得的分先得来，然后剩下的时间再把不会的死心研究。第二个全等辅助线，绝对不是蒙猜错，而是每一个都要有理有据，并且初一学的对未来初二有没有影响，大有影响，所以初一就要把每一个东西 都学透，比如说角分线，你不能说角分线，就是等倍分，只能倒个角，你还要知道毕老师这是什么，双角分线到底是 怎么回事，角分线的对称性如何做全等辅助线，当你把这些东西都掌握透的时候，没有题能难住你，你就是那个顶级学霸。所以大家距顶级学霸你们还差在哪个题上？都可以下方评论区留言点赞超过十条，老毕专门给你讲一期！

有这么样一类期末考试题，他看上去非常简单，但是这道题能拿着分的同学却少之又少，哎，这种就是我们常说的 期末考试中的陷阱题，也就是孩子们说的坑题了。比如说咱今天这个陷阱，哎，就是咱们典型的多解陷阱。咱们整个初中啊，有四种情况容易出多解，你要小心谨慎。第一种情况就是咱们这种叫什么？叫做无图。 你想一个几何题，他既然没给你画图哈，什么原因？因为这个图未必只有一个，就需要你自己能想到啊，他有好几个。好。紧接着第二种叫什么呀？就叫做直线，有的时候一个点在线段还是射线还是直线上运动， 大家就要注意了，直线是特别自由的，往往容易戳多结。那另外两个陷阱是什么呢？哎，先积累着一个，就是未来咱们要学习的 等腰。还有一个就是三角形的高，为什么？因为锐角三角形的高都长在里面，但钝角三角形呢？有些高是长在外面的，所以这就是多结的四个特征。当你知道这个特征的时候，哎，这道题你就明白了。说我第一个条件角 a o b 等于七十二度，哎，这个东西它是固定不变的呀， 啊，那我就给它画在这了，这个角七十二度，嗯，紧接着第二个角 a o c 啊，等于五分之三倍的 b o c。 那 有一个问题啊， 我这个 o c 到底在哪啊？我这个 o c 是 在这个角之间呢，还是在 o b 这边呢？还是在 o a 这边呢？这事确定吗？ 是不是不确定啊？那既然不确定，我就得怎么样，就得分类讨论呢？所以一分类讨论，那不就出多解了吗？是不是？哦，所以无图。为什么多解？因为它暗含了分类讨论思维，所有带这种思维的，是不是就是孩子容易丢分的难点？哎，所以把这一道题学会，你学会了非常多东西。 那咱就现在来一下。第一种情况，我就让这个 o c 长在这个角的里边。哦，那我 a o c 等于多少啊？五分之三倍的 b o c， 也就是 a o c 比上 b o c 等于三比五呗。哦，那见着比例毕老师教给大家怎么样 设 k？ 那 在角度问题中，我们就把 k 换成二法吧。也就说，你不就是三倍的二法吗？那我这边不就是五倍的二法吗？所以咱们两个之比就是 三比五啊。哦，那我整个加在一起多少呢？八倍的阿尔法，八倍的阿尔法等于七十二度，所以一倍的阿尔法八分之七十二，也就是九度呗。那一个阿尔法是九度，你要求的谁啊？要求的 a o c 啊，你是三倍的阿尔法，那就是三九二十七度。所以 一个答案咱就写出来了。那紧接着第二种情况，我能不能让 o c 长在这样靠近 ob 这边啊？那你要看一下了啊，假设它靠近这，那 a o c 大， 然后 b o c 小， 然后 a o c 比 b o c 还等于三比五，这可能吗？ 各位？显然不可能啊。嗨，你得让谁啊？让 b o c 更大一些。哦，那我这个 o c 就 继续旋转，旋转，旋转，旋转到直到到这边哦，靠近 o a 的 时候， 我才能实现。什么？实现 a o c 是 三倍， b o c 是 五倍。那这个时候又该怎么求呢？啊？你这是三倍的阿尔法，我用过了，那我还可以用贝特吧， 我假设它是三倍的 beta， 可以 吧？那 b o c 是 不是就是五倍的 beta 呀？哦，你是三倍 beta， 我是 五倍 beta， 那 a o b 就 等于多少啊？是不是等于五倍减三倍，也就是两倍的 beta？ 哦，那最后我们就列出来两倍的 beta， 现在等于七十二度，所以一个 beta 就 等于 三十六度，而我要求的叫 a o c 吧。啊，那么角 a o c， 它是三倍的，三个三十六，也就是一百零八度。那最终我们让这条线从头转到尾，一共就这俩答案，所以这题只有 两个答案，两个全写上，此题就必对无疑。所以一个多解问题，当孩子能做到我这道题不需要别人跟我判，我就特别肯定我自己对的时候， 那才是真正把这类题吃透了。所以一个高效的期末复习，就应该帮孩子实现这样的效果。如果你听过毕老师上一期视频，你会知道我们这种题就叫什么呀，就叫做啊角度推导问题。 关于角度的推导一共有三种题型，第一种题型叫已知角度，求角度，那我们就求每一个。上期视频毕老师已经给大家讲完了，那么第二种题型呢？就叫做未知角度，求角度。哎，我们怎么破解？ 设阿尔法，贝塔是不是今天就用的这个方法呀？当然还有未来，还有更难的叫做什么叫做由动线产生的动角问题，那我们就设时间 t ok， 整个角度。作为命题老师，我们的命题方法，命题策略就这么多，你只要把这三类都掌握了，那各位角度推倒就没有能难的住你的。 同样大家，我们这学期的几何不仅有角度推导，还有什么？还有边长吧各位，边长也是这样的，已知边长求边长怎么啊？求每一个未知边长设 x y 啊！那我如果是动点产生的动变问题呢？各位，那就设 时间题。所以当你这样给孩子进行高效复习的时候，你会发现，我只需要做六道题，就能把整个这学期的几何计算彻底帮孩子提分的 理气。无论孩子在哪个年级，无论他哪一个教学版本，哪一个章节的知识有问题，毕老师其实都按章节给他总结好了，想要领取的家长直接留言，期末复习四个字，毕老师能帮你！

我们继续分析，对于三角形 c、 e、 f 来说， c、 f 等于 e、 f， 这是它的内关联条件，不能让它自己沿这个关联条件做贴靠。由于 c、 e 是 等于 b、 d 等于 a、 d 的， 它可以沿 a、 d 或者沿 b、 d 做单靠，得到这个全等三角形，或者这样的全等三角形，也可以得到这样的全等三角形 和这样的全等三角形。经过分析发现，这四种贴靠方法并不能拓展关联，所以对三角形 cf 做这样的单靠都是不能解题的。对中心三角形 cf 而言，还有没有其他的构造方法来解题呢？当然是有的， 我们可以对三角形 c、 e、 f 沿这个定角做拉伸贴靠，使 f 一 贴靠到 fa 的 位置，得到这样的图形。 假设这一点是 m。 由于三角形 m、 a、 f 是 三角形 c、 e、 f 拉伸贴靠得到的，所以这个角等于这个角，这个角等于这个角，而这个角是等于这个角的，所以这个角也等于这个角， 那么这个三角形就是等腰三角形，于是这个边等于这个边。又因为 e、 f 是 等于 c、 f 的， 所以 a 一 就是等于 m、 c 的。 另外，由于 c、 e 是 平行于 m a 的， 而 d 是 ab 的 中点， 所以 c、 d 是 三角形 m、 a、 b 的 中位线，因此 m、 c 就是 等于 b、 c 的。 这样也可以证明 a、 e 等于 b、 c。 特别说明一下，这个贴靠方法就不是全等贴靠，而是后面将要讲到的相似贴靠了。这是要解答的第一个问题， 要解答的第二个问题是三角形 c、 d、 b 在 第一问的证明过程当中，不是中心三角形，只是目标三角形。为什么在第二问的证明过程当中，它又成为了中心三角形呢？ 在证明第一个问题的时候，通过刚才的分析，我们知道三角形 c、 e、 f 当中有三组关联条件，而三角形 c、 d、 b 当中只有 b、 d 等于 a、 d 和这个角等于这个角等于这个角这两种关联条件。所以在证明第一个问题的时候，由于三角形 c、 d、 b 的 关联条件的种类没有三角形 c、 e、 f 多，所以它不是中心三角形，只是目标三角形。 在证明第二个问题的时候，已经有了第一个结论，也就是说有新的关联条件产生，这个时候再来观察三角形 c、 d、 b， 它就增加了 b、 c 等于 a、 e 这个关联条件， 这个时候三角形 c、 d、 b 和三角形 a、 d、 e 当中就都有三组关联条件，所以它们都是这个阶段的中心三角形。通过这两个中心三角形的双靠都实现了解析。 通过三角形 c、 d、 b 关联地位的变化可以说明两个问题。第一个问题是中心三角形是一个思维概念，并不是指某个固定的三角形，它指的是当前关联条件之下，图形当中关联条件最集中的那一个三角形。 在解析的不同阶段，三角形的中心地位是可能发生变化的。第二，中心三角形的中心地位依赖于关联条件的充分挖掘，关联条件挖掘的越充分， 三角形的中心地位越准确，因为它的关联条件最多围绕它去做几何构造才对解析最有利。

这是第五十题。这道题有两问，书上都给出了具体的证明方法，这里先对书上的解法做一个小结。第一问当中，是对目标三角形 c、 d、 b 绕中点， d 做中点旋转，贴靠得到与它全等的三角形 g， d， a， 这点是 g， 然后通过等腰三角形 a、 g、 e 得到 a， e 等于 a， g 等于 b、 c。 要证明的第二个问题，需要用到第一问的结论。 得到 a、 e 等于 b、 c 之后，就可以对当前的中心三角形 a、 d、 e 或者 c、 d、 b 做双靠构造解析，如果是对三角形 a、 d、 e 做双靠构造，它可以贴靠到这里 得到全等三角形 b， p、 c， 这里是 p， 这样 a、 d 就 转移到了 b， p， d、 e 转移到了 p， c。 由 d， e 等于 p， c 可以 得到 d， p 等于 c、 e， 而 c、 e 是 等于 b、 d 的， 所以 d、 p 也是等于 b、 d 的， d、 p 等于 b、 d。 因为 b、 d 是 等于 a， d 等于 b p 的， 所以三角形 p、 b、 d 是 等边三角形，因此这个角就是六十度。这是三角形 a、 d、 e 的 双靠接法。如果对三角形 c、 d、 b 做双靠构造，它可以贴靠到 eq、 a 的 位置， 这里是 q， 这样 b、 d 转移到了 a， q， c、 d 转移到了 e， q 由 c、 d 等于 e， q 可以 得到 c， e 等于 d q， 而 c、 e 和 b、 d 是 相等的，所以 d、 q 和 b d， a、 q 以及 a、 d 都是相等的，那么这个三角形也是等边三角形，所以这个角等于，这个角是等于六十度的，通过这两种双扣构造都可以证明。第二个结论。刚才所讲的是书上解法的简要介绍。 围绕这道题，下面解答两个问题。第一个问题是三角形 c、 e、 f 是 不是中心三角形？能不能通过它的构造来解析？在证明第一个问题的时候，分析已知条件， 我们可以看到三角形 c、 e、 f 当中 c、 f 是 等于 e、 f 的， 那么这个角就等于这个角。 另外还知道 c、 e 是 等于 d b 等于 a、 d 的。 因此三角形 c、 e、 f 当中有三组关联条件，它的关联条件是最多的。 所以在求解第一个问题的时候，三角形 c、 e、 f 是 中心三角形。既然是中心三角形，那能不能够通过它的构造来解析呢？

当一个知识点真正学透的时候，大家题自然就变简单了。很多同学遇见这种需要做辅助线倒角问题的时候，总是做不出来。那今天毕老师就给大家讲一道九年级这一期咱们的期末考试题，看看我们是如何了解。说，在四边形 a、 b、 c、 d 中，嗯， 角 a、 b、 c 这个角等于角 a、 d， b 这个角等于四十五度啊，你得四十五，我也得 四十五。好，再来说，角 b、 d、 c 等于九十，嘿，这边还得九十。最后问我们谁啊？ b， a、 c 这个角，问它等于多少度？各位，这个问题该如何解决呢？ 其实非常简单，比如说，你要是系统跟 b 老师学过圆这个知识点的话，老 b 最后会给大家讲到什么？讲到四点 共圆问题。什么叫四点共圆呢？其实常见的就是你圆周角定里逆运用啊，说，我如果在一个圆上，哎，同一条弦所对同侧的圆周角是不是就得相等啊？ 那倒过来呀，假设有一个八字这样的两个角相等了，那倒回来这四个点就怎么样长在同一个圆上啊？同样道理，圆周角定里还告诉我们说，我圆内接四边形对角怎么样啊？ 互补吧。哎，那各位倒过来，如果一个四边形对角已经互补了，这四个点肯定怎么样长在同一个圆上，这就是咱们简单版的四点共圆。好吧，哦，你要是知道四点共圆这道题，不就了解了吗？大家，我这九十，你四十五，所以我这大角得多少吧？ 是不是一百三十五，你是一百三十五，我这是四十五，咱们一共得几吧？加在一起是不是一百八？一百八就意味着咱两个互补，对角互补，所以四点哦共圆。于是乎 我所有这些点，它就长在哦同一个圆上。毕老师说清楚了吗？那既然在同一个圆上哦，再用一下另外一个圆周角定里，你刚刚是你俩互补来的是不是？我这回干嘛？我这会同弦所对， 同侧圆周角相等，因为你得九十，所以这得九十。所以这道题 b、 a、 c 直接口算九十度。但是 各位同学做一个解答题，你这么写一分你都得不来。所以老毕还得教大家写过程。那说四选公务员的过程该怎么写呢？因为他分析的逻辑跟别的完全不一样，是吧？这么分析太简单了，那过程大家记住四个字，以后 老师想给你扣分都难。凡是四点共圆，皆用二次相似。画家说四点共圆，学校不教也不让用，对吗？相似，你总教过我吧？哦，你总让我用吧，那我用两次相似就可以了。那怎么样两次相似把这个问题解决掉呢？你看 咱这道题，之所以四点共圆，不是因为你得四十五，我得幺三五吗？咱们对角互补吗？对角互补怎么照相似啊？非常简单呢啊，相似得有角相等啊，咱是互补，但是 我这延长一下子，你这个角得一百三十五，我外角是不是就得四十五了？四十五跟你这个四十五是不是就相等啊？我跟这边再延长一下，各位，一个反 a 字不就来了吗？也就是说，这个大白 跟这个小白，咱们有个公共角 m， 还有个四十五度角相等，是不是啊？所以第一个相似三角形 m、 a、 d 这个小家伙啊，它就相似于三角形 m c b 这个大家伙，是这个道理吧？好，那这样相似以后，我是不是就得到对应边乘比例啊？啊？那就是 m a 比 md 来了啊，比上 md， 它就等于这边 啊， mc 比上对应的 mb 吧， mc 比 mb 啊。大家都知道相似对应边乘比例的时候，我可以竖着找三角形吗？你两个围成一个三角形，你两个围成一个三角形，哎，我还可以怎么样 横着找三角形，这才叫学偷。 ok 啊，那 m a 和 mc 我 围成了一个，谁啊？ m a 和 mc 就是 这个黄色三角形，对吗？好，再来， 那我这边 m b 和 m d 呢？啊？ m b 在 这， m d 在 这，它是不是又围成了一个这个红色三角形啊？红跟黄 相似。这道题的第二组相似是不是就来了啊？没有地表示不写了啊。但是相似以后，对应角相等，大家帮我找到，说，我这个红色三角形哪个角我知道， 各位，哎，你这一角是不是得九十啊？所以我这个角是不是得九十啊？九十度，我知道你得九十度，那我这黄色三角形对角这边是不是得九十啊？你得九十，人家问这边，这边还剩九十呗。所以二次相似必减四点共圆。 到时说清楚了吗？把一个东西拿过来，就能分析，并且能写出来完美的过程，这才是把一个知识点真正学透了。所以大家孩子为什么丢分，只因为一句话，他还没学透。