沪科版九年级数学圆24.1基础题

九年下册必考题圆的综合计算我们先来读题，如图，在 r、 t 三角形 abc 中，角 a、 c、 b 等于九十度标上去 点 o， 在 b、 c 上以点 o 为圆心， o、 c 长为半径的圆 o、 b 相切于点 e， 交 o， b 于点 d， 若 b、 d 等于一，然后摊平它角 a、 o、 c 等于二， 然后则圆 o 的 面积。想要求圆 o 的 面积，我们首先得求出圆 o 的 半径，所以我们的重心就放在了半径为多少，我们来看一下。因为圆 o 与 ab 相切，所以我们很自然做的辅助线就是连接圆心和切点 好，连接好以后，我们就可以得到 o， e 与 ab 是 垂直的， 那么此时我们设圆 o 的 半径为 r， 所以 在图上把所有的半径都标注出来， o、 c 是 r， o d 是 r， o e 也是 r， 所以呢， o、 b 就 等于 r 加一，那么 bc 就 等于 二， r 加一，那么在这个直角三角形 o、 b、 e 中，我们就可以表示出 b e 根号下 o， b 方减去 o， e 方代入进去， 减去 r 的 平方进行开方整理，结果是一个 根号下二， r 加一，所以 b、 e 就是 一个根号 二， r 加一。那我们来看一下三角形 o、 b、 e 和三角形 abc 是 否相似呢？因为它们两个三角形是不是都有一个直角，还有一个公共角角 b， 所以 我们很自然就得到了 三角形 o、 b、 e 相似于三角形 a、 b、 c。 那 我们来看一下这两个三角形 o、 b、 e 的 三边我们都表示出来了， a、 b、 c， 我 们只表述出一条边是不行的， 那我我们还有一个条件，就是探进的角 a、 o、 c 等于 r， 我 们还没有用。我们来看一下探进的角 a、 o、 c 在 这个三角形 a o， c 中，我们就可以表示为 ac， 比上 oc 等于个二，又因为 oc 呢是 r， 所以 我们就表示出 a c 等于二 r， 那 这两个三角形相似的话，我们是为了得到对应边乘比例，所以就得到 o e 比上一个 a， c 等于长的直角，边是 b， e 比上一个 b c， 然后代入 o， e 是 r， a c 是 二 r， 然后 b e 是 根号。二 r 加一， 然后 b c 是 二， r 加一，交叉相乘，我们就可以求出 r 的 值， r 一 就等于二分之三， r 二就等于负二分之一，负值肯定是不合提议的，所以我们舍去。那么此时很自然我们就求出圆 o 的 面积等于 pi， r 的 平方就等于 四分之九。派好，最后把结果填进去。好，同学们，你听懂了吗？听懂的话请给老师点点关注吧！

九上数学最难的圆的常用定律全部练熟，逆袭班级前三！关于圆的八个常用定律，圆心角定律、圆周角定律、垂线长定律、 香蕉弦定律、割弦定律、弦切角定律。

九、上数学最难的圆的十大定律全部吃透！逆袭班级前三！一、圆周角定律二、垂径定律三、切线长径直定律四、三角形外切圆六、定角定弦定律 七、相交弦定律八、割线定律十、最大章角问题完整版分享！

一个圆的小综合题，圆的证明题，最喜欢正直线是圆的切线，这个就是我们直线是圆的切线的定义就是过半径外端，并且和该半径垂直，这条直线就是圆的切线。 现在 e 是 a、 c 和圆交的点，这个地方就告诉你， e 是 咱圆，上一点是半径的外端。那你接下来任务要想正直线与圆相切，只需要连该半径正，这个地方是直角就行了。 好，这是这道题，咱们给他简单做个梳理，基本上都是这样一个套路。好，那怎样证这个角是九十呢？哎，隔壁有一个角是九十，那咱的目标就是证这个 a、 b 和 o、 e 平行平行。平行的话， 那咱可以用咱平行的判定定理，和角有关，同一角相等，两直线平行，或者同一角相等，两直线平行，那在哪里呢？咱看一下，给了一个等腰， 是不是想提供这两角相等呢？还有咱园内自带等腰，以为半径围成的三角形都是等腰，这两个角也相等。好了，找到了吧，同一角相等，两直线平行平行，这垂，这也是垂，第一问就得正， 第二问也好正，咱们的 g f 是 二倍根三， g b 是 四，勾股令里算出来这是二， 立马发现这个角，那应该是三十度吧。在直角三角形中，三十度，对的直角边是斜边一半，反过来，在直角三角形中，如果有一个锐角的，那对的这个边是斜边一半，那这个就是三十度，或者是直接用 c 三十度 都可以。好，那他是三十度。太好了，咱们放到这个小红三角形里，你要求半径吗？你得放到有半径的三角形为 r 法吧。好，就用三十度对的直角边是斜边一半 交叉相乘积相等建立 r 的 方程，解方程就可以了。 ok。

快喊你的朋友来一个视频速通圆的八大定底！先看第一个定力，圆形角定底， 圆形角、弦、弧、弦心距四者关系的定底，在同圆或等圆中，圆形角相等，它所对的弧弦弦心距也相等在左凸中角一如果等于角二，那么我们可以得到，弧 a、 b 等于弧 c d。 弦 a b 等于弦 c b o e 等于 o f。 以上四个的量关系，我们知道其中任意一个可推出另外三个，正所谓之一推三。第二个定律，圆周角定律， 同弧或等弧所对的圆周角相等，并且圆周角的度数等于它所对的弧上的圆形角度数的一半。在所图中，就由角 c 等于角 d 等于二分之一角 a o b。 第三个定力，垂径定底， ab 是 弦， cd 是 直径，当 ab 垂直于 cd 的 时候，我们可以得到，弧 a、 d 等于弧 b d。 弧 a， c 等于弧 bc a e 等于 b e。 第四个定力，切线长定点 p 是 圆外一点 p a， p b 是 圆的两条切线就有 p a 等于 p b。 第五个定力，相交弦定力， 圆内两条弦 abcd 相交于点 e 就 有 a e 乘 b e 等于 c， e 乘 d e。 第六个定力，割线定力， 点 p 是 圆外一点 pa， pc 是 圆的两条割线，与圆交于点 b 和点 d， 那 么就有 pa 乘 pb 等于 pc 乘 p d。 第七个定律，切割线定律， pa 是 圆的切线， pc 是 圆的割线，与圆交于点 d， 那 么就有 pa 方等于 pc 乘 p d。 第八个定律，弦切角定律， 点 p 是 圆上一点 p c 是 圆的切线， p b 是 圆的弦，角 a 是 裂弧 b p 所对的圆周角就由角一等于角 c。 搞定，收工 so easy！

是应用的非常的灵活啊，非常的非常灵活，不要总说以后啊，不要总想着还有明天，我们人生中的每一寸光阴都不应该被虚度， 扎实的过程必然结果。大家好，我是大张，讲述讲数学，今天给大家讲一个初中几何之四十九种模型之模型三十六、圆内接四边形的定义是什么？就说在一个圆当中有个圆内接四边形 a、 b、 c、 d， 它满足的 他会有一个什么样的定义呢？咱们看一下这个图啊，这是个圆的一个四边形，当中角 a 和角 c 之间呢？ 得一样八十度，对，为什么得一样八十度呢？我们凡是遇到一个数学问题，我们多问一下自己几个为什么？那这样的话，我们是把这个就想清楚了，想明白了来龙去脉，想通之后，我们把这个什么定义就永远记住，所以有的同学说我记不住公式，记不住定律，是吧？你 老师教你个简单的方法，你凡是遇到这些定义和公式，你自己去推导一遍，你永远记在你的大脑里面啊，这个方法很有效，我们看一下为什么角 a 加角 c 的 一个衍化呢？啊？我连接了 o、 b 啊，还有连接了 o、 c， 你 们会发现，你看这个角， 这个角是不是这个弧 bc 的 所对的圆心角，那么它所对的圆心角和圆中角之间的关系是什么呀？是不是二倍关系啊？对不对？也就是说这个角角 b， 那是角 a 啊，是角 a 是 不是二 b 的 角 a 是 不是等于角 b？ 无得对不对？那么这个角 c 呢？这个角 c 的 意思是等于这个圆心角所对的圆珠角，那么他俩之间的关系是什么呀？ 对，我们知道这个角加这个也是三百六，是不是也等于二倍的角 a， 再加上二倍的角 c， 是 不是就等于三百六十度啊？那所以说角 a 加角 c 就 等于什么？一百八十度，那么同理是不是我们可以得到什么？对，同理可以得到角 b 加角的等于一百八十度。 对，这是圆内接四边形的一个定力，是不是？那我在这里再给大家补充一下啊，圆内接四边形的外角定力是什么啊？我现在说外角啊，就比如说我把这延长一下，是吧？那这个角，这个角等于什么呢？ 这个角等于和他相邻的这个角的对角，也就说这个角等于这里的角位啊，也就是这个圆内接四边形的外角定义是什么？任意一个外角等于和他相邻的内对角，内角的对角，是不是啊？讲，也就是说我写什么 内接四边形，对吧？外角定义 啊，就任意一个外角等于和他和他相邻的内对角啊，任意一个外角。我简写了啊，任意一个外角等于和他 相邻的内对角，内对角啊，那么也就是这个外角等于和他相邻的角的对角，也就是这个得 c e 的 角 a 啊，那这个是圆内接四边形的外角定义。这很简单啊，证明起来很简单。怎么证明呢？你看咱们说内角是不是角，这个角加这个角是不是也八了？是不是？那同理这个角加这个角是不是也八？同角的与角角是不相等，所以说这个角与这个角。 所以说你一下子圆内角四边形的定义和圆外角四边形的定义和圆内角的外角定义，内角定义和外角定义你是不是都知道？那么接下来我们做这种题就非常简单了啊，我们看一下啊，在这个圆内角四边形圆 o 当中， a c， 弧 a c， 弧 a c 啊，弧 a c 在 这啊，往这连一下啊，对，弧 a c 等于弧 bc， 那 么在同一个圆当中， 弧相等，那是不是弦相等，对吧？等弧对等弦是吧？那么同样在同圆或者等圆当中，同弧或者同弧或者等弧所对的什么？圆心角或者圆中角相等，那弧 a c 和弧 bc 所对的圆中角和圆心角都相等，是不是？对？但角 b 得 c 是 什么？五十度，这个角是五十度 啊，这个角是五十度。好的，那现在让我们求什么？求角 a 得 b 的 度数，求求这个角 啊，求这个角是多少？那其实很简单，你看，我刚才说了，弧 a c 的 一个弧 bc， 那 么弧相等，那么他所对的圆中角或者圆心角是不是也相等？但是这个条件，这个定义是必须在什么同圆或者等圆当中，那么也就是说你弧 a c 所对的圆中角是不是角 abc 啊？ 哎呀，我这么写吗？其实角 bc 吧。啊，那他是不是应该等于多少呢？ 等于多少呢？不知道是吧？但是我又知道弧 bc 所对的圆中角是什么？ b 得 c 是 吧？那么同弧所对圆中角，像的也就是这个角和这个角是不是像？这是五十度，是不是？那所以说这里是不是应该选五十度呀？ 是不是？那这里是五十度，或者这里是五十度啊？对，这个我没写啊，就是说，呃，又因为啊，我写一下吧，又因为角这个 b、 a、 c 等于一个什么角 b、 d、 c， 是 不是这两角是相等，是五十度，对吧？ 那又一还还有什么呢？这是圆的一节四边形吗？对，角是互补，对吧？也就说角 abc 加上这个角 a、 d、 c 等于一二八十度。那你想想，这两个角加起来一二八十度，这是五十度，这是五十度，是吧？那这就是多少 啊？或者说这是五十度，这时候就是一百三十，一百三十，再减五十的时候就八十度啊。对，所以说这个角 a 的 b 就 等于个一百三十度，减去个五十度就等于个什么八十度啊，很简单对不对？也就是说你把这个圆内接四边形的 定力和圆外接四边形的定力，你是不是都知道了？你用用这个圆内接四边形的定力做这个题，是很简单，是吧？再加上同弧所对的圆中角和圆心角相等，很简单。这个应该选什么？对，选 d 选项啊。那么同理这本书，那么也是 啊，我手里拿的这本书上的模型三十六讲的就是圆内接四边形的外角定力， 当然这个模型后面已经备注了一些经典的练习题啊，我们讲的只是一个核心的母题啊，这个母题非常经典，就是说它把这个圆锥的四倍镜， 那么这里面总共有四十九种几何模型啊，这本书挺不错的。好的，那么这道题就给大家讲到这里，拜拜。

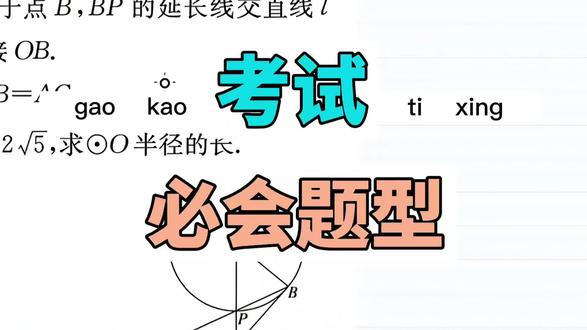
人的基础题型，我们看一下已知条件， o， a 垂直于 l， o， a 等于五， o， a 与圆相交于点 p， a， b 是 圆 o 的 切线，所以我们能知道 o b， a 这个角等于九十度， 那题目让我们证明 a， b 等于 ac， 那 么找边相等，所以在这里面我们通过角的关系去找一下，那我们看一下啊，角一表达为角二，角三，角四， 那通过题目所给的条件，我们知道角一加角二等于九十度，那我们标这个角为角五吧，那根据切斜的性质，我们知道角四加角五等于九十度，那题目让我们证明角一等于角五， 那所以我只需要去证明角二等于角三角三又等于角四， 那所以角一等于角五，那这是这个题的思考过程，嗯，把这个思考过程反过去写，就是它的证明过程。 我们再看第二个 pc 等于二倍根号五，去求半径的长，那么在这里面我们出现两个直角三角形，一个是 a p c r t 三角形 o， b， a， 那 所以 ap 的 长 二倍根号五解 r， 那 么在三角形 a， p， c 中，我们知道 a， c 的 平方等于 p c 的 方解去 ap 的 方，那把它带进去，就变成了二倍根号五的方解去五解 r 的 平方，我们在这里面 a b 的 平方，我们在 r t 三角形 o， b 中可知道 等于 o， a 的 方解去 o， b 的 方，由于 o， a 的 方是五， o， b 的 方， r 的 方，那题目低问，我们证明了 ab 和 ac 是 相等的，所以在这里面二倍根号五的方五减 r 的 方 等于五的方， r 的 方，那通过这个式子，我们可以去求出 r 等于三。记得点赞关注哦！

每天一道必考题，期末多考二十分，今天我们一起来学习一道九年级上册期末考试比较喜欢考察的一类题型。圆的切线的证明。如图，在二次角形 a、 b、 c 中，角 c 到九十度啊，那就是直角三角形，这个角九十度点 d 为边 a、 b 的 中点， 点 o 在 边 b、 c 上以 o 为圆心的圆或 c 点与边 a、 b 相交于点，则那就是说明这个地点在圆上，并且和 a、 b 的 相交。 第一问，求证直线 a、 b 是 圆 o 的 切线，那我们先看这个切线的证明。其实讲到切线证明的话，咱往往来说是两种方法，一定要先判断这个圆和直线有没有公母点， 如果有公母点的话，就发现如果它们相切，那个公母点必然是切点，那有公母点行，咱们就是连接切点，证明垂直就行。如果是无公母点行，那咱们就先做垂直，做完垂直以后，证明它是半径， 那这里边很明显，因为这个说了这个圆与 a、 d 相交一点得，那说明是有公共点形，那 d 点就必须是且沿就连接 o、 d， 只需要证明 o、 d 和 a、 d 垂直于这行。这时候我们再看其他套件， 在直角三角形中，角 b 是 三十度，那其实计算出来的角 b 就 六十度，这是我们还发现，因为角 b 是 三十度的话，那么根据直角三角形中三十度角所对应直角边是斜的一半，说明 a、 c 是 不应该等于二分之一的 a、 b。 其次还有一个点 d 是 中点，说明这个 a、 d 也是二分之一的一，那虽然说我们是能得到这个 a、 c 等于 a、 d 的， 这是我发现角 a 还是六十度，那说明 a、 c、 d 是 一个等边角形呢？那我把它连起来，我们连接 c、 p 以后，我们就发现了啊，那这个角也是六十度，这个角也是六十度， 这个角 a、 c、 b 是 一个九十度，它是六十，那说明下面这个 o、 c、 d， 它就三十度，再加上 d 点一位在圆上，那 o、 d 就是 半径了。 o、 d 是 半径， o、 d 就 等于 o、 c， 那 它是三十度，说明这个角也是三十度。那最终这个角 a、 d、 o， 它不就等于六十度，加三十度就等于九十度。九十度的话，说明这个半径和这条直线 ab 垂直的， 说明它就是个切线。这是我们再来看第二个，第二个跟计算阴影面积有关， a、 c 等于根号三，那它就是根号三呢？求阴影部分的面积，那我们现在观察求阴影部分面积，这个很自然就是三角形 b、 o、 d 的 面积。减去这个扇形，咱们比如说再标一个 e， 减去这个扇形 o、 d、 e 的 面积就行了。而且在计算扇形面积时候，一定得知道圆心角，那就需要算出来这个角 e、 o、 d 是 这个三角形 o、 c、 d 的 外径， 两个三十度数的差是六处。那还有一点，你就判断得到扇形的半径长度，那也就是这个 o、 c 的 长，也就是圆的半径，因为这里面它很多毫。三、两套切线方法，我们其实能想到切线长定力的就是如果连接 o、 a， 根据切线这条定义，我们知道 这个 o、 a 是 平分，这两条切线的夹角那一半就是三十度，那在这个三角形中是有一个含三个矢度的直角三，那咱们知道三边比例是一比二零毫三， 是否 o、 c 都等于一，那当然 o、 d 也等于一，这个角是三十度，那说明这个 b、 d 是 刚好三，那这个白色的面积就等于三角形 b、 o、 d 的 面积减去扇形 o、 e、 d 的 面积， b、 o、 d 的 面积二分之一，底乘高二分之零，刚好三乘以这个扇形的面积呢？三百六十度分之 n， pi 二方，那就三百六十度分之六十乘以 pi 二方，那叫 pi r 分 之一，所以最终结果就等于二分之零，靠三减去六分之派，这就咱们这个应用的面积。这也是咱们期末考试里面比较喜欢考的题型，咱们下去以后可以多看几遍。有什么问题了在评论区给我留言。