指数函数性质总结
挑战七分钟,带你速通高一数学第四张,指数函数与对数函数所有必考知识点主要包括 n 次方根与分数指数密指数密计算性质、对数计算性质、指数函数计算性质、函数的零点存在性问题等 等等所有必考知识点弹幕区打上,高考必胜!我们开始第四张指数函数与对数函数一、 n 次方根于分数指数密指数密运算性质若 x 的 n 次方等于 a, 如果 n 为基数,则 x 等于 a 的 根号 n 次方。若 n 为偶数,则 x 等于正负根号下 a 的 根号 n 次方。二、 a 的 n 次方开根号若 n 为奇数,则等于 a, 若 n 为偶数,则等于 a 的 绝对值 a 的 根号下 n 次方整个是指再进行 n 次方等于 a, a 的 n 分 之 m 次方等于 a 的 m 次方。 根号下 n 次方,其中 a 要大于零, n 都属于正整数,且 n 大 于一, a 的 负的 n 分 之 m 等于 a 的 m 次方。然后再开根号, n 为分母, 分子为一,零的正分数,指数为零,零的负分数指数没有意义。 a 的 r 次方乘以 a 的 s 次方等于 a 的 r 加 s 次方, a 的 r 次方括号外面乘以一个 s 次方等于 a 的 r 乘以 s 次方 b 的 r 次方等于 a 的 r 次方乘以 b 的 r 次方。第二,对数对数计算性质 a 的 x 次方等于 n。 能推导出 x 等于 log 以 a 为底, n 的 对数,其中 a 大 于零, a 不 等于一。 第二 log 以 a 为底,一的对数等于零。 log 以 a 为底, a 的 对数等于一。以 a 为底, a 的 m 次方等于 n。 以 a 为底, a 的 m 次方的对数等于 m, 其中 a 大 于零, a 不 等于一。以 a 为底 m 的 对数等于以 a 为底 m 的 对数。加上以 a 为底 n 的 对数,就等于以 a 为底 m 的 对数,减去以 a 为底 n 的 对数,以 a 为底 m 的 n 次方的对数等于 n 乘以以 a 为底 m 的 对数。换底公式,以 a 为底, b 的 对数等于 以 c 为底 b 的 对数,除以以 c 为底 a 的 对数。其中 a 要大于零, a 不 等于一。 b 要大于零, c 要大于零, c 不 等于一。一 a 的 m 次方为底, b 的 n 次方的对数就等于 n 除以 m。 以 a 为底, b 的 对数,以 a 为底, m 的 对数,以 a 为底, b 的 对数乘以以 b 为底, c 的 对数乘以 以 c 为底, a 的 对数等于一。对应条件, a 要大于零, a 不 等于一, b 要大于零, b 不 等于, c 要大于零, c 不 等于一三。指数函数 y 等于 a 的 x 次方 a 要大于零,且 a 不 等于一 及其对应性质。在定义域,负无穷到正无穷。直域为零到正无穷过定点零。一、单调性,当 a 大 于一时, 函数 f、 x 在 r 上是正函数。当 a 大 于零小于一时,函数 f x 在 r 上是减函数。在 y 轴右侧,指数函数的图像底大图高,对数函数 y 等于 log。 以 a 为底, x 的 对数及其性质,定义域为 零到正无穷,直域为负无穷到正无穷过定点一、零。单调性,当 a 大 于一时,函数 f、 x 在 零到正无穷上是真函数。当 a 大 于零小于一时,函数 f、 x 在 零到正无穷上是减函数。在直线, x 等于一的右侧对数,函数的图像底大图低。五、指数函数 y 等于 a 的 x 之密与对数函数 y 等于以 a 为底, x 的 对数不为相反数,它们的图像关于直线 y 等于 x 对 称。六、不同函数增长的差异性线型函数模型 y 等于 k, x 加 b, k 大 于零的增长特点是直线上升,其增长速度不变。指数模型 y 等于 a 的 x 是 密, a 要大于零。增长特点是随着质变量的增大,函数值增大的速度越来越快, 呈现指数爆炸状态。对数函数模型 y 等于以 a 为底, x 的 对数的增长特点是随着质变量的增大,函数值增大速度越来越慢, 即增大速度平缓。密函数模型 y 等于 x 的 n 次方,其中 n 要大于零的增长速度介于指数函数和对数函数之间。七、函数的零点在函数 y 等于 f x 的 定义域内, 使得 f x 等于零的时数叫做函数的零点。八、零点存在性定律如果函数 f x 在 b 区间 ab 上的图像是连续不断的一条曲线,且有 fa 乘以 f b 小 于零,那么函数 y 等于 f x 在 开区间 a 到 b 至少有一个零点,即存在 c 属于开区间 a b, 使得 f c 等于零,这个 c 也就是方程式 f x 的 根。九、二分法。对于 b 区间 a b 上图像连续不断且 f a 乘以 f b 小 于零的函数 y 等于 f x, 通过不断把它们的零点所在区间一分为二,使得区间的两个端点逐步逼近零点, 进而得到零点近视值的方法。十、给定精度 sigma 用二分法求函数 y 等于 f x 零点 x 零近视值的步骤。一、确定零点 x 零的初,使区间 b 区间 a b, 验证 fa 乘以 f b 小 于零,再求区间 a b 的 b 区间的中点 c, 计算 f、 c, 并进一步确定零点所在的区间。若 f c 等于零,则 c 就是 函数的零点。若 fa 乘以 f c 小 于零,此时 x 属于开区间 a c, 则 b 等于 c。 若 f、 c 乘以 f b 小 于零, 此时 x 零属于开区间 b、 c, 则令 a 等于 c。 四、判断是否达到精确度 c 个码,若 a 减 b 小 于 c 个码,则得到零点的近似值 a 或者 b, 否则重复上面的二之四。好了,以上就是必修一、所有的重点知识和必备公式,一定要点赞收藏哦!
粉丝1309获赞9628
相关视频
 03:00
03:00 05:35查看AI文稿AI文稿
05:35查看AI文稿AI文稿指数函数的性质,记住图像就搞定了,今天告诉你哪些常见题型, 同学们,好呀,今天我们来讲一下指数函数的问题。指数函数的形式是 f x 等于 a 的 次方,注意和 b 函数它们之间的区别, b 函数是 x 的 a 次方,指数函数是 a 的 x 次方,这两个的区别特别注意一下。 然后接下来的话,我们要了解它的性质,其实只需要把它的图像给记住就可以了,注意 a 大 于等于小于, a 大 于两种情况, a 大 于小于的时候,它的图像是单调递减,大概是这样的草图, a 大 于的时候,图像是单调递增, 大概是这样子的草图,那么这些草这个除知道之后的话,那么我们很多的性质就可以直接由图去看出来。那首先常考的几个常见题型是什么呢?第一个定点问题, 这定点问题的话,他一般来说他考试的时候他不会单独的去考,他不会说直接像我出了这么一个问题,他可能会跟基本不等式结合起来去考,等等啊,我们来看一下最原始的一些出的问题,定点问题的话,只要抓住什么呢?抓住一个 关键点,就是说里面的参数 a, 我 要让我们的 a 失效,就说这个 a 对 我产生不了任何的影响就可以了。 那么怎么样才能不影响呢?只要抓住 a 的 零次方等于一,那 a 的 零次方等于一的话,这样子的话 a 就 消失了,那这样子的话,它自然而然对我们产生不了影响了。所以说这边只需要我们令二 x 减三等于零的话,也就是我们 x 等于二分之三的时候, f x 等于二,所以说它的定点是二分之三的二,这是一个定点问题。第二个是减我们的不等式, 正常来说的不等式一元二次不等式我们是会解的,如果说是这种的指数型的不等式的话,我们该如何处理呢?我们处理的时候,我们只能使用它的单调性来进行解决。来看一下这边这个形式,二的 x 减平方减二 x 次方大于等于八,我们的八可以把它写成二的三次方,然后的话它的对应的函数是 f x 等于二的 x 次方。我们知道 a 大 于一的时候,这是一个真函数, 既然这是一个增函数的话,我们就可以知道二的 x x 平方减二, x 等于大于三的,因为咱们左边的形式其实就是假,就是我们的 f x 平方减二 x, 右边的形式就是假,就是我们的 f 三, 现在的话相当于就是什么呢?已知一个函数的单调性,让我们去求你们的范围,不就是两个自变量的代沟关系的比较吗?好,所以说解出来范围就是这个,这边其实也用到用到单调性了,只不过这边是一个指数和单调性的问题。然后第三个是值域问题, 具体问题的话,老师这边举了一个最近考试的简单个例子,求这个函数的值域,这函数的值域的话是一个数值形,但是它的话它的形是一个分数的样子。那么首先第一个值域的话,先看定义域, 定义域是什么?定义域是 x 是 r 的 情况,然后我们分子分母同时除以二的 x 的 四方,我们为什么要这么除呢?为的是减少 x 的 数量, 这边减少了 x 的 数量之后的话,你看一下我们这边式子就变成了二分之三的 x 次方减一,除以二分之三 x 次方加一,然后我们把二分之三 x 次方看成个整体就变成了 t, 而 t 的 情况它是什么大于零的,所以说问题就变成了这个情况, 这个式子的话,它其实是一个什么?是一个复合函数,我们内层函数的值域变成我们外层函数的定义域,而这个式子我们在除以一次的形式呀, 所以说分叉之后变成这个样子之后,然后我们的 t 是 大于零,那 t 加一大于一, t 加一分之一是零到一, t 加一分之负,二是负二到零,那么自然而然我们的 f x 范围也就是负一到一了。好,下面一个 这个也是一个指数函数类型里面常考的问题是二的 x 次方加上二的负 x 次方的一个情况,那么这里面的话,我们先咱们先把 h x 先写出来, h x 它是一个这样子的形式,我们在换元的时候,大家注意啊,不要只换二点 x 脂肪,因为换完之后的话,我们还得再换一次,我们不妨就直接把这个整体换成什么呢?换成 t, 然后看一下这个和这个之间的关系,我们只要平方一下,再减个二, 就可以得到我们的结果。 好,这边的话,我们 t 方就等于这个形式,那么我们的 h x 可以 化成什么呢?化成一个 five t 的 形式, five t 是 等于 t 加上 t 方减二, t 是 属于二分之二到二分之五的情况。画圆时候的话注意一下,看一下它们的单调性的情况。哎,这个式子它是一个单调递增的,它是在 零到一上单调递增的,所以说我们的 t 的 范围要紧跟其后。这是一个画圆时候的注意事项。然后我们就把一个 二次指数型的一个情况变成一个二次函数的题目。二次函数题目的值域的话,我们直接看一下它的对称轴和我们端点值的一些关系,就可以直接求出我们的值域问题了。好,这边的话答案是等于四到四分之二十七。 好,这是一个指数问题的一个常考的情况,我们后面的话会再把指数题目再拿出来说。那边的话一般来说是跟零点的问题结合的紧密一点。这边我们就先讲到这边。好,下课下期见,拜拜。
50数学何math 12:25查看AI文稿AI文稿
12:25查看AI文稿AI文稿上课,同学们,好,请坐!上一节我们学习了指数函数的概念,那谁来回顾一下它的内容呢?嗯,好。第二排那位同学, 嗯,很好。函数 y 等于 a 的 x 次幂,其中 a 大 于零,且 a 不 等于一,叫做指数函数。其中这里的 x 是 自变量,定义域是 r 的。 好,请坐。并且上一章呢,我们也学习了逆函数,那同学们回顾一下,我们是如何研究逆函数的图像和性质的呢?我们的研究经验是什么呢? 嗯,好。第三排这位同学,嗯,很好。我们研究逆函数的时候,是通过解析式来求出定义域, 也可以由描点法来做出函数的图像。 然后呢,由图像和解析式来讨论,哎,函数的值域,单调性,基友性这些性质。 那本节课呢,我们就按照逆函数的图像和性质的性质。 那接下来,请同学们在草纸上画出 y 等于二的 x 次幂,以及 y 等于二分之一的 x 次幂的这两个指数函数的图像。 这是 y 等于二的 x 次幂的函数图像。 这是 y 等于二分之一的 x 次幂的函数图像。好,那同学们来观察一下这两个函数图像具有怎样的关系呢? 好,同学们都发现他们两个是关于 y 轴对称的,那这只是从图像的角度进行直观感受,那能否进行严谨的说明呢? 我们可以从解析式入手,我们看 y 等于二分之一的 x 私密,我们是不是可以将其写成二分二的负 x 私密啊? 那下面我们在 y 等于二的 x 次幂的函数图像上任取一点 p, 我 们将其坐标设为 x 二的 x 次幂。那下面我们做出点 p 关于 y 轴的对称点 记为 p 撇,那 p 撇的坐标就是 i 负 x, 二的 x 是 m, 哎,那这个 p 撇是不是就在这个函数图像上? 那因此 y 等于二的 x 次密图像上,任意一点关于 y 轴的对称点都在 y 等于二分之一的 x 次密的函数图像上。哎,那是不是就说明这两个函数图像是关于 y 轴对称的呀? 那请同学们观察这两个指数函数的底数具有怎样的关系呢?哎,它们都是互为相反数的。哎,那是不是只要这两个指数函数互为相反数,它们就是关于外在对称的呢?那我们来看 y 等于 a 的 x 幂和 y 等于 a 分 之一的 x 幂,我们是不是可以将这个解析式写成 a 的 负 x 幂呀? 哎,那按照同样的方法,哎,是不是只要底数是会倒数的,那么这两个图像,哎,就是关于 y 轴对称的。 那因此呢,我们只需要画出其中一个图像,根据对称性,我们就可以画出哎底数或倒数的另一个指数函数的图像。那下面请同学们在同一个直角坐标系中画出 y 等于三的 x 四次密的图像。 哎,那么我们通过对称性就可以画出 y 等于哎三分之一的 x 四微的图像。 那我们画出 y 等于四分之一的 x 四微的图像。哎,我们是不是就可以画出 y 等于四的 x 四微的图像了? 这是 y 等于四分之一的 x 次幂的图像。哎,根据对称性,我们就可以画出哎 y 等于四个 x 次幂的图像。 好,那下面呢,请同学们观察 函数的解析式以及函数的图像,他们具有什么共同规律呢?同学们可以从定点的角度以及单调性的角度去发现问题。 好,谁先来说一说,嗯,好,第二排。那同学,哦,你发现他们每一个函数图像都经过定点零一,哎, 那这是为什么呢?哎,当我们把 x 等于零带入,那么 y 就 等于 a 的 零次幂,哎,任何数的零次幂都为一,因此横过定点零一。好,那谁来说说单调性的规律呢?嗯,好,后中。 哦,你发现当 a 大 于一的时候,函数图像都是递增的哦,当这个底数,哎,在零到一之间的时候,都是单调递减的, 非常好,请坐。那,因此我们就可以将 a 分 为两种情况,一种是 大于零小于一的情况,哎,另一种是 a 大 于一的情况, 当零大于 a 小 于一的时候,它是单调递减的,它是在整个定义域 r 上都是单调递减的,哎,那因此它就是一个减函数。 那当 a 大 于一的时候,在整个定域上都是单调递增的,那因此它是哎增函数。 那下面呢,我们就可以做出哎函数图像,当 零大于 a, 当 a 大 于零小于一的时候,函数图像,哎,在整个定域上都是递减的,并且呢,它横过定点零一, 那这就是 y 等于 a 的 x 次乘以,此时 a 大 于小于一,那当 a 大 于一的时候,在整个定域上都是单调增的,并且横过定顶零一, 那这就是 y 等于 a 的 x 次幂,此时 a 大 于一的函数图像。哎,那我们通过函数图像呢,我们可以观察到它们的值域都是怎样的呢? i 都是属于零到正无穷的,哎,那这个零可以取到吗? 嗯,取不到,它们都是无限趋近于零,但是不与零相交的。 那这样呢,我们就从图像中归纳出了性质,并且呢,也由性质做出了函数图像。下面我们学以直用, 请同学们判断下面三组数的大小。第一个, 一点七五的二点五次米与一点七的三次米的大小。第二个,零点八的负根号二次米与零点八的负根号三次米的大小。 第三个,一点七的零点三次米与零点九的三点一次米的大小。 我们是不是都可以将他们抽象成指数函数啊?哎,那对于第一个而言,他的底数是大于一的,因此他在图像上应该是递增的。嗯,那自变量越大,函数值就会越大,因此,哎, 前者小于后者。那第二个呢?哎,我们发现他的底数是介于零到一之间的,因此他在图像上是递减的。嗯,哎,这里的自变量, 哎,负根号二是大于负根号三的,因此前者就是小于后者的。 那对于第三个呢,我发现他们的底数和指数都不相同,哎,那我们还可以去分析一下,这里的 a 是 大于一的,嗯,哎,他是零点三,那他是不是在是在这个位置, 那因此它的值一定是大于一的。那再看零点九的三点一次密,它的底数是介于哎零到一之间的,那么它是 满足这个函数图像,它的指数是三点一,介于哎这个位置,那因此它的函数值应该是介于零到一之间的,那因此前者一定大于后者。 本节课呢,我们类比密函数的图像和性质的研究方法,又研究了指数函数的图像和性质。好,课下呢,请同学们完成书后习题,本节课就上到这下课。
86g(0) 55:35查看AI文稿AI文稿
55:35查看AI文稿AI文稿函数嘞,这个东西,如果我们去纠结他的这个定义的话,他是蛮严谨的东西,蛮严谨, 但是呢,我们这个基础考试,对于严谨的东西没有必要,咱们也不不考研究生,不搞证明。所以我简单的给大家讲一下,什么叫函数啊?什么叫函数? 就是说题目里边,比如说给的是这种形式, y 等于 x 的 平方加三, 这种我们就叫函数,就叫函数。那这个函数呢?我们叫做什么呢?叫做具体的, 具体的函数,就是说 y 和 x 的 关系,它们是,哎,明明确确的,我 y 就是 你 x 的 平方加三, 这个叫具体的函数。那如果题目给的是这种,比如说 y 等于 f x 啊,或者是 g x 啊, 这种形式,当然或者说大 f x 都没关系,就说像这种他没有明确的给出来。像这种呢,我们就叫抽象函数 啊,叫抽象函数,哎,大家懂这个意思就行了,懂这个意思就行了。好,现在咱们讲另外一个问题,比如说这是 y 等于 x 的 平方加三。好,他会限定你,比如说他给你个要给你个前提条件, 比如说,哎,人的寿命,比如说人的一个寿命,人的寿命至少也,呃,不说别的,至少也大于等于零嘛, 都不可能说一一天都没活到嘛,是不是?哎,他就是有个范围,比如说他给你个范围, x 嘞,是大于等于一小于等于三啊,我举个例子, 那么给了这么一个 x 的 范围,那么这个范围,哎,它是 b 区间啊,这个是 b 区间, b 区间呢?就这样写 啊, x 呢,属于这个范围,如果是 x 大 于一小于等于三啊,那就这样写。开区间,左边是开区间,那么就是一到三,右边是 b 区间,那么这一个呢?就叫做什么呢?就叫做定义域, 叫定义域,就是说 x 的 取值范围就叫定义域。 好,那么对应啊,对应,这样就是说你 x 有 一个范围,那么我问一下大家,这个 y 是 不是也相当于确定的一个范围,对不对? 你 x 的 范围定了,那么 y 的 范围它也就定了,那么 y 的 范围就叫什么嘞? y 的 范围就叫直域。 好,定义域,直域的意思懂了没有啊?懂了没有,哎,懂了,好, 好,这是定义域值域的一个概念。好,现在咱们来简单的看一下定义域常见的三个限制条件,就是说,呃,比如说啊, y 等于 x 的 平方加三,就是说, 呃,题目他会特别的说明,比如说,我就说 x 是 在一到三这个范围, 这个这个定义域呢,就是人为约定的,或者是说有条件的定义域。那如果说,我不说这个, 哎,我不说这个,那么比如说啊,像这个我不说, x 大 于等于一,小于等于三,那如果单独的给你这么一个函数,我问一下大家, x 是 不是任何值都可以, 是不是任何值都可以,对不对?那么不给他约束条件的这么一个定义域,那么这个叫做什么呢?叫自然定义域, 叫自然定义域啊,自然定义域就是我不人为的去约定他,或者是说,呃,有一些,呃约束条件,约束 就跟咱们人人的寿命一样,人的寿命至少是大于等于零的,就是这个是相当于约定俗成的东西啊,有条件限制的啊。好,现在咱们来看一下 自然定义域啊,自然定义域的三个限制条件。比如说这么一个函数,这么一个函数,我问下大家,分母能不能等于零?我问下大家,分母能不能等于零? 不能等于零,所以他不说,我们也知道列 x 是 不能等于零的, x 不 能等于零, 这个就是说这个函数的性质。哎,有这么一个要求,就是函数的一个性质有这么一个要求, 像这种,你看像这种,我问一下大家,因为它是带根号,带根号,那这个 x 能不能取负? 能不能小于零?就根号线能不能小于零啊?都不能。所以就是说这种函数就要求了 x 要大于等于零, 对不对? x 要大于等于零啊。好,来看下这种像这种呢,哎,这个是对数,这个叫对数啊,对数呢?哎,也是必须大于零的, 这就是函数的性质,哎,对,他这个定义了有一个限制条件。好,这一个一说,大家应该都没问题啊。来看一下这个,来看下他, 来看下他的自然定义域啊,自然定义域,首先这边是不是就要求了 x 不 能等于零,就是说这个地方 啊,这个地方要求了 x 不 能等于零。好,这边呢,这边就要求什么,一减 x 的 平方是不是要大于等于零? 一减 x 的 平方大于等于零,所以 x 呢,你必须大于等于负,一小于等于一, 那么这两个合起来,这两个合起来,所以他的定义域呢,就可以写成负一到零,并上零到一,就说他的定义域,我们就搞定了。好,懂这个意思没有? 兄弟们懂这个意思没有?懂了吧?好,这就是定义域的意思。好,定义域呢,我就讲这么多啊,后边虽然也给了两个,给了两个我不讲了啊, 因为定义域呢?呃,考试他没有,呃,这么多年好像没有单独去考这个定义域这个东西 啊,因为这是也是咱们高中,高中函数呃,知道的东西啊。最后提一下,好,现在咱们来看一下什么叫分段函数。分段函数就是这么个意思,分段就像这种,你看 这种呢,叫分段函数。比如说啊,我们刚才讲的 y 等于 x, 方加一,比如说 x 大 于等于一,小于等于三。大家看一下在整个的定义域, 就是说在整个的定义域,它的表达式是一样的, 就是在定义范围内,它的函数的表达式是一样的,那么这种它就没有分段,像这个你看像这个就不一样,你看啊,它在 x 小 于零的时候, x 小 于零的时候,它的函数表达式呢,就是 y 等于负 x, 在这个范围的时候,它是这种函数关系式。哎,在这个范围的时候, a y 等于 x 有 这种表的关系,也就是说不同的段 它的函数关系式是不一样的,那么这个呢,就叫分段函数,叫分段函数。好,这个分段函数的意思明白没有?明白,咱们敲个一,好吧, 好, ok, 好, 现在咱们来看基本的初等函数,基本的初等函数,呃,这一个大家我今天也提前给大家发了。 呃,大家要知道啊,要知道第一个 y 等于 sin x, y 等于 cos x, y 等于 twenty x, y 等于 quarter x, 还有 y 等于 a 的 x 次方。注意这一个的话,大家记住有一个是 a 大 于一, 一个是 a 大 于零小于一这种情况,然后就是 y 等于 log a x, 同样的他也有两种情况,一种是 a 大 于一的,一个是 a 大 于零小于一。这几个函数的图像 我呃,提醒大家要要自己去复习一下,就是说我们的考试范围,我不要求你太复杂,比如说像这种函数,它的图像你说你不知道就不知道了 啊,你说你不知道就算了。呃,我们在正常的考试范围内,这几种函数图像,当然,呃,还有一个 y 等于 x 的 平方, y 等于根号 x, 这几种图像大家要知道,因为我们做题的时候呢,呃,经常会用到这个函数图像 啊,经常会用到,所以大家自己,哎,脑补一下,回去自己补一下。好吧,我这里呢,也不不讲了, 关于这个图像这个文件我上传到了微盘啊,微盘里边啊,大家不需要知道的太多太多,你就知道这几种基本的就行了。好吧,好,现在咱们来看一下啊,基本的初等函数呢,像这种我们叫密函数, 像这种呢,我们叫指数函数,像这种呢,我们叫对数函数。好,三角函数,三角函数的变换公式很多,变换公式很多 啊,我要求大家记得,当然 y 等于三 x, y 等于 cosine x 等于 cosine x 等于 cosine x 等于 cosine x, cosine x, cosine x, cosine x 等于 cosine x。 当然还有个三个 x, sec, sec 叫郑,叫郑戈,这个叫于戈啊,应该是这个戈吧啊,郑戈和于戈,那么 sega x 等于扩散 x 分 之一, cosine x 等于 cosine x 分 之一,这个关系大家要知道啊,这个关系大家肯定要知道,就是 cosine x 等于 cosine x 分 之一, cosine x 等于 cosine x 分 之一好,同时三角函数的变化 我在前面也提到了,你那些什么棒角啊,什么和差画几啊,什么积画和差呀,那些都不要管,你就知道这两个就行了,你就知道这两个就行了。三 x 等于二倍三 x 和三 x, cosine x 等于 cosine x 的 平方减 cosine x 的 平方等于二倍的 cosine x 发减一等于一,减二倍的 cosine x 发。 就是说三角变化,你有了这两个就可以了啊,再复杂你也不要去记了。我也没有记,因为我觉得呢,哎,我记这些就够用了, 够用就可以了,你千万不要说你想着去储备,没有必要。这么多年都考试都没用到。那按六年考试,实在用到了这道题不会就不会嘛。我们又不是造火箭,又不是发泄卫星, 又不搞原子弹,我们搞一百三十二分就行了,你实在要要考超超出这个水平就算了,是不是那一分也无所谓,是不是啊?好,现在呢,咱们讲这个,这个叫什么呢?这个叫反 阿格三 x 叫反正弦啊,这个叫反正弦, 叫反证钱。大家要记得这个 x 的 范围是从负一到一啊,那么 y 的 范围呢?就是,呃,负一到一的话,也就负二分之派到二分之派。 好,阿根廷的 x 嘞,这个 x, 这个 x 啊,是从负无穷到正无穷,那么对应的 y 就是 负二分之派到二分之派啊。负二分之派到二分之派好,这是基本的出场函数。好。常用的 运算公式常用的运算公式啊,这个有这几个就行了啊。有这几个就行了。你看现在这个我都写了的啊。 哎,这个我都写了的啊,这个我都写了的。好像这种 a 的 x 次方乘以 a 的 y 次方,就等于 a 的 x 加 y 次方,这个也不详细讲了啊,那么 a 的 x 次方比 a 的 y 次方等于 a 的 y x 加 y 次方。好,这个我都不讲了啊, 哎,这个给大家强调一下这个给大家强调一下。 a 的 x 次方在 y 次方是等于 a 的 x, y 好, 烙印 x, y 是 等于烙印 x 加烙印 y, 烙印 x 比 y 等于烙印 x 减烙印 y 好,烙印 x 的 y 字方是等于 y 倍烙印 x。 这个都是性质啊,大家也不要问我怎么来的,大家知道当姐妹记住就行了。好,最最重要的,当然这个也重要啊,这个也重要, 这个也重要。好,现在最最重要的是这个。注意,这里的 a 不是 单纯的, 不是单纯的 a r, 大家不要说,哎,我如果是 b 行不行呢?我问一下大家,这个地方如果是 b 行不行啊? 你不要说看到是 a 就 一定要是 a r。 我 发现咱们兄弟们有比较死板,他他,这,如果我给的是这样的 x 等于一的绕 x, 那 他就一定认为,哎,这里是 x 啊,这里是 x 啊。 那如果说我搞成这样, x 的 平方等于一的绕 x 的 平方呢?他说了,哎,老师,你这里是 x 的 平方啊, 你这里是 x 啊,好像不一样啊。注意啊,这个 a 代表什么嘞? 代表一坨,我管你是一坨什么,是一坨屎也行, 是一坨黄金也行,反正这一坨和这一坨一样,就对应起来了,就对应上了。注意啊,这个变换经常用,我们在求极限的时候啊, 或者是求导数的时候,那家伙是经常用,哎,比如说他可以是这样,比如说 f x 等于一的烙印 f x, 只要他们对上了就 ok 啊,大家记住啊,他不是单纯的 a, 他 是代表一坨东西啊,这个地方大家明白没有?这个地方明白没有?明白,敲个一过了,好吧, 好注意啊,这一页都是干货啊,这一页都是干货,在咱们后边的计算的过程当中,会经常的用到,会经常的用到啊,好,现在咱们讲符合函数, 哎,符合函数大家懂意思就行了啊,比如说啊,比如说 y 等于 x 加五 这种函数呢,我们叫简单函数,也就是说 y 和 x 呢,就直接对应的这么一个关系,但是如果是这种 y 等于什么呢?等于 sine x 的 平方啊,假设大家看一下, 首先呢,哎,它这里,这里是直接的 x, 它这里呢是 x 的 平方, x 的 平方以后再加了个 sin, 那 么它这种形式就是可以写成 y 等于 f g x 这种形式。 哎, g x, g x 就 相当于这里的 x 平方, f 呢, f x 就 相当于 sin x 这种关系, 就是说这个 x 呢,先组合,组合以后再取了一种函数,这种呢,我们就叫复合函数,所以我们,呃,面临的基本啊, 基本都是符合函数啊,基本都是符合函数。好,现在咱们来讲函数的性质。哎,奇偶性,奇偶性, 呃,我看一下啊,有奇偶性,单调性,有界性,还有一个周期性, 周期性啊,这几种性质,像周期性呢,一般考的少,呃,主要就是考极偶性啊,单调性啊, 呃,这个呢,是高中数学学过的啊,你就死扣定义,注意 死扣定义就行了,死扣定就是满足什么条件呢?就是注意啊,是对任意 x 属于,属于什么呢?属于定义域啊,注意,只要这个 x 定义域。注意啊,定义域是这样写啊, 我这里用的文字就是说对于任意一个注意一定是任意一个啊,不是说特殊的一个字满足就行了,是任意 x 属于定义域,只要 x 属于定义域, 他都满足一个什么呢?第一个,如果你这个 x 属于 d, 那 么这个负 x 也属于 d, 意思就是什么意思呢?就是说你首先定义域,首先是对称的, 首先你这个定义域你要是对称的,比如说啊,像这种, 比如说像这种啊, y 等于 x 的 平方 x 呢?它是属于这个范围,负三到四这个范围。那我问一下大家对于这么一个定义域的,呃,有没有必要去讨论奇偶性 啊?有没有讨论奇偶性的前提了? 首先你这个定义域就不对称,他必须是这样的,哎,就是说一定是复式到式这种,一定是关于原点对称的 这么一个,我们才有讨论酒性的前提条件。好,这个地方明白没有?明白,敲个一。好吧, 这个地方明白,咱们挑个一。好, ok, 这里明白了啊,好,第二一个大家注意,对对任意的啊,注意,任意的 x 属于 d, 任意的 x 除以 d, 如果满足什么呢? f 就是 说取一个负 x 值,它是等于,哎,等于这个的就是满足这个,我们就叫什么呢?叫偶函数。 那如果是这种呢? f 负 x 等于什么呢?等于负的 f x, 满足这个的呢?就是奇函数,那你碰到奇偶性就死抠这个定义,你就死抠就行了。 好,第二个,记住,好,记住啊,奇函数的图像关于原点对称,偶函数图像关于 y 的 对称,那么这个呢?选一下就知道,比如说 y 等于 x, y 等于 x 就是 奇函数,你看它的图像是这样的,哎,是这样的, 你看它是不是关于圆点对称,关于圆点对称吧,你看这是圆点,你看这边, 转一百八十度就到了这边,它关于圆点对称的偶函数。偶函数呢?你 y 等于 x 方, y 等于 x 方,它是这样的,你看,哎,是这样的。抛物线嘛, 是不是?它是不是关于 y 轴对称,关于 y 轴对称啊?好,这是偶函数 g 函数的一个性质。来,我们看题啊,哎,看一下题, 已知函数,已知函数满足这个,这 f x 是 什么?哎,这个题稍微有点点难度啊稍微有点点难度,这是我搞的模拟题啊,我自己搞的题,立体 像这种题,哎,他比较抽象,他也没给你具体函数像这种呢。首先,像这种题我们都是干什么呢?哎,我们一般像这种情况,我们先取一个什么呢?取特殊值啊, 都是取一个特殊值来,取一个 x 等于 y 等于零, 先取一个特殊值,搞一搞,大家看下。搞一搞啊,你看就变成了,也就说 f 零加零等于 f 零加零, f 零加零就是 f 零嘛, 就是 f 零,也就是说可以推出 f 零等于多少啊? f 零等于多少, 是不是等于零?哎,等于零来,先搞了一个 f 零等于零了。哈,第二个啊,第二个, 第二个,注意啊,兄弟啊,这个是函数形式,注意,这一个 y 和这个 x 只是一个变念啊, 就说这个 y 和这个 x 是 没有任何关系的,这只是给了一种一种函数形式,就说这里边的 y 和这里边的 x 都是自变的, 他们之间没有任何关系。啊。啊,好,得到了 f 零等于零,好,第二一个,第二一个取特数字啊,这个呢,大家一般想不到,要熟练的做,熟练的就知道取一个什么呢, 你不要说,哎,我再取一个 x 等于 y 等于一,那你就你就误入歧途了。像这种呢,一般是取什么呢? y 等于负 x, y 等于负 x, 你 看 y 等于负 x, 也就说 x 加上 y, y 就是 负 x 等于什么?等于 f x 加 f 负 x, 大家看下这个是不是就是 f 零 x 加负 x 是 不是就是零 x 加负 x 就是 零啊?哎,等于零,大家看下它等于零了,也就是是不是可以得出 f x 等于负的 f 负 x, 也就是说 f 负 x 等于负 f x, 所以 就是积函数,所以就积函数。好,这道题大家明白没有?明白咱们敲个一好吧。哎,明白,你敲个一, 这很多兄弟嘞。哎,这一步有点想不到啊。想不到没关系,你能听明白就行了,后边做的多了你就想的多了,对不对?熟能生巧嘛,是不是啊,你咋能听明白就 ok。 好, 来我们做题 啊,我们做题来像考试了也考过九星,你看他说问这里是什么?基函数,偶函数,来,我们先搞后边,好吧。 呃,先搞前面吧,先搞前面啊,搞完前面再搞后面,可能会简单一点点,大家看看判断偶函数还是判断基函数,一般都怎么判断? 你看 f x 这个它这个具体函数,具体的函数。对,我们就是取一个什么呢?取一个负 x, 我就看一下你们俩是什么关系,如果是这个关系,那你就是加数,如果是这个关系就是偶函数,那我现在我就来看一看,是不是我看一看,你看取一个负 x, 大家看一下啊, x 的 时候这里就这样的,那我负 x 呢?我负 x 是 不是就是一的负 x 减一,一的负 x 加一。 首先告诉我这个有没有问题?兄弟们,首先告诉我这一步有没有问题?没问题,好,再给它变形, 再给它变形这个基本的运算啊,哎,你的一的负 x 是 不是一的二 x 分 之一? 好,这一不变形有没有问题?告诉我兄弟们,这一不变形有没有问题?没有吧。好,那么我同分,我分子分母同时乘一个,分子分母同时乘一个,这个鬼东西 这就变成了一减一的 x, 再一加一的 x, 是 不是?好,我提一个符号出来,分分母,分母提啊,分子提一个符号出来就是负的 一的 x 减一,分母嘞,就一的 x 加一,提一个括号出来,是不是就等于负的 f x 啊? 啊?对不对?大家看一下,是不是就是奇函数?是不是就奇函数? 是奇函数,好奇函数。来,现在我们讲啊,讲一下另外一个问题,咱们讲了奇函数的图像关于什么对称, 就说我们刚才讲了奇函数的图像关于什么对称? 对,关于原点,就是说他要么像像,比如说我取一个啊,比如说 y 等于三 x, y 等于三 x, 你 看,哦,不行,这个不行啊,你除非限定那个范围,就 y 等于 x 吧。 它关于原点对称,它就是说随着 x 的 增加,要么就是单调,干什么?哎,马上就要讲单调线啊,要么就是单调增,要么就是干什么, 你要么就是增加的,要么就是干什么,是不是要么就单调减, 知道,要么就是增加的,要么就是递减的好,所以像这个求值域,你看求值域啊 求值域,你既然是单调增,单调减,那我 x, 我 就取一个什么,取一个负无穷,取一个正无穷,我代入算一下 就可以了。但这个就涉及到求极限了啊,以极限的内容呢,我们又还没减,没关系,在这里不影响。你看,我取一个,我 x 取富无穷,取富无穷的话 啊,娶富不穷的话啊,娶富不穷的话,大家看一下。娶富不穷,这个就是多少啊? x 取负无穷,对,它就是零,也就说 f 无穷呢,是不是就是负一? f 无穷就是负一,那么 x 取正无穷呢? x 取正无穷,那么这个就是多少?是不是无穷大?我问下他取无穷大的时候,这个负一和一,呃,可不可以不要了?我们这里就涉及到求极限了啊。 啊,就涉及到求极限了,就是说在无穷大面前,你这个负一一都可以不要了吧啊,这个东西是不是可以不要了? 那么一比, f 正无穷是不是就是一就一,对不对一,所以它的值域范围就是负一到一, 负一到一。好,这就是这道题,这道题。好,现在咱们来看这道题,注意,这道题呢?呃,有公式啊, 这道题有公式,但是嘞,那公式我不建议你去记,没必要我们就分析啊,大家看一下啊, f x 是 偶函数, g x 是 奇函数,它说下列函数中为奇函数的来,答案是 d 啊,答案是 d, 我 就减 d, 好 吧,因为这些呢,都是偶函数啊,这些都是偶函数,我就给大家减一下 d, 好 吧, 我就给大家减一下 d, 你 看,它是奇函数, 它是 g 函数,那么 g 负 x 就是 多少啊?啊, 是不是就是负的 g x, 是 不是负的 g x, 那 它在前面再加个 g, 也就说 g g 负 x 是 不是就相当于是 g 负 g x 到这一步,是不是?那么因为它是 g 函数,所以它呢,是不是就等于负的 g g x? 有没有理?有没有理啊?没问题吧?没问题,所以大家看下,它是等于它,所以它就是计算数, 他就是这样说啊,他就这样说。好,这个题大家明白没有?我们判断极偶性就一点,就一点,你是这个,你就是偶, 你是这个,你就是吉。哎,这就是判断吉偶性的出发点啊,判断吉偶性的出发点。好,这道题大家明白了没有?明白的话咱们往后走好吧。 啊,没问题吧?兄弟们,没问题,咱们敲个一,好吧, 好, ok, 现在咱们讲单调性,现在讲单调性啊,什么叫单调性呢?最呃讲单调性肯定是对于任意的啊,一定是任意的, 就是说对于任意的 x 属于,属于这个定义域啊,就说对于任意的 x 属于定义这个范围,属于定义这个范围。如果或者说只要 x 小 于 x 二, 就说你的定义值 x 小 于 x 二,如果满足什么呢? f x 一 小于 f x 二, 就是说我的 x 值比你大的时候,我的函数值比你大,那么这种情况我们就叫什么呢?就叫增, 就是说你 x 变大, y 也变大,这叫增,那如果反过来, x 一 是小于 x 二的,但是呢,我的函数值反而比你大, 那么这种呢,就叫减,也就是说你这个定义值变大了,函数值反而变小了,这就叫单调减,单调减啊,这个就是判断单调性的 定义条件,定义条件,注意一定是任意的, 任意的 x 小 于 x 都满足这个条件,它不是个别的啊。如果说,比如说我三小于四,那么 f 三小于 f 四,那单纯的说说这两个词,那你不能这么说, 你不能说它单调性,对不对啊?比如说像这种函数嘞,像这种函数嘞,哎, 像这种函数呢?比如说三,假设这里是三,这里是四, 你不能说 f 三小于 f, 四就是单调增啊。像这种我们就要干什么呢?就要分区间,就要分区间,哎,在这个区间,在这个区间, 在这个区间是单调增的,那么这个区间是单调减的,这个区间又是单调增的,所以像这种情况我们就要分区间去讨论。在整个的区间它是没有单调性的, 在整个的区间,你看它一会增一会减,一会增一会减的,在整个的区间它是没有单调性的。像这种情况我们就要分区间 啊,比如说在这个区间是真单着,真的在另外一个区间是单着减的啊,就去分区间讨论的,这是单调性。好,大家在这里你就记住这一个,记住这个定义就行了, 我们做题的出发点就从这定义出发。好,现在咱们讲有界性啊,什么叫有界性? 就是说对任意的 x 属于 d 啊,对于任意的 x 属于 d, 这个 f x 嘞都小于等于 k, 像这种情况我们就叫它叫什么嘞?叫有上进,就说你的最大值, 你的最大值有一个什么,咱们叫做什么?叫天花板 哎,有个天花板,你的最大值只只能到 k, 这个叫有上界。那如果是反过来这种情况呢? f x 大 于等于 k 呢?这个叫叫做什么?哎,叫有地榜, 这个就叫有下界啊。有下界。那如果整个 f x 比如说大于等于 k 一, 小于等于 k 二, 最小值也有限定,最大值也有限定,这个就叫又有上界又有下界啊。又有上界又有下界 啊。又有上界又有下界。来,我们来随便看一个函数,好吧。呃,看一下它吧,你看看下它 y 等于三 x, y 等于三 x, 它的函数图像是这样的。 这样的 y 是 不是大于等于负一小于等于一 对不对,它最小只能小到负一,最大只能大到一,所以它有没有界?我问一下它家有没有界, 他就有借吧。他又有上借,他又有下借。注意又有上借又有下借,我们才叫有借啊。 单纯的有上界不叫有界单纯的有下界也不叫有界,就又有上界又有下界才叫有界啊。来看这个,看这个最 x 有 范围啊。你看它的函数图像,它的函数图像就这样的 啊它的函数图像是这样的啊它的函数图像是这样的。我问一下大家像这种情况,那 y 总是大于啊,大于零啊, 等于取不到等于取不到啊。呃,没有等号也也是有借的啊没有等号也是有借的啊。没有等号也是有借的。好大于零。但是呢,他有没有上借? 它有没有上进?它没有上进。因为 x 取无穷的时候它取无穷啊,它没有上进没有上进。好像这个来 y 等于 x 分 之一啊。这个函数图像大家记得吗? 啊,这个函数图像大家记得吗? 它是这样的啊, 这样的,当然 x 零到一, x 零到一啊,假设一在这里,也就是说这边就不取了啊,你看零的话,到了这边是不是,是不是无穷大, 对不对?你 x 趋,呃,趋近于零的话,它趋近无穷大,所以它是没有商界的, 他没有上界,他有下界啊,下界的话就是一啊,下界的话就是一啊,这个叫有界性。这个了解一下就行了啊,了解一下就行了。这个也没考过啊,也没考过。好,来看下题目,好吧, 看下题目来看下这个题啊,当然偶函数还没讲偶函数没讲啊,但这个题也不涉及到偶函数。好吧, 也不是啊,干脆我把周期性讲了吧,把周期性讲了就。哦,函数已经讲了啊,因为这里涉及周期函数,干脆把周期函数这点讲了。好吧,周期性,周期性的定义。 什么叫周期性的定义?你就记住,如果存在,存在一个正数题啊,存在一个正数题,满足什么呢?满足 x 等于 x 加 t, 满足这么一个条件,我们就说它是周期函数, 我们就说它是周期函数,那么这个题呢就叫周期。这个题呢就叫周期啊,叫周期。 好,咱们现在减一下返航数啊,返航数也给大家减一下。好吧,什么叫返航数呢?就这个意思,比如说啊, y 等于 x 的 三次方。 哎,这个呢是函数,函数就是 y, 是 x 的 函数, 那么现在呢?我把它反解,注意,反解,反解出来的 x 就 等于 y 的 三看三次方啊, y 看三次方,那么这种呢,我们就称之为反函数, 我们就称之为反函数。好,大家注意,反函数呢,严格就是 x 就是 y 的 开三次方门,但是注意,我们解除反函数来以后,我们还是习惯这样写, 就说按道理是 x 等于 y 的 开三次方,但是我们后面的习惯还是这样写习惯呢?还是写成 y 等于 x 的 开三次方 啊?这些只是一种习惯啊,只是一种习惯,那么返航数就记住了这种形式 啊,这个图像呢,大家不要管,反正这个一般不考也没考过啊,也没考过。好吧,好,这就是返航数,大家注意啊,就是说我们反解出来以后, 最终我们习惯干什么呢?习惯这个 x 呢?还是用 y 来代替这个 y 呢?还是习惯用 x 的 代替? 就相当于我们还是表示自变量的时候,还是喜欢用 x 来表示,表示自自观量, 就这个意思啊。来,我们来看一道例题,你考试你不考,那我就搞搞例题来解,你看 y 等于这一个的反函数 啊,他等于这个的很繁琐,那我就反解,大家给讲反解怎么解啊?来,就是 y 减一就等于烙印 x 加二。 好,这一步变化大家可能就不会变了,大家还记不记得啊?我刚才讲的啊,呃, a 就 等于 e 的 烙印 a, 大家记不记得 啊?就这个大家记不记得哎,记得,那我问一下大家,呃, y 减一等于绕引 x 加 i, 那 我变成这种形式, 它应应不应该相等啊?就说你 y 减一是等于烙印 x 加二的,那我一的 y 减一是不等于一的烙印 x 加二,就说这个等式成不成立, 这个等式成不成立啊?我们讲的这个等式成不成立,应该成立的吧,你成立那这个肯定成立。好,那这个等于什么? 这个是不等于 x 加呀?就这个变化嘛,它是不是等于 x 加呀?那么反过来 x 是 不是就等于一的 y 减一再减二, 对不对?对不对?就是说他的返航数应该是这个。好,咱们讲了你返航数是这个,但是我们还是习惯写, 习惯写,哎,所以就习惯就到这里了,就把这里的 x 变成 y, 这里的 y 变成 x, 所以 答案选 d。 好, 这个题大家明白没有?明白咱们敲个一好吧。 啊,明白,咱们敲个一啊。好, ok, 呃,反函数给大家讲了,现在咱们就回头来讲一下这个题。好吧,讲下这个题啊,来,首先告诉我这种函数叫什么函数? 这种函数我们叫做分段函数吧。分段函数。好,来,先看一下啊,先看一下,他说在负无穷,正无穷内,哎。呃,单调减少, 单调减少是错的,像这种的可以画图啊,就说你可以画图,你可以画图啊, 可以画图,当然你也可以排除,也可以排除啊,也可以排除法。呃,来,我先看一下 c 对 不对吧。有界应该是不对, 有键应该不对。你看 x 大 于等于零,那 x 等于无正无穷的时候, x 等于正无穷的时候,它也是正无穷啊。它有没有键?它肯定没键,肯定没键。那是不是偶函数嘞? 是不是偶函数嘞?你取一个嘛,比如说,哎,我,我就取一个 f 一, 哎。 f 一 等于多少? f 一 等于二, f 负一呢? f 负一就在这里边在这里啊, f 负一在这里,一减负一的平方等于零,哎,偶函数肯定也不对, 有界肯定也不对,好判断,单链减少,单链增加了,你可以直接取值啊可以直接取值,我们对不对? 我们只要把分搞对了就行了嘛。不一不一定要严格按定义去搞,是不是啊? 好,这个题不讲了啊。比如说你可以取个二,再取个三,对不对啊?取个二,你看 f 二呢,是朝着你等于三, f 三呢?哎,就是四哦,增加的, 增加的至少不是减少的。那就就 ok 了啊,就 ok 了啊 哈。来看这个在定义域内,注意在定义域内,首先大家注意它的定义域就是 x 不 等于零, 对不对?就是 x 不 等于零吧,因为 x 在 分母,所以它不能等于零,就是 x 不 能等于零哈。像这种 这里边不管多么大, 就说你这个 x 分 之一 x 也好, x 分 之一也好, x 平方也好, x 平方之也好,我不管你这里边这一坨, 哎哎,我不管咱们,哎。以前的康师傅老师举的例子就是说我不管你是亿万富翁也好还是千万富翁也好,对不对?前面加了个什么东西呢? 加了个赛赢赛赢的就相当于加你一个败家子,对不对?加你一个败家子,你是千万富翁也给你败家了你是亿万富翁也给你败家了。就是说你这个东西不管你多么的大,我给你加个赛赢,那么 他的范围是不就是永远是负一到一,能不能逃出如来佛的手掌心?我只要给你框一个 set, 我 只要用个 set 给你框起来,你就是在负一到一这个范围。所以是有界函数啊,所以就是有界的。呃,是不是单调的呢? 注意它不是周期啊,它不是周期,如果 y, 呃,或者说如果 f x 等于三 x, 如果是这个啊,如果是这个是周期函数,但是 x 分 之一就不是了, x 分 之一就不是了,如果是三 x, 它就是周期函数, x 分 之一就不是的了啊,像这个肯定做的这个都可以排除的。啊。啊?为啥为啥?你就举个例子啊?好吧 好吧,你为啥就不去讲了啊?那就是真的就就就就。我这里只能说告诉你意会一下了。啊。啊?意会一下了,如果要去证明,那真有点难度。好吧,有点难度啊,好吧哈,来看一下这个题 啊,大家看这个题啊,在这个范围是奇函数啊,在这个范围是奇函数。好,它在零一上单调增,那么在这个上面就应该干什么? 基函数在定义域,我们讲过基函数在定义域它是有相同的 单调性的。你不行,你就用这个举例,哎,你就用这个举例, 哎,用这个举例,你看零到一,哎,增加的,零到一是增加的,那负一到零也应该增加, 就是说基函数在定义域内是有相同的单调性的,有相同的单调性的,这一个是基函数的性质啊,基函数的性质。
 04:18查看AI文稿AI文稿
04:18查看AI文稿AI文稿在机器学习或者说是其他群众的,含群众的这种算法里,我们通常都会见到指数函数的影子。今天呢,我们单独把指数函数拿出来说一下,那么指数函数通常指的是 e 的 x 这个指数函数,那他有什么特点呢?标准的指数函数占一,然后这是急速上升的,这是急剧趋于零的。 那么对于这种我们数据的划分,我们可以看到指数函数他的特点是啥?他超过一之后,这个是急剧上升 啊,小雨的部分,他会快速衰减至零。那对于整体数据来说的话,这一部分我们可以看成是什么东西呢?这一部分我们可以看成是他消失的部分,而这一部分呢,我们可以看成是啥呢?他是一个无限高的一堵墙, 就是当我的数据在这一部分的时候,我认为他是数据就是趋零的这一部分是一个无限无限高的一个墙, 就是急速上升。那我们实际在算法中,我们对于数据的处理基本上就是在干什么呀?其实就是在做数据、做标识、做分类 或者做预测,那么做分类标识预测的时候,就是对数数据打标签。那么对于指数函数来说,他这部分趋于零的,我其实相当于是给他变相的打一个零,趋于这种高阶的这种趋于这种特别大的这个数值的时候,我们尽是相当于在这个地方他是一个划分数零。嗯,那么常见的我们像逻辑回归, 逻辑回归在这里面它是一加上了 e 的 w、 t、 w、 x, 这有时候会有个 b, 有 时候也会有个复数,它其实是这是逻辑回归,逻辑回归呢,对吧?它是这样一个函数。嗯, 那我们在神经网络里面,它的激活函数也大概是这样一个形式,其实逻辑回归就是一个没有没有隐藏层的一个多元, 就是多多路输入,然后单元输出的一个最简单的一个基本的一个神经网络可以看成是这样,那么他其实就是在这样一个, 就是他把指数函数放到蜂母上了,是因为这个地方我要去做度量后,我要给他给一个上确解,就是我让他去 我不想要的部分,让它无限趋于零。而它上一部分的时候,我们为为什么神经网络一开始要用这个 sigma 的 这个占了个函数? sigma 的 和这个是很像的,也是在分母上加了一个指数的一个东西,那么其实就是给它限定了个上确界, 就我我,我去做分类的时候,要么是一,要么是零,我不希望它是个很大的数,因为我回头还需要去做整理,就是它是加了一个外一的分享,就是加了一个上确界的一个形态。嗯, 这是在逻辑回归神经网络里面的 sigma 的 计算函数。那么我们在以群算法里面, 在以群算法对于信息素的释放,对于信息素的释放,也是用到了一个指数函数,它是一个 alpha beta, alpha 加 beta 的 一个。这个式子回头我在评论区放一下,有点复杂,但是它依然用到了指数函数,只不过它的指数的这个底,它不是一个自然数 e, 我们常见的大部分用自然数 e, 主要是为了就是因为 ex 它的一个微分或者积分对它求的还是它函数本身嘛?嗯,它它是个自然增长的,所以要这样去用,那么在已知算法我们通常也是用这样的, 那么再把这个进阶一下,我们正态分布,正态分布 e 的 x 减六平方,负的,然后是二的七个满平方,然后前面一堆 根号下二派,然后是一个马分之一。我们看到这一部分,他也是用的指数函数,就是说他描述了一个基本的一个自然逻辑,我在有效区域内的东西,他其实这些值差值,我们看到他其实是相对衰减偏弱的,当 突然到某一个值的时候,外围延拓的时候,他突然就会衰减到零。我们通常就是取这个就像一个平台,就像一个平面上我突然顶起来一个凸起一个东西,对吧?他其实就是我从 数据这种超微空间的数据是这样的,我中间的部分我要做区分,我就是把中间给他凸起来,我从水平界面凸起来之后做一个切割就能做区分。嗯, 那么正态分布,我们看到他就是这个用指数函数套了一个二次函数,做了一个对称形态,形成了一个中间一个平台,凸凸的一个台子,那么通过凸的台子去顶起之后,就是把空间 进行非限性的这种切割。所以说指数函数的算法有大量的运用在群智能里面,以群算法在逻辑回归、激活函数,诸如此类,他指数函数有太多的地方去用。
94哲衍同师 02:39查看AI文稿AI文稿
02:39查看AI文稿AI文稿一个口诀,教会大家指数运算,另外关于指数运算的必备公式,李姐都给大家整理好了,如果你还不知道背哪些公式的话,那你一定要拿去记一记,拿去看一看。好,那我们来看一下这里的指数题目。碰到这种 右上角是分数的题目,我们用四个字可以解决,它叫做母外子内,母是指的分母,子是指的分子,外是指的分母放在外边,内呢是指的分子放在内部。拿第一个题来说,四的二分之三次方,这个三是指的分子,这个二是分母。直接写一个大根号,这里的四直接照抄下来, 然后分母放在外边,二放在外边,分子放在内部,三放在内部,所以他就等于四的三次方,然后给他开二次根号,也又等于四的三次方是等于六十四的根号六十四,所以这里是等于八的。接着我们来看第二个同样的道理,母外子内直接写一个根号,八照抄, 这里是分母,这里是分子,分母放在外边,分子放在里边,所以这里是根号下六十四啊。对,它开三次根号,那三次根号下六十四等于多少呢?它是等于四的,因为四的三次密是等于六十四的,所以这里结果是四。好,接着我们来看, 如果右上角他出现了负号,这里有一个负的二分之三啊,负的三分之二,这个时候该怎么办?我们把它称为负号变长,用这四个字解决这种题目。负号变长,把这里的小符号变成大横线,变长了,直接四的二分之三放在分母底下,分子直接一个一, 比如说这里的小负线变成了这里的大横杠了,所以剩下的东西就是四的二分之三次方,直接放在分母底下,然后分之一就行,那剩下的我们就又变成了,哎,右上角是一个分数,那又用到这个母外子内了, 所以这里四的二分之三次方,母外子内。刚才我们已经算过是八,再算一下就是给四,然后母是分母放在外边,分子三放在里边 就是根号下六十四,所以这里是八。好,那结果就是八分之一。接着我们来看一下八的负的三分之二次方,好,这里的小负号给他变长变成大横杠 就变成了八的三分之二次方。分之一,那又要求这个八的三分之二次方等于多少?好,同理给他母外子内一下,这也是分,母是三三放在外边,子呢是放在 内部,所以这里得出来是等于四的,那分之一的话就是四分之一,所以碰到指数右上角是分数或者是负分数的时候,可以用这两句口诀直接解决,它就是母外子内和符号变长。同学们,你们听懂了吗?听懂的同学记得点个关注和收藏,免得下次找不到了。
646梨姐单招数学 03:02查看AI文稿AI文稿
03:02查看AI文稿AI文稿考前急救系列零基础速通指数函数必考点,扔掉书本当研法,让你考试直接口算 每年必考的指数函数三大项,增减性、过定点求值域我们先看第一个增减性问题,指数函数 y 等于 a 的 s 方,当中的 a 控制了它的增减性,如果 a 大 于一,它就是一个增函数。如果 a 小 于一大于零,它就是一个减函数。 比方说二大于一二的 x 方,随着 x 增大, y 值就是增大的。比方说二分之一的 x 方分之一就属于一到零,随着 x 增大,二分之一的次方就会变得越来越小。来看第一题,若 y 等于一,减 a 的 s 方在 r 上是增函数,则 a 的 取值范围 值。函数函数是增函数,那么就是这一部分必须是大于一的,也就是 a 小 于零,对应的选项就是负无穷到零。大家看第二道 已知函数 f, f 等于 a 的 s 方, a 小 于一大于零,则 a 小 于一大于零,说明这个指数函数它就是一个减函数,那么减函数随着 s 值增大, f x 值是在减小了,看选项哪个满足这个条件。负二增大到三,但是 f 负二大于 f 三,说明选项 a 是 对的。第二个过定点问题,这里考到了一个 a 的 零次方等于一,当然这个 a 有 要求 a 不 能等于零, 任何一个非零数的零次方等于一。那么看第一题, f, x 等于 a 的 x 加一次方的图像过定点,那么它过的定点一定是 a 的 零次方等于一,那么对应这个零的位置就是 f 加一,也就是有 f 加一等于零,解出来就是 f 等于负一, f 等于负一时, a 的 s 加一次方,也就是 a 的 零次方等于一,也就 f 负一等于一 零点就是负一。一看选项,选择 c。 第二题,已知函数 f s 等于 a 的 s 加一次方,减一,横过定点,是在第一问基础上减去了一个常数项负一。我们分开先看,先看 a 的 s 加一。刚刚已经说了,当 s 等于负一时,有 a 的 负一加一次方,也就是 a 的 零次方等于一, 那在这个基础上,我们再减去一个一就可以了,也就是它 a 的 负一加一次方,减去一个一,也就是一减一等于零。那过了点,那么这个呢?就是当 s 等于负一时的 f 值,那过了点就是负一零。 这道题选择 f。 第三个,只有你函数 y 等于一加三的 x 方的值域,这里考到了我们说的 a 的 x 方是大于零的,当然 a 有 要求 a 是 大于零的,那么这道题呢?是三的 x 方, 三个 s 方必然是大于零的,在这个基础上加了一个一来不等式,两边三个 s 加一,右边也要加一,那么这个不就是 y 的 值域,也就是 y 是 大于一的,那么对应的值域就可以写成一到正无穷。选择 c。
236中职数学老邵(单招对口) 24:07查看AI文稿AI文稿
24:07查看AI文稿AI文稿抖音寒假公开课,我们一起来学习中职数学基础模块下册的内容。本视频参考教材为左下角高等教育出版室基础模块下册第三版,视频中所有内容为零基础的讲解,基础差的同学也可以放心观看。 下册的第一章就是指数函数与对数函数,我们先来看一下他的知识结构,我们要学习的内容有五个点,第一个就是实数指数密,我们会介绍到有理数指数密和实数指数密,第二个就是指数函数, 前两个也就构成了我们第五章指数函数的内容。第三个内容就是对数,会介绍到对数的概念,记商密的对数, 第四个就是对数函数,那第三个和第四个就构成了对数函数的内容。最后就是指数函数与对数函数的应用,这个应用我们目前不要求大家掌握,考试的考点也是比较少的, 我们在学习的时候主要还是要知道指数函数与对数函数,它们的一些运算规则,大家一定要非常的熟悉, 这是他的知识结构。我们来看一下具体内容的讲解。第一个内容,实数指数密,我们先来看第一个有理数指数密, 我们在中学的时候呢,已经学习过了整数指数密的知识点,但是呢,在实际的应用中,密的指数呢,不一定是整数,他还可以是有理数,无理数,也就是我们的实数。那我们中学的时候呢,已经学过了 n 个相同因子, a 的 连乘积呢,我们记住了 a 的 n 次幂,这里面呢, a 呢,我们称它为幂的体数,简称的就是底, n 的 话呢,就是幂的指数,那我们把它展开之后呢,就是 a 的 n 次幂呢,就是 n 个相同的 a 连乘, 当 a 不 等于零的时候呢, a 的 零次幂呢是一,这个呢大家应该是比较熟悉的,如果是 a 的 负 n 次幂的话呢,我们就可以给它变成分数的形式,也就是 a 的 n 次幂分之一,那我们给它括号,括起来之后呢,就是 a 分 之一的 n 次幂。 如果数 b 的 n 次方呢,等于 a, 也就是 b 的 n 次方等于 a, 那 么我们就乘这个数, b 呢为 a 的 n 次方根。这个概念呢,我们简单了解一下, 当 n 为偶数的时候呢,哎,正实数的 a 的 n 次方根呢有两个,那当 n 为基数的时候呢,输入 a 的 n 次方根呢,只有一个,这个呢大家也是比较好理解的,如果是偶数的话呢,我们分别用负的 和正的来表示,如果只有一个的话呢,就用单独的正的来表示。另外呢,这个负实数 a 的 n 次方根呢,它是没有意义的。这个有个印象, 零的 n 次方根呢?还是为零,那我们形容这样的根式呢,我们称它为 a 的 n 次根式,其中的 n 称为根指数, a 呢就成为被开方数。 如果指数为最减分数呢,我们就可以得到,当指数为正分数的时候呢,比如说 n 分 子 m, 对 吧?这个 n 呢是大于一的, 那我们就可以得到这样的,当指数为负分数的时候呢,也就是说负的 n 分 之 m。 这里面要注意一下,我们这个 a 呢,它是不能为零的,为什么呢?我们可以看到它呢,写成这样的时候,我们这个 a 呢,它在分母下面,所以呢分母呢,它是不能为零的, 所以要注意一下,也就是我们下面文字描述的,当 n 为偶数的时候呢, a 的 取值呢,应使它们有意义,这样的话呢,我们就把整数指数密推广到了有理数指数密,这些文字描述呢,大家看起来是比较头疼,那我们很多内容呢,是中学已经学过的, 我们再来看一下下面的总结。当 a 大 于零, b 也大于零,且这个 p、 q 呢,都属于有理数的时候呢,有下列的运算法则,我们来看。第一个 a 的 p 次幂乘上 a 的 q 次幂呢,就等于 a 的 p 加 q 次幂。第二个就是括号,对吧?它就等于它们成在一起。第三个 ab 的 p 次幂呢,就等于 a 的 p 次幂乘上 b 的 p 次幂。那我们这里呢,还可以补充一下大家可能会遇到的,比如第四个 带分数的 a 的 p 次幂呢,比上 a 的 q 次幂,就等于 a 的 p 减 q。 第五个, 那 a 比 b 的 q 值密呢,就等于 a 的 q 值密比上 b 的 q 值密。那我们来通过一些例子来帮助大家更好的理解。比如说第一个同底数密相乘的话呢,三的平方 乘以我们三的三次方,那他呢,就是三的二加三,对吧?就等于三的五次方。比如我们第二个密的乘方,对吧?他就可以是三的平方的三次方,那他呢,就是 三的二乘三,对吧?就等于三的六次方。那第三个 g 的 乘方呢,那他就可以是二乘以三的三次方,对吧?那他就是二的三次方乘以 三的三次方。答案呢,大家可以自己算一算。那第四个同底数密相除的,比如说我们的三的 三次方比上我们三的六次方,那他呢就是三的三减六次方,就等于三的负三次方,对吧?那第五个上的乘方呢,对吧?就是有三分之二的三次方,那就是二的三次方比上三的三次方, 这是他的一些运算法则,我们简单了解一下,那我们来通过一些例子来进一步的了解。例题五点一,将下列各分数指数密呢写成根式的形式,我们先来看第一个 a 的 五分之二次密, 这个呢我们就可以看到前面呢提到的一般是,对吧? a 的 n 分 之 m 次幂,那他呢就是根号下 a 的, 嗯,那我们给他代入的话呢,这个 n 的 话就是五,对吧? m 的 话呢就是二,那我们给他代入的话呢,就是 a 的 二五,对吧?第二题,那我们同样的给它的一般式写出来,它呢就是我们这个的负 n 分 之 m, 那 它呢就是刚好像 a 的 m n 分 之一,这里面呢, n 的 话呢就是二,对吧? m 的 话呢就是三,那我们同样的话,代入的话呢,就是刚好像 a 的 三二一, 这里呢,这个平方的话就可以省略到,所以呢答案呢就是这个。第三个。哎,同样我们可以看到,这个呢,同样也是这个 n 的 话呢就是七,对吧? m 的 话就是三,所以呢我们就可以直接写答案,它呢就是啊,像 a 的 三七, 那第四个呢,它呢也是我们的 a 的 n 分 之 m, 那 它呢就是 a 的, 嗯,我们这里面 a 的 话呢就是八分之三, n 的 话呢就是五, m 的 话呢就是三,那我们直接代入写答案的话呢,就是 这是立体五点一,这个呢是比较简单的,我们来看立体五点二,将下列各根式写成分数指数幂的形式,这个呢就是和我们五点一它们两个反一下,对吧?我们来看一下第一个 四次根号下八的立方,那我们通过分数指数幂的定义, n 次根号下 a 的 m 次方呢, 它呢就等于 a 的 n 分 之 m 次方,那我们这里直接代入的话,这个 m 的 话呢就是三, n 的 话呢就是四, a 的 话呢就是我们的八,对吧?所以呢他的答案就是八的四分之三次方,那我们来看第二个五次根号下 a 的 立方分之一,这个呢看着是比较难的,我们来看一看,首先呢我们还是要根据分数指数密的定义,对吧?我们找到它的通向 这里呢,我们根据分数指数密的定义,我们先给下面这个,对吧?分母下面的我们给它写出来,那他的话就是 a 的 五分之三,对吧?我们同样用过这样的方法给它写到分母下面,写出来之后呢,我们再根据负值说明的定义, 那 a 的 五分之三是方分之一呢,它就是等于 a 的 负分之三, 这里面要注意一下,我们这个 a 呢,它是不能为零的,对吧?那题目中呢也给出来了,那我们来看第三个,这个是比较简单的,对吧?那我们还是根据 分数指数密它的定义,对吧?你还是看到第一个 m 的 话呢,就是一, n 的 话呢就是三,这个就是比较简单的,我们直接写出来的话呢,它答案就是十的三分之一。 第二个呢就是实数指数密,当密的指数为五位数的时候呢,五位数指数密, a 的 r 方次方 a 大 于零, r 呢是五位数,是一个确定的实数,那我们有位数指数密的计算法则呢,同样也适用于五位数指数密, 所以这样的话呢,我们就将密指数呢推广到了全体的实数。下面的一些运算法则大家要理解, 比如第一个 a 的 r 法乘以 b 的 r 方呢,就等于 a 的 r 加贝塔。第二种带括号的这种,它是两个是相乘的。 第三个呢就是可以把它们拆分开。这三个公式大家一定要非常的熟悉,很重要,大家要记一记指数函数,我们先来看一下什么是指数函数,形容 y 等于 a, x 这种类型的呢,我们称它为指数函数, 一定要注意和我们前面学习过的密函数它的区别,那我们这里它的底数 a 呢要大于零,并且呢要不等于一, y 等于 a, x 呢,它的 a 呢,我们称它为指数函数的底数。 指数的 x 呢为自变量, x 呢是属于时数 r 的, 比如 y 等于六 x, y 等于六分之一 x, y 等于零点六 x, 这些呢都是指数函数。那我们可以看一下下面它的图像, 如果是在 a 大 于一的时候呢, y 等于 x 呢,它的图像呢就是这个,它是一个增函数,如果抵除 a 的 取值范围,在大于零小于一的时候呢,它的图像呢就是这样的, 那它呢就是一个减函数,比如你们以后会经常见到的 y 等于一的 x, 它的函数图像呢,就是这样的,它是一个增函数。 那我们通过下面的表格来具体的来看一看,指数函数具有下列的性质,首先呢,它的图像,对吧?我们刚才也提到了,当 a 大 于一的时候呢,它的图像呢,就是这样的,它是过零一这个点的。当 a 大 于零小于的时候呢,它的图像呢,就是这样的,同样呢,也是过零一这个点, 他们的定义域呢,都是实数 r, 也就是负无穷到正无穷,子域呢,是零到正无穷,图像呢,是过零一这个点的。那当 a 大 于一的时候呢,它是一个增函数。 当 a 大 于零小于的时候呢,它是一个减函数。当 x 小 于零的时候呢, y 是 大于零小于的。当 x 大 于零的时候呢, y 是 大于的。接着右面的,当 x 小 于零的时候呢, y 是 大于的。当 x 大 于零的时候呢, y 是 大于零小于的, 这是他的一些性质。那我们通过具体的题目来看一看例题五点五,比较下列各组中两个数值的大小。我们先来看第一个二的三点一次方与二的三次方,他们两个对比,我们可以看到他那边的底数呢,都是二, 而指数呢,是不同的。我们在做这种类型的题目的时候呢,我们要回想到我们这个函数的图像,当我们指数函数 y 等于 a x, 它的底数 a 大 于一的时候呢,那它的函数图像呢,就是这样的, 这个点呢,就是零一 y, 我 们可以发现呢,它是一个增函数,也就是单调递增的。 那我们在做对比的时候,有三点一呢,他肯定是大于这个三的,指数越大呢,他的数字呢,肯定是越大的。所以我们就可以通过函数图像,或者是根据他的性质就可以得出来,二的三点一呢,他是大于二的三的。 同样呢,我们就可以看到第三题,他的底数都是一点九,那他的指数呢,一个是二点五,一个是三,那我们可以发现他的这个底数呢,也是大于的,那函数图像呢,也是类似于这样的, 那我们只需要比较它的指数大小就可以了,二点五呢,是小于这个三的,所以呢,一点九的二点五次方呢,它是小于这个一点九的三次方呢?这是我们第一题和第三题,那我们来看第二题 零点三的四次方和零点三的负次方。我们在做的时候就会发现这个零点三呢,它是大于零小于一的, 那他的图像呢,我们再给他画一下,就是这样的,他是一个减函数,这个也是零一点,这 x, 这个是 y, 那 减函数的话呢,因为他的指数越大,他反而会越小,所以呢,我们就可以得到零点三的四次方是小于零点三的负四次方的。 这是我们例题五点五。接着我们来看例题五点六,求下列函数的定域。我们先来看第一个 y 等于零点五的负 x 分 之一,那我们看到有分母的,就要想到分母呢,它是不能为零的,对吧? 接着呢,我们要把下面这个分母零点五的负 x 给它进行一下变形。那我们知道根据指数的运算法则,对吧? a 的 负 x 呢,我们就可以写成 a 的 x 分 之一, 这里呢, a 呢,是不能为零的,对吧?这里呢,我们可以看到零点五呢,它是不为零,那么这里面的零点五的 x 呢,我们就可以写成零点五的 x 分 之一,我们接着给它变形,就可以写为 零点五分之一的 x, 那 零点五的话就是二分之一,对吧?我们给零点五变成二分之一,再进行代入的话,它就变成了 二分之一的分之一的 x, 对 吧?最后我们整理一下呢,就是二的 x, 那 这些步骤呢,就是你在延长纸上面写的,我们把它代入到原式里面呢,就可以写成 y 等于二的 x 分 之一。 那我们知道指数函数的值域呢,是零到正无穷,所以呢,二的 x 呢,它不等于零,它是横乘以的,怎么样它也不会等于零,所以呢,我们就可以得到它的定义呢,就是我们的实数 r, 你 可以写它的实数 r, 或者是呢,就是负无穷。好,正无穷, 这是我们第一题,它的定义域。第二个 y 等于三的 x 分 之一,那我们知道指数分式的时候呢,分母呢,也是不能为零了,所以呢,指数的 x 分 之一呢,它是 x, 不 能为零, 那我们就可以得到它的定义呢,就是负无穷到零,并上我们的零到乘无穷, 这是我们第二题的答案。接着第三题, y 等于二的 x 减七,那我们对指数函数 y 等于 a x, 它的要求呢,就是只要 a 大 于零,并且 a 不 等于一就可以了, 所以我们这个指数 x 减七的一次函数呢,它无论怎样取,它都是有意义的。所以我们第三题呢,它的定义呢,也是实数 r, 或者是呢,你也可以写成负无穷到总无穷。 首先呢,我们先来看一下什么是对数,第一个呢,就是对数的概念,一般来说,若 a 的 b 次方等于 n, 这里面 a 呢大于零,并且呢,它不等于一,我们就称 b 呢,是以 a 为底 n 的 对数。记住这一个,其中呢, a 呢,我们就成为对数的底数, n 呢就称为真数。比如二的立方呢,等于八,我们就可以得到三呢,是以二为底八的对数,记住呢,就是这一个。 那当 a 大 于零,并且呢, a 不 等于一, n 大 于零的时候,指数式的也就 a 的 b 次方等于 n 的 与对数式的具有下列的关系,大家可以看一看。由此呢,我们就可以得到已知底数 a 和密 n 求指数 b, 就是 求以 a 为底 n 的 对数。那根据对数的定义,我们具有下列三个性质,第一个呢,就是 log, 以 a 为底, e 呢,它是等于零的,以 e 的 对数呢,它是等于零。 第二个,这个等于一呢,以底数的对数呢,是等于一。第三个, n 大 于零的时候呢,其零和负数呢,是没有对数的。那由于以十为底的对数呢,用上比较简变,并且呢我们见的也比较多,通常呢把它称为常用的对数,我们就可以减记为 log n, 这里要注意一下,这个呢,就是大家见的比较多的这个五位数 e, 那 他的对数是这样的,我们就从这个对数呢为自然对数,减去呢就是了 n, 对 吧,我们见到这个了, n 的 话呢,一般都是以 e 为底的, 有这个呢,就可以减去为二三,这个大家有个印象。第二个呢,就是基商密的对数,我们这里呢,最好要记一下它的对数计算法则。这里面有个前提,就是 m 大 于零, n 大 于零, a 大 于零,并且呢它不等一 n 呢为任意的实数,我们来看一看, 第一个呢就是对数的积,那么对数的积呢,就可以转变为对数相加,第二个对数的商,我们就可以转变为对数相减,那它密的形式呢?我们就可以把这个 n 提到前面来, n 倍的 绕个 m, 这个有印象。最后呢,还有一个就是换底公式,这四个公式呢,大家要学会灵活的应用, 特别是前面这三个非常重要,大家要非常的熟悉。那我们学完了对数的概念,我们来看一看 我们的重点内容,对数函数形容 y 内洛克斯,那这个是以 a 为底的, x 大 于零,并且呢 x 不 等于的,我们就称它为对数函数,它的图像呢,大家有个印象,如果底数 a 大 于的时候呢,它的图像呢就是这样的,它是一个单调递增函数,如果 d 数大于零小于一的时候,它的图像呢就是这样的,是一个减函数。 那如果以 e 为 d, 那 么 e 的 话,就是论 x, 它的图像呢就是这样的。大家常见的这些图像呢,要熟悉,那论 x, 它在令到正无穷是一个单调递增的一回音响。接着 对数函数的定义呢,就是零到正无穷,对吧?零和负数是没有对数的,我们来看一下下面这个表格,这个中间具有下列的性质,首先呢图像,对吧?这个大家要熟悉, a 大 于的时候,它的图像呢,就这样的,比如说 a 大 于零小于的时候,它的图像就这样的,是一个渐函数, 定义呢就是零到正无穷。子域的话呢,就是负无穷到正无穷,图像呢是过一零这个点的, 这性质里面,对吧,在零到正无穷上呢,当 a 大 于一的时候,它是一个增函数,当 a 大 于零小于一的时候呢,在零到正无穷上是一个减函数, 这些性质呢,大家要记一记,那我们通过具体的题目来看一看。例题五点十,求下列函数的定域。第一个呢,就是 y 等于 log, 以二为底, x 减五, 那我们通过前面对数的概念里边, y 等于 log 也为底,这个 x 的 话呢,把这个 a 呢,它是要大于零,并且呢它是不等于一,那我们这里发现二呢,它是大于零的, 所以呢,我们只需要看后面这个 x 减五,它这个真数就可以了,我们只需要得到真数 x 减五,它只要大于零就可以。 x 减五,大于零的话呢,我们就可以得到 x 呢,它是大于五就可以,所以呢,它的定义域呢,就是 五到正无穷。接着第二个带分数的,我们看到带分数的,对吧?首先要考虑到分母呢,是不能为零的, 所以呢,第一个呢,就是这个零点五, x 呢,它是不能为零,那我们对数呢,首先呢,这个 a 它是满足的,对吧? 它的真数呢要大于零,也就是说 x 它要大于零,那我们根据前面函数图像,对吧?零点五呢,它是大于零小于一,它是一个减函数,对吧? 并且我们这里这个 log 零点五, x 它不能等于 log 零点五,这个 x 呢,它是不能等于一的,所以呢, x 大 于零,并且呢, x 要不等于一, 那我们就可以得到,它的定义域呢,就是零到一,并上我们的一到正无穷。第三题,我们看到带根号的这种,我们要知道根号的话呢,对吧,根号下面要大于等于零, 也就是说我们这个整体 x 呢,它是要大于等于零的,同时呢我们这个真数 x 它也要大于零,我们根据 a 大 于一的话呢,我们知道这个函数图像呢,它单调递增的,如果如果 x 等于一的话呢, 用我们这个 log 二 x 它呢就等于零了,那因为我们这根号下面是可以等于零的,所以呢 x 它是可以等于一的,这样的话我们就可以得到 x 大 于等于一,它都可以满足它的定义,那我们就可以得到它的整体的定义呢,就是 一到正无穷,这里要注意一下,一的话他是 b 区间,他是可以等于的。恭喜大家完成了第五张指数函数与对数函数的内容,我们来看一下这一张的章节回顾。 我们这里呢主要要提醒两个点,第一个关于指数函数里面的像实数、指数密,他的一些运算法则,这三个呢大家一定要非常的熟悉,我们在做题的过程中会经常的遇到。 第二个呢就是关于它的图像, y 等于 a x, 如果 a 大 于的话呢,它就是这个图像,如果 a 大 于零小于的话呢,它就是这样的一个图像,这个大家图像的话一定要非常的熟悉。再一个呢就是 y 等于 y 的 x, 这个也是我们 非常重要的一个点,那 e 的 话呢,就约等于二点七,这个大家要非常的熟悉。第二个呢就是对数函数里面的一些运算法则,这三个大家也要非常的熟悉,以及像后面的换题公式大家可以了解一下。 最后呢我们再强调一下,很多同学可能有时候区分不了论和 log, 他 们的区别论的话呢,它是以 e 为底,而 log 的 话呢,它以实为底,这个注意一下就可以了。 好,这是我们这一张的全部内容,如果这个视频对大家有帮助的话呢?大家可以多多点赞转发分享一下,我们下个视频见,拜拜。
2392李师傅上课啦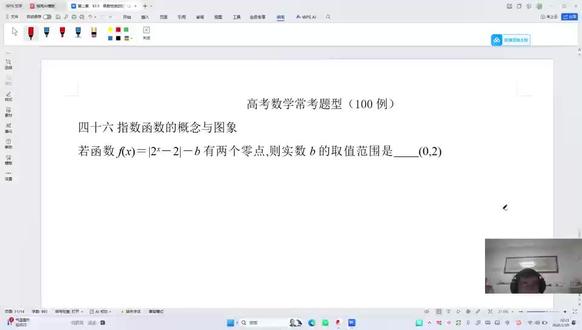 03:15查看AI文稿AI文稿
03:15查看AI文稿AI文稿各位同学,大家好啊,今天我们开始学习高考数学常考题型一百例的第四十六的递减指数函数的概念与图像。 我们把形容这样的函数 v 等于 v 等于 a 的 x 方, a 大 于零。切 a 不 等于一的函数叫做什么函数?指数函数,它前面的系数必须为一,底数必须大于零,小于几不等于几啊,以这个指数比十多少 x。 现在我们看这个题, 若函数 f 等于二的 x 方减二,绝对值减 b 有 两个零点,则实数 b 的 取之分又是它有两个零点,实质上就是二的 x 方减二的绝对值减 b 等于零,有几个根啊?两个根,这样的话一般用什么方法?竖形结合法? 我们讨论零点的个数问题,或者零点所在的区间问题,一般用的方法都是竖形结合法,你看如下, 二的 x 方减二的绝对是等于 b, 这样的话就说明二的 x 方减二的绝对值。这个图像与 v 等于 b, 这头直线有几个角点,两个角点。现在我们画图啊,竖形结合法啊,用竖形结合法解决问题啊。画图, 这个我们画图的话,你首先画出二的 x 方减二图像,带有绝对值以后,把负值变成什么值?正值?你看我们首先画二的 x 方图像,因为二是大于一的,它单调递增横通过哪一个点 零一点,这样的话,我们画出 v 等于二的 x, 这个减二相当于把它向下平移两个单位长度啊,这个零一就平移到什么零负一这个点,但在这个里面 总以出错这样,因为它与 x 轴无交点,说明它向下平两个单位长度与 v 等于负二无交点,这是一个什么点?易错点? 一错的这个大拇同学就搞错了,现在他向下平,及格点数到两个,哎,通过零度负一, 现在对角对折以后,负值要变成什么值?正值,因为他与 v 等于负二五九点,说明他翻上去以后与 v 等于二,有没有点?没有,你看把这些复制变成正值,这样翻上去他做他关于 x 轴对称的,现在你做出来是这样的, 哎,对,这样的一个图像,做这以后我们画 v 等于 b 这条直线,你看我们画了 v 等于 b 这条直线, 现在你看这是一个角点,这是一个角点,这样画几个角点?两个角点。如果 b 等于零的话,只有这样一个,如果 b 等于二的话,只有这样几个。一个这样的话,说明 b 的 曲值范围在什么零到二之间,特别是在这个里面, 出错的原因就在这了啊。因为指数函数图像横在 i n 刻子中下方,它向下平移以上方。指数函数图像横在中上方,它向下平移两个单位长度, 对吧?这样它相当于把 i n 刻子只要向下平移两个单位长度,这样的话就说明它就位等于负二十度的无交点的,这是一个易错点啊,我们今天就分享这,谢大。
34俊哥初高中数学 02:27查看AI文稿AI文稿
02:27查看AI文稿AI文稿我每天给你一千块钱,连续一个月,但是同时你要第一天给我一分钱,第二天给我两分,第三天四分,以此类推,每一天都是前一天的两倍,也是连续一个月,你愿意吗? 大家可以在弹幕或者评论区打出你第一反应的决定。很多朋友估计猜到我要讲一个关于指数函数的案例,那么揭晓答案。我每天给你一千块,一个月就要给你三万块,你第一天给我一分钱,之后的每一天都是前一天的两倍,那么单单最后一天,你就要给我五百三十七万, 加上前面二十九天的累计,你要给我一千零七十四万。我猜很多朋友跟我一样,理论上知道指数函数很厉害,但是直觉上没想到这么厉害。这个游戏更加震撼的是,如果在第十五天结束游戏的话,那么你就只需要付给我三百二十八元, 对比一千零七十四万的收益,实在是九牛一毛。理论上来说,一张纸只要折四十二次,它的厚度就能从地球到达月球。 纳瓦尔说,所有的利益,无论是财富、人际关系还是知识,都来自于复利。我觉得了解指数函数对于普通人最重要的意义就是我们可以重新对坚持进行定义。我认为不管什么信念、自律、远大理想,都不如理解指数函数能让人更容易的坚持下去。 因为普通人做了一百天,发现没有见效果,就觉得努力没有用,这条路肯定不对,于是就放弃。但是高手他也是做了一百天也没有见到任何效果,但是他心里知道,太好了,我离那个指数函数的拐点又近了一百天, 同时理解了指数函数,我们也就能更加深刻的理解,种一棵树最好的时间是十年前,其次是现在。因为如果事物的发展是限性的,那么我比别人早一天出发,就只能够比别人早一天到达。但是在指数函数的世界里面,早一天出发,最后收获的可能是比你晚一天人的非常多倍。 其实理解了指数函数,也就能够理解了生活当中很多看似不公平的现象。比如说为什么那个领导每天只需要开几个会就能够拿大几万的月薪, 比如说为什么有些人能够在一天之内赚到普通人几辈子也赚不到的钱。巴菲特说,我的一生都在享受指数级的增长带来的福利。 我的财富并不是靠某一次重大的成功,而是靠长达六十年的不间断的微小的指数级增长。祝大家都能够在自己的领域拿到指数级的结果。
 09:58查看AI文稿AI文稿
09:58查看AI文稿AI文稿上课,同学们好,请坐上一章。我们学习了函数的概念和基本性质,并且通过对 m 函数的学习,掌握了研究一类函数的基本过程和方法。那本节课呢,我们将研究其他类型的基本初等函数,指数函数。 请同学们仔细听庄子天下中的一句话,一尺之锤,日取其半,万事不竭。如果将一尺之锤的长度看作单位一, 那第一天得到的长度就是 i 二分之一, 那第二天呢?哎,就是二分之一的一半四分之一。那第三天呢?哎,四分之一的一半,八分之一, 哎,那第 x 四天得到长度是多长呢?那我们可以把这些数写成具有规律的形式, 这是二分之一的一次幂,这是二分之一的二次幂,这是二分之一的三次幂。哎,那第 x 天的长度就是 i 二分之一的 x 四次幂。 那下面记 y 等于二分之一的 x 四次幂。同学们思考一下, y 是 关于 x 的 函数吗?谁来说说?好第二排念上去, 嗯,非常好。根据函数的概念,对于任意一个确定的天数 x 按照这种对应关系都有唯一的长度, y 与之对应,因此 y 是 x 的 函数,其中呢, x 是 自变量。非常好,请做 同学们听第二个例子。我们知道,在营养和生存空间条件充足的条件下,细菌会不断的繁殖,某种细菌呢,每二十分钟就会通过分裂繁殖一代, 那一个细菌分裂一次会产生几个细菌?哎,两个, 那分裂两次呢?哎,就是二的两倍,四个 来分裂三次呢,哎,就是四的二倍,八个来分裂 x, 四呢,哎,我们可以将这些数写成具有规律的形式, 这是二的一次密,这是二的二次密,这是二的三次密。那记 y 等于二的 x 次密, y 是 关于 x 的 函数吗? 啊,对于每一个确定的次数 x, 按照这种对应关系都有唯一的个数 y 一 致对应,因此 y 是 x 的 函数, 其中这里的 x 是 自变量。好,那现在请同学们观察这两个函数的解析式,它们具有什么共同特征呢? 嗯,好,第一排这位同学,嗯,很好,你发现这两个函数都是以 me 的 形式出现,并且都是以 me 的 指数为自变量,而 me 的 底数是常数。非常好,请坐, 那下面我们用常数 a 来代替底数二分之一和二,那么这两个函数解析式都可以表示为 y 等于 a 的 x 次幂, 那像函数 y 等于 a 的 x 次幂呢?我们就叫做指数函数, 其中 x 是 自变量, 那 x 的 取值范围呢?其实我们在前面学习逆函数的时候,我们已经将指数的范围推广到了全体实数,因此 x 的 范围是属于 r 的, 那么定义域就是 r。 哎,那既然 x 的 取值范围是 r, 那 这里 a 的 范围也是 r 吗?那同学们可以前后四人一组合作讨论一下,给大家一些时间。 好,哪组?来说说你们组的结果。好,你们这组哦,你们将 a 分 成了三种情况, a 小 于零, a 等于零和 a 大 于零的情形哦,当 a 小 于零的时候,如果这个 x 取二分之一, 那么 y 是 a 的 二分之一,次密是根号 a, 而 a 是 负数,它没有意义,因此 a 小 于零不可以。那当 a 等于零的时候呢? 哦,当 a 等于零的时候, y 是 零的 x 次密哦,如果取 x 等于负一,就是零的负一次密等于零分之一, i 分 母为零,没有意义。 那 a 大 于什么时候呢?其实呀,当 a 等于一的时候呢,函数值为 y 等于一的 x 次幂横为一,也不具有研究意义。因此,我们规定这里的 a 不 光要大于零,并且呢,要不等于一。 因此,函数 y 等于 a 的 x 次幂, a 要大于且 a 不 等于一,才叫做指数函数。其中 x 是 自变量,定义域是二,那么这便是指数函数的概念。 那老师在强调指数函数的一些细节,如果一个函数是指数函数,那么 a 的 x 自命的前面的系数一定是一, 并且呢,它只能是一项,不能是 a 的 x 次幂加一加 x 两项或多项的形式出现。还有,它的自变量只能是单个的 x, 不 能是 x 的 平方, x 的 立方。这样 好,那下面请同学们判断这些函数是否是指数函数。 第一个 y 等于三倍的二的 x 次幂。第二个 y 等于二的 x 次幂的平方。第三个 y 等于三的 x 次幂。加一, 第四个 y 等于 x 的 次幂。第五个 y 等于二的二分之一的 x 次幂。 好,那从这组开始,从前往后依次。第一个,哎,不是因为二的 x 密,前面的系数不是一。第二个, 嗯,它的指数不是以单个的自变量出现,因此它也不是指数函数。第三个,哎,它有两项,那第四个, 哦,他是我们之前所学习的密函数哎,密函数是以密的底数为次变量,而我们今天所学习的指数函数是以指数为次变量。第五个呢, 哦,你说它的指数不是单个的 x, 因此它不是指数函数。那请同学们回顾一下我们之前所学习的指数幂的运算及其性质。那我们是不是可以把它写成二的二分之一是幂的 x, 它等于什么呢?哎,它等于根号二的 x x 米。哎,那它是不是以根号二作为底数,它满不满足大于零减不等于一啊?哎,满足,因此它是指数函数。 所以啊,有些指数函数不是那么明显。但是呢,我们通过变形可以哎,发现它是指数函数。 好,本节课呢,我们既逆函数这种基本出等函数,又研究了一位新的基本出等函数。指数函数。那课下呢,请同学们完成数后习题,本节课就上到这下课。
349g(0)
猜你喜欢
最新视频
- 1281阿老师







