北师版八下第一章和第三章几何练习题
哈喽,大家好,欢迎来到明老师初中数学课堂,我们今天一起来进行第一章第一节等腰三角形第一个课时的习题练习。 来看一下常见的题型啊,一共是有三种,先来看第一种题型,等腰三角形的分类讨论,这个呢,其实在我们学习这个啊,轴对称图形啊,讲怎样三角形的时候,已经做过类似的题目了啊,我们呢就相当于一起啊,再进行一下回顾啊。 首先第一题,若等腰三角形中有一个角等于七十度,则这个等腰三角形的顶角的度数是多少度? 我们谈到啊,解决等腰三角形的问题的时候,经常会涉及到一种分类讨论的思想。这道题也是一样,他首先呢给了一个角等于七十度,那问我们顶角的度数, 那首先就要考虑了,他给的这个七十度角啊,到底是不是顶角,对吧?如果说给的这个七十度角就是顶角的话,那很显然顶角的度数很显然有一种情况就得是七十度,对吧? 哎,所以呢,这是第一种情况啊,给的这个七十度就是顶角,所以呢,答案就是七十度。那么对于第二种情况是什么呢?给的这个七十度啊,他是底角哎, 他如果是底角的话,那很显另外一个底角也得是七十度,对吧?哎,这是怎样三角形的性质啊,两个底角相等,那么这个时候呢,他顶角的度数是不是就得用这个一百八十度减去七十度,然后再减去七十度啊,对吧?哎,就减去两个七十度,这里算出来呢,应该就是等于 四十度,哎,所以呢,这道题啊,应该是有两种答案,一个呢是七十五,另外一种情况呢,就是等于四十度,所以呢,答案应该是 c 选项。 好,接下来第二题,怎样三角形底边长十厘米?一、腰上的中线分此三角形的周长为两部分,若其中一部分比另一部分长四厘米,则该怎样?三角形的腰长为多少厘米? 哎,这道题啊,首先我要说一下啊,他有没给画出这个图形啊,这个图形呢,是我们后画的,为了节省点时间,省的我们先画图嘛,对吧?那我们把图形画出来之后,我们一起来分析一下。首先呢,这是一个等腰三角形,这是两个腰,哎,这是 bc 呢,是底边,也就是底边的长是十厘米。 然后同时呢,这个 bd 啊,他呢是腰上的中线,也就是说什么呢,这个 ad 和 cd, 哎,这两段是相等的,然后他说呢,分此三角形的周 周长为两部分,那也就是什么呢?分成哪两部分?一部分是 ab 加上 ad, 哎,另一部分呢,是这个 bc 加上 cd, 哎,他把这个周长分成了这两部分啊,上面一部分,下面一部分, 然后他说呢,其中一部分比另一部分长四厘米,到底谁比谁长啊?这里是不是又需要分类讨论了,对吧?哎,如果第一种情况,我们讲啊,如果 ab 加 ab 这段比较长,那上面这部分比较长的话,那么也就是他减去这个等于四厘米,对吧? 哎,那这样呢,这两个 ad 和 cd 是不是可以抵消掉啊?哎,那也就是说呢,是 ab 减去 bc 等于四,哎,那 bc 是十,对吧? 这里算出来呢, ab 就应该等于十四厘米啊,等于十四厘米。好,这是第一种情况,那么第二种情况呢,是什么呢?是下面这部分比较长。哎,那也就是应该是 bc 加上 cd, 然后呢,减去这个 ab 加上 ad, 哎,这个等于四,这是不是又是另外一种情况啊,对吧?哎,这里一减呢,这个 cd 啊,和 ad 同样可以消掉,哎,所以就变成了 bc, 减去 ab 等于四,哎,那 bc 是十,对吧?哎,这里算了, ab 呢,就应该是等于六厘米。好,那么根据这两种情况,所以 我们这道题应该得到两个答案,对吧?也就是说呢,这个等腰三角形,他的腰长可以是十四厘米,或者是六厘米,所以这个答案啊,应该是有两种情况的。 好,接下来我们看第二种题型,利用等样三角形的性质,求边长和角度。第三题,如图,在三角形 abc 当中, ab 等于 ac, 哎,是一个等样三角形了,然后呢, ab 啊,他呢是角 b ac 的角平分线,他就是顶角的平分线呗,对吧,那我们就很容易想到什么呢,等于三角形的性质了,三线合一,也就是 ab 这条线段呢,既是顶角平分线,同时呢,他又是底边 bc 上的中线和 bc 这条边上的高,对吧?哎,这里还应该是垂直的好,如果告诉我们啊,他说若 ab 等于十三, ad 这段等于十二,求呢?求 bc 的长是多少?那我们一看,这里十三,这里十二,那我是不是很快应该可以求出 bd 的长啊, b d 的长怎么办?利用勾股定理啊,对吧?哎,这是我们上学期刚刚学过的一个内容哎, b d 的长呢,就应该等于根号 下啊, ab 的平方减去 ad 的平方,对吧?哎,这里算盘应该就等于五好, bd 的长如果是五,那很显 cd 的长是不是也得是五啊,对吧?哎,因为这个 ad 也是底边上的中线 啊,他俩都是五,所以呢, bc 的长是不是就应该等于五加五啊,对吧?哎,所以呢,这里算出来应该是等于十啊, 哎,这个呢,也是利用了啊,怎样三角形三线合一的这样一个性质,对吧?同时结合了勾股定理,求边长啊。第四题,如图,三角形 abc 当中, ab 等于 ac 等于 cd, 看一下啊, ab 等于 ac, 然后呢,还等于 c, 哎,这一下告诉我们什么呢?首先,三角形 abc 是一个怎样三角形?同时呢,这个三角形 acd 也是一个怎样三角形,对吧?好,继续啊,又说呢, bd 又等于 ad, 哦,这两条边又相等,那也就是说,这个三角形 abd 又是一个怎样三角形? 然后,让我们求三角形 abc 中个角的度数,也就是角 b, 角 c, 还有这个角 b ac 的度数呗,对吧?哎,以致条件当中没有给出其他的角度方面的信息,那这种情况下,我们应该怎样来求角度呢?而且就利用等腰三角形的性质, 两个底角是相等的,对吧,我们观察一下,首先,在这个大三角形 abc 当中,等边对等角,那是不是这个角 b 和这个角 c 应该是相等的,对吧?哎, 同时呢,我们再来看啊,在这个三角形 abd 当中,又是一个怎样三角形?那这个角 b 很显然应该跟上面这个角,我给他起名叫角一啊,哎,角 b 是不是还应该等于角一呀?哎,同时呢,还应该等于角 c, 哎,这三个角应该都是相等的,还有些什么其他的信息呢?既然角 b 和角一相等,那我们看下面这个角啊,这个角如果叫角二,这个角如果叫角三的话,我们看角二, 他是不是应该等于角 b 加上角一啊,对吧?哎,那角 b 和角一又相等啊,所以他就应该等于二倍的角 b, 好,那同时这个三角形 acd 呢?他是一个怎样三角形?所以角三和角二是不是相等的,对吧?哎,所以就是角三也等于二倍的角币。好,角三等于二倍的角币 啊,画两道杠这样画,那这个角一等于角 b, 所以我是不是知道这个角 b ac 啊,他等于角一加角三,那就等于角 b 加上二倍的角 b, 所以他应该等于三倍的角 b, 对吧? 好,那现在呢,在这个大三角形 abc 当中,我就知道了,这三个角啊,都可以给他转换为角币,他是等于角币,他也等于角币,那上面这个顶角呢?又等于三倍的角币,我根据三角形的内角和是一百八十度,对吧?我就可以知道,角币 加上角 c 加上角 b ac, 哎,应该等于一百八十度,所以呢,把它全部转化为角 b 啊,那就变成了角 b 加角 b 再加上三倍的角 b, 对吧?哎,就等于一百八十度,这是不是一个关于角 b 的一个方程啊?哎,解说呢, 角 b 的度数应该就等于三十六度啊,角 b 如果三十六度,角 c 也应该是三十六度,对吧?那么角 b a c 呢?就等于一百八十度,减去二倍的角 b, 对吧?或者呢,可以直接利用我们刚才所说的角 b ac 等于三倍的角 b, 也可以求出啊,角 b ac 就应该是一百零八度,哎, 用这个方法就可以求出来了,虽然题目当中没有给出我们角度的信息,但是我们所利用的呢,就是啊,三角形的内角和是一百八十度这样的一个啊条件, 然后呢,找到了这个三角形三个内角跟角壁之间的关系,然后列出方程,最后求出角壁的度数,哎,这样呢,求出其他两个内角的度数,这就是我们这道题的一个解题的思路啊,看下答案啊。在这接下来第三种题型,等腰 三角形和全等三角形综合应用来看。第五题,如图,在三角形 abc 当中, ab 等于 ac, 他是个等腰三角形,对吧?然后呢,欧式三角形 abc 内部的一个点,并且告诉我们的这个 ab 啊等于 oc, 哎,他俩也是相当的, 然后让我们求证啊, a o 垂直于 bc, 我们这样一看呢,哎呦,这,这里是一条线段的,对吧?哎,这个线段和他应该怎么样才能垂直啊?是不是应该判断的是这个线段 ao 所在的直线呢?他跟 bc 是垂直的,对吧?哎, 那这样的话,我们应该就能想到,我首先应该把这个 ar 给他延长一点,延长之后呢,让他与这个 bc 啊相交,相交之后我再来判断这个 ao 所在的直线跟这个 bc a 之间的一个位置关系,对吧?好,那我呢,首先要做的事,我应该把这哎呦延长一下啊,延长之后呢,射他与这个比赛亚相交于点地, 好,那我接下来就可以证明什么呢?我想证明这里是垂直的,对吧?好,那我看这样应该怎么样来证明呢?已知条件当中,给我们 ab 等于 ac, ob 等于 oc, 是不是都集中在这三角形 abo 和这个三角形 aco 里面了,是吧?我发现这里呢,有一条公共边, 哎,那是不是边边边?我根据这个边边边这个判定条件,可以判定出三角形 abo 应该是全等于三角形 aco 的,对吧?哎, 编编编吗?三组编分别都相等好,判定出他俩全等之后,下一步我又应该怎么办呢?既然他俩全等,那是不是 就有上面的这两个角角一和角二啊?他俩是一组对应角,所以角一就应该等于角二好,角一如果等于角二了,那么我们观察一下 a d 这条线段,是不是就是这个三角形 abc 的角平分线呢?对吧?好, ad 如果是角平分线,那同时呢,这个三角形 abc, 他又是一个等腰三角形,我们根据等腰三角形三线合一这样的一个性质, ad 如果是等腰三角形顶角的平衡线,那么他一定是底边上的高,所以呢,这里就是垂直的,对吧?这里要如果垂直,我就可以说明什么呢? a o 就是垂直于 bc 的,对吧?哎,所以呢,这道题啊,咱们是把这个全等三角形以及等腰三角形的这个性质啊,做了一 一个综合的应用。首先判定出了两个三角形全等,利用全等三角形的性质,判定出了 a d 平分角 b ac, 哎,然后再利用等腰三角形三线合一这样一个性质,判定出了 ad 与 bc 是垂直的啊,好,看下解决过程啊。好,接下来 最后一题,如图,在三角形 abc 当中啊, ab 等于 ac 又是一个怎样三角形啊?然后呢, ad 他呢?垂直于 bc, 也就 ad, 他是底边上的高,对吧?那也很容易想到他是底边的中线,也是顶角的角度中线。然后呢, ce 啊,他又垂直于 ab, 哎, 这里是垂直,这里也是垂直的。然后告诉我们呢,这个 ae 啊, ae 他等于 ce, ae 和 ce 相等。好求证。第一个问题 求证的是三角形 a, e, f, 哎,这个是一个直角三角形,对吧?他呢全等于三角形 c, e, b, 哎,这里也是一个直角三角形, 根据已知条件我已经有了。什么呢?这个 ae 啊,和 ce 是相等的,你看 ae 和 ce, 这已经是一组对应编了,对吧?好,一条边相等,并且还知道呢,有一个直角相等,是吧?相当于我们是不是只差一个条件了,就可以判定出他俩全等,对吧?那个条件我们应该怎样来找呢? 我们观察一下啊。首先我看一下这个角,这个角如果给他起名为角一,他可不可以想办法证明跟这个角二是相等的,哎,这两个角能不能证明出他是相等的呀?应该是可以的,因为 a d 呀,和 b a 是垂直的,这里是直角,所以呢, 我就应该有角一加上角 b, 是不是应该等于九十度啊?直角三角形,两个锐角互余吗?对吧?他俩相加等于九十度, 同时呢,你这个角二加角 b 是不是也应该等于九十度吧,对吧?哎,角二加上角 b 也是等于九十度的,因为这里又是一个直角,对吧?好,那也就相当于呢,这个角一和角二啊,都是角 b 的与角,哎,我们根据同角的与角相等,对吧,我就可以得出啊,角一就是等于角二的。 好,那我们观察一下,在这个三角形 ae f 和这个三角形 ceb 当中,角一等于角二,一个角相等了,然后呢, ae 又等于 ce 一条边相等,然后又有两个直角相等,对吧?那这是不是角边角啊? 根据角边角,我就可以判定出这两个三角形就是全等的啊。所以,到这啊,我们第一个问题就给他证明完毕了。 好,再看第二问题,他说呢,求证, a f 等于二倍的 cd, a f 在这, cd 在这二 倍的 cd 是谁呢?二倍的 cd 很显就应该是 bc, 对吧?哎,因为这个 ad 呢,他是底边的高,那他就是底边的中线吗?哎,所以呢,我就有这个 bc, 他是等于二倍的 cd 的,那我只要证明 a f 等于 bc 就可以了呗,对吧? a f 等于 bc, 考证吗? 别忘了,我们刚刚证明出两个三角形全等,对吧?你这个 a f 和这个 bc 是不是刚好是一组对应编呢?哎,所以呢, a f 啊,他就是等于 bc 的,那么他如果等于 bc, 所以他自然而然就等于二 倍的 cd, 对吧?哎,那第二问题不就正完了吗?哎,所以呢,这道题同样是考察的是什么呀?等腰三角形和全等三角形的一个综合的一个应用。 首先呢,根据已知条件判定了两个三角形全等,哎,得到两个三角形全等之后,我知道了对应边是相等的,对吧?也就是说, a f 是等于 bc 的,同时利用等腰三角形的性质, bc 等于二倍的 cd。 哎,那所以呢, a f 就等于二倍的 cd 啊。好,我们看一下紧接过程。好,在这里,好,今天的习题 练习呢,就和大家一起做到这里,我们下一节课和大家一起来进行第一章第一节等腰三角形第二个课时的学习,欢迎大家收看,如果喜欢,请关注明老师初中数学课堂。如果大家在学习中有问题,欢迎留言或者给我发私信,我们下次再见!
粉丝18.6万获赞66.8万
相关视频
 01:27查看AI文稿AI文稿
01:27查看AI文稿AI文稿同学们好啊,今天起给大家整理一下八年级下册数学的全册预习重点预习抓主线,破难点,重点盯公式定律和题型逻辑,按章节拆分, 明确核心重点,预习关键易错点,方便直接用来规划预习,精简实用。第一章三角形的证明一、核心重点全等三角形判定边边边角边角边角角边是基础。 重点预习等腰三角形、等边三角形的性质与判定,等边对等角三线合一直角三角形的判定,即三十度角所对直角边等于斜边一半。二、预习关键, 分清性质定理有结论推特征和判定定理有特征推结论,比如等腰三角形性质是等边等角判定式等角等边,避免混淆。三、易错点,直角三角形全等用 h l 使。 必须先明确两个三角形都是直角三角形,再找斜边和一条直角边相等。怎么做才能提高预习效率呢?给大家分享几个实用的操作方法。一、 先看教材例题,先精读定义和定例,再看例题步骤,搞懂每一步的依据。二、抓核心公式定律, 把定和定力抄在笔记本上,反复背诵。三、基础题优先练预习时不用攻难题,重点做教材课后基础题,砥实基础比刷难题重要。四、标记疑问点,遇到不懂的地方做好标记,开学后重点听老师讲解,针对性突破。
122初中数学肖老师 30:03查看AI文稿AI文稿
30:03查看AI文稿AI文稿各位同学们大家好,我是你们的阿川学长,今天我们讲八下第一章三角形的证明的第一节等腰三角形的这个性质。那我们观看我们本节课,也就是我们之后的一些课程会讲的一些什么东西。 第一个关于等三角形的话,我们会涉及到它的性质,以它特殊的一个等边三角形的性质,以及如何去判定等三角形,以及如何用反证法去证明等三角形。而且还有关于等边三角形的判定及含三角三十度角的这个直角三角形的一些性质。 然后后面就是关于这三角形啊,以及角平分线啊,还有线段的垂直平分线这一些方面的知识,然后其中这一堂课的这个规模是最大的,难度是极高的,所以我们需要好好听啊。那我们现在呢,我们这个第一课是啊,首先我们来看三部图片, 埃及金字塔,他是一个三角形斜拉桥梁,这里有个三角形,以及关于我们这个体育观看台架啊,他有一个三角形,所以说我们会发现三幅图片都存在一个等腰三角形吧,所以说我们来看啊, 那现在问题一,在八上的平行线的证明这一章中,我们学了哪八条的基本事实?我们来小伙伴来一起回想一下平行线的证明的一些基本事实,我们想想是不是有两点确定一条直线以及两点间线段最短, 然后如何去正平行? c 边形是不是有同位角相等两直线平行以及同方内角互补两直线平行。 然后关于到我们的平行正比线,有很多很多事实吧,那现在我们来例举八条,第一条是确定直线,第二条是关于距离的问题,第三条是同一平面内过一点,有且只有一条直线与已知直线垂直啊,必须同一平面内啊,这个是我们的心理条件 啊。第四条就是我们的证明平行线的一个呃呃,这个判定判定条件。然后第五个是过直线外一点,有且只有一条直线与这条直线平行。然后第六个是两边及其夹角分别相等的两三角形全等,相当于是一个边角边关系。 第七个两角及夹边分别相等的三角形全等啊,这是角边角以及三边分别相等的两三角形全等,这个是边边边。 所以说我们这里涉及到的是关于全等三角形的知识,这里问的是关于如何证明平行,第三和第五相当于,是啊,确定了他们些关于线的性质,而第一个和第二个相当于是其他类型的一些条件。 那我们来看到我们的第一个探求心之定理是两角分别相等,且其中一组对等角的对边相等的两三角形全等,也就是角角边,这个属于新的一个判定性质了。现在我们用基本事实以及学过的定理来证明这个推论。 我们来看啊,咱们画出来了,已知如图,角 a 和角 d 是 相等的两个角,角 b 等于角 e、 bc 等于我们的 e、 f。 现在要你证明三角形 abc 比三角形 d、 e、 f 全等。那刚刚我们是不是说过,在证明我们的平行的时候,我们学过了我们的这个边角、边 角、边角以及边边边吧。那这道题的话,我们要想一想,用这三个哪一个好证明啊?我们得知道边边边是什么,三条边都要相等吧。 但这道题我们会发现,我们没有办法得到关于除了 bc 和 e、 f 的 其他边的性质,所以边边边用不了 边角边行不行?也不行吧,因为我们只有一个性质,所以说我们就要首选的是关于用角边角来证明三角形 a、 b、 c 与三角形 d、 e、 f 的 全等。那好,我来证明一下啊!首先我会发现他的两组对应角分别相等,是不是也明白,因为角 a 等于角 d, 角 b 等于角 e, 又因为角 a 加角 b、 加角 c 等于角 d、 加角 e 加角 f 等于一百八十度啊。所以说我们可以一点一点 t 吧, a 和 d 相等, b 和 e 相等,所以说什么角 c 和角 f 是 不是也相等的呀? 那很好,现在你知道了角 c 和角 f 相等,所以说我们来标注一下啊。 所以同学们是不是由此可得,在三角形 a、 b、 c 和三角形 d、 e、 f 中,因为角 b 等于角 e、 b、 c 等于 e、 f 以及角 c 等于角 f, 所以 三角形 abc 与三角形 d、 e、 f 是 不是全等的呀?对吧?所以说是角边角的性质,所以得到了关于这个的证明。然后同时角 a 等于角 d, 角 b 等于角 c, 角角 e、 b、 c 等于 e、 f, 所以 说它也是不是我们刚刚的推论的角角边的一个顺序关系,所以说这个定律就得正了。这是我们关于啊探讨的第一个的性质,也就是关系到我们的这个 角角边的定力的一个合理性。两角分别相等,并且其中一组等角的对边相等的两三角形全等,这是定力啊,所以根据确定下三角形定义可以得到什么?得到我们的全等三角形的对应边相等,对应角也相等, 那现在我来探求一下他的这些一些其他的性质定力。等腰三角形的两个底角相等,这个很明显吧,等边对等角以及他的推论, 等腰三角形的顶角的平分线,底边的中线,底边的高线,三线合一这个性质,这个是我们的最最重要的性质啊,重要到极致的性质,你的考试中,你的作业中, 你的啊。之后咱们上了这个九年级的时候,以及我们的这个一轮复习,二轮复习, 三线合一贯穿始终,他的重要性没有办法比你的存在。所以说我们一定要记住三线合一,三线合一,哪三条线顶角的角平分线,底边的中线,底边的高线 三线合一。而且三线合一只在等腰三角形以及等边三角形中才会有,其他三角形是没有的啊。那现在我们要用基本事实和已知定力来证明这些结论,那我们一起来证明一下啊。首先我们引出了一个东西, 七下的时候,我们学个轴对称法,我们利用折叠的方法说明了这个等三角形,它是一个轴对称图形,且两个底角是相互重合的,折过去的话,所以说他们应该是相等的底角,那现在我们把它用图的形式表示出来了, 这个折痕,将这个等腰三角形分成了两个全等的三角形。那现在由这个解题要得到一些启发,那我们把它变为我们的数学语言,就是 如图,在三角形 b、 c 中, a、 b 等于 a、 c, 现在要你正到角 b 等于角 c, 它都要正到等边,对等角的一个性质,那我们来用两个方法来进行证明。首先第一个方法,我们可以做底边的中线,比如说我现在 在 bc 上取一中点 d, 此时我连接 a、 d。 好, 这第一个方法啊,我现在通过中线来证明在 bc 上取一中点 连接 a、 d。 为什么这么,为什么这么正呢?同学们,角 b 等于角 c, 要正到两个角相等。我们之前是不是说过要正到类似的几何性质相等,要么你去找全等吧, 要么去干嘛?去通过计算吧,就说什么等量代换,对吧?这道题里面我们想一想, 你觉得第一个合理还是第二个合理啊?等量代换意味着得有足够多的数据和条件支撑我去进行第二个这么操作吧。 那这道题里面很明显没有这么多条件,所以说我们要通过构造全等找全等三角形,通过证明它们的对应边相等,得到对应角相等。那 ok, 现在我们来进行第一个方法啊,中线, 那此时意味着做完这图就知道我们的这个 b、 d 是 不是等于 a、 d 啊? 好, b 点 c、 d 吧。好,现在相等。那现在 ab 等于 ac 了, ad 是 不是公共边啊?所以说同学们在三角形 a、 d、 b 和三角形 a、 d、 c 中,因为 ab 等于 ac, b、 d 等于 cd, ad 等于 ad, 这个是已知的,这个是通过作图得到的,这个是公共编码,所以此时三角形 a、 d、 b 和三角形 a、 d、 c 是 全等的关系。 通过 b、 b 边证明此时角 b 等于角 c 啊,对应角是相等的,这是第一个方法,通过做中线的方法得到的。那现在第二个方法我们可以去尝试着做 角平分线啊,现在我做了一个角平分线啊,这个 a、 d。 我 们来说一下啊,这第二个方法啊,不是这个等它再换的方法了啊,我是说证明这个角的方法有两个啊,是这个方法其中第二个方法是用不了的啊, 好,第二个方法要通过做角平分线来进证明。首先我们做 a、 d 平分角 a b 角 b, a c 交 bc 于点 d, 这是我们的这个作图的一个表述方法啊,此时我们可以得到这个角命名为角一,这个角命名角二,所以只知道角一等于角二, 那之后是不是也显然可以得到啊?在三角形 a、 d、 b 和三角形 a、 d、 c 中, 是不是 ad, 呃, ab 等于 ac, 角一等于角二, ad 等于 ad 啊?所以说通过我们的边角边证明我们的这个圈的条件是成立的, 所以此时写上,所以三角形 adb 全等于三角形 adc 通过边角边证明,所以此时我们的这个什么,呃,角 b 等于角 c, 这是我们的第二个方法,那能不能通过做底边的高线呢?我们来尝试一尝试一下。好吧,我们来尝试一下可不可以做高线来进行证明 啊。现在我做 a、 d 垂直于我们的这个 b、 c 了,那现在这里是一个啊,直那个 公共边,这里是我们的,我们的什么?我们的斜边吧。那同学们勾股定律会不会啊?好,第三个方法,咱们换一个图好不好?换一个图,换一页啊,换一页。第三个方法,我们做 a、 d 垂直 bc 交 bc 于点 d。 好 的同学们,我们做垂直下来了, 我们会发现 ab 等于 ac, ad 等于 ad 的 话,那是不是意味着还少一点东西啊?因为我们在这个时候其实没有学 h l h l, 你 还没学到 这个,在同学们如果说你们已经学完这节课的时候来看我的课的话,会觉得我讲的非常的奇怪,为什么不用 h l? 因为我这节课的话是针对没学过的同学讲 h l, 同学们还没学到,所以说我们会通过边角边或角边角或角角边进证明不会用 h l 哈,在在这个学到之前,我们都是用的这个一些比较基本的证明条件。 h l 的 话,同学们不用着急啊,我们在大概是在第几节课?应该是在第二节, 呃,第二章,呃,叫叫第叫叫叫第二节吧,叫第二节吧。第二节关于直角形的这个性质的时候会讲的 h l。 哈,不用着急啊,咱们在这节课的话,不是这个 h l 涉及到别的东西啊,那咱们来看啊,首先我们用固定力可以得到 是不是 ab 的 平方等于 a、 d 的 平方加上 b、 d 的 平方啊? 然后 ac 的 平方是不等于 ad 的 平方加上我们的这个 cd 的 平方啊,因为 ab 等于 ac 吧, ad 等于 ad 吧,那所以什么?是不是 bd 等于 cd 啊?所以说此时 因为 b d 等于 c、 d, 又有我们的这个 ab 等于 ac, 还有什么 ad 的 ad 吧,所以说可以利用边边边的性质得到关于此时三角形 abd 和三角形 acd 全等。那当然呢,也可以用边角边吧,怎么用?是不是通过 b d 等于 c d? 角 a d b 等于角 a、 d、 c 等于九十度, a、 d 等于 a、 d 得到此时三角形 abd 确定三角形 a、 c、 d 啊,所以说第三个方法也是 ok 的 啊! 咱们就讲了这么多,咱先想一想同学们,我们由三角形 b、 a、 d 全等于三角形 c、 a、 d 图中线段 a、 d 还具有什么性质?为什么?同学们,我们来想一想啊,刚刚我会发现,我们做这条线的话 啊,这有点糊啊,有点糊,都好糊啊!咱们就啊,把这里擦了吧,把这里擦了啊! 我们会发现,我们无论是做平分线,做垂线还是做中线,他们貌似是不是同一根线? 朋友们,是不是啊,在同一个位置吧。因为我也发现,如果我挣到了全等的话,很明显他们的对应角是相等的,他们的对应边是相等的,对应的角还相等吧。所以说我只挣到三角形 a、 b、 d 全等,就会得到一 堆的条件吧。所以此时如果我能挣到 b、 d 等于 c、 d 的 话,所以说此时证明什么? a、 d 是 b、 c 的 中线, 如果我用圈的知道了角 a、 d、 b 等于角 a、 d、 c 等于九十度的话,说明什么?说明我们的这个角是九十度角,又以此说明此时 a、 d 垂直于 b、 c, 那 我如果由圈的条件推出了角一等于角二的话,是不是意味着此时 a、 d 还平分了角 b、 a、 c 啊? 所以会发现两个三角形全等引出的很多的蝴蝶效应吧。所以此时就明白 a、 d 它是一个非常非常特殊的线,它既是底边的中线,也是底边的高线,还是顶角的角平分线吧。所以说,此时我们可以很轻松的回答出陈哥现在说的这一问, 得到的结论是,此时他是底边的中线,你是底边的平分线,还是底边的高线?这些都是由全等所引出的蝴蝶效应 啊,很简单,同学们啊,如果咱们不记得了三线合一的话,同学们可以在淘宝纸上啊,在现场上你就直接啊画个等三角形出来,做条垂线下来,因为我明白这个垂,这个,这根线才是我们这个剪的核心所在 啊,这里是 a, 这里是 b, 这里是 c, 这里是 d 啊,这全等三角形全等, ok, 那 现在我们得到对应边关系,对应角关系,由此推出关于 a、 d 的 所有性质也可以的啊,三线合一很好推的,咱们可以在考场上现推啊,只要你有空的话,那现在我们来看到下个知识点 啊,刚刚挣到的等边对等角,以我们的这个三线合一,用几何语言的话,就是因为 ab 等于 ac, 所以 角 b 等于角 c, 三线合一啊,重点好,我们来练一练啊,练一练, 知道全是题目了啊!同学们,已知如图,三角形 a、 b、 c 和 a、 d, e 是 全等的角 b、 e、 d, 呃,哪里啊? b、 e、 d 到二十度, 现在要你要问你的是角 a、 e、 d, 问了,这个角是多少度,我们来看一下啊。同学们,首先这个是二十度的角, 这个角角一等于角二,为什么呢?很明显通过全等得到了吧,角一等于角二, 那现在意味着对顶角也相等吧,对应角也相等啊,这对顶角,这对应角啊,所以此时我们的角 d、 a、 b 这个角,它也是二十度,对不对?同学们, 那现在好了,这个角是二十度的话啊,那现在意味着我要挣到这个角,还还有没有别的条件呢?很明显还是有的啊。我们来看,如果说我要挣到这个角的话,我可以能不能推到这个角呢?因为我们知道角 a、 e、 d 其实也等于角 c 吧, 对吧?等于角 c 吧,那现在我们又要知道角 c 在 这个位置,角 a、 e、 b 在 这个位置,那我们去怎么证明? 好,我们再来看一下啊,那如果说我现在这个角和这个角相等呢?因为很明显吧,角 b、 a、 c 等于我们的角 d、 a、 e 吧,对不对?同学们,那所以呢,此时意味着这里 我们来用大题写起来写吧。啊,用,用小的题写的话,我有点说不清楚啊。由全等得到, 我们命名为这个角为角三啊,这个角四,这个是角五 啊,有趣的得到我们的这个角 d、 a、 e 等于角 b、 a、 c, 因此角三加上角六等于角四加角六,所以说角三等于角四吧。 又因为角一等于角二,也是个全等得到的吧,这就是全等条件啊。 角一等于角二,所以此时意味着角三等于角五,这里还是个对零角,所以此时角等于角五等于二十度, 那意味着此时它也是二十度吧。好,角四是二十度的话,那怎么求到角 c 呢? 我们是不是会发现由全等得到 a、 e 等于了 a、 c 啊?所以说什么?所以角 a、 e、 c 等于角 c 吧,等边对等角吧。那现在知道角 a、 e、 c 加角 c 加上角 e、 a、 c, 嗯,这里是角四啊,这里是角四,就是角四啊,加角四 等于一百八十度,那角四是二十度的话,所以说角 a、 e、 c 加角 c 是 不是一百六十度啊?它又相等,所以说此时角 a, e d, a e d, a, e, c 等于了八十度吧, 等于角 c 吧,那又全能又得到我们此时角 a, e, d, 它又等于了角 c 吧,所以说,答案是我们的八十度,答案是我们的 c 选项啊。第一题,它是一个有点像俄罗斯套娃的感觉啊,比较呃,稍微有点 繁琐,但是难度不是很大啊。这是我们的这个第一问,那例题, 这道题的话,我们来讲一下关于第一问就 ok 了。第二问,同学们可以课后自己去证明一下啊,很简单的,其实一样道理, 第一问都听懂了,第二问也很好证的。那现在看到第一个已知 a 点点 d 和点 e 在 三角形 abc 的 bc 上, ab 它等于了 ac, 若 ad 等于 ae, 让你证到此时 bd, b, d 等于 c e, 那 这道题怎么证?同学们,我们来看一看啊。首先,我们可以过点 a 做 a 句,垂直于我们的这个什么,呃, bc 为什么这样证呢?因为我这样证的话,我可以得到什么些性质?什么性质呢?是不是可以得到我们的 d 句等于 g e 啊?那此时一减,是不是得到 b, d 等于 c e 啊? 是不是?这是不是这么个道理啊?哎,我是不是没听清我,我在讲什么?同学们啊, b d 等于 c e, 它等于我们的 b g 减去 d g 等于 c g 减去 g e 吧 啊,所以说,我只需要知道 b g 等于了 c g, d g 等于了 g e 就 ok 了。这个很好证明吧,刚刚是不是证了很多次了? 我们通过证明边角边或者边边边得到此时 a g, e, a a, d g 和 a e, g 全等啊,我们来翻页啊!翻页,我们来证明一下啊! 首先我做了这么一个辅助线,此时它是一个垂直的关系,垂直的关系好,因为啊, a, d 的 平方等于 a g 的 平方加 d g 的 平方, a e 的 平方等于 a g 的 平方加 g e 的 平方。所以因为 a d 等于 a e, a g 等于 a g, 所以 d g 等于 g e, 那 所以在三角形 a, b, a, d g 和三角形 a, e, g 得到我们的这个什么 a g 等于我们的这个 a g 公共边角 a g, d 等于角 a g, e 等于九十度 得到,此时还有 d g 等于 g e, 那 现在是不是可以得到此时三角形的 a, d、 g 全等于三角形 a、 e、 g 了? 所以此时我们的这个什么, 呃, 一些低聚零聚异哎。哦,好像没必要挣全等了。好,同学们,我们已经挣到低聚零聚异了啊,没必要挣全等了啊,有点画蛇添足了。同学们 啊,咱们刚刚这个属于啊,翻车了啊,翻车了,忘了我要挣什么东西了。突然一下子不是全等了。同学们,我已挣到了低聚零聚异了啊,由这个固定里得到的,他现在同理是不是一样的?同理, 同理的话怎么同理啊?因为 ab 的 平方等于 a g 的 平方加 b g 的 平方, 然后这个 a, c 的 平方等于 a g 的 平方加 g c 的 平方吧。 所以此时是不是意味着我们的这个 b g 等于 g c 啊?那现在一减 b g 减 d g 是 不是等于我们的这个 g c 减 g e 啊?所以此时很明显吗?我们的这个 b d 等于了 c e 了吗? 同学们,也可以用三线合一来写啊!三线合一怎么写?同学们,因为我们知道 a、 d 等于 a、 e, 所以 三角形 a、 d、 e 是 一个等三角形吧。我们来写一下三线合一怎么写啊?这是我们的第一个方法。第二个方法,三线合一啊,因为 a、 d 等于 a、 e, 所以 三角形 a、 d、 e 是 等腰三角形。 因为 a、 g 是 d、 e 的 高线, 所以同学们,所以 a、 g 又是 d、 e 的 中线, 这里我们可以写上三线合一,所以此时 d、 g 等于 g、 e, 那 之后你写同理可得 我们的 b, g 等于 g、 c, 所以 之后再重复这一步操作就 ok 了。这是我们第一问很简单,第二问的话也很简单啊,咱们可以课后自己去写一下啊,咱们就不多做讲解了。 课堂小结,我们本节课学习了关于新的一个判定的条,判定的一个辅助条件是角、角边, 以及学习了关于对应边相等和对应角相等,也学习了此时他们那些性质叫做等边、对等角。还有我们的三线合一,其中三线合一是最重要的点,这个东西同学们在小学也学过了啊,咱们没必要再进行追究了, 咱们只需要知道咱们初中所学的重点是三线合一就 ok 了。那咱们看到我们的课堂练习已知, a、 b 等于 a、 e, 角 b, a、 d 等于角 c a、 e。 要是三角形 a、 b、 c 确定三角形 a、 e、 d, 还要添一个条件,这条件可以是什么 啊?我们可以试什么呢?同学们,我们来标注一下, ab 等于 a e, 角 b, a、 d 等于角 c、 e, 所以 说这两个公共角啊。所以此时角 b、 a、 c 等于角 d、 a、 e。 那 现在意味着我需要得到 条件,从而证得 abc 和 ad 全等股数。可以写 ac 等于 ad 啊, 因为这是边角边吧,你也可以写角 b 等于角 e 吧,这是角边角啊。所以同学们答案很多啊,咱们就不多做讲解了,这道题没啥意思。好,第二题,在第一问, 等腰三角形,一个底角为七十五度,那他另外两个角的话,很明显,一个是七十五度,一个是三十度。第二问,如果他说他的一个角是三十度的话,这个角可能是顶角,可能是底角啊,所以同学们及其分类讨论。 所以说答案是三十六度或一百零八度,这个答案是很明显吧?是,如果是底角的情况下,是底角的情况啊,底角的情况,这个是顶角的情况。 第二问,咱讲完了。第三问,等腰天线,一个角为一百二十度,另外两个角的度数为多少?很明显两个角的度数为多少?很明显,两个角的度数为多少?很明显,两个角为一百八十度的话,总和就超过了一百八十度吧。 所以说这个不可能为底角,只能为顶角。所以说这道题答案就是三十度负三十度啊。咱们的一些基本结论呢,咱们可以借鉴一下。顶角加上两 倍的底角等于一百八十度,顶角等于一百八十度。减去两倍的底角,底角等于一百八十度。减顶角的度数除以二。好,第四个和第五个是它的限定条件啊,这个很明显, 所以说同学们在等式教学中需要注意对讲的分类和讨论。那么本节课讲到这里,到此结束,我是你们的阿奇学长,我们下期再见,拜拜!
52阿橙学长 28:51查看AI文稿AI文稿
28:51查看AI文稿AI文稿哈喽,大家好,欢迎来到明老师初中数学课堂,我们今天一起来进行第一章三角形的证明的复习课。好,首先我们一起来进行一下本章知识点的大归纳, 我们在本章的内容学习当中,首先我们一起来学习了等腰三角形。好,咱们一起来看一下,在等腰三角形,三角形这部分内容当中,我们都学习了哪些知识啊? 我们学习了等腰三角形的性质,哎,每说到一点的时候,大家都可以按下暂停键,自己先回忆一下,那等腰三角形的性质是什么呢? 他有一个性质定理,对吧?哎,等腰三角形的两个底角相等,我们呢也可以简称为等边对,等角,对吧?哎,那么同时呢,他还有一个性质,可以简称叫做什么? 怎么样?三线合一,对吧?哎,也就是说等腰三角形呢,他这个顶角的平分线,底边上的中线以及底边上的高,哎,那么是互相重合的,哎,简称为三线合一。 好,继续。那在等腰三角形的判定这一方面,我们可以有哪些判定方式呢?首先我们可以用定义来进行判断,对吧?哎,如果我能说明啊,他有两条边是相等的,哎,那么他就是等腰三角形, 那么同时呢,我也可以通过一个判定定理来进行判定,对吧?哎,如果有两个角相等的三角形,那么他就是等腰三角形,哎,那这个判定定理呢,可以简称为等角对,等边。 好,那接下来我们又一起学习了等边三角形啊,那等边三角形呢,它是一种特殊的等腰三角形,那因此 呢,他具有等腰三角形的啊,所有的这个性质,除此之外呢,他有一些比较特殊的性质,对吧?哎,哪些特殊性质呢?一个等边三角形,他的三个内角都是相等的,哎,并且呢都等于每个内角都等于六十度, 哎,这个呢,就是属于等边三角形啊,他一个比较特殊的地方,对吧?那对于等边三角形的判定,我们都有哪些方式呢?我们首先可以根据定义,三条边都相等,这样的三角形呢,就是等边三角形, 同时呢,我们还可以用其他的方法进行判定,比如说我们可以通过角来进行判定,对吧?三个角都相等的三角形,就是等边三角形,或者呢,我们也可以利用什么呀,如果有一个角等于六十度的等腰三角形,那么他也是等边三角形,哎,这 几个呢,都是我们常用的来判定等边三角形的方法。好,继续在直角三角形这部分内容当中,我们又一起学习了什么呢?首先我们学习了直角三角形的性质,性质主要包括哪些呢?首先直角三角形两个锐角互余,对吧? 然后其次呢,还有一个呢,就是如果说呀,在这个直角三角形当中,有一个锐角等于三十度,哎,那么这个三十度的锐角所对的直角边等于斜边的一半,哎,这个也是属于直角三角形的一个性质,对吧? 除此之外呢,还有我们在上个学期所学过的勾股定理,哎,他呢,其实啊啊,也应该把它归纳在这个直角三角形的性质当中了,对吧?哎,两个直角边的平方和等于斜边的平方,好,那么对于直角三角形的判定,这部分内容当中, 首先可以用定义,哎,如果你能说明啊,这个三角形当中啊,有一个角是九十度,那么呢,这个三角形你就可以判定他为直角三角形,哎,那还有其他的方法吗?如果有两个角互余的三角形,是不是也应该是直角三角形啊,对吧?这个也是直角三角形的一个判定的定理。 那么除此之外,还有一种判定方法,就是我们所说的勾股定理的逆定理,对吧?如果三角形两边的平方和等于第三边的平方,那么这个三角形就是直角三角形,哎,这个呢,是用边来判定这个直角三角形的。 好,接下来我们一起学习了两个全等直角三角形的判定。除了我们之前学习的那个啊,边边边角边角角角边以及边角边这几种判定方法之外,对于直角三角形来说, 还有一种特殊的判定方法,就是斜边直角边,这个判定定理简称为 hl, 哎,他呢是专门用来判定直角三角形的。好, 我们继续。那么在后面呢,我们又一起来学习了线段的垂直平分线,哎,那么他的性质主要有哪些呢?线段垂直平分线上的点到这个线段两个端点的距离相等,这就是他的性质。 那么他的判定呢,刚好啊,就是把这个性质啊给他秘密提一下,对吧?哎,到一条线段两个端点距离相等的点 就在这条线段的垂直平分线上,哎,这个就可以用来作为垂直平分线的判定了。好,继续一个三角形,他三条边的垂直平分线有什么样的性质啊? 三角形三边的垂直平分线相交于一点,并且这个点有什么特征呢?这个点啊,到三角形三个顶点的距离都相等,哎,这个呢,就是三角形三条边的垂直平分线的性质。 好,继续。接下来角平分线,它的性质是什么呢?角平分线上的点到这个角两边的距离相等, 哎,那么他的判定这里要注意了,我们也必须要加一个前提条件,就是在一个角的内部, 哎,到角两边的距离相等的点,在这个角的角平分线上,哎,一定要注意加上一个在一个角的内部,哎,否则的话呢,这个命题啊,就是错误的啊。好,再继续。三角形三条角平分 线有什么样的性质呢?三角形的三条角平分线相交于一点,并且这个点到三角形三边的距离相等, 哎,这个呢,就是三角形三条角平分线的性质。好,那么以上呢,就是我们本章啊所进行的一个知识点的归纳,咱们在学习的过程当中,一定要及时的复习,及时的归纳。好,接下来我们再通过一些例题来让大家强化一下我们对这一章知识的掌握。 首先第一题,满足下列条件的三角形不一定是直角三角形的,是,注意啊,他说的是不一定是啊, 好,我们看 a 选项,三条边的比为,五比,十二比十三。看到这三个数啊,应该很熟练的反应数,这是一组勾股数,五,十二,十三,常见的勾股数啊,五的平方加十 十二的平方就等于十三的平方,哎,所以呢,这个满足勾股定理的逆定理啊,他呢,可以判定出这个三角形是全等啊,是,是这个啊,直角三角形啊,好。 b 选项,三个角的度数比为二比三比五,这个呀,就得把角度给他求出来了,对吧? 哎,根据比例关系,你可以分别设置三个角为二 x, 三 x, 然后呢,还有五 x, 对吧?哎,那么他们三个相加呢,等于一百八十度,哎,这里呢,就可以算出 x 的度数了。一百八十度啊,哎,这里呢,算出来 x 应该是等于十八度。 好, x 等于十八度的话,那这个二 x 呢,它对应的就是三十六度,对吧?它呢,三 x, 它就应该是五十四度,它是五 x, 五 x 对应的就是九十度,哎,刚好它有一个 九十度的角,对吧,所以他也一定是一个直角三角形。好, c 选项,有一边等于另一条边的一半, 那这个呢,不能判定一个三角形是直角三角形,对吧?哎,满足这个条件的三角形,我们可以画出其他的形状的,所以呢,他不能判定他。也就是说呢,满足这个条件啊,不一定是直角三角形。好。 d 选项,三角形的三边长分别为二十四、二十五和七, 这个呀,也是一组购物数哎,七的平方加上二十四的平方就等于二十五的平方, 哎,所以呢,他满足勾股定理的逆定理,哎,所以呢,他可以判定出一定是直角三角形。所以呢,这个题啊,最后答案应该就是 c 选项。好,接下来第二题,下列能判定三角形 a、 b、 c 为等腰三角形的是, 哎,这个又是等腰三角形的判定,对吧?我们看给了角 a 和角 b 的度数,那我自然可以想到,我想求角 c 呗,对吧?这里算出呢,角 c 应该是等于一百八,减三十减六十,应该等于九十度的, 哎,那也就是这个三角形是一个直角三角形,对吧?哎,并且呢,他应该不是一个等腰三角形,哎,所以呢,这个啊, a 选项他不能判定他是等腰三角形。好。 b 选项,角 a 等于五十度,角 b 等于八十度,那这样算出来,角是应该等于多少度啊? 一百五八十度,减八十,再减五十,角 c 算上应该是等于五十度的,哎,那角 c 和角 a 的度数是不是相等的呀? 哎,根据等角对等边,对吧?哎,有两个角相等,这三角形他就是等腰三角形,所以他是可以判定的啊。答案现在就出来了, b 选项啊,我们看一下 c 吧,角 a 等于二倍的,角 b 等于七十度,那这个二倍的角 b 等于七十度,角 b 就应该等于多少啊?角 b 就应该等于三十五度,对吧?哎,角二等于三十五度,角 b 等于三十五度,角 a 呢,是他的二倍啊,已经是算出来七十度,那角 c 的度数我是不是可以求出来了?一百八十度,减去他再减去他算出来应该等于七十五度,这三角度数都不相等,对吧,所以他不能判定 好。 d 选项, ab 等于四, bc 等于五,给了两条边长,又给了个周长,我是不可以求第三边的长度来。第三边呢,应该就是 acac, 就应该等于十五减五,再减四,算出来应该是等于六, 也就是说,这个三角形的三边呢,分别应该是四五六,对吧?哎,没有两条边是相等的,所以呢,它也不能判定出是等腰三角形。所以呢,这个答案应该就是 b 选项。好,接下来第三题,如图,在三角形 a、 b、 c 中, b、 d 平 分,角 abc 平分,那这两个角,哎,他俩应该是相等的。好,然后呢,这个异地和 bc 他俩是平行的啊,这样,他俩呢,是一组平线好,已知 ab 等于三, ad 等于一。 求,这个三角形 aed 的周长是多少?哎,想求周长呢,你肯定就应该用三边相加呗,对吧? ad 加上 ae, 再加上 de。 哎,根据已知条件,我只知道一个 a d 的长是等于一,那这个 a e 加 d e 的长应该是多少呢? a e 在这儿, d e 呢在这儿。 哎,已知条件当中给的是 a b 的长等于三,对吧?哎,那这个 a e 和 d e 他那么的和跟这个 a b 有什么样的关系呢?那就得利用其他的已知条件了。首先他俩是相等的角,平行线,然后又给了一组平行线,根据平行线的 性质,两直线平行内错角相等,我就可以得出这个角啊,应该是等于这个角的,对吧?哎,角 cbd 应该等于这个角 edb, 对吧?他俩应该相等。哎,那是不是这三个标出红色的这三个角应该都是相等的呀? 所以我就得到这个三角形 b, e、 d 来观察啊。这个 b, e、 d 当中是不是有两个角都相等啊?它是一个等腰三角形 好,如果他是等腰三角形的话,我根据什么呢?这个 b e 和 d e 就应该是相等的,对吧?哎,所以他们三个相加呢,我就可以把它转化为 a d 加上 a e, 然后再加上谁呢?把这个 d 啊,就可以用 be 给他表示出来,对吧?哎,再加 b。 好,那 ad 我照常写下来,加上这个 ae 加 be, 那是不就是 ab 啊? 哎,所以它这个周长啊,我就把它转化为 a、 d 与 a、 b 这两条线段的和,那这两条是不是都是以这条件的?一个三,一个一,对吧,他俩相加就等于三加一呗,就等于四。所以呢,这道题答案应该就是分享一下啊。 哎,他呢,是把这个啊,角平行线,平行线,还有这个等腰三角形的内容都结合起来了。好,第四题,如图,在直角三角形 abc 中,角 c 等于九十度。标一下啊,哎,这里是一个直角,然后呢,角 b 等于三十度。 好,边, a、 b 的垂直平分线 d、 e 啊,这个 d、 e 啊,它是这个 a、 b 的垂直平分线,根据垂直平分线的性质,垂直平分线上的点到线段,两个端点距离相等,对吧?那这个 a、 d 和这个 b、 d, 它俩肯定就应该是相等的。好,继续 告诉我们, c、 d 的长等于三啊,他等于三了。然后呢,求,这个整个的啊,这个 b、 c 的长是多少? 那这个我们应该怎么来考虑?这有三十度,刚才我就看出来这两条边是相等的,那这个啊,三角形 a、 b、 d 啊,它应该就是一个等腰三角形, 对吧?哎,那所以呢,这个角是不是也应该是等于三十度啊?两底角相等,对吧?哎,角 b、 a、 d, 他应该是等于三十度,他如果等于三十度,那这个角呢,角 c、 a、 d 应该是等于多少度啊?我们看一下,这里是角 c 是九十度,角 b 三十度,那么这个角 b、 a、 c 是不是应该等于九十度减三十度啊?哎,他应该等于六十度,整个这个角 b、 a、 c 等于六十度,那角 b、 a、 d 呢?等于三十度,那所以呢,这个角 c、 a、 d 也应该是等于三十度,对吧?好,他既然是三十度,我们继续看, 那么这个三角形 acd, 他是不是就是一个含有三十度角的直角三角形啊,对吧?三十度角所对的边是 cd, 斜边是 ad, 所以呢,我是不是应该就有这个 ad 就应该等于二倍的 cd 啊,对吧? cd 长是三,二倍 cd 长应该就是六,所以这条边的边长应该就是六。 a、 d 如果等于六了,那么对应的这个 b、 d 的长是不是也应该等于六啊,对吧?好, b、 d 等于六, c、 d 等于三,那你说 b、 c 的长应该多少?是不是应该就用六加上这个三呐?哎,六加三等于九,对吧?所以呢, b、 c 的长就是九啊,这个答案呢,就是 c 选项,它呢是一个角平分线与这个 啊线段的垂直平分线相结合的这样的一个题目,同时呢,又结合了一个含有三十度角的这个直角三角形,它的性质,对吧?好,第五题,如图, a、 b 平行于 c、 d, 哎,他俩这俩都是平行的啊,标一下他俩平行,然后呢, b、 p 和 c、 p 分别平分角 a、 b、 c 和角 d、 c、 b 啊,就是说这里他俩是相等的,那下面这个角 d、 c、 b, 哎,他也是平分角平线啊,这两个角也是相等的。 好, a、 d 呢?经过点劈,并且呢与 a、 b 垂直啊,这里是一个直角,好,告诉我们, a、 d 的长是八, 你看 a、 d 的长啊,它的长是八,我,我标在后面呢啊,哎,它的长是八,求什么呢?求这个点 p 到 b、 c 的距离, 点 p 到 b、 c 的距离,那我是不是应该过这个点 p 向这个 b、 c 做一个垂线呢,对吧?好,我把这个垂线做出来啊,设垂足为 q, 哎,这里呢,是垂直的,也就是这道问题呢,要求我们求出的 是这个线段 pq 的长度呗,对吧?好,那怎样来求呢?很显然,我们得利用角平行线的性质,对吧?好,点, p 呢,在这个角 abc 的角平行线上,那么他到这个角两边的距离应该是相等的,也就是说呢, ap 应该是等于 p q 的,对吧?哎,它俩相等,那同样道理呢,点 p 也在这个角 b c、 d 的角平行线上,这里也是角平行线的,对吧?那这两边也都是垂直的,为什么这里是垂直的呢?因为它俩平行, 哎,平行的话,这里是一个九十度角,他俩应该是同方内角互补啊,对吧?那他是九十度,所以这里肯定也应该是九十度,哎,所以这里也是垂直的,哎,所以呢,我就应该有这个 pq, 还应该等于 pd, 也就是说呢,这个 a p, p q 还有 p d 这三条线段啊,都应该是相等的,哎,在都 相等的情况下,我就有什么呢?其实这个点批啊,就应该是这个线段 ad 的终点,对吧?哎,那线段 ad 的长是八,所以呢, ap 的长肯定啊, ap 的长肯定就应该是四,对吧? 哎,那这个 p d 的长也应该是四,那我是不是就得到这个 p q 的长,是不是也应该是四啊,对吧?哎,他们三个都相等吧,那 p q 的长如果是四的话呢,也就是说,点 p 啊,到这个 b c 的距离应该就是四,对吧?所以呢,这个题答案应该是 c 选项。 好,第六题,下列命题一二三四,哎,其中原命题和逆命题都是真命题的,有几个?这里要注意了啊,他不光问这个原命题,哎,他还问这个逆命题, 他俩要求都是真的才行啊,大家自己暂停思考啊,因为有四个命题,对吧?思考一下他们每一个问命题的这个逆命题都是什么, 再判断一下他们的真假啊。好,第一个谜题,钝角三角形有两个内角是锐角, 这个命题肯定是正确的。我首先说,对吧,一个对角三角形吧,你除了一个角是钝角以外,另外两个角肯定都得是锐角啊。哎,那原命题正确了,那逆命题呢?是不是应该是说有两个内角是锐角的三角形,是钝角三角形,这应该是他的逆命题,对吧? 那么这个逆命题是不是真命题呢?如果一个三角形有两个内角是锐角的话,那它第三个角一定是钝角吗? 很显然不一定,对吧?第三个角既有可能是锐角,也有可能是直角,也有可能是钝角,也就是这个三角形啊。呃,什么形状都有,对吧?所以他不一定是钝角三角形,所以他的逆命题是错误的,原命题正确,逆命题错误。所以呢?他呀,不能计算在我们这个啊,两个 都是这命题的这个范围里面,对吧?好,第二个命题有两个角是六十度的三角形,是等边三角形,那这个命题对不对啊?如果一个三角形有两个角都是六十度, 那么他第三个角是不是一定也是六十度啊,对吧?哎,这三个内角都相等,这样的三角形就是等边三角形,原命题正确。 好,我们看下秘密题。秘密题应该怎么说呢?是不是啊?如果一个三角形是等边三角形,那么他有两个角是六十度啊, 这应该是他的逆命题,对吧?啊,那如果三角形是等面三角形的话,那他三个角都是六十度,那,那,那我要说有两个角是六十度,那肯定也正确啊,对吧?哎,所以呢,他的逆命题也是正确的。哎,他就符合条件了。这有一个了啊,我们再看第三个,直角三角形的两个锐角互余,那这个圆命 题啊,肯定是正确的。这直角三角形的性质反过来怎么说呢?逆命题就应该是啊,如果一个三角形有两个锐角互余,那么这个三角形是直角三角形。 哎,那你想想,如果两个角互余的话,那第三个角怎么样啊?是不是肯定得等于九十度啊,对吧?哎,两个角互余,就是比如角 a 加角 b, 哎,他俩等于九十度, 那你想想,你这个角 c 是不是一定也得等于九十度啊,对吧?哎,角 c 如果等于九十度的话,那这个三角形一定就是直角三角形,对吧?所以他的逆命题也是正确的啊,有两个角互余的三角形是 直角直角形,也是正确的。好,他也算了,哎,现在我们找到两个了,对吧?好。第四个,成轴对称的两个图形能够互相重合,这个肯定是正确的,对吧?原命题肯定是正确的啊,那逆命题呢,是不是应该 说能够互相重合的两个图形成轴对称的,那这个对吗?这个肯定是错的,这个不一定。我们说轴对称,他的定义是什么呀?必须要沿着一条直线翻折过来,对吧?翻折过来能够互相重合才行。 哎,所以呢,并不是说只要能重合就一定是轴对称就匿名题啊,他是错的啊,原命题正确,所以呢,他这个一和四不能进入在这个最后满足条件的这个个数里面,所以二和三是满足条件的。所以呢,啊, 答案应该就是 b 选项啊,有两个都是圆命题与逆命题,都是真命题的选项啊。 好,接下来第七题,如图, a、 b 平行于 c, e 啊,它俩是平行线哎,它俩是平行的。然后呢,又告诉我们 d, e 等于 d f 啊,它和它相等,也就这个三角形。 d, e, f 是等腰三角形呗,对吧,然后呢,角 f, 哎,角在这啊,他呢等于二十度。好球呢,这个角 b 的度数是多少?刚才分析完这个三角形是等腰三角形啊,对吧,两个底角分别为角 e 和角 f, 角 f 等于二十度,那角 e 应该就也是二十度呗,对吧? 好,那这对于求角臂有什么样的帮助呢?那看平行线了,对吧,他俩平行,那是不是这个角我给起名叫角一啊,角一是不是应该就等于角臂啊, 对吧,那我只要把角一求出来是不是就可以了?两直线平行,同位角相等,哎,求角一,角一呢,又是这个三角形 d, e, f 的一个外角,对吧? 哎,那外角应该等于与他不相邻的两个内角之和,所以呢,这个角一啊,应该就等于角 e 加上角 f, 对吧?哎,就等于两个二十度,加在一起应该等于四十度。 角一等四十度,那角 b 很显然也应该是等于四十度,对吧?哎,所以呢,啊,这个答案应该就是四十度,哎,这个又把等腰三角形和这个平行线给它结合在一起了啊。 第八题,如图, b d 垂直平分线段 a c 啊, b d 啊,是这个 a c 的垂直平分线。 哎,那我们是不是首先考虑可以利用性质了,性质里面应该具有什么呢?这个 a b 啊,和这个 b c 他俩应该是相等的,对吧?这个只不过是横过来放了,大家要适应啊。不不不,仅能看出来这个竖着的,横着的,应该也能看出来 三角 abc 是个怎样三角形呗,对吧?好,我继续看垂足,这个 ae 垂直于 bc 啊,这样,这里是一个垂直的。然后呢,告诉我们, pe 的长 pe 等于三厘米啊, p, 这这这小线段它等于三厘米, 求这个点劈啊,到直线 ab 的距离是多少到 ab 的距离,那我得得这样,得画个垂线呗,对吧?哎,这样,哎,这个起名叫 f 吧,哎,我就是想求一下这个 pf 的长度是多少呗,对吧,我们刚才已经分析过了,这个呢, 三角形 abc 是一个等腰三角形,哎,那这个 bd 呢,应该既是底边的中线,又是底边的高,同时是不是还应该是顶角的角平分线呢,对吧?哎,三线合一嘛,所以这两个角啊,应该是相等的, 也就是点 p 啊,它实际上呢,就是这个角 a b c 的角平分线上的一个点,对吧?根据角平分线的性质啊,角平分线上的点到这个角两边的距离是相等的,所以呢, p f 的长度应该就等于 p e, 哎,那 p e 的长度也给我, 我们呢,是等于三厘米,对吧?哎,所以 p f 就等于三厘米,那么也就是说这个点 p 啊,到这个啊,直线 a b 的距离应该就是三厘米。 好,接下来第九题,如图, a, d 平分角 b, a, c, a, d 平分角 b, a, c 啊,这两个角它俩是相等的啊,然后呢, d, e 垂直于 a, b, d, f 垂直于 a、 c, 那我首先是不是可以看出这个 d, e 和 d、 f 它俩应该相等啊,对吧?这里应该就很熟练了啊,角平行线的性质。好,继续,又告诉我们 d, b 等于 d, c, 我看一下啊, d, b 是它 d, b 又等于 d c, 好,让我们求证这个 b, e, 它和这个 f、 c, 求证它俩相等。看这个图,这样标了以后啊,很自然应该就会想到,我们应该利用的是全等三角形了,对吧?哎,因为这个三角形 b, d、 e 和这个三角形 c, d、 f 啊,是两个直角三角形,对吧?哎,两个直角三角形当中,我们观察这两条斜边分别是 d、 b 和 d、 c 两个斜边相等,对吧? 那这个,这个 d、 e 和 d、 f 呢?又是两条直角边,两条直角边也相等,那我是不是其实就可以判定出这个三角形 b, d、 e 应该是全等于这个三角形 d、 c, f 的,对吧?他俩是全等的哎,依据呢,就是这个斜边和直角边这个判定定理啊,他俩如果全等的话,那你看,求证这个 e, b, e, b 在这,对吧?和,这个啊, e, e, b 和这个 f, c 看一下 b, d, e 和 c, c, d, f 啊,这是写错了啊,啊,对对,对应的顶点写错了,应该是 c, d, f 啊。 啊, c, d, f 啊,那这个 b, e 对应的和这个 f、 c, 它俩是不是刚好就是一组对应边啊,对吧?哎,所以我就得到这个啊, e、 b 呢,确实就是等于 f、 c 的了。好,我们一起来看一下解题的步骤啊。 好,首先由角平行线判定出了 d e 等于 d f, 然后根据已知条件, d b 还等于 d c, 哎,然后我就可以判定出两个直角三角形全等,哎,然后接下来呢,就可以得到对应边相等,所以这个 e b 和 f c 就相等。哎,这道题呢,就把这个啊角平行线和这个直角三角形全等的这个判定结合在一起啊,好, 接下来第十题,如图,在直角三角形 a、 b、 c 当中,角 a、 c、 b 等于九十度,在这里啊,这里是一个直角。好,然后呢, d 和 e 是 a b 边上两个点,且 c e 注意看啊, c e 所在的直线垂直平分线段 a d, 哎, c e 是 a d 的垂直平分线, 那我就很快的应该想出什么呀,这个 ac 和这个 cd 他俩是不是应该是相等的呀,对吧?线段垂直平行线的性质吗?哎,然后继续看,还有时候 cd 呢,要平分角 bce, 我看啊, cd 平分角 bce 啊,就是这个角和这个角,他俩呀又是相等的, 哎,然后呢,告诉我们 a c 的长度是五厘米,求这个 b d 的长度应该是多少? 这道题呢,我们首先还是得利用这个线段垂直平行线了,刚才我们已经分析过了啊, a c 和 c d 相等,也就是说这个三角形 a、 c、 d 呢,是一个等腰三角形,对吧?哎,那这个 c、 e 根据三线合一,他也应该就是这个顶角角 a、 c、 d 的角平分线,对吧?哎,所以呢,我这里应该会得到一个角度的一个等量关系啊,应该是谁呢啊,角一跟这个角二 是不是应该是相等的?哎,角一等于角二,这个是等腰三角形的性质,对吧?好,我继续来看,因为这个 cd 呢,他又平分了角 bce, 对吧?哎,也,所以呢,我就说这个角二和角三是不是也应该是相等的呀?哎,那我就得出角一、角二、角三这三个角都相等了呗, 那这里呢,是一个直角,对吧?比如说他们三个相加等于九十度,那他们三个又分别又相等,所以我是不是其实可以求出他们的度数了,对吧?哎,他们三个呢,就应该都等于三十度。 好,度数我可以求出来了。求数度数之后呢,我接下来看,这里角一等于三十度,这里是个直角,对吧?所以我是不是可以把角 a 的度数求出来呀?角 a 求出来应该就等于六十度, 角 a 求来以后呢,那什么角 b 就可以求了,他俩又互余啊,对吧?角 b 求来呢,也应该等于三十度,到这,我发现角 b 和角三是相等的,他俩都等于三十度,对吧?也就是这个三角形 bcd, 他呢应该是一个等腰三角形。 好,那如果他是等腰三角形,等角对等边,我就应该有这个 b d 应该是等于 c d 的, 对吧?哎,那经过刚才的分析呢,这个 c d 和 a c 又相等,对吧?哎,这上面 a c d 也是一个等腰三角形啊,所以呢, c d 又等于 a c, 所以呢,就是 b d 要求的,这个他和 a c 呀,是相等的,就应该是等于五厘米,对吧?哎,这个五厘米呢,就是最后的答案了。哎,所以呢啊, b d 长五厘米。其实这道题呢,也不止这一种减法啊,当我们证明出这个角一角二角三相等之后呢,其实你 你也可以不用急着马上去求这个度数到底是多少,我们还可以怎样来做呢?我考虑一下啊,我们还可以说角一加上角 a 等于九十度,对吧?哎,这个三角形 ace 是个直角三角形嘛,那同时在这个大三角形里来看呢,是不是有这个啊,角 b 加上角 a 是不是也等于九十度啊,对吧?哎,那这两个条件我就可以得出什么呢,角一应该是等于角 b 的,对吧,因为他们都是角 a 的余角啊,同角的余角相等嘛?角一等于角 b, 哎,那角一就等于角三,对吧?哎,所以呢,角 b 就等于角三,哎,所以呢,我在不求出度数的情况下,我也可以直接证明出角 b 和角三是相等的。哎,那所以我也可以得到这个 cd 和 bd 也相等呗,对吧。哎,那所以呢,也可以求出最后 bd 的长度啊。好,哪个方法 都可以啊,大家可以根据自己的这个解决习惯来做啊,咱们看一下解决步骤啊,这个呢,是用的是我们后面所说的那种方法,没有直接求出角度啊。 好,今天的复习课呢,就和大家一起学习到这里,我们下次课和大家一起来进行第二章一元一次不等式 与一元一次不等式组的学习啊,下次课呢,是第一节不等关系,欢迎大家收看,如果喜欢请关注明老师初中数学课堂,如果大家在学习中有问题,欢迎留言或者给我发私信,我们下次再见。
86明老师课堂 01:06查看AI文稿AI文稿
01:06查看AI文稿AI文稿北师大办八下数学一元一次不等式核心考点之含餐问题。若关于 x 的 方程三, x 减二 m 等于一的解为正数, 则 m 的 取值范围。这道题的关键是求出方程的解,并且让解为正数。首先,解这个方程三 x 减二 m 等于一,三 x 等于一加二 m, 从而可以得到 x 等于三分之一加二 m。 因为解为正数, 所以三分之一加二 m 大 于零, 于是一加二 m 就 大于零, 所以二 m 大 于负一,最终二 m 大 于负二分之一。
7长江老郭 01:32查看AI文稿AI文稿
01:32查看AI文稿AI文稿朋友们好啊,今天继续给大家整理八年级下册数学的全册预习,重点预习,抓主线,破难点,按章节拆分, 明确核心重点,预习关键,衔接考点,方便直接用来规划预习,精简实用。今天关注第三张图形的平移与旋转。一、核心重点,平移的性质,对应点连线平行且相等, 对应线段平行且相等,形状大小不变。旋转的性质,对应点到旋转中心距离相等,旋转角相等,形状大小不变。中心对称图形的判定,绕中心旋转一百八十度,与圆图形重合, 比如平行四边形。二、预习关键,动手画图,平移抓方向和距离,旋转抓旋转中心方向、角度,这三个要素缺一不可,通过画图理解,性质更直观。三、衔接考点,后续平行四边形的学习会用到平移旋转性质预习时打好基础, 记住常见中心对称图形,平行四边形、矩形、菱形、正方形。如何才能提高预习效率呢?给大家分享几个实用的操作方法。一、先看教材立体,先精读定义,再看例题步骤,搞懂每一步的依据。二、抓核心概念性质,把相关定义、平移旋转的性质、 中心对称图形的判定抄在笔记本上反复记。三、基础题优先练预习时不用攻难题,重点做教材课后基础题,磋识基础比刷难题更重要。四、标记疑问点,遇到不懂的地方做好标记,开学后重点听老师讲解,针对性突破。
113初中数学肖老师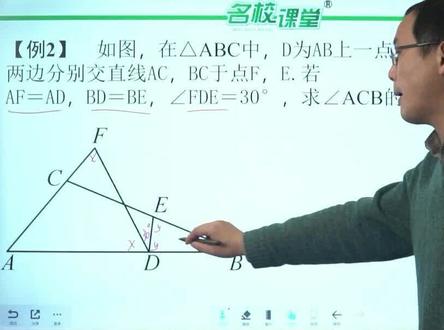 02:50查看AI文稿AI文稿
02:50查看AI文稿AI文稿各位家长,各位同学,欢迎来到名校课堂,我们今天来看一下整体思想在三角形内角和当中的应用, 一起看一下。如图,这是一个三角形, d 是 a、 b 上一点角 f、 d、 e 的两边分别交直线 a、 c、 b、 c 与 f、 e 两点,对吧?若 a、 f 等于 a、 d、 b、 d 等于 b, e 角 f、 d、 e 等于三十度,对吧?啊,这个角是三十度 啊,求 a、 c、 b 的度数对吧?好,我们在这个地方有两个相等的条件,对吧?那么根据我们等腰三角形的性质啊,就可以知道他们两个底角也是相等的,那这个时候我们不妨设这个, 下面这个角是 x, 那么这个角 f 也是 x, 同样的,我们设这个角 e、 d、 b 等于 y, 那么上面这个角也是 y, 对吧?好,那我们来看一下。那根据这个平角 是一百八十度,可以知道 x 加 y 加三十度等于一百八十度,所以就得到 x 加 y 等于一百五十度。好,那么我们就可以进一步得到一个式子,在左边的三角形当中啊,在三角形 a、 fd 中, 我们知道角 a 加上二 x 等于多少啊?等于一百八十度啊!在右边的三角形 b、 d、 e 中, 那这个时候角 b 加上二 y 也等于一百八十度,对吧?所以,那么把两室一加,就知道,角 a 加角 b 加上二 x 加上二 y 等于三百六十度。我们知道 x 加 y 等于一百 五十度,所以二 x 加二 y 就等于三百度,所以这个时候角 a 加角 b 就等于六十度。再根据三角形 a、 b、 c 当中内角和一百八十度, 就可以知道,角 acb 加上角 a 加上角 b 等于一百八十度,这个时候角 a 加角 b 等于多少啊?等于六十度,所以角 acb 就是一百二十度。 这个题目呢,我们是没有办法分别求出角 a 和角 b 的,那我们利用一个整体思想求出角 a 和角 b 的和, 然后的话就可以求出角 a、 c、 b 了。那角 a 和角 b 的和呢?怎么求呢?那也是再次利用整体思想,在三角形 a、 f、 d 和三角形 b、 e、 d 中再用两次得到两个方程相加,就可以得到角 a 和角 b 的和了。那么像这种整体思想在等于三角形当中的应用 大家都掌握了吗?那么这道题的详细解题思路就写在这里,留给大家巩固一下吧。最后给大家留了一道同类型的题,评论区告诉我答案吧! 连续答对三道题的同学,可以私信客服领取一本学霸秘籍,周末练一练哦!
147周末好搭档 23:25查看AI文稿AI文稿
23:25查看AI文稿AI文稿哈喽,同学们大家好,我是你们的阿山学长。今天我们讲第一张一点一的第二课时等边三角形的性质,我们回到我们的这个流程图, 我们到了第二节的一个知识了啊,现在我们再往下讲,就是下节课就是等边三角形的判定,以及我们的这个反正法。那我们先看到本节课的知识,在期下我们已经知道了三边相等的三角形是等边三角形。 生活中有很多这样的等边三角形,比如说我们的这个交通图标,又比如说咱们台球厅的三脚架,他们的这个形状都是等边的三角形, 那同学们我们归我们来思考一个问题,在上一节课我们证明了等腰三角形的两底角相等,那等边三角形的各角之间的关系是什么样的?那我们回归归我们的重要性质, 首先在等腰三角形中画出一些线段,比如说角平分线,中线以及他的高线等, 我们能不能发现其中一些相等的线段,通过证明相等的线段来得到它的性质呢?我们来看一下啊,我们第一个猜想是底角的两条平分线相等,第二个猜想是他的两条腰啊,他的中线相等, 第三个猜想是两条腰上的高线相等,现在我们来进行证明,第一个证明 等腰三角形的两底角的平分线是相等的啊。如图,在三角形 a、 b、 c 中, ab 等于 ac, b、 d 是 b、 d 和 c、 e 分 别是角 a、 b、 c 和角 a、 c、 b 的 角平分线,那这 b、 d 等于 c、 e, 那 这个很明显是通过证明全等三角形来进行求证的吧,所以说我们只需要证到三角形 e、 c、 b 全等于三角形 d、 b、 c 就 可以证到我们此时我们的 b、 d 等于 c、 e 了。那现在我来证明一下啊。首先因为 a、 b 等于 a、 c, 所以 由等边对等角得到角 a、 b、 c 等于角 a、 c、 b。 又因为此时 d、 d、 c、 e 是 角平分线, 所以角一等于二分之一的角 a、 b、 c。 角二等于二分之一的角 a、 c、 b, 所以 角一等于角二。 那现在角一等于角二,知道了角相等,又有一条公共边, 那现在意味着我还需要挣到别的条件才行吧。要么挣边角边,要么挣角边角吧。 那现在我们来看哈,边角边就要证明是两边及夹角,所以要挣到 c 一 等于 b、 d。 我 们发现这是我们要存在的条件,所以说我们利用边角边没办法证明。那现在我们只能用角角边来证明了吧。 好,现在我们使用直角边,所以说我只需要正到我们的角 abc 等于角 dcb 就 行了吧。那因为角 abc 等于角 abc, 是 不是它不是同一个角啊?所以说在三角形 abc 和三角形 d、 c、 b 中,因为角 e、 b、 c 等于呃 e、 b、 c 啊, 等于角 d、 c、 b 以及 b、 c 等于 b、 c。 还有角一,角二等于角一,所以三角形 e、 b、 c 全等于三角形 d、 c、 b 是 由角边角得到证明的。那所以此时 b、 d 等于了 c、 e 啊,得正,很简单,这是我们的猜想一。 那现在看猜想二,等腰三角形两腰上的中线相等 已知如图啊。在三角形 a、 b、 c 中, ab 它等于 ac, 然后 b、 m 和 c、 n 是 两两要素的中线,要证 b、 m 等于 c、 n, 怎么证? 一样道理吧,也是通过证三角形 b m a 全等于三角形 c n a 就 可以了吧, 我们只需要找到它对应的三角形全等就 ok 了吧。那现在我们来看啊,已知我们的 ac 等于 ab 啊,标上 ac 等于 ab, 那 现在 nc 又和 bm 分 别是 ab 和 ac 的 中线,所以说词是什么? ac 的 与 bc 的 中线,所以说词是不是意味着 an 又等于我们的 am 啊, 是不是这样的那些同学们,所以此时我们又要找到一个角就 ok 了吧,是不是公共角角 a 啊,那所以我们的思路就是通过证明边角边来得到 b m 全的 b m 等于 c n 吧,那所以我们来进行证明, 因为 ab 等于 ac, 又因为 b m c n 是 两腰上的中线, 那现在可以得到呃 am 等于二分之一的 ac, 以及我们的 a n 等于二分之一的 a b, 所以 此时 a m 等于 a n。 那 现在就可以写在三角形 b m a 和三角形 c n a 中 a m 等于 a n 角 a 等于角 a 以及 a c 和 ab 等于 ac, 所以 三角形 a m b 全等于三角形啊, a n c 证明是边角边成立啊,所以此时 b m 等于了 c n 得证了啊,很简单, 那我们看到第三个猜想,证明等腰三角形两腰上的高相等。已知如图的三角形 a b c 中 ab, 它等于 a c bp 和我们的 c q 是 两腰上的高,要证 bp 等于 c q。 我 们来看啊,首先有一组公共角,并且呢有一组对应角相等吧。 那现在我们来看啊,还有 ab 等于 ac 吧, 是不是很明显了?通过角角边证明全等吧,同学们,那现在,所以同学们,我们来进行证明啊,因为 啊 b p、 c、 q 是 啊,两腰上的高, 所以我们把它命名为这个角一,这个为角二。好吧,所以角一等于角二等于九十度。那现在就是在三角形 a、 q、 c 和三角形 a、 p、 b 中证明全等吧。所以此时角二啊,角一 等于角二等于九十度。角 a 等于角 a 以及我们的 a、 q 等于我们的这个哦,不是 a、 q 啊,是我们的这个 a、 c 等于 ab 啊, ac 等于 ab, 所以 三角形 a、 q、 c 全等于三角形,我们的这个 a、 p、 b, 所以我们的这个 b、 p 等于 c、 q 啊,比较简单,这个利用的是角角边啊,角角边。 当然呢,你也可以证明下面的这个 c、 q、 b 和我们的这个啊 b p、 c 我 画一下啊,可以证明,也可以证明 c、 q、 b 和我们的这个啊 b p、 c 全等也是可以的啊,我设了上面的一个全等,没啥太大的关系啊,同学们, 所以这道题是两个方法的,那现在问题是还有没有其他的结论?那现在我们来看一下下一页。我现在换个条件,如果角 a、 b、 d 等于三分之一的角 abc, 角 a、 c、 e 等于三分之一的角 a、 c、 b, 那 么 b、 d 和 c、 e 是 否相等? 然后现在第二问,是我们的,如果角 a、 b、 d 等于四分之一的角 a、 b、 c, 角 a、 c、 e 等于四分之角的角 a、 c、 b, 那 现在是否相等?那我们先证第一问好不好啊?先证第一问。首先我们得明白,因为 ab 等于 ac, 所以他们的底角一定是相等的吧,所以此时角 a、 b、 c 等于了角 a、 c、 b 吧。所以只要角 a、 b、 d 和角 a、 c、 e 能够同与 abc 或者 abc 它们产生一样的数量关系的话,这个 b、 d 等于 c、 e 是 一定可以挣到的。 我们来看啊,我们把这个完整的步骤写一下啊,所以角 a、 b、 d 等于角 a、 c、 e, 那 现在角 a、 b、 d、 a、 b、 d 啊,在这里,角 a、 c、 e, 在 这里 ab 还等于 ac, 此时角 a 又是公共角,所以通过证明角边角可以得到此时的 b、 d 等于 c、 e 吧。所以同学们第二问就也能写出来了。如果他们都成了四分之一的关系,是不是不影响我的全等条件啊, 对吧?只要角 a、 b、 d 和角 a、 c、 e 与我们的 abc 和 a、 c、 b 是 一样的数量关系的情况下,他们 所证的全等条件是不会有任何变化的。那既然全等条件不会变化,意味着三角形 a、 b、 d 和三角形 a、 c、 e, 它都能证明全等,那意味着此时他们对应边 b、 d 和 c、 e 是 不是也是全等的呀?啊,也相等的吧,所以此时第二问,他们 的 b、 d 和 c 的 关系还是相等的,没啥变化的啊。那现在第三问啊,如果是 n 分 之一,还算道理,还是相等的,没有任何变化的。所以只要记得一句话啊,只要它是等腰, 只要角 a、 b、 d, 角 a、 c、 e 与角 a、 b、 c 和 a、 c、 b 的 关系,他们的数量关系是一模一样的情况下,在我的缺的条件不被破坏的情况下, b、 d 和 c、 e 他 一定是相等的。这第三问啊,所以同学们结论就是, 在三角形 a、 b、 c 中,如果 a、 b 等于 a、 c, 并且角 a、 b、 d 等于角 a、 c、 e, 那 么 b、 d 等于 c、 e, 这个是我们的条件啊,咱们的之后的一些证明课上对于这一类的题目证明还是比较多的啊。 那现在我看到咱们的第二个是关系到我们的这个,呃, 第二个结论已知如图啊,巴拉巴拉一大堆啊。第一问,如果 a、 d 等于三分之一的 a、 c, a、 e 等于三分之一的 ab, 那 么 b、 d、 c、 e 是 否相等?为什么 我们明白 ab 等于 ac 的 情况下,是不是意味着 ab 如果等于三分之一, a、 c、 a、 e 等于三分之一 ab, 是 不是此时 ab 和 a、 e 又是相等的呀? 那所以同学们边角边就能证明三角形 a、 e、 c 和三角形 a、 d、 b 全等吧。一组公共角一个,一组一组对应边,还有一组对应边长的, 是不是就证明全等了呀?所以同学们通过证明 a、 e、 c 和 a、 d、 b 全等,很容易得到 b、 d 等于 c、 e 吧。所以跟刚刚一样,如果不管是三分之一也好,四分之一好,或者第三问,我们的 n 分 之一也好, 只要我们的 a、 d 等于 a、 e, a、 b 等于 a、 c, 那 么 b、 d 和 c 的 关系一定是相等的,这是我们的啊。第二个猜想的一个啊,进阶的一个结论。 那所以这是由特殊结论归纳出一般结论的一种数学思想方法啊。那现在我们来讲关于等边三角形的性质啊,我们知道等边呢,其实是特殊的等腰,那么等边的内角有什么特征?这个很好理解吧, 三个内角相等,并且都是六十度,这个是小学的知识都知道吧。那现在同学们,我们来证明这个定力,小学没证明过吧,我们初中来证明一下这定力啊。现在一幅图要出来了 啊,一幅图如图,在三角 a、 b、 c 中, a、 b 等于 a, c 等于 b、 c。 要证角 a 等于角 b 等于角 c 等于六十度啊,刚刚说过,这不是可以利用等腰的性质来进行证明。 等腰怎么性质?是不是等边对等角啊?那现在看成哥来操作啊,因为 ab 等于 ac, 所以 角 b 等于角 c。 因为 ac 等于 bc, 所以 角 a 等于角 b。 那现在是不是连等,所以角 a 等于角 b 等于角 c 啊,那因为角 a 加角 b 加角 c 等于一百八十度。是不是就很简单,角 a 等于角 b 等于角 c 等于了六十度啊!啊,非常简单的一道题啊, 那现在例题四,如图,要你啊证明 e、 d、 a 的 度数, 并且 a、 b、 c 是 一个等边三角形, b、 d 是 a、 c、 b 上的中线,此时 b、 d 等于 b、 e。 让你求 e、 d、 a 的 度数, 我们来进行证明啊。首先我们得明白,等边三角形,它所有的内角都是六十度吧,所以此时六十度,六十度。然后 b、 d 是 a、 c 边上的一个中线。那同学们,我现在要再问同学一个问题,三线合一 是哪三线?是不是底边的高线, 里边的中线以及顶角的角平分线, 对吧?一条线三个性质,就跟我们地理的秦岭淮河一线一样,道理对不对? 那所以同学们,我们这道题他现在问等边,但我们知道三线合一是等腰的性质。那现在同学们问你个问题啊,等边有没有这样的性质啊?很明显也有吧,因为等边是特殊的等腰角形意味着等边 的的性质,等腰它不一定有,但等腰的性质等边它一定是有的吧,所以三线合一在等边,这样形中还是一样的,可以进行使用和操作的。那些同学们, b、 d 是 a、 c 的 中线的话,所以此时根据三线合一,它就是 点顶角的角平分线吧,所以这里也是三十度,这里也是三十度,那现在 b、 d 等于了 b、 e 意味着什么?等边对,等角,所以说这两个都是七十五度吧。 那现在角 b、 e、 d 是 三角形 d、 a、 e 的 外角,那外角的性质是什么?是与它不相邻的角的两个角之合吧, 对吧?所以此时角 b、 e、 d 又等于角 a, 加上角 e、 d、 a 等于七十五度, 那现在角 a 他 什么六十度吧,那 e、 d、 a 是 不是就十五度了呀?答案就是,这是我们的历次啊,咱们就讲一下咱们的思路啊,如果要写字的步骤啊,其实没必要写的,因为考试呢,考这道题的话可能性不大啊,比较简单,咱就不会再进行比较细致的讲解了。这历次, 那现在看到我们的单项小节,等腰的角平分线,两腰上的高,两上的中线的相关性质如下啊,底底角的两条平分线是相等的啊,两上的中线也是相等的,以及两腰上的中高线也是相等的。 定力就是啊,等边三角形的三个内角都相等,并且每个角都等于六十度,那现在看他练习, 如图,三角形 a、 b、 c 和 a、 d、 e 都是等边三角形,如果在 a、 b、 c 的 周长为十八厘米, c、 e 为两厘米。现在问的是三角形 a、 d、 e 的 周长是为多少?首先 都是六十度角吧,所以很明显可以知道平行,那根据平行的性质呢?我们在上节课讲过,对应线段成比例关系,对不对?所以此时意味着我们的这个如果 c、 e 等于两厘米,那它也是两厘米吧,对吧? 那现在意味着我们看一下啊,三角形 abc 的 周长呢,是等于我们的这个 b, c 加 ab 加我们的这个什么 bc 加 ab 加 ac 吧,等于十八厘米,而且它等边的吧,所以此时三条边都是六厘米吧,所以这里是四,这里是四,那这里是六,那这里是不是 a、 d、 e 也是一个等边的,所以它它也是四吧,所以答案是十二厘米啊, 咱们看第二问,第二问呢,是我们之前的一堂课讲过的,叫做手拉手模型啊,手拉手模型,这个是我们的这个专题模型课,在合集里有啊,合集里是有这这个课的啊,专题模型课是我们的这个手拉手模型。 那现在我们来看一下啊, 如图所示,三角形 a、 c、 m 和我们的 b、 c、 n 都为等边三角形,要证 a、 n 等于这个 b、 m, 很 明显也是通过证明全等来证明我们的对应边是一个呃,相等关系,那 a、 n 和 b m 是 不是只需要证到 a、 c、 n 和三角形 m、 c、 b 全等就 ok 了,对不对?同学们,那现在我们来进行证明一下啊,我们把这个角变为角一,这个角为角二,这个角为角三啊。首先因为 三角形 acm 啊,是等边的 哎,我直接写一写一,那个写一长串吧。三角形 a、 c、 m 和三角形 b、 c、 n 是 等边三角形。 那现在所以此时我们的这个什么角一等于角二等于六十度, 并且 c、 m 等于 cn, 还有 ac 等于我们的这个啊, cm 啊, cm 等于啊, cm 等于 ac 啊,不好意思啊, cm, ac 以及我们的这个啊, nc 等于 bc, 看错了啊,那因为角一加角三等于角二加角三,所以此时角 a, c, n 等于角 m, c, b, 所以 在三角形 a, c, n 和三角形 m、 c, b 中证明全等就 ok 了。那这里是我们的这个什么 a, c 等于我们的 c m, 角 a, c, n 等于角 m, c, b, 以及我们的 n, c 等于 bc。 那 现在所以此时三角形 a, c, n 全等于三角形 m, c, b 了吧,所以说利用的是边角边的性质,所以此时 a, n 等于我们的 b m 啊,这第二问, 那第三问呢?还是手拉手模型吧,咱们就不多讲解了,做法是一模一样的啊,咱们可以同学们感兴趣的课后自己做一下啊。这个方法是一模一样的,刚刚步骤一模一样的,没一点变化啊。这第三问, 那现在辨识啊,如果利用的是不全等的啊,还有道理,方法一模一样啊,方法一模一样的, 只不过大小发生了变化,但它们其实对应的性质没一点变化啊,同学们可以自己下课后自己尝试一下啊。答案是,这个方法是一模一样的,答案呢,也是这个。呃, a, e, b 的 这度数啊,它要问度数的话,那就可能会要要复杂一点,但方法是一模一样的啊,同学们, 咱们就不多讲解了啊,那本节课呢,就讲完了啊,那我们回顾一下咱们这节课学了些什么东西。我们这节课呢,学的比较杂啊,主要学的这个三线合一,复习了一下,包括刚刚讲过的一些性质啊,两 两个比较的,两条平分线相等,两条腰的中线相等,两条腰的高线相等,这些东西是比较重要的啊,但是最重要的还是三线合一啊,三线合一最重要, 然后其次呢就是我们的粉面的一些性质,咱们需要记住一下啊。那那那本节课呢?讲到这里,到此结束,我是你们的阿才学长,我们下期再见。拜拜。
19阿橙学长 57:20查看AI文稿AI文稿
57:20查看AI文稿AI文稿好,大家好,从这节课开始,我们来学习北师大版八年级下册咱们这个数学的课程啊,今天呢,我们来学咱们第一章的第一节,叫做三角形内角和定力, 你看他的大标题啊,是三角形内角和定力,那么通过这个标题你能想到什么呀? 那么提到三角形内角和咱们熟不熟悉啊?咱们很明显是很熟悉的,对吧?那我们之前有没有学过这个三角形内角和 咱们是学过的,对吧?那我们的这个整个的第一单元啊,整个的第一单元实际上相当于是一个复习的内容。 好,那么三角形的内角和实际上呢?我们小学的时候就已经学过了。提到三角形的内角和,那我们立刻可以想到的是三角形内角和它是一百八十度,对吧? 那么你想一想,我们的三角形内角和为一百八十度,我们当时是怎么证明的呀?咱们是怎么去证明三角形内角和是一百八十度的? 咱们首先第一个的话呢,就是 我们把三角形的三个角我们可以给它剪下来,对吧?剪下来呢,或者说把它撕下来啊,然后呢,那么我们把它可以拼成一个平角,拼成一个平角的话呢, 那么一个平角它就是一百八十度,对吧?由此咱们得到三角形它的三个内角和是一百八十度,是吧?那也就是呢,咱们的叫做剪拼法, 对吧?接下来把它拼在一块的啊,也就咱们的剪拼法, 对吧?减拼法。那么第二个方法呢,咱们可以用量角器把它的三个角给它量出来, 对吧?也就是度量法,对吧?度量法把它的三个角给它量出来,量出来之后呢,给它加总求和也能得到一百八十度,但是呢度量它是会有一点误差的, 对吧?那包括我们,呃,把它剪掉来拼接,把它撕下来来拼接,也是会有点误差的。 那么接下来的话呢,咱们今天啊,咱们用正明的方式,用非常精确的这个方式来推导推导三角形内角和为一百八十度。 好,那么咱们的这个第一个知识点啊,就是让咱们去证明这个三角形内角和或者是多种方式来证明三角形内角和定力啊,那这个定力怎么来推的啊?咱们呢接下来 来学习一下啊,接下来的话呢,大家这个 就可以看着啊,看着我给大家去补充的这个拓展内容啊,就先不用看书了啊,看我给大家补充这个拓展内容, 用多种方式来证明三角形内角和为一百八十度。 那么我们先来看第一幅图啊,第一幅图呢是已知三角形 abc, 那 我们求证呢,这个角 a 加角 b 加角 c, 它等于一百八十度。 那大家通过看图,咱们想要得到三角形三个内角的和是一百八十度,咱们最容易想到一个什么方法?咱们最容易想到一个什么方法? 是不是咱们可以过这个点 a 来做一下 b、 c 的 这个平行线,对吧?咱们可以过这个点 a 来做 b、 c 的 这个平行线, 来做一下它的平行线好比如它的平行线是 这个 e、 f, 那 我们做了这个平行线之后呢, 咱们能够得到,哎,这个角咱给它叫角一,这个角给它叫角二,你说我们得到这个角一和哪一个角是相等的? 这个角一和哪一个角是相等的?是不是?角一它和这个角 b 就是 相等的。角二呢,和这个角 c 这个角是相等的,对吧?这个咱根据什么呢?咱们根据的就是 两直线平行内错角相等,对吧?角一和这个角 b 是 内错角,角二和这个角 c 呢?是内错角, 是吧?那么我们知道这个角一加上原来的这个角,原来这个角角 a, 那 现在的话呢,我们加了辅助线了,我们就应该说它是角 b、 i、 c, 对吧?角一加角 b i、 c, 再加角二,它是一个完整的平角,那么它是一百八十度,于是呢,也就相当于是咱们的角 b 来加上角 b i、 c, 再来加角 c, 它的和是一百八十度,对吧? 那么这个过程咱可以来写一下啊,就是咱们的过这个 a 点来做 e、 f 平行于 b、 c, 那 么则 角一等于这个角 b, 角二等于角 c, 那 么因为角一加上角 b、 i、 c, 再来加上角二是等于一百八十度的,对吧?这个平角一百八十度,所以呢,也就是咱们的这个角 b 加上角 b i、 c, 再来加上这个角 c, 它是等于个一百八十度,对吧?咱就得到了三角形它的三个内角的和是一百八十度。 那这个呢,我们是用了平行线的,这个什么 利用了加辅助线啊?加辅助线,然后呢,过 a 点来做 b、 c 的 平行线的这个方法,对吧?我们来通过平行线来倒角来倒角,得到了三角形内角和为一百八十度, 对吧?这里面呢,我们主要利用了什么?利用了内错角, 主要利用了两直线平行内错角相等,是吧?那我们除了利用内错角,我们还可以利用什么? 咱们还可以利用什么? 咱们是不是还可以利用一下这个同位角啊? 是不是可以用同位角?咱看第二幅图,看第二幅图啊,同样是已知这个三角形 a、 b、 c 来求证呢,角 a 加角 b 加角 c 等于一百八十度。 那我们来用一下同位角。好,首先呢,我们把这个 bc 呢,给它稍微延长一点, 再稍微延长一点,延长到这个 f。 然后呢,我们过这个 c 来做, 来做这个 c、 e 平行于我们的这个 ab, 好 做 c、 e 平行于 ab。 那 么你看啊,我们做了 c、 e 和 ab 平行了, 我们把这个角给它角角二,那这个角 b 和角二是不是就属于同位角?那么同位角呢?是不是就相等?同位角是不是就相等了? 那这里面呢,同样还有一组这个角和这个角呢?哎,它是内错角,这个角咱给它叫角一,那么角一和这个角 a 呢,是相等的,角 b 和角二是相等的, 是吧?那角二、角一,还有我们的这个角 a、 c、 b 的 核也是一百八十度,也是一百八十度,对吧?那所以呢, 我们就得到了角 b 加角 a, 加上我们的角 a、 c、 b 的 核也是一百八十度,对吧? 好,那所以这个过程啊,咱们同样来写一下,咱们呢,可以延长 bc 至 f, 然后呢,过 点 c 来做 c、 e 平行于 ab, 那么则角二等于角 b, 角一等于角 a, 因为角 b c、 i 加上角一加上角二是等于一百八十度, 所以呢,也就是角 b c、 i 加上角 a 加上角 b, 等于一百八十度,对吧?那这里面咱们是用了 同位角,用了两直线平行,同位角相等,同时呢还用了内测角 是吧?那你看我们除了用同位角内错角,还有没有其他的方法?还有没有其他方法? 哎,有的同学说,老师可以用同旁内角互补是吧?好,同旁内角互补也是可以的。那你看,我们看一下第三幅图, 同样的啊,这个三角形 a、 b、 c 啊,已知三角形 a、 b、 c, 让我们求证呢,角 a 加角 b 加角 c 等于一百八十度。 哎,这样的话呢,就是说我们现在要去想第三个方法, 我们要想第三个方法,你看前面两个,我们过了 a 做平行线,过了 c 去做 ab 的 平行线,那第三个我们如果想用同旁的角互补的话,我们要怎么去加辅助线了呢? 我们可以来做 i c 的 这个平行线, 同时来做我们的 ab 的 这个平行线啊。比如我们做 ab 的 这个平行线,咱们先做一下 做 ab 平行线,叫做 d e 吧,叫做 d e, 再来做 a c 的 平行线, 叫做 e f。 好, 咱们做了这个平线之后, 做平线之后啊,咱们现在来看一下角,假如说这个角是角一,这个角是角一啊,那么既然这个 e f 和 i c 平行了,这个角一和 下面这个角我给它叫角二,这个角给它叫角二。角一和角二的和是不是就是一百八十度? 角一和角的和是不是就一百八十度,对吧?因为它是两直线平行,同旁的角互补呀。那么同样的,我们的 b a 和 d 平行,那么这个角二和这个角呢? 和这个角的和是一百八十度,或者说呢,我们的 ab 和 d e 平行,那么我们的角一和角 a 的 和呢?它也是一百八十度,现在角一和角二的和是一百八十度,角一和角 a 的 和也是一百八十度,所以这个角二和角 a 是 相等的,角二和角 a 是 相等的, 是不是?好,那么咱们的这个 角 c、 角 c 啊,和这个角是不是相等的?这是属于同位角相等,对吧?这属于同位角相等, 因为呢,这个 e f 和这个 i c 是 平行的,对吧? e f 和 i c 平行的,那么它这是同角相等,那么这边这个角我给它叫角四, 这个角四和我们的角 b 呢?它是相等的,对吧?角四和角 b 平行,那么两直线同角相等, 对吧?那我们能知道的是角三加角二加角四,这三个角的和是一百八十度, 这三个角的和是一百八十度,那所以呢,我们就把它替换成了角 a 加角 b 加角 c 的 和是一百八十度,对吧?好,那么这个过程咱们写一下, 就是咱们做 d e 平行于 ab, ef 平行于 a c, 所以 角 a 加角一等于一百八十度。 角二加角一也等于一百八十度, 所以角 a 等于角二。又因为 e f 平行于 i c, 所以 角三等于角 c, 又因为 d e 平行于 ab, 所以 角四等于角 b。 因为角三加角二加角四 等于一百八十度,所以角 c 加角 a 加角 b 就 等于一百八十度, 对吧?好了,那你还有别的方式吗?那实际上还有啊, 别管用哪种方式,实际上都是什么,都是倒角。就是呢,把三个角给它怼在一块,给它弄在一块啊,利用的平角 一百八十度得到的三角形内角和为一百八十度,对吧? ok 啊,好,这个呢,是我们三角形内角和为一百八十度的这个证明。这个咱能过了吧? 这个咱能过了吧?能过的话呢?我们那个啊,咱们来看两个小题啊。 来看两个小题, 看第一题啊,二,如图 l 一 平行, l 二,就是那两条线平行的啊,来,现在出现平行了啊,由平行,你能想到什么啊? 平行线是用来干什么的啊?现在告诉你这个两条线平行了, 那么平行的话,你能想到什么?平行线是用来倒角的啊,平行线是用来倒角的好,那角一是等于四十度,好,就这个角是等于个四十度了, 它是四十度。角二是等于七十五度,好,这个角它是七十五度了,则角三等于多少度啊?这个角三啊,这个是角三, 角一是四十度,角二是七十五度,问角三是多少度,那么平行线是用来倒角的。既然这两条线平行了, 那么角一和我们的这个角和这个角是不是就是同位角?同位角相等呀,就能够导出来这个角它是四十度, 那我们的角二是这个七十五度,这个角跟它是什么关系啊?对顶角,对顶角是什么?对顶角相等,就能导出来它是七十五度,这个角是四十度,这个角是七十五度,那这个角三呢? 那我们根据这个三角形内角,它是一百八十度,对吧?角三呢, 就等于一百八十度,减去个七十五度,再减去个四十度,能算出来它是多少度,它是等于个六十五度,那就选 c 是 吧?所以咱这个题呢,就是 c 选项。好,第二个, 在三角形 a、 b、 c 当中,角 a 告诉我们是六十度,角 b 比角 c 是 等于个一比五,现在让我们求角 b 的 度数是多少, 那么这里面有一个比啊,我经常给大家讲的话呢,鉴别要干什么? 见比射开对不对?见比 射开,当然你也可以,就是不射开,你可以射什么? x、 y、 z, 对 吧?射 abcdef, 那 都是可以的。但是的话,这里呢,我想告诉大家,就是你见到这里这个比的关系的时候, 要能想到用方程的思路来解决,好吧,我们呢, 如果设这个角 b 是 x 度,那么角 c 呢,就应该是无 x 度,那么既然我们用方程了, 那我们就能够得到一个等式,对不对?那这题里面的这个等量关系是根据什么来得到的呢?咱们根据什么能够得到一个等量关系呢? 还有这个角的关系啊,那就是我们刚刚学的这个三角形的角和为一百八十度,所以呢,我们要利用这个三角形的角和为一百八十度来列方程,对不对?好,那么我们 来写过程啊结, 那我们就设角 b 是 等于 x 度,那么则角 c 等于五 x 度, 那么因为角 a 加角 b 再加角 c 是 等于一百八十度, 所以呢,角 a 是 六十度,对吧?把它带进来,那么就是六十度。加上角 b, 咱们设成是这个 x 了,所以呢,就是加 x, 角 c 呢,是五 x 了,所以就加五 x, 它等于一百八十度,于是呢,我们就得到了这是六 x 等于多少?一百八十度,减掉这个六十度,对吧?一百二十度,那所以我们得到 x 呢,就是等于个二十度, 对吧?就是二十度, 那 x 二度也就什么?因为咱们设角 b 是 x 度呀,所以呢,就是这个角 b 是 等于个二十度, 对吧?所以就角 b 啊,它等于这个二十度。好,那关于第一个知识点啊,第一知识点,咱们学的是三角形内角和定力。哎,三角形内角和是一百八十度,这个能过了吧? 这能过了,咱们来看一下咱们这个课本上面的这个例题啊。课本上面的例题, 看一下咱们的这个课本上面的例题。例一, 看这个例题一啊, 说呢,如图一,杠五,在三角形 a、 b、 c 当中,角 b 等三十八度。好,这个角 b 是 三十八度,咱标一下,角 c 六十二度。好,角 c 六十二度 a、 d 呢?它是三角形 abc 的 角平分线。好,那么我们通过读题,既然告诉我们角平分线了,你立刻想到什么呢?这两个角是相等 的,是吧?现在让我们求这个角 a、 d、 b 的 度数,求这个角的度数是多少的,是吧?那我们可以先分析一下, 我们刚刚学的是三角形内角和定力,而三角形三个内角的和是一百八十度。 那么呢,我们想得到这个角的度数,我已经得到什么三,这个角是三十八度了,我只需要得到什么,只需要能知道这个角 b、 i、 d 的 度数就行了呀。我如果能得到这个角 b、 i、 d 的 度数,这个角的度数不就出来了吗? 那么现在我要得到这个角的度数呢?我知道这个角和这个角是相等的,所以呢,我们如果能知道这个整体就是整个的角 b、 i、 c 的 度数, 就能得到这这个 b、 i、 d 的 度数,是吧?现在要得到角 b、 i、 c 的 话呢,要把它放在大的三角形 abc 当中来, 把它放在大三角形 a、 b、 c 当中来,那我们就能够得到这个角 b、 i、 c 了呀,现在你看角 b 知道了,角 c, 知道了这个角 b、 i、 c 的 度数,那不就知道了吗? b、 a、 c 度数,知道了,这一半的度数知道了,这一半都知道,所以呢,这个让我们求的这个度数不就出来了吗?是不是如果说我们这个我们分析的过程的话,如,如果我们分析的过程啊,咱们来说一下,就是我们的这个角 b、 i、 c, 它是等于什么呢?我们的这个角 b、 i、 c, 哎,它是等于一百八十度,来减掉这个三十八度, 来减掉这个六十二度,哎,得到呢?它是八十度,得到它是八十度,它是八十度了,那么这个角 b id 呢?角 b id 是不是就等于咱们得到这个角的一半?角 b、 a、 d, 它是等于二分之一倍的角 b、 i、 c, 哎,它就等于个四十度, 对吧?那么这个角是四十度了,现在让我们求的这个角 a、 d、 b 呢,就应该等于一百八十度, 减去这个四十度,再减去这个三十八度,那么算出来是等于多少?一百零二度不就完事了吗?就给他算出来了,对不对?那如果说让我们写格式, 如果让咱们写格式的话呢,咱们就把格式写一下,是吧?刚才是分析的啊,格式的话,这个呢,大家要把它去学会啊,写这个格式 好,比如说咱们写一下这个格式,或者说,呃,咱们来写一下过程啊,大家可以看这个图,那么呢,我们首先哎就是写个结,首先结 在三角形大的三角形啊, abc 当中,在三角形 abc 当中, 这三个角的和是一百八十度,对吧?因为角 b 加角 c 加角 b i、 c 等于一百八十度, 所以呢,那么这个角 b 它是三十八度,加上呢?角 c 是 六十二度, 再加上角 b a、 c 等于一百八十度,所以角 b、 a、 c 是 等于个一百八十度,减去三十八,减去六十二,哎,算出来就是等于八十度, 是吧?那又因为这个 ad 呢,它平分了 这个角 b、 i、 c, 哎, ad 平分的角 b、 i、 c, 这是给我们的条件,所以呢,那么这个角 b、 i、 d, 哎,这个角 b、 i、 d 呢,就是这个大角的一半,它等于二分之一倍的角, 这个 b、 i、 c 也就等于个四十度,对吧?它的一半四十度。好,那么接下来 再放在小的三角形里面啊, a、 b、 d 当中,那么就是在三角形 a、 b、 d 当中, 角 b 加上角 b、 a、 d、 b, 再加上角 a、 d、 b, 就是 再用一次三角形内角和是一百八十度啊,再用一次,那么所以 三十八度加上四十度,对吧?他知道了,他是三十八,他是四十了,再加上角 ad 等于一百八十度,所以角 ad 就等于一百八,减掉他俩得到呢,是一百零二度就完事了,对吧?好,那么接着呢,咱们看一下, 这个咱能过了吧,关于我们的这个三角形的要和定理的这个应用啊,就是这个例题,实际上就是关于三角形的要和定理的应用,对吧? 好,接下来我们接下来啊,接着往后看, 来看咱们课本的第四页, 看咱们课本的第四页啊, 看这个尝试思考 或呢,我们已经探索过两角分别相等, 而且呢,其中一组等角的对边相等的两个三角形全等这个结论。 那你能用相关的基本事实和已经学过的定力证明它吗?我们看关键字啊,这里有一个什么呢?基本事实, 已经学过的定力证明它。那我们学过的这个基本事实, 咱们学过哪些基本知识?有哪几条啊?谁能告诉我在哪里学的呀?这个基本知识还有没有同学能记得的? 咱们来看啊,在我们的八上册啊,在我们八上册的课本,大家打开啊,咱们是学过的, 来看一下啊,关于八条基本事实,看了吗?这里面说九条基本事实作为证明的出发点和这个依据。 那我们呢,已经认识了其中的八条,第一条是两点确定一条直线,第二条是两点之间线段最短。第三条 同一平面内过一点,尤其这一条直线与已知直线垂直啊。第四条,巴啦啦这一堆啊,我就不去读了啊,第五条,第六条,第七条,第八条,这里面有这么多条,有这么多条啊, 那么这八条基本事实里面呢,它只有三个判定,是我们的证明三角形全等的基本事实, 也就说呢,只有这三条是我们的基本实施啊,就我们公认的哪三条呢?看一下啊,就是两边及其夹角分别相等的两个扇形全等。这叫什么呢? s a s s a s。 再一个呢,是两角及其夹边 分别相等的两个三角形全等,也就是我们的 a s a 就是 角边角,上面这个是边,是边角边,下面这个是角边角。那么第三个呢,就是三边分别相等的这个两三角形全等,就是我们的边边边啊, s s, 对吧?那么就这三条是我们的基本事实,它是公认的啊,它是不用你去证明的,不用你证明的啊,就是你可以拿过来就用,它是一个基本事实呀,拿过来就能用啊, 那么而其他的以其他的方法要去得三两个三千全等的话呢,你得需要证明,比如说我们的 这个 a a s 啊,也可以说什么叫做角角边,这个你是需要通过证明的,当然你把它证明出来之后呢,你后面你就可以直接用了,但是你在用之前你是需要证明的,而这三条你是不需要去证明的,这是可以直接用的。那现在我们呢? 这个现在我们课本上说的什么呢?哎,他说的就是让我们能不能用,哎,刚才我们看到的基本事实,已经学过这个定律去证明他, 那么证明呢,就是我们现在想去证明,就是两角分别相等,而且呢其中一组等角的 对边相等的两个三角形全等啊,就是想来证明他用我们的基本事实,用我们学过的定力来证明他。 那我们刚刚才刚刚看过了啊,我刚才呢把那个上册的,把上册的给他打开给他看了,就是我们的这个基本实示里面, 基本事实里面有 s a, s, a, s a 和 s s s, 是 吧?有这三个,这三个呢是你可以直接用的,是不需要你去证明的,那么这三个 我们不用证明,能直接用。可是我们如果利用这三个,如果能够证明出来这个 aas, 那 以后的这个 aas 我 们就可以直接去用了啊,咱们就可以直接去用了。 好,那么接下来咱们就来去证明一下,咱就来证明一下啊,这个通过我们已经知道的基本事实来证明一下这个 角角边啊,这个 a、 a、 s。 看一下我这里的这个,咱们关于第二个这个定律啊, 全等三角形的判定定理,这个 a、 a、 s 以及它的性质。第一个呢,我们用所学的基本知识来证明这个角角边, 那么这里面呢,有两个三角形啊,已知角 a 等于角 d。 好, 这个角和这个角相等,这个角和这个角相等, b、 c 呢?等于 e、 f, 哎,这个边和这个边相等,这就符合什么了呢?符合他所跟我们说的就是由 两个角相等其中一个角的一组对边相等,是吧?这个条件啊,现在我们呢让我们求证这个三角形 a、 b、 c 和这个三角形 d、 f, 哎,这两三角形是全等的, 那么当然你看这是不是很明显就是我们的角 a 和角 d 相等了,角 b 和角 e 相等了,那你说我们的这个角 c, 你 说我们的角 c 和这个角 f, 它是不是必然相等呀? 因为这三角形内角和都是一百八十度的,他跟他相等,他跟他相等,那我用一百八减他减他不就等于了?一百八减他减他就得到了角 c 和角 f 相等呀,因为这个角 c 等于 一百八十度减,角 a 减角 b, 角 f 呢,等于一百八减角 d 减角 e, 那 么 a、 a 和 d 相等, b 相等,所以我们得到角 c 和角 f 相等, 对不对?那我们得到角 c 和角 f 相等,我们是不是就可以用?这叫做什么?角边角角边角不就得到两个三角全等了吗?角边角就是咱们的这个 a、 s、 a 啊, 咱们不就用了我们前面的那个基本事实,就得到了这个角角边了吗?就证明出来角角边 能够得到两个三进全等了,对不对?所以这个过程呢,咱们把它写一下啊,证明。 因为角 a 加角 b, 加角 c 等于一百八十度,角 d 加角 e 加角 f 也等于一百八十度, 而角 a 呢,它等于角 d, 角 b 呢,它等于角 e, 所以 咱得到的是角 c 等于角 f, 那么又因为 bc 这个边是等于 e、 f 这个边的啊, bc 这个边等于 e、 f 这个边,那么所以呢,咱就得到了三角形 a、 b、 c 全等于三角形 d、 f。 这个咱们根据的是角边角,这个你要写出来啊,根据你要写出来,因为他让我们用基本事实, 对吧?来去证明的啊,这个你要写出来。好,那么既然我们现在已经证明了 这个角角边能够得到两个三全等,那所以以后的话呢,我们就直接可以用这个角角边了啊,也就直接能用了,也就说我们证明出来的,我们就直接能用了。 好,那么接着呢,咱们来看一下这个关于角角边他的考题,他考的时候,他是怎么去考啊?他是怎么去考?咱们来看这个题目啊, 来看一下题目, 如图,在四边形 a、 b、 c、 d 当中, ad 平行于 b c, 角 b 等于角 d。 好, 这个角 和我们的这个角是相等的,然后呢,告诉我们呢,它俩是平行的, a、 d 和 b、 c 是 平行的,平行用来干什么的呢?那我经常给他说,对吧?平行用来干什么的?平行是用来倒角的,对不对?平行是用来倒角的啊,平行来倒角的, 那么现在呢?它又连接了 ac, 把 ac 连上了,它让我们干什么了呢?求证 ab 等于 cd, 求证 ab 这个边等于 cd 这个边, 那我标个这个角啊,这个角的话呢,我们给它叫做这个角一,这个角我们给它叫角二。 好,那么现在你看,我们怎么能够证明出来 a、 b 和 d、 c、 d 是 相等的呢? 首先,它俩既然平行了,角一和角二什么关系啊?内错角对不对?内错角相等是吧?这是一个。 然后呢,这个角 b 和角 d 相等,咱们得到什么了?有两组这个,有两组 这个角相等了,是吧?还有一个隐藏的是什么?还有个隐藏的边吧,就是我们的 a、 c, 它等于 c, a 啊,这个 a、 c 既是三角形 a、 b、 c 的 边,也是三角形 c、 d、 a 的 边, 是吧?这个 i、 c 的 既是 a、 b、 c 的 边,它也是 c、 d、 i 的 边,所以它是一个这个公共边,那就是我们的 i、 c 等于 c、 i, 对 吧?这不就能够得到这两个 c 全等了吗?是吧?所以这个过程咱们写一下 证明, 因为 a、 d 平行于 b、 c, 所以 角一等于角二,又因为角 d 等于个角 b, a、 c 等于个 c、 i, 所以 三角形 a、 d、 c 全等于三角形 c、 b、 i。 这个就是根据我们的角角边了, 对吧?这就是根据角,这个角跟这个角相等了,这个角跟这个边相等,这就叫做角角边, 是吧?那么所以既然两个三全等了,那么对应的边 a、 b 呢?不就等于 c、 d 了吗?对应的边 a、 b 和对应边 c、 d 相等呀, 对吧?哎,这个呢,就是我们利用这个角角边啊,来去证明这个全等就可以这样来用了啊。 好,然后呢,我们那么关于这个这个小题大家都能会了吧, 那我们接着呢,来看咱们的课本啊,来,接着来看咱们课本的第四页的上面啊, 课本第四页上面呢,咱们现在刚才学完两个那个定律了啊,学完一个三角形的内角和定律,接着又学了一个 咱们的两角分别相等,而且呢其中一组等角的对边相等的两三角形全等这个定律,那我们接着来看第三个啊,这是我们刚刚已经学过的,接下来我们看第三个,第三是什么呢?就是咱们的叫什么呢?全等三角形的 对应边相等,对角相等,实际上这是什么?就是我们的 全等三角形的性质,实际上就是全等三角形的性质啊,那么它的性质咱们接着来学, 那么全等三角形的性质啊,有哪些呢? 书上其实虽然给了,但是呢,实际上不全,但是我们了解就行啊,就是全等三角形它的性质,全等三角形 它是对应边相等,然后呢还有就是对应角相等, 对应角相等,其实还有什么呢? 其实还有对应边的中线、高线、角平分线也都是相等的, 对吧?就是还有啊,就是我们现在呢,就书上他只给了这一点,就说呢,全等三角形对应边相等,对应角相等,那实际上你也要知道,其实还有对应边他的中线相等,对应边的高线相等,还有对应边的角平,还有这个 角平分线它也相等,就对应边它所对的那个角的角平分线,它的长度相等,对吧?说的更透彻的话,好,这个呢,大家知道行了啊, 好,然后呢,那么咱们学了这第三个定律了,咱们来看一下,哎,这个题目啊,咱们看一下题目, 看下面这个题目,那如图这个点 a、 b、 c、 d 在 同一直线上, a、 b、 c、 d 啊,这四个点在同一直线上, a、 e 呢?等于撇腹,这条线等于这个撇腹,角 a 等于角 b。 好, 角 a 等于角 b。 还有呢,角 a、 c、 e 等于角 bdf, a、 c、 e, 这个角等于 bdf 等于这个角啊,这个角和好这个角,它是相等的。 第一个呢,让我们第一位,让我们求证三角形 abc 全等于三角形 bdf, 求证 啊,求证这个 a、 c、 e, 这个小的啊,这个小的三角形 和这个小的 b、 d、 f, 那 我们求证这两个三角形是这个全等, 是不是咱们可以用什么? 这叫什么? 是不是角角边呀?你看这个角和这个角相等了,这个角和这个角相等了, 还告诉我们一个边 a、 e 和 b、 f 相等了,这不是角角边吗?这不就角角边了吗?对不对?刚刚学的是吧?好,那么第一问啊,咱们来过程写一下。第一问证明 在三角形 a、 c、 e 和三角形 b、 d、 f 当中 有这样的三个相等关系,角 a、 c、 e 等于角 b、 d、 f。 角 a 等于角 b。 边 a、 e 等于边 b、 f。 所以呢,三角形 a、 c、 e 就 全等于三角形 b、 d、 f。 这根据的是角角边, 根据角角边, 对吧?这叫什么呢?这叫全五行啊,全五行,一行两行,三行,四行五行,对吧?我们经常用的全五行,就把这个过程完整的展现了 啊,正全等的这个全五行啊,这个格式对吧?大家知道就是这个格式啊,好,第二问的是什么呢? a、 b 等于个八,整个 a、 b 等于八, a、 c 等于二。好,这个 a、 c 它说是二, 这个 c 问我们 c、 d 等于多少?那么 a、 c 如果是二的话呢?我们刚刚证明这两个三角形全等了,那我们的 b、 d 不 也是二吗? 对不对? a、 c 是 二, b、 d 也是二呀,那么整个是八,你中间的这个 c、 d, 它不就是四吗? 中间 c、 d 咱们得到,咱们得到不就是四了吗?是不是分析就可以这个分析出来,是吧?然后这个过程呢,我们同样写一下。 第二问的 就是呢,咱们由第一问,我们能够得到三角形 a、 c、 e, 它是全等于三角形 b、 d、 f 的, 那么既然两个三全等了,咱们刚才学的第三个定律是什么?全等三角形对应边相等,对应角相等,对吧?那我们得到对应边相等呀,就所以呢,这个边 a、 c, 它等于边 b、 d, 对 吧? a、 c 等于 b、 d, 那 么 所以我们的这个 b、 d 呢?不就也应该等于二吗?对吧? a、 c 是 等于二的, b、 d 也等于二呀。 那么又因为呢, c、 d 等于什么?整个的中间的线段等于整个线段减掉两头呀,等于个 ab 减去 a、 c, 再减去个 b、 d, 所以呢, cd 就是 等于个八减二减二等于四,是吧?好了,关于这个题目的两问没问题了吧? 关于这个题目两问应该没问题了吧? 一共呢是我们到现在学了三个定理了啊,一个呢是三角形内角和定理,就三角形内角和一百八十度。第二个呢就是我们的 a、 s, 第三个呢?就是全等三角形,它的性质这个能过了吧?
 05:42
05:42 01:41查看AI文稿AI文稿
01:41查看AI文稿AI文稿朋友们可以去这个粉丝群当中去领取啊,最近我们其实在学习八上的数学,是不是?对,然后呢,我们学习的你们的版本是北师大版,但是呢,很多同学用的是人教版,嗯,但是不管人教版还是北师大版,我们都发现他的七下的第一章都是什么? 香蕉线与平行线吧?对,香蕉线与平行线其实它作为的是一个几何的初步,初步几何的基础,对,其实挺简单的,是不是?所以大家很多同学认为简单,但是有的时候你发现真正做难题的时候,哎,你做不出来,做不出来就怪了,所以它是有难题的, 然后很多家长在问这个事情,对吧?然后呢,我也整理了一下啊,想了半天终于找了一套题,这套题呢,我管它叫做培优拔尖,应该是平行线和 这个香蕉线香蕉线当中最难的部分了,最难的部分了就是培优八件的部分啊,他是一套卷子,一共呢是二十四道题,有大题,有选择题,也有这个,就是这个啊,你也做一做之后啊,因为我觉得这道题非常的重要啊,很重要的。 然后我们呢,还会以电子版的这个形式,把这套香蕉线平行线这个培油拔尖的发到我们的粉丝群当中啊,朋友们可以去这个粉丝群当中去领取啊。但是我们第一版呢,现在先没有答案,大家先做先做啊, 这个答案我尽快整理,尽快整理,整理出来以后呢,发给大家好不好?然后呢,大家你也得做一做啊,咱们一定要把这个东西给它做出来好不好? 咱们看一看真正的几何的初步到底难不难?如果大家都能做对了,那证明咱们几何不错了,就可以接下来的三角形了,等等这些难难点的学习了,是不是?好吧,就这样。嗯,就这样。
80壹壹带俩娃









