高二数学试卷答案扬州过程分
我们来看一下这次扬州市的高二期末考试的几道压轴题。 首先看这个第八题,第八题它给我们的一个递推关系是这个式子,然后它让我们求后面的这个值可能是什么。 那么我们一般拿到递推关系的话,他如果里面带 sn, 通常我们会把它整理成 sn 等于 an 加一乘以 an 这种形式啊,然后我们不喜欢看 sn 嘛,因为递推关系是要的 an 和 an 加一的关系,所以我们可以往后再写一下, sn 加一就等于 an 加二乘以个 an 加一, 我们做差两个式子做差就可以得到 an 加一就等于 an 加一,括号 an 加二减 an 两边可以把 a n 加给约掉,因为呢,他这个呃竖列的象啊,他是做分母的,所以他不可能会有象是等于零的,所以我们在这边约的时候,不需要考虑到他这个象是否会为零这种情况, 所以我们就可以得到 a n 加二减去一个 a n 就 等于一,那么我们会发现它实际上是隔两项为一的,一个等差数列,也就它基数项乘一个等差数列,偶数项也乘一个等差数列,那么既然如此的话,我们就非常想弄清楚它的首项是什么。 呃,所以我们可以根据这个递推关系,我们可以带一些特殊值,比如说我们带 n 等于一的时候,我们会发现 a 二就等于 s, 一 就是 a 一, a 一 比 a 一 就等于一啊,那么我们已经有了偶数项的第一项, 但是我们这个基数项的第一项也就 a 一 是不清楚的,那么不清楚的话,我们可以先去试试看,我们就用 a 一 去写他这个式子的一个表达式,那么他前面是前六项和啊,前六个偶像和就是一加二加三,一直加到六。 好,我们可以求一下,手项加末项乘以项数除以二,所以这里算出来是等于三七二十一。 好,后面是从第一个计数项,第一个计数项就是 a 一, 第二个计数项就是 a 一 加一。好,一直到第七个就是 a 一 加六,不是加七哦,因为首先是 a 一, 然后我们把它加起来, 然后再除以一个啊,不用除了,那么这个东西它就等于七个 a 一, 再加上一个二十一。好,所以它的一个做差,实际上的结果就等于负七倍的一个 a 一, 那么负七倍的 a 一 可能是下面哪一个呢?如果是他的话,那么 a 一 就等于一,如果是 b 选项就是 a 一 等于零,如果是这个,那就 a 一 等于负一 啊,如果是十四的话,那么 a 一 等于负二啊,我们可以把这个排除掉,因为他不能有任何项为零。然后后面两项他虽然不是零啊,但是他会导致 a 二就等于零,这个会导致 a 三等于零啊, 写错了啊,这个是 a 三等于零啊,这个是 a 五等于零,他都是不可以的。所以这道题目我们选 a, 这个第十一题,第十一题的话,他的 a、 b 选项都是比较好判的,但是 c、 d 选项是有难度的。 我们先看 a 选项,如果它关于 y 轴对称,也就是说你带 x 进去或者带负 x 进去,它应该式子是不变的,那么我们会显然发现它里面出现过的 x 都是 x 平方,那你带 x 和带负 x 进去,这个式子是没有变化的,所以 a 选项是正确的, b 选项我们要看它与坐标轴有几个公共点,我们可以令 x 等于零解 y, 令 y 等于零解 x, 那 么这边我们可以解出来,它实际上应该是有四个公共点,然后 c 选项, 他说他任意一点的重坐标的取值范围,也就要求 y 的 一个取值范围,那么我们怎么去求解 y 的 取值范围呢? 在这里如果我们分餐就会有一点点麻烦,比如我们从分餐的策略去走, y 减去 x 的 平方的平方,就等于一减 x 的 平方一下,然后你就要开根,但是开根的话,你会发现平方开根实际上是要套绝对值的,它就等于一减 x 的 平方, 那么这时候你要去绝对值,它就变得非常的麻烦啊,所以我们用分餐的角度画,其实并不是特别好,那么在这里我们可以考虑整体进行一个讨论 好比如说我们可以令 x 的 平方等于 t, 那 么我们可以写一下 t 的 范围,由于啊,它是两个平方加和等于一,所以 x 方是一定不会超过一的,所以我们就会得到 t 的 取值范围应该是小于等于一,大于等于零。 好,所以它就变成了 t 加上一个 y 减 t 的 平方等于一,我们可以把它打开,它是关于 t 的 一个方程, y 是 这样式的函数,我们可以写成 t 平方减去一个二 y, t 加上一个 t, 再加上一个 y 平方减一等于零。 整理一下变成 t 平方加上一个一减二 y, t 加上一个 y 方减一等于零。那么到这里的话,我们就需要他要在零到一上面要由解 好,那么我们可以看一下,它是一个二次函数,我们可以把它当二函数看,那么它需要在零到一上有解的话,我们可以先看一下,我令这个函数为 f x f t, 我们就可以得到。先带下两个端点值观察一下情况,我们可以得到 f 零就等于 y 方减一, f 一 就等于一加一减二, y 加 y 方减一就等于 y 减一的平方, 那么我们会发现,如果说 f 零是小于零的, f 一 是大于零的,那么它中间一定会传出一个根出来,所以也就是说我们如果让 y 方减一小于零,同时让 y 减一的平方大于 等于零啊。由于零和一是可以取的,那么没关系,可以大于等于零,那么就可以做到它中间一定会有根,所以这边我们可以解出来是 y 要大于等于负一小于一,这边我们解出来是 y 啊,一定是会大于等于零的, y 除以二,所以在这种情况下,我们可以解到 y 的 一个范围,那么如果说他在零的时候是正的,那么我们就需要这样 啊,他才会有根,对吧?因为一的时候肯定是大于等于零的嘛,所以这时候我们就要要求他的对称轴负二 a 分 之 b 要大于零小于一,同时我们要求他的第二大要大于等于零,往他对准时候可以取到等,那么这时候我们就可以再解出一段 t 的 范围。 第一个式子,接下来是一减二, y 要大于等于负二小于等于零,两边先解这个二, y 要大于等于一, y 要大于等于二分之一,再减后面这部分, 二 y 要小于等于三, y 要小于等于二分之三。好,再看点它大于等于零, 而他的话,我们就可以得到 b 平方一减二, y 的 平方减去一个四 a c 四倍的一个 y 方减一要大于等于零,那么这边我们打开一加上一个四 y 方减去一个四, y 减四, y 方加四 大于等于零消掉。所以我们可以得到四 y 是 小于等于五的, y 小 于四分之五,所以在这种情况下,我们可以得到 y 的 一个取值范围要大于等于二分之一,小于等于四分之五。最后我们再把这两段取一个并集,就可以得到 y 的 取值范围是大于等于负一小于等于四分之五,所以啊, c 选项就正确了。 那么 d 选项的话,它其实是比较难判的,但是在这里同学们可以尝试去找一些特殊值进去,那你就会发现它可以超过根号二,所以 d 选项就是错误的。 好,我们来看十四题,十四题他说在平面直角坐标系内,我们可以先画一个圆, 他的圆心是一,逗号二,半径是三,那么 a 点坐标是二,逗号四,我们可以把它带到圆里面,会发现它是小于九的,所以它在圆内。然后呢,他要求 ap 是 垂直 a q 的, p q 是 圆上的两个动点,我们可以画一个矢图, a p 垂直于 a q, 然后他要我们去求 p q 这根弦的一个最大最小值的差值。 我们知道,如果我们想要研究弦的一个长度的话,实际上就要研究什么呢?啊,圆心到弦的距离,也就是说我们实际上是需要找到 p q 的 中点 m 点的一个变化啊,我们要求出 cm 的 一个取值范围,那么 c 点是定点,那么我们就要去看这个 m 点它是怎么动的,只要有了 cm 长度的取值范围,它的弦长的变化就出来了, 也就是说我们要求动点 m 点的一个轨迹,那么在这里我们可以尝试用圆的参数方程。在这里我们可以假设 p 点坐标为 三 cosine 阿法加一,逗号三 sine 阿法加二。 同样道理,我们说 q 点三 cosine 为它加一,逗号 cosine 为它加一加二。 好,那么我们看一下它满足的一个等量关系啊,就是这个垂直,垂直的话我们可以理解为向量相乘等于零,所以我们就可以写出三 cosine, 哈发减一,乘以一个三 cosine 被它减一,加上一个三 sine 哈发 减二,乘以一个三 cos, 三 cos 被他减二等于零,好,我们可以把它乘开来,乘开来我们就可以得到九倍的一个 cos 算法, cos 算法 后面也有九 cos 算法,算法减去一个三倍的 cosine 算法加上一个 cosine 被他 减去六倍的一个 sine 打法,加上一个 sine 被它。好,那前面还有一,后面还有四,所以加五就等于零。那么我们要看 m 点的一个轨迹,那么我们可以先表示一下 m, 利用中点坐标公式,我们可以得到 m 应该是等于二分之三个 cosine 算法加上 cosine 比特再加一,它的中坐标应该是二分之三个 sine 算法加 sine 比特 再加二。好,我们要求它横轴坐标满足的等量关系,我们可以令它为 x, 令它为 y, 我 们先尝试去表示这个部分,那么这个部分怎么得到呢?我们可以啊,把 x 减一,再乘以二 平方,再加上一个 y 减去一个二,再乘以二平方,那么它写下来就等于三 cosine 符号加上三 cosine 比特括号的平方加上一个三 cosine 比特括号的一个平方,那么它整理下来就变成了一个十八,加上一个十八倍的一个 cosine 比特, cosine 比特 加上十八倍的三个法三倍的。好,这就出现了我们要的这个部分,所以我们只需要把十八移过去,再除以二,所以他就可以得到 两倍的一个 x 减一的平方,再加上一个两倍的一个 y 减二的一个平方,再减去一个九。好,这里就比较容易了。这里的话我们可以直接把它写成 x 减一,再乘以二。这边减去一个部分,就是 y 减二,再乘以一个四, 减去一个四倍的一个 y 减二,加上一个五,等于零。两边同除二, x 减一的平方减去一个 x 减一,加上一个 y 减二的平方,减去一个两倍的 y 减二,再减去一个二,等于零。 配方,他可以写成 x 减一,减去一个二分之一的平方,加上 y 减二减一的平方就等于二,加上一个四分之一,再加上一个一, 所以我们可以得到它就是 x 减去一个二分之三的平方,加上一个 y 减三的平方等于四分之三四一,十二十三,所以我们就可以得到它的圆心是二分之三,逗号三,它的半径是等于二分之根号十三, 那么在这里我们就可以求到 c m 长度的一个取值范围了,那么我们要求 c m 的 长度取值范围,我们先聚在 c 点到这个圆心的一个距离, c 点到圆心的距离我们可以计算一下,它应该是等于二分之一的一个平方,再加上一个一的平方再开根,所以它算出来应该是等于二分之根号五,所以我们可以得到 c n 的 距离的取之范围应该是 大于等于二分之根号十三,减去一个根号五,小于等于二分之根号十三,加上一个根号五。 而 p q 的 一个长度应该是等于 r 方减去一个 c m 的 一个平方再开根,再乘以二,所以我们就可以知道 p q 就 等于根号下。嗯,九减去一个 c m 的 平方,再乘以一个二。 那我们当 c m 取到最小值的时候, p q 会取到最大,那么此时可以得到 p q 的 一个最大值,应该是等于根号下。九减去一个四分之十三,加上一个五,再减去一个两倍的根号六十五,再乘以二, 那么我们可以进一步运算,它就等于四分之十三,加上一个五,加上一个二,根号六十五,再乘以二,所以它算下来的话,就可以写成根号十三, 减去一个,加上一个根号五。那么同样道理,我们可以算出 p q 的 一个最小值,它最小值就等于根号十三减去一个根号五,所以它的最大值最小值的差是等于两倍的根号五。
粉丝618获赞2734
相关视频
 00:15查看AI文稿AI文稿
00:15查看AI文稿AI文稿如果没有天赋,那就一直重复,当你重复到闭上眼都能做的时候,那就是别人眼里的天赋。天赋不是天生的,它是拼尽全力的结果,不断重复直到完美,你就是那个天赋的创造者。
16戴数之路 07:11查看AI文稿AI文稿
07:11查看AI文稿AI文稿我们来讲解一下这次扬州市高二期末的一个呃,十九题,二十题。 那么在这里的话,我们第二问实际上可以考虑用椭圆参方的方法去做,那么什么叫椭圆参方呢?就是对于椭圆上面的任何一个点啊,我们可以设它的一个点,坐标为二, cosine 阿发,逗号根号三 sine 阿发。那么我们可以这样去假设, 那么在这里的话,我们可以再优化一下它,比如说在这里我们可以把 cosine r 写成 cosine 二分之 r 的 平方,减去一个 sine 二分之 r 的 平方。 那么我们再其次画一下底下除以一个 cosine 二分之 r 方,加上一个 sine 二分之 r 方,再同时上下同除 cosine 二分之 r 的 平方,我们就可以得到它,就等于一减去添进来的平方,底下就变成一加上添进来的平方。 同样的道理,我们再处理这个 cosine 啊法, cosine 啊法可以写成两倍的一个 cosine 二分之二法, cosine 二分之二法,底下也除以一个 cosine 二分之二的平方,加上 cosine 二分之二的平方,所以上下一同除之后,它就变成一加上一个天渐的的平方,上面变成两倍的一个天渐的。所以对于像这个椭圆上面的点,我们都可以去进行假设, m 点可以写为一加 m 的 平方分之啊二减去二 m 的 平方逗号一加 m 的 平方分之二,根号三 m。 好, 同样的零点坐标,我们可以设为一加零方分之二减二零方逗号一加零方分之二,根号三 a 好,那么由于这个 q 点的坐标是 p 点坐标两倍,所以我们可以得到这样三倍,所以我们可以得到这样的一个关系, k a m 乘以一个负三,就等于 k b q。 好, 那么我们来表达一下这个关系。 k a m a 点的坐标是负二多号零, b 点的坐标是二多号零,所以 k a m 可以 写为 一加 m 的 平方,二根号三 m 减零,一加 m 平方,二减二, m 方加二, 等于一加盈方,二根号三盈减零,一加盈方二减二,盈方 减二。可以进行一个化简,它可以写为上下同乘,一加 m 的 平方,底下就变成了二减二 m 的 平方。加二加二, m 方,上面就变成了负六根号三 m, 那 么这边的话上面就变成二根号三零,底下就变成二减二,零方减二减二零方。 这边可以约掉,那么这边可以约掉,所以我们就可以得到四分之负六根号三 m, 就 等于负四零平方,二根号三零。 所以在这里我们可以得到三 m 等于零分之一,所以我们可以得到三 m 零等于一。 好,有了这个关系之后呢,我们来看,它要我们求的是 number, number 就 等于 k b m 比上一个 k a n。 好, 我们先写 k b m, k b m 就 等于一加 m 方,二根号三 m 减零,比上一个一加 m 方二减二, m 方减二,那么它要除一个 k a n, 就是 相当于乘以 k a n 的 倒数,所以这边就是一加零方分之二根号三零 减零,一加零方分之二根二减二,零方,再加二。 好,那么第一个式子我们可以稍微化解一下。上下同乘一加 m 的 平方,所以上面就是二根号三 m, 那 么底下算下来就等于负四 m 的 平方。好,上下同乘一加平方,所以上面算下来就等于四,下面算下来是二根号三 n, 所以 这里我们最后算下来应该是等于负的 m n 分之一,所以它就等于,就这里我们可以得到 m 零就等于三分之一,所以它等于负三。我们会发现,如果用椭圆的餐方的话,那么这个第二文的计算量实际上并不大啊,它都是一个,别看它式子复杂,但是它在计算的时候它都能约掉很多。我们再来看它的一个最后一问, 最后一问他说过, o 点做 m 的 一个垂线,好,我们连接 m 做大的一个垂线,然后他要我们去求 b h 的 一个长度。如果我们在这里用非常常规的做法,你会发现它的计算量还是很大的,所以我们不妨先研究一下 m 零这条直线它有什么样的一个特征好。在这里我们可以假设 m 零 为 y 等于 k x 加 b, 那 么由于 m 点和零点带进去,它都能成立,所以我们就可以得到 一加 m 方,二根号三 m 等于一加 m 方, k 二减二, m 平方加 b 是 成立的。同时一加零方, 二根号三零等于一加零方, k 二减二零方加 b 等于零也是成立的。所以不如我们就去 构建一个同构的方程,一加 x 方分之二根号三 x 等于一加 x 方分之 k, 二减二 x 的 一个平方,再加上 b, 那 么我们会发现这个方程的解实际上就是 m。 好,我们继续两边同乘,一加 x 的 平方,它就变成二根号三 x 等于二 k 减去一个二 k x 的 平方,再加上一个 b, 加上一个 b x 的 平方,好,我们把它整理一下,移向移到左边来,就变成二 k 减 b。 括号 x 的 一个平方加上一个二根号三 x 减去一个二 k 减去一个 b 等于零。根据几何定律,我们知道他的两根 m 乘以是等于三分之一的,所以我们就可以得到二 k 减 b 分 之负,二 k 减 b 等于三分之一。交叉相乘负六 k 加三 b 减三 b 就 等于二 k 减 b 一 项,我们就可以得到八 k, 就 等于负二 b 得到 b 就 等于负的四 k, 所以 我们就可以得到这条直线,实际上可以写成 y 等于 k x 减四 k, 那 么就意味着他会经过四零这个点横过四零,那么既然横过四零,而 b 点坐标又是二零,我们就会发现他实际上是直角三角形斜边上的一个中线,所以他就等于斜边的一半, 我们就可以得到 b h 等于二。所以我们会发现,如果这道题我们用乘方结合同构,那么它的计算量就会大大的减少了,同学们学会了没有?
23扬州董老师数学 00:12查看AI文稿AI文稿
00:12查看AI文稿AI文稿请监考老师拆封并分发试卷,指导学生填写个人信息。
902奋发向上 00:17查看AI文稿AI文稿
00:17查看AI文稿AI文稿徐州高一高二的期末考试今天终于考完了,现在试卷和答案也都已经出来了,高一高二的同学都反映数学题目比较难,高一英语难度适中,高二相对难一些。阅读理解呢是重灾区。高一和高二所有科目的试卷和答案都已经给大家准备好了,扣一二三,大家可以找我免费领取。
 01:00
01:00 00:12
00:12 00:10查看AI文稿AI文稿
00:10查看AI文稿AI文稿二零二五到二零二六上中山高一高二期末真题加答案来啦!快来评论区领取吧!
 00:17
00:17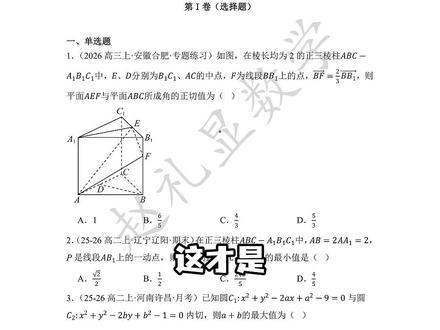 00:19查看AI文稿AI文稿
00:19查看AI文稿AI文稿这才是最值得高二生刷的期末试卷。我花费三天时间,把高二上数学出错率在百分之九十五以上的知识点会编成了这套全是错题的高二期末试卷,每道题都是高频丢分考点限时练习能拿到一百四十分的九八五线。建议家长同学下载打印检测掌握情况。
2402数学赵礼显 00:47查看AI文稿AI文稿
00:47查看AI文稿AI文稿试卷相较于去年嘉兴期末卷,整体难度平稳,由易到难,命题人注重通信通法,由特殊到一般的数学思维引导。其中第八题属于难题,陌生题,升级并隐藏了常见的地推式关系,实际令 n 等于一就是常规题了,对于学生的观察能力有较高要求。第十一题 几何动点问题毋庸置疑,几何法难想少算,代数法异想难算,还是推荐基础中等。以下注重代数法。十四题经典的交半径比例问题,结合双实线定义、勾股定律,属于中档题、常考题、高考真题卷、高考模拟卷,数次考察过 十九题,此题当之无愧,难度极大。模仿二十四全国两卷压轴题,第一问常规,第二问点差法即可,非常考验计算能力。第三问的命题计算起来计算量特别大,特别具有挑战性。
10英华教育 00:16
00:16 00:08
00:08







