八下数学全等三角形模型怎么画辅助线
粉丝1167获赞6012
相关视频
 22:02查看AI文稿AI文稿
22:02查看AI文稿AI文稿标准答案中的辅助线是如何想到的?这期视频会告诉你答案,其实我们常考的也就三类,要么是终点,要么角平分线,要么垂线那么亮。今天就把这三种常考的辅助线思路给大家梳理清楚,以后我们遇到了就可以快速拿分了。 那遇到终点呢?我们一般倍长中线,比方说给出一个三角形,那 d 是 底边的中点,那么也就是 b、 d 呢,等于 c, d 好, 连接 a、 d 就 产生中线了。有终点或者中线的时候,我们一般可以把这个中线呢延长一倍,也就是使得这两条蓝边相等。 那最后你会发现我们还有对顶角,等于对顶角,所以如果你连接 c、 p, 那 么我们一定可以挣出这两个三角形全等,那我们挣出全等之后呢, 我们就可以利用全等三角形的性质来进行边角条件的转化了。你看亮亮在这里放个乌漆嘛黑的屁,臭死人,听一半就逃跑的各位同学们,亮亮这么简单的东西,我也知道,他真的能搞定我们的难题吗?好,我们一起来看一下今天的第一题。 首先给出一个它就不太常规五边形对吧? a、 b、 c、 d、 e。 好, 我告诉你, a、 b 等于 b, c 等于七,也就是我们这个边是七,以及我们这个边呢,也等于七,两边相等。还告诉你, a、 e 等于 e, d 等于八,也就是这两条蓝边相等,并且每一条边的长度呢,都等于 八八。接下来还有一个条件,角 abc 加角, a、 d 等于一百八十度, abc 也就是这个角加上角 a、 e、 d 也就是这个角,对吧?这两个大角相加等于一百八十度。 其实很多同学特别怕这种条件,为什么呢?因为像这种角,我们把它叫复合角,它是由多个角重复组合而成的,像复合角的问题,很多同学看到就比较怕。好,我们先继续,往后我还告诉你, m 是 c d 的 中点,也就是这条边等于这个边 o, 这里面会有很多过中点的线段, 那么其中一条 b m 呢?等于九,还有另外一条 m e 呢,它是等于十的,我们把所有条件全都标注在图形里面,好,问题来了,让我们求整个五边形的大大的面积等于多少?该怎么处理?根据我们刚才所提到的,有终点或者有中线,我们可以尝试背成, 比方说在这里面我们把 b m 呢延长一倍,也就使得我们这条边等于这条边,嗯,亮了,在这里依然放个乌漆嘛黑的屁,看到没有?好,我们再连接 d p, 那么首先根据我们背长中线,我们知道我们很容易挣出 m、 c, b 这个三角形一定全等于 m、 d p 这个三角形,也就是这两个三角形全等,那全等三角形对面相等,你这个边是红边,那我们立马知道,也就是这条边一定也是红边,所以我们知道它的长度呢 等于七。然后该怎么办呢?你会发现我们好像就没有思路,对吧?哎,亮亮,我平常就跟你一样,对吧?就是做完之后呢,就不知道该怎么办了。你要知道题目中告诉你,这两个角相加一百八十度有什么用呢?我们知道 a、 b、 c、 d, 它是个五边形,五边形的内角和是五百四十度,对吧? 那我们再减去一百八呢?所以我们知道剩下的三个角相加一定是三百六十度,也就是我把这个角标做 a r 法, 我再把这个角标做 beta, 以及我再把这个角标做伽玛。我们知道 alpha 加上 beta 加上伽玛一定等于三百六十度。我跟大家说一下,其实在我们整个全等的判定以及应用里面,其实最难的就是我们角度的推导。 那一般需要我们利用什么三角形的内角呀、外角呀啊,平角一百八,直角互余哎等等,包括我们的周角三百六来进行角度的转换。比方说, 那这个三角形,我们知道跟 m d p 这个三角形全等,你这个角是 beta, 所以 我们知道这个角也是 beta, 对 吧?好,接下来怎么办? 我们说了, alpha, beta 加伽玛呢?相加等于三百六十度。喏,我这是伽玛,我这是 beta, 并且你会发现整个大角已经是三百六十度了。请问那我们这个角等不等于 alpha 角呢?很明显我一定和你相等。到这里之后,你会发现整个题目我们又获得新的思路了。喏, 我们有红边,有蓝边,加角是 alpha, 所以 我们很容易想到我要把 b、 e 连接起来,对吧? 以及我把 e p 连接起来,我可以怎么样?我可以证出 a、 b e 和我们的怎么样呢?呃, d p、 e 这两个三角形全等,我们知道全等三角形对应边相等,所以你这个三角形的 b、 e 一定跟我们这个三角形的 e p 是 对应相等的,也就是这两条绿边一定相等。你会发现我们通过全能把这个小三角形的面积转化到这里了, 以及通过全能把这个小三角形呢,我们把它转化到这里了,所以整个大五边形的面积其实就是我们等腰三角形 e b p 的 面积。好,那整个等腰的面积该怎么处理呢?大家不要忘了, 我们刚才证明过,这个小三角形跟这个小三角形全等,对吧?全等三角形对边相等,你这个边是九,我这个边呢,也等于九,也就是 m 点,它是整个 b p 的 中点,对吧?哎,两个边都是九,对不对? 好,那我们知道等腰三角形有三线合一的性质,你过顶点连接底边的中线,那么一定是底边上的高,所以整个 e、 b、 p, 我们的底边多少呢?啊?也就是二分之一,两个九十八再乘以高呢?十,所以我们最终求出来的面积等于九十。搞定 这里有没有难度?的确有,但你会发现本质是什么?不就是背长中线吗?背长完毕之后呢,跟我们题干中的角度,跟我们题目中的面积稍微的结合一下,就呈现出我们千变万化的不同的题目,仅此而已。那如果我们遇到角平分线呢?你就需要掌握三种和全等相关的角平分线模型。 我们首先看第一种,比方说呢,喏, o c 是 一个角平分线啊,也就是这两个角相等,对吧?那如果在角平分线上有一个点屁啊,向两端做垂线,向两端做垂线,我们能够知道 这两个三角形一定全等,并且呢,哎,你这两条垂线段它是相等的。那问题来了,如果有的题目只是像这样给出一部分呢?那么请问你能想到的辅助线构造是什么?那肯定是过屁点向另一端做垂线了,构造我们的全等以及我们的 等边,对吧?好,那么第一类量就拿出一个比较常规的题目了,那我告诉你,角 b 等于角 c 呢?等于九十度,也就是这个角呢是直角,以及这个角呢,也是直角。 好,问题来了,告诉你, m 是 bc 的 终点,那就是这两条线段是相等的。好,第一步,让我们求证 am 平分角 d a b a m 平分角 d a b, 也就是求证 a m 是 一个角平分线,对吧?就是证明这两个角相等,那该怎么处理呢?首先,大家有没有发现?那你有没有发现这是不是一个角啊?这是个角对不对? 好,在这个角里面是不是已经出现了一条角平分线了?各位,关键是我已经过这个角平分线上一点向一端已经做了垂线吧,所以接下来你所想到的全等模型, 我们只要过 m 点向另一端也做垂线是不就可以了?哎,就差不多哎,放个红色的屁是吧?我们知道,那你这两端一定相等,就是我们的 c m 一定等于 d p 吧, 而我们知道 c m 呢,还等于 a b m, 所以 这两条线段一定相等。好,当我们知道这两条线段相等时,接下来你会发现 那一个点到角两端的距离相等,对吧?你是不是在角平分线上?一定是的啊,所以这两条垂线段相等,你可以直接推出 a m 是 角平分线搞定, 也就是在这里面,我们甚至可以推出两组全等,就是这个三角形跟你全等,以及我们这个三角形呢,跟它全等,对吧? 好,那接下来我们处理第二种就简单的多了,为什么呢?那如果我把你这个角标做 arfa, 标做 arfa, 我 再把你这个角标做 beta, 你 这个角呢?也是 beta。 好, 我们知道整个大角呢,一百八十度,也就是两个 arfa 加上两个 beta 呢,等于一百八,我们同时除以二,也就 arfa 加 beta 呢,等于九十度。而 arfa 加 beta 不 就是我们的 dma 吗?九十度推导完毕,因此二者呢,是垂直的。 那么第二类呢,就是在角平分线上依然有一个点。好,现在我不再过屁点向两端做垂线了, 我是过屁点做角平分线,自身的垂线,对吧?就像这个样子。好,因为你要知道角平分线,这个角等于这个角,对不对?好,在这里面大家可不可以挣出上下两个三角形全等?那其实证明非常简单,在下面这个三角形中,有锐角,有九十度夹着一条 o p, 上面这个三角形有锐角,有九十度夹着一条 o p。 所以 我们可以推出上下两个三角形一定是全等的,也就是这条边一定等于这条边。好,那问题来了,如果以后在角平分线上有一个点,我过他做自身的垂线,但我只做一半的垂线,请问你能不能想到 去把这条垂线段延长,来还原我们刚才的图形呢?比方我们今天的这道题,首先我给出一个直角三角形, a b c 角 a b c 等于九十度啊,给你标出来一个比较小的直角,好,告诉你 bc 是 八,哪个边 哦,就是这个边等于八,对吧?好,把它画一下,就是这条边的长度呢,它等于八。好,剩下 ab 等于六,这个边是六, 以及呢? a c 等于十,哎,这个边等于十,好,告诉直角三角形三边的长度。好,现在我出现一个角平分线, a、 d 是 b, a、 c 的 角平分线, a、 d 平分整个角, b, a、 c, 也就是这两个蓝角是相等的,然后过 c 点呢?做你这个角平分线的垂线,垂足是我们的地点。好,我们连接 b、 d, 让我们求三角形 b、 d、 c, 它的面积 亮亮,这个跟我们刚才的模型有关系吗?首先你会发现我们给出了一个大大的角大概长这个样子,然后各位,关键是你会发现我过角发射了一条角平分线, 不仅如此,而且在角平分线上有一个点,并且过这个点做自身的垂线。呐,这个角九十度。请问接下来你所想到的辅助线构造, 所以我们很容易想到把 c、 d 延长嘛?延长完毕之后,比方这个点我们把它叫 m 点好不好?也就是这条线段一定等于这条线段,以及我们的 a、 d、 c 这个三角形一定全等于 a、 d、 m 这个三角形, 也就是整个图一大概长这个样子,那我们知道,因为整个 a、 c 等于十,所以我们知道 a、 m 的 也等于十,你拿走了六个单位,所以我们知道 b、 m 的 一定等于四。那然后怎么办? 那此时你要知道,因为 md 是 等于 dc 的, 也就是 d 点是整个三角形底边上的中点,对吧?因此 bd 是 中线,而我们知道 中线最主要的性质是什么?是平方面积,对吧?你要取个中点连一下,左右两个三角形的面积一定相等,那你会发现整个 bmc 这个三角形的面积可不可以求出来,因为这个角是直角啊,九十度延长出来的 一个边是四,一个边是八,所以面积二分之一乘以四乘以八等于多少等于十六,整个三角形的面积等于十六,底边上取个中点连接中线,所以我们知道这个三角形的面 积一定等于 b、 d、 c 的 面积都等于整个十六的一半,也就是面积呢,等于八,搞定。 当然了,并不是所有的角平分线都会出现垂直,比方说呢,我们在角平分线上放一个 p 点,现在没有垂直了。 哎,我在这里随便连一个什么呢?连一个,像这样,比方说,哎,这个叫 a e 点吧,有什么特殊性呢?没有。 那么请问接下来我们能够构造的辅助线是什么呢?注意,你在 o b 上截取 o e 相等的线段,比方说来一个 f 点好不好,也就是使得 o f 等于 o e, 那 么接下来有什么好处呢?那因为你是角平分线,你这个角本身就等于这个角,对吧? 所以你把 p、 f 连接起来,那么在上下这两个三角形中, o e 等于 o f, 公共边等于公共边,对吧?而且呢,还有夹角相等,所以我们可以推出上下这两个三角形一定全等, 也就是在出现角平分线且没有任何垂直的情况下,我们往往是截取等长来构造全等。 好,现在我告诉你,在整个三角形中,角 a、 b、 c 是 六十度,也就是咱们这个角呢,是一个固定的六十度。好,现在我告诉你,有两组角平分线, a、 d、 c 分 别平分这两个角啊,就是 a、 d 呢,平分整个大角,也就是这两个蓝角是相等的,我们令它都是 a r 法好了, 还有 c e 呢,平分底下的这个角,那么这两个小角呢?我们就索性多把它叫做 beta 角,多把它叫做 beta 角啊,把它标在图形中。 好,第一问,让我们求 a o e 的 度数,也就是这个锐角,对吧?啊,其实这个题本质上是想让你求 a o c 这个大的钝角。 好,怎么求呢?首先我们知道啊,三角形内角和是一百八十度,所以二倍的阿尔法。哦,二倍的阿尔法加上二倍的贝塔。啊,两个贝塔再加上你这个六十度,对吧?我们知道等于多少呢?等于内角和一百八十度,因此两个阿尔法加上两个贝塔呢,一定等于一百二十度, 则两边同时除以二 a r f 加上贝塔呢,等于六十度。好,接下来你会发现哦,一个 a r f 加一个贝塔等于六十度。在我们三角形 a、 o、 c 中, 两角相加等于六十度,所以我们知道剩下你这个大大的钝角一定是一百二十度,所以我们可以求出来,这个小角呢,等于六十度。搞定 好,第二个,让我们求证, a c 呢,等于 a e 加 c d, 就是 整条线段呢,等于我们这条边加上我们这条边。那很明显啊,我们一般求证两边之后,等于第三边都是通过构造全等来进行处理的。那可是怎么构造呢? 此时你会发现他给出了一个角,然后在里面呢,发射一条角平分线,因为没有任何的九十度,所以我们可以截取等长。怎么截取呢?我们只需要在长边上截取短边,比方说我们在这里面取一点屁干嘛呢?使得我们 a p 这个边呢, 等于我们 a e 这个边,哎,两边相等,所以接下来我只要求成 c p 这个边等于 c d 就 可以了。 此时我们连接 o p, 你 会发现我们左右这两个三角形,红边等于红边,中间二者的公共边以及加角都是相反, 所以我们可以正出左右这两个三角形全等。因为你这个角等于六十度,所以我们可以求出来这个角呢,也等于六十度。而我们知道整个平角一百八十度,也就是我们可以推出这个角也等于六十度。 那当然首先我们把这个对角把它标出来,也就是这个小角呢,他也等于六十度。这次我相信很多同学看得出来,上下这两个三角形,红角等于红角,六十度, betta 等于 betta, 而且二则呢有着相等的公共边,所以我们可以证出上下这两个三角形也是全等的,也就是我们 c p 这个边呢,我们的确证出了等于 c d 这个边,所以你会发现很多题目,你只要大胆的构造辅助线,最后你会发现你想要什么就有什么。 那这个题让我们求成 a c 呢,等于 a e 加上 c d, 我是 红边加蓝边,你是红的,我是蓝的,所以证明完毕。那我们角平分线平常见的也就这三类,大家只需要根据题干中的条件来进行选择判定即可。 那如果我们遇到垂直该怎么办呢啊?垂直一般不会单独的出现,他一般会告诉你,同学们有这两条线段既相等又垂直,那么此时我们可以用到的也就是三垂直模型,他一般情况下是这么考的,比方说过 a 点呢,画一条线,对吧?然后你过端点分别往下做垂线, 过端点分别往下做垂线,我们能够推出来的也就是这两三角形,一定全等学完了,对吧?哎,一起来做题啊,大概长这个样子,我们直接来处理这个题的最后疑问,他是这么描述的, 辉煌小组深入研究和谐小组提出的这个问题。呃,不用管了,就是他发现一些什么探求点之类的。就是首先告诉你,在正方形 a, b, c, d 中啊, a, b, c, d, 它是个正方形好, e 点呢,是 b c 边上的一个洞点,你可以理解,从 b 点出发啊,他慢慢往右边跑好不好? 但是不管怎么运动呢, ap 永远是一个等腰直角三角形,哦,就是 a e, p, 也就是我们知道这两条边永远是既相等又垂直的。那题目中也告诉你,这个角呢,它等于九十度, 好连接 ap 与 cd 呢,交于 m 点啊,并且连接 d p, 好, 现在告诉你,如果正方形的边长 ab 等于四啊,整个边等于四了。请问, 当我们这个 a d p, 也就是 a d p, 当我们这个三角形的周长取得最小值的时候,让我们求什么呢?求 dm 的 长度, 也就是我们这个边的长度。首先你会发现这两条红边既相等又垂直,而且过我们的直角顶点已经画出一条线了。最关键是,我们已经过 a 点往下做了一个垂线, 所以我们很容易想到过屁点往下做垂线,大概这个样子去构造三垂直模型,也就是这个三角形全等于这个三角形,但你发现正全等好像没有用,对吧?我们这个三角形周长的最值,跟你这个全等好像一点关系都没有。我们大胆引入未知数,比方说令这条线段的长度是小 m, 全等三角形对边向的你是 m, 所以 我们知道这条边的长度呢,也等于四。 接下来我们可以把这里的每一条线段都表示出来,因为正方形的边长等于四,所以这个边的长度呢,也等于四。你拿走了 m 个单位,所以剩下的 e、 c 是 四减去 m, 而我们知道 整个边等于四,你拿走了四减 m, 我 们用四减去四减 m, 你 会发现不多不少,我们刚好等于 m, 也就是这条边的长度刚好等于 m, 你是 m, 我 也是 m, 二者既相能又垂直。所以我们想到如果连接 cp, 一定会产生一个等腰直角三角形,说白了,也就是我们这个角永远是四十五度的。 我们知道 e 点是个动点,并且在整个运动过程中,我永远是个等腰直角三角形,所以 p 点呢,它会随着 e 点的运动而运动,也就是你也是个动点。但你犯不管怎么运动,我连接 cp 这个夹角永远是四十五度, 也就是不管 p 点在这在这在这,不管在哪里,你连一下 c p 和水平线的夹角是一个固定的角,所以 p 点就一定在把 c、 d 绕着 c 点 旋转四十五度,在这条射线上运动。好知道 p 的 运动轨迹之后,我们来处理周长最值问题。因为正方形的边长是四,所以这个边呢,也等于四。因此我们只需要使得 d p 这个边加上 a p 这个边,只要使得这两边之和最角就可以了, 这不就是我们常规的将军印码吗?你只需要做 a 点或者 d 点关于这条直线的对称点就可以了。为了方便大家理解,我延长 a d 和对角线呢,产生一个焦点, 然后在我们下方呢构造一个大大大大的正方形,根据对称性,我们知道 d 点关于对角线的对称点就在这里,这个就是我们的 d 一 撇,也就是你连接 p d 一 撇呢,你可以把这个边转化到这里,也就接下来我们只要使的这条线段 加上这条线段,二者之合最小就可以了。这就相当于从 a 点出发,然后经过我们的某一个 p 点,最终呢再回到我们固定点,第一撇,从一个点到另外一点,我们知道两点之间线段最短,所以我们知道连接 a 点跟我们的第一撇就可以了。此时呢,我们 p 点在这 m 点呢,在这里。好,接下来我们这个 dm 怎么求呢?因为我们知道正方形的边长是四,并且你靠着 d c 向外也构造一个正方形,所以这个边呢也等于四,我们很容易挣出上下这两个三角形全等,因此呢,也就是这条边等于这条边, 那所以呢,我们的 d m 等于整个正方形边长的一半,也就是等于二。搞定,你会翻很多题目,考察我们的辅助线,但辅助线只是第一步,你能不能想到过屁点往下做垂线,构造我们的三垂直模型, 那接下来就考察我们的引入未知数的思想,你敢不敢大胆的引入未知数去把这个等腰直角三角形构造出来,这是第二个,也就是你得推出这个角呢,等于四十五度。当你推出我这个角等于四十五度之后,你能不能挣出屁点的运动轨迹?是像这样的一条射线, 以及第四步,你能不能通过轨迹来求出我们整个三角形的周长最值,也就是什么时候我的周长可以取得最小值,说白了也就是和我们的将军一马连了一起来。所以你会发现我们所谓的压轴题难题,无非就是由若干个比较简单的知识融合在一起形成的,仅此而已。 其实你会发现,所谓的辅助线就是我们几何模型的还原,在遇到什么样的条件,我们该怎么做,还原什么样的几何模型,它就是我们辅助线的构造思路。 那么模型有两类,一类呢就是还原类的,需要你构造辅助线的。还有另外一个结论类的,同学们可以把想听敲在我们弹幕上,亮亮火速更新。为了让大家快速的掌握这三类辅助线思路,完成复仇,亮亮给大家整理了我们针对性的资料,跟着亮亮无脑学习。
41.5万亮亮巧解数学 00:28查看AI文稿AI文稿
00:28查看AI文稿AI文稿垂直,那么此时我们可以用到的也就是三垂直模型,他一般情况下是这么考的,比方说过 a 点呢?画一条线,对吧?然后你过端点分别往下做垂线,过端点分别往下做垂线,我们能够推出来的也就是这两三角形,一定全等学完了,对吧? 哎,一起来做题啊,大概长这个样子。
30.2万小灯动画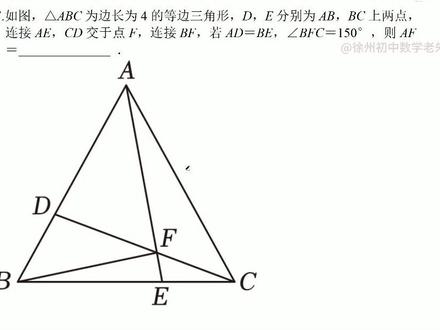 08:44查看AI文稿AI文稿
08:44查看AI文稿AI文稿全等三角形辅助线的构造是很多娃头疼的地方,说想不到这个辅助线该怎么画,那今天咱们化身小侦探带你复习一下怎么构造辅助线,那来吧,说三角形 a、 b、 c 啊,它是边长为四的等边三角形,那接着说这个 a、 d 等于 b e 角 b、 f、 c 一 百五十度,让我们求 af 的 长度,那乍一看呢,这个 af 和这边的几个条件没什么关系, 这个三角形内部呢,可谓是迷雾重重,但是碰到了咱们小侦探,这个三角形的天就要亮了。那既然从问题不好直接找呢,我们就从条件先来,顺着分析。那咱先从这个等线段开始, 你从这个线段两端去看,你观察这个线段的两端呢,能发现它和等边三角形有一个六十度角呢,是有联系的,那这里的边角边 就和这里的边角边对应全等了,所以第一个线索全等就找到了三角形这个 d、 a、 c, 它就全等这里的 e、 b、 a。 那 有了全等显然不能干放着,我们顺着新线索继续往下挖。全等是个工具,能带来对应的边角相等,那就找一下对应边角,这里的 a、 c、 d 这个小圈呢,就和这个角 b、 a、 f 对 应相等,那另一组就是这个叉和这边的小叉对应相等, 那除了角呢,还有我们正圈等没用的一组边,这个 c、 d 和 a、 e 相等,看起来 af 呢是在 a、 e 上边,但是它和 c、 d 的 关系不好找,那咱就可以从角来入手, 顺着新来的线索继续往下找。那你看这个小圈,它和这个六十度有一个关系,圈加三角是六十,那作为相等的圈呢?这里的圈加三角也是六十, 是不是能发现这两个角在一个三角形中,所以我们就得到了 dfa 作为外角,也就是六十度,这是通过全等得到的关键线索。六十度怎么用? 那说之前把它怎么来的?简单写一下,把这里的符号呢?改成一二三,这是角一、角二和角三。我们因为全等得到了角一等于角二, 那角一加角三是等边的六十度吗?所以得到二加三也是六十度,这样就得到了外角 dfa 的 度数。那接着来一名合格的侦探,得充分利用他手上的线索,这边的一百五十度我们现在还没用, 那结合新得到的六十度,是不是能发现一百五他的补角三十度和这个六十度组成了一个直角, 那这个新的直角继续往下追查,是不是和 a f 有 关系?那咱们就能发现这个 a f 呢?它在一个这样的直角三角形里边。那这个直角三角形它浮出了水面,到底有什么特殊的? 我们来观察一下。它的斜边是四,它的内部呢?这有一个角一,另一个角呢?没啥背景,但是这角一很特殊,它和刚才的角二相等,而这个角一挨着一条边是四,这角二挨着一条边,它也是四。 那已经出现了一组对应边和一组这里的对应角了。这个 a f 的 长度在角一的另一条边上, 所以我们就在角二的另一条边上,也给他截取一段 a f 的 长度就行了吧。这是其中一种想到的方法,也就是说我们在 c d 上截取一段和 a f 一 样长,你看我们取一下,大概在这吧, 这个点记为点记,现在把这绿的先擦掉,那我们只要把这个 a g 给它连上,因为我们截取的 c g, 它是等于 af 的, 再结合这个角二和角一是相等的,以及这里都有一个长度为四的边, c a 等于 ab, 那 是不是三角形就全等了? 这不边角边吗?所以 c a g, 它就全等三角形,看好对应顶点是 a、 b、 f, 那 这个全等三角形显然会有新的边角关系。我们待会说,除了这样去截长补短之外, 我们还可以利用刚才发现的这个 a、 b f, 它是个直角三角形,我直接就过点 a 往下做垂直能带来直角,那用角角边也能证明全等这里的直角角二和四,以及这边的直角角一和四, 那接着从全等来入手了,也是有新的对应边角。这个特殊的九十度咱已经对上了,那我们要求的 a f 呢? 他就等于这里的 c g 了,那剩下的就比较明显了,结合我们这里的九十度啊,以及这个新得到的相等的线段,你看九十六十这个角就是三十度, 那么三十度角对的直角边,也就是 f, g 是 af 的 一半,所以我们设 f g 是 x, af 就是 二 x, 那结合 a f 和 c g 相等, af 是 二 x, f g 是 一个,所以 c f 也是 x, 那 怎么求 x, 这是二 x, 这是 x, 这又是直角直接勾股定律吗? a g 就 等于四 x 方减 x 方,三 x 方开根号根三 x, 所以 最后在这个直角三角形 a g、 c 中,我们就能得到这里的根三 x, 它的平方加上这个二 x 方, 就等于斜边四的平方,这边就是三加四, x 方呢,是七 x 方等于十六, x 方是七分之十六,那 x 就 等于根号,七分之根号十六就是四。这里注意,有的地方还没学分母有理化吗? 像这种分数里边,分母带根号的,按照规范把它整到分子上,所以分子分母同时乘根号七,这就变成了七分之四倍。根号七, 那 x 有 了,我们的 a f 是 二, x 就 出来了,也就是七分之,这边乘二八倍根号七。那咱们接着再来分享一个分析方法,来帮助你提高想到辅助线的概率。先把这个辅助线擦掉,就从咱们这正了六十度开始。正了六十度发现直角, 那刚才我们是把目光聚焦在了左边 a b f 这个直角三角形,那现在我们看一下 a f 的 右边, 它所在的三角形,也就是 a f c 这个蓝色三角形里,那观察这个三角形的边和角,这有一个等边的四有一个小角,角二是刚才和角一相等的对应角。 那既然如此,我们构造和 a f 有 关的全等三角形,就可以利用这里的两个蓝角以及等边三角形的两条边。那你观察这里,它是 a c 和这个角一现在对应相等。 如果想构造全等,按照边角边来说,是不是得有一段和 c f 相等的边?所以既然角二的另一条边是 c f 这么长,我就在角一的另一条边上截取一段和 c f 一 样长,因为另外一条边已经对应上了嘛。 那这样截取完之后,我们把它一连这个点记为 m, 你 会发现这里有边是四角一和 am, 这边呢也是边是四角二和 cf, 所以 我们截取之后就有全等了。 am 等于 cf 之后,三角形 b a m 全等。三角形 a c f, 这也是咱们之前讲过的顺藤摸瓜嘛。顺着这个 a f, 我 们的目标看一看它和条件的联系,有等边有等角,自然就构造了第三条边相等。那有了全等之后还是一样,我们的目的是转化边角嘛, 所以这个 a f 就 和 b m 是 相等的,那接着把 b m 求出来,还是利用全等,我们除了说边相等,还有角相等,这个角三作为全等的对应角,是不是来到了这里,即为角四, 那角三和角四相等,一加三是六十度,那一加四也是六十,所以这个角作为外角, 它就等于角一加角四也是六十,再加上这个九十度。哎,三十度特殊角来了,那三十度角对的直角边,这个 f m 我 们设为 x, 那 b m 就是 二 x, 所以 b f 就是 根三 x, 那 再结合对应边相等, b m 就是 a f 也是二 x, 所以 你就能发现 a f b 中, 在这个直角三角形中,用割股定律二 x 方加根三 x 方,就等于这里的四和这边是一样的,只是辅助线换了一个思路去构造出来。 所以说这个顺藤摸瓜呢,顺着问题, a f 和已知的条件 a c 和角能够提高你想到辅助线的概率,那就到这每天进步一点点,咱们下期见。
692徐州初中数学老朱 01:30查看AI文稿AI文稿
01:30查看AI文稿AI文稿一个视频讲清楚八年级常考重难点模型背长中线模型。首先得知道什么是背长中线, 背长中线的做法, d 是 bc 的 中点延长中线 a d 使 d e 等于 a d 连接 b, e, c e 构造全等三角形 何时使用背长中线?一题目给出终点信息。二、需要证明边长相等。三、建立三角形三边关系四、转化为平行四边形问题。
 12:19查看AI文稿AI文稿
12:19查看AI文稿AI文稿江苏初二的家长和同学们注意了啊,如果说您孩子的分值是在八十分以上,那么一定要看一下这道题目如何用手拉手模型去构造辅助线做全等啊, 是我的学生刚才问我的题目,那么他们学校呢,是正好在讲这个手拉手模型与构造权等啊这个专题。那这里面我觉得如果说孩子想要在期末考试冲刺一下更高的分数,那么这种类型的题目一定要会做。 来看一下这个题目啊,这个题目用到的知识点呢,就是我们在学三角形啊,里面会讲到一个模型,叫做手拉手模型,还记得吧,手拉手模行为呢,为什么会想到手拉手模型呢?因为这里面他说做等边三角形,而在我们手拉手模型里面,哎, 我们回顾一下之前讲过手拉手模型也就子母模型,那它里面也会用到什么呢?比如说啊,像两个等边三角形进行顶角相连, 他这种模型里面就一定会存在一个全等,对吧?我们当时讲到的一定会存在一个什么样的全等呢?啊?分别是利用左边这个三角形的一条边 和右边的这个等边三角形一条边所连接形成的这个三角形,以及啊,同样左边三角形形成的一条边和右边三角形的一条边所形成的这样的一个三角形, 对吧?这两个三角形一定是全等的,以及他们他们的角是拿来的,是他们中间的这个公共角,对吧?中间公共角是六十度加公共角,以及这边的六十度加公共角啊,是这样的一个手拉手的模型,这个是最常规的,那么这道题目也同样的,他说 a、 b 是 等于六的, b、 c 是 等于二的,然后这个角是三十度,他说把以啊,以 a、 c 为边做等边三角形, a、 c、 d, 那 么这个题目要注意了,他说以 a、 c 为边做等边三角形, a、 c、 d 没有说是往那里做吧, 是吧?啊,如果说他是确定的位置的话,应该他把图直接给你,他没给让你自己去画啊。所以,所以说这个地点呢,可能是在上面,也可能是在下面,对吧?所以要分两种可能性,那么地点也可能在下面,在这边,我们大概先换两个位置啊,有可能是这样子的,对吧? 好,那这边上面的话,那就有可能是这样子的,哎,然后打滑一下,好,地点在这边。那同样的啊,我们要做个辅助线了啊,要用什么辅助线呢?用刚才手拉手的一个模型,我们在他的右边这里,右边这边以 bc 为边,也作为这样的一个短片三角形, 也做这样的一个等边三角形,那这样子,这个点就大概是在这里的,大概是这样子的一个图形, a、 b、 c、 d, e 吧,叫做 e 点,那因为题目让我们求的是 b、 d 的 平方, 对吧?不是让我们直接求 b、 d, 那 遇到这种情况,一般来说啊,可能会把 b、 d 放在某一个直角三角形里面,对吧?你才能会有平方出现嘛,对吧?才会有平方出现,那所以说 b、 d 的 平方可能是在某一个三角形里面的,那么我们先把 b、 d 先连接一下, b、 d 连接完之后再把 a、 e 连一下,对吧?这是手拉手模型里面基本的一个全等,这个我们之前提到过, 那这两个三角形肯定是全等的,对不对啊?这两个三角形肯定是全等的,怎么证明就不说了啊,这个是手拉手模型里面就肯定要会了啊。这两个三角形全等之后,我们就可以知道了,这个 b、 d, 那 就等于 a、 e 了,对吧?全等对应边相等,那 b、 d 的 平方是不是就等于 a、 e 的 平方? 所以我们就把 b、 d 转化为 a、 e 的 平方,所以我们就把 b、 d 转化为 a、 e 的 三角形里面的 啊,这样的一个三角形,那这个三角形是不是直角三角形了?我们来看一下。那这边的话三十度还没用,对吧?三十度,那三十度我们这边来看一下,那因为这边的这个角啊,这边的这个角是一个六十度,那题目里面给了一个三十度条件,那这是不就垂直了, 对吧?这边就是垂直的啊,这里垂直的,所以我们就知道了三角形 a、 b、 e, 它是个直角三角形吧,它是一个直角三角形,那么 a、 e 的 平方是不是就等于这个 a、 b 的 平方加上 b、 e 的 平方, 那因为 b、 e 呢?我们是怎么来的?是做等边三角形来的,对不对?这边是做等边三角形来的,那所以说他的边长为二啊,边长是二,这跟这个题目中的 bc 是 相等的啊,这个就是二, b、 e 是 二,那么还差一个什么呢?差一个 ab, 那 ab 题目也给了 ab 是 六,对吧?那这就出来了,所以 a、 e 的 平方就等于六的平方加上二的平方,对吧?那这边就是三十六加上四啊,等于四十, 所以 a、 e 的 平方等于四十,那么也就说 b、 d 的 平方啊,也就是四十吧,那这就出来了,对吧?那么同样的下面这一题呢,也用同样的方法,也用同样的方法,那么只不过它这个可能求法上会有点不一样啊。 呃,然后他这里也是向下做了一个等边三角形,那么右边这一块啊,右边这一块我们还是向上做,跟刚才一模一样做这样的一个等边三角形向下做,可不可以?你可以自己探索一下啊。这个我就刚没有试, 那这边我们也做一个这样的一个啊,大家这边刚知道这边右边是垂直啊,这边应该是垂直画的,可能有点歪,重画一下 这图可能有点歪啊,那这个叫做一点啊,叫做一点。那么根据刚才我们讲的手拉手模型,同样的 我们把它这个连接一下,对吧?找一下全等啊,是左边三角形的一条边和右边三角形的一条边, 呃,有没有全等呢?我们来看一下啊,正好有了一个 a、 c、 b 啊,三角形 a、 c、 b, 这个三角形和哪一个呢?和这边的这个连接啊,在这里这边连接一下,因为他们现在的旋转点是 c 点了,旋转点是 c 点啊,把这个连接一下, 所以说是这个三角形和这个三角形,三角形 a、 c、 b 全等于三角形。看一下 a、 c b, d, c、 e 吧, d, c, e 这两个三角形全等的。 呃,这两个三角形全等之后我们就知道了啊,就把这个三十度,这个角是转化出去了,所以这个角是不是也三十度,那这个角是不是也三十度,对吧?因为这是等边三角形吗?这个长度是二,这个长度是二啊,这边长度六,我们都标一下。二 啊,都标一下,然后求的是谁呢?求的是 bd, 我 们看 bd 在 哪? bd? bd? bd 在 哪? abc 啊? bd 在 这里, bd 在 这里,我们把 bd 连接一下。 bd 我 们用红色标一下啊, 这个是 bd 啊,因为 b 点在这,对吧?这个是 bd, 那 我们就看一下 bd, 这个怎么求呢? 对吧?因为现在 b、 d 不是 这个。呃,全等三角形里面的边长了,对吧?它就没法去转化了。 b、 d 目前是没法转化了,那不能转化,那就看 b、 d 它自己所在的三角形能不能是一个直角三角形, 对吧?刚才是因为上面是因为 b、 d 正好是在那个全等三角形里面啊,所以说它可以转化,但现在它不是在那个全等三角形里面了 啊,那这里我们就还得往下看一看了啊。因为啊,刚才说了这边是九十度,这个 a、 b、 e 是 九十度,对吧?因为是六十度加三十度吗?他是九十度的。那么 b、 d 所在的三角形目前没有直角三角形,没有直角三角形得自己构造了,怎么构造?把这边往下延长一下, 往下延长一下,把它进行连接啊?这个三角形它恰好是一个直角三角形,对吧?恰好是一个直角三角形。而且呢,呃,题目里面现在 ab, 刚才我们上一道题目是把 ab 转化,上道题目是看一下是把 ab, 这个尺就不要了啊,是把 ab, ab 在 哪? ab 转化成了 db, 是 吧? ab 转化成了 db, 那 现在看一下 ab 可以 往哪转化?根据全等,对吧?那么 ab 它是等于 ab 是 等于谁的?看一下全等 ab 是 等于 d、 e 的, 对不对? ab 是 等于 d e 的, 那么 d e 现在在什么三角形里面呢?在它这个,哎,这里是不是有个直角三角形, 对吧?这里也有个直角三角形吧啊,因为我们是做做做辅助线过来的啊,自己做的一个辅助线,垂直的标一下。自己做了一个辅助线 啊,这里也是垂直的,那现在这里面我们 d e 知道了,是 ab 等于 d e 是 等于六的,然后 e b 是 等于二的吧,然后刚才说了,这边的度数也出来了,这是个什么?三十度的直角三角形,是不是 他是在三十度的直角三角形里面,那么这个 f 点吧,叫 f 点,那所以说这个 d f 是 不是就等于二分之一的 d e 的 对不对?因为三角形用 r t 三角形 d e f 啊,有一个 三十度的角,对吧?三十度组对的直角边等于斜边的一半,所以 d f 就 等于二分之一的 d e, 那 d e 是 转化过来,是等于六,那么 d d f 就 等于他的一半,那是不是三?所以这段长是不是就三好?然后还有一个 b f, 还缺一个 b f, 那 b f 不 就好求了吗?因为在三角形 d e f 里面, d e 知道了, d e 知道了,然后这个 d f 也知道了,那么 e f 不 就可以求了吗?对吧? e f。 当然我们求的是 e f 的 平方, e f 的 平方 是等于 d e 的 平方,减去 d f 的 平方就是三的平方,等于三十六减九等于二十七 啊,那么 e f 的 平方就是二十七,那么 e f 开个根就是根号二十七,那要是会化简的话,那就是等于啊,三倍的根号三, 等于三倍的根号三,那么这样子 e f 知道的是三倍的根号三,那么 e b 呢?又是等于二的,对吧?那么 b f 不 就出来了吗?所以 b f 就 等于 e f 减去 e b 吧, e f 减去 e b 等于三,根号三减去二,那 b f 就 出来了, 那么在这个下面这个三角形里面, b f 有 了,是三根号三减去二的,而 d、 f 呢是三,所以 b d 的 平方是不就等于这个 d f 勾股定律, d、 f 的 平方加上 b、 f 的 平方, 是不是就等于 b、 f 的 平方是三的啊? d、 f 的 平方等于三的平方,加上 b f 的 平方,加上三倍的根号三减二的平方,对吧?这边自己计算一下啊,算一下,这边就是等于, 呃,我看一下啊,等于三三九九,四十啊,四十减去呃,十,呃,十二倍,十二倍 减去十二倍的根号三,对吧?我看一下是不是四二六啊?对,四十减去十二倍的根号三 啊,那么这个就是 b、 d 的 平方啊,所以这道题们应该是两个减,一个是 b、 d 的 平方,等于四十啊,刚刚上面算的一个是 b、 d 的 平方,等于四十减去十二,根号三啊,这两种情况 用的是手拉手模型啊,做的稍微复杂一点啊,稍微复杂,第一种情况很好理解啊,上面这个情况好理解,主要下面这个情况他用了一个双勾股,对吧?啊,这样的一个直角三角形,然后下面呢还有个小的直角三角形,两个直角三角形,主要这边辅助线会比较多一点。
 11:39查看AI文稿AI文稿
11:39查看AI文稿AI文稿关于全等的这个模型,大家怎么理解?模型这个概念就是一个模板,一个模板感觉差不多 他就像一个包一样,就他是一个工具包啊,他能帮助你把一些结论快速的得到,不影响你去思考啊,所以这个叫模型。在看到一些结构的时候啊,或者说看到一些特殊的这种几何的构型的时候,我们可以通过这种模型的结论和技术, 他能帮我们直接抓取一些特殊的结论。这个事就是模型,比如说大家在小学,实际上在其他的一些数学的分支里面见过模型, 比如说组合的模型,组合技术里面大家就见过模型,举两个例子啊,大家马上就能明白这是模型,比如说大家有没有印象插板法,插板是什么意思啊?怎么理解的? 在空里面做组合对吧?或者做排列对不对?所以这叫插板法,比如说捆绑,捆绑法怎么用啊?几个人站在一起对吧?那我把他们视成什么? 一个整体是成一个整体,所以但凡看到这种结构,你是不是就想到用捆绑法,对吧?所以一样的,对于这个几何的模型而言也是一样的啊,看到一些结构,我们马上就要反映出来这个东西应该是一个模型,它能帮助我们提供出来一些结论啊,所以 这里面呢,我们对于几何的模型啊,几何的结构这个事是最重要的啊,那么这里呢,我们只讲一些非常简单的基本的模型啊,就是够大家初中还有高中还有联赛的基础使用的啊。那么对于全等的模型呢,我们能看到全等的模型呢,实际上核心就包括六个, 这六个模型能帮助大家解决刚才我们说的这个啊,只要出现了特殊结构,马上抓取特殊结论,他能帮助我们解决百分之八十这样的问题。第一个,对于全等的模型呢,我们将他们分成三类, 第一类呢,是能直接提供给我们全等,就是说看到了这个模型以后,马上就产生全等,不产生全等,你这模型就没有用上的啊,这是第一类,那这一类呢,我们一共有三个模型啊,第一类,这个第一个 叫手拉手模型,第二个呢叫做半角,第三个呢叫倍长中线。那么第二类呢,就是说在这个全等的结构中,他只提供给我们角相等的条件,全等除了角相等条件还有什么条件? 边相等的条件对吧?好,所以只给我们提供角相等的条件,那我们想产生全等,你就得找边,对吧?所以这里面呢,角相等条件只负责提供这个事的。有两个模型, 第一个叫三垂直,第二个叫做一线三等角。那么第三个还有一类,他只提供给我们边相等的模型,所以这个模型叫做截长补短。那有的人说,哎,老师,你这个倍长中线和截长补短,你这不是辅助线吗? 辅助线它仍然也是模型提供给我们的结论和技术之一。说白了,你看到了这种结构,你想到连这个辅助线也没问题。那么大家觉得模型最重要的有哪些?或者想了解这样一个模型最重要的有哪些点? 你要先了解这个模型是什么特征,显然说的非常好。第一个啊, 首先呢,这些模型大家能看到这些词并不是数学里面的官方词汇,什么叫官方词汇?比如说全等三角形,你不能叫一样三角形,对吧?所以 这些词他不是官方词汇的意思就是这些词大家在我这你听到的是这些词,可能在别的书上你就看到别的词,但是本质上 特征一致,那他就是一个模型,能理解啊,所以别说什么王老师讲的手拉手,那个老师讲的脚拉脚,所以我们对于模型的理解最核心的第一个问题叫做特征, 模型的特征是我们要关注识别的啊,那么有特征以后还要了解模型的什么,你光认识特征了,用出来的方法,对吧?也就说白了,这个模型带给你的结论以及这个结论的证明路线,所以这是我们最关注的问题啊。第一, 一个模型的特征是什么?第二,这个模型的结论以及他的证明的路线是什么?所以接下来呢,我们从手拉手模型开始说起啊, 手拉手的特征教材上有写叫做什么共顶点的两个顶角相等的等腰三角形。第一个关键词叫共顶点的共顶点的 两个顶角相等的等腰三角形,只要产生了这个结构,它就是手拉手模型的特征,这就是手拉手模型的特征。 第二个特征啊,顶角相等。那么现在给大家一分钟的时间,在你自己的笔记上随便画一个满足要求的结果。接下来我画一个图,你来识别对应的特征,共顶点的顶点相等的啊。 首先一条边两条边一个的二三角形,再来一个顶角相等的一条边, 两条边,一个等腰三角形,那么这两个等腰三角形,现在大家把头对准这个共顶点,左手就是这个点和这个点,对不对?那右手呢? 这边和这边对不对?来连一下,连完以后这两个点一连,这个就是手拉手的结构。 来连上啊,你在你自己的图里面找着左手和右手,不用看我这个图画了啊,好,所以这个结构啊,这个结构就叫做手拉手。 那么这个共顶点呢?我们给他标记一下啊,这个共顶点我们给他记成一起记啊,你的符号跟我一致,这个共顶点你要记成 a, 左手 b, 右手 c, 另外一个三角形,左手 b 撇,右手 c 一 撇。那么这个时候我们能看到有没有全能啊?有,第一个,哪个三角形和哪个三角形全能, a、 b、 b 撇和 a、 c、 c 一 撇,全能。好,把它记起来啊,全能找到了第二个条件, 大家能看到我在里面连的这个拉手线, b、 b 撇, c、 c 撇这个拉手线,这个拉手线给大家 五秒钟的时间,把它延长出一个焦点,如果你的拉手线没有焦点,就延长出来,有焦点无所谓啊,比如说你看我这个没焦点,对不对?我把它延长出一个焦点来,交在这两条拉手线延长出一个焦点, 让我这两条紫色的线有一个焦点。如果你已经有焦点了,没关系,如果没有焦点,现在让他有一个焦点,不要玩赖啊,不要看我画啥,你们画啥图,你们就画你们自己的。明白,画完了 把这个焦点设成 m, 仔细看啊,这个焦点 m 会有一个交角,对吧?这个交角不管是钝角还是锐角,你看你自己的这个大的三角形的顶角, 它一定会有,要么是这个锐角,要么是那个钝角,跟这个三角形的顶角是一样的。 b、 m、 c 和这个等腰三角形的顶角 b、 a、 c 是 一样的。 如果你画的是两个钝角顶角三角形,那你就找那个钝角,锐角就找锐角。我就说 b、 b 撇和 c、 c 撇的交角和顶角相等,不管你交角在哪,这个角一定和顶角相等。来 说一下为什么?仔细看啊,倒角的技术,我们之前讲过倒角的方法论,倒角方法论有哪些?内角外角一套,全等,全等,全等可以,对吧?还有什么?平线,还有 同角的与不角,非常好,同角与不角在这个图里仔细看啊,全等告诉我们,这个角 abb 撇等于 acc 撇,对吧? 全能给的,那么 a、 b、 b 撇等于 a、 c、 c 撇,同时 a、 c 和 b、 m 交于这个点,对不对?所以还有一个对顶角, 对吧?那么同角的与补角相等,这就是同角的补角相等,对吧?三角形里面,双弧线的角加单弧加叉一百八, 在 a、 b 这个焦点的过程中啊,在这个三角形里差加单弧线加双弧线一百八,所以这两个双弧线的角一样,对不对? 明白明白,好,所以这是第二条结论,叫做新三边,或者叫做拉手线,或者也叫做第三边啊,或者叫新三边,都可以, 这个新三边的夹角等于顶角,就是你新拉出来的这条边夹角等于顶角。说一下啊,第一,我为什么让大家自己画这个图? 大家思考一下,为什么几何模型要比组合的模型或者代数的模型更复杂,因为 大家处理你的几何模型是需要你在几何的途中观察的,对不对?就这一个模型, 你跟处理代数的模型在脑子里的处理器用的地方就不一样,你处理图用的不是 cpu, 是 gpu 图像处理器,对吧?大家的图像处理器不是一个规格的。 很多时候你会发现,虽然我讲了手拉手模型,但是这图一模一样的图转一下你就看不出来。所以几何模型需要大家去理解, 这个图形在不同位置,不同大小,旋转到不同角度产生的结构,大家都得能看得出来,所以我让你们自己画,就转成什么样,你都得能看得出来。这是一个手拉手。如果刚才你没找到这个角, 那么你现在把这个角找着,看一下你的全等带来的是哪个角。先不用研究证明,就先看这个事。几何是初中几何证明里面啊,是初中数学里面最深刻的部分。 他不是说难,是说你的观察是需要做积累的。什么叫观察需要做积累?有的同学比如说先天硬件不错,一看就能看出来,有的就怎么看不出来,这事谁也帮不了你, 所以怎么办?怎么弥补这个事,就多练多看就行了。
17卓易数学









