粉丝1158获赞4354
相关视频
 04:09查看AI文稿AI文稿
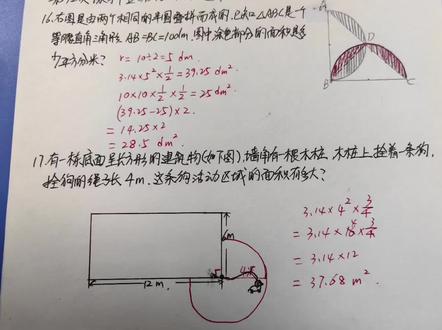
04:09查看AI文稿AI文稿大家好,我是讲数学的小红老师,今天我来讲解六年级上册数学第七十二页练习十五的第十六题和十七题。 第十六题右图是由两个相同的半圆叠拼而成的,已知三角形 abc 是一个等腰直角三角形 a、 b 等于 b、 c 等于十分米。图中图色部分的面积是多少平方分米? 那么在这条题当中呢,他要求的是涂色部分,那么这个涂色部分可以怎么来求呢?我们可以这样来看,我连接 b、 d, 也就是把中间这个叶子形的 这个阴影给他分成两部分,分成两部分,然后呢,那我们看这个阴影部分在这个半圆里看。好啊,在这个半圆里,他的阴影部分是这么两块, 看懂了吗?应该是这么样的两块,那么另一个半圆里,这两块的面积与这两个红色阴影的这个斜杠的阴影面积应该是相等的,所以我可以先求这一部分,然后再乘以二即可。 那这一部分呢,它就应该是半个圆的面积减去一个三角形面积,而这个三角形面积又是整个大三角形 a、 b、 c 面积的一半。 所以按照这个思路,我们可以先来求半圆的面积,那么 a、 b 和 b、 c 呢?是十,这个十呢,就应该是半圆的直径,所以半径就应该等于十除以二等于五分米, 然后用三点一四乘以五的平方,再乘以二分之一,就等于三十九点二五 平方分米,这是半个圆的,然后再减去一个三角形面积,这是最大的一个三角形面积的一半,然后等于二十五平方分米,之后用三十九点二五减 需二十五,也就是求这个红色的阴影他的一份,那么因为整个图形阴影呢,占了两份,所以他乘以二就等于十四点二五,乘以二等于二十八点五平方分米。 这是第十六题,第十七题有一栋底面呈长方形的建筑物,如下图, 墙角有一根木桩,这了这木桩说木桩上呢,拴着一条狗,说拴狗的绳子长四米,也就是这根绳是四米的。 问,你这个狗的活动区域,它的面积有多大?那么你想这个绳子是四米的,那我把这个绳子拉直啊,拉直那, 那么这个狗所能活动的区域就是以四为半径的。看好到这到这到这 啊,他能不能扯到这个墙里边去,走不到,走不到里面去啊。所以呢,这个狗的活动区域就应该是以四为半径的。一个圆面积的多少呢?这个角是直角吧,所以呢,是整个圆面积的四分之三, 那也就是说用三点一四乘以四的平方,这是整个圆的面积,然后再乘以四分之三,等于三点一四,乘以十六,乘以四分之三, 所以等于三点一四乘以十二,就等于三十七点六八平方米。
56讲数学晓红老师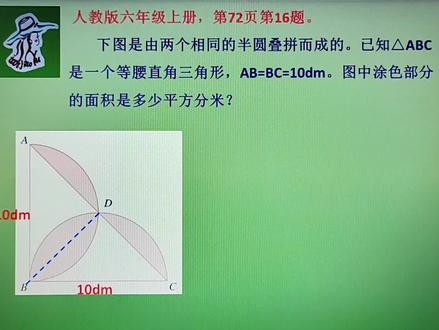 01:18查看AI文稿AI文稿
01:18查看AI文稿AI文稿我今天讲的是人教版六年级上册第七十二页第十六题。下图是由两个相同的半圆叠拼而成的。已知三角形 a、 b、 c 是一个等腰直角三角形 a、 b 等于 b、 c 等于十分米。图中图色部分的面积是多少平方分米? 我在这里面加了一条辅助线,这样的话呢,这个 s 半圆,这个半圆的面积减去这个 三角形的面积 b、 d、 c, 那就得这两块小的应分涂色面积好,那 s 半圆,这个半圆减去上面这个三角形 a、 b、 d 的面积,也就是这两块小的涂色部分合起来就是整个涂色部分,也就是半圆加半圆是整圆,整圆减去这个大三角形的面积,就是这些涂色部分的面积, 也就是派儿平方减去十乘十除以二。最后结果呢,就是二十八点五平方分米,你看明白了吗?
122周游谈教育 02:54查看AI文稿AI文稿
02:54查看AI文稿AI文稿这个视频我们来说说比例尺。在绘制地图和其他平面图形的时候,需要把实际距离按照一定的比例扩大或缩小,再画在纸上。 比如,我们要画一幅操场的平面图,这个操场的长是八十米,宽是四十米,肯定不能在图纸上画这么长,这就需要我们按照一定的比例缩小。我们将长定为八厘米,宽定为四厘米。画在纸上, 我们将实际的长度八十米和四十米成为实际距离图。纸上的八厘米和四厘米称为图上距离。图上距离与实际距离的比, 我们就叫做这幅图的比例尺。我们这幅图中八厘米代表八十米,也就是涂上一厘米,表示是记十米, 也就是一千厘米。这幅图的比例是一比一千,他表示涂上距离是实际距离的一千分之一, 也表示实际距离是图上距离的一千倍。我们在计算比历史时,可以这样算,八厘米比八十米等于八厘米,比八千厘米等于八八千等于一比一千。当然,我们也可以写成分数形式, 计算比例尺时一定要注意单位统一。另外,我们一般把比例尺的前线化为一,在绘制地图或其他平面图时,都要标出比例尺,例如比例尺一比六百万或六百万分之一, 这是数值比例是还可以标出这样的线段,像这样用一条线段表示图上距离与实际距离到关系时,我们 把这样的比例吃叫做线段比例吃。他们都表示涂上一厘米的距离相当于实际距离六十千米。这是一幅北京地图,这个线段比例是表示涂上一厘米的距离相当于实际距离五十千米。 我们现在将线段比例值转化为数值比例值,一厘米比五十千米等于一厘米,比五百万厘米等于一比五百万。 我们看这三幅中国地图,这三幅地图都是把实际距离按照一定比例缩小后画出来的,虽然三条线段的长度一样,但表示的实际距离却不同。 在现实生活中,科学家会根据地图的用途所表示地区范围的大小等等不同情况,选用不同的比例尺进行绘图。这是我们都非常熟悉的笔记本电脑,在这个笔记本电脑中有很多 揭秘的零件,在设计时,为了大家看的更清楚,需要把这个非常精细的零件按照一定的比例放大以后画在纸上。背幅图的比例尺和前面我们学习的比例尺不大一样, 大家表示涂晒的距离是实际距离的六倍,也就是涂上六厘米代表实际的一厘米。现在你认识比例纸了吗?赶快做几道题试试吧!
2752赖课数学 02:01
02:01 10:04查看AI文稿AI文稿
10:04查看AI文稿AI文稿今天我们来学习一下小学六年级数学上册说这个半年, 描一下这个半年跟哪个半年?跟这个半年,这个半年 大家可以描好一点啊,我这手有点抖啊。这两个半年,嗯,叠拼而成的。已知三角形 a、 b、 c 是一个等腰直角三角形,等腰直角啊,直角三角形,这个是直角三角形啊。 a、 b 等于 b、 c、 a、 b 这个十,这个也是十,嗯,这两个都是十的话,等同于这个半年的直径是十,对不对?图中图色部分的面积是多少平方?后面也就是说要求图色的话,我们来观察一下,观察一下这个,如果我们把这条连接上来, 这刚好是不是这个三角形的这个 a、 c 为底边的一个高 这条啊,对不对?嗯,就把这个分成两半,对不对?那好,如果我们把这个一,嗯,这个写二,这个三,这个四,分成这个几小半,一二三四,嗯, 分成四半啊,分成四半,我们这条要画上去啊,这样把它切分开来。好,我们一和二连一起来看啊,一和二 一,一和二,一和二连立起,我们就没有办法可以直接把它求出来。一和二,一和二引领,我们把它当成一个引领部分呢。一和二会等于什么?这个 半年的面积减去这个三角形,这个三角形对不对?这个三角形,也就是说 a、 b、 d 这个三角形面积,对不对?也就是说这个的面积哈,面积 会等于什么?会等于这个半年,半年的,半年的面积,嗯, 半年也是半年,也是半年的面积减去这个三角形 a、 b、 d 的面积。对于 x 三角形 a、 b、 d 的面积啊,是不是?这个这个半圆减去这个 a、 b、 d 的面积,是不是剩下一和二?是不是剩下一和二,嗯, 是吧?嗯,然后这个,这个我们就有办法求了,对不对?是不是有办法求?嗯,那 然后呢?我们再来看三和四的面积,三加四的面积会等于什么?也就是半年, 也就是说这个的这个半圆的面积减去这个内部三角形,这个三角形的面积,对不对?这个三角形的面积,是吧?减去 x 三角形 b、 d、 c、 b、 d、 c 的面积啊,是不是? 是还是不是?嗯,那好,那要求的是什么?涂色部分的面积,涂色部分面积是不是一加二加三加四的面积啊? 是不是上面加下面的这个面积,那自然就会等于 x 半年加 x 半年啊? x 半年加 x 半年, 上面加下面动力也是半年,也就是说也是整个圆的面积啊,一个圆的面积减去啊,三角形 a、 b、 d、 a、 b、 d, 再减去这个三角形 b、 d、 c。 啊,这个刚好是减去一个大三角形,也是刚好是减去 a、 b、 c 的 三角形 a、 b、 c 的面积,是不是?这样我们就回到球了,对吗?那就是一个圆的面积等于八平方,太二了。二, 直径是十,那二就是五,对不对?五的平方再减去 s 三角形 a、 b、 c, s 三角形 a、 b、 c, 那就二分之一十乘十,对不对?二分之一 乘十,再乘十,嗯,这个底,这个高度力,嗯,这样我们就求出来了。嗯,那答案我们把它求一下, 这个就是二十五乘一,三点一四,三点一四,七十八点五,这是七十八点五,减去这个五十,对吧?五十,嗯,最终得到的结果是二十八点五,嗯,单位平方分米, 这个要理解清楚啊。好,接着我们来看课本的第十七题,有移动底面成长方形的建筑物,从长方形的建筑物墙角有一根木桩,墙角有一根木桩,木桩上拴着一条狗,拴着一条狗,这是一条狗啊, 三绳的绳长是四米,也就是他拉直之后,这条绳长拉直之后,他是四米啊,四米,那这条狗的活动区域面积有多大? 那我们我们来简单画个草图啊,简单画个示意图,比如说这个,这是墙的一面啊,这个是墙的另一面啊,然后这里呢有个有个木桩啊,然后绳子拉长,是这样的, 这个,这个这个长一点,这个绳长是四米,那他的活动范围是不是他就成一个圆,对不对?成一个圆,成一个圆,但是这个是墙顶住了,他里面进不去了,对不对?是不是? 嗯,然后它的呢?绳长是四米,那它的活动分为数数这个阴影部分,我们来看一下,这刚好四分之三的圆, 四分之三的圆的面积,是不是?然后呢?他的半径刚好是就是四,对吧?那弧度面积就是四分之三 x, 嗯,那就是 四分之三了,那就四分之三乘一,这个是派二平方,对不对?派乘一,四个平方,是不是十六, 或者你写四个平方啊?大家看得懂一点啊,那这个把它求出来,这个十六十六跟这个约分是算是十二等于十二派啊,十二派把它求解出来啊,这个就是他活动的面积,大家一定要。哎,这个要怎么怎么说呢?哈, 就是灵活一点啊,然后呢?根据,根据我,我们要想象到实际,实际当中啊,那就就十二乘一三点一四,就等于三十七, 等于三十七点六八,单位平方米。好,接着我们来看课本第十八题, 一根绳子长三十一点四米,用这根绳子在操场上围出一块地,怎样围面积最大?请你画一画绳子哈。围一块地,我们肯定是围成什么?围成圆形的面积会是最大?这根绳,这根绳这样围过来, 围成一个圆的面积最大。为什么?我们想如果围成一个,一个中花园, 这个怎么说?嗯,正方形它是边长,从边长丢裂边长从边长,那你也可以去算一下啊,可以去算一下,如果围成的是一个正方形,它的边长是 多少?嗯,然后围成一个圆啊。围成一个圆,我们也可以求出他的面积,是不是因为我们知道周长,这个周长是三十一点四,对吗?三十一点四,我们自然能够求出他的,他的半径,对不对啊?然后自然能够求出他的面积。我们面积, 然后和正方形的比较,正方形看四边都相等,对吧?求出他的什么?求出他的边长,然后边长和边长求出正方形面积,然后对比一下,那哪个大,肯定是围成圆的面积大,对不对?最终比折是不圆的面积大, 这个自己自己大家自己去算一下。好,然后你这题要怎么解答呢?就答围乘圆的面积最大。嗯,围乘圆的面积最大。这样就可以了。看第二题,为什么草原上蒙古包底面是圆形的,底面是圆形的?为什么绝大多数植物的根和井横截面是圆 的?根据上面的研究,请你试着解释一下啊,一样的道理,他会达到面积最大度的草原上蒙古包底面为什么要做成圆形的啊?因为同等的材料,同等的材料, 同等的材料,看围成圆啊,围,围成圆的面积最大, 这个是解答这个蒙古包的啊,这个是解答这个蒙古包的。为什么会成圆的啊?为什么绝大多数植物根和颈横截面积是圆圆形的啊?这个根和颈 你乘的面积是圆的啊,这个什么?因为他是圆形啊,就会导致这个这个面 最大,面积最大,面积最大,那就 最方便什么?嗯,就是最大限度的,最大限度去吸收水,根是不是要吸收水,吸收水和养分啊?这样写就可以了哈。 啊,你能够写出写出这个基本上就让你对了啊, 也就说他,你要知道他为弄成圆呢,他就最大啊,面积最大,达到面积最大,我们点到这个点基本上就那么对了啊,因为我们也不是说专业的,专业的他他这个说 这个植物需要需要什么,但是我们知道他肯定需要水用力,肯定需要养分啊。嗯,这样就可以了啊,好,那就这样。
48傲世教育 00:21
00:21 01:27查看AI文稿AI文稿
01:27查看AI文稿AI文稿比例尺应用题,在一副比例尺为一比二十万的地图上,梁德甲乙两地的距离是六厘米。在另一副比例齿为一比四十万的地图上,甲乙两地的图上距离为多少厘米?读完这个题,我们发现甲乙两地的距离被 画在了两副比例尺不同的地图上。但是不管是画在了哪幅地图上,甲乙两地的实际距离是不变的。所以我们根据第一幅图的比例池一比二十万和第一幅图的图上距离六厘米来求出他的实际距离。 因为图上距离比实际距离等于比例尺,所以实际距离就等于图上距离。除以比例尺,那么我们用图上距离六来除以第一幅图的比例尺二十万分之一 得到实际距离,再用实际距离和第二幅图的比例尺一比四十万,那么我们来求出在第二幅图的图上距离。那么我们要根据 图上距离等于实际距离乘以比例尺,这个实际距离是不变的。在乘以第二幅图的比例尺四十万分之一, 得到第二幅图的图上距离三厘米。解这个题的关键就是我们要把比例尺的公式灵活运用,赶快收藏。
824小学数学慧慧老师
猜你喜欢
- 5182野生茜茜酱












