三角形脑筋范围探测怎么做
粉丝61获赞513
相关视频
 07:58
07:58 00:56
00:56 10:30
10:30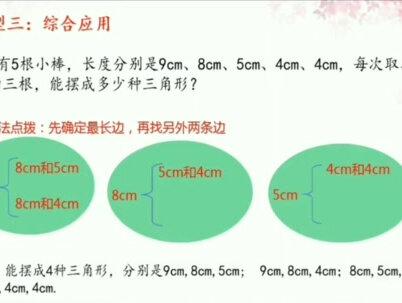 03:25查看AI文稿AI文稿
03:25查看AI文稿AI文稿大家好,欢迎来到萤火课堂,今天我们学习三角形的判定问题,体型一,下列三根小棒能拼成三角形吗? 根据三角形的判定定理,较短的两边之和大于第三条边,很显然这三根小棒是不能组成三角形的。我们通过一个动画加深印象, 你发现了吗?旋转过程当中,他们始终不能阻止分量型。 体型二,给定两条边 ab, 判断第三条边 c 的长度,此时 c 的曲值范围是大于 a 减 b, 小于 a 加 b。 已知三角形的两条边分别是三厘米、七厘米,第三条边可能是多少举整数,我们先将这两条线段相交为一个顶点, 在三厘米线段不停的旋转的过程当中,会产生出不同的三角形, 比如在此刻只需要再加一条线段,例如红色的边就可以组成三角形,但当蓝色边继续旋转的过程当中,红色边会逐渐的变长, 接着再变长,而在此刻是达到最长,最长是七厘米加三厘米,但此时已经不是三角形了。若是蓝色的短 边继续往下旋转,那么红色的边会越来越短, 此时达到最短红色边仅仅是七减三等于四厘米,但此刻也不能组成三角形, 所以红色的边的曲值范围最长不能超过七加三,最短不能低于七减三,并且两端不能取等于号。体型三,综合应用 有五根小棒,长度分别是九厘米、八厘米、五厘米、四厘米、四厘米,每次取其中的三根能摆成多少种三角形?既然是摆成三角形,必然要满足 两短边之和大于第三条辫,那么我们不妨采用控制辫量法,先确定最长边,再找另外两条短边。 若是最长边为九厘米,此时另外两条短边只需要满足相加大于九即可。于是我们可以选择八厘米和五厘米、八厘米和四厘米两种三角形。 那么当最长边为八厘米的时候,另外两条短边可以选择五厘米、四厘米。 当最长边选为五厘米的时候,另外两条短边只能是四厘米和四厘米,于是我们一共摆成了四种三角形。要注意将四种三角形的三条边分别列出来。
 02:58
02:58 10:38
10:38
猜你喜欢
- 2496以父之名












