尺规作图对称轴怎么画。没有刻度来画
粉丝1829获赞2.9万
相关视频
 07:16查看AI文稿AI文稿
07:16查看AI文稿AI文稿好,我们接下来开始系统现在讲一下隔点无刻度尺作图啊,我们有些地方他每年都会考,那我们首先把基本的六大做题手法啊,给大家讲一下。 那接下来我们先看如何做平行线,是吧?我们这种题型他只有一个无刻度咫尺啊,别的啥都没有。首先我们看第一个 ab 是格点,然后做 c 点,关于 ab 他平行线,那我们做平行线要注意什么呀?第一种手法就是平移嘛, 比如说我们这个 c 点是不是可以看作 a 点,向上平移三个单位啊?所以我们把 b 点也向上平移三个单位,一二三,哇,就这个点,然后连接 c 点跟这个点,这个线就符合要求 啊,这就是最简单的一种,能够直接看出来,然后大家需要系统资料,是吧?看这里。好,接下来我们看第二个 ab 是边的终点, 然后做这个 c 点,关于 a b 他平行线,那么第一种方法还是平移吗?我们看一下把 a 点平移到 c 点,是不是向左平移一个单位,向上平移半个单位啊?啊?所以说我们 b 点也一样,向左平移一个单位, 然后向上平移半个单位,他是不是就这个隔点,他正中心呢?是吧?那么正中心怎么做出来啊?因为小格子都正方形嘛,连接两个对角线,那么这个焦点 他就是必点,向左拼一个单位,向上拼半个单位之前连接 c 点跟这个点, 是吧?这个线就是平行线,然后我们做平行,还有没有其他的方法啊?也有,我们可以用相似是吧?或者是平行线分线段成比例, 常用的就是 a 字相似,用相同的比例把这个平行线找出来啊,那我们还是以这个图,你看我们连接 ca 延长,他是不是会到达这个格点呢?是吧?因为 a 点是这个线,他终点嘛,然后我们再连接,是吧?这个点跟 b 点 这延长出去,他会到达哪个格点啊?我们这个点地点到地点是不是向左平移一个半单位,向上平移两个单位啊?所以等被延长币地的话啊,应该会达到这个点,这个 b 点是第一, 他的终点就是数格子,那我们这个 c 一是不是就是 ab 他的平行线啊?啊?此时 ab 是这个三角形, c d 一他中微线啊,就是一个相似的思维,只不过这个相似 b 是一比二。 那接下来我们再看一个相似,比他不是一比二了?好,我们看第三个,这个题目还没改,这就不是中间啊。 ab 是隔点还是做 c? 关于 ab 他平行线,那我们首先也是用相似的这个手法来做,我们如果连接 ac 的话,把延长出去,是不是会加到这个点啊?这个隔点, 并且也穿过这个格点,假设这个地点,是吧?他比他是不是一比二的关系啊? 所以我们连接 bd 的话,只用找到 bd 他的三等分点就行了。那么 bd 这个线他的三等分点在哪里啊?是不是在这里啊? 哇,我们看竖排就行了,一个隔点,两个隔点,三个隔点,选择于这个呈现他的焦点就是三等分拣, 然后连接 c 点与一点,把这个线也平行于 ab, 那我们这个图能不能直接平移来做 也是可以的,你看我们 a 点平移到 c 点是不是向右两个单位,向上一二三四四个单位啊,我们都是隔点的话,是吧?就平移简单一些,所以我们 b 点平移两个单位到这里,然后 向上平四个单位,一二三,发现格子不够了,是吧?应该到这里才行。那我们在考试中,如果格子不够,我们不能私自把这个格子是吧给扩大, 所以说 b 点平移不行, b 点平移不行,那我们可以找别的点平移啊,找到这个线 ab 中间的特殊点, 那我们也发现特殊点也没有呀,没有隔点怎么办呢?找终点,这个终点还是挺好找的,你看我们 ab 水平距离一二三四五,那么终点是不是在这个终点啊?这个格子终点,这个点他就是我们这个格子正中间,所以我们把这个点 向上平移四个单位,一二三四,再向左平移两个单位,一二哇, 那么应该在这个格子,所以我们找到这个格子,他终点啊,也就是正中心,中心啊,中心点啊,那么还是跟前面一样连接对角线这个点就行了啊。假设地点啊,那么 cd 这个线, 他也是我们 ab 他的平行线。好,那么接下来看第四个啊,这个就比较复杂一些, 做这个基点,关于 ef 他的平行线,那么这个基点是 ab 与这个啊,这个少写个字母与 cd 他的焦点,那么 abcd 是隔点,那基点就不是隔点了, ef 都是隔点怎么办呢?是吧?我们做平行线第一反应还是平移嘛,那我们看一点平到几点,他不规则是吧?所以我们看 看一点平移的 f 点是不是向右一二三四个格子,向上一个格子啊,所以我们如果把基点 也向右四个格子,向上一个格子就可以了,但这个基点单独平移我们做不到,我们可以把这个,对吧?这个东西整体平移嘛。啊?整体平移之后,基点也是整体平移过去,所以我们 a 点是吧?又是上一在这里, 这是 a 铁点,然后 b 点又是上一一二三四在这里啊,然后 c 点一二三四 这点平行到这里,地点一二三四在这里。然后我们还是连接,把 a 撇、 b 撇,再连接 c 撇。第一撇 啊,这个焦点就相当于机撇,也是又是上衣,然后连接几点跟这个点,他就是我们 ef 平行线 啊。那我们来总结一下,做平行线最好用的就是平移嘛,直接平移,平移的方向和距离一样,保持一致原则,然后如果平移解决不了,就用相似来做,他就是我们需要平移的比例,是一致的原则 啊。那么我们关于平行线就讲到这里,那么下节课我们就做垂线该怎么做? ok。
2168数学唐老师 13:54查看AI文稿AI文稿
13:54查看AI文稿AI文稿同学们好,欢迎来到大众数学啊,前面一次课呢,我们已经知道 怎么样去画一个图形的对称轴,是吧?那么画对称轴啊,实际上就是画图形一些特殊线的垂直评论线,是吧?啊,那么利用垂直评论线的画法呢,我们基本上就解决了。 好,那么现在呢,我们来看这样一个问题,好,我们椅子一个图形啊, 而且还知道一条直线。好,那么现在我们的问题是,我们想在这个直线的字一侧 再画出一个图形,让我们画的这个图形呢,跟这个图形关于这条直线 l 对称。 好,也就是说现在我们椅子一个头型跟对称轴,我们要画他的另外一个部分啊,就是与他对称的另外一个部分,是吧? 好,那么这个问题呢,我们稍微回忆一下,我们发现我们在小学的时候,我们做过,但是那时候呢,我们怎么样呢啊?我们在方格子上做过, 但是现在呢,我们这里没有换个字,是吧?没有换个字我们该怎么办? 那么在那个时候,我们在方格子做的时候啊,我们是怎么做的啊?我们首先回一下,那在我们读小学的时候,我们在方格子做这个图形的轴对称图形,我们是不是 找几个点呐?是吧?好,实际上呢,在那个时候啊,我们就会运用一种方法,就是什么呢?找关键点, 因为点是构成这个图形啊,最基本的元素,那么我们只要知道一个图形,它是有哪些 关键点不成的,我们把这几个点来找出来啊,那么我们的思路就出来了,是吧?好,那么找关键点啊,我们知道 直线,我们用两个关键点是不是就可以了?那,那么这里呢是个三角形,那么三角形呢?我们需要几个点?什么?三个就可以了?好,分别是他们什么点点?好,那么思路已经出来了啊,好,那么这个思路有了, 接下来呢,我们再看看,那既然我们要找关键点,那意思就是说我们要找出 abc 这三点关于 l 这条直线的对称点,对吧?好,那么对称点怎么找?好,那么 我们最后一个问题, 如果我们把这个问题解决了啊,那么我们的整个问题呢,我们就解决了,是吧?好,那么至于这个对称点到底怎么找?我们来这里看一下啊。 好,比如说有个点 a, 这里呢有一条直线,现在我们在这边找一个点啊,比如说 a e p。 好,如果这个 a a 撇是关于 l 对称的。好,那么我们看看 他们之间有什么关系?好,首先呢我们把它连起来,那,哎,哎, 这个线段跟 l 什么关系呢啊?从前面我们是不是知道他们一定怎么样啊? 垂直是吧?啊?垂直,因为对称走就是他们的垂直平分线,对吧?好,那又是垂直,而且呢又是平分的,你说他跟他怎么样啊?要相等 是吧?两个问题啊,就是背成轴又是他的垂直平衡线啊,也就是 l 要垂直 a a, 是吧?啊?而且 l 呢平分 a, 那么这个问题我们通过前面的学习,我们是不是都可以解决呢?好,那么现在我们具体的来看啊。好,那么这个 a 点 好,首先呢,我们画出这个 a 关于这个 l 对称的另外一个点出来,是吧?好,我们先用圆规来。好,首先呢我们要画跟 l 垂直的线,是吧?好,意思,就是画垂线。 好,然后希望你可以为圆形 画一条湖。好,那么这条湖呢,跟这个 l 相交在两个点上是吧?好,然后呢,我们再分别以 这一个点啊,我原先画一条胡,同样呢,再以这个点回原形画一条胡啊, 那么他们两个相交在这个点,那你们讲,我们连连 a 一根这个点好,我们把它连起来。好, 好,那么这一条线跟 l 是不是一定是什么 垂直的是吧,因为我画的实际上就是这一条线段的垂直平衡线是吧?啊,前面已经介绍过了啊,那肯定是垂直的,那第一个问题垂直的解决了, 第二步我们再来解决一下平分的问题,是不是就可以了? 那解决平分啊,那意思就是 a 到这个的距离跟另外一个点到这个距离是一样的,是吧? 那只要我们用圆规把它量就可以了。好,注意啊,这里不能用尺量是吧?因为我们说此规作图,这个尺子呢,不能有刻度是吧?那么我们用圆规来量啊,好,现在呢,我们把 a 到这个的距离把量出来,你看这么长,是吧?紧接着呢,好,这里,那么我们要找的这个 a 点啊,关于这个还要对称的点呢啊,就是这个 a。 好,这一点呢,我们也做出来了,是吧?思路呢,我们也有了。好,那么下面呢,我们接着来找 b 点。好,用同样的方法啊,好, 然后呢,我们先啊,以臂为圆形的,这画一条弧,好 啊,画一条胡啊,为了不死的,这些线条密密麻麻啊,让人头昏眼花啊,我只画跟他相交的这个地方了啊,啊, 到这里啊,用这条线画的稍微短了一点点啊,每次我们把它裹上啊, 啊,这里啊,那么这两个交联呢?在这里是吧,那么现在我们用另外一种方法啊,我们可以省略第二步,就不用量了,是吧?什么方法呢啊?刚才你看好了,我们是以 b 点为原先 这样画胡,是吧?好,那圆规的两角张开的角度就是这么大,是吧?那现在呢,我们不改变这个圆规他的这个两角的距离。好,我们然后以这个点为圆心画弧,紧接着呢,又以这里为圆心再画一个, 那么这个点好,这个点我们就说他是 b, 一撇就是 b 的对称点,接下来呢,我们来解释一下 b 撇跟 b 为什么关于 l 对称是吧?好, 我们先把它连起来。好, bb 瓶呢,我们连起来, 因为他们垂直,这是肯定的,是吧? 里面放的就是垂直平行线。好,接着呢,我们这个点啊,这个点呢,我们随便记,我们记为 m, 我们连一下,我们连接 bm, 再连接什么呢? b pm, 好,因为这里已经是垂直了,是吧?那只要我们在说明啊,这里给我假如文具是什么?嗯呐, 因为我们知道这个 b 撇等到 s 才值得了,那我们只要再能够说明这个什么 bn 等于 b 撇 n 是不是问题就解决了,就相当于 做了第二步了,是吧?好,那现在我们既然连接啊,这两端,我们来看看这两个三角形前等不前等啊,我们看一下啊, 好,因为我我们知道 bm 跟 bkm 啊是相等的,因为刚才我们说了,我们不改变这个圆规两角的距离,是吧?啊,他们都等于那个圆的半径,所以相等是吧?好,紧接着 巩固边是吧,那你看这里是垂直的,所以呢,这两个三角形都是什么啊?踢三角形啊,都,是啊,踢三角形, 那这也是啊,这三角形你看这两边是什么?斜边,这条是直角边,所以人家都 hl, 是不是就已经可以判断这两个三角形全等他,那既然他们两个全等,所以 bn 跟 bpn 是不是相对好,那么我们利用这个圆规两角啊,不改变距离啊,我们就直接就能够把它找出来,第二步都不用做,是吧?好,那么说明这个问题呢,我们都解决了,是吧? 好,那接着呢,我们就用这个方法呢,把 c 点再找出来就可以了,是不是?好,然后我们画一下 c 点,好用做 b 点的这个办法啊,首先 c 点以它为圆形啊, 好,两个交流旁边在这里啊,好,然后呢,圆规的大小不改变啊, 好,那么这一个点呢,就是十一点了,那么呢, abc 这个三角形呢,他的三个对称点我们都做出来了,是吧?好,那现在呢,我们把它连接起来啊, 那么连接过后啊,我们通过视觉观察呢,他们应该是关于 l 对称的,是吧,虽然我们用此规则图呢,他会存在着一些误差, 但是呢,做出来图形还是比较标准的,是吧?好,那么在这里呢,我们就完成了我们今天的这个问题啊,就是画走对称图形, 好,从这里呢,我们也知道啊,尽管没有换鸽子啊,现在我们用此规作图的方法呢,也可以把它做出来,是吧,你看,随着我们学习的知识啊,逐步的增加,是吧?啊,我们就能够处理以 钱呢没办法处理的问题,是吧?那么这个轴对称图形呢?他在世界上是吧?啊,用处很大,因为你只要画出啊他的一部分,然后根据他的什么对称性 设计出他的另外一部分,是吧,那么得到这些图案是相当的美观啊。好了,关于这个慈悲做图呢,我们就先介绍这么多啊,以后呢我们碰到的时候呢,我们再慢慢的介绍啊,那么我们的客呢,就先到这里,再见。
114大众数学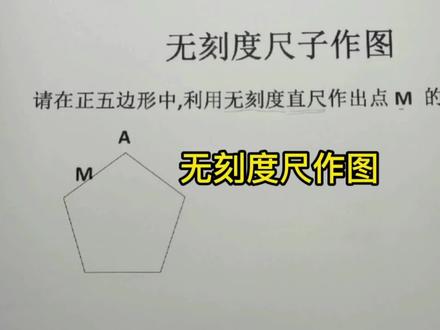 03:18查看AI文稿AI文稿
03:18查看AI文稿AI文稿大家好,欢迎来到校行课堂。今天我们来看一道作图题。这一部分内容中考经常考,但容易,但往往呢,同学们忽略了他。 我们来看看题目,要在正五变形当中,利用无刻度及时做出点 m 的对称点。 n 是 m 要等于 n, 也就这个意思。 我们首先要弄清楚,无刻度支持没有四句的。一把尺子,我们能做一些什么东西?它不是不同于指挥作图啊,我们一般没刻度的尺子,首先我们可以用利用它,它的边是直的固定的,我们可以用它来画直线,这是第一个作用。 第二个作用是,如果以这样两点,我们可以把这两点连起来,做出一条线段。 第三个作用是我们引进的一条边,我们可能可以做他的延长线 直尺做图,他能发挥的作用也就这一些。我们下面在这个图层当中要找到 n 点是 a m, 要等于 a n。 那我们同学说这还不容易,我用眼睛瞄一瞄,咕一下,在这上面做一个这样的,做一个记号可不可以呢?不行,那就等于是有刻度的做法了,我们不能这样做, 那不能够用刻度,也没有圆规,我们该怎么办呢?来看啊,题目说的是对称点,对称点那肯定就有对称轴嘛。我们正五边形的有五条对称轴,分别是顶点到对边中点的连线,顶点到对边中点连线,我们要做 a m 等于 a n。 你在这条边上的话,我们肯定要这条对称轴,但终点我们找不到,没有圆规说不出准,找不到,终点 找不到。我们要想别的办法,把这条对称轴给找出来,先找到这条对称轴,然后 再来找 m 的对称点,那我们清楚的是这样的连起来,再调边这样的连起来。两个不相邻的顶点连起来的线段,他们一定会相等,我们来连一下,看来看啊,这样一连, 这样的线一连这里有个角点的,这个角点呢,就一定会是在他的对称轴上,所以我们只要把这点和 a 点给连起来,那么对称轴就找到了。 当然你找这点的时候,还可以把这两边呢进行延长,汇聚到这点上面来两个线的延长线的交点,也可以 找到了他的对称轴了。然后我们来看,你可不可以这样去给他做过来就是了, 这样不行,这样的话你要不标准,你到底是怎么做呢?这样连起来啊,做他的平行线也要往上推是可以的。但呢还有一个方法,我们看啊,我们把这一点跟 m 点连起来, 他与对称轴有一个焦点,根据对称性,我们把他的这个点的对称点跟对称轴上刚才的焦点,这个焦点,我们把它连起来,并把它延长 到这里,这个点就是我们要的 n 点,还有 a m 就会等于 a n 了,这个 n 点就是我们要求的了。 这种题目呢,最主要注意是不要跟此规作图。分为一坛,点赞加关注,学习不迷路!
17深圳优师服务 02:46查看AI文稿AI文稿
02:46查看AI文稿AI文稿各位同学好啊,做对称点是初中数学的必考考点,比如在将军一马列的最值问题中,做对称点是常用手段。那么你是否知道如何用无刻度指使来做对称点呢? 有的同学可能觉得做对称点是一件很容易的事情,比如下面这个图中,过格点 c 做直线 ab 的对称点,只需要把 c 沿着 ab 的方向往下移动两格,就得到对称点 c 撇。可事实上,如果直线 ab 稍微变动一下,比如这样,那么做对称点的难度就大多了,因为最后的对称点落在了非隔点上, 这个真需要动下脑筋,同学们不妨暂停视频思考片刻 好了,一起分析一下对称点性质。一,过点和对称点的直线垂直于对称轴 c 的对称点叫 c 撇。 由于 cc 撇垂直于对称轴 ab, 利用这一点,我们先过 c 做直线 ab 的垂线,那么 c 撇将落在这条垂线上。做垂线的方法在前面的视频中有讲过,建议不会的同学可以看一看。对称点性质二,点与对称点到对称轴的距离相等。 为了利用这条性质,我们延长 c a 一倍到点 e, 使 c a 等于 a e, 同时延长 c b 到 f, 使 c b 等于 b f 连接 e f。 我们看,由于三角形中卫线的性质 ab 平行于 ef, 并且 ab 和 ef 的距离刚好等于 c 到 ab 的距离,所以 c 的对称点 c 撇就一定落在线段 ef 上。现在对称点 c 撇记在垂线 m 上,又在线段 ef 上, 那么这两条线的焦点就是 cp 了。老师问个问题,如果刚才把 cb 延长一倍时,格点不够怎么办? 这个问题特别好,如果右边的隔点不够了,刚才的 f 点不能用,那怎么办呢?其实只要点 e 在隔点内,我们通过点 e 来做对称轴 ab 的平行线,一样可以解决问题。本题中,将 e 先往右移四格,再往上一 e 格到 g 点连接 eg, 那么 eg 平行于 ab, 连接 eg 与垂线 m 的焦点,即为对称点 c 撇。这个方法比上个方法所需要的格子更少,所以我建议同学们以后就使用这个方法。 最后,我们走一遍完整的过程。第一步,用数格子的方法做对称轴 ab 的垂线 m, ab 是横四竖一,因此 此我们过 c 做出四横一的垂线 m。 第二步,延长 ca 一倍,倒点 e, 将 e 先往右移四格,再往上一格,倒点 g 连接 eg。 第三步,取 ege 与垂线 m 的焦点,即为所求的对称点。你学会了吗?
617春雨知行 07:37查看AI文稿AI文稿
07:37查看AI文稿AI文稿你好,欢迎来到学霸数学,今天开始我们来讲无刻度直尺做图问题。我们知道无刻度直尺做图正成为某些地区的中考的热点题型,因为是无刻度的直尺做图,所以限定非常之多。 做此类问题的关键点是找点,找到点,然后再做出。当然你所要找的点可能在格点上,可能在图形的特殊点上。当然单就是找特殊点,对于很多中学而言也 是有困难的。这类题给同学们的感觉似乎并没有章法,没有特定的方法或者技巧。其实呢,这类问题不仅 有方法,还有技巧,当然前提是同学们一定要掌握好基础知识。好,我们接下来来介绍一下这类问题他的特点。第一个,只有 无刻度的直尺,一把无刻度的直尺我们只能画直线吧,所以他的线钉 非常多的。第二个,利用特殊点进行作出,所以这里最关键的点就是找特殊点。第三个,和你们 对图形的性质非常熟悉,这个是基本前提,所以要解决此类问题, 不仅要掌握相应的方法和技巧,还要对图形的性质等基础知识非常熟悉。 无刻度值此作图包含的问题有六点,第一个是 角度问题,第二个是对称问题。第三个旋转问题,第四个是比例问题。第五,特殊图形问题。第六,切线问题,也就圆中的阳光问题。下面我们来 举几个比较典型的问题。第一个,特殊角问题,找一格点 c 使角 b ac 等于四十五度, 那么这里找法部为一。我们可以这样画线,也可以在下面画这个线。当然,虽然是简单的画一条线,他所蕴含的原理是有些同学 是掌握不了的啊,或者并没有掌握的,那么这里包含的原理是一二三四五模型啊。第二个,找特殊点,找线段 ab 的中点,这条线呢, 是两个端点在格点上,那么直接去找点肯定找不到,那么这个时候要借助格点,这样, 然后他的焦点就是 ab 的中点,那么他所蕴含的原理是平行线分线段成比例。 再比如找三等分点或者四等分点,找一点 p, 使 p a 等于三倍的 pb, 那这个时候你们可以借助平 线分线段成比例这个特点去找这个批点啊,这样一斜拉,那么这个焦点就是我们所要找的这个批点 所硬含的原理。同学们可以用平行线,分线等成比例去理解,或者相似三角形去理解,这两个三角形明显是相似的吧。再比如做特殊的 线,做垂线啊,当然这个点可能不在格点上,那么这题呢,你所要找的点并不在格点上,需要借助平移和全等的姿势去找到,否则的话,你找不到就做不出来啊, 我们这样画线,那么这个垂线就做出来了啊,当然还有特殊 正方形,然后做一个,是吧菱形,那么怎么做呢?首先连接, 那么这个对角线的焦点也是菱形的中心啊, 然后借助正方形的对称性找到另一个点,然后呢再斜拉,那这样的话, 中间这个四边形就是菱形,那么对常人的要求就是正方形,菱形的性质要非常熟悉啊。再比如在圆 中去找圆心,或者找相等的弦长确定圆心呢?我们首先要知道圆心在旋 的垂直平衡线上,所以呢,你关键是找垂直平衡线,或者找九十度的圆周角,因为可以确定直径吧啊,那么这里首先找到 eb 这条弦的中垂线,因为 eb 都在格点上,所以找中垂线相对简单。那后面呢, 我们可以找 ab 的垂线,找到直径,那么他们的焦点就是圆心啊。那么如果要找相等的弦呢?那么这里要借助什么相等的 圆周角所在的弦相等啊,利用对称性找到什么相同的 圆轴角,然后再做出来这条线就是 fg 啊。那么同学们要对圆的相关性质要非常熟悉啊。本周呢,按照问题 的顺序来进行讲解,角度问题,分特殊角问题,角平分线问题,还有直角垂直等问题。第二个对称旋转问题,第三个比例问题, 第四个特殊出行问题,第五个特殊点问题,第六个与原有关的做出问题,比如切线问题,圆心弦等等。按这些问题来进行讲解, 这些问题包含了中考命题的多数问题和你们掌握这些问题, 那么基本没有问题啊。那么详细情况和更多问题呢?请同学们继续关注专栏课程的更新内容啊!
251学霸数学 02:53查看AI文稿AI文稿
02:53查看AI文稿AI文稿这是一道专门用来考导中学生的中考题,叫直尺之轴。什么意思呢?就是只是用一把直尺,没有刻度啊。去找到这个长方形的对称轴啊,大家挑战一下。好多同学都认为做不出来啊,实际上可以的。 我们看看如何解决这个问题啊。首先标记这个点,然后好同学都知道怎么把它的对称中心找到。连接 bd, 连接 ac 这个点哦,就是他的对称中心。如果我们能够找到 ab 的终点 m, 连接这个延长,就是他的对正轴了。但是 ab 的终点 m 不是那么容易找到的,需要一点点技巧。那怎么找到 ab 的终点呢?首先,我们 随意的在长方形 abcd 外面取一点,假设这点是一吧。然后连接 a, 连接 b 这两个焦点。假设是,假设是 f 和 g, 我们连接 b, f 连接 ag, 交这个点与 n, 然后连接一 n, 把它延长交 ab 与 mm, 就是 ab 的终点。所以我们找到他的对称中心呢,找到他的终点,连接延长, 就是他的对联轴了。好同意。很疑惑啊,为什么这样作图能够找到 ab 的终点呢?实际上啊,这涉及到一个初中可能考过,但是很少人去记的一个定理啊,叫赛瓦定理, 我个人喜欢叫他旋转不变定律。什么叫旋转不变呢?就是绕着这个三角形啊,我们转 圈最后得出的比值是不变的。具体的讲就是 am 比上 mb 乘以 bg 比上 eg 乘以 e, f 比上 f a, 他实际上是等于一的。不管这个恩典如何变化。假设这个恩典在这里啊,我们同样的 过三角形内的一个点,就能够构成这样的定理啊,这是三角形内啊,三线共点的一个非常有趣的定理。而这个题目呢,我们知道 fg, 在 cd 上, fg 是平行于 ab 的,这个平行我们就能够得到 ef 比上 f, a 是等于一, g 比上 gb 的,也就是 e f 除 e, f 乘以 gb 比上 eg 是等于一的。这一部分等于得到 ammb 等于 am 等于 mb, 就得到了这个结论啊。 大家也可以自己给他取个名字啊,方便自己记就行了。好同学可能会很疑惑啊,这个是怎么得来的啊?点赞过千,下个视频分享!如何证明更多的有趣的数学问题,可以翻看我的合集和专栏,关注我,让学习变得更有趣一点!
2021火星课堂 11:14
11:14 01:38
01:38 04:11
04:11
猜你喜欢
最新视频
- 1265琪琪同学
![[初二数学补充内容]尺规作图(一)A #每天跟我涨知识 #涨知识 #记录校园生活 #初中数学 #课堂](https://p9-pc-sign.douyinpic.com/image-cut-tos-priv/751e32838c86b43b0b4a89eac7f9017f~tplv-dy-resize-origshort-autoq-75:330.jpeg?lk3s=138a59ce&x-expires=2079349200&x-signature=luc2qrT%2B0jZ1g3b2c6F0WTcG9Io%3D&from=327834062&s=PackSourceEnum_AWEME_DETAIL&se=false&sc=cover&biz_tag=pcweb_cover&l=20251124210340D2A833CBE0E3EC24190F)

![[初二数学]尺规作图(一) 五种基本作图#每天跟我涨知识 #课堂 #努力学习 #初中数学](https://p3-pc-sign.douyinpic.com/image-cut-tos-priv/d825fa3050f3660ec4d89396aa57180b~tplv-dy-resize-origshort-autoq-75:330.jpeg?lk3s=138a59ce&x-expires=2079349200&x-signature=Dhx51qoPrAbJY7TmcIzBPcn0YiI%3D&from=327834062&s=PackSourceEnum_AWEME_DETAIL&se=false&sc=cover&biz_tag=pcweb_cover&l=20251124210340D2A833CBE0E3EC24190F)






