数学七年级上册第四章角怎么画
粉丝10.6万获赞31.4万
相关视频
 06:58
06:58 02:51查看AI文稿AI文稿
02:51查看AI文稿AI文稿这个视频我给你讲讲方向角。东南西北四个方向你在地图上都见过了,而以这四个方向为基础,你也可以给各个方向起名字,比如这两个方向都介于北方和东方之间,他们明显不一样,可要怎么区别呢? 这就需要方向角来帮助你了。方向角是指从正北或正南方向到目标方向所形成的锐角,所以呢,这个方向就可以叫北偏东三十度。 而这个方向,显然他与东方的夹角是三十度,那他的方向就是冬天被三十度。你要是这么果断的得出答案,我也会果断的告诉你,做错了。 别忘了,方向角一定是从正南正北开始的哦,所以只会有北偏东、北偏西、南偏西以及南偏东。于是你果断修改答案,说他的 方向是南偏东一百二十度啊哦,我只好遗憾的通知你又错了,方向角一定是锐角,所以他的方向只能说是北偏东多少度?这个角是三十度的雨角,显然就是六十度。那这条线的方向也就是北偏东六十度,怎么样?不难吧? 你只要记住方向角一定是南偏沙或北偏沙的锐角就行了。特别的,像北偏西四十五度这样的方向,也可以称为西北方向。 类似的,南偏西四十五度也叫西南方向,南偏东四十五度是东南方向,而这个方向则是东北方向,也就是北偏东四十五度。那嘎达, 看图,任方向角的技能你妥妥会了。但是有一些题目很不友好,他们木有图,比如这个也知有一只虫子 a, 他在青蛙 b 的北偏东五十度处, 另有一只虫子 c, 这只虫子位于青蛙的难偏心十度处,就叫 a、 b、 c 的度数。没图没关系,自己画呗。题目中无论是虫子 a 还是虫子 c, 都是以青蛙的位置来描述方向的。所以你就把青蛙所在的 b 点当成基准位置,上北下南,左西右东,标好方位。 虫子 a 在 b 到北偏东五十度,在图上标出。就是这样,虫子 c 在 b 到南偏西十度,也可以在图上标出来。 题目要求角 abc 的度数不就是这三个角的度数和吗?这个角是十度,而这个显然就是九十度。最后这个角是五十度的余角,也就是四十度了,把他们加一加,就是一百四十度, 这就是角 abc 的度数。看来,画方向角时,一定要先确定基准位置,再根据描述画出其余方向。好了,题目 都做完了,你该催我总结了,那就赶紧的,方向角一定是北偏啥或南偏啥的锐角,你得会在图上读出它。 如果碰到木有图的题,画图时一定要先选中基准点,标好方位,再根据其他点的方向把图画出来,答案自然就搞定了。为师这就讲完了,图案们快去做些题目操练起来。
415高斯竞赛数学-G 03:04查看AI文稿AI文稿
03:04查看AI文稿AI文稿这个视频我来讲讲角平分线。像这样在纸上画一个角,剪下来对折,那形成的这条折痕恰好可以保证把角平分成两份。我管这种从角的顶点出发,把角平分成两个相等的角的射线,叫角平分线。 你可以说 oc 平分,角 aob。 既然是角平分线,也就意味着角 aoc 等于角 boc 都是角 aob 的一半。继续做 om 评分角 aocon 评分,角 boc, 给角 aom 起个代号叫角一,那么这四个角的度数都等于角一。 现在问题来了,度数是两倍,角一的角有哪些呢?像这种美举技术的问题,咱得按照顺序一个一个涨。以 oa 为边,向下找两个角,一是叫 aoc, 顺次移动一下。以 om 为边,向下找两个角,一是 mon, 再移动一下角 cob 也可以满足要求的角有这三个,可别落一个。所以技术的时候要按照顺序一个一个的美举 技术问题。欧了,咱再来看看计算。叫 aob 是平角,也就是一百八十度,做射线, oc 是角, aoc 等于三十度, om 是他的角平分线,做射线 od 是角 bod 等于六十度, on 是他的角平分线。现在问题来了,请求角 mon 的度数。 角 mon 显然是这三个角的核,可咱一个度数都不知道咋办呢?别急,要淡定,一个一个来呗。 om 是角平分线,那这个角就是角 aoc 的一半了呗,也就是十五度。类似的, on 也是角平分线,那这个角就相当于角 dob 的一半,那不就是三十度吗? 如此这般,两个角搞定了,就差中间的角 cod 了。观察一下,发现他跟旁边的这两个角拼在一起是平角,也就是一百八十度。于是角 cod 的度数就是一百八十度,减去左边的三十度,再减去右边的六十度,算一算就得九十度了。 各个击破的任务已经完成,把这三个角加在一起,就是角 mon 的度数了,也就是一百三十五度,这就是答案。 角度计算问题通常是条条大路通罗马的,你换个思路,把角 mon 看成是平角 aob 减去这个角,再减去这个角,得到的也没问题。还记得 om 是角平分线,那这个角就是角 aoc 的一半,也就是十五度。 on 也是角平分线,所以这个角就是 bod 的一半,也就是三十度。那角 mon 就是一百八十度, 减去十五度,再减去三十度,答案还是一百三十五度了。你放心,不同的方法计算出来的答案肯定是一样的,否则那肯定是你算错了。 以上就是角平分线的全部内容,我来给你总结一下。角平分线就是把角分成两个相等部分的射线。在计算问题中,先确定目标角如何通过角度加加减减得到, 再利用角平纹线分出的两个角度数相等且都是一半的特点,算出所需角度,答案自然就搞定了。为师这就讲完了,徒儿们速速刷题去吧!
81高斯竞赛数学-G 02:23查看AI文稿AI文稿
02:23查看AI文稿AI文稿同学们大家好啊,我们期末期中考试结束以后啊,很多学校都开了我们第四章的课程。下面我来看一下七年级上册第四章平面几何中的一个关于脚的内部 数角的问题。他说在角内部画一条射线可得三个锐角,画两条射线可得五个锐角,三条射线呢,可得十个锐角。 到此规律下去,画十条不同的射线可得多少锐角呢?那么实际上这个题啊,我们是有公式的。在我们研究线段的时候呢,我们就知道有一个公式叫二分之 n 乘以 n 减一,那么这个公式呢,他同样应用于我们的角,但是这一题他是有坑的。 因为这一题的公司里边啊,就像我们上一题说车票的时候是一样的,他一定要把两个端点加上,那么这一题你会发现他中间一条 条线,这是 n 等于一的时候。实际上我们用这个公式呢,我们应该变成三,把首尾的边界加上呢,因为一共是三条线,这样的话才会出现三乘二除以二是三条。那么 n 等于四的时候呢? 画两条射线是这样, n 等于四,那么四呢?乘以三除以二应该是六条。所以这一个题目中印刷与错误啊,他应该是得到六条六个这个锐角,那画三条就是五乘以 四除以二应该是十个。那因此他说里面画十条的时候呢,我们要把两个端点加上啊,加上端点是十二个,乘以十一除以二等于六十六,所以呢,我们选二 b 啊。所以他应用公式的时候,我们记得要把首尾加上。那么如果单纯的去 记忆中间的这个为 n 的话,我们怎么推倒这个公式呢?如果中间是 n, 那我们要把 n 呢?带入这个公式的时候,要变成 n 加二,因此这个公式就可以变形为 n, 变成 n 加二啊。心里边的 n 加 n 减一呢,这里边的 n 也要变成 n 加二,去减这个一,然后除以二。所以我们这一题里边啊,它的公式呢,实际上是 n 啊,这里边是二啊,是 n 加二括号, n 加一括号除以二。 如果你直接带入的话呢,你也可以用这样一个公式啊,这是我们线段里面和脚里面应用的公式最为广的这个公式的一个啊,变形啊,有没有听懂呢?
81老房教数学 03:30查看AI文稿AI文稿
03:30查看AI文稿AI文稿这个视频咱来讲讲角,别乱想了,这可不是生物课,我要讲的是这个角。角在生活中很常见,比如这个,再比如这个。在几何中,角有自己的定义,而且还有两个。第一个定义是描述性的,有公共端点的两条射线所围成的图形叫做角。 公共端点是角的顶点,射线就是角的边。第二个定义是动态的一条射线绕端点转动所形成的图形就是角 射线端点即角的顶点,射线出发的位置叫始边,停止的位置叫中边。你要注意,两种定义都强调了,角的两边为射线,也就是可以无限延长,而这并不影响角的大小。 知道了什么是角,你还得会给一个角起名字。比如这个角的端点是 b, 你就可以叫他角 b。 记住,角 b, 这是角的符号,就是一个迷你的角吗?下面的这条边横着画,可别跟小鱼号弄混了。好了,如果我给这个图在天条设限,这时候就有点麻烦了,以 b 为顶点的角有三个,你说角币都不清楚再叫谁了, 那就需要再来几个点辅助。这个角就得叫角 nbc 了,顶点 b 必须在中间,你叫他角 cbn 也愁。两种写法都一样, 类似的这个角是角 cba, 而这个则是角 nba。 如果你觉得写仨字母太麻烦,也可以给角起个新名字,只要用数字或者小写希腊字母就行了。 比如你觉得叫 cba 很二,就可以叫他叫二,名字充分的体现了人物性格。再比如,你觉得叫 nba 很洋气,就可以给他起个希腊名,叫阿尔法,写出来就是这样,有点像个小鱼, 那这个角就多个名字叫角阿尔法,你看这样只用一个数字或字母就可以表示角了,是不是很方便? 在这里,我有必要给你普及几个希腊字母。刚才的小鱼念作阿尔法,而这个像耳朵一样的念作贝塔,这个有点像 y 的念作伽马,放射性的伽马射线就是它。陆续的,你在数学和物理课上还会见到这些希腊字母,咱以后再慢慢说好了。 言归正传,知道了什么是脚,以及怎么表示他,咱接着说脚的分类,脚按照脚的大小来分类,脚的大小用角度来表示。 一条射线沿端点旋转一周,与自己重合,他所转过的角是周角。规定周角为三百六十度,周角的一半是平角,也就是一百八十度。平角的一半是直角,也就是九十度。比直角大而比平 角小的是钝角,其度数介于九十度到一百八十度之间。比直角小的是锐角,他的度数介于零度到九十度之间。学会了角的定义、表示和分类,就可以来总结了。 角是一个傲娇的几何元素,他有两种定义方式,两条射线围成的图形是角,一条射线旋转形成的图形也是角。角还有四种表达方式,第一种,在没有奇异的时候,你可以用顶点字母表示角,比如这个角 b。 第二种,用顶点字母表示。出现起义的时候,你得用三个字母表示角,比如角 nba 和角 cba, 而顶点 b 必须在中间。 第三种,你可以用数字给角起个新名字,比如角二。第四种,你也可以用小写希腊字母给角起名字,比如这个角阿尔法。 另外,根据角度大小,角还可以分为周角、平角、钝角、直角以及锐角。为师这就讲完了,徒儿们快去做题吧!
134高斯竞赛数学-G 15:00查看AI文稿AI文稿
15:00查看AI文稿AI文稿同学们好,今天我们来认识一下角,那在现实生活中,我们经常会见到上面的图形,那这些图形到底是什么呢? 今天我们主要来认识一下角的几何图形,然后理解一下他的概念,并且会表示, 然后再了解一下度量单位,角的度量单位有什么呀?度分秒,知道了他之后,还得会进行简单的换算和角度的计算,这是这几盒我们需要掌握的 好。首先来看一下下面的图形,你发现红色的部分他都是什么样 样子呀?好,所以我们思考一下脚,他的概念是什么呢?有公共的短点,然后有两条射线, 这就叫做角。那换句话说,他有两个条件,一是顶点,也就是公共点,另一个是什么?两条射线,这是他静态中,那如果他在动态当中,他又是什么概念呢? 哎,绕着一点,就是绕着他的短点进行旋转,旋转到某一位置所组成的图形就叫做脚。 我们看一下,比如说我以哦为短点,然后以射线 oa 作为开始编,然后进行转动,转动到某一角度的时候,你会发现他有一个中指边, 那这种情况所组成的角就称之为哎,我们所说的角。那同学们再想一下,我如果继续旋转呢?旋转开始边,旋转到哎,成一个直线的样子,那此时又是什么角啊? 这个叫平角,我们引入的概念叫平角,也就是 oa 绕着 oa 进行旋转,旋转的 oa a 和欧 b, 他们共同重合于欧点,就像一条直线时的时候,那就叫做平角。 好,那同学们再想一下,我如果还是绕着 oa 进行旋转,旋转到和 oa 重合,这种情况下又成为什么角啊? 圆周角。好,那同学们想一下,我们现在知道了平角和圆周角,那平角是多少度啊? 一百八十度,圆周角呢?三百六十度。好,以后啊,这个一定要记住背下来,因为后面的题都要设计到这个角度,平角和圆周角,那接下来 迅速的判断一下,哪些是脚,哪些不是脚啊?很显然他不是脚,为什么没有端点?也就是公共点。 好,那我们再看一道题,我们说说法正确的是,平角是一条直线,我们说不管你怎么样,这个角他是两个条件,一个是由公共的 顶点,另一个是要么动台的,是绕着一条射线进行旋转,要么是镜台的,是由两条射线和一个短点所组成。所以这道题自己下去看一下,答案是,第, 不管你怎么变,这道题考的就是角度的概念,那你看看哪些 不对的?我们首先看平角,跟大家讲一下吧,因为咱们的时间特别紧张,每次时间都不够用。我们看啊,平角是一条直线 对吗?我们说他绕着哎,这条直线射线进行旋转,可以旋转成一条直线,但是呢,他说平调就是一条直线,对吗? 我们说单独的一条直线,它可不叫平角,一定要理解角度的概念,知道了吗?它有一个短点,还有一个哎,开始的射线起势边还有一个中指边,这是角度的概念, 如果是动态的话,静态的一定要清楚啊,它是由两条射线,有一个公共的端点,有一个公共的顶点端点所组成的,叫做角。 那么看一条射线是一个圆轴,哎,一条射线他构不成任何角,对不对?只能是两条射线,两条射线组成的图形叫做角,两条射线 必须有什么?哎,端点啊,一定要清楚,这些都是不对的,要理解一下我们脚的概念。 好,我们看教如何来表示呢?首先知道了他的概念之后,我们首先标商字母,他可以由大写 怎么来表示?比如说 aob, 或者就是你不管用哪个方向,你这样标也是可以的,你这样逆着标也是可以的,不管哪个方向都是可以的,但是我们顶点一定在中间就行了,你看你不管怎么变,他顶点是不是在中间呀? 好,那比如说我此时就这一个角,那我可以用角欧来表示,也就是定顶点,没有任何设限, 明白吗?顶点的字母在中间,他除了这个角度之后,再没有任何角度组成的时候,他可以写成角欧。如果老师在中间加一个射线,就不可以这么写。为什么?比如说他是 c, 你写个角欧,这个 o 到 b 代表的是 aoc 还是 cob 呢?对吧?所以说我们说除非他就是单独的有两条射线所组成的角,我们可以直接写成角 o。 好,那同学们再想一下, 比如说我还可以用什么来表示?比如说刚刚老师说 ios, 那我还可以用数字,阿拉伯数字,前面带上脚的符号就行了, 还可以怎么写?比如说我这还可以用一个啊,什么希拉字母?除了阿拉伯数字,我还可以用希拉字母来进行表示。阿尔法贝塔噶嘛,这都称之为希拉字母。那 图中有几个脚啊?同学们自己数一数啊,一二,还有个大脚三,对不对?三个脚。好,那这种同学们下去自己练练啊,非常简单,要知道角度是什么即可。 我们再来看一个难点,角的度量,角的度量在我们小学的时候就学过了,就如何来量这个角是多少度, 但是我们怎么来换算呢?这个东西就是两脚气,但是我们怎么来换算这些东西啊?比如说度分秒如何来换算啊? 我们说一个圆周,刚刚老师说是三百六十度,对不对?一个平 角是一百八十度,那么看如果把这个三百六十度,每一度记着一上面那个,哎,小圈 那么大一度,是不是啊?就六十等分呐?所以每一份就叫做一分一分,我们上面表示的是一带个小偏, 把分再等分成六十分,然后每一秒我们就记住啊,矮一两个小片,这就是精细的。 比如说这个整个角度是三百六十度的时候,每一度把它精细到六十等分,每一分我们又把它记作成这样,每一分又可以画的床六十秒。所以一个 圆周其实是三百六十度,一个平角是一百八十度,一度是六十分,一分是六十秒,这个换算单位一定要背下来。好,接着我们看如何来换算。 刚老师说了一度是六十分,那我们做的时候前边就是五十七度, 那么后边的小数点如何来划分啊?零点三二。同学们,零点三二如何来划分?先把它划分成分, 画分完分之后你会发现他是十九点二分,还有个小数点,实际上他就是五十七步,十九分,十九分。后边的零点二如何画成 秒啊?零点二分如何画成秒?哎,一分是等于六十秒,那紧接着我们就把这个小数点的零点二再乘以六十秒即可, 最终就是五十七度,十九分十二秒。所以化解这个的步骤同学们一定要清楚。首先小数点前面的就是度, 小数点后边的也是小数点的零点多少度,我们说了一度是六十分,所以你先画分,因为他让你画成度分秒的形式,你一步一步来,一步一步来,不要着急。 然后我们把它画成分分,后面还有小数点的时候,我们要把哎小数点再拿出来画成秒,秒又是一分 等于六十秒,所以我们把零点二拿出来,再乘以六十秒,最终就画成我们其中要求的形式,度分秒知道了,哎。如何用整体的度画成度分秒?那同学们,如果反过来你会画吗? 你在我们正着画的时候是成,那反过来呢?哎,跟数学的道理是一样的,是除。好,接下来我们看一下, 你比如说这种形成如何来画呀?一秒是不是就等于六十分之一?哎,分呐, 那一分呢?六十分之一度,你知道了这种关系之后还是同理,一步一步来画。我们说刚开始画的时候,上一 熊化的时候,是从正着从度开始来,小数点后面进行化,你看五十七度,然后把零点三二乘六十。好,如果逆着来进行划分的时候, 简化的时候,我们还是要从逆着开始,比如说三十六秒,我先把它进到分分,画完之后再拿分进到度,最终就画成度的形式。 你知道了这种方式之后,你然后再来进行化解。好,这就是我们题中要求下句,自己练一练啊,老师再讲都不如你练。 接下来我们再看这道题,我们需要理解的是,圆周是三百六十度,对吧?那我们 说表盘上有十二小时,十二小时, 那同学们告诉老师,每小时是多少度啊?哎,每小时肯定是三十度吗?对吧?每小时是三十度。知道了这样一个一知条件之后,好,接着你再判定十点十分是什么样子啊? 十点十分是什么样子?九十十点十分是这个样子。那同学们看一下,十点十分,哎,我们说经历了多少啊? 哎,经历了几个小时,但是你会发现十点十分,他这个要往前走十分。往前走十分,那就需要你 知道十分钟是多少度。你知道一个小时是三十度,那一个小时有几个十分钟啊?六个,所以十分钟是五度, 对不对?同学们,十分钟是五度,那我们想一想,实际上一二三四,四个三十度,再减去五度就行了。四个三十是多少? 一百二,再减轻的往前走了十分钟是五度,所以是答案是第一百一十五。 我希望同学们做题的时候,咱不要着急去往下看,你要搞懂,你要知道他的步骤,你要知道他的思路,然后来进行解题。 好,接下来这道题就没必要讲,同学们自己看一下啊,他说的是小于平角啊,看清题,平角 ioe, 他就不能再算在其中数啊。 好,紧接着我们看这道题,这道题又是考脚的概念啊,同学们一定要把脚的概念认识清楚,所以答案选第。那首先看第一个为什么不对, 两条直线相交组成的图形叫做角,两条直线相交,同学们告诉我他是个什么呀?对顶角吗?你比如说角一角二,是不是对顶角啊?哎,所以,哎,是不对的。 两条有公共短点的线段组成的图形。角做角是线段吗?同学们告诉老师。
39假如 17:30查看AI文稿AI文稿
17:30查看AI文稿AI文稿hello, 大家好,欢迎来到明老师初中数学课堂,我们今天一起来学习第四章基本平面图形的第三节角。 说起角啊,我相信大家应该都不陌生,因为这个在我们小学的学习当中啊,都学习过,对吧?所以呢,今天我们主要是在这个小学学习的基础上啊,对他进行进一步的一个学习。 但如果在小学的时候啊,对这个掌握的很清楚的话,我们今天其实也可以当做是一一节这个复习课了啊,好,我们看一下知识点清单啊,主要包括四个知识点。首先来看一下第一个角的定义,以及分类 角的定义,哎,什么是角呢?角呢?它是由两条具有公共端点的射线组成,哎,注意这个啊,是由公共端点的射线组成的,那么这两条射线的这个公共端点,哎,就叫做这个角的顶点, 那这两条射线呢,就叫做角的边,哎,这是角的有关的一个定义啊,我们画一个图,比如这是一条射线 oa, 对吧?哎,那么另外一条射线呢,肯定也是要以这个点 o 为这个端点,他俩的端点应该是相同的,对吧?画一个这个 ob, 哎,这就是两条射线,那么这两条射线就一起组成了一个角,对吧?哎,那么这个公共的端点就叫做这个角的顶点,哎,那么这两条射线呢,就分别叫做角的两条边, 这个呀,其实相当于是从一个静态的角度给这个角下了一个定义,对吧?那同时我们可以想想一下啊,我们也可以从动态的角度给他下一个定义,哎,如何下这个定义呢?如果我们把 oa 哎定义成一条射线,对吧?我们想一下,这条 o a, 我如果把它绕着这个点哇进行旋转,对吧?比如说往上这样旋转,哎,一直旋转到现在 o b 这条射线的这个位置,那你看他是不是也可以形成一个角,哎,对吧?所以呢,我们说我们这个角啊,也可以把它看成是由一条射线绕着他的端点旋转而成的, 哎,这两个角度对这个角给他下定义,其实都是可以的,对吧?一个是以从这个静态的角度,那这个呢,就是从这个动态的角度来给他下定义的啊,两种其实都可以。 好,接下来看一下角的分类啊。第一个就是平角和周角,这个概念我相信大家也都了解啊。啊,那什么叫做平角呢?我们刚才说可以从动态的这个角度啊,给给这个角下定义,对吧?哎,也就说一条射线绕他端点旋转, 那么如果说呀,他的中边和始边成一条直线时,什么是中边和始边呢?始边就是起始的那条射线吗?对吧?那中边呢,就是他绕的端点旋转,旋转之后停下来那 边那个位置就叫做中边,如果这两条边成了一条直线的时候,那么这个时候所成的角就叫做平角,哎,我们还是把这个图画一下啊,还是以射线 oa 为例,他绕着这个点后这样旋转,旋转,旋转,那什么时候旋转到这两条边成一条直线呢?那是不是旋转到哎,往这个方向了,对吧? 哎,你就选择现在 ob 这个位置,那么这个时候所成的角,那当然是这个角了,对吧?哎,我给你标一下啊,也就是这个角,这个角就叫做平角。 好,那什么叫做中,呃,周角呢?如果这条边继续旋转,你看啊,如果又旋转回来了,也就旋转了整整一圈,对吧?哎,他又跟这个 o a 又重合起来了,那么这个时候说 成的这个角就叫做周角,哎,就是绕了照这个这个绕了一圈又回来了,对吧?哎,那么也就是应该是这样的一个角转了一圈,哎,这个角 就叫做周角,那这个时候呢,他跟初始的这条边是重合的,哎,他俩重合到一起去了,这个角就叫做周角。那以前我们也知道这个度数啊,周角, 平角,他们的度数分别是怎样的呢?一个平角应该是等于多少?一百八十度的,哎,那么一个周角呢,应该就是等于三百六十度,哎,这都是我们以前曾经学过的知识了,对吧?好,那除了平角和周角之外,这个角还可以怎样分类呢? 还可以把它分为直角、锐角和钝角。首先什么是直角呢?等于平角一半的,这样的角就叫做直角,比如这个,哎,这样的角就叫做直角。 然后呢,什么叫锐角呢?大于零度,并且呢,小于直角的角就叫做锐角,比如这样的,哎,这样的角叫锐角啊,那什么叫钝角呢?就是这样的啊,大于直角,对吧?他比这个角 直角大,并且呢,他要小于平角的角就叫做钝角,哎,这是直角、锐角和钝角的概念。那具体跟度数有关的话,我们看一下,直角呢,应该就等于九十度,对吧?那锐角的度数应该是怎么样啊? 应该是大于零度,并且呢要小于九十度,这样的角才叫做锐角,那钝角呢,那肯定应该是大于九十度,注意啊,他还必须要小于一百八十度,对吧?因为人家说了,必须要小于平角,对吧?哎,钝角的度数范围就是大于九十度,小于一百八十度。好, 这道例题啊,下列说法正确的是这里,大家可以先暂停一下啊,有答案以后我们继续啊。第一个啊,一条直线就是一个平角,这说法对吗?虽然说一个平角啊,他是两条边,这个成一条直线,对吧?看上去好像是一条直线,但是这两这是两个完全不同的概念,你线怎么可能是一个 角呢,对吧?角的话,我们有端点呢,有两条边,对吧?哎,那线和角,这完全是不同的概念,这个说法肯定是错误的。那必也同样啊,这射线就是一个周角,这肯定也不对,对吧?哎,虽然样子差不多,但他们是有本质区别的啊。 c 呢,两边成一条直线的角是平角,哎,这个应该是没错的,对吧?哎,这是跟我们平角的这个定义就是这样表达的啊。那第四个呢,两个锐角的和一定大于九数,这个对不对?这很明显也错的,我们可以随便举个例子,对吧?比如两个锐角都是十度,哎,你十度加十度, 可能大于九十度吗?不可能的,对吧?所以呢,这道题最后答案就是 c 选项。好,接下来看第二个知识点,角的这个表示方法。我们怎样去表示一个角角啊,通常是用这个符号来表示的,我们乍一看,好像有点像小于号,对吧?但是要注意下面这条,这条边是 平的啊,你不要不要写成这样了,那这样就真成小于号了,对吧?哎,写法要注意,下面这边是平的啊,他是用这个符号表示的,哎,常见的话有以下几种表示方法。首先第一种看这个图,哎,如果是这样的话,我想表示这个角的话, 我们可以用呢三个大写英文字母来表示,比如这个图上可以记住角,这个就读啊,读,就读成角啊,角 aob aob, 对吧?当然你读成角 boa 也是没有问题的, 但是要注意的是必须要把这个 o, 因为 o 是这个角顶点,对吧?他必须要放在中间,哎,他不能这个这个 o 啊,不能跑到前面和后面去,哎,把这个顶点必须要放在中间的位置,这是书写的一个要求。好,这是第一种表示妈妈。 那第二种呢,是可以用一个大写的英文字母来表示,但是呢,前提啊,是必须是什么啊?以这个点 o 为 顶点的角,只有一个的时候才能用这种方法来表示,哎,我们还是给他画个图啊,还是刚才这个角,这个角我可以把它表示为角 o, 没有问题,哎,可以表示为角 a o b, 角 boa 或者表示为角 o 也可以啊,但是他说既然可以有一个字母表示,我们干嘛还要用这种三个字母来表示,那多麻烦呢,是不是?哎,这就涉及到这个前提了,为什么他要求是以这个点 o 啊为顶点的角必须只有一个?比如说,我们看一下下面这种情况,如果是这样的, 我如果还想表示这个角,那怎么办?我还可以用这个角 o 来表示吗?那肯定错了,因为我们看以这个点 o 啊为顶点的角不止这一个角,对吧?你看它是有哪几个角?这里这个角就是一 这个点 o 为顶点的,同样呢,这个角也是以这个这个这个点 o 为顶点的,对吧?那再包括这个大的这个角, 哎,这三个角都是以点欧为这个顶点的,那你说角到底是表示哪个角啊?所以我们不能这样表达了,对吧?我们如果还想表达这个大角的话怎么办?那这种情况,那就只能用这个角 a o b 或者是角 b o a 来进行表示,对吧?哎,所以说呢,我们要根据不同的情况,你如果以它为顶点,角只有一个,哎,那你可以这样表,否则的话,就不能用这种方式来表达好。 第三种方法呢,就是用这个数字或者是用希腊字母来表示了,哎,那么用这种方法表示的时候,要在靠近顶点的这个地方一定要画上一个小弧线啊,然后呢,把它标上数字,或者是这个希腊字母啊,比如说这种情况, 哎,这里有画一个小弧线,比如角一,那角一呢,跟这个角 b o c 其实是同一个角,对吧?哎,下面呢,我再画一个小弧线,标上角二,角二,实际上就跟这个角 a o c 是同一个角,对吧?哎, 那用希腊字母的话,其实也一样啊,这角二发和角贝塔,哎,这也是一样的啊。好,这再看一道例题啊,如图所示,下列表示角的方法,错误的是, 哎,第一,这个角一和角 p o n 表示同一个角,我们看一下,角一在这儿啊, p o n a, 它俩应该是表示同一个角,对吧?好,那 b 呢,是角二发,表示的是角 m o p, 角二发在这里, 那角 m o p a 也表示的从这个角,对吧?哎, b 选项也正确,那 c 呢,角 m o n 也可以用角 o 来表示,看,角 m o n 是这个大的钝角,对吧? 他是用角 o 来表示,那肯定是错了,对吧?因为以点 o 为顶点的角不止这一个 mon, 角一和角二发都是以这个点 o 为顶点,对吧?所以 c 选项这个肯定是错误的啊。那 d 呢?图中共有三个 角啊, m o n, 角 m o n, 角 p o m 和角 p o n 一二再加一个大的,正好就三个角,对吧?哎,所以呢,这道题啊,他说要选择这个错误的,对吧?所以呢,答案就应该是 z 选项啊。 好,第三个知识点,角的单位换算,哎,角,他都包括哪些单位啊?其实除了度以外,他还有其他的单位,就像我们学长度一样,对吧?长度单位不只有一个米啊,对吧?哎,他还有什么有分米啊,厘米,毫米或者什么千米等等,对吧?哎,我们需要对他, 有时候需要对他进行一些更精确的一些测量,是吧?哎,所以呢,为了更精确的度量这些角,我们作出以下规定,一度我们把它分成六十份,哎,那么每一份呢,就叫做一分,也就是说,一度他的六十分之一就叫做一分。那记做什么呢?就这样记一个小撇啊,这就叫一分, 也就是说一度呢,是等于六十分的,那同样呢,一分的六十分之一,我们把它叫做一秒,哎,记住,这有两个小撇,也就是说呢,一分是等于六十秒的,哎,这里一定要把它记清楚了。那我现在如果问你, 这个一秒等于多少度啊?大家能不能,能不能说一秒应该等于多少度啊?那是不是应该等于六十分之一度,对不对啊?这个一分等于多少度啊?那一秒应该等于多少分呢?一秒等于多少分啊?那是不是同样应该等于六十分之一分呢?对吧? 这里呢,要注意,他是六十进制的,这里啊,跟我们所说长度啊,这种十进制的是不一样的,对吧?这里也可以怎样来记忆呢?这种六十进制,其实呢,他与我们的时间单位换算其实是一致的,大家想一想,对吧?一个小时等于六十分钟,哎,一分钟等于六十秒, 这同样是六十禁止的,哎,我们角的这个度数啊,同样也是六十禁止的,哎,这里要把它分清楚。好这个例题啊,第一个,零点四五度等于多少分等于多少秒,哎,那我们知道一度应该等于六十分,对吧?哎,那两度呢,是不是就二乘以六十啊? 哎,那零点四五度是不是就应该是用零点四五,怎么样啊?再乘以个六十就行了呗,对吧?哎,就等于这么多的分, 那等于多少秒应该怎么办?那就在分的基础上再乘一个六十,是不是就等于多少秒了呀?对吧?啊,这就是单位的这个换算的方法。 第二个问题,他是反过来的啊,告诉我们多少秒了,问这个秒等于多少分,那思路其实一样的啊,一秒,我们知道一秒是等于六十分之一分的,对吧?那现在一千五百秒呢,是不是有六分六十分之一 再乘以个一千五百就可以了,对吧?哎,这些就是换算成多少分,那把这些分再换算成度呢?又怎么办?因为一分等于六十分之一度,对吧?那这些分等于多少度呢?是不是再乘以一个六十分之一就可以了呀?哎,这就是我们这个角的这个单位换算的一个方法啊。 好,看一下这个答案啊,我写的看不是特别的规范啊,大家注意书写的时候要注意一些。好, 接下来最后一个支点叫做方向角啊。那什么是方向角呢?叫做以正北或正南为基准, 他以偏西或偏东的角度来描述方向,他主要是来描述方向用的啊,比如说我们确定一个中心点,我把它放在这个十字的这个中间,哎,这个点,那现在呢?有另外的一个点,我们要描述一下另外的这个点在这个点的什么方方 像,哎,那这样怎么样描述呢?对吧?我们假设如果说另外一个点在这上面,哎,我们可以把这个中心点啊,和另外一个点给他连起来,比如说这样连起来,哎,另外一个点,我就假设他就在这里啊,在这里这两个点,哎,那这个点在这个点的什么方向上呢? 我们首先要量哪个角啊?这里我们必须要量的是这个角,大家要注意啊,我要量出来这个角是多少度,哎, 如果说打个比方,这个角我量出来刚好等于六十度,那这个点在这个点的什么方向?我怎么描述呢?首先我要描描现成是北,对吧?哎,因为他在上面吗?对吧?上北下南吗?对吧?哎,他是大概是在这个点的上面,所以说北北。然后怎么样呢?往这个方向是偏哪呀?是偏东,对吧? 哎,所以我要把它描述成北偏东多少度啊?六十度。哎,所以这个描述方法就叫做北偏东六十度, 所以我们是以北和南为基准,我们这里不把它说成是东偏北多少度,我们不这样说啊,我们必须要把北和南放在前面,哎,这里呢,比方说北偏东六十度, 这里要注意。好。那么另外一种情况,如果说这个点换位置了,他跑到下面来了,比如说在在这个位置啊,那同样我还是把这两个点给他连接起来,如果另外一个点在这里啊,好,连起来之后,那这个点又在这个中心点的什么方位上呢?这样怎么来描述?首先他是在他的下面,对吧?哎,那就应该是男 南偏哪呢?又往又往这个方向偏了,对吧?哎,所以呢,我要量的是这个角应该是南偏西,那这个角度数量出来,比如说他是三十度,那这个方位就应该描述为这个点在这个中心点的南偏西三十度这样的一个方向上,哎,对啊, 南偏西三书,这就是我们所说的这个方向角。在这里还有几种特殊的一些说法,叫做什么呢?就以下四种啊,大家看一下东北方向、 东南方向、西北方向和西南方向。我们看一下东北方向什么概念?应该就是东和北的正中间,哎,大概是这样的一个方向上,正中间这样的一个方向。哎,所以呢,这两个角啊,其实都都是四十五度,也就这个角他是四十五度的啊, 二十四十五度,我们可以把它说为北偏东四十五度,你也可以直接说他叫东北方向,这两个说法其实都是可以的, 那其他的东南、西北和西南,大家自己看一下,都是四十五度,对吧?哎,也就是说在这个西和北的正中间,哎,这样的一个方向上,我就把它描述为西北方向,哎,这两种说法其实是相当于是等价的,大家自己可以在 图上可以练一练。哎,量一下角度,自己找一下。这个点。以后啊,我们看到东北方向,你就不用管他到底多少度了,他表示的就是北边中四十五度这个技术就行了啊,这是一个特殊的一些说法,好,再看立体啊,教材上了,请在中国地图上测量出这个 哈尔滨在北京的北偏冬大约多少度,哎,这里如果有地图的同学可以自己找一下啊,哎,首先把北京和哈尔滨这两个点给他找到,哎,比如说是这样的两个点,对吧? 他问的是哈尔滨在北京的什么方向,那我当然要以北京为中心点了,对吧?好,我把这个方向给他标出来,把北京放在中间,然后怎么办?我把北京哈尔滨要连起来了,对吧? 哎,我把它连上。这时候你要测量的是哪个角度呢?这里一定要注意,你要测量的必须是上面的这个角,哎,要从正北开始到这条线,你要测的是 这个角的度数,哎,这个角度数测量出来之后,那么我就可以说哈尔滨在北京的北偏,什么北偏东,哎,然后呢?多少度, 哎,这就是这个答案,哎,具体的度数呢,我想大家自己量一下,我这里就不再帮助大家一起去量了啊,大家有地图的话,自己去测量一下就可以了。好, 总结一下今天内容啊,我主要学习了角,其实主要还是以复习为主了,对吧?哎,那角这部分知识我们主要复习了哪些知识点呢?首先角的定义,哎,我们从这个静态和动态两个方向对他的定义啊进行了一个归纳,对吧?这两个方向其实描述这个角定义都是可以的。 接下来呢,我们学习了这个角的分类,对吧?哎,分哪几类呢?锐角,直角,钝角,平角,周角。哎,他们的各自的度数,或者说是度数的范围,大家 一定要把它记清楚。好,接下来呢,又学习了角的表示方法,对吧?哎,那有几种表示方法呢?一二三三种,三个大写的字母,或者是一个大写字母,或者是用数字和这个希腊字母,对吧?哎,那什么情况下适用于哪种表示方法?一定要把它分清楚,尤其是这个用一个字母来表示的, 什么情况下适用,一定要把记清楚。好,接下来呢,就是角的单位换算,对吧?这个也没什么好说的,六十进制吗?对吧?好,最后一个呢,讲了这个方向角,哎,他是以正北或正南为基准,一定要记清楚了,配以偏西或偏东的这样的一个角度来描述方向。 好,那今天的内容呢,就和大家一起学习到这里啊,下节课呢,和大家一起来进行一个习题练习,欢迎收看啊,如果喜欢的话记得点下关注,如果大家学习中还有问题,可以留言或者给我发私信,我们下次再见。
210明老师课堂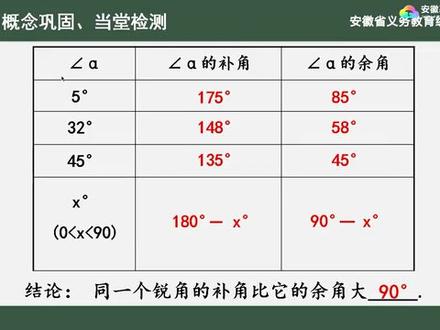 29:41查看AI文稿AI文稿
29:41查看AI文稿AI文稿同学们好,今天我们将继续学习户科版七年级上册第四章第五节角的比较。于捕鱼角第二课时, 首先让我们来共同回顾一下上节课所学习的相关知识, 如何比较两个角的大小。通过上节课的学习,我们知道 比较两个角的大小方法有叠合法和度量法。叠合法的关键点在于要将两个角的顶点于一边 互相重合,而另一边要放在重合边的同一侧。所以叠合法是通过观察形的角度来比较两个角的大小。 而度量法则是利用量角器去度量出量角的度数的大型。所以度量法是通过测量数的方法来比较角的大型。以上两种方法都可以用来比较角的大型。 此外,我们还学习了角的和叉形式, 如下图,请把其中一个角写成其他角的和叉形式。 观察图形可得,角 i o b 等于角 i o c 加上角 b o c, 这是角的和的形式。角 i o c 等于角 i o b。 减去角 b o c, 这是角的差的形式。 角 b o c 等于角 i o b。 减去角 i o c, 这也是角的差的形式。 同学们,你能求出下面两个角的和是多少吗?若 o 为直线, a b 上一点, o m 为任意一条射线,角 i o m 与角 b o m 的和是多少? 数学家华罗庚曾经说过,树缺行驶少直观。因此,我们首先要根据提议画出符合要求的图形。同学们,你们画出图形了吗? 观察图形,角 a o m 加上角 b o m 等于角 i o b, 而角 i o b 是一个平角,平角等 等于一百八十度,所以角 i o m 与角 b o m 的和是一百八十度。 我们借助几何图形的直观性来帮助我们解决数学问题的方法,我们在数学上称为数形。结合思想, 同学们,下面图形中每对角的和又是多少? 请大家计算一下。 通过观察 图形和计算,我们发现不论两个角有怎样的位置关系,两个角的和都等于一个平角一百八十度。 那么除了两个角的和是一百八十度这个特殊值之外,同学们,你们认为两个角的和还有什么特殊值? 通过观察图形,我们可以发现,除了两个角的和是一百八十度之外, 两个角的和还可以构成一个直角九十度。因此,不论两个角有怎样的位置关系,两个角的和都 等于个直角九十度。我们把两个角的和等于一百八或九十度的两个角赋予他们新的定义, 补角。如果两个角的和等于个平角,就称这两个角不为补角,简称不。 例如,角一加角二等于一百八十度,则角一与角二互 角一是角二的补角或角二是角一的补角。 余角。如果两个角的和等于一个直角,就称这两个角不为余角, 简称互愚。例如,角一加角二等于九十度,则角一与角二互余。角一是角二的余角或角二是角一的余角。 通过读角与者定义,我们可以发现,我们只研究两个角的数量关系,而与位置关系无关。 我们还可以用数学的三种语言来表示。古角语角的概念 有文字语言角一与角二互补,符号语言可以表示成角一加角二等于一 一百八十度。文字语言角一与角二互余,用符号语言可以表示称角一加角二等于九十度。 同学们,学习完补角与角的定义之后,你会求一个角的补角或余角吗?请填写下列表格。 当角阿化等于五度时,角阿化的弧角、角阿化的余角各是多少呢? 通过补角与角的定义,我们可以得知,当角 alpha 等于五度时, alpha 的补角是一百七十五度, 脚阿法的雨脚是八十五度。当脚阿法得以三十二度时,脚阿法的补脚是一百四十八度,脚阿法的雨脚是五十八度。 同理,当角 alpha 等于四十五度时,通过计算我们可得角 alpha 的补角是一百三十五,角 alpha 的余角是四十五。 那么当角阿法为正义的一个锐角时,它的古角又可以怎么表示呢? 根据补角的定义,我们可以得到角 r 的补角为一百八十度减 x。 同理,角阿法的余角可以表示成九十度减 x 度。那么请问大家同一个锐角的补角比他的余角大多少呢? 下面我们通过具体说例进行观察。当角阿法分别等于五度、三十二度、四十五度时, 角 off 的弧角减去角 off 的余角,我们发现都等于九十度。 那么当角阿法为任意的一个锐角时,这种结论还成立吗?我们用角阿法的独角一百八十 度减 x 度,减去角 r 化的余角九十度减 x 度。通过计算可得两种角的差仍然是九十度。由此,我们得到一个一般性的结论, 同一个锐角的弧角比它的余角大九十度。 下面我们来研究一下补角和余角又有哪些性质呢? 如图,若角一与角二互补,角一与角三互补, 角二与角三的大小关系是什么? 因为角一与角二互补,所以角一加角二等于一百八十五。 因为角一与角三互补,所以角一加角三也等于一百八十。 观察右边的两个等式,有等式的传递性,可得角一加角二等于角一加角三。 再有等式的基本性质,我们可以得到角二等于角三。观察图形,角一与角二互, 所以角二是角一的五角。角一与角三互补,所以角三也是角一的五角。 我们可以发现角二和角三都是同一个角的五角, 结果角二等于角三。如果我们用语言来归纳一下我们刚才所发现的结论,我们可以这样描述横角的补角相等。 如图,角一与角二互,角三与角四互,且角一等于角三, 角二与角四的大小关系是什么? 分析题意可得,因为角一与角二互补,所以角一加角二等于一百八十。 因为角三与角四互补,所以角三加角四也等于一百八十。度。 观察右边的两个等式,有等式的传递性,可得角一加角二等于角三加角四。 又因为角一等于角三,所以有等式的基本性质,我们得到 角二等于角四。观察图形,因为角一与角二互补,所以角二是角一的五角。 因为角三与角四互补,所以角四是角三的五角。而角一等于角三,我们称为等角,结果得到他们的补角也相等。 同样的,我们也可以用语言来归纳一下刚才我们得到的结论,挡脚的补脚相等。 结合上一题当中我们得到的结论,由此我们可以归纳出补缴的性质是 同角或等角的补角相等。 余角有无与上面补角类似的性质呢?同学们,这时我们不妨可以先进行一个猜想, 同学们猜想是什么呢?猜想同角或等角的与角也相等。 下面我们来分别叙述一下结论是否正确。 已知角一与角二互与,角二与角三互与,是说明角一 等于角三。同学们可以试着用自己的语言叙述一下相等的理由, 因为角一与角二互余,所以我们得到角一加角二等于九十度。 因为角二与角三不一,所以我们得到角二加角三也等于九十度。 利用等式的传递性,我们可以得到角一加角二等于角二加角三。 再有等式的基本性质,我们可以得到角一等于角三。 观察图形,角一与角二互余,所以角一是角二的余角,角二与角三互余,所以角三也是角二的余角。 角一与角三都是同一个角的余角。结果我们得到角一等于角三, 由此我们得到结论,同角的与角相等。 那么对于猜想等角的与角相等, 同学们能不能用自己的语言来说明一下他们相等的理由呢? 结合上一题当中我们得到的余角的结论,由此我们可以归纳出余角的性质是同角或等角的余角相等。 在研究语缴性质的时候,我们是类比补缴的性质进行说明的,因此这种方法在数学思想上称为类比思想。 下面我们通过习题进行巩固提升。一如右图点 i o b, 再 在同一直线上 o c。 平分角 i o b, 角 d o e 等于九十度回答下列问题, 首先我们来看一下第一问,通过分析题目的已知条件点, i o b 在同一支线上, 所以角 i o b 是一个平角,等于一百八十度。 o c 平分角 i o b。 利用角平分线的定义,我们可以知道角 i o c 等于角 b o c 都等于 于九十度。而题目当中还知道角 d o e 等于九十度,所以图中所有的直角有三个,分别是,角 i o c、 角 d o e、 角 b o c。 二、图中与角一相等的角。 观察图形,我们要从图形中去寻找与角一有关系的角。 有一中的结论,我们可以发现,因为角 i o c 等于九十度,所 所以角一加角二等于九十度。角一与角二固于,因为角 d o e 也等于九十度,所以角二加角三等于九十度。 角二与角三互余,我们从图中发现角一、角三都是同一个角,角二的余角。 那么根据与角的性质,同角的与角相等,所以我们得到图中与角一相等的角是角三。 三, 图中所有的余角有哪些?根据余角的定义,如果两个角的和加起来等于九十度,我们称这两个角互为余角, 有体翼可得。因为角 b o e 等于九十度,所以角二加角三等于九十度,所以角二是角三的余角。 同时我们还可以发现角 b o c 也等于九十度。 角三加角四等于九十度,所以角四也是角三的余角。所以 在第三问当中,角三的余角有角二和角四。 同时进一步观察图形,我们发现由于角二和角四都是角三的余角,利用余角的性质,我们还可以进一步得知,角二是等于角四的 四。图中角二的鼓角。观察图形,有的同学可能会说,角二的鼓角是角一、角三、角四, 因为角一加角二加角三加角四等于一百八十度。同学们想一想, 这个答案正确吗? 回顾一下补角的定义,我们可以发现,补角是指两个角的和加起来等于一个平角, 而刚才所说的角一加角二加角三加角四是四个角之间的关系,因此它不符合补角的定义。 很显然答案是 to。 另外,从图形上当中,我们无法直接找到与角二互为补角的角,怎么办呢? 结合第三问当中我们得到的结论,在第三问当中,我们寻找角三的余角,我们可以得到余角是角二和角四,并且角二等于角四。 因此我们可否这样可以想寻找角二的补角,我们只需要把它转化成去寻找角四的补角就可以了。 而在图形当中,角四的补角是什么呢?很显然是角 i o e。 因此角二补角其实也就是角四的补角。答案是角 i o e。 我们把寻找角二补角的方法, 把转化成寻找角四的补角的方法,在数学上称作是转化思想。 同学们,其实我我们身边的作图工具一副三角尺当中也蕴含着今天我们所学习的数学知识,下面我们来看一下。 如图,将一副三角尺按不同的位置摆放,在哪种摆放方式中,角阿法与角 bat 布。于哪种摆放方式中,角阿法与角 bat 布。 哪种摆放方式中,角阿法与角白塔相等。我们先来看第一幅图,观察图形可知, 角 alpha 与角白塔和上面直角三角尺的直角三个角构成了一个平角,因此角 alpha 加上角白塔加上九十度等于一百八十度。 进一步计算,可得角阿法加上角白塔等于九十度,因此角阿法与角白塔关系是互逾 图。图形二,我们发现两个直角三角尺中间有互相重合的角,我们称为公共角。观察图形,可得角 baca 与公共角形成一个直角, 角 alpha 与公共角也形成一个直角。那么由此我们发现角 bat 与公共角互与,角 alpha 也与公共角互与。 例如同角的与角相等,我们可以知道角 alpha 与角 bet 的数量关系是相等的。 图形三,观察图形,我们知道上面直角三角尺的两个底角都是四十五度, 而角阿法和角白塔分别是这两个四十五度角的五角。因为两个四十五度的角是相等的,所以我们利用 等角的五角相等,从而得到角 a 法与角 b 的关系是相等。 图形四,通过图形,我们可以直接观察到角 r 法与角 pet 形成一个瓶颈,因此在本题当中,角 r 法与角 pet 的关系是不本关系。 数学源于生活,用于生活,我们今天也可以用所学的数学知识来解决我们生活中的实际问题。下面我们来看一下实力。 如图,两堵墙为一个,角 i o b 大人不能进入围墙, 我们如何去求这个角的大小呢?由于不能直接去测量出角 i o b 的大小,所以我们必须去寻找与角 i o b 有关系的角。 通过今天这节课的学习,我们知道两个角的关系有互补或互余的关系。进一步观察图形,我们可以发现,如果我们能找到角 i o b 的补角, 测量出角 l b 的股者大小,我们就可以计算出角 l b 的大小。因此我们延长 l 到点 c, 此时 使角 i o c 是一个平角,角 i o b 与角 b o c 是互补的关系, 同时角 b o c 是通过测量可以得知角度的大小。因此我们再利用互补的关系得到角 i o b 等于一百八十度, 减去角 b o c, 从而得到这个角的大小。 好,下面呢,我们将和同学们一起对本节课的知识进行一个回顾再成长。首先,我们学习了 捕鱼角的定义,在定义当中,我们结合了树形,结合思想,从一般的两角河到特殊的两角河,一百八十度九十度赋予了捕鱼角的定义。 在捕鱼角的概念领域当中,我们由特殊的数据入手,得到了一个一般性的结论,同一个锐角的捕角比它的鱼角大九十度。 而在捕鱼饺性质当中的学习当中,我们利用了猜想验证类比的思想,从而归纳出捕饺和鱼饺的性质。而在捕鱼饺的性质定义当中,其中第四位 我们把寻找角二的孤角转化成了寻找角四的孤角。利用了数学的转化思想,最后我们发现数学源于生活,要回归生活。 同学们在数学知识的学习当中,学习数学知识固然重要,但是比知识更重要的是数学学习的方法,而比方法更重要的是我们学习数学的思维, 而比思维更重要的是同学们学习的兴趣和探索精神。通过本节课的学习,相信大家对于数学问题的研究的方法 和思想有了一定的感受和理解,希望同学们能够借鉴今天所学习的数学知识,借鉴今天所用到的数学方法和思想,尝试着在以后的学习当中去解决相关的数学问题。 同学们,今天这节课我们就上到这,下次再见!
10空中课堂 12:35查看AI文稿AI文稿
12:35查看AI文稿AI文稿哈喽,大家好,欢迎来到明老师初中数学课堂,我们今天一起来学习第四章基本平面图形的第四节角的比较。 首先来看一下这节课的知识点清单啊,这个知识点就比较少,对吧?有两个知识点。好,我们先来看一下第一个, 比较两个角的大小,在学这个内容之前啊,我们先思考一下啊,复习一下上次这个学的内容啊,就怎样比较两条线段的长短,对吧?哎,大家想一下,这有什么方法呢?我们当时一起学习了两种方法, 第一种方法就是测量,哎,第二种方法叫什么呀?叫做叠合,对吧?哎,有这两种方法,那叠合法呢?他具体应该怎么操作,大家自己回忆一下啊,如果不清楚了的话,赶紧回去复习一下啊。好,那接下来再思考一下,我们用啊类 类似的方法,你能不能想出哪些用来这个比较两个角的大小的这样的方法呢?哎,这里呢, 我们看啊,首先第一组,哎,如果让你比较这两个角大小,你应该用什么样的方法? 人家说这太简单了,这用眼睛看都能看的出来,对吧?那很明显是第一个角比较大一点,对吧?因为他张开的这个,这个这个范围比较大,对吧?这个呢,这个比较小,所以呢,我用眼睛看就能看出来,对吧?哎, 确实啊,这个方法是可以的,这个也就叫做直接观察法,对吧?它适用于什么呢?两个角啊,如果它的大小相差比较多的时候,对吧?我们可以通过直接观察的方法 就能看判断出这两个角大小,这也可以算得上是一种方法。好,那接下来呢,我们再看一下第二组啊,如果人比较这两个角大小 好像就不是很容易了,是不是没有眼睛,好像没有办法直接的给他观察,哎,那这应该用什么样的方法呢? 哎,别说,应该能想到我们可以用量角细意,对吧?哎,我直接量出来,哎,他是多少度,他呢又是多少度?我比比大小是不是就可以了?哎,那这个是不是也可以叫做这个测量法?哎,这种方法也是可以的。那还有没有其他的方法哎,有没有这个跟这个叠合法类似的一种方法,用来比较两个角的大小呢? 我告诉大家这个方法也是可以我们用来比较这样的两个比较接近的角啊,我们同样可以用度量法和联合法。哎,度量法和测量法其实是一个意思啊,他是用量角器来量的, 那杜兰法我就不多说了,两脚气我相信大家都会用,对吧?哎,那现在呢,我们主要讲讲这个叠合法。叠合法的话应该怎样来操作啊? 是用叠合法来比较两个角大小,这个为了看的清楚一点,我把那分别标成蓝色,我现在如果想比较他俩大小,我用用的是什么叠合法,对吧?哎,那我思考一下参照这个线段的这个方法线段是怎么样?是把这个两条线段先放在一条直线上,要把他这个端点重合呀,对吧?哎,看看另外一个端点是 哪一个在左边,哪个在右边呗,对吧?那这个呢,我其实同样我可以怎么样把他的顶点给他重合到一起,哎,然后呢,把他的下面这条边也给他重合到一起,也就说呢,我让这个 oa 和这个 opa 一撇重合到一起,哎,比如说把他移过来,对吧?哎,让他俩顶点重合,然后呢,这个 下面这条边也重换到一起,哎,这我观察一下上面这条边是不是,哎?谁在里面,那现在这个蓝色的在里面,红色的在外面,对吧?哎,谁在里面谁就小,谁在外面谁就大,那这样 比较很明显,红色这个角应该是比较大的,对吧?那这个呢,其实就是我们使用这个叠合法来比较两个角大小,我们可以归纳一下他的方法具体应该是怎样的呢?啊,也就是说呢,啊,将两个角的顶点以及他的一条边重合, 然后呢?说什么呀?另外的一条边呢?是放在重合边的同一侧,哎,注意这个很重要,对吧?我们刚才是把啊 oa 和 o 撇 a 撇重合在一起了,然后呢,我把这个 ob 和 o 撇 b 撇怎么样?放在了他们重合这条边的同一边, 你不能说 o 撇 b 撇在上面, o b 你把它弄下面来了,那这个是肯定是没有办法比较大小,对吧?哎,放在同侧之后呢,我们通过比较另外一条边的这个位置来比较角这个大小, 好,那如果说,哎,我们比较出来最后是这种情况,那说明什么?那肯定红色的比较大呗,蓝色 比较小,因为蓝色的这个在在内部,对吧?在里面,那这个呢,得到的结论就是应该是角 a 撇, o 撇 b 撇,也就是红色的角比较大,对吧?啊?那如果说通过叠合得到了一个这样的一种情况,那又说明什么?那肯定蓝色的比较大,对吧?那也就说明呢,是这个 a o b 是大于角, a 撇 o 撇 b 撇, 如果说经过叠合,我们发现这两个边完全重合在了一起,那就说明那就是他想等呗,对吧?这就是我们用叠合法啊,好,再来做一个立体啊,如图所示。这里这个这个图啊,有两个问题,第一个,比较角 doe 与这个角 dof 的大小,看一下 doe 在哪? doe 应该是这个角,对吧?有点像一个直角。第二个呢,是角这个 dofdof 应该是这个角,对吧?那这两角谁大呀?这个直接观察其实也就可以, 如果说想量一下的话,当然也这个没有什么问题,都可以,那肯定是这个角这个 b o e 比较大,对吧?好, 接了。第二个啊,他说呢,要比较叫这个 fod, 我看一下 fod 在这里,对吧?哎,然后叫 foe, foe 在这里, 这个通过职业观察肯定也可以啊,那肯定叫 foe 比较大,对吧?那同时我们看这里其实是不是也是可以用这个叠合法呀?因为你看他俩都有这个 fo 这条边,对吧? 哎,相当于把这个 fo 对角边重合在一起,并且他们顶点也都是点 o 也重合在一起,对吧?哎,那 od 呢,很显然是在内部, oe 呢是在外部,所以呢,就是叫 foe 比较大,对吧? 好,这个题啊,其实都都很简单啊,我想大家理解起来应该都没有什么问题。好,先来看一下第二只 啊,角的平分线,那角的平分线啊,其实呢,呃,我们可以参照的这个线段的终点来进行。什么线段终点呢?把线段分成两条相等的线段,这样的点就叫终点,对吧?哎,角的平分线,其实它的概念跟那个其实是类似的,对吧?只不过名称不太一样, 那这个线段的终点,我们也可以认为是这个线段的平分点,只不过他不这样叫而已,对吧?好,那我们就直接看一下角中线定义了啊,从一个角的顶点 引出的一条射线啊,他呢,把这个角分成两个相等的角,那么这条射线就叫做这个角的平分线,是不是非常简单画头啊,这个 你看,从这个角,我们看这个角 a o b 啊,它顶点是顶 o, 对吧?我从这个顶 o 引一条射线出来,叫射线呢,又叫 o c, 那这条射线 o c 呢,可以把这个角 aob 分成两个相等的角,也就是呢,这个角 aoc 和这个角 boc, 对吧?哎,如果这两个角相等的话,我们就把 oc 叫做这个角 aob 的角平行线。哎,这里要注意一点什么呢?这个 oc, 这个角平行线啊,他一定是一条射线,这个一定要记清楚, 这个射线的端点就是这个角平点,哎,所以呢,我们说角平分线,它是射线,我们不要把它当做是直线或者是线段,哎,这是一个概念上的一种错误,这里一定要给它记清楚。好,那么如何用数学语言把这个角平分线给它描述一下啊? 好,可以这样啊,如图涉险。 o c 是角 a o b 的平衡线,那么有以下结论啊,第一个角角 a o c 等于角 b o c, 对吧?这两角相等,并且呢,它们都等于角 a o b 的一半,这应该很好理解,对吧?那也可以说呢,这个角 a o b 呢, 等于二倍的角 a o c, 哎,同时也等于二倍的角 b o c, 这个应该是啊,很容易理解的啊。好,接下来再做一道例题啊,他说射线 o c 再角 a o b 的内部 下列条件不能说明 oc 是角 a o b 平分线的事,这看怎么样来判断这个角?呃,这个射线是不是他的这个角平分线,对吧?所以清楚起见,我还是把这个图给他画出来,假如说就这样的一个图,因为他也没说角日币有多大吗?对吧?就这样画了一下,那这个 根据哪个条件啊?他是不能说明 o c 是零件。我看第一个啊,角 a o c 等于二分之一倍的角 a o b, 角 a o c 是这个角,他呢,等于角 a o b 的一半,那是不是可以啊?他等一半的话,那角 b o c 肯定也等于一半,对吧?哎,他俩相加刚好呢,是等于角 a o b, 并且呢,他俩又 相等,对吧?哎,所以呢,这个 a 是可以的啊,可以说明,那 b 呢?角 b o c, 它呢也等于角二分之一倍的角 a o b, 那这个是不是也一样啊?哎,所以它也是可以。第三个角 a o c 加角 b o c 等于角 a o b, 我看角 a o c 这个角,对吧? 而这个角呢,加上角 b o c, 他俩相加等于这个大角,乍一看好像也没有问,但是我们这里要注意什么呢?他说的是通过这个条件能不能判断出 oc 是平衡线,对吧? 我们如果说假设,假设 oc 已经是贫困线的话,那这个 c 啊,肯定是正确的,对吧?因为他俩相加肯定要等于这个大角,但是呢,如果说只给你他俩相加等于这个大角,能不能说明 oc 是贫困线?这里不一定,因为什么呢?我过点哦,做任意的一条射线,哎,我 都有这个结论,比如说我的 oc 在这,对吧,那很显这里上下两个角不相等,但是呢,他俩相加是不是一样等于这个角 aob, 对吧?所以呢,通过这个呀,是不能判断出 oc 是这个评论线,对吧?哎,那反过来,如果说我们已经知道 oc 是评论线,那这个结论当然是成立。 所以呢, c 选项它是不能说明这个 o c 是平衡线,对吧?对,它不能说明。那这个 d 选项呢,叫 a o c 啊,他说角 a o c 等于角 b o c, 就这两个角相等呗,对吧?哎,那当然可以说明 o c 是这个文件了。所以呢,这道题答案应该就是 c 选项。好, 再看一个例题啊,教材上了,如图, o c 是角 a o b 的平分线,角 a o b 的平分线,也就就是说,这个角 a o c 和 角 b o c, 它俩相等呗,对吧?这两角相等啊,它是等于它的,好,就告我们,角 b o d, b o d 是这个角,对吧?它呢,等于三分之一倍的角 c o d 啊,它是这个角的三分之一。 然后呢,哎,又给了我们角 b o d 的度数,这个角是十五度啊,你看,是不是这个角十五度。哎,他已经告诉我们这个角好,接下来求什么呢?第一个,他问啊,角 c o d, c o d 等于多少度?那这很简单呢,哎,根据这个条件就可以了,对吧? 它等于十五度,然后呢,它又等于这个角 c o d 的三分之一,那角 c o d 很明显应该是等于这个十五度,再乘以三呗,对吧?所以呢,它应该是等于四十度。好,第二个角 b o c 等于多少度?那求角 b o c, 那我们看角 c o d, c o d 的度数我已经知道了,对吧?然后呢,角 b o d 的度数我也 已经知道了,那所以呢,这个角 b o c 它应该等于什么?它是不是应该等于角 c o d, 然后呢,减去这个角 b o d 啊? 他是不是应该是这个,对吧?哎,所以就应该等于四十五度,减去十五度。所以呢,这个角 b o c 应该是等于三十度,对吧?哎,这个我们可以求他们应该是等于三十度。好,接下来他求角 a o b a o b 啊,求的是这个角,那我们知道 o c 是他的贫困线呢,对吧? 所以呢,这个角 a o b, 它是不是应该等于这个角 b o c 的二倍啊?也就是应该等于三十度,再乘以二,对吧?所以呢,这个角 a o b 应该是等于六十度。哎,这就是利用我们角平分线的这个定义啊,来求角的度数,这也是一个经常出现的一种。 接下来呢,我们把今天的这个学的内容啊进行一个小节啊,主要学的就是讲的比较啊,内容不多, 一个是比较呃,角质比较的一个方法,另外一个就是学了角平分线,是吧?哎,那角比较的方法呢?就是这个度量法和叠合法,直接观察法的话,这就不假,对吧?度量法这个用连角器也没什么好讲。 那叠合法呢?主要就是啊,把这两个角的顶点及一条边重合,把另一条边呢放在重合的这条,这两条边的同一侧,通过比较另一条边的位置来比较大小。 好,接下来呢,角的贫困线,哎,他是定义是什么呢?就是从一个角的顶点引出的一条射线,哎,注意是射线,然后呢,把这个角分成两个相等的角,那么这条射线就叫做这个角的贫困线。好,概念性的东西,一定要把它记清楚。 好,那下一次课呢,我和大家一起来啊,做一个这一次的一个习题啊,欢迎大家收看。好啊,今天的内容呢就到这里,如果喜欢的话记得点下关注,如果大家学习中有问题,欢迎留言或者给我发私信,我们下次再见。
151明老师课堂
猜你喜欢
- 2656火星课堂









