粉丝3006获赞1.4万
相关视频
 00:41查看AI文稿AI文稿
00:41查看AI文稿AI文稿初中几何不管怎么考,都逃不出这六十八个解题模型,让孩子把它吃透,数学拿满分都有可能!初中常考必考的几何模型,这本书都帮你汇总好了。像三年二十九考的八字模型、三年四十二考的双角平分线模型、三年二十九考的将进一码模型等等, 每个模型都有立体讲解,从审题到图解分析,教孩子一步步完成解析,遇到选择题、填空题,就能直接套用结论写出答案,节省答题时间。看不懂也没关系,扫码还有视频讲解, 学完再做,对应便是练习,有学有练才能成长更快,让孩子把它吃透,初中三年不用愁!
 04:32查看AI文稿AI文稿
04:32查看AI文稿AI文稿跟着高师走,数学幺幺九。哈喽,同学们大家好,我是数学高老师,今天我们来讲解初中数学几何模型中的另一个最具模型,那就是瓜豆模型。什么是瓜豆模型呢? 它出自一个成语,叫做种瓜得瓜,种豆得豆,也就是说在这类模型中啊,它有两个动点,一个动点叫做主动点,这就是我们说的瓜,另一个动点叫做从动点,这就是我们说的豆。 而这个从动点的轨迹呢,会和主动点的轨迹呢,是完全一致的,如果主动点的轨迹是一条直线,那么从动点的轨迹也是一条直线。如果主动点的轨迹是一个圆呢,那么从动点的轨迹也会是个圆。那么如果主动点是个其他的几何轨迹,那么从动点呢,也同样是相同的几何轨迹,这就是我们所说的刮豆原理。 那么经过我这么简单一说呀,相信很多同学们还是处在云里雾里,所以要想识得庐山真面目,我们就要跳出此山中。那么下面呢,通过一个动画来给大家简单的展示一下什么叫做刮豆恶心 好这道题呢,是辽宁省的一道中考题,我们来看一下他这么说的,他说点 a 啊,在双曲线 y 等于负 x 分 之六的第二项线上的一个动点啊,这个 a 点可以动连接 a o 啊,并且交于另一只一点 b, 那 么这个 b 点跟 o 跟 a 点呢,必然是关于 o 点是对称的,那么以 a b 为底啊,做等腰三角形 a b c, 且 a c b 是 等一百二十度的, 那么点 c 在 第一项线随着点 a 这个运动啊,这个点 c 的 位置也在不断的改变,并且告诉你这个点 c 啊,它也在一个 k 值是多少, 那么这就是个典型的刮动模型了,我们先让这个点运动运动,大家来看一下这个轨迹啊,我们发现 a 点的运动过程中呢, b 点跟 a 点是对称的,所以它也会运动, c 点呢,当然要保持这个角不变,它也会跟着运动,那大家发现没有,这个点 c 的 轨迹是不是也像个双曲线啊?那么这个就是我们说的刮逗了模型了, 其中这个 a 点呢,称之为刮,也叫做主动点,而这个 c 点呢,是跟着 a 点的运动而运动,所以它称之为从动点,也就是我们说的逗。 那么主动点的运动轨迹呢,是一个双曲线,自然这个点 c 的 运动轨迹也就是个双曲线了,那么为什么这个曲线就是个双曲线,或者这个双曲线的 k, 我 们该怎么去求呢?哎,这时候我们先要了解一下瓜豆模型的一个基本的一个模型的定位是什么? 不只有两个动点, a 和 c, 还要有个定点,那么在这个时候里边这个定点呢,就是 o 点,因为 o 点始终是没有动的,我们连接 co 啊,做出来一个辅助线连接 co, 那么我们我们知道,因为 a、 c、 b 是 个等腰三角形,所以根据三线合一,因为 o 是 a、 b 的 中点,对吧?根据三线合一, c o 呢,必然是垂直于 a、 b 的, 所以这个角是直角,那大家发现没有,呃,这块呢,还有个角边线啊,这个角呢,应该六十度啊,三线合一嘛,而这个角是三二, 所以这个 c o 和 a o 的 比值啊,也是个固定的比值,应该是一比二、三比二,所以这里边那个 o、 a 比 oc 啊,应该是根号三比一,它是固定的比值。那么这就是我们所说的刮豆模型啊。比如说刮豆模型里边必须还有两个动点, a 点和 c 点,当然还得有个定点是 o 点,同时这个角 aoc 还得是个定值,这个角度是个固定的啊,那么在这道题里边是个九十度角, aoc 等于九十度, 并且它还要满足这两个动点到定点的这个距离的比值得是定值啊,那这道题里边是根号三比一的啊,固定,所以这就是我们说的刮豆模型。 那么接下来这个 c 点,这个 k 值该怎么去求呢?那么很简单,大家发现这是个直角三角形,我们直接利用一线三等角模型,所以我们分别往 a 过 a 点做 a、 d 垂直做 c、 e 垂直。那么根据这个一线三等角模型,我们知道这个三角形 a、 d、 o 和这个 c、 e、 o 自然是相似的,而且它的相似比是根二、三比一, 那么相似比,我们知道这个,因为我们知道根据绝对值这个 k 的 一个几何意义。我们其实求 k 值,就是求这个三角形的一个面积,那么这两三角形因为相似,它的这个面积比呢,应该是相似比的平方,也就是三比一,所以这两个 这个图形里边这个 k 值的绝对值之比也是三比一。那为什么是绝对值呢?因为 a 的 这个 k 值是负数,而 c 的 这个 k 值呢?它是个正数,它的绝对值之比是三比一, 而这个 a 点,它这个 k 值呢?它这个是负六,所以它的这个 k 二啊,那么这个 c 点的 k 值呢?应该是等于二的,那么它的这个六比二就是三比一嘛,所以我们求出来这个 c 点这个 k 值呢,它应该是二,那么这道题呢,也就解决了, 所以大家体现了没有,这就是我们所说的这个最简单的一个刮豆模型的原理。那么当 a 点运动轨迹是一条直线,当 a 点运动轨迹自然也就是个圆,这就是我们说的刮豆模型。
35我师老高 03:39查看AI文稿AI文稿
03:39查看AI文稿AI文稿同学们,今天我们一起来看一道八年级上册的手拉手模型的题目。看题,在直线 a、 b、 c 的 同一侧做两个等边三角形,也就是三角形 a、 b、 d 与三角形 b、 c、 e。 我 们做完这两个等边三角形后,又把 a、 e 与 d、 c 连接起来了。 第一问,我们要证明 a、 e 与 d、 c 是 相等的,这个时候我们应该如何证明?一般是通过三角形的全等得出对应边相等,这个时候我们发现它所在的三角形 a、 b、 e 与 d、 b、 c 应该是全等的。我们应该用到哪些条件呢?因为它是个手拉手模型,中间的 b 点就是它们的公共点。 从公共点出发,我们发现 b、 d 与 b、 a 是 相等的, b、 e 与 b、 c 也是相等的,有一组边了。然后我们再找对应角,因为等边三角形的三个角都是六十度,所以角一等于角二等于六十度。 这个时候我们发现中间还有一个公共角,所以我们角一加角三与角二加角三的和是相等的,那么我们就可以通过边角边、边角边来正全等就出来了。我们应该如何书写呢?第一步,先写证明。 因为我们要用到等边三角形的对应边相等,所以第一问,我们要先写上三角形 a、 b、 d。 三角形 b、 c、 e, 它们为等边三角形, 所以我们就得出来了, a、 b 是 等于 db 的, 同理 e、 b 也是等于 c、 b。 还有一个角一等于角二等于六十度,这个时候因为角一加上角三等于角二加上角三,所以我们就可以得到角 a、 b、 e 是 等于角 d、 b、 c 的, 这个时候就可以证全等了。在三角形 a、 b、 e 和三角形 d、 b、 c 中,首先我们先写边,就是 ab 等于 db, 然后我们再写角角 abe 等于角 db、 c, 接着我们再写最后一组边,就是 e、 b 等于 c、 b, 那 么所以三角形 a、 b、 e 就 全等于三角形 d、 b、 c。 我 们的判定依据一定要写上是 s、 a、 s, 判定完以后,它所以对应边相等就正出来了。 a、 e 是 等于 dc 的, 这是第一问,第二问,我们要求线段 a、 e 与 dc 所夹的角 a、 f、 d。 这个时候我们一般会通过八字模型来找看老师给你画的这个线段,我们把它描起来以后,看这个八字模型, 首先我们这标上一个四和五,四和五,通过第一问的全等我们就可以推了出来了,这个时候发现六和七又是一组什么呀?对顶角,因为三角形的内角和是一百八十度,八字形现出来以后,我们就可以得到所求的角与角一是相等的,也就是六十度。写的时候我们应该如何写?先写解, 然后第一问,我们是正完全等了,我们应该写由全等可知,我们角四是等于角五的,然后又因为什么角六等于角七,它们俩是因为是一组对顶角,所以它们是相等的。 然后同样在三角形里面,我们发现角 d、 f、 a, 它是等于一百八十度,减角四,再减角六, 然后角一呢,它也是等于一百八十度,减角五,再减角七的,所以说我们就可以用等量代换得出来了,角 d、 f、 a 是 等于角一的,所以就是等于六十度,也就是所以角 a、 f、 d 的 度数 为六十度。这就是我们今天讲的手拉手模型,同学们喜欢的话给老师点个关注吧!
19辉县市昂立教育 00:26查看AI文稿AI文稿
00:26查看AI文稿AI文稿八上数学最难的四十八个几何模型全部吃透,逆袭班级前三。八上数学四十八个几何模型一, a 字模型、鸡爪模型,腋下两角合等于上下两角合。 八字模型,三角形中五大模型见八字除对顶,剩余的两角之合会相等。飞镖模型也叫燕尾型、双角平分线模型。三个结论完整版分享!
 12:51查看AI文稿AI文稿
12:51查看AI文稿AI文稿初二期末必考的手拉手九大结论,今天明天老师一次性带大家彻底掌握考试,遇到必定多拿二十分。 前提条件, abc 是 一个等边三角形, a、 d、 e 也是一个等边三角形,并且 b、 a、 e 在 一条线上,那左手拉左手 b 拉 d, 右手拉右手 c 拉 e 来第一个结论,三角形 a、 b、 d 全部全等于三角形, a、 c、 e 呀, 好,这里是 a、 b、 d, 这里是 a、 c、 e, 这是我们熟稞熟的经典结论了,只要拉上了手,就有全等。为什么标下条件啊? ab 等于 a、 c, a、 d 等于 a、 e。 这个大角是我们的六十度加上六十度一百二,这个大角也是六十度加六十度一百二,所以第一个必定全等,全等的依据是 s、 a、 s。 再来看,大家会发现这个大三角形被 a、 c 这条边是不拆成了一个 f 出来,就会产生 a、 b、 f 和 a、 f、 d 这两个三角形一大一小。然后我们看这个 a、 c、 e 啊,这 a、 c、 e, 它也被拆成了上面这一个大的,被这个 g, 这个点底下这个小的。 那你看这个大的跟这个小的有什么区别?全能吗?来看这个 a、 b、 f 跟 a、 c、 g。 全能吗? a、 b 等于 a、 c, 你 这有六十度,我这都是六十度,还缺一个条件。别忘了啊老师,这个顺序其实就是大家的证明顺序,包括大家在做题的时候,他也是一二三四给大家选项了之后你一定是从前往后,因为上一个很可能给你,下一个是提供条件的,是台阶。 咱们上一问正出了 a、 b、 d 全等于 a、 c、 e, 现在你有俩条件,缺一个,那你看看上一问能不能给你提供一点条件,我们会发现哦,这个小角 跟这个小角是上一问全等中的对应角,就能用上了。第二个全等就用上了,在一个三角形中去看判定依据啊,两个角一个边,边是夹边,所以它是 a s a 全等,这大的 和这大的全等了,那剩下的这个小的呢?也就是我们第三个 a、 f、 d 和这个 a、 g、 e, 它俩呢?也自然全等了。你想证明的话,那可以是用一样的 说,那我这圈也等于这个圈哦,你这个边也等于这个边,你这俩还都是六十度,也可以用 a s a 去中。 接下来我们看第四个结论, b、 o、 c 是 六十度,这个小角是六十度。 手拉手必备的,就无论这题是什么样的三角形,只要是两个等腰三角,不一定是等边啊,只要是两个等腰三角形共顶点,并且拉上手了。大家记住,必须有两个经典的结论,第一个是拉手之后形成的三角形全等,第二个就是 拉手线啊,拉手线是谁呀?我 b 拉上 d 了,如果我管 b 跟 d 交左手的话,那这个右拉右 c 打上 e 了。 拉手线的夹角必定等于什么?必定等于你这个等线段的夹角。一开始你不是等腰三角形吗?你这不有一个顶角吗?等线段的夹角为啥呢?其实它更本质的呢是旋转等,我们到这个初三的时候会学,那现在呢,咱们怎么去挣这两个角相等? 就是这学期我们学的经典的倒角模型,当你不知道怎么倒角的时候,你就去瞄角的两边, 大家看啊,那你说我描 o 的 两边,我去描这 a 的 两边,你看围成什么图形?是围成一个八字,八字的结论是这个加这个,等于这个加这个, 那它俩还什么关系啊?相等啊,所以呢,那这俩自然也相等。你说这个结论咱是怎么导出来的?咱是用了全等加八字, 如果你发现这道题说万一没有八字呢?有没有可能?也有可能,如果用的不是八字,那一定是四边形内角盒,你碰到过吗?来第五个三角形, a、 f、 g, 我 如果把这个 f g 这块给连上了,说它是等边三角形,大家看怎么整?上面这几个结论,我要用到哪一个? 要用到这两个边相等,这两个边是第几个结论的?是不是第二个结论的?这两个三角形 a、 b、 f 和 a、 c、 g 是 不全等于角是多少度?假角是六十度, 于是有一个角是六十度的。等腰三角形是等边三角形,所以我们也用到了一个全等,加上我们等边三角形的判定,用的是两边一角。好,第六个, f g 平行于 b 一, f g 平行于 b 一, 那是不是得看同位角内角啊?你先看到哪一个?哎,内错轻松解决。根据第五个,你看一环扣一环,根据第五个,你是整边三角形,所以你这必然是六十度,那我这也是六十度。内错角相等,两只线平行。好,我们这里用的是内错。 第七个。从第七个开始上难度了啊,同志们可能会考到选择填空的压轴题,也可能会考到大题的压轴题。说如果你连上 o a, 你这必然是角平分线, o a 平分这 f、 o g, 那 我怎么正呢?这两个角相等呢?大家会想到什么?其中的一条路就是角平分线的判定。 角平分线的判定说的是什么?你要想正,这个是角平分线,你就过这上面的点,这里上面有,除了这 o 还有谁?也只有这个 a 了,咋着?向两边做垂,过 a 向这边做垂,假设这是 m, 过 a, 向这边做垂,好,这是 n, 我 要证出来。 am 等于 an 的 话, 根据角平分线的判定,你在角的内部,你到角两边的距离还相等了,那你就在角平分线上,那我怎么证明 am 等于 an 呢?这里的方法非常多,我们可以用法一 全等。什么意思啊?你看一下 a m 跟 an 四角形有没有全等的,这时候你会看到了 abm 和 acn, 你 去证吧,轻松就能证出来。这老师不说了。 第二个方法是迷你老师想重点给大家拓展的,因为它非常快,而且这个方法呢,在整个初二初三经常会被用到,就叫面积法。 a m 咱是向谁做垂的?咱是向整个 b、 d 这个边做垂的,它就相当于咱们第一个三角形,这 a b d 这三角形 b、 d 边上的高, 那你 an 呢?你是向 c e 做垂的,就是跟它全等的这个三角形 c e 边上的高。那你 b、 d 跟 c e 是 不是对应边?是对应边吧,你面积相不相等?你全等了,面积相不相等还相等,那你对应边上的高呢?是不自然就相等了,所以咱用面积法就能做出来了。两种方法分享给你啊。 好,接下来第八个,第八个跟第九个咱挣一个就行了。一个意思,第八个说的是,来,再往这擦一下, o b 等于 o a 加 o c。 来看一下这三条边, o b、 o a、 o c, 这是米老师之前讲过的什么鸡爪子鸡爪图,而且它的关系还是求和,所以你可以往哪里去想?这思维也非常多,你可以往截长补短上去想。 好,这是第一个思路,第二个思路还可以往哪去想?还可以往构造旋转全等去想。什么叫旋转全等? 当有等腰三角形存在的时候,你就可以转,对吧?你就绕着一个点转,那第三个就是说我就从等边三角形的性质,你这题不是有等边三角形吗?我就够等边三角形,非常多的思路啊。 然后很多同学的难点就在于说我不会走第一步,那现在米老师就告诉你如何走第一步,第一步就是你要选三角形, 无论你用什么方法,你得选出目标三角形来,因为啥?因为你无论构造谁跟谁全等,你是不是都要转移边?转移角, 那你转移谁呀?你不要转移你这些目标边、目标角吗?对不对?好,所以你就要关注他们仨所在的三角形, 而且条件比较多的。为什么?因为你要构造全等,是不需要等线段,需要等角啊,你要当然关注条件多的,大家的选择其实非常多,当选择非常多的时候,我一般会选择小的那个,因为小的那个接上节就可以了,如果你选大的,可能还得补。来吧,大家看看它们都围成哪些三角形? 你比如说这个 o a 是 我们的目标边, o c 是 我们的目标边, a c 是 不是一组等线段?是非常好的一个构造跟它全等的一个三角形啊?这三角形 a、 o c 可选 好,那看还有谁可选?你看这个 o b, 这个 o a 也是我们的目标边,那 b a 呢?是不是等线段?哎?它跟它的地位有什么区别吗?没什么区别,三角形 o a、 b 可选,别的还有吧?别的就没啥,就这俩。那这俩选哪个?我选小的,是不是它小一些,其实它都可以做出来,我选小的,这个好。然后第二步,假如说我们是从截长补短的,这是我的等线段, 所以你要构造跟我全等的话,你,你得有这条边,你得有跟我相等的这条边,那就是 bc 和 ab。 这么多方法,咱们选哪个呢?那这样吧,因为如果说我选这个截长补短的话,大家可能说我在谁上截呀?或者说我在谁上补啊?方向特别多,那咱们这个题结合它是等边、三角形以及未来旋转全等,会是我们的压轴难点,咱们就讲旋转。 接下来咱们看这个三角形,我要转它,我绕着谁转,绕谁呢? 绕着等线段的端点转就行了。你比如说 c, 这是不是有一组等线段, c a 等于谁? c a 等于 c b, 我 就可以绕它转,当然你绕着 a 转行不行?哎,也行,你说这辅线到底咋做呀?老师,你先把图转过去,你自然就知道辅线怎么做了。来,大家先转,说我 c a 转到这转了多少度? 是不转六十多,于是你这个 co 就 得怎么样?是不是绕着它转也转多少度也转六十多? 你发现,那我转六十度,我这个 o 点假设是点 p, 转到六十度之后,这个 p 点是不是正好落在 b o 上的呀?你是不会纠结这个问题, 那它是不是一定落在为什么?因为你这样的话就会把 o a 带到这儿,这不正好截长不短的那个方向,所以它一定落在这儿。接下来你就看一下你这辅线如何描述能让你有这个权能。 这个描述方法也非常多,比如说我们这个第四问,说正了这个角是六十度了,那我就直接结这个三角形,是不一定是等边三角形啊?因为这两个粉色的相等,这还是六十度,是不一定等边三角形,那我就直接结,结谁?你没法说结 o p 结 cp 对 不对?你在这说结 o p, 所以 我就结 o p 等于 o c, o p 等于 o c, 于是你看你这个 o c 是 不是产生了一个,现在是不是就已经产生一个截长的效果了,它就已经挪到这来了?我产生了一个等边三角形 o c p, 我 还产生了一个截长的效果,我只要证什么?我是不是只要证这个 b p 是 不是等于这个 o a 就 好了? b p 等于 o a 吗? 那我怎么正? b p 等于 o a? 正线段相等全等,我就看这样做。这个等边三角形之后,产生了一个截长的效果之后,这俩三角形能不能全等?一旦全等了,那就好了, 来屡条件吧。第一个条件, c b 等于 c a。 第二个,等边三角形,是不是 c p 等于 co 两组边了,就差啥了? 你不可能第三组边,第三组边是你要正的相等是不一定差角,我一定是要关注一下你这个小不点假角等不等于我这个小不点假角等不等?当然等,因为你得出它是等边三角形之后, 那这个角自然就是多少度。六十度,两个六十度减去中间公共部分是不剩下的,就相等了。两个点点就相等于是 s a s, 我 就正出了这两个三角形全等, 最后三角形 c, b, p 全等于三角形 c, a, o 全等的依据是 s a, s。 好 了,这你也证出来了, b p 等于 o a 了,那 o a 在这转移到这, o, c, 咱转移到这,是不是一加第八个出来了,那第八个出来了,第九就出来了,第九就是反方向, o e 等于 o a 加 o d 就是 完全把那个大的啊变成反回来这个了。好,九个结论你学会了吗?跟着问题走,数学不用愁。
158初中math铭迪老师 06:03查看AI文稿AI文稿
06:03查看AI文稿AI文稿手拉手模型是我们八年级数学几何的重要模型,是我们一定要掌握的啊,考试经常会考到, 这是一个期末考试的真题啊,我们来看一下,如图,点 c 是 线段 ab 上除 ab、 y 的 任意一点,分别以 a、 c、 b、 c 为边,在线段 a、 b 的 同旁做三角形 a、 c、 d 和做等边三角形 a、 c、 d 和等边三角形 b、 c、 e, 也就这是等边三角形,这是等边三角形, 然后去连接谁,连接 a、 e, 再连接 b、 d, 然后交于 m, 交于 n 啊。 第一问,让我们求证 a、 e 等于 b、 d, 我 们看啊,它是等边,让我们求证谁? a、 e, a、 e 在 哪里啊? a、 e 在 这里,我们的 a、 e, 它等于谁啊?等于 b、 d。 那既然是两个等边三角形,它的顶点又对在一起,这就符合了这个手拉手模型啊,也就是三角形 a、 d, c, a、 d、 c 这个三角形,它的左手 去拉三角形,谁呀?哎,这个左手啊,点 e 和点 a, 拉左手拉起来,右手,这右手去拉右手, 然后形成我们新的三角形,一定会全等哪三角形呢?也就是我们的三角形 a、 c、 e, a、 c、 e, 这个三角形和我们的 啊 b、 c、 d 相等,那我们看啊,这里,这里, b、 c、 d, 它就等于我们的 c、 e 啊, b、 c 等于 c、 e, 然后我们的这条边 c、 d、 c、 d 是 不是等于我们的 a、 c 啊?然后我们又有,又有谁呢?有这个啊!六,这个六十度的角啊,六十度的角。呃, 我们这个角,这个角和这个角这个角, 因为这是六十度这个小角,这是六十度小角啊,所以这个角一百二,这个角一百二, 所以这就构成了一个 a、 c、 e 和 b、 c、 d 全等,全等以后,我们的 a、 e 和 b、 d 就 相等,这是一个典型的手拉手模型。 好,第一题,第一个问,我们处理好,我们再看,请判断三角形 c、 m、 n 的 形状,并说明理由。三角形 c、 m、 n 让我们判断这个三角形,那首先我们知道啊,这是六十度, 这也是六十度,很明显,这三点共线啊, abc 三点共线,那这个也是六十了啊,直觉已经告诉我们了啊,这个三角形应该是一个等边三角形,那么有一个六十度,我们再去找 两条边相等就可以了。我们现在的观察,我们还能在这里找到一个全等, 也就是三角形。谁啊?这个,呃, a、 c、 m 这个三角形 a、 c、 m 和我们的啊,这个 c、 d、 n 这个三角形。 好,我们这个这个三角形应该是全等的。第一问当中,我们已经证明了,这个大三角形啊,全等,那么全等呢?全等之后,这个大三角形的 大三角形的这个角,这个角是不是等于我们这个角,哎,这两个角等,这两个角等,我们再找啊,再进去找。呃,我们的这个角, 这个角是六十,哎,这个角,这个蓝色的假角,它也是六十。 好,已经有两个角,两个角相等,那我看 a、 c 的 边和 c、 d 的 边是不是也等,所以角,边角,角,边角,所以我们的三角形 a、 c、 m 和 d、 c、 n 全等。 有三角形 a、 c、 m 全等于三角形 d、 c、 n 全等,我们要怎样?哎,我们就看啊, 我们这个短的短的边,蓝色三角形短的边和红色三角形短的边是不是相等?所以我们 c、 m 它等于 c、 n 啊,假角又是六十度,所以这个三角形 c, m, n 是 等边等边三角形啊。这个题希望对你有帮助。
38那些年 03:58查看AI文稿AI文稿
03:58查看AI文稿AI文稿手拉手模型是我们这次八上期末考试的必考模型哎,他的考频非常之高,今天老师一个视频带你一起复习手拉手模型的四大经典结论,一起来看。首先啊,在做题之前,我们要识别清楚到底什么是手拉手 哎,它主要有三类,第一个是等腰三角形手拉手,第二个是等边三角形手拉手,然后就是我们的正方形手拉手, 其中最常考的就是等腰三角形手拉手,今天老师就以这个为例,比如说现在给了我们两个等腰三角形 a、 b、 c 和 a d、 e, 你 看它俩有什么样的特点呢?首先它们有公共的顶点,并且它俩顶角,也就是角 b、 a、 c 和角 d、 a、 e 是 相等的, 你看共顶点有相等的边,并且顶角相等,这就是非常典型的手拉手模型的特征。 好,我们来看,左手是 a、 b 和 a、 d, 所以 说连接 b、 d, 右手是 a、 e 和 a c, 所以 说连接 c、 e。 那 么辅助线做完之后,第一条最核心的结论就是 b 出全等,我们看这两个组成的全等三角形,也就是黄色和蓝色的三角形,一定就是全等的。为啥? 你看 a、 b 和 a、 c 是 两个等腰相等, a、 d 和 a e 也是两个等腰相等。同时我们看,如果中间这个小角是 alpha 的 话, 此时角 b、 a、 d 还有角 c、 a、 e, 它俩是不是都是等于这个相等的顶角减去 alpha 呀?哎,所以说这俩角一定就是相等的,那么边角、边它俩就是全等的。这是我们手拉手模型最最核心,也是最为重要的一个全等三角形的结论。 好,那它俩全等,我是不是就可以得到 b、 d 和 c、 e 是 相等的呀?哎,对应边相等,这就是第二条核心结论。 好,我们继续来看。那么第三条结论呢?就是角 d、 h、 c, 它应该和顶角 b、 a、 c 是 相等的, 也就是这两个拉起来的手,哎,把它延长,它俩组成的这个角应该等于顶角。为什么?我们来观察,现在在三角形 a、 g、 b 和三角形 h、 g、 c 中,我们刚才知道它俩是全等的, 对吧?所以说角一和角二这俩角是相等的,这里还是一组对顶角。那你看这两个三角形中 剩下的这一组角,是不是应该就是相等的角了?哎,也就是等腰三角形的顶角还有两个手,他俩组成的这个角就是相等的。这是第三条结论。接下来我们再来看第四个结论, 也就是 h、 a 平分角 d、 h、 e 什么意思呢?也就是这两个手,哎,通过延长,它俩出现了一个焦点 h, 把这个焦点 h 和顶点相连接,此时组成的这个 a、 h, 它一定平分这个角。怎么去正?可以使用面积法。 哎,其实这一切的源头还是来源于它俩是全等,那它俩全等是不是面积相等啊?所以说,如果我此时以 b、 d 和 c、 e 为底边的话,所以说它们这个底边上做出来的高一定就是相等的。 好,那你看 b、 d 为底边,现在我过 a 点做 a、 g 垂直于这条边,现在我再过 a 点做 af, 垂直于 c、 e 这条边。 那出现的这两个高是不是 a、 f 和 a g 应该就是相等的?那同时这还是两个直角,所以说再加上 a、 h, 这是一条公共边。那么在直角三角形 a、 g、 h 和直角三角形 a、 f、 h 中是不是 h、 l 它俩全等啊? 它俩全等是不是就可以得到对应角相等?也就是,哎,这俩角是相等的,那么 a、 h 自然就是角平分线。以上就是我们手拉手模型的四大核心结论,一定在考前复习完!
166阿畅讲数学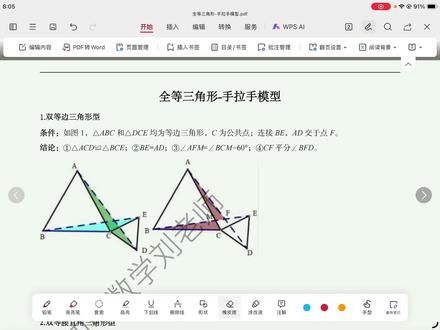 18:18查看AI文稿AI文稿
18:18查看AI文稿AI文稿同学们大家好,今天我们讲的是全等三角形手拉手模型。手拉手模型是初中几何中非常重要且常见的模型,它的核心是共顶点、共顶点、等线段 等顶角。通过旋转构造全等三角形, 主要用于证明三角形的全等或相似。我们今天只讲全等。他得名于两个三角形共享一个顶点,就像这个三角形,这个三角形他是一个人,这是另一个人,这个顶点 是这个三,这个人的右手,这个顶点是他的左手点。 a 是 这个三角形,相当于一个人的右手点。 b 相当于这个人的左手,左手牵左手, b、 e 相连, a、 d 相连,他就相当于一个人左手牵左手,右手牵右手, 这两个顶点一定得相对应。将两个等腰三角形绕着公共顶点旋转,某一个角度完全重合自这两个三角形 构成的手拉手全等也叫旋转型全等,常用边角边判定定力证明全等。掌握该模型有助于快速识别图形关系,简化证明过程。在复杂图形中 常需要添加辅助线构造手拉手模型来解决问题。该模型通常涉及等边三角形、 等腰直角三角形,还有等腰三角形或者正方形等特殊图形,通过旋转产生全等三角形。下来,我们言归正转让第一种,它是双等边三角形, 他总共有以下四个结论,我们逐一证明。首先我们看条件,三角形 a、 b、 c。 三角形 d、 e、 c。 三角形 d、 c、 e 均是等边三角形, c 为公共顶点连接 b、 e、 a、 d 交于点 f, 这个点是 f。 让我们开始证明第一个三角形 a、 c、 d。 全等于三角形 b、 c、 e 这两个三角形都是等边三角形的话,我们就知道了 a、 c 他 和 bc 他 是相等的, 而又有 c、 e 和 c、 d 也是相等的。我们又知道这两个角它都是六十度,这又是一个公共角, 所以呢,这个角和这个角它就是全等的。因此呢,我们就运用 边角边就可以证明这两个三角形全等。这两个三角形全等了以后, b、 a、 d 是 它的一条对应边。接下来我们看第三个,第三个的话,它是要让证明角 a、 f、 m 这个角和角 b、 c、 m 是这个角。我们通过第一个结论三角形全等,我们已经知道了这个角 f、 a、 m 还有这个角 m、 b、 c, 它是三角形的对应角,也是相等的。同学们看,这里还有一组,这是对顶角。又知道三角形的内角和一百八十度角 a、 f、 m 等于一百八十度减 角 a、 m、 f 再减角 f, a、 m 角 b、 c、 m 等于一百八十度减角 b、 m、 c 减角 m、 b、 c 这两个是对顶角相等,这两个是对应角相等。因此呢,我们也可以就可以得出来这两个角也是相等,等于六十度,这个我们也没问题。接下来我们 连接 cf, 他 说 cf 他 平分角 b、 f、 d, 我 们也知道了,如何证明他是平分呢?是不是只要知道了这个点到角两边的距离相等,就知道这个这条 cf 这条线 就平分角 b、 f、 d, 我 们先做辅助键过点 c 分 别做 b、 f 和 d, f 的 垂线,分别交于 p、 q。 有 这个图像我们可以看出来,这 p 它是不是三角形? a、 c、 d 在 a、 d 边上一条高了,而 c、 q 呢,它又是 b、 c、 e 三角形,在 b、 e 边上一条高。前面我们第一个条件我们已经证明了这两个三角形它是全等的,全等的话,它的面积也就是相等面积的话,等于二分之一,乘以 a、 d, 再乘以 c、 p, 因为它们全等,所以面积也是相等二分之一。 b, e 乘以 c q a d, b, e, 它是对应边相等,又有二分之一,所以呢, c、 p, 它等于 c、 q 两条高线,它是相等的。因此呢,是不是就可以得到结论, c、 p, 它平分角 b、 f、 d。 所以呢,第四个结论我们也就知道了。这四个结论呢,都是我们做题通常很常见的结论, 同学们一定要知道证明他的方法。接下来我们看这个手拉手模型,是由两个等腰直角三角形手拉手而来的,我们看 c 仍然是他的公共点 连接,这,这就让他们牵手了 b 和 ad 对 应点,然后再继续证明。我们看第一个 abc, 它是一个等腰直角三角形,这两条边相等,呦呦,这两条边也是相等, 这是一个公共角,这个角是不是九十度加公共角,这个角又是九十度加公共角。因此呢,还是运用边角边来证明三角形全等,全等了的话, b、 a、 d 仍然是对应边相等。这两个结论没问题, 现在他要证明第三个,是需要证明这垂直。来我们证明一下这个角是不是仍然是他们手拉手形成的一个夹角,夹角等于他的三角形的一个顶角,也就是这个结论。来我们证明一下。看 b m c, a, m n 这两个三角形,我们已经知道了这两个三角形全等,因此呢,这个角和这个角它是对角相等的, 而这又有一个对顶角也是相等。因此呢,和上面这一样,一百八十度接上 这两个角,角 a、 n、 m, 等于一百八十度。减角 a、 m, n, 再减角 m a, 嗯,这个角呢,它是角 a、 c, b, 等于一百八十度。减角 b、 m、 c, 再减角 c, b、 m, 这个是对应角相等,这个是对应角相等。没有。在这个三角形里面, b、 m、 c 中,我们知道这两个角加起来是 九十度,所以这两个角加起来也是九十度,所以这这两个角我们就知道相等的,它是九十度。所以第三个我们就证明出来了。接下来我们看第四个结论。第四个结论,我们连接 c、 n, 它仍然是要证明 c、 n 平分角 b、 n、 d。 我 们还是和上面一样,分别做两条边的垂线, 分别交于 p、 q 两点。第一个结论,我们已经证明这两个三角形相等,因此这两个三角形的面积它也是相等的,所以三角形面积它就等于二分之一。 a、 d 乘以 c, q, 这是 s 三角形 a, c、 d, 它就等于二分之一,乘以 b, e, 再乘以 c、 p, 这是 s 三角形。 b、 c、 e, 它俩是相等的。又有 a、 d、 b、 e, 它是三角形的对应边,所以这两个角也是相等的,所以我们仍然可以退出来。 c、 q, 它是等于 c、 p 的, 因此呢,结论也就出来了。 一个点到两条边,它的距离它是相等的,因此呢,这个点也在角平分于角 b、 n、 d。 这个结论我们也就求出来了。 接下来我们看两个都是等腰三角形的,这种情况说是 a、 b, c 和 d c, e, 它是共顶点 c 的 等腰三角形,然后在手拉手连接 d、 a、 b、 e, 这个点是 f。 我 们首先看第一个 a、 b、 c、 d、 c、 e 都是等等腰三角形,说明这两条边相等,这两条边也是相等。我们又知道了这个角,这两个角也是相等,这又是一个公共角,这个角它等于这个角。 所以呢,这个这两个三角形我们就可以站出来,他是全等的,仍然是要用边角边三角形全等以后,这是两条对应边也相等,没问题,他仍然是要证明 角 a、 c、 m 三角形,一个顶角和两条手拉手交界的这个角是相等的。接下来我们证明这是一个对顶角,这是一组对应角,用一百八十度剪, 我们方便的话,它会标成九二九三九四,一百八十度接九一接九三, 一百八十度减角二,减角四,这两个是对应角,这两个是对应角。角 a、 c、 m 和角 b、 f、 m 这两个角也是相等的,我们也就证出来了。 这证明的话,同学们还可以这样,你们看这个角分别这两个三角形, 它的一个外角,外角,这个是外角的话,它一个外角是不是也就等于这个角加这个角, 这个角也是加这个角,仍然等量等会还是一样的,还是这个角,这两个角相等,这个我们就证明出来了。接下来我们看第四个结论,但是要证明 c、 f、 c、 f 平分角 a、 d 平分角 a、 f、 d 这个角,因此呢,我们仍然是正因此,我们仍然是过点 c 做它的垂线,分别做这两条边的垂线。 我们已经证明了三角形 a、 c、 d 全等于三角形 b、 c、 e。 仍然我们还知道三角形 a, 三角形全等的话,它们面积三角形全等的话,它们面积仍然相等的。 这个是 p, 这个是 q 还是三角形 a, c、 d, 它等于二分之一 a, c、 d, 嗯,这个错, 这个是 b, 这个是 a, a, c、 d, 它等于二分之一的 a、 d 乘以 c, p, s。 三角形 b, c, e 则等于二分之一 b, e 乘以 c, q, 面积相等 a, d, b、 e, 它对应边相等。因此我们就可以得出来 c、 p 等于 c、 q, 是 不是我们又可以证明了 c、 f, 它平行角 a、 f、 d, 这个面对吧?这里我们都知道。接下来我们看双正方形四边形 a, b、 c、 d, 四边形 c、 e、 f、 g。 同学们看下这个有没有很熟悉?这个双正方形是不是和我们上面这个等腰直角三角形它是相似的呢? 是不是就 b、 c、 d, e、 c、 g, 它就和上面这个等腰直角三角形是不是就类似了? 只不过这个是在正方形还是一样的?我们看一下这四个结论的正面都是正方形的话,这两个 边相等,这两台边相等,这是九十度,这个是公共角。然后我们就用九十度加公共角,这边是九十度加公共角,因此这两个三角形它是全等的,还是运用边角边 全等了以后,这是对应边,这两条线仍然是相等的。接下来我们看还有证明它的正方形的一个顶角和这个手拉手这个夹角,它俩相等。 我们用就是刚才咱说三角形外角的那个方法,证明一下这个角分别是三角形 bcm 和 d、 m、 n。 外角。所以我们可以知道了,角 b、 m、 d, 它是外角,它等于角 b, c, m。 加角 m, d, n 又等于角角 d, n, m, 加角 m, d。 嗯,这一组是对应角,它是相等的。这有一个公共角,一个外角,因此呢,这两个角它是相等的。我们又知道了角 b, c, m, 它是相等的,等于九十度。 第三个结论,我们也就这样占领了。接下来,我们看第四个结论,他说, c, n。 仍然平分角 b, n, e。 因此,我们还是和上面一样,做垂线过 c, 做 d, e 的 垂线交于点 q 过 c, 作 b, g。 的 图形, b, g 的 垂线交于点 p。 我 们知道了这两个三角形相等,所以它的面积它也是相等的。 s, 三角形 b, c, g 等于二分之一 b, g 乘以 c p, s。 三角形 d, c, e, 它等于二分之一 d, e 再乘以 c q, d, e, b, g, 它是对应边,它是相等的,面积又相等。因此,我们可以得到 c, p 等于 c, q。 仍然,我们这个结论也就出来了。 c, n, 它的平分角 b, n, e。 的 同学们看一下手手拉手这四个模型的它共同的结论,它是不是都类似了?都是出现了 一组对应的全等三角形,而且手拉手形成的这两个线段它是相等的。手拉手这两条线段,它形成的夹角,与这个等腰三角形的顶角它是相等的。 我们又知道了顶角与这个手拉手模型这个交点连线,手拉手直线,它形成的一个夹角, 他俩是平分的关系。这就是我们这节课所学的知识点。手拉手模型,这个很常见,同学们一定要知道。好,这节课就上到这里,下次再会。
23数学刘老师 00:26查看AI文稿AI文稿
00:26查看AI文稿AI文稿八上数学最难的四十八个几何模型全部吃透,逆袭班级前三。八上数学四十八个几何模型一, a 字模型、鸡爪模型,腋下两角合等于上下两角合。 八字模型,三角形中五大模型见八字除对顶,剩余的两角之合会相等。飞镖模型也叫燕尾型、双角平分线模型。三个结论完整版分享!
20小王老师爱分享 01:39查看AI文稿AI文稿
01:39查看AI文稿AI文稿哈喽,大家好,我是爱与堂数学赵老师,今天跟大家分享的呢,是我们人教八上几何的一些常见模型。首先我们可以看第一个模型啊,叫飞镖模型,那它由来也很好理解啊,就是,呃,它的长相像一个飞镖一样。首先我们看一下它的结论,就是角 b、 d、 c, 也就说这个角 它等于 a, 角 a 加角 b 加角 c。 那 么说直白一点,就是我们飞镖里边这个比较大的这个凹角等于三个小小的核。那接下来我们来证明一下这个结论,它是为什么有这样的一个结论啊? 好,那首先我们来看一下,根据三角形的外角有一个这样的性质,我们可以稍微做一下辅助线,我们把这 哎画虚线,延长 b d, 这这个 e。 那 么根据我们三角形外角的这个性质呢,我们就有了这个角 a 加上角 b, 它等于哪个角啊?哎,它等于这个角, 我们可以写成角 e 啊,就是角 a 加角 b 等于一个角 e。 那 么再根据三角形的一个外角性质呢?角 e 和角 c 加起来,它对应的外角又是哪个呢?哎,那显然它就是一个这个角啊,所以呢,我们这个角 e 加上角 c, 它就等于角 b dc, 那 么把上下两个结合起来,我们就有了,呃,这个角 a 加上角 b, 再加上角 c, 就 等于我们的角 b、 d、 c。 哎,因此我们的飞镖模型的结论就出来了,哎,以后我们在应用的时候,如果是选择填空题,可以直接用,但如果大体,可以进行一下简单的证明。好,这是我们第一个模型。
猜你喜欢
- 2943秒杀小数









