太原实中12月月考数学22题方法
据说很多同学看到做图题就两眼发黑,我们来看一下这道做图题,他说有一个问题,在图一当中,角 abc 知道是九十度,在线段 a、 c 上一边要取一个点 d 连接 b d 之后要使得 b d 等于二零 a c, 那 我们自然联想直角三角形斜边中线定的,如果点 d 是 a c 的 中线,就等于就等于斜边的一半,所以这个问题我们搞清楚了,其实就是要取 a、 c 的 中线,就等于就等于斜边的一半,所以这个问题我们搞清楚了,其实就是要取 a、 c 的 中点,我们看一下他是怎么做的。 他说在图一的基础上,利用网格构造线段 a m 和 c n, 要使得它平行且相等如图,然后它就连接 m n, 那 么 不难得到上下两个三角形全等,这个是显然的证明,我们就略了,所以全等之后,点 d 就是 a、 c 的 中点,进而就可以得到 b d 等于二分之 a c。 哦,他的逻辑呢?其实也挺简单,那么我们做一下总结,其实这也是网格当中常见的问题。网格 取终点,对于网格取终点,就是我们这个思路一的方法。什么方法构造平行八字全等的方式来取终点?好,这是思路一,我们对它的什么?这叫理解, 也就是对于问题一的理解,我们能够理解到这个程度就可以了。好,继续。问题二,他说点 d 是 ab 上的终点,规定的是终点了。 在线段 a、 c 上边做一个点 e, 大 概吧,我们先大概做一个点 e 连接 d e, 要使得 a b 等于 d, e 等于二分之 a b, 那 么这段要等于二分之一的 a b, 那 么就三段都相等,那要想使得三段都相等,我们自然联想这个图特别像斜中半,只需把这个这个 b e 连起来,如果我们能做出来这是直角,是不是就进一步结合点 d 中点,就可以进而利用斜中半得到 d e 等于二分之 a b 好, 那么我们现在理解了问题了,说白了就是要做一 一个 b e 垂直, a c 做个直角,那我们看看他怎么做的。他说在图三基础上,利用网格做了个 a q 垂直, b c 好 垂直,然后发现 a q 和 b c 都是五格好,这两条线相等,然后从 c 往上做了个垂直,并且取了个 c q 一 样长的 ok, c q 和 c p 一 样长,然后他就连接 b p, 后来呢就发现了点交点,就是这个点 e 连接 d e 之后就可以得到这垂直。那为什么垂直呢? 也不难证明,因为我们在刚刚做的时候,其实它有所引导,相当于让我们发现了 a q 和 b c 相等,并且还让我们发现了 c q 和 cp 相等。那么再结合这两个直角,我们不难发现这个蓝色的直角三角形和这个黑色的直角三角形,它俩是全等的。 那么全等之后,自然我们就可以知道这个角加这个角是九十,而全等这个圆圈角是不也等于这,所以这两个角也将相加九十,内角和一百八的情况下,他就九十对顶过去,他是不也就九十,所以是不就挣出来九十,进而斜中半就挣出来了一半, 这就是思路二。这也顺带就是第二小问要让我们补全的剩余的证明过程,那么我们做一个停顿,我们要做好理解,理解什么呢?就是理解第二小问,他想要让我们做的是什么?他其实想让我们做的是网格做直角,或者说叫网格做垂直。 那么他的做法呢?在思路里边已经给我们引导,并且在证明过程中我们也进一步理解了,他是怎么做的呢?他的做法是构造 全等,构造什么类型的全等呢?我们来看一下刚刚是不是这组和这组全等,那么这两组全等属于什么类型全等呢?他其实属于三垂直全等的变形。 我们看一下为什么是三垂直全等的变形,比如在这个空白网格当中做个理解,我们现在呢有一条线段,取了这个网格的这两个格点做了一条线段,现在如果我让你做这条线段的垂线,你会不会做?你可以暂停视频三秒钟思考一下。 那么做垂线的方法其实很简单,这条线所在的网格的网格直角三角形,其实是不是就是这个直角三角形? 那么这个直角三角形如果我们把它做个延伸,再把这个直角三角形躺平,那我们很容易能构造出来了一个与之全等的,并且是躺平着的三角形。 那么这个时候这两个三角形的两条斜线根据全等不难得到两角相等,然后这个三角形当中两锐角互余,进而得到它俩互余,进而得到垂直。 而我们这种做垂直的方法,利用的是不是就是构造一个三垂直全等这两个三角形,三垂直全等就可以得到直角。而本题当中构造方式我们做个对照,其实就 其实就好比我们把这个蓝色的三角形做了个平移,我们现在试着平移感受一下, 比如我们把它平移到这,因为平移呢,是相当于线段平行,所以我们平移之后的蓝线,蓝的这条斜线和黑色的这条斜线也应该是垂直的,而这组全等是不是就好比我们刚刚的这组全等, 大家再对照看一下,是不是就几乎是一样的,无外乎就是多了一次平行对不对?所以我们网格当中做垂直的,做直角或者做垂直的方法就是什么构造三垂直权的, 那么这个构造三垂直全等呢?其实我们可以平移到这,我们甚至其实可以平移到任意位置,比如说刚刚是最开始这样的,我们能不能平移到这?可以,还可以平移到这,我们甚至可以平移到这,而且一旦平移到这之后,这两条线不止互相垂直,这两条线还互相平分,你有没有发现 为什么呢?我们把这个蓝色的这个直角三角形再延伸变为一个长方形,把黑色的直角三角形也延伸变为一个长方形,你会发现这两个长方形也是互相垂直,而且是互相平分的。 关于他们的中心对称对不对?好,这就是网格当中做垂直,做直角,构造三垂直全等。而本题就是三垂直全等,加了个什么?加了个平移。 那么有了这两层理解之后,接下来我们再来看一下第三小问,看一下他还是不是很难。第三小问,他说是 三角形 a、 b、 c 中顶点, a、 b、 c 均在格点上点, d 是 靠近 ab 的 四等分点,请用无刻度的直尺在线段 a c 上取一个点 f, 我 们就先大概取了取个点 f, 要使得 d f 等于四分之一 ab 好, d f 是 一份,那 ab 就是 四份,再结合点 d 又是四等分点,那点 a d 与 b d 的 比本身就是一比三,换言之,和 d f 的 一份单位一是一样的。 哎,这个时候我们就发现了, d f 要等于四分之 a b, 而 a d 本身也等于四分之 a b, 说白了其实就是 a d 和 d f 相等。那么这个和我们上面的有什么关联呢? 这是我们应该思考的,如果没有任何关联,那这个题你要当一个纯新的一个题去思考,那有点难,但如果你能发现和上边的关联,那当然题目的难度就降低了,那有什么关联呢?我们把四等分点做个变形, 所谓的四等分点,如果我们取 ab 的 中点 m, 那 么原题当中做 d f 等于四分之一 ab, 当知道了 ab 中点 m 之后,是不是可以也转化为做 d f 等于二分之一 a m 好, 那么要做 d f 等于二分之一 a m 该怎么做? 这个时候发现 d f 是 不是也就等于 ad 等于 dm 了?那如果要等于 ad 等于 dm, 是 不是又让我们联想到,如果此时连接 m f 是 不是相当于我这儿只要能做出来一个垂直,就可以结合直角三角形斜边中线定力,得到所谓的 d f a r v a m, 于是我们做法是不是就是可以做 m f 垂直 a c 好,这样我们是不是就明确了,本题其实就是两步,第一步我们要取那个终点 m, 第二步就是做垂直,而取终点怎么取?前面交了,而做垂直怎么做?前面也交了,所以这个题到此,我们应该难度就大大降低了。好,接下来我们来实操一下。 第一步取终点,我们取 a、 b 终点怎么取呢?构造平行八字的方式来取终点,所以这样呢,我们可以构造一个一组平行线段,然后连接平行且相等的线段,然后连接,那么这个焦点即为我们所要的点。第一步达成,然后第二步要做垂直。 做垂直该怎么做?做垂直的话,我们就需要先找到黑色的那个直角三角形,直角三角形在这, 然后我们又构,我们要构造一个与之全等的,并且是三垂直全等的蓝色直角三角形,大概我们可能要画到外边,对不对?但是我们之前也说了,把这个直角三角形平移之后,是不是始终垂直的?所以我们不妨画到网格里边去构造,所以这个时候我们可以 数一下格一格,然后这边是一二三四五格,所以我们很躺着来一个一格五格的直角三角形。 好,然后接下来我们是不是就可以任意平移了,对不对?那么任意平移的话,我们任意平移到任意位置,我们是不是就都能做出来 a、 c 的 垂线,就是这条蓝线,但是我们这条蓝线不行,为什么?因为题里边所要让我们做的蓝线是得经过点 m, 那 该如何让它经过点 m 呢? 那么这个时候我们可以分析一下,我们会发现当这个三角形刚好落到这个位置的时候,他就经过点,这是为什么?因为这个点应该是根据之前的推导,应该是这个正方形的中心,而如果我们这个蓝色的三角形放到 正方形的左右对称的正中间的时候,那么这条斜边是不是也刚好经过点?所以我们这个三角形是不是可以放到这?那么放到这之后,我们是不是就可以得到这条线既经过点 m 又和 a、 c 垂直?于是这个时候我们就发现这个 这个点焦点就是我们所要的点 f, 此时我们如果连接 f 就 可以得到垂直,进而得到一半, 这就是这个题,那么这个题呢?当然我们在取中点的时候,可以这样构造平行八字,也可以其余的方式来构造平行八字。第二步做三垂直,全等平移到这个位置的时候呢, 这个是必定要平移到这个位置的,所以大家可以看下,看一下大家的做法是不是你所做的那个所谓的 m、 f 是 不是延伸之后能推理得到一定经过这两个格点的?如果没有经过,那说明你的做法一定错,如果推理得得到了,一定经过这两个格点,或者你本身就经过了这两个格点,那说明你的做法一定就对。 这就是这个题,这就是我们的阅读型理解的网格作图题。对于网格题来说,其实我们往往需要做的就是两步,第一步叫理解,第二步叫应用。好,我是七哥,关注我带你学习更多压轴题。
粉丝132获赞296
相关视频
 11:29【初三数学】2025-2026学年实中12月考22题 【初三数学】2025-2026学年实中12月考22题
11:29【初三数学】2025-2026学年实中12月考22题 【初三数学】2025-2026学年实中12月考22题
二次函数建模问题,二次函数平移,范围问题
#山西中考改革 #二次函数建模 #新中考 #数学压轴题查看AI文稿AI文稿山西省实验中学十二月份的这个月考二十二题啊,应一些孩子的要求,我本来是讲了这个十五题和这个二十三题,发现这个二十二题啊,这个道题也比较好,有一定的难度。嗯,好些,有有好几位小孩啊, 让我给大家讲一下。我给大家讲一下啊,这道题啊,这个山西省实验中学出的特别好啊,这是个非常好的题目,因为他特别贴合山西的这个中考改革的一个方向。山西中考二四年,二五年他已经中考做了调整,就是二次函数,最明显的特征就是二次函数那道压轴题现在 变成了二十二题,他叫做二次函数建模题,或者叫做二次函数实际应用题啊,而这道题其实就完美的契合了中考,所以他出的特别好啊,我们一起来读一下,说这个山西省实验中学被贯彻等等等,这些信息其实都是废话啊。我们继续往后呃 看,说设计了一辆有笼子的投石车,并用沙包完成目标沉池的打击。比赛场地如图一啊,这是一个比赛场地,沉池的尺寸, a、 b、 c、 d, 它的底面是一个正方形,六十厘米乘六十厘米的正方形 a、 b、 c, 三个沉池都是一样的。 然后样式图如呃,图二,我们眊一眼就行啊。然后接下来沙包在最大档位和最小档位力度发射出去。 从头实线看头头一有个头实线,从头实线开始的路线可以抽象为平面直角坐标系中两条抛物线的部分图像已经明确告诉,这个路线啊,就是个抛物线, 如图三,抛物线方向始终与水平方向保持一致啊,抛物线打出去的方向和水平方向是保持一致的,然后最响档位发射的抛物线可以看左,由最大档位发射的抛物线向左平移得到。好,这句话很关键啊, 最小档位和最大档位说明力度不一样,力度不一样,但是可以抛物线可以通过平移得到,而平移的话是不改变图形的形状和大小的,也就说这个抛物线啊,它的形状大小始终保持无变,是吧?最小力度的话,嗯, 是一个抛物线,最大力度是一个抛物线,他们左右平行之后啊,就可以重合了,是这样一个情况,然后最小档位可以精准命中目标成是 a 处。好,大概看一下这个图三啊,从头实线嗯,处发射出来之后,最小档位他命中了目标 a 处最大档位的 最大的有抛物线,最高点离投实线水平距离是两米,最高点那就是最高点,那就是顶点的意思啊,说明顶点他的横坐标我们可以认为是二,然后最高高度是二,纵坐标也知道了,然后恰好命中目标成是 b, 最大到位命中了目标乘以 b, 达到了最大射程六米。好,首先这个这道题出的比较好啊,但是他少了一些关键的信息,比方说这个坐标系咋建的,他是没有说出来的, 他正常的话或理论上应该表达清楚啊,谁谁谁是 x 轴,谁谁是 y 轴,谁是圆点,要表达清楚啊,但是这个题其实已经默认成怎么建了啊,我们看图三角 ok 了。 从题干的信息我们可以得出,叫最大档位的时候,我会发现最大档位的时候,它的顶点坐标是二度或二, 二度或二,并且命中了目标乘以 b, b 的 话,它在 x 轴上,也就是 b 点的坐标,我们是能看出的是六度或零啊, 知道零点,知道一个点,所以这个最大档位时的,呃,这个抛下的警示可以搞定啊。我们看问题,第一问,说,最大档位时,沙包经过投射线上方的高度是多少?经过这个投射线上方的高度啊?从图中看的话啊,比如说这个,这个字母标的不太清晰,我们改一下啊,就是 q 点吧。啊, 头线啊, q 点是经过头线的那个位置,所以它相当于求的什么呢?就是最大脑位是那个抛线有弯折的焦点的坐标,所以我们算出解析式就 ok 了啊。好,第一问,我们来简写过程啊,因为顶点知道,所以我们设为 y 等于 a, b 的 x 减二,括号的方加了个二, 这里面 a 不 等于零。然后接下来,因为 b 点是在这个抛物线上, b 点左右是六度零,把 b 点代入上式啊,代入上式我们就可以得出这个抛物线了,我们快速的算一下啊, y 呢,是等于零, x 等于六,所以 a 倍的六减二十四,四个平方是四四十六,所以前面其实就是十六 a 啊,所以是十六, a 加二等于零,所以我们可以解,解出了 a 呢,应该等于负八分之一啊,所以是 y 等于负的八分之一,被的 x 减二的平方再加二,这是最大档位,是抛物线的解析式。 然后现在求的是什么呢?求的是最大档位是沙包,嗯,经过投射线上方时的高度。哎,我们只需要令 x 等于零, 嗯,则这个 y 我 们可以算出来, x 等于零的时候应该是二分之三啊,所以这个答案就是二分之三米啊。答案算出的是二分之三米,也就是图中这个 q 点坐标是应该是零度二分之三, 这是第一个啊,它是个比较常规的考法。第二个说目标成尺 a 中心与投射线间的距离是多少啊?目标成尺 a, 看错啊, a, 呃的中心与投射线的距离,也就是最小档位的时候,这个抛线啊,它命中了 a 点,现在求的是 a 点与投射线的距离。看图的话,其实求的是什么呢?求的是 o a 这一段, 而 o a 这一段取决于什么呢?取决于 a 点坐标,而 a 点坐标取决于什么呢?取决于抛物线的解析式。抛物线解析式。 所以我们相当于这道题,我们要核心是要求出最小档位时,那个抛物线解析式是多少?那最小档位抛物线解析式 啊,解这个抛物线和最大档位的抛物线,它是有关系的。其中已经说了啊,说最小档位发射的抛物线,可以看作是用最大档位发射,抛物线向左平移,那怎么向左平移呢?哎,这里面关键信息是,这个 q 点是同时在最大档位和最小档位的抛物线上, 所以 q 点如果我们认为在最小档位这个抛物线的话, q 点坐标是零度或二分之三,那么它左右平移的话,那 q 点是由谁平移过来的话,由谁平移过来的呢?它就是相当于是在最大档位时的那个抛物线,它的对称点 啊,对称点啊,因为我发现最大档位的时候,那个抛下的对称轴 x 应该是等于二的,所以 q 点坐标是零度和二分之三的话,那么我们可以看出它的对称点 q 撇二应该是重点坐标公式,二乘二减零是四度和二分之三。由此我们 可以看出啊,这个大抛物线它是怎么到这个最小档位时抛物线的呢?它就是向左啊,向左平移了四个单位 啊,向左平移了四个单位,所以接下来我们可以把最小档位的抛物线及时算出来啊,这就有数了,或者呢啊,或者我们直接可以看出来啊,最大档位时,这个 b 点坐标是六子六的话零, 然后最小档位它其实对应的是 a 点啊, a 点坐标是谁的零呢?因为是向左平移四个单位啊,所以就是二的零, 所以我们得出了啊,所以我们得出了这个啊,目标成尺 a 中心与投实线间的距离应该是啊,这个 o a 的 长应该是两米啊,两米。好了,这是第二个的做法。 第三,我们继续看啊,说目标成尺 c 放置在投实线啊,四米的 离头视线四米的一个位置,然后离地面约是七十厘米的高度啊,这个目标城市 c 啊,他在感觉在空中的这样一个感觉啊,离头视线水平距离是四米,然后他的高度是什么呢?高度是七十厘米, 且城池边缘高度啊,因为这个城池他是个长方体,他的底面是个正方形,他啊,边缘的高度是三十厘米,换句话说,这个城池 c 啊,他的啊,他的这个最高点离什么呢?这个地面的距离应该是七十厘米,加上个三十厘米 应该等于一百厘米,就是一米啊,一米的位置投时机后测地米可保证命中目标乘十 c 的 内部请直接写出 d 的 取法。这道题的关键啊,就是理解上可能有问题,他什么叫做后测?后测,后测完之后他就 他就这个命中了目标乘十 c 呢?或者说一开始怎么就没有命中呢?啊?一开始为什么没有命中呢?这个我们可以做一个感直观的感觉啊。 嗯,对于这个最大的,这个最大的位置,这个抛物线,因为解氏已经知道了,我们把 x 等于四啊,因为这个 c 乘值离投投直线的水平距离是四,把 x 等于四,我们带进去之后啊,发现啊,我们感受一下啊, 啊, x 等于四,带进去的话,这个 x 等于四的时候, y 应该等于负的八分之一乘以。我看一下啊,乘以 啊,前面已经算过了,其实啊,已经算过是二分之三,二分之三,也就是说啊,就是最大方位抛物线上有一个点叫做四度或二分之三, 而现在 c 乘值的这个,呃,横左边啊,我们可以认为是四,它的高度是一米,它相当于从 c 乘值的头顶给飘过去了,所以我们需要什么呢?把这个投时机向左平移上地米之后啊,他才有可能命中目标。这道题和二五年山西中考的那个, 呃,二十二题有点像啊,那个机器蛙啊,机器青蛙的那个啊,就是机器蛙,这个打的打的太猛了,他跳过去了,要把那个跳板来一个跳台,就是把抛物线上下平移,这样感觉或者左右平移都其实道理是一样的啊, 所以那到底平移多少呢?我们假后撤了,后撤了这个地名,我们假设啊,啊,后撤,后撤后的这个 后车后的抛物线,我们直接可以写成 y, 等于负的八分之一倍的 x 减二,因为是向左左加,所以加了个 d 啊,加了个 d, 块了个平方,再加上个二, 这就是后车之后的那个抛物线,这个抛物线它要命中乘以 c 的 内部。什么叫命中乘以 c, c 的 内部呢?它其实只需要我们在中阶段啊,我们只需要研究特殊位置就 ok 了 啊,正常的话其实要系统的进行理论的计算啊,在中间呢,他是只是让我们做一个特殊位置的这个计算就 ok 了。那特殊位置是哪两个位置呢?啊?第一个叫做四等会一这个点, 这个点我们可以认为是乘十 c 靠近投实线,嗯,这个部分的这一侧的最高的那个点,然后还有一个点是什么呢? 他是啊,四加上一个六十厘米啊,四米加六厘米就是四点,四点六,逗号一,所以接下来我们需要把这两个点啊,这两个点,比方说一个是 p 点,一个是 q 点啊,这两个特殊位置的点啊,特殊点, 把这两个特殊位置的点带入新的这个抛物线解析式啊,带入这个新的抛物线解析式之后,我们算出那个地址就是两个零界值,而这个地两地的两个零界值就是地的曲折反 啊。所以关键信息啊,就是把 p 点和 q 点往新的抛物线里面往进带,带完之后啊,算出那个 d 的 答案,就是 d 的 范围了。好了,具体带啊,孩子们自己带。张老师不在这个计算了啊。
 12:37查看AI文稿AI文稿
12:37查看AI文稿AI文稿哈喽,伙伴们大家好,我是初中数学尤正华老师,那么我们接下来继续看一下三大附中的第二十二题的这道题目啊,难度和二十三题相当啊,非常难。来,我们看一下这道题,大家需要这个三大附中试卷的,一定要私私信尤老师,然后问尤老师来领取一下,好吧, 来,他给了一个题,说是 a o b 呢,是一个一百二十度的角和一个直角三角板进行做旋转,将这个直角三角板六十度的顶点呢,和这个 a、 o b 的 o 点重合, 然后呢, o e 呢是角 b、 o d 的 角平分线。他说,第一问来,我们看图一啊,说 d o c 呢,在角 a o b 的 内部, a、 o d 呢是四十度。求 c o e。 来,咱们常规倒角一下啊, 这个总共的一个大角呢,它是一个一百二十度,然后其中还给了中间这个角度呢是个六十度,旁边这个角呢是四十度。那大家很容易能够算的出来, b、 o、 c 应该是多少度,对了,二十度, 然后呢,再加上 o e 是 平分角 b、 o d。 来,我们看一下这个 b、 o、 d 到底是多少度啊? b、 o d 呢,是不是刚好是六十和二十之和,也就是多少度?哎,八十度平分八十度,那一半对应的就是 四十度,那中间这个角呢?哎呀,很轻松算出来,四十减二十等于二十度,所以我们的第一空直接写答案,二十度 来。接下来我们看第二问,第二问当中呢,他问我们的是说,哎,这个在图一的基础之上,将这个三角板进行旋转,使得 o c 落在脚外面, o d 落在脚内部。然后呢,让大家判断一下 a o d 和 c o e 的 数量关系啊, 来这个题呢,大家常规思路呢,就是直接记住图二,直接研究就行了,但是我们在这出了图二呢,还要教大家一个方法叫特殊位值法,这个特殊位值法呢就是用来处理我们这种几何的变量关系所使用的。 来,我们先来根据这个一般的情况,我们来先分析一下,他的意思就是我要求的是这个 o e, 我 们把它记做叉叉,还有谁呢?还有这个 c o e, 哎,这个小三角,求这两之间的关系就可以了。 来,我们题当中有一个角分线,大家不要忘了啊,他平分谁呢?平分 b o d, 也就是有两个圈圈相等,然后题当中还有两个定量的角,也就是一百二十度和 c o d 的 六十度角,这是个六十度, a o b 是 一个一百二,我们就往这两个固定角上去探讨这几个叉叉和三角形以及圈圈的关系就行了。来,我们直接分析一下,大家看图,这个叉叉与谁呢?与这个一百二十度是有关系的,他是一百二十度,刚好去掉两个圈圈就能得到了。 那么接下来我们看这个小三角,小三角呢?他在哪呢?对了,他正好在这个六十度以内,也就是六十度呢,去掉一个圈圈就能得到小三角,那么很明显这两个关键你能看出来 叉叉和三角形什么关系?对了,一个叉叉等于两个小三角二倍关系,所以这道题的答案就是角 a o d 等于二倍的角, c o e。 好 了,然后你证明就可以了。好吧,我们在这就只带大家做分析了来,那么这是我们直接通过图当中大家的常规导角,必须做熟练,你就能把这样的关系找到,那么除了他以外呢?来我们还有一个技巧方法 介绍教给大家了,叫做特殊位置法,或者叫临界指法。我们说特殊位置法呢,跟大家强调过,特殊位置法在初中阶段就三种,分别叫贡献、重贡献、垂直和平行。所以这第一道题呢,我们主要采用的叫贡献 共线,包含两种,一种叫重合,一种叫在同一条直线上,都叫共线来,那么比如说像我们的这道题来给大家画一个图啊,那么他不是说让大家要保证好这个 o d 在 内部, o c 在 外面吗? 那我们就找他的临界位置, o d 保证在内部, o c 保证在外部,哎,首先第一个临界点,那就是 o c 是 不是刚刚好,在你这个 o b 位置的时候, 对吧?是不是就可以?哎,这个位置就是我们其中的一个临界位置来,那我们就把它画好,这就是一个特殊位置,此时的谁呢? o c 和 o b 刚好重合, d 在 这。好了,那么角平分线呢?我们顺便画出来 来角平分线在这, o e, 好, 我们接下来倒角呗,我们来找角度关系来,我们看这个 a、 o d 标准的多少度,六十度,然后再看这个 c、 o e, 很 明显这两个角都是三十度,是不是很明显六十度,三十度,两倍角的关系有, 哎,对了,但是这只是其中一种特殊位置啊,我们要用特殊位置法,大家就必须得把所有的特殊位置你都得找到,哎,他只负责帮助大家研究出结论, ok 吧?来第二种特殊位置应该怎么画呢?对了,就是 o d 即将出去的时候, 对了,那就是我们图当中这个位置了,点 d 点呢? o d 呢?落在了 o b 上,哎,这个位置也是个特殊位置,来,我们再把它的角平分线画出来,刚好也是重合在一起了, 所以我们来开始看角度吧, a o d 多少度呢?一百二十度? c o e 呢?哎,六十度,你看是不还是一百二十六十度的两倍,所以这个答案和我们结论完全吻合,没问题, 所以这就是特殊位指法,帮助大家去找寻这个结论。那么这个特殊位指法特别在第三问的时候,非常非常能够让大家用的很好,也就是第三问不需要写过程,只需要猜结论,那猜结论大家就可以采用这个方法去求,那么我们看一下啊,他说在图二的基础之上呢,继续旋转,要让他这个三角板旋转一周, 然后呢说当三角板都整体在 l b 的 外部的时候,因为他不能在内部啊,就在外部,也就是说,哎,在我画红线的这个圈圈范围之内,让大家还是写出他俩之间存在的数量关系来,直接写出。那么伙伴们,第三问,你的探讨逻辑呢?就要采用好我们的特殊位置法了, 来特殊位置法呢,那么我平常就跟伙伴们说过了,一定要回去多拿着三角板选择感受这种贡献的情况来。那么我们接下来一个一个特殊位置来帮大家找一找。 首先我们先看我们找上一个它的起点吧,我们就从图二开始出发往外转,那么首先第一个特殊位置呢,就是说这个 o b 和 o d 刚好重合, 哎,也就是 o d 在 这, o c 在 这,而且你此时会看到不仅 o d 和 o b 重合,这个 o c 和 o a 也刚好是在同一条直线上一百八十度。 好了,这是其中第一种情况。来,咱们再继续来旋转,来第二种 a、 o b 继续第二种的旋转呢,那我们在旋转过程当中,大家知道了,那接下来该谁呢?该这个 o d 和这个 o a 共线了,来,咱们重画一个啊, 好,也就是说 o d 在 这, o c 在 这,刚好是 o d 和 o a 在 同一条直线上, o d、 o c。 好 了,这就是我们第二种特殊之就逆时针方向,顺时针方向继续旋转下来了啊。来,接下来我们再画第三种情况, 那第三种情况又该谁和谁重合了呢?来,这个图往右边挪一挪,来,我们画一下 a、 o b, 哎,该画到哪了呢?对了,是该这个 o c 和 o b 共线了, 哎,也就是这个特殊位,哎,这是个点 d, 这是个点 c。 好, 继续旋转,伙伴们 继续旋转,它还在外面的这种特殊情况,那就是该谁了?该这个 o d 和 o b 重合啊,或者换句话讲,叫做 o c 和 o a 能重合来画出来,这其实就是一回事,记住啊,要做到不穷不漏。 好,我们来划过来啊,好,我把它划到这,哎,这不就出来了,我们的 o d 呢,落在了 o a 上了。 好了,这四种情况,这不就是它在外面旋转过程当中的四大特殊位置吗?哎,你画出来之后,在这特殊位置上找关系就可以了呀。来,接下来我们开始标它的角平分线,第一个 o e 重合来第二个 b、 o、 d 的 角平分线 o 一。 第三种, b、 o、 d 的 角平分线。来第四种, b、 o、 d 的 角平分线呦, b、 o、 d 角平分线,第四种,大家特别注意了, b、 o、 d 的 刚好是个平角一百八,所以它要分的是上下两种情况。 好,我们把它标好之后,开始在每个图当中研究就可以了。来,我们先看第一个图,当中 a、 o d 一 百二十度,而 c、 o e 呢,六十度。对了,还是符合 a、 o d 等于两倍,两倍的角 c、 o e 的 关系。好了,和我们这个第二题得到的这个结论是完全吻合的。来,接下来咱们看第二种情况,来第二种情况,大家可以看到这个 a、 o、 d, 哎哟, 这个 a、 o、 d 刚好变成多少度了?对了,平角一百八十度,角 a、 o、 d 是 平角幺八零。来,接下来咱们看这个 c、 o、 e, 咱们倒一下角啊,来,上方的这个角, 这个 a、 o、 b 呢是幺二零度,那么旁边这呢,必然就是六十度,再加上一个角分线,所以得到三十度,三十度,旁边这个呢,是个六十度,也就是说这个角 c、 o、 e 呢,是多少度?九十度哟,大家看到了这个 a、 o、 d 好 像又是等于 c、 o e 的 两倍, 两倍的角 c、 o e, 对 吧? a 好 像还是吻合的。来,咱们再看第三种。 第三种图当中,我们来也是倒角,来,先把这个角的是幺二零度,旁边这个角呢是六十度,下方这个角呢是六十度。那么大家可以知道 b、 o、 d 呢是一百二,那么平分角呢?六十度,六十度呦,你刚好发现 o e 正好和 o e 在 同一条线。 来,咱们不要操心这么多,咱们来找我们需要的角,角 a o d, 哎,刚好是多少度呢?一百二十度。来,再看我们的角 c o e 好 像是一百二十度 哟,这两个关系好像是相等关系,没有二倍关系了,对吧?但是呢,你不要着急找相等啊,我们此时是不是要把这个二倍的 c o e 一 般都是要扩大 两百两倍的,你根据前面的结论来往出走规律好了,你此时可以看到它变成是 c o e, 变成是 a o d 的 两倍了, 大家可能会有一个关系,哎,他是是反过来了,或者呢,你仔细再仔细观察,二四零和幺二零刚好是多少度,哎,和是三百六,对啊,所以这里面的关系比较复杂。别着急,咱们再看下一个。 来,咱们再看最后一个。最后这种情况呢,我们也是先倒角,哎,这呢是个九十度,旁边这个角呢,哎,三十度,这呢是一个六十度,下方都是直角,九十度 来,那么我们接下来看角 a o d 来, a o d 的 度数呢,就是六十度不变,关键是这个角 c o e 呢,有两种度数了。来,咱们看第一种角 c o e, 如果说是这个 e 点在上方, c o e 就是 多少度, 三十度,哎,此时这俩不是还是符合角 a o d 等于二倍的角 c o e 吗?还吻合。来,咱们再看第二种,如果说这个点 e 跑到下方去了,咱们看这个 c o e 是 不是刚好变成一百五十度了? 哎呦,这个一百五十度和六十度之间,你看就没有明显的两倍关系了吧,所以这个关系不通用。不过没事,咱们先把这个角 c o e, 因为前面都是研究两倍的,我们把它变形一下,哎,刚好是三百度哟,这个三百度和 a o d 好 像也没有直接的两倍关系,但是你会发现 角 a、 o d 加上二倍的角 c、 o e 刚好等于多少度,哎,三百六十度来,那么你回到刚才第三种情况,你是不是也能够把这两个结果就统一起来了?加上二倍的角 c、 o e 是 不等于三百六十度 哎,你看我们的这种情况,这种情况吻合了哟,出现了全新的一个答案,除了他们有两倍的相等关系以外,另外的关系就是和式三百六。 好了,这个特殊位置法就帮我们分析出这个答案,所以我们最后直接填答案就行了,角 a、 o d 要么等于二倍的角 c、 o e, 要么就是角 a o d 加上二倍的角 c o e 等于三百六十度,答案就出来了。 好了,这就是我们说采用特殊位置法来帮帮助大家快速的能够把这种旋转的题目的答案快速解决清楚。 好吧,好了,这就是我们的第二十二题要教给大家的一个方法,难度还是非常大,所以大家好好的来把这道题吸收吸收,特别是姚老师刚刚教大家的特殊的指法,要学会学,也学会灵活使用了。好吧,好了,那么这道题呢,就给大家讲解到这。
88游中华讲数学 10:29查看AI文稿AI文稿
10:29查看AI文稿AI文稿上大附中十二月月考初一的这个二十二题啊,关于角度的一个压轴题,那么我们来先看下这道题目吧啊,数学课上啊,同学们以一个固定的一百二十度角 a o b 和一个直角三角尺啊,这三角板为背景, 探究有关角的一个问题,然后将这个叫三角板,六十度的这个,呃,角的这个顶点呢?与 a、 o b 顶点 o 重合啊,然后呢,呃,三角板,其于两边即为 o c 和 o d, 其中 o e 是 角 d o b 的 平分线啊。首先 我们一定要知道,看到角平分线啊,看到相相等的角,所以我们先把相等的角给他标出来,那 o e 平分角 d o b。 所以 我假设这儿是耳法的话, 呃,这儿是不也就是耳法啊? o e 平分角 d o b, 那 d o e 是 耳法的话, e o b 也是耳法。好,那么我们来接下来再看其他的题目啊。首先你把题里边条件搞明白,不要把这弄糊涂了啊,这个中间这个三角板是六十度, 那么这个第一题说啥呀啊?如图一角 d o c 在 a o b 的 内部。然后呢,问你,若 a、 o d 是 四十度啊, a o d 是 四十度,那我们把 a、 o d 给它标出来, a o d 是 四十度。 然后呢, c o e 的 度数为多少啊?要求的是 c o e。 好, 你就看这个图, c o e 应该怎么求呢啊? c o e 是 不是可以用这个角 a o c 去减掉 啊?这个 aoe 也可以用什么呀?也可以用 r 法去减掉 c o b 吧。那么我们到底要怎么算呢?啊,很明白啊,这里边这是一百二十度对吧? 那么这四十,这是不就八十?说明一个 r 法是不就是四十角平分线吗?角一个 r 法是四十的话,他这是六十,那这个小角是不是二十,是不马上就取出来了啊?很多同学不爱在这个图上面勾勾画画,其实我们这个角勾画画,答案就直接明了的出来了, 我们继续来看这个。第二问,他说在图一的基础上呢,将三角板点 o 啊,绕点 o, 顺时针旋转,使得 o c 在 a o b 的 一个外部, o d 去外部了, o d 呢?还在 a o b 的 内部,其余条件不变啊。如图二所示,菜菜提出了如下的一个问题,请你判解答。判断 a o d 和 c o e 的 一个数量关系, 首先看到了要求数量关系,就是主要是之前视频里边说的啊,你从初一开始就要有这样的思想,你让我求关系见比设餐为什么要用三个字母去表示一个角的时候,我在题里边找会很麻烦,所以我 习惯上用一个字母一个字母去表示一个角度。那么标角度的时候呢,我们一般是设阿尔法和贝塔啊,阿尔法,贝塔,伽马这些希腊字母。那么啊, a o d 呢?我把它设成阿尔法, 然后呢,还有个什么呀? c o e 啊, c o e 能把它设成北塔,也就说我只要最后得出阿尔法和北塔间的关系就可以了。那这里边有一个非常重量的重要的题头里边的条件,也就是刚刚老师读题的当中圈出来的 o e 呢?不管在哪个图当中,它始终是平分角 d o b 的 啊,因为它是提头的条件,提头的条件是为三问所用的啊,每一问都可以用的,所以 o e 平分角 d o b 的 情况下,我们是不是就啊,如果我标出这个角是伽马的话,这个角是不是也是伽马? 那么由在这个题当中我们能得出一些什么样的一个等量关系呢?啊?你会发现所谓的这个,呃,九十度啊,什么六十度啊?这个角是六十度,以及啊,这个角呢, 他是一个一百二十度,是不是都可以用了?那我们看图能得到什么呀?你会发现尔法加上两倍的伽玛呢,是一百二十度。这是啊,题里面给的 a u b 是 一百二十度这个条件,还有一个就是这个三角板本身的六十度吧,也就是说啊,北塔呢加上伽玛呢是一个六十度, 那我想要得到阿尔法和北塔间的关系,我是不是就需要把这个伽玛给他约掉?那么伽玛如何才能约掉呢?啊?我们让啊第二个式子去乘以二,也就是二倍的北塔加上二倍的伽玛呢,等于一百二十度。好得到这两个式子 啊,这两个式子有什么关系呢?我要把伽玛削掉,两个式子一减,伽玛是不就没了啊?阿尔法, 看啊,阿尔法减上二倍塔,是不是还是阿尔法减二倍塔,而二嘎玛减二嘎玛没了,一百二减一百二也没了,等于零,说明阿尔法是不等于二倍的贝塔。阿尔法等于二倍的贝塔,是不就证明角 a o d 应该等于二倍的角 c o e。 此时这个结论就推出来了啊,这就是他们之间的一个二倍关系,我们要学会啊,把这个问题简单化,我能用一个希腊字母去表示一个角,我就不用三个字母去表示一个角,因为太费劲了,太费时了啊,看的太麻烦了,容易把你绕糊涂。好啊,那么我们再来看第三问, 第三个说啥呀?说到菜菜的启发,露露将图尔这个三角板绕点 o 顺时针旋转了一周啊,绕点 o 顺时针旋转了一周,从这转转转转转了一周, 并进行了如下的思考,当三角板转到 a o b 外部时,你看啊,刚才这个 d o、 c 是 不是在内部,后来呢? d o c 一 半在里边,一半在外面,后来呢,他又说了,直接转到全部转到外面去了。请直接写出 a o d 和 c o e 存在的数量关系大会发现什么呀? 你看啊,这个问题当中,第一问是不是 a o d 和 c o e 是 一个二倍关系?而第二问当中,你是不是也是求出了 a o d 和 c o 是 一个, c o e 是 一个二倍关系?如果说这道题你在考场上已经没时间了,马上要收卷了,剩下一分钟两分钟的时间了,我们是不是懵也要懵?一个角, a o d 的 二倍的角, c o e 啊, 对吧?那么这道题,哎,如果在你有充足时间的情况下,我们如何去思考它呢?要求 a o d 和 c o e 间的关系,那么 a o d 会有几种 情况呢?那我们一定要确定下来一个角的位置,然后再来定别的边的位置,从而啊进行分类讨论啊,因为这道题呢,他是有两种结果的,那么你怎么去分类讨论呢啊?首先大家思考啊, 这个,这个角本身是六十度,这个角呢,本身是一百二十度,他俩如果是共线的情况下,就是整个构成一个直角情况下,那是不是这个假角小,这个 a、 o d 就是 一个锐角呢?啊,我们分类的标准是什么呢?啊?让 a、 o、 d 分 别为锐角、直角、 钝角去分类讨论,你会发现啊,如果啊,这个呃,直角三角形绕到了靠 a 的 这个左边的话啊,我让 a、 o d 先先是一个锐角,然后你就会发现啊, a o d 如果是一个锐角,那始终不要忘了它小平分线这个条件啊。 那么 a o d 是 不就等于六十度加上这个小的锐角,而这个小的锐角怎么算来的呢?是不是就是 a o c 就 应该等于大的三百六十度减六十,再减两个尔法,再减一百二,所以 a o d 是 等于六十加上啊,三百六减一百二,减两个尔法,再减六十,你会得到它是二百四十减二尔法, 而此时的 c o e 呢,它是六十度加一个尔法。那他们俩之间这啥关系呢?还是不是二倍的关系啊? 啊,两倍的 a o e 是 一百二十度加上阿尔法,哎,他俩好像不是二倍关系,那什么关系呢?你快去把他俩一起加, 阿尔法就没了啊。所以这儿的关系是 a o d 加上两倍的 c o e 等于三百六十度。那么啊,这是 a o d 是 一个锐角的时候,我们得到的一个答案。那么如果 a o d 还是等于六十度加上三百六减一百二,减二十减六十。哎, 不管啊,不管,说这个 a、 o d 是 锐角也好,直角也好,他们的公式是一样的,那 c o e 也是六十加 r 法。 而如果说 a、 o d 是 一个钝角,但是这个钝角开口是朝左边的话啊,开口朝左的话发,你会发现跟前面两种情况是一模一样的, a o d 和 c o e 的 表示是一模一样的。也就是说,当这个 cod 啊,只要在这个 o a 所在这条直线的左边的时候呢,它所表示的这个结论都是 a o d 和 c o e 的 关系是 a o d 加上二倍的 c o e 等于三百六十度。那么还有什么样的一个情况呢?既然题目里边提示你了 a o d c o e 和 d o b 指 指均指小于平角的角,那么这个钝角是不就有可能在 o a 这条直线的右边呢?如果在右边的话啊, a o d 如果在右边的话,你会发现角 a o d 它等于啥呀? a o d 应该等于一百二十度,加上这两个而法 啊。而 c o e 呢,它等于的是什么呀?是六十度加上一个而法,此时是二倍关系。所以说这个题的答案是有两个的,要么就是啊角 啊,要么就是角 a o d 等于啊,二倍的角 c o e, 要么就是角 a o d 加上二倍的角 c o e 等于三百六十度啊,两个答案一定要大家考考虑明白我为什么要分类讨论?我分类讨论的时候以什么为标准? 大家会问,朱老师,你为什么要以 a o d 为标准区分它是锐角、直角、钝角在 o v 这条直线的左边还是右边?为什么要这样讨论,而不去去把这个 c o e 给他定出来, c o e 在 这个呃, o a 的 左边还是右边?这样去取,你会发现啊 c 点本身图中没有对吧?啊 c 呢?呃, c 点它是有 o d c 这个三角形决定的啊,它怎么也好说 d 和 c 是 同等地位啊,但是呢, 这个一点一点在哪里呢啊?一点还在角平分线那里。所以说我一定是先确定 o a o d 是 最方便的啊,确定 c o e 他 在两个动的图当中 啊,他都在动,而 a o d 呢,只有点一个点 d 在 动,所以说我是去把 a o d 去分类讨论,这样是更合理的一个方法,也是更让你的这个呃预算更加 会计的一种分类讨论的方式啊。呃,这就是这个老师给大家讲的关于二十二题啊,一个分类讨论。那么这道题呢,也是给了大家一个非常啊痛的一击啊,应该是很多孩子照样应该会丢个一半分的啊,也大多数孩子都只写了一种情况。好,就讲到这里。
26初中数学周老师 03:05查看AI文稿AI文稿
03:05查看AI文稿AI文稿满分为一百二十分,高质量十二月考数学测试题,这份测试题非常值得我们花时间从小题到大题完整的过一遍。 客观选择题,看似某些题目并非放在了选择压轴的位置,但他的坑却一点都不浅,你也来看看这道题他到底选什么呢?可以把你认为的正确答案打在我们的评论区。 我们会发现,平时如果老师提醒学生这道题易错且坑点很多,那么学生做这道题就会极其谨慎,然后正确率就相对提高了。但如果没有这样的提醒,是不是就容易掉到题目设置的陷阱当中呢? 所以我们平时做题,无论他是否处在压轴题的位置,都要细心谨慎,越简单越要仔细小心,这才是决定成败的关键,这也才是学习应该有的状态。 而对于填空压轴十五题,考察学生见到终点应该联想到的辅助线构造。之前视频当中我们提到,山西中考当中有关终点的考法只有八类,利用排除法一定可以找到适用于这道压轴题最优的解法。 而对于解答题部分,新加入了项目化学习二十二题,这也是中考改革后中考数学的新考点。这类题会跟二次函数结合实际应用问题对学生们进行考察,同时也是我们寒假陪游学习大纲中的一大模块。 学生对于联系实际情况的二次函数问题,如何通过函数建立联系来解决项目化的问题。 比如像二零二四年以及二零二五年,山西中考二次函数压轴题比较头疼,也难得分,这也变成必须是我们解决的学生痛点之一。其次便是这份试卷上难度最高的题目,十三分的几何压轴二十三题。 而这道题涉及的考点手拉手相似正是我们目前学习的专题内容。所以对于在读学员来说,这道题并非无从下手, 也正好与我们讲过的同类型题矩形中的手拉手相似,也同样是考察第三边比例以及夹角问题,然后再应用求解线段长。 所以我们说,学生考试见到平时学过的同类型题,那么他不仅不那么焦虑,甚至更有信心得更高的分。 另外不得不说的是,手拉手相似是中考数学必考考点,他一定会出现在中考或模拟考试当中, 他一定是学生的重中之重,他也一定是学生必须研究透彻的模型之一。关注江涛数学,让你知道更多的学习技巧和方法。
2江涛在线 02:55查看AI文稿AI文稿
02:55查看AI文稿AI文稿初二月考不是已经结束了?咱们初二月考的时候,好多学生会遇到一个问题,就是给你一个图,给你两个一字函数的图像,让说时他就形成了一个真际问题,或者相遇问题,或者谁与谁 相差多少,用了多长时间。对于这个题,好多学生干嘛呢?在考察那一刻根本就看不懂题, 那为什么他看不懂题呢?因为他在那里,他在那想的,记住他把他想成一个,他在一个静态的里面去想的,在在坐那里,要要去想象出来的,这样来说对好多学生都给都比较难,那咱们干嘛呢?咱们做这个题的时候一定要把它动态, 什么叫动态?看他就是两种类型的,一种是一个快车,一个慢车,慢车先走,快车后面追击,你看 你要注意一个问题,咱们就划这么长,就是 ab 的 距离,然后慢车先走,那快车追击他是不是追上了?追上之后快车是不是又超过他了?这是不是两个?如果他俩相距多少,是不是两种情况了?然后有可能快车嘟嘟嘟到头了之后,然后再返回来, 是不是他有第三种干嘛呢?相距以及快车又超过了,慢车跑过来时,他是不是有第四种相距了? 你把它变成了咱们的初一的什么速度与时间那个表格,你记住他给你那个图,咱们只要看见第一个会算出他的速度就行了。第二个能分清楚哪个是假,哪个是乙,第三个他有可能有的有停留,停留了几个小时,你能会求,这就行了, 这是第一种情况,那第二种情况是相什么相遇的问题吧,一个在左,一个在右,看好啊,一个在左,一个在右,他俩走走走,往往过走了吧?往过走了之后干嘛呢?他俩是相距多少米?这是不是相距了然后干嘛呢? 有一个过,他俩相遇之后,然后又过来之后是不是相遇了?这里面肯定有一个快车和一个慢车,如果反过来了,反过来了之后干嘛呢?他俩是不是这有个相距的? 然后呢?这个快车是不是又追上?这个慢车是不是也有个相距的?你要这么去思考,然后你把每一个线段,哎,这个车走了,另一个车走的,然后把它的路程算出来,你这样来说就比较简单了。记住咱们坐那里千万不要去去想说,哎呀, 他这个这个线是这个点的什么意思呢?就是到出发点的距离, 不要去这么去想,你要去看,这么去想对好多学生来说都非常难,所以说你把这个题你要具体化, 具体化来说就相对来说比较简单了。所以说咱们特别是做到一次函数解决行程的问题,咱们一定要去想法,一定要想让它变成一个动态的,当你变成动态的之后,它就比较简单了。
5高效学习 00:42查看AI文稿AI文稿
00:42查看AI文稿AI文稿十二月中下旬,太原市很多学校会进行十二月月考,由于刷题比较少,袁老师在这里呢给大家整理了一些去年哎优秀初中的 月考真题,这些呢是三大附中初一、初二、初三的考试题,这些是智大中学初一、初二、初三的考试题, 还有一些是师院附中初一、初二、初三的考试题。每道题目都藏着孩子的学习漏洞和进步空间,通过专题,我们各能精准的找到孩子需要发力的地方, 辛苦各位家长抽点时间督促孩子刷题并且复盘,我们一起努力,有需要的家长请在评论区留言。
 10:08查看AI文稿AI文稿
10:08查看AI文稿AI文稿据说这道题的第二小问拦住了一部分同学,第三小问更是拦住了绝大部分同学,那么他真的有那么难吗?我们来看一下这道题。如图一,矩形 a、 b、 c, d, 点 m、 n 分 别是中点,沿着这条中线剪开之后,得到 am 和 b, m 分 别是三, a、 d, m, n, b、 c 分 别是四,得到两个矩形,然后长度呢?如图标上了第一小问,他说将下边这个矩形绕着点 m 旋转,旋转到点 c 与点 d 重合的时候,判断四边形 d, e、 m、 f 是 一个什么形状,并说明理由。那么这个四边形结合之前,我们的 a、 d 和 m, n 是 矩形平行的,所以这个四边形的两条边平行。在结合之前, 矩形下边那个矩形的 n 撇 m 和 d、 b 平行的,所以我们不难得到这个四边形的 m、 e 和 d、 f 平行,所以这个四边形目前两组对边分别平行,可以得到它是平行四边形。再一细看,我们发现这个三角形和这个三角形 首先都是直角三角形,其次对顶角相等,再次这条 d、 n 撇是等于 a、 m 等于四,所以这个三这两个三角形是全等的,所以我们可以得到这个四边形的蓝线和红线是相等的,所以有一组邻边相等的平行四边形是菱形,所以我们就挣得了它的形状。 这是第一小问,还比较简单。我们再来看第二小问,当点 b 落在矩形 a, m、 d, n 的 对角线上,换言之,就是下边这个四边形继续旋转,点 b 落到对角线上的时候,求 四边形 a、 m、 b、 p 它的面积。那我们在求这个四边形的面积之前,我们发现这个四边形貌似它的形状呢,比较特殊一点,那我们继续做一个分析。我们不难发现 a m 和 b m 它是相等的,都等于三。 既然他俩相等,我们可以得到等边对等角,这两个角就相等。既然这两个角相等,再结合我们最开始的矩形直角,下边那个矩形也直角,所以我们不难得到 与之互余的两个角也相等。既然这两个角也相等,那我们可以得到 a p 和 b p 也相等。此时我们发现这个四边形应该是两组邻边相等,这是个真形,而且是一个直角真形。那么对于直角真形来说,我们求它的面积,当然我们可以联想它的对称性。于是我们连接 mp, 我们可以把这个直角真形分成两个直角三角形,这样的话,我们两个直角三角形的面积面积总和就是这个真形,而且这两直角三角形应该是全等的。所以我们接下来的方向就落在了如何能求得 ap 的 场, 那么要求 ap 的 长。我们再观察一下,我们发现 ap 所在的这个直角三角形 a m p, 这个直角三角形貌似和我们的另一个直角三角形全等,哪个和我们的这个直角三角形 应该是相似,不是全等。为什么和这个直角三角形?因为这个直角三角形的另一条边 m n 是 四。 而通过发现 amn 的 形状,它的两只角边是三比四,我们不难得到红色这个三角形的两只角边也是三比四,所以我们列一个比例式,根据相似,我们可以得到 ap 比 am 就 等于 ambn, 而 am 是 三, mn 是 四, ap 是 要求的 am 是 三,所以根据这个比例式就可以求得 ap 的 长,求得 ap 的 长之后,这个直角三角形的面积搞定,将来乘以二,就是我们所求的四边形的面积,那么最终答案呢,是四分之二十七,大家可以自行求一下, 这就是他的第二小问,貌似也不是很难,关键呢就是需要你发现这个四边形的形状,确定它求面积的方法,进而确定求 ap。 而求 ap 呢,需要找到相似第三小问, 在旋转过程中,两条直线 c n 撇和 d n 交于点 q, 请直接写出 d c q 是 等边三角形时候的比值, 那么现在要想直接写出它是等边三角形时候两线段的比值,我们当然就需要知道旋转过程中何时这个三角形为等边三角形, 于是我们接下来需要把这个四边形做个旋转,看一看何时为等边三角形。那么为了方便旋转呢,我们把这个,我们把这个四边形呢先做一个复制,上下两个四边形应该是全等的,所以我们把这个上边这个四边形做个复制, 然后为了好旋转呢,我们就在下边这个图形当中做一个旋转,那么旋转过程当中呢,这个点是 c, 这个点是 n 撇, 呃,而且我们在旋转过程当中更多的需要关注一下那个点 q 到了哪了,而这个点 q 是 直线 c n 撇和直线 d n 的 交点,直线 d n 老师已经用黑线把它画出来了,那么直线 c n 撇呢?我们用蓝色的线来代替它,那么接下来呢,我们来开始旋转这个四边形, 当然这呢大家如果在试卷上做的时候可以怎么办呢?可以考虑把这个四边形,把老师蓝色画出来,这个部分呢画到透明纸上,那么接下来就可以达到像老师一样旋转,旋转透明尺就可以达到像老师一样旋转的效果,这样就更为直观。 好,那么在旋转过程当中,我们需要重点关注一下那个黑线和蓝线它的夹角啊,它的焦点为什么呢?因为这个焦点其实就是 d n 与 c n 撇这两条直线的焦点,也就是点 q, 那 么我们重点需要关注一下那个焦点 q 到哪了?比方说我们旋转到这,旋转到这之后那个三角形,我们就会发现三角形 c d q 很 明显是一个钝角三角形,对不对?所以一,所以不太满足,我们继续旋转,旋转旋转,这个时候旋转到 c d 重合了,我们继续旋转, 这个时候过了,过了之后那个点 q 是 不是焦点,是不就到了上边了?到上边我们还不太满足,我们继续往上一点点,哎,这个时候发现三角形 cd q 貌似快变成等边三角形了,约摸差不多到这个位置的时候,他到等边三角形了,我们把它做一个调整 好,这就是我们的第一种情况,三角形 c 这个焦点就为 q, 三角形 c d q 就是 我们所要的等边三角形。好,现在他要求什么?求 c d 与 n n 撇的比值,那么我们把 n n 撇也连起来, 那么根据这个三角形是一个等边三角形,再根据这两条边是相等的,不难得到平,不难得到。这个三角形和这个三角形是相似的,所以大的三角形也应该是个等边三角形, 于是我们可以做一个转化,它所要求的是 c、 d 与 n n 撇的比值。而我们发现等边三角形 c、 d 应该是等于 d q 的, n n 撇等边三角形应该是等于 d n 的, 所以就可以转化为 d q 与 d n 的 比值。这样就好比一些,那么 d q 的 长,我们是不是就能知道? n q 和 d q 就 能知道比值,那 d q 的 长又该怎么知道呢? 这个地方我们会发现,旋转的旋转完之后,我们貌似有一个特殊角度三十度,而且 大的这个四边形也应该是一个真形,不难证明,自行证明。所以,呸,六十度大的是一个真形,所以我们利用真形的对称性,如果还连接对角线 m q, 我 们会发现 这个应该是一个三十度的直角三角形,所以我们就可以利用 m n 等于四, a d n 之前是三,不要错了。利用 m n 等于四,我们可以求得 d n 一 比根号三, d n 就是 四倍根号三,所以这个时候我们就可以求得 d q 就是 四倍,根号三减三, 而 n n q 就是 四倍,根号三。上下同时除以根号三,下边除没了,变成四,上边四倍,高三除以高三是四,三除以高三是根号三,所以得到它的比值是四分之四减杠三。于是这就是它的第一种情况,我们就求得了。 由于我们其实还没有旋转完整个过程,所以它极有可能存在另一种情况,所以我们理应继续做旋转 好,于是接下来我们继续旋转。和刚刚的情况类似,我们依然需要重点关注那个焦点,所以我们需要把 c、 n、 p、 r 这条所在直线呢也画出来,然后接下来我们开始旋转, 好旋转,旋转到第一个位置,大致就是我们刚刚所画的这个位置的时候,出现第一次等边三角形,大家重点关注那个交点和 c、 d 三个点连成的三角形形状好继续,这个时候三角形变成锐角,三角形继续,这个锐角越来越小,越来越小,直到平行的时候锐角没了, 好继续旋转。哎,这个时候发现 c、 n 撇和 dc 黑线、蓝线的交点到了下边了,下边很远的地方,那么再关注一下 c、 d、 q 这个三角形是一个锐角,三角形好继续旋转,我们发现这个锐角越来越大,越来越大,越来越大一定存在某一时刻这个锐角变为六十度,大致 在这个位置我们稍微做一下微调,那么在这个位置的时候,我们会发现它应该就是我们所要找的等边三角形 c、 d、 q, 它要求的是 c、 d 与 n、 n 撇的比值,所以我们把 n、 n 撇连起来。 好,那么此时我们不难发现它是一个等边三角形, c、 d、 q 还是一样的做一个转化,此时的 c、 d 比 n、 n 撇,它是不是 c、 d 可以 转化为 d q, 而 n、 n 撇是不是可以也转化为 d q, n q? 于是我们在知道 d、 n 等于三的情况下,依然是只需知道 n、 q 就 可以知道。 再于是刚刚我们在上一个里边发现这个四边形是一个真形,而在这个地方的时候依然是一个真形,而且是一个六十度的真形。所以我们如果连接对角线 m q, 我 们可以发现这个三角形 m n q 是 一个三十度的直角三角形,于是我们再次利用 m n 可以 求得 n q 是 四倍根号三,于是我们就可以知道 d q 就是 四倍根号三。加三 n q 就是 四倍根号三。于是再做一个化简,上下同时除以根号三,就可以得到比值为四分之四,加根号三。好,这就是这个题的第二个答案。好,关注我,我是七哥,下次见。
287哥数学 04:45查看AI文稿AI文稿
04:45查看AI文稿AI文稿二零二四到二零二五太原市师范附中啊,初一十二月份月考的一道几何压轴题,冻脚问题啊,最近问冻脚问题的比较多啊,我给大家讲一下这个题,这个题除了第四小问稍微需要思考一下,其他的都很简单哈,所以碰到这种冻脚问题一定要去做。 首先他怎么说的?他说 aoc 是 六十度,老三角板放在如图所示的这个位置啊,图一所示,这个时候问你 boc 多少度,那想都不用想,一百二十度,这个是一百二十度,对吧?那 c o n 呢?就是六十度,加上这个九十度,也就是一百五十度。 第二个题,它转转转,转到什么时候呢?转到 o m 去平分的 b o c, 而 b o c, 刚刚我们第一小问写了,它是一百二十度,所以平分成两个六十度,而这个角就直接出来了,用这个九十度减去六十度,也就是三十度 啊。第三小问,它在图二的基础上把 o n 啊反向延长了一下,得到射线 o d 啊,这个时候问你 a o d 多少度,那一样的呀,这个是六十度,整个这个是九十度啊,或者说是这是个平角,那这个就会是个三十度,那整个 a、 o c 是 六十度, a o c 是 六十度,所以这个也会是三十度,所以 a、 o d 是 三十度,那这个时候你会发现 d o c 多少度三十度, b o n 多少度,刚刚求过了,这个也是三十度, ok, 所以 它俩什么关系?相等的关系。唯一一个需要大家思考的啊,就是第四小问, 好吧,第四小问,他说将图一中的三角板绕 o 点啊,按每秒五度的速度啊,顺时针方向进行旋转,旋转到什么时候呢?旋转到直线啊,注意这个直线啊, o n 恰好平分 a o c, 那 这个时候什么叫直线 o n 啊?就是 o n, 你 把它从射线看成直线啊,就直线啊,它要平分谁平分 a o c, 这个时候你会发现,图三刚刚就满足了呀,图三这个就满足了呀, 对吧?红笔画的这个叫直线 o n, 它平分了它呀,对吧?那此时要注意啊,它不仅仅有这种情况,现在 o n 是 相当于是朝下的,那 o n 也可以朝上,所以它还有一种情况是,大概是这个样子的一个图, 这个是 m, 这个是 n 啊,这个是 m, 这个是 n, 平分了这个 a、 o c。 这个时候我们只需要看一下我画的这两个图啊,一个是红色的这个, 一个是蓝色,这个都是直线 o n 平分这个角,它到底转了多少度?然后根据你顺时针转的度数,每秒又转五度去求这个时间。比如说我们怎么找这个呢?我们要找它的初始位置,找出始位置啊, o n 从什么时候开始?从这个时候开始 啊,你找 o m 也行啊,转到什么时候转到这块啊?先看蓝色的 o n 是 从这里开始的啊,我换个颜色的笔给大家看一下啊。 从这里转到哪里转顺时针啊?顺时针,那反了啊,顺时针,那应该是往这个方向转多少度?一百二十度,对吧?一百二十度顺时针吗?这个方向叫顺时针, ok, 从 o n 垂直这个 ab 的 时候开始啊,往这里转,先转九十度,再转三十度,也就是第一种情况,一百二十度, 一百二十度,每秒转五度,那一共转了多少秒?二十四秒呗,二十四秒, 对吧?然后或者红色的这个啊,红色的 o n 也是从这里走的, 你发现这么转,转多少度?转了六十度,但是不好意思,人家是顺时针转,那顺时针转转多少度?转了三百度吗?三百度,每秒转五度,那这个时候就得六十秒。六十秒,好吧,六十秒,那 不难吧啊,所以大家一定要去做哈动脚问题,虽然说是个压轴题的考点哈,但他并不一定会考特别特别难的那种,特别难特别难的那种。一般怎么考呢?两条射线啊, 分别动动的速度还不一样,就类似于我们数轴里面的相遇和追击问题。 好吧,那种才是比较难的,并且有那种超过一百八十度要跨,就是超过一百八十度他技巧方式改变的,并且加了各种角分线的条件在里面的这种综合的题才算难的。 好吧,像现在就是我讲的这个题啊,他实际上我觉得同学们是可以做出来的。好吧,加油。
63支点数学徐老师 50:31查看AI文稿AI文稿
50:31查看AI文稿AI文稿hello, hello, 各位同学,大家好,我是雪源老师。今天我们来给大家去讲解一下二四年十月十二月月考的解答亚洲题,也是我们的最后道大题,是道动角问题已知。那么我说了点 o 的 话呢,在 直线 a b 上说 a、 o、 c 的 话呢,等于六十度,顺带的话呢,我们来标一下,那么 b、 o、 c 的 话呢,为一百二十度。那么我会发现的话呢?哎,直角三角把 m、 o n 的 顶点在 o 处,那么所以说 m、 o n 的 话呢?为什么呢?九十度。来把题目中的条件在图上去表 表示一下,表示完之后,咱们再来看一下。第一题说,如图 e、 o m 的 话呢,在射线 o b 上, o n 在 它的下方。那么题目中说 b、 o、 c 的 度数很明显是一百二十度, c o n 度数要注意了。有些人说,老师一百二加九十是二百一, 我们说过,一般情况下只研究小于一百八十度的角,那么因此通过计算,你会发现 a、 o、 n 是 不是也是九十度,所以说 c、 o n 的 话呢,应该是 o c、 o n 是 对应的这个角,所以说六十度加上九十度,答案等于什么呢?一百五十度。第一题相对而言比较简单,中规中矩,咱们再来看一下第二题说如图二, o m 恰好在角 b、 o c 的 角平分线上,那么同样的话呢,把题目中的条件标一下,那么说了,这里呢是六十度,然后 b、 o、 c 为一百二十度,那么角平分线一半一半的话呢?这里为什么呢? c o m 的 话呢,为六十度。那么 b、 o m 的 话怎么样呢?也为六十度。来读题了, o n 在 直线下方说问 b o n 的 度数,很明显, m o n 等于九十度,随着 b o n 这里等于多少度呢?三十度,随着第二题答案呢是三十度,也比较简单,接下来看一下第三题,说延长的话呢, n o 的 话呢,得到射线 o d, 如图的话呢,三 a o d 的 度数的话呢,那么应该为多少度呢?来咱们接下来去思考一个问题,在图二中,图二中的度数的话,那么刚刚说了,这里呢是多少度呢?是六十度,这里呢是六十度,对吧?这边呢是三十度。给它延长出来之后,咱们再来思考一个问题,先考虑 c o d 的 度度数, 这大的是六十度来 c o d 度数,因为你会发现 n o d 度数,所以 c o d 的 话呢,应该是等于三十度, c o d 等于三十度,所以说 a o d 的 话呢,六十度减三十度也应该等于三十度。答案就出来了,题目中说 d o c 和角 b o n 的 数量关系, d o c o d 在 这, c o c 是 三十度,那么 b o n, 那 么 b o n o b 在 这, o n 在 这也是三十度,所以说很明显是相等的关系,是等于的。接下来我们来看下最后一问, 说三角板按照每秒五度的速度的话呢,沿顺时针,要注意了,是顺时针旋转一周,我们在我们的课堂上给大家讲过是逆时针,要注意了, 他就是给你进行一些小的变化,然后呢大家去出出错,那么在旋转过程中, o n 恰好是它的角平分线,那么这个时候呢,问 t 的 值,其实这道题目当中的话呢,已经给你把一种去画出来了,来看好了,说在图三当中的话呢,已经给你把一种去画出来了,来看好了。说在图三当中的话呢,已经给你把一种去画出来了,来看好了。说在图三当中的话呢,是直线 o n, 那么来想一个问题,那么直线 o n 的 话呢,是它的角平分线,那么我们说过,正常情况下,第一种情况来给大家去画一下 o n 呢,是不是旋转到这样的一个位置,角平分线,那么一半一半,这里是多少度呢?三十度和什么呢?三十度, 那么因为是顺时针,所以说方向呢是这样转的,看好了,所有的方向是这样转的,那么所以说请问各位同学来看好了,那么 o n 呢?从这个位置转到这样的一个位置转了多少度呢? 九十度加上三十度的话呢是什么呢?是赚了一百二十度,所以第一个答案的话呢, t 一 就等于什么呢?一百二十度的话呢,除以五度,那么答案就等于什么呢?二十四秒, ok 吧,这是第一种情况, 那么第二种情况的话呢,来说呢,就看好了。那么第二种情况才是我们说的这里大家不容易注意到的,我们在课堂上强调过是直线 o n, 所以 这里图三在明确的告诉大家,看好了 o n 的 直线是不是 d n d n, 这里是不是恰好是他的角平分线?所以说第二种情况就是我们说的图三的这种情况,所以说一定要去读题。那么当时这种情况的时候,请问各位同学一个问题,他转了多少度?因为是顺时针转的,我同样给大家分析一下, o n 一 开始的位置在这,那么因此呢,他转了多少度呢?他转了这么一圈,那么所以呢,把这些度数加一下,九十度,加上三十度,加上三十度,那么很明显, 九十度加上三十度是一百二,一百二加三十是一百五,一百五加上六十的话呢,是什么呢?二百一,二百一,加六十是二百七,再加上三十的话呢,是什么呢?三百度,他一共走了三百度, 所以说他的 t 二的话呢,等于什么呢?等于我们的三百度,除以五度答案等于多少秒呢?等于六十秒。 那么还有一个方法是什么?有人说老师这里三十度,说明这里的话呢,应该是六十度,总共三百六十度,那么说明这边总共转了应该是三百度,也可以快速的得到答案,具体题目具体分析。所以这道题的话呢,两个注意点,一是顺时针,第二个是直线 o n, 那么以此,所以说最后一道题答案是六十二十四秒或六十秒,所以说的话呢,跟着袁老师把对应的题型学过之后,就用题目的话呢,难度就不会很大了。好了,那么关于今天题目就给大家讲到这里,有什么不懂的话呢?欢迎大家随向袁老师提问,每天一道题,让我们直接考试,从容应对。各位同学,我们明天的话呢,不见不散! goodbye, hello, hello, 各位同学,大家好,我是薛媛媛老师,今天我们来给大家讲解一下二十年质达十二月月考的解答压轴题,同样呢是我们的动角问题,来读一下题说如图,以点 o 的 话呢,为 直线 d 上的一个点过点 o 的 话呢,做射线 o c 角 e o c 的 话呢,等于什么?一百三十度, e o c 等于一百三十度,说明角 a o c 的 话呢,等于五十度。来把咱们的已知条件呢,标在咱们的图上, 将直角三角板 aob, 那 么 aob 的 话呢?这里呢,有一个顶角的话呢? oab 的 话呢,是三十度,说明它是一个三十度,六十度,九度的直角,三角板的直角顶点放在了 o 处。然后呢说 oa 的 话呢,在射线 o d 上, 另外一边 o b 呢,在直线 d, e, f 的 上,直线 d e 的 上方。然后呢,说了一个非常关键信息,将直角三角板按照每秒六度,第一个速度是每秒六度,第二个 逆时针旋转一周。那么逆时针的话呢,是沿这个方向怎么样去旋转一周? ok 吧?好,然后咱们接下来的话呢,来继续去看了,是旋转的时间的话呢,为 t。 第一题,当 t 等于四的时候, t 等于四,那么很明显四六二十四,他从 o a 的 话呢,从 o d 开始旋转,因此的话呢,他转了多少呢?他转了二十四度。因此呢,把题目中的条件呢去表示一下, e o c 一 百三十度, c o d 五十度。那么因此呢,这里转了多少度呢?这里转了呢?二十四度。那接下来看好了,说 a o c 等于多少度? 五十度的话呢,减去二十四度的话,那么很明显, a o c 的 话呢,等于多少度呢?等于二十六度。不要着急,一个一个来叫 b o e 呢?那么 b o e 的 话呢,那么很明显呢,同样呢去进行计算 啊。我们题目中说了,角 a o b 的 话呢,是九十度,那么 b o e 的 话,就等于一百八十度,减去九十度,减去二十四度,也就等于九十度,减去二十四度等于用,说的什么呢? 六十六度, ok 吧,所以第二个答案的话呢,应该是多少度呢?为六十六度, 说 b o e 减去角 a o c, 那 么 b o e 的 话呢,减去角 a o c 六十六度,减二十六度的话呢,答案等于什么呢?等于我们所说的四十度。第一题,答案就出来了,那么相对而言的话呢,比较简单,只需要咱们按部就班的把题目各角表示出来,答案就出来了,所以说难度的话呢,不是很大,那 所以咱们接下来的话呢,来一起呢,去看一下我们说的什么呢?第二题,当三角板 o a b 呢?旋转,至于 o e 相交的时候,如图三,请你写出来 a o c 与 b o e 的 关系, a o c 在 这, b o e 在 这,而且 a o c 和 b o e 的 关系。那么接下来为了方便去进行分分析的话呢,同样不要着急来,首先 c o e 的 话呢,一百三十度, 这里呢?五十度,这里呢是一个九十度,不,不给大家标了,那么刚好了,我们来去先去思考一个问题啊, 让我们怎么样求的是不是先表示出来了 a o d, 然后呢把这些一表示,答案是不出来了。那么同样我们来也是各位同学,先去把咱们的 a o d 表示一下, a o d 的 话呢,来分析一下,速度是几?速度是六度,然后时间是 t, 所以 说呢,六度的话呢,乘以 t 就 应该是什么呢?六 t 度,总共是不是六 t 度对不对? a o d 的 话呢,是六 t 度,来看好 这里是多少度呢?五十度。所以首先第一个 a o c 出来了没有?很明显交 a o c 的 话,就等于六 t 度,减去多少度呢?减去我们所说的是不是五十度,对不对? a o c 就 出来了, 接下来我们来再来去思考一个问题,那么请问思考一个问题,那么 a o e 能不能求出来呢? a o e 是 不是也可以求出来了?那么 a o e 的 话呢?来一步一步来交 a o e 的 话呢,就等于 一百八十度。减去什么呢?刚刚说了,这里是六 t 度, a o e 等于一百八十度呢?减去什么呢?六 t 度, 这个时候最后呢角 b o e 的 话呢?是不是答案也可以表示出来了?所以说它就等于 题目中说了这里的话呢, a o b 是 九十度,所以就等于九十度。减去一百八十度,减六 t 度就等于九十度,减一百八十度,加六 t 度,也就等于六 t 度,减什么的九十度。 所以呢,这在课堂上老师给大家强调过的,利用什么呢?利用我们的方程思想的话呢?最主要的精髓求简。 当我们把各个角都表出来之后,那么最后的话呢,说 aoc 和 boe, aoc 是 我们说的什么?六 t 度减五十度, boe 是 六 t 度减九十度,那么很明显 刚刚给的是什么呢?两个的差,那么请问这里谁大? aoc 比 boe 大, 所以说我们很明显不可能用 boe 减了,换一个思路,用谁呢? aoc 减 boe, 所以 aoc 减 boe, 也就等于六 t 度减五十度,减去什么呢? boe 六 t 度减九十度,所以说去掉括号就等于什么呢?六 t 度减五十度,减六 t 度,加上怎么九九十度?六 t 度一约九十度减五十度,答案等于什么呢?四十度,所以说这个就出来了, 所以说通过第一问的话,我们可以去适当求出来。第二问,所以说它的数量快,就是角 a、 o c 减去什么呢?是等于四十度, 所以你一个一个去做难度不大,关键在于我们能不能合合理的把这个角去表示出来。接下来第三问是重中之重了,说在整个旋转过程当中,是否存在某个时刻, o a、 o c 和 o d 中的某一条射线, 是另外两条射线竖成加角的角平分线。若有,请写出来 t 的 值,若不存在,请说明理由。 o a、 o c、 o d 的 某一条射线是另外两条射线所所成的角平分线。正常情况下,那么大家应该能够分下发现有几种情况呢?有三种情况, o a 是 角平分线, o k 是 角平分线和 o d 是 角平分线。 对于这道题的分析来看了,题目中很认识一点,图二和图三已经给你把两种情况表达出来了。第一种情况怎么样呢? o a 平分什么呢?叫 cod。 第二种情况不要着急, oc 平分什么呢?角 a、 o d。 第三种情况是谁啊? o d 平分什么呢?叫 a o c。 老师,这张第三种情况好像没有图,不要着急,一个一个来嘛来, o a 平分 c, o d, c, o d 多少度?五十度,那就说明什么呢?刚说了,所以说 角 a、 o d 就 等于什么呢?很明显,二分之一角 c、 o d 是 不是也就等于我们所说的二十五度? 那么所以说 a、 o d 是 什么呢?是不是六 t 度?刚刚就给大家用 t 表示过,所以说六 t 度等于二十五度,那么 t 就 等于什么呢? a 六分之二十五。第一个答案是不出来了,六分之二十五。第二种情况, oc 平分 a、 o d, 那 么很明显,角 a、 o d 是 不等于二倍的角,什么 c、 o d 对 不对?看这个图, o c 平分,它说明 a、 o、 d 是 它的二倍,二倍是多少度呢?是一百度, 而 a、 o、 d 是 什么?六 t 度等于一百度,所以说 t 就 等于什么呢?六分之一百三分之什么呢?五十。第二个答案也出来了,你看,哎呀,老师我不管怎么样是不知道能学来两个答案。第三个, o d 平分 a、 o c。 来,咱们来看好了,我给大家画到第一个图当中, o d 平分 a o a 的 话呢,这样呢?转了一圈 o a, 当转到这样的一个位置的时候,是不是成成为了角平分线对不对? 那么所以说当他转了这么多多度的时候,请问一下各位同学, o d 平分角 a、 o c, 这个时候角 a、 o、 d 是 多少度?角 a、 o、 d 的 话呢?是不是就等于角 c、 o d 等于什么呢?五十度,这里是五十度。 那么请问一下各位同学,六 t 度等于多少?谁是六 t 度呢?他转了这么一圈,这个是六 t 度,他不是 a、 o d, 这里是五十度,是 a、 o d。 所以 说六 t 度等于三百六十度,减去五十度,是不是因为他总共转了是不是等于转了三百一十, 那么 t 就 等于什么呢?六分之三百一十,六分之三百一十,同时约去二三分之什么呢?一百五十五。 所以说因此的话呢,这道题几个答案呢?这道题的是不是三个答案就全部都出来了?所以说我给大家在课堂上强调过, 题目中一定一定会给大家告诉他最终的未知情况,这道题虽然是一句话,但是他把未知情况都给大家告诉出来了,只要你按部就班分析,答案就出来了,所以说对于这道题目而言,属于一道偏中规中矩的题目。所以呢,下来之后,大家好好的把这道题去看一下, 有什么不懂的话呢?欢迎大家去向袁老师提问。每天一道题,让我们直接考试重一对。各位同学,我们明天的话呢,不见不散,拜拜! 哈喽哈喽,各位同学大家好,我数学袁老师。今天的话呢,我们来给大家去讲解一下 二四年五中十二月考的解答压轴题,同样呢是一道动角问题,来读下题说在射线 o c, 在 角 a o c 和 a o b, 那么说如果有一个角的度数是另外一个角度数度数的两倍,这我们做了 a o o c 的 话,就是他的巧分线给了他一个新的定义。正常情况下,有些人说,老师我读完题,我去看第一问就可以了,而不去进一步思考,他们说了一个角是另外一个角的两倍,请问有几种情况 看好了,有人说,老师我们来去看一下,我们是不是可以是 aob 是 aoc 的 两倍,你想个问题, aob 是 aoc 的 两倍,他是不是也就是 boc 的 两倍?因为 aob 是 他的两倍的话是,他是不是就是角平分线?所以说的话呢,我们来正常去分析了,来第一种情况的话呢,很明显这个大的角 可以是什么呢? aoc 的 两倍,也可以是什么 boc 的 两倍,这是第一种情况来。第二种情况呢?各位伙计们, aoc 可不可以是 boc 的 两倍,可以,没问题。 那么第三种情况,我们说了 boc 可不可以是 aoc 的 两倍,也是可以的, 那么还有其他情况吗?有人说老师, aoc 是 aob 的 两倍,怎么可能呢?你小小怎么能是大小的两倍呢?所以说这是这三种情况多问。题目之后来看,第一题说一个角角平分线是不是它的角平分线,那么很明显是的,我刚才给大家说过了,对不对?所以第一题答案呢?是是没有任何问题 来看下第二题,说 a o b 的 话呢,等于 r 法, o c 是 他的巧分线,那么问他有 a o c 有 几种情况?我们说了三种情况来分析一下。第一种情况,他是这两个的二倍,所以他一半一半是不是都是二分之 r 法,对吧?所以说这是第一种情况, 所以你会发现有些人做到第二问就蒙了,为什么呢?因为第二问他不知道怎么做。其实如果说在你读完题目之后,跟着袁老师把三种情况都分析出来,这道题就比较简单了。第二种情况, a o c 是 b o c 的 二倍,那么咱们看好了, b o c 我 设为什么呢? x, a o c 为二 x, 加起来三 x 是 不等于 r 法, x 是 不就等于三分之一倍的 r 法,那么 a o c 是 减, x 是 二 x, 所以 说它就是减了三分之二倍的 r 法。这第二种情况。 那么第三种情况的话呢? boc 是 aoc 的 二倍,把 aoc 设为 x, boc 就 为二 x, 加起来同样三 x 等于 r 法, x 等于三分之一倍的 r 法,那么 aoc 是 x, 所以 就是三分之一倍的 r 法,那么因此的话呢,所以说这道题的话呢, 也是三分之阿尔法。所以呢,对于这道题目而言,是不是分为三三种情况了,把没用情况分析到就可以了,第一种情况,二分之一阿尔法,第二种情况三分之二倍的阿尔法,第三种情况,三分之一倍的阿尔法。读懂这道题目之后,才可以去继续去进行研究。好的,那么所以呢,不敢说看完题目之后,什么都必须都 不去想,再来看一下,深入研究。说有一个三角板的话呢,拼接到了一起, b、 c 的 话呢? b、 f 的 话呢,分别与直线 g、 h 重合, abc 的 话呢?为什么呢? abc 的 话呢,是六十度, 当三角板绕点 b, 以每秒五度的速度。好了,关键一个速度啊,每秒五度的速度的话呢,逆时针旋转, abc 要逆时针旋转,逆时针的话呢,是这样的一个方向,给大家一分分析出来,那么来观察观察一下, 当同时呢,三角形 b、 e、 f 的 话呢,以每秒十度的速度的话呢,也是逆时针旋转,它还比较快,哎, 一个呢是五度每秒,一个的话呢,是什么呢?十度每秒。接下来,当 ab 恰好落在 b g 上的时候呢,它停止旋转。 来想一个问题, a、 b 要落在了 b g 上的话,这里是一百二十度,所以一百二十度的话呢,除以五度,他,各位同学,他旋转了多少秒呢?他有个范围,所以说范围的话,应该是多少秒呢?是不是二十四秒,对不对?所以说这道题的话呢,他说了总共呢旋转了二十四秒, 关键啊,有一个二十四秒,你呢,可以像我一样标到旁边继续去读题了。 那么说,当运动时间为 t 秒,说直接写出来,当 b f 是 我们所谓的 abh 的 巧分线的时候, t 的 值, b f 是 abh 的 巧分线,那么这个时候的话呢,是不同样,我们要干嘛呢?进行分类讨论。 b f 是 abh 的 角 巧分线。咱们接下来先去思考一个问题,来去表示一下 abh 怎么表示呢?来,看好了 ab 的 话呢,它要运动了。看好了 ab 的 话,你要说运动到这样的一个位置 对不对?这里是六十度,它运动的呢是速度是五,时间是 t, 那 么所以说它是不是运动了五 t 度对不对?所以你会发现,表示一下角 abh 就 等于什么, 等于什么呢? a 五 t 度呢?加上什么呢?六十度?这是我们说的第一个 abh 的 情况对不对?接下来第二个的话呢,来去观察一下 bf 运动, bf 要想是它的巧分线的话呢,请问一下, bf 是 不是从这边开始运动了? 那因此呢,速度是十,所以对于 bf 而言的话呢,看好了,运动了,它的角 bf h、 f, bh 的 度数是多少呢?是不是十 t 度对不对? 角 f, b、 h 的 度数呢?就等于什么呢?十 t 度? ok 吧,刚刚给大家分析了,就不给大家画到一起了,看好了, 速度是十,时间是 t 是 不是等于十度?乘以 t 是 不是十十 t 度?好的,明白了这个之后,咱们就来去思考一个问题啊,来看好了, 题目中说的话呢说,嗯,他最后运动时间是二十四秒每秒,运动十度的话呢, bf 的 位置话呢,最终有可能到哪里呢? 最终的位置的话呢,他会转二百四十度,最终的话你也会转到这样的一个位置,所以说这个时候的话,你就得去注意了啊, bf 的 位置是可以在什么呢?在他的里边是不是也可以在他的外边,对不对?那咱们接下来去分析一下,假如我们说了,当怎么样的 bf 怎么样的在里边的时候对不对? b f 在 里边的话有几种情况呢?我们说过有三种情况来看好了,第一种情况 好, b f 在 里边的话呢,我们说了第一种情况的话呢,很明显这个大角是它的几倍呢?两倍,它是不是角平分线?所以第一种情况我们说过, a 五 t 度加六十度等于什么呢?它的二倍二乘以什么呢?十 t 度,所以来算一下吧, 我们一起二十 t 度等于五 t 度加六十,所以说二十减去五的话呢,是十五 t 度等于六十,所以说 t 的 话呢,就等于什么呢?二六十除以四的话呢?六十除以五十五的话呢,是几秒呢?是四秒,第一种答案的话呢,是四秒,答案就出来了。 那第二种情况的话呢,咱们来下来去思考一个问题,来请问一下,他是不是可以是他的三倍, 对不对?来想一个问题啊,就是 a、 b、 f 是 不可以是它的两倍,那么假如说我们说了这个是 x, 这个是二 x, 那 么所以说总共的话呢,是三 x, 所以 说 a、 b、 h 是 它的几倍, a、 b、 h 是 不是它的三倍,对不对?我们说了啊,所以 a、 b、 h 的 话呢,是它的三倍, 所以呢,五 t 度加六十度的话呢,等于什么呢?三倍的是不是十 t 度,对不对? 有人说,老师,那我能能不能用刚刚这个方法去?可以,没问题,你要能反应过来,能行,要是反应不过来,向袁老师去进行分析,这个是为 x, 这个是为二 x, 总共是不是三 x, 这是他的三倍来通过计算,所以呢,三十 t 度就等于五 t 度加上六十度,所以说二十五 t 度等于六十度,那么 t 就 等于什么呢?二十五分之六十,同时约去五,是不是五分之什么呢?十二,第二答案是不是五分之十二? 那么第三种情况的话呢,大家来去思考一个问题, 那么第三种情况的话呢,也可以是什么呢? f、 b、 h 是 它的二倍,所以这个是 x, 这个是二 x, 总共是三 x, 说明这个大角是它的几倍呢?说明,很明显你会发现,大角乘以三,小角乘以二,说明五 t 度加上什么呢?六十度的话呢,是什么呢?是三 x, 不好意思啊, 这个是二 x, 这个是三 x, 说明的话呢,角 a、 b、 h 是 三 x, 那 么所以说角 f、 b、 h 呢,是二 x, 两个一比的话呢,是它的几倍呢?是二分之三倍,对不对?所以呢,五 t 度加上我们所说的六十度的话呢,是它的二分之三倍, 所以通过计算的话呢,来看好了,这里一约的话呢,是几呢?是不是十五 t 度等于五 t 度加上六十,所以说的话呢,十 t 度的话呢,等于六十 t 的 话呢,怎么样呢?等于六秒, 二分之三。刚说了,这里的话呢,是等于几秒呢?六秒。哎,那么这个时候的话呢,我们说过了,怎么样呢? b f 的 话呢,应该是什么呢啊? b f 的 话呢,是 a b h 的 这个啊,巧分线。那么有些人说老师的话呢,那当他运动到外边的时候呢,来看好了,运动到外边的时候呢,是这样的一个情况, 那你说老师,那这种情况下怎么办?那你说咱们要去思考一个问题啊, 要想是他的巧分线,看好了 oc 是 他的巧分线,请问 oc 在 一个角的什么呢?在一个角的内部题目中一开始说了,那么请问各位同学,那么当他转到外部的时候,还是不是他的巧分线了,不是了,对不对? 所以说的话呢,对于这种情况而言,转到外面要不要去咱们所说的思考的不用。其实所以说这道题的话就有几种情况呢,有三种情况。好了,那么关于今天题目呢,就给大家讲到这里,有什么不懂的话呢?欢迎大家学小雨老师提问。每天一道题,让我们只期考试重温一对,各位同学,我们明天不见不散! goodbye, hello hello, 各位同学,大家好,我数学袁老师。今天我来给大家去讲解一下二四年意外十二月月考的解答押注题第二十三题。对于这道题目而言的话呢,是一道非常特别难的题目,那么好多同学的话呢,全军覆没了,咱们接下来呢,来去看一下这道题。 一副三角尺,按照如图所示的方式呢,摆放在两角器上, p d 边的话呢,与零度重合 啊,边 a p 的 话呢,与咱们两两角七呢一百八十度重合。那么通过看图的话,能够发现他是不是相当于走的是内圈这部分,对吧? 然后的话呢,说 a p b 的 话呢,等于四十五度,那么我说了 c p d 的 话呢,等于什么呢?六十度,将 a b p 的 话呢,绕着两角七的中心点 p 啊,以七度每秒的速度的话呢,顺时针旋转啊,七度每秒, 当 p b 的 话呢,与我们所谓的零度线重合的时候的话呢?哎,停止运动,说它的时间为 t。 其实呢,大家来思考一个问题,这边的话呢,是我们说的四十五度,这边的话就应该为什么呢?一百三十五度,所以说 b p 的 话呢,它最多转多少呢? 那么说了,所以就相当于是一百三十五度的话呢,怎么样呢?除以七,所以说要转这么长时间,大概也就是个十几秒的情况。了解之后啊呢,来看一下。第一题说当 t 等于五的时候, p b 经过的是咱们来思考问题, t 等于五, 那么很明显,五七的话呢,它这里原本是四十五度,那么五七的话呢,怎么样呢?是三十五度,大概是这样一个位置啊,我们说是对应对应的情况啊,来看好了, 对应的是两角形刻度线,对应的度,度数是我们刚刚说过,他看的是内内圈,内圈这边是零度,所以看好了,这边应该是八十度。那么所以说这边的话呢,应该走了大概多少,对应的应该是多少度呢?应该是一百度,对不对?所以说就怕大家不认真审题,你认真审题之后呢,才能够发现这题答案是什么呢?一百度, ok, 这是第一题, 那么来看好第二题。第二题说当 t 等于几时? p b 开始平分? c、 p、 d, 我 们能够发现这边的话呢,是一个什么呢?六十度。这边的话呢,六十度角平分线一半就应该是三十度。那么来看好了, 那我从这里画这边的话呢,对应的是三十度角平分线。那么所以说 b 的 话呢,从这个位置运动到这个位置,所有人来看一下,应该运动了多少度呢?用我们说的一百八十度怎么样呢?减去什么呢?四十五度。减去什么呢?三十度 运动了一百零五度。所以说的话呢,时间的话就等于什么呢?一百零五度除以什么?七度?答案应该是等于什么呢?十五秒, ok 吧。所以第二题答案的话呢,当 t 等于什么呢?十五秒的时候的话呢,怎么样呢?它平分,所以大家注意一下,前两位的话呢,偏中规中矩,比较简单。咱们再来看一下第第三题。 第三题的话呢,题目中是这样去说的,来看啊,来说三角 使 a、 b、 p 旋转的时候的话呢?三角尺的话呢? a、 p、 c、 d 的 话呢?沿绕点 p 怎么样呢?以什么呢?以三度每秒的速度的话呢?怎么样呢?沿逆时针的方向运动,这边三度每秒。 当三角尺 a、 b、 p 停止旋转时, p、 c、 d 也停止旋转。那么很明显我们能够发现 这个的话呢,它能不能旋转到与这边发生重合?很明显不够,这是一百二十度。除以三,它要旋转四十多秒。而刚刚的话呢,我们能够发现这边是什么?是不是一百三十五度?所以呢,一百三十五度的话呢?除以什么呢? a, 除以我们说的七,它就大概呢旋转多少秒呢?旋转十九秒, 所以当这个 a p b 啊,最终的情况给大家画一下,就当 a p b 哎,旋转到这个位位置的时候的话,这个 p p c d 哎,可能才走了这么样一点的距离,所以说的话,大家明白它的这个起始位置和咱们的中轴位置。好的,明白这个之后的话说,当 t v 合值时, p b 平分什么呢? c p d? 那么对于这种情况而言,袁老师在课堂上呢,给大家去说过,他就相当于变相的话呢,怎么样的哎,告诉大家他最后的运动情况了,那么因此呢,我们根据他的情况呢去画图就可以了。那么接下来看好了第三题的第一个, 首先来看好了这边的话呢是什么的? c p 这边的话呢是什么的? p d 好 p c d 呢?这样的一个位置,他说了 b p 要怎么样呢?平分什么呢? c p d 对 不对?那么 b p 的 话呢,要去平分 c p d 的 话,那么大家来看好了,原本的话呢, ab p 的 位位置的话呢,是这样的一个情况, 是不是 ab p 旋转之后的话,它要平分的话呢? b p 是 不是应该是在这 好 b p 平分我们所要的 c p d 的 话,那么请问各位同学一个问题,这个时候如何找他们的等量关系? 乍一看的话呢,很难,实际上的话呢,还是比较简单的,我来问大家一个问题啊,来,咱们来把这个图当中的条件的话,角度的话分别去表示一下,这里呢我给用虚线去 表示,这里呢是原来的 b 撇啊 b 的 位置,现在的话呢, b 的 位置是 c p d 的 位置。那么来看好了,题目中的等量关系呢?答案就出来了,老师呢,给大家写一下来,请问各位同学,这个度数是多少度? 那么我们说过速度是三,那么时间是 t, 那 么所以说三度乘以 t, 是 不是三 t 度,对不对?来分析,那么会发现这里呢,是三 t 度,那么这个时候的话,我们来发现这里呢,这里还是角平分线六十度,角平分线一半,这里是三十度, 那请问各位同学,这个呢,速度是几呢?七,时间是 t, 所以 他走了七 t 度,这里一开始多少度?是不是四十五度,所以等量关系是不就出来了?四十五度加上七 t 度,加上三十度,加上三 t 度,答案就出来了,那么以此的话呢,所以说列一下关系,四十五度加上七 t 度,加上什么呢?三十度 或者是加上什么呢?三 t 度, 答案呢,等于一百八十度,所以我们来去快速的计算一下吧,七 t 度加三 t 度是十 t 度,那么这边的话呢,应该是加起来是七十五,等于一百零五度,所以 t 就 等于什么呢?一百零五度的话呢,除以十度,所以应该是什么呢?十点五秒, 那么第一题的话呢,答案就出来了,所以呢,作为对于这种题目而言,袁老师曾经给大家强调过,题目中一定会给你把它对应的情况去说出来,角平分线,我们随便换一种情况是一分析就可以了,所以说根据他给的图,我们去找等量关系,答案就出来了,这是我们说的第三题的第一题, 第二题的话呢,很难啊,我直接说了,第二题很难,正常情况下,第二题要想去做出来的话呢?袁老师来给大家说一下,我们应该干嘛呢?说摩羯士格是否存在 a、 p、 c 等于二倍的 b, p、 d, 若存在,请说明理由。若不存在的话,若存在请求来 t 的, 则若不存在呢?请说明理由。 对于这个而言,袁老师给大家说,为啥,为什么说他难呢?他正常情况下的话呢,分五种情况,分哪五种情况的话呢?我们来去分析一下这个,这个图看好了,第一种情况,哎,他开始转了 对不对?它也开始转了,两个图没有任何交叉,这是第一种情况。第二种情况, a、 p、 c、 d 还在转的情况下的话呢,你会发现怎么样呢? a、 b 到了内部,这是第二种情况,对吧? 那第三种情况的话呢,还在转的过程当中,你会发现怎么样呢? a、 a、 b 是 不是都可能到了内部,对不对?那么第四种情况的话呢,说 p、 c、 d 还在转的过程当中, 很明显 a 还在里边, b 怎么样呢?是不出来了。那么第五种情况的话呢,就是 p、 c、 d 还在转的过程当中的话呢,怎么样呢? ab 的 话呢,是不全部都出来了?所以说是不分为这五种情况,我们正常情况下,应该是把这五种情况的 a、 p、 c 和 b、 p、 d 表示出来, 答案是不就出来了,那么因此哈,所以对这道题目而言,分析五类分,分类讨论五种情况就得到答案,确实很难。那有没有什么比较快速的方法帮我们进行分析?有表示角 abc 的 表示呢?可以把它讲成一个相遇问题,那么对于相遇问题而言,老师给大家去写一下, 那么 a p 的 a p 的 速度的话呢?来看好了, a p 的 速度的话呢,往这个方向走速度的话呢,是七 t 每秒,那么这个时候呢, c p 的 速度的话呢?是什么呢?是不是三度每秒对吧?两件的距离是不是一百二十度,那么把它分成相遇问题的话能够发现, 那么所以说两人最后 a p、 c 的 话呢,它们之间的夹角就等于什么呢? a 一 百二十度减去什么呢?七度 t 这边是不是走了三度 t 对 不对?那么因此,所以说角 a p c 的 话呢,就等于什么呢? a 一百二十度减去七度 t 减去三度 t, 相当于就减去什么呢?哎,我们说的十 t 度, ok 吧?好的,但是既然是相遇问题,我们刚刚在画那五种情况时候,大家应该能够发现了,有什么呢?有相遇前 有什么相遇后?既然有相遇前和相遇后的话,请问相遇后的角 a b c 怎么表示?因为我们能够发现,太阳在某一时刻 a b 和 c b 发生了重合,重合之后的话,是不是就是错开了,对不对? 那么所以说呢,来利用相遇问题去考虑看好了。哎,假如说我们来看这里了,那么 a p 的 话呢,走到了这,这走了什么呢?很明显七七 t 度对不对? c 的 话呢?走到了这,那么这走了多少度呢?是不是三 t 度对不对?那么因此你会发现, 这走了七 t 度,这走了三 t 度,那么它俩加起来之后,比一百二十度多了一个中间的 a p c, 所以 它就等于什么呢?七 t 度加三 t 度减什么呢?一百二十度是不就等于十 t 度减一百二十度了? 等于十 t 度减一百二十度的话,那么一个是一百二十度减十 t 度减去一百二十度,那么很明显各位同学 这道题我该怎么进行分析?我们老老师呢,给他个建议,利用绝对值,因为我带他绝对值之后,那是不是就说明我们相遇前和相遇后的两种情况就都包含了?那明白了这个之后,咱们接下来看一下角 b p d 呢? b p d 的 话呢,也是这边呢,原本四十五度,这边是一百三十五度,那么这个时候的话呢, b p 的 速度的话呢,是七度每秒, d p 的 速度话呢,是三度每秒,是不是也是相遇问题 分为什么相遇前和相遇后,相遇前就等于什么呢?这边七 t 度,这边三 t 度,那么它就等于什么?一百三十五度减七 t 度减三 t 度,对不对?所以说是不是就等于一百三十五度减去十 t 度, 这是不是 bpd? 相遇之前,那么我说了分为相遇前还有什么呢?还有相遇后,那么相遇后的话呢,袁老师再给大家进行分析,看好了, 和刚刚一样,这个走了七 t 度,那么这个走了什么呢?三 t 度,那么这个时候你会发现七 t 度加三 t 度加起来比原本的一百三十五度是不是多走了这么一个角,所以减去一百三十五度,是不是刚好是角? b p d 一整理是不是十 t 度减一百三十五度,那么所以说他同样也分为相遇前和相遇后,那这个时候怎么办?老师给大家说要干嘛?带上什么绝对值进行分析,这个时候我们就不用再去考虑他在什么样的一个位置了,因为带上绝对值是不是就相当于把所有的情况都考虑到了? 那么题目中的关键来看好了,说角 a p c 开始求了,求过他小的角 a p c 等于什么呢?角 a p c 等于二倍的角,什么呢? b p d。 那 么换句话说,一百二十度减十 t 度,等于二倍的一百三十五度 减十 t 度,那这个时候呢?乘以二之后呢?我把二乘到里面是不是就等于什么呢?二百七十度减去什么呢?二十 t 度。那么请问各位同学一个问题,当我们带上绝对之后,老师来问一下各位同学, 当 a 的 绝对值和 b 的 绝对值相等的情况下, ab 有 几种情况?两种情况,要么怎么样相等,要么怎么样呢?是不互为什么呢?相反数是不是? 那所以你会发现就不用画图画五种情况了,所以说应该怎么样呢?要么怎么样相等?一百二十度减十 t 度,等于二百七十度减二十 t 度,通过计算,那么所以说十 t 度就等于一百五十度 t 就 等于什么呢?十五, 那第二种情况呢?一百二十度减十 t 度减去二十 t 度,对不对? 这个时候去括号就等于一百二十度减去十 t 度,等于负的二百七十度加上二十 t 度,所以说来去算一下, 那么三十 t 度的话呢?这边就等于什么呢?三百九十度 t 就 等于什么呢?十三,是不是因此的话呢?我们把最后一问,复杂的一道情况的话呢?变成了什么呢?变成了我们所有的方程求解的,所以说这道题的话呢, 所以呢,这道题的话呢,当年很多同学哎,全军覆没,那么所以说的话呢,与其说去分析分类讨论五种情况,还不如把它给它想成我们所要的怎么样的方程思想进行求解,就可以很快的得到答案了。 好的,那么关于今天题目就给大家讲到这里,有什么不懂的话呢?欢迎大家学校袁老师提问,每天一道题,让我们直接考试从容应对。各位同学,我们明天的话呢,不见不散! is bye bye bye! hello, 各位同学,大家好,我是薛媛媛老师,今天我们来给大家讲解一下二三年秋季三大副十二月月考的解答压轴题。那么同样的话呢,是一道动角问题,题目中说的话呢,一块三角板按照如图一的位置呢摆放, o a 的 话呢,与 e f 重合, a o b 的 话呢,题目中说的是三十度射线, oc 的 话呢,在 e f 上方前 e o c 的 话呢,是四十六度。 那么这个题目说做角 b o c 的 角平分线很明显,通过计算的话呢, b o c 的 度数应该为一百八十度,减去咱们说的三十度,减去呢,四十六度等于什么?一百零四度,那么所以说角平分线那么一半一半应该是多少度?应该为五十二度。 那么第一题的话呢,相对而言比较简单,我们正常去进行计算就可以了,所以第一题就不给大家耽误时间了,来看下第二题。第二题题目中说 三角板 a o b 绕着 o 逆时针旋转,看好了,这两是逆时针旋转一个角度,而法在转动过程中的话呢,它 说 e, 呃,三角板一直处于 e f 的 上方。好的啊,这是关键,这是分类讨论的一个限制范围。 e f 的 上方 说当 cod 是 二十度的时候,咱们就来看一下旋转角 r 法的话呢,等于多少度?如图二, cod 呢是二十度,这里是角平分线,那么这边呢是二十度,这里呢是用原本的三十度,这边的话是什么呢?四十六度。所以旋转角的话就等于什么?一百八十度, 减二十度,减二十度,减三十度,减去四十六度,对不对? ok 吧。那么所以说最后的话呢,答案等于什么呢?六十四度。所以说阿尔法的话,这里应该是对应的是六十四度。这里呢,特别注意一下题目中给了什么了,题目中已经给了度了,所以这道题应该直接写什么呢?六十四就出来了, ok 吧。 好,接下来看一下第二题,也是最难的一道题了,题目中说,在循环过程中是否存在 b o e 等于三倍的 a o c? 若存在,请写出来,请直接写出来啊。阿尔法的度数若不存在的话呢,请说明理由。 那么这个时候的话,咱们去关关键的一个点在于哪里的,哎,我们说在整个循环过程中, b o e 等于三倍的阿尔法,这三倍角 a o e 等于三倍角 a o a a a o c 啊,题目中说了 b o e 等于三倍角 a o c, 它 f 分 为的是三种情况,怎么样?三、三种情况呢,就是 a o b 的 位置。第一种情况就是如图所示的位置, a b o e 是 这样的, a o c 是 这样的,对不对?第二种情况我们来看好了,如果 a o b 的 位置呢?怎么样呢? 出现了这样的一个情况,看好了,那么这里是 a, 这里是 b, 对 不对?哎,当 aob 的 话呢,怎么样呢?转到 ob 在 oc 的 下方时候,是不是有当它和 oc 发生交叉的时候, be 和 oc 又是第二种情况, 那么有些同学,同学说,老师,那有没有第三种情况以后继续去进行分析看好了, 那么假如说它怎么样呢? o a 也在它下方的时候,那么因此的话呢?所以说总共的话呢,我们说了分为这几种情况呢?分为这我们说的三种情况。哎,那么三种情况的话呢,老师呢,给大家把三个图的话呢,分别去画,去画出来, 把三种图都画出来之后的话呢,来去求一下咱们对应的答案就可以了。来看好了,那么因此明白了之后的话呢,来去看一下第二题。 那么第一种情况的话呢,来表示一下我们说的 b o e, 那 么这里的话呢是什么呢?四十六度。 a b o e 的 话怎么去表示呢?很明显也比较简单,呃,不用看那个四十六度,这里呢是 r 法度,那么这里边的话呢是什么呢?三十度,所以说 b o e 的 话呢,就等于 一百八十度,减去什么呢? r 法度也就等于什么呢?一百五十度减 r 法。我 好这第一个,接下来我们来看下第二个来 aoc 怎么表示?各位同学们, aoc 的 话呢,是这样的一个位置,那么这里是阿尔法,这边呢?是什么呢?哎,这里是不是四十六度,所以说它是不是等于一百八十度减什么四十六度, 那么也就等于我们说的一百三十四度减 r 法,好,那这种情况来求下 r 法是多少度? boe 等于什么呢?三倍角 aoc, 说明我们说的什么呢? a, 一 百五十度的话呢?怎么样呢? 减 r 法就等于什么呢? a, 三倍的一百三十四度,是不是减 r 法,对不对?所以通过计算,一百五十度减 r 法等于三百,看一下三四十二, 三三得九,应该是四百零二,减去三 r 法度, ok 吧,去整理一下三 r 法,减 r 法等于四百零二度,减去一百五十度,所以说二 r 法的话呢,就等于什么呢? 一四百零二度减去一百五十度,应该为我们所说的二百五十二度,所以说 r 法呢?除以二答案应该是等于我们所说的 一百二十六度, ok, 那 么通过计算的话呢,我们算出来 r 法等于一百二十六度,但是的话呢,我来问大家一个问题,第一种情况的话呢,我们说什么呢?哎,我们说他怎么样呢? 一百二十六度的话,请问一下 ob 运动到了哪里了?阿尔法是一百二十六度,加上这个三十度,他应该运动到了一百五十六度, ob 运动到了这样的一个位置,很明显和图第一个图是不相符的,所以这种情况怎么样呢?分析出来,但是他怎么样呢?不存在,所以两个字怎么样呢?舍去 不符合题,这是第一种情况,来看一下第二种情况, 这时候同样问大家, boe 怎么表示 boe 的 话呢?这边的话是什么呢?三十度,这边是不是 r 法度,所以说也是什么呢?一百八十度减三十度,减 r 法度也是什么呢?一百五十度怎么样呢?减 r 法, 那么这个时候呢? aoc 呢?很明显 aoc 在 这,这边的话呢,是 r 法度,是不是一百八十度减四十六度?减 r 法度,是不是我们说的一百三十四度 减 r 法,那么这个时候同样是三倍加上出来 r 法等于一百二十六度,那么因此这种情况下,它是复合题的 o b 在 里边, o a 在 什么呢?外边是不是这样的情况,所以这种情况下流出来,明白了吗?各位同学,所以说正常情况下就应该把这三种情况都分析清楚,接下来看一下第三种情况, 角 b o e 等于什么? a, 那 么角 b o e 的 话呢?还在这里, 那么这里边的话呢,是三三十度,那么这个时候的话呢,我们来去观察一下这边呢三十度,这个呢,是不是说的 r 法度也是一百八十度减三十度,减 r 法度是不是等于一百五十度减 r 法,这 b o、 e 呢?始终都是一百五十度呢?减 r 法,那么请问一下角 a、 o、 c 呢? 各位同学,请问一下 aoc 在 哪里? aoc 在 这,那么各位同学,这里是多少度?这里是不是 r 法度对不对?那么这个是相当于 r 法度减去了什么叫 cof? cof 的 话应该是相当于什么呢?一百八十度减四十六度,应该是不是一百三十四度, 所以这里是一百三十四度的情况下的话,那么所以说 aoc 就 等于什么呢? r 法减什么呢?一百三十四度, 这个时候,那么最终的话呢,存在几倍的关系呢?我们说了是不是存在三倍的关系来算一下,所以呢,一百五十度减 r 法等于三倍的 r 法,是不是减去一百三十四度?所以说一百五十度减 r 法等于三 r 法减去四百零二度, 所以说三 r 法加 r 法等于一百五十度,加上四百零二度,所以呢,四倍的 r 法的话呢,等于五百五十二度,那么 r 法的话呢,就等于什么呢?哎,用我们说的这个五百五十二的话呢,除以四五百五十二的话呢? a 除以四的话呢,刚好是我们说的一百三十八度。 好,那么咱们接下来去思考一个问题, r 法等于一百三十八度,看好了是否符符合题意。 那么题目中说了这边的话呢,我们刚刚所说的是不是说的一百八减去什么呢?一百八减去四十六的话呢,是不是一百三十四度?他一百三十八度,说明 o a 确实转到了 oc 的 下边,所以这个是什么样的?是不是也是符合题的? 因此的话呢,通过计算的话呢,总共的话是不是有三种情况?三种情况的话呢,就有几个答案呢?是不是有两个答案?那么所以说最终的话呢?所以说,综上所述, 阿尔法等于什么呢?一百二十六度或阿尔法等于什么呢? a, 一 百三十八度? ok 吧。好了,那么关于今天题目呢,就给大家讲到这里,有什么不懂的话呢?欢迎大家说一下。于老师提问,每天一道题,让我们直接考试重音,对各位同学,我们明天的话呢,不见不散! respect! 拜拜!
 02:09查看AI文稿AI文稿
02:09查看AI文稿AI文稿不废话,直接说结论,这张试卷再加五到十分,大概就是你期末的分数。这份试卷的题目类型那不止与难度和往年期末考试极其类似,当做期末的模拟卷完全没有问题。但是这个月考考出来,对县级段的孩子们来说还是不好做的, 且一个半小时的考试时间虽然不短,但对中等生而言依然比较紧张。小题方面没有无脑的送分题,都需要孩子们进行一定程度的思考,比较考验学生的效率与日常学习。 大题方面非常符合素质教育,题目长且要画图,过程严谨,还考验现学现卖的能力。大部分同学们做的应该是比较累的。 孩子们的差距主要体现在后面三道大题上。二十一题考察新定义加尺规做图,虽然难度不是很大,但这种考察方式较为新颖,有点类似于中考试卷中尺规做图的考法。咱们以前的尺规做图都是明确告诉你需要做什么, 比如题目中会直接说让你做脚等或者线段,而现在的考法更多的是把技能当做工具去用,就比如二十一题,让你做巧分线, 那就是让你去结合题意去想我应该做一个什么样的图,读懂题目的要求才是关键。两道压轴大题对绝大部分孩子们来说还是压力很大,尤其动态问题,对孩子们很不适应,期末的时候可能会好很多,但是现在这个阶段,大部分孩子肯定还是不太行的, 只要图行动起来,它就不好进行准确的想象了。二十二题考察转角问题,前两问不是很难有个好的标记习惯,人也不懒,基本上可以解决。但第三问需要同学们根据题意画图, 还能想到这题不止一个类型,这就比较考验人了,很有难度。做这类问题的核心就是敢于下手,不要空想。二十三题考察行程问题的综合题,与太原市以往的期末考试非常类似,最后一问难度较大,极有可能答不全。这类问题的核心就是时间的表示。 总结来说,虽然这张试卷难题的难度很大,但是最难的题占分倒是不多,所以说整个试卷总体难度适中,考察知识点比较全面。无论做没做过这张试卷,都要把这份试卷当做期末的模拟卷,千万不能错过这张卷子。
 32:43查看AI文稿AI文稿
32:43查看AI文稿AI文稿好了,各位同学大家好,我是资点教育的艾老师啊,那今天的话呢,由我来带着大家呀,复习一下咱们在十二月月考可能会涉及到的一些知识点。好,那当然,在这次月考的过程中,呃,第一呢就是部分学校他的教育进度,教学进度不太一样, 所以呢,可能会出现考试的范围稍有区别,这个正常啊。第二个呢就是还有呢,我们在期中考试前的内容,这次月考的话呢,也是会涉及到的,所以呢,涉及到期中考试前的一些内容,我们会简单带大家串一下,就不再去详细重点去复习了啊。 好了,那么先说这次考试的核心的知识点,第一个呢就是方程模块,也就是一元二次方程啊,函数模块的话呢,重点就是考察这个反比例函数,个别学校啊,考这个目前的话呢,教学进度比较快一点,可能已经开了二次函数会,考察一些基础的二次函数的题目, ok, 再然后呢就是三角函数模块啊,然后呢这个正弦余弦正切这种类型啊,然后呢再有就是概率统计,概率统计的话,一般来说比较简单啊,都是送分题,但是同学们不要在这些地方丢分啊。最后呢就关于啊 重难点分值占比比较多的啊,叫几何模块。好,那么先来说方程模块,方程模块的话呢,大家需要简单的复习一下,因为这个的话呢,是在咱们期中考试的时候,基本上就已经考过这些题目了啊。 好,第一呢就是关于一元二次方程的定义,标准形式和判别式,可能会在一些送分题里面考到,比如说把某个一元二次方程化成标准形式是长什么样子,或者说这个一元二次方程有没有根,有几个根这种问题,那标准形式呢,就是 a x 方加上 b x 加上 c 的 形式是吧?好,然后呢,判别式也就是 b 方减四 ac。 有 个别同学如果还没有记住公式的, 需要好好复习一下了啊。好,再然后就是一元二次方程的解法,我们常用的三种解法的话呢,就主要是以配方法,因此分解法和公式法为主。那么在什么情景下用什么方法,或者优先考虑什么方法,大家呢,一定要注意,不要只说哎,老师我会公式法,万能的就搞定结束了 啊,其他的方法也一定要去多注意,多了解,多去分析它在什么情况下使用更合适啊。待会说。 那再然后呢,就是一元二次方程的应用题,那么这种的话呢,一般是以解答题为主,个别学校呢,会在小题里头还会再出一道说给你一个材料,让你去判断根据这个材料应该列出的方程符合要求的是哪一个啊?那这种题的话呢,倒是比较简单啊。 最后呢,就是个别学校可能会在拓展一些关于伟大定律,也就是根与系数关系,那么可能会出一道小题,不会,通常来说不会太难啊。 那么伟大定律的简单复习一下,就是两根之合等于负的 a 分 之 b, 两根之 g 等于 a 分 之 c。 然后呢,如果是考到的话呢,稍微注意一下啊。 好了,那么接着我们来说一下,呃,在实际考试过程中,解方程的常考的两个地方,一个呢就是第十六题会给你一个哎,这个两道解方程的题,通常来说啊,这种两道题的话呢,它会考察两个不同的方法啊,常考的就是 因子分解法和这个叫呃,配方法,或者说是公式法啊,通常来说的话呢,就是三个里面挑两个好,以这个为例, 那么这个的话呢,呃,有个别同学就是分析的不太到位啊,容易去在这里面的采用的方法就是先全部打开,然后合并变成标准形式,再考虑实际相乘因子分解或者直接公式法。那这个叫这个方法呢,就太麻烦了,注意观察 有个 x 减二的因子,这里面你仔细去观察,它相当于也是一个二倍的 x 减二,所以呢,这实际上应该是一个因子分解法的逻辑啊,因子分解法的逻辑 好,那至于这个,那么考虑到这个是 x 方,这是减八 x, 它实际上可以比较简单的配方,也可以考虑呢,直接是公式法进行处理啊,公式法进行处理,如果说这个地方啊,它是一个七 x, 那 么配方的话呢,系数算起来就稍微麻烦点了,不要犹豫,直接公式法啊。 好了,那这个的话呢,是关于第十六题可能考察的逻辑啊,那接着来说一下十九题,一般这种的话呢,相信大部分同学都是能够读懂题,并且列出来对应的方程的, 往往难度不大啊,但是呢,在接下来的计算过程中,需要跟大家去啰嗦几个问题啊。第一呢,就是关于这个式子的化简,有些同学呢,就是属于叫硬算啊,不是不行, 但是啊,但是往往呢,我们可以同时在等式两边除以一个系数,让他的计算量稍微降低一点。比如说,以这老师为例,我们先把这个中括号里面的化解一下,他应该是 x 减七括号乘中括号,那这秒上去到最后应该减十 x 再加一百二,那应该是二百八 十,减去十 x。 好, 呃,应该是中括号,然后呢减二百八十,然后呢等于八百,那这个时候你如果直接去把这个括号给它成开,计算量稍微有点大啊。好,那么如果我们考虑这里面是不是二百八十,这里面是不是十 x, 这里面有二百八,这里面有 八百,我等式两边同时除以一个十,再去化简,是不是计算量就会稍微小一些了?好,那这个呢,是需要给同学们去啰嗦的一个点,怎么去尽可能降低自己的计算量,但是的话呢,呃,同学们,一般来说应算的话呢,也 ok。 好, 那化简到最简形式之后, 呃,就个别同学开始出现一些困难了,就是老师,我确实能划到这一步,但是我接下来的算我比较费劲,我感觉计算量特别大。好,那这里的话跟大家啰嗦一下,我们从结果倒推, 大家如果注意这种类型的题,应该知道它的结果往往是比较整的数,所以这种题优先考虑什么呢?优先考虑十字相乘一日分解,如果你平时十字相乘一日分解,就不是特别熟练 多练啊,这没有什么可说的啊,多练,多想,多琢磨。好,那么实在,你在考试的过程中说,老师,我也琢磨了,我也花了一点时间了啊,但是我确实就是想不出来,那也不要在上面一直的想你该换方法,换方法,比如说我就 全公式硬算,能不能算出来应该也是可以的,只不过就计算的稍微大一点嘛,但是优先考虑实体乡镇一日分解。好吧,以这道题为例,还是带大家呢去啰嗦一下,比如说这是 x 方 减去三十五 x, 再加上三百零四等于零,对不对?那十的相乘一的分解怎么去分析呢?首先第一步,你把它的这个平方向拆开, x 方拆成 x 乘 x, 对 吧?然后呢,这个三百零四,我们就说要拆成两个数相乘吧,然后让它们交叉相乘之后再相加等于负三十五 x, 所以我们可以大胆的猜测,这里面呢应该是减 a, 这里面是减 b, 那 么其中 a 加 b 就 应该是就相当于减 a x, 减 a x 减 b x 加起来等于减三十五 x, 所以 a 加 b 等于三十五,以及负 a 乘负 b 等于三百零四,也就是 a 乘 b 等于三百零四。 我们如果要直接分析 a 乘 b 还是比较困难的,所以呢,这个题就优先建议先去分析, a 加 b 等于三十五, a 加 b 等于三十五,那 a 加 b 等于三十五,还有乘起来等于三百零四,立马就拆一个相对比较整的,比如说什么呢?哎,十五加二十是不是等于三十五?那这个时候你发现十五乘二十,它是不是等于三百,比这个三百零四要 小一点,那这个时候呢,我们就把这两个数呢稍微调整调整就行了。那怎么调整呢?我们知道当两个数合一定的时候,应该是差小积大,差越小积越大, 所以我们现在想让这个三百变得稍微大一点,那我们这个十五是不是应该变得大一点?二十是不是应该变得小一点?那么我们接下来就可以去尝试十六乘十九,以及十七乘十八,以及这个十八再乘十七,这就重复了, 所以我们接下来要去努力尝试的就是这两组,看看他会不会就是我们想要的东西,是吧?那这个时候你去看一下个位基本上就出来了,六九五十四、七八五十六,那应该是他合适的,简单去验证一下,发现十九乘十六确实等于三百零四。好,那所以我们的十字相乘就猜出来了, 那这两个数就应该是减十六,减十六和减十九,那所以呢,他对应的十字相乘一的分解的形式是 x 减十六乘 x 减十九啊,然后呢等于零,那么两个根就是十六和十九, 是吧?好,这就是所谓的十字相承音质分解,当你碰到一些比较大的数的时候,怎么去分析?好,那我们还是那句话,如果你在考试的过程中,确实说,老师我也分析了一两分钟了,就是没有头绪,那么平时要多练,考试的时候不要犹豫, 该配方配方,该十字相乘以十,呃,该公式公式啊,那当然,这个地方呢,它是一个减三十五,如果你想要用这个叫配方法,呃,这道题呢,就不是特别合适了,如果这个题它是三十六,那我们知道它的配方呢,就应该配一个十八的平方,这个还是比较好的。 那这个三十五的话呢,就建议直接求公式吧,那求公式的话呢,列一下 x 呢等于二 a, 那 就是二分之负 b, 呃,三十五加减根号下 b 方减四 a c, 也就是三十五的平方减去四乘三百零四,你会发现这个计算量呢,还好吧,哈哈,还好吧, 这个三十五的平方呢就等于一二二五,然后呢减去四乘三百零四,那应该是等于四四十六三四十二,一二 一六。好,然后呢再开方三十五呢,加减再除以二,那一二二五减去一二一六的话呢,等于二十五减十六对吧?啊等于九,开方的话呢等于三,所以它结果呢就应该等于二分之三十五加减三。哎,那你看也就搞定结束了 是吧。所以的话呢,呃在计算的过程中一定要算的比较准确。好吧,那总结一下这类的问题,第一在列方程的时候列完之后再去化简的过程中尽可能降低自己的计算难度。 第二再去解这个最终的数比较大的一元二次方程的时候呢,优先考虑十指相成一日分解。 呃在考试前要多练啊。然后呢如果思维相册一的分解卡住了,没思路了,找不出来到底是哪些数进行配凑了,那怎么办呢?不要犹豫啊,公式法或者是配方法去处理就行了啊。 好,那这个呢是关于呃这道题给大家的一个建议啊,考前的一个建议啊,那再然后呢就是函数模块好,那么函数模块的话呢,跟大家唠叨一下就是 呃考的反比例函数吧,因为我们最近这个刚学啊,所以的话呢,有部分同学这个可能在这一块的知识点如果不是特别扎实的,一定要去看一看。哪些地方呢,还需要巩固练习一下啊。 一、反比例函数的话呢,可能会考察的基础,比如说它的解析式,怎么去求它的图像大概有哪些特征,以及比较容易常考的 k 的 几何意义,需要着重去说一下啊。 好,再然后呢,就是反比例函数和一次函数的综合题啊,就是这里面的话呢,它既有反比例函数,也有一次函数,比如说他们的焦点啊,怎么去求他们的焦点呢?连立啊,他们的解析式啊,解方程,然后呢,去求他们的焦点就可以了啊。 好了,那再然后呢,就是反比例函数的一些应用题啊,注意它里面的一些各种数据,比如说你像往年可能会考一些大家经常会调侃的啊,数学题怎么变成了物理题,是吧?啊,也有这种可能性啊,也有这种可能性。好了,那么接着说 举两个例子吧。啊,去年的话呢,你看有这么一道题,说给了一个反比例函数,问他的图像是否会经过一斗士,是否会经过哪个点呢?很简单,你就把这个点带到解析式里面,看是否成立,成立就经过,不成立就不经过啊,就是这么一个知识点。 好,再然后呢,函数图像的对称性啊,轴对称和中心对称。那我们也简单复习一下,反比例函数是中心对称函数啊,中心对称图形,他的图对称,中心呢,就是圆点, 同时呢,它也是轴对称图形啊,这个句前半句话是对的,但是呢,对称轴不是外轴啊,它的对称轴应该是什么呢?我们画个图,比如说以一三象限的反比函数为例, 它的对称轴有两条啊,第一条呢,是这个一三象限的角平分线,是它的对称轴,除此之外啊,二四象限的角平分线也是它的对称轴啊,好,所以它是有两条对称轴的啊,这个需要了解一下。 说之外呢,还有就是它的图像经过哪些象限,那我们知道,如果说它的 k, 这个 k 是 正数,那么它就经过一三象限, k 如果是个负数,它就经过二四象限。这些基本图像的性质需要了解啊。说之外, 也有一些题呢,会考察啊,通过图像呢去比较,比如说横坐标或者纵坐标的大小关系,那这种题的话呢,不要犹豫,画图就行了。 比如说你像这个题,他说,哎,这个反比函数 k k 大 于零,那就是在一三象限的图像上,然后你去把图像一画,再去找到复式啊,比如说复式在这,那逗外一外一呢,就是在这个地方, 是吧?好,然后呢,负二逗 y 二能找到,负二好,找到点,那这个地方呢,就是 y 二,是吧?然后呢,再找到三逗 y 三啊,三找到。好,那这个地方呢,对应的就是 y 三,那你去比较 y 二, y 一 和 y 三的大小关系,也就一目了然了。这种题的话呢,不要去 偷懒啊,该画图画图,从图上呢,就很简单,一目了然啊,好,再然后呢,就是我们刚才强调的反比例函数里面常考的一目了然啊,好,那我们简单复习一下, 假如说给你一个反比例函数,给你一个反比例函数,好,那么我们在上面呢,随便找一个点过,这个点呢,去做 x 轴和 y 轴的垂线,得到一个矩形,哎,那这个矩形的面积,哎,就刚好是等于这个 k 的 绝对值。我们需要再重复一下,是 k 的 绝对值, 原因呢是因为如果你的图像是在二四象限,那这个时候你的面积依然是正数,但这个时候你的 k 它是个什么?说它是个负数,所以面积呢,是等于 k 的 绝对值。除了 长方形之外,我们大部分时候呢,可能还会再考到另外一种形式,就是三角形。比如说过这个点做 x 轴的垂线得到一个直角三角形,它其实就相当于是这个长方形面积的一半吗?所以呢,如果是直角三角形,那么它对应的面积就是等于 k 的 绝对值的一半啊, k 的 绝对值的一半。 好,那么复习完这个知识点之后,我们来看一下这个去影的这道题啊。呃,怎么说呢,有两个函数, 一个是 y 等于 x 分 之二,一个是 y 等于 x 分 之 k, 一个是在第一项线,一个是在第二项线。好,找到这么一个三角形啊,这个地方是三角形符号啊,说它的面积等于三,那这个怎么处理呢?很简单啊,我们先把这个三角形呢调整一下,这不是 a、 b、 c 吗? 我们给他做一个等级变形,把它变成三角形 o、 b、 c。 那 我们知道,在等底等高的情况下,那么这个三角形 abc 呢?的面积就应该等于三角形 abc 的 面积 也就等于三。那对于这个 abc, 我 们是不是可以猜成刚才这个所谓的两个直角三角形的形式了?一个是这个直角三角形 好,它的面积呢,就应该是等于这个 二的绝对值的一半,所以我们可以得到对应的结论就是啊,二分之 k 的 绝对值,哎,加上这个二分之二的绝对值啊,当然二的绝对值就是二,是吧,加起来呢,等于三。好,那搞定结束是吧, k 就 可以求出来了。好的,那这个呢是关于 k 的 绝对值这一块,大家呢需要简单复习一下啊。 好,然后呢,关于涉及到的这种,呃,实际应用题啊,实际应用题的话呢,就 不再去啰嗦了。大家的话呢,如果需要这种题的练习题,包括啊,这个如果在这道题上觉得还有些问题的需要答案或者说需要讲解的,可以找 私信艾老师,艾老师呢给你发一下往年的这些真题以及对应的答案,以及呢,可以在艾老师的主页上翻一翻,可以找到一些往年的讲解啊。往年的讲解 好了,那这个呢是关于第十题。第十题的话主要想说一个什么问题呢?就是关于反比例函数,它只要知道图像上的任意一个点都可以去求出它的 k, 比如说你像这个地方,他告诉你这个地方呢,是三斗八,对不对?三斗八, 那这个三斗八它是不是在反比例函数图像上?那我是不是可以去根据三斗八先求出它的 k, 也就是求出它的 解析式之后,比如你像我还需要知道,呃,当 x 等于十的时候, y 等于几,那我也就可以直接去算了,是吧? 类似的依次函数呢,我们需要知道两个点对不对,但是对于正比例函数,因为它一定过圆点嘛,所以呢,只要再额外知道一个点,这个正比例函数和反比例函数的解析式都可以求出来啊,根据这个三角八这个点就可以求出来了。好的, 接下来我们说一下三角函数模块啊,三角函数模块的话呢,其实主要呃考察的就是两大块啊 啊,一块呢是关于具体的锐角三角函数的定义啊,那么基于这个定义所涉及到的他的三角特殊的角的三角函数值。好那么啰嗦一下啊,第一,什么是正弦呢?就在直角三角形里头,我们用对 比斜啊,这个谁比谁不要弄错了,然后在余弦呢,那就是用零比斜,正切呢,就是用对比 零啊,那这几个呢不要弄错了啊。再然后呢,就特殊角的三角函数值,大家呢最好是能熟记,如果实在记不住,那你至少知道咱们手头上的两个三角板,一个呢就是三十度,六十度和九十度,还有一个呢就是四十五度,四十五度 和这个九十度是吧,那他们所对应的三条边的边长比分别是一比根号三比二和这个一比一比根号二,那么你就可以根据这两个图再 快速的得到三十度,比如说他对应的正弦余弦和正切,六十度,所对应的正弦余弦和正切,以及四十五度的正弦余弦和正切的值啊, ok, 那这个呢是关于啊第一个大模块吧,算是第二大模块呢,就是在具体的题目中,我们需要去解直角三角形,是吧,通常来说就是需要同学们自己去建模了。 ok, 那 这里面的话呢 啊,第一题咱就不啰嗦了啊,就是求一个角 a 的 正弦值啊,送分底。然后呢,这个题也就是我们常考的这种类型,给你一个具体的生活中的实际情景,然后给你一个图像,让你需要根据这个图像呢,首先抽象的建模出他所对应的一些边长角度的图形, 再根据这个图形呢去求出某些线段的长度也好啊,某个高度也好,然后呢去处理问题。好,那这种问题呢,核心的关键点啊,先找角, 找完角之后呢,一定要把这个角放在直角三角形中,但你看这个一百三十八度肯定不行,对不对?那这里面的话呢,人家也给到提示了,就后面给的这些信息也都是在提示你要用哪个角呢?四十八度的角, 那这个角是等于一百三十八度,怎么去找四十八度呢啊?第一个想法就是我给他去掉九十度不就行了吗?那去掉九十度,我可以在这边呢做个线,但是这样的话呢,你就发现这条边和这条边呢就不是特别好去处理了,那怎么办呢?可以捯饬一下,我们实际上可以在这边做个垂线, 然后呢在这边做个垂线,那这个是一百三十八,这个是一百三十八的补角,他的补角的余角呢,就应该是四十八度, 是吧?好,然后他是四十八度,这个呢跟他互余,那这个呢?跟他也互余,所以这个也是四十八度。好,你把这些角度捯饬之后,你会发现我们构造了两个直角三角形,然后这两个直角三角形里面都有四十八度这个锐角,再根据正弦余弦正切去,根据边去求出剩下的边就行了。 你像去年这里面呢,给到了什么呢?给到了 ab 场,给到了 bc 场,以及给到了 cd 场啊, cd 场他知道,那么我们就可以去算这条边和这条边对不对?好,然后呢, bc 知道,我们就可以去算这条边,最后呢, ab 知道,我们把这个所谓的 d e 就 相当于分成了三段 啊,这是一段啊,这是一段,然后呢这是一段,然后把这三段最后呢加起来就搞定结束了啊,所以呢,总结下重点啊,就把他给到的角的条件放到直角三角形中,如果没有,我们就需要做辅助线去构造直角三角形啊。 好了,接下来统计和概率模块啊这块的话呢,送分题。但是呢,往往有一部分同学啊,也不是说学的不好,而是属于什么呢?就是太 粗心啊,太粗心的小孩啊,容易呢出错。简单说一下这块的话呢,有两个常考的题型,第一个呢,就是用竖形图或者是用表格去求概率, 这个地方的话呢,就大家一定尽量啊,就平时容易在这个地方丢分的,尽量呢老老实实,踏踏实实的把这个塑形图或者是表格去画一画,写一写。之前有个同学容易丢分,最容易的产生的问题就是脑海中一想,哎,好像应该是几个总的情况 啊,然后,哎,满足条件了,好像总共是几个条件,但是呢,就这种想的过程中非常容易出错好吧,所以呢,该画图画图,该列表格表格,好吧, 还有第二种图形呢,就是用频率去估计概率,这个呢比较简单,基本上就送分体,你观察一下,当重复的次数足够多的时候,它的频率会逐渐稳定在某个相对比较整数附近啊,比较整数附近, 然后去梳理就可以了。好,那这个的话呢,就是去年的一道真题,那主要呢就是大家把图一画啊,一定要做到所有的总的可能性的话呢,就是要做到不重不漏啊,比如说这里面一共就有一个男生,抽两个人啊,抽两个人,那能不能抽到两个都是男生呢?不可能啊,不可能,好注意,不重不漏啊。 好了,几何模块,几何模块的话呢,我们给大家简单串一下,就是基础的模块和呃这个重难点的模块啊分开去串 来。先说基础模块,第一个呢就是大家需要注意的就是在期中考试前,我们就已经去带大家复习过,然后呢,大家应该在期中考试的时候也去练过的题型就是特殊的平行四边形的判定和性质。 呃,但是呢,在呃期中考试包括以前的题里面的话呢,经常暴露出来一个问题,就是个别同学看到这种菱形的证明啊,他有部分同学就是只是证明了他是个平行四边形就停了啊。 跟大家说一下,大部分情况下啊,往往都是让你去证明他是个菱形啊,证明他是个矩形,甚至有可能让你证明他是个正方形,所以一定要去多观察题目中还有没有一些条件是你没有用到的啊? 好,那像去年的这个月考题的话呢,通常来说就是在前面的中等的大题里头会给到直接让你去证明某个 四边形是一个什么样的图形的啊。再然后呢,就是压轴题的第一问或者第二小问,往往也可能会出一道让你去证明它的形状的啊,这个地方的话要稍微注意一下 好。再然后呢就是平行线分线的成比例以及未知。平行线分线段成比例的话呢,通常来说就是送分题,这个就没啥可说的,大家呢,呃,注意观察好是谁对应谁啊,谁对应谁啊,是哪些线被平行线分开了,然后呢做好对应关系,不要弄混了就行。 那至于未知稍微要给大家强调一下,就是大家经常容易出现的问题,就是漏的一个情况,比如你像这道题,他说的是 a o b 三角形啊,那么同学们去画一个图,在坐标系中把这几个点描一下, 然后呢与沿点为未知中心相似比呢是三分之一,然后呢将 a o b 缩小,问 b 的 对应点是谁?这个的话呢,一定要注意,就是它可能是这种 以 o 为正中心是吧?好,它有可能是这种的,叫包含在里头的。呃,三分之一,咱们画的再小一点,这是 a 撇,这是 b 撇是吧?也有可能是什么呢?哎,叫头对头的 啊,往这边延长,往这边延长啊,然后呢这个是 b 撇,这个是 a 撇,也就是说,嗯,可以理解。我们用相似里头的话来说呢,就是一个是 a 字形的相似,一个是八字形的相似啊啊,这个的话呢,大家不要漏掉一种情况,不要漏掉一种情况啊。 好了,那接下来说一下相似的判定性质和应用这块的话呢啊,主要涉及到的。相似的判定性质和应用这块的话呢啊,主要涉及到的编编编的, 以及啊,就是三条边对应成比例的是吧?再有呢就是边角边的啊, s a s 的, 再有呢就是角角的啊,角角的 ok a a。 好, 那这个呢是关于呃这个相似的判定性质啊,和应用,那么当然呃实际上涉及到应用的话呢,一般来说就是综合性比较强的一些题目了啊,那么接着说啊,小题里面也有 除此之外的话呢,对于黄金分割比是一个比较容易常考的题型啊,知识点吧,所以呢,在考试前一定要注意 大概了解一下黄金分割比例是多少啊,那经常的,去年啊,经常这个考完试之后啊,老师我忘了黄金分割比例是多少,考试的时候是蒙的啊,这个呢不要不建议啊,那最后呢,投影和视图往往考的比较简单啊,大家呢简单串一下就可以了啊,这块呢就过 好。那么这个呢是去年的一道黄金分割比例的题,大家呢可以去截图,然后去做一做,练一练啊,考试前还强调下黄金分割比例的比例,一定要稍微注意一下啊。好了,那最后呢 几何的压轴模块啊,几何的压轴模块,简单串一下这一块呢,大家再去思考和琢磨的时候呢,怎么去处理啊,很难给大家讲的特别细啊。好了,那么接着说 填空的压轴,通常来说呢,就是线段求值问题,那么这里面的话呢,建议大家的入手的思考的点,第一,我们能用的东西是什么?比如说勾股定律全等相似 啊,那当然这个相似的话呢,我们更多的是用什么呢?就是所谓的直角三角形的三边比啊,比如说三比四比五,一比二比根号五,一比三比根号十,也就是我们经常说的有可能在这里面呢,还会出现一些一二三四五模型啊,一二三四五模型, 好吧,那么对于相似的话呢,我们就知道某个角以及和他相等的角的所在的直角上行,他对的三边比一定相等的,所以当你知道某一个角他是对应三边比,比如说三四五也好,二比三也好,那么其他的所有的这个跟他相等的角所在的直角上行 对应的三边比,你就都知道了。那在这个基础上,我们经常会出一些所谓的背靠背或者欠套的问题,什么意思呢?就比如说告你这个角 他的三边比知道了,这个角他对的三边比也知道了,那怎么办?做一个垂直构造,两个直角上行,这个时候在这个图里面的任意一条线段的长度,如果知道了之后,那么其他的所有的线段,我们都是可以根据这个两个角的三边比去算出来的,去算出来的啊, 好了,那么嵌套的就什么意思呢?比如说,哎,这个角,哎,他也是个特殊角。 好,那这个时候怎么办呢?我们在这个地方做个垂线,是吧?那然后这个三角形三边比知道,这个三角形三边比也知道,我们再找一条线段的长度去,进而求出其他的线段的长度,也就搞定结束了。好吧, 那这个呢是在小题十五题里头常用的处理逻辑啊,常用的处理逻辑,那么对于大家的建议呢,就是 额外的建议啊,第一呢就是题目条件的翻译啊,比如说题目中给了哪些中点,怎么去用,给了哪些啊?这个相等的线段怎么去用是吧?啊?给了哪些角?相等怎么去用?给了正方形怎么去思考?那这些的话呢,我们今天就 没法去带大家一个一个去创了,因为确实涉及到知识点还是比较多,建议大家呢把之前咱们课上讲过的一些辅助线的做法可以去梳理梳理啊。 那另外呢,就是合理添加辅助线往往是需要去添加的,那在什么地方添加就基于你刚才条件的翻译,是否翻译到位啊? 最后呢,还有就是直角三角形的合理构造,我们现在界限阶段既然是要求线段的求值,大概率是需要借助于勾股定力,需要借助于直角三角形的,所以的话呢,那我们在构造这个辅助线的时候,一定要尽可能去看一看有没有构造出比较适合去求这条线段长度的直角三角形啊。 好了,那么举个例子吧,你像去年这个第九题啊,第九题给了个什么呢啊?三十米每秒的速度,七十五度的方向飞行了二十分钟,那就相当于告诉你这条线段的长度高了,应该相当于是三十乘二十五,三十乘二十五呢,是七百五十米 啊,七百五十米,然后呢从 a 处到达 b 处,然后给到的角度是这个俯角三十度,这个呢是七十五度。那我们可以得到什么呢?可以得到的是这个是三十度 平行吗?是吧?呃,这个地面和这个水平线平行,然后呢还有就这个是七十五呢?这个是不是也是七十五?那这个的话就可以确定,那这个的话呢应该是四十五, 那你发现四十五是特殊角,三十度也是特殊角,还知道一条边,虽然这个三角形是一个普通的三角形,它不是直角三角形,对不对?那没关系,我们自己去做垂直嘛,做一个垂直之后,那就可以产生一比一比啊,这个线画的稍微有点歪啊,好, 可以得到一个一比一比根号二和一比根号三比二的这个三角形。那么我们可以通过七百五十度最后要求什么来的?求 ab 两点之间的距离,根据七百五十度先算出它,然后再去算出 ab, 就 搞定结束了。那这个就是关于去年的第九题这么一道题啊,好 注意条件以及处理方式啊。那这个第十五题,大家的话呢,有兴趣的话呢,可以去做一做啊,那就不再去展开去演示了。好吧, 接下来我们说一下大题的压轴题,就是说大家怎么去处理呢?通常考的就是图形的变化问题,包括折叠,平移和旋转啊,折叠,平移和旋转,那么 通常来说可能不会考的太复杂,比如我就考折叠,或者就考平移,或者说就考旋转。但是也有一些题呢,可能就考的会比较多啊,比如说我这道题呢,第一小问给你来个平移,第二小问呢,来个旋转啊,不重要,重要的是大家知道折叠会带来什么, 折叠会带来的就是轴对称,那么就是折叠前后的线段啊,是相等,折叠产生的这个角会有相等,一定要找它里面的等量条件。 平移的话呢,就注意啊,平移会产生相等的线段,相等的角以及平行的线,平行的线啊,是吧,那旋转的话呢,就注意找它的旋转前后的线段以及旋转角啊。旋转角 那么在这种题目的情况下,低于,比如说特殊平行四边形的,特殊的四边形的判定啊,这个呢就不多说了。然后这样呢,就利用全等和相似去判断线段之间的关系,那至少同学们要大胆的去猜一猜啊,比如说这两个线段之间是不是相等关系,还是倍数关系, 如果是相等关系,我们通常就是利用全等去处理,然后如果是有倍数关系,那么也可能是利用全等或者说是相似去处理啊。 那么除此之外呢,还有可能会涉及到多条线段,那比如说有平方的啊, ab 的 平方, cd 的 平方,那这种的话呢,甚至还可能会考虑到勾股定律去构造直角三角形,先把线段 捯饬捯饬,把它们放在同一个直角三角形里头,然后再去处理啊。最后呢就是动态问题,就是在旋转的过程中啊,比如问有没有可能在这里面呢产生平行,或者产生哪个角跟哪个角相等,或者产生垂直的时候,那这种动态问题的话呢,第一 大家一定要去快速的尝试去画图,那么这个画图怎么办呢?呃,两个方式,第一个就是你拿一个小纸片,把这个它旋转的图形给它裁下来,然后呢去绕着这个图去旋转旋转,观察一下在什么时候画出一个大字图形,再去求他所要问的问题。 第二个就是现在有一些尺子上面去能画,用铅笔画一些图形,也可以用这个尺子画出来它的图形,描出来图形之后,再去用这个尺子去旋转,总而言之,用尽可能形象直观的东西去旋转, 找到大致的位置之后,把这个图先画出来,再用静态的图像去分析问题。最后呢注意,有可能是要分类讨论的,有可能是要分类讨论的,可能有多个不同的位置都能够符合要求,那然后会产生不同的结果。 好了,那么咱们关于月考的知识点的串讲呢,今天就串到这,那么最后呢,再啰嗦一下,如果各位同学呢,需要啊,这个往年的试卷的真题想要去刷一刷啊。可以呢,跟艾老师私信, 包括往年的这个题目,如果有不太明白的,可以来艾老师的主页去翻一翻往年的真题的讲解视频。好的,那各位同学拜拜。
16支点数学艾老师 01:20查看AI文稿AI文稿
01:20查看AI文稿AI文稿上头又下头的,真是让你给全占了。本套试卷循序渐进,紧跟山大附的十月份和期中考试承上启下,前两次考试总结到位的这套试卷就比较友好,如果遗留问题没解决,那这套试卷依旧有问题,比较难。 一到五题送分题,不喜欢看材料的同学,第七题就是搞你心态选择压轴题。第八题是最难的,单调性即偶性,外加求只能做做不能做猜就行。三个多选难题占了俩 最基本的体面分,估计都拿不下,只能靠平常多做好事,积累运气。填空压轴题又提高了难度,好几个大题看似不友好,其实静下心来还是能完全写出来的,前提是时间够考的。就是你考场的心态, 会参变分离,会双变量问题,如果你还会倒序相加,前四个大题基本拿下,那已经很牛了。最后一个压轴大题是真的看着复杂,但确实也很不容易做出来,估计只能做出来第一问,第二问也只能做一小部分, 整体来说上一百分没有任何问题。想要取得更高的分数,得多看,多做一些长得就抽象的题目来练习。
30王哲物理 01:39查看AI文稿AI文稿
01:39查看AI文稿AI文稿月考不愧是内部考试啊,名校们对自己人下手还是比较狠,这份试卷所有小题都要动脑或者动手去做,没有送分题,选择天空的亚洲题也有期末考试的难度,而且后三个大题, 它的难度已经等同于期末的亚洲题难度,这就相当于有了三道亚洲大题。比较有特点的像是十九和二十题这种考一次函数构造的大题,因为它更加偏向于理论型的内容, 其实已经不太符合当下的中考和期中期末考试的方向了,但是智达还是作为重点考察出来,而附加题的这种应用题类型才是期末考试的重点, 反而被当成了附加题。这种安排还是稍微奇怪一些,因为这次考试只有一个小时的时间,对于大部分孩子来说,他其实做不到附加题的位置,那么就导致这道题没有给期末起到一些强化作用。 这张试卷对思维能力不是很强的孩子来说不太友好,对专注力不高的孩子来说更是很大的打击。走走神,你的时间就没了。而且对比较扎实,习惯好,但是思维还没练到那个程度的孩子来说,咱们千万不能用这份试卷的答题习惯去应对期末考试。 这份试卷的核心就是难题多,过程少,时间紧,看到不会的就跳过的孩子,反而会得分高一些。 但是想扎实做题,仔细想的孩子可能就会吃点小亏。而期末考试呢,他时间是足够的,期末考试的时候,我们还是要沉下心来,好好去想,好好写过程。所以说我们 习惯还比较好的小孩,思维能力没有那么强的小孩不能把月考的这个经验拿到期末里面去啊。所以我建议啊,同学们把这份试卷就当成一种拔高训练就可以了。
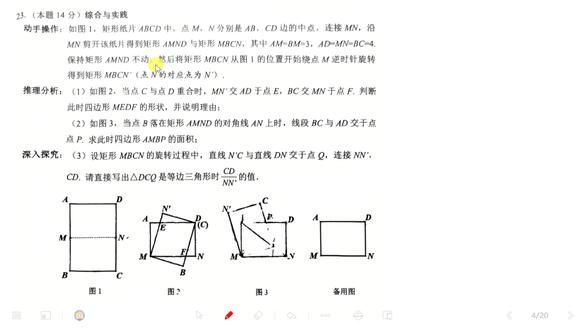 14:47查看AI文稿AI文稿
14:47查看AI文稿AI文稿啊,它就是一个四边形加一个几何变换,再加上这个线段长问题啊,我们一起来读题。如图一,矩形纸片, a, b, c, d 中, m 和 n 分 别是中点,它是中点连接 m, 沿着 m n 把这个矩形这边剪开,剪成了两个矩形,其中 am 的 长是三, b, m 的 长也是三,然后 ad 的 长也是知道的是四,所以这个矩形啊,两个矩形 amd 或者是 mbcn, 它都是三四 啊,对角线连上的话就是五啊,三四五的这样一个直角三角形,所以他全部这里面有特殊角啊,然后保持上面这个矩形是不动的,下面这个矩形绕着 m 点开始 逆时针方向旋转,得到了一个新的矩形啊,典型的旋转问题,旋转问题啊,关键还是那个那句话,找到旋转角 好,我们看第一码啊,因为如图二,当 c 点和 d 点重合的时候,当 c 点和这个 d 点重合旋转的时候,我们找,找到起点啊,找到起点,本来看图一的话, c 点在如此这个位置, mc 啊, c 点转到了 d 点,所以如果我们看图一的话,大概啊可以把它 连一下,我们能发现什么呢?发现这个旋转角,它这个旋转角到底用不用另说,反正是我们能知道这个旋转角的相当于 mc 转到了 md。 然后啊,这个图中这个小角如果是 r 法的话,也就说贪婪者 r 法,他是三比四的,那所以他的第一种情况的旋转角就是两个 r 法啊,就是两个 r 法, 这叫 c 点和 d 点重合,此时呢,这个 m n 撇与 a d 交于 e 点, bc 呢,与这个 m, n 相交于 f 点,看图能看出来啊,让我们判断四边形 m e、 d、 f 它的形状,这个形状啊,相当于说好判断一点,它明显是个菱形啊,我们直接写结论,它是个菱形,它为啥是菱形呢?首先这个两组对边分别是平行的,因为这个 d 和这个 m f 都是 原来的这个矩形的对边。同样道理, m e 和 d f 也是原来矩形的对边,所以是两组对边分别平行啊。也就说它首先可以正数,它是个平数。 平数要变成菱形的话,那么只需要证明一组菱边相等就行了。这个途中啊,可以证明圈一和圈二这两个三角形是全等的。全等的原因是 am 是 圆矩形的一条 啊,宽它是三, mb 也是三。然后这里面有个套角模型啊,两个九十度套在一起的话,那所以这个角一和这个角二它俩是相等的,角一等于角二,顶点 b 处九十度,顶点 a 处也是九十度,还有一条边是三,所以啊,它是全等的。全等之后得到了 m e 等于 m f, 所以相当于是平四加了个一组零边相等。图中是 m e 等于 m f, 所以 第一步是个菱形,这个难度不大。 嗯,第二步说,当 b 点落到了矩形 a m n, d 的 对角线 a n 上。啊,落到了矩形的它对角线 a n 上。这个图啊,画的不是特别清晰啊,我们把它大概连起来 说 b 点啊, b 点落到了原来矩形的这个对角线 a n 上,那把这个 a n 我 们也给它补充完整。 图中这个点是 a 点,好落到了 a n 上。读到这句话的时候,说明什么呢?这个旋转的角度是定的,我们也是一样从原图中找啊,通过这个起点,我们找到看它到底转了多少度,或者转的这个旋转角是怎么样的呢? 他说 b 点啊, b 点,本来啊 b 点,看图一,在这个位置转到了对角线 a n 上,转到了对角线 a n 上,所以我们在原图中啊,在图一中把对角线 a n 线连起来, b 点转到了 a n 上,大概画出来 是这样一个位置,这样一个位置啊,这是 b 点。此时我们会发现什么?这个旋转角什么呢?这个旋转角就是角 bmb 啊, b m b 撇吧啊,这个旋转角是角 b m b 撇,而这个角的话,我们也是确定的,因为此时三角形 m a b 撇,角旋转 b 处等腰的话,那么它这个 三角形 m a a 哎哎,三角形 m a b 撇,它是个等腰三角形,并且它的底角数啊,如果我们用这个 r 来表达的话,那么此时啊,这个底角数的 r 法,它其实是一个, 它的 r 法等于四比三的一个 r 法啊,那底角也就知道了,所以这个角啊,其实就是两个 r 法,且我们发现这个贪政策 r 法,此时是四比三的,是这么一个情况, 转到了什么呢? b 点落到了原原来举行的对角线 a n 上,之后说线段 bc, 找一下啊,线段 bc 与 a d 相交于 p 点啊,图中这是个 p 点,让我们求四边形 a m b p 的 面积,四边形 a m b p 的 面积。首先这个四边形它是个不规则的图形,不 规则图形要么是割,要么补,要么是等级转化,等级转化做一个转化。那这道题很明显啊,我们能发现什么呢?如果我们把 m p a 和 m p b, 它是全等的,全等的原因是啊,直角 边啊, m m a 和 mb 都是三,它是确定的,然后还有个九十度,还有公的斜边,所以它也是全能。全能之后,我们只需要算出一个直角三角形的面积,再然后再乘二就搞定了。而一个三角形的话,它的直角边啊,一条直角边是三。 如果我们知道这个旋转角的话,那么此时啊,这个三角形 a m p, 它就是一个特殊的三角形。 因为如图一啊,我们刚刚分析了,当 b 点跑到 a n 这条对角线上的时候,这个假角,这个假角角 a m b 这个大角角 a m b 这个大角,它是一百八十度减去二十法 又全等之后,所以每一个小角就是九十度减二法,而二法是三比四比五的直角三角形的大锐角,所以九十度减二法就是那个小锐角。所以第二个的关键啊,关键是什么呢?就是旋转角,我们发现 旋转角,我们发现是两个阿尔法,其中这个阿尔法是攀着的,阿尔法是四比三,所以我们得出了啊,三角形 a m p 啊,它其实也是一个三比四比五的一个直角三角形。 并且我们知道三角形 a m p, 它是全等于三角形 b m p 的, 它俩是全等的,所以这个面积好算了啊,所以 s, 我 们写个 s 总,它应该等于两倍的 s。 三角形 a m p, 它等于二,乘以二分之一,乘以个三,再乘以什么呢?乘以这个 ap 的 这条边,因为九度角 r, 它是三比四比五的直角三角的小锐角,所以它所对的这个 ap 应该占三分,而 am 占四分,所以是三除以四代表一分,再乘以个三, 此时这个这个四分之三乘以三,他就是 ap 的 长度了,所以我们把它快速的算出来啊,算出来应该是等于四分之约掉啊,四分之三乘三,再乘三,三九二十七啊,四五百二十七,这是第二吗? 关键还是找到旋转角啊,旋转的问题我们做了无数遍啊,发现核心就找到旋转角,如果找不到旋转角的话,这个题啊,可能就看的很很很尴尬,很零零碎碎的啊,总是找不到那个关键的条件。 好了,我们看第三个啊,第三个有点难度啊,说设矩形下面这个矩形 m, b, c, n, 这个矩形旋转过程中,直线 n 撇 c, 直线 d, n 相交于 q 点啊, n 撇 c 和 d n 相交于 q 点,然后把概念的连起来,请直接写出啊,三角形 d, c, q 是 等边三角形时后面这个比值。所以啊,我们首先得搞清楚它什么情况下出现一个等边三角形或这个 q 点到底在什么位置呢?啊, 好还是一样?第三个啊,还是一样。旋转的问题,我们一定要找起点动态嘛,我们来感受一下。这个 n c 是 没有动的 啊, n 撇 c 其实就是 n c, 然后 d n 也是没有动的,此时他俩是共线,共线的话,他俩一旋转交点是 q 点,并且顶点 q 处要是出现一个, 出现一个等边,也就说顶点 q 处要出现一个六十度的话,所以大概率接下来啊,他要么旋转什么呢?要么旋转六十度或者旋转什么呢?哎,一百二十度 啊,当然由于时间关系啊,这个六十度的这个角啊,孩子们可以自己尝试一下,我们发现如果旋转六十度之后啊,顶点 q 处那个角正好是一百二十度,所以我们把旋转六十度就排除了。换句话说,此时我们就能分析出来啊, 我们就能分析出来,如果要出现三角形 d、 c、 q 是 个等边三角形的话,那么得转,得转一百二十度。那转的过程中可以啊,比如说逆时针,逆时针转一百二十度 是等边三角的话,那继续转上一百二十度,也会是等边。也就是说这道题啊,大概率是两个答案,第一个是旋转一百二十度,第二个是旋转 啊,在一百二十度的基础上,再旋转上一百八十度,或者说我们可以认为是逆,这个换一个方向啊,换一个方向,他就是逆时针一百二十度啊,顺时针一百二十度。 好了,那我们就一个一个来画啊,比方说这道题啊,我们先来逆时针旋转一百二十度,逆时针旋转一百二十度的话,嗯,大概我们画一种情况啊, 一开始这个 m n, 一 开始 m n, 呃, m, n 撇和 m 是 重合的,它要转一百二十度,我们大概把它画出来, 比方说这个点是 n 撇,那 n 撇知道的话,那这个整个这个长方形,我们就可以把它大概画出来了啊, 好,大概把它画画出来, n 撇我们知道了,然后这个点是 c 点,还有这个点是 b 点啊,此时它转的是一百二十度。那根据题目的意思,我们先把这个 q 点找到啊, q 点是 n 撇 c 与 n d 的 交点, 把 n 撇 c 和 n 的 给它分别延长之后,分别延长之后啊,交点是 q 点,然后还要连接 n、 n 撇,好,我们根据题目的意思啊,把该连的连起来,连接 n、 n 撇,还要连接 c、 d, c、 d 啊,好,此时它转了一百二十度,所以此时顶点 q 是 这个假角,它应该是六十度,所以三角形 c、 q、 d 它首先一个内角是六十度了,它到底是不是等边的话,取决于 有没有这个 q c 等于 q d, 就 这两条边啊, q c 和 q d 是 不是相等的?这个啊,非常好证明,因为它旋转完之后,如图啊,各位,我们把 q q 连起来的话, 连起来的话可以正得三角形 m q d 和 m q n 它俩是全等的,它俩全等之后, 全等之后啊,说明这个 n 撇 q 和 n q 它是相等的,并且 n 撇 c, 它是原来长方形的一条边,它是三,而 n d 也是三,所以长的长的相等,短的相等,所以也就说可以正得啊。顶点 q 处是等于六十度,且 q c 是 等于 q、 d 的, 也就是说这个条件相当于啊,等价于说,此时三角形 d c q 就是 一个正三角形。 所以这个图啊,我们画的是没问题的啊,所以接下来我们只需要算一下最终的这个比值,比值是 c d 比上 n 平。 图中这个 n 撇非常好求 n 撇,它是一个因为旋转了一百二十度,所以它是一个顶角处为一百二十度的一个等腰三角形的底边,它的腰长是四,所以 n 撇就是四倍根号三,这个是没问题的啊,所以问题转化成又转化成求向量长,求 c d 的 长, c d 的 话,此时 c d q 是 个等边三角形。所以如果假设 c d 是 x, 那 么这个 d q 也是 x, 刚刚啊,我们在证明它是等边的时候,把 m q 是 需要连起来的话,如果连起来的话,那此时三角形 m n q, 它是一个三十六十的直角三角,三十六十九十的直角三角形,然后三加 x, 也就是 n q 是 根号三分的那条边, 它是根号三分的边,然后这个 m n 啊,它是一份的边,也就是说啊,所以我们会得到叫什么呢?叫四比上,四比上三加 x, 应该是一份,比上一个根号三分,由此我们可以把这个 x 给算出来, x 应该是等于四倍根号三,减了个三,而 x 的 值其实就是 cd 的 长。所以第一个答案, cd 比上一个 n n 撇,它应该是四倍根号三减三,比上一个四倍根号三。这个结果是一减去, 一减去月线是四分之根号三啊,一减去四分之根号三。这是第三问的第一种答案。第二种答案啊,做法类似,接下来我们只需要什么呢? 只需要把这个矩形叫顺时针方向旋转一百二十度,转完之后,他的做法和肛肠做法基本一致啊,张老师不再赘述啊。 哎,这道题确实难度还不小,但是我们如果要去总结的话啊,它的关键信息是什么呢?它的关键信息旋转,各位记好了啊,旋转类的问题,旋转啊,它的关键是找这个旋转角。 哎,那如何去找旋转角呢?啊?动特类,动特类的问题啊,一定是找起点啊,首先找起点,然后看变化得结果。
 01:41查看AI文稿AI文稿
01:41查看AI文稿AI文稿其实咱们各个名校月考卷一般都考的比较窄,但是考的是很深的,但是咱们晋源这个卷子不愧是大机构,出的卷子非常不同,很像太原市的期中期末卷,考的很全面,不会仅仅是只考这个月的,而还会考一些期中以前的那些期末考点啊,突出一个全面,考察 在题目设计上呢,试卷的小题部分啊,不存在这种中分题,这个和太原市的期中考试就很像了,要么就是题意简单,但是计算很复杂,要么就是题意很隐晦,需要好好去思考。小题部分,对于进入状态慢,专注度不够高的孩子来说,拖的时间就比较多一些。 那从作答的体验来看呢?试卷整体上没有那种超高难度的题目,但对于每道题目都需要持续的有强度的思考, 学生在完成试卷的过程中啊,并不会感到很轻松,而且数学量也很大呀,家长可以问问自己的孩子们,从二十题开始做的累不累对吧?从二十题开始到后面每道题都要答很长很长,那么现在考试对于学生的表达能力真的要求越来越高了,孩子们其实就是怕这种需要文字表述的题目, 可能本身题不难,但是答题的过程中啊,真的不好说,会不会写着写着就出错了。 而且对于像二十二题这种,其实最后一问问的很容易,但是就是有一部分同学读完问题之后,可能不知道自己在干嘛。从学情的吃亏角度分析的话,这份试卷对于中等生是十分友好的, 只要你基础扎实,审题是细致的,很容易取得高分。反之,如果基础比较薄肉的孩子来说,做起来就会多点开花。最后建议还没有做过这份试卷的同学,建议大家都做做这份卷子不太累,还能看出来哪里掌握的不够扎实。
 13:18查看AI文稿AI文稿
13:18查看AI文稿AI文稿学数学难吗?一点都不难。大家好,我是 banana, 不 难老师。今天呢,咱们来看一下上午刚刚考过的山大附初一十二月份月考的这个卷子。呃,咱们来着重讲解一下它里边的一些难题啊。首先,整份卷子呢,是比较难的啊,尤其是最后的这三道题,二一二二二三, 这二十一题呢,他是考察了一道这个材料题和尺规作图相结合的一道题。但这个材料题呢,比较巧的是,咱们刚好在课堂上啊,就在咱们的讲义里边刚好提到了这个巧分线,而且给大家的这个练习题里边又出现过一次, 所以说大家应该学过这个的同学对于这个概念是比较理解的啊,或者说他是比较好理解的啊。 这个第三问的话呢,他其实就是,呃,给设置了一个背景,然后需要你耻归做角啊,做出一个角等于已知角,但是可能比传统的这种直接耻归做图的题啊要稍微的难一些,毕竟需要大家有这个理解的成本在里边。 所以这是二十一题。二十二题呢,是考察了一道动脚问题啊。这道题的前两问啊,还是可以通过自己的努力做出来的。但第三问呢,是比较困难的, 包括最后一道题是考察了一道行程问题,也是一样的第三问,呃,比较难一些。所以大家在这个考场上有限的时间内,想把这个卷子做完啊,就是一件不容易的事了, 然后再把这两个压轴题做对啊,这就更难上加难了。所以大家如果要是对这些题有问题的话,可以下去再研究一下,或者没有做过的同学可以做一下啊,然后没有这套试卷的同学也可以私信我。 那咱们今天呢,就来看一下这个二十二题,这个动角问题。数学活动课上,同学们以一个固定的一百二十度角 a、 o b 和一个三角形啊,直角三角板为背景,探讨有关角的问题, 将三角板的六十度角顶点和 o 重合,然后其余既为 o c o d, 然后 o e 是 它的平分线。那这种 动脚问题或者这种动态问题,其实给大家说过很多遍了,咱们一定要学会动中取静,也就是找不变的东西,那在这有什么不变呢?首先角 a、 o b 是 不变的,所以作图的顺序,首先先把角 a、 o b 先画出来,然后接下来呢, 再画这个三角板啊,三角板 d o c 把六十度的角靠在这,最后再画这个角分线啊,因为 o e 是 d o b 的 平分线,那你这个 d o 在 动,所以 o e 也在动啊,那这就是整体的一个作图顺序了。那咱们来看这个第一问, 呃,角 d o c 在 角 a o b 的 内部,弱角 a o d 等于四十度啊,这个角是四十度,然后整个大角是永远不变的,是一百二十度,所以咱们就可以得到,此时下边这个大小是八十度,然后上边这呢是六十度,所以下边这个小角就是二十度。 题里边呢,又给了一个条件,是平分的条件,大家看清楚是谁平分谁啊, o e 永远是角 d o b 的 平分线啊,那 o e 是 在这 d o b 是 整个大小,整个大小多少度呢?是八十度,所以平分下来以后,各自是四十度。 那而最后咱们要求的 c o e 啊, c o e 是 在这啊,那就一目了然了,用四十减去下边的这个二十就可以了。所以第一问是二十度啊,相对的有容易一些啊,大家应该是能呃标完角以后就能分析出来了。来看第二问, 在图一的基础之上,将三角板绕着点 o 顺时针旋转,使得 o c 在 a o b 的 内部, 然后 o d 在 角 a o b 的 外。呃,这个是在外部啊,下面这个是在内部,其余条件不变,然后让你找这两个角的关系。那咱们来看一下啊,这个三角板呢,是转到外边来了啊,然后不变的是什么呢?不变的是 a o b 这个角永远是一百二十度。 呃,在这还能用到的一个条件就是平分啊,那咱们是知道这条线是平分角 d o b 的 啊, o e 是 平分角 d o b 的, 那第一个办法啊,那咱们就往图上标一标这些角度啊,能标的就是这个一百二,这个是六十,然后其他的角都标不出来了,或者说标这九十三十呢,对于咱们其实是没有什么意义的。那怎么办呢? 也就是说在这种条件比较少,或者说大家束手无策的时候,一定要学会一个啊。这个也给大家强调过很多遍了,要学会假设射谁啊?一般咱们射最小的角,或者是射有等量关系的角,那在这哪有等量关系呢?平分不就有等量关系吗? 所以咱们就假设这个角为 r 法,所以下边这个角也是 r 法了,那由此咱们就可以得到角 c o e 的 这个度数了啊, c o e 其实就可以表示出来了,它等于整个这个大角是六十度,然后 c o e, c o e 呢,刚好是从六十度里边把这个 r 法角减掉就可以了,所以角 c o e 等于六十度减 r 法, 那接下来再去表示角 a o d 就 可以了啊,角 a o d。 好, 那咱们再来看看题里面的哪些条件没用呢?整个这个大角 a o b 是 一百二十度,所以说 a o d 的 话,那就是一百二十度减二而法 一百二十度减二而法。写完之后大家就一目了然了,那这两个分别是两倍的关系,所以整个就是两倍的关系,所以咱们就可以得到最终的结论,角 a o d 等于二倍的角 c o e。 那大家在答题的时候,一定要先把这个结论先写了,然后再写理由啊。所以第二问的关键点就是大家一定要打大胆的去假设,假设完之后去表示就可以了,来第三问,第三问的话就比较复杂了, 呃,受到这个菜菜的启发啊,露露呢,接着将这个三角板进行旋转,当这个三角板旋转到角 a o b 的 外部的时候,刚才呢,其实都是在内部,或者说和内部是有一部分重叠的,那旋转到外部的时候,仍然是让你研究这两个角的这个数量关系。 那首先大家在做到这一问的时候,可能第一个啊,就是觉得比较难了,第二个呢,可能时间也比较紧张了,那大家可以去猜一猜这个关系 啊,那这个关系可能跟第二问会有一些关系啊,就是会有一些联系,所以如果要蒙的话,那大家可以把这个蒙上啊,或者说反过来蒙一下, c o e 是 a o d 的 二倍,那可能就是其中的一个答案了。那不知道大家这个这个题究竟做出来没有啊?或者做出来几种情况,咱们来具体的分析一下。 首先在这这个题是需要分类讨论的啊,为什么需要分类讨论呢?咱们看这个角,角 a o d, a o d 是 这个角,对吧?那 o d 再往下转转转转转 转的位置可能不一样,这个角的表示方式也可能不一样,咱们所说的角呢,是小于等于一百八十度的角,那目前 a o d 是 右边的这半部分,但是 o d 在 旋转的过程中,他可能会转到左边,那此时 a o d 这个角就变成左边这一部分了, 所以在这呀,就需要分类讨论了。那第一种情况呢,就是 a o d 还是在右边,只不过它在下边一点啊,那咱们把它画出来,这是 d, 然后接着再画这个 点 c 啊,这再画的时候,这也有些技巧啊,这个 d, 这是个直角,所以咱们保证它是直角,然后再把 c 画出来就可以了。画完之后,接下来还是往里边去,呃,看看这些条件,标标角啊, 呃,在这儿呢,咱们知道这个上面这个角永远是一百二十度,然后还有一个平分线,咱们没有标啊,这个 o e 是 角 d o b 的 平分线啊, d o b 是 在这儿,所以 o e 是 它的平分线 啊,这就得到 o e 了。那咱们接下来同样的做法,还是去假设这个角为阿尔法,这个角为阿尔法去表示 a o d 就 行啊。角 a o d, a o d 的 话,那大家可以发现这个角应该是一百二十度加阿尔法。好,接着再去表示角, c o e c o e c o e 这个角的话应该是这是 c o e 啊,这个角很明显六十度加阿尔法, 呃,加 r 法。所以大家发现第一种情况的话,仍然是符合两倍的关系的,也就是角 a o d 等于二倍的角 c o e。 所以 大家如果要是蒙的话啊,就有一些做题经验啊,也可以大概的去蒙一下。那这是第一种情况,就是 o d 还是在这这条 a o 延长线的右边,那他可能 o d 转到左边啊。因为时间原因,所以我就直接给大家把这个图就画出来了啊。那接着咱们再来分析一下,同样道理, 这个是一百二十度,然后 o e 呢?是平分角 d o b 的 啊,那我画出来 o e 平分角 d o b, 这个是 r 法,这个也是 r 法。然后接下来再去表示表示题里边的一些角啊。首先是 c o e 啊,那咱们表示 c o e c o e 是 比较好表示的, c o e 等于 这个角啊,也就是六十度加上这个 r 法就行,所以他还是六十度加 r 法。然后接下来再去表示角, a o d a o d a o d。 好,是在这 a o d 这个怎么表示呢?这个是一个一百八十度角,我从一百八十度里边把这个下边这个小角减去就行,那下面这个小角究竟是多少呢?他是在阿尔法这个角里边,我先把这个打对勾的小角求出来啊,这个对勾的小角怎么求呢?是用一百八十度减去阿尔法,再减去一百二十度, 也就是六十度减 r 法。这个角是六十度减 r 法,那所以左半边就用 r 减去六十度减 r 的 叉,其实就是 r 减六十度,再加 r 法,那也就是二 r 减六十度。 然后最后咱们表示角 a o d 的 时候,就用一百八减去下面这个小角就行啊,减去下面这个小角,也就是一百八减阿尔法,再加六十度,其实就是二百四十度减阿尔法, 二百四十度减阿尔法,那这样的话就把角 a o d 表示出来了,表示完之后这个问题还没结束,这个也是大家可能会卡的一个地方啊,就这俩角, 这怎么表示他俩的关系呢?他也不存在这个倍数关系,直接的倍数关系。那怎么办呢?在这首先大家要明白啊,就这有阿尔法,这也有阿尔法,这个阿尔法一定是不能在最终的结果里边出现的 啊,为什么呢?因为你设的是阿尔法,他设的是 beta, 也就是这个是你引入的一个未知量,所以咱们最后的关系里边一定要把阿尔法消掉,那怎么就能把阿尔法消掉?这是正阿尔法负阿尔法,这样就能抵消掉了。所以咱们给角 coe 乘个二,也就是二倍的角 coe, 它是等于一百二十度加阿尔法的,然后再跟 a o d 去求和就可以了,这样的话正负二阿尔法就抵消了,也就是说二倍的角 c o e 加上角 a o d, 它应该等于三百六十度,那这个是最终的结果,那这个所以这个情况的话,一来不好分析,分析出来以后很多同学可能也一脸懵,不知道最终应该怎么写结果,所以这个比较,嗯,困难或者比较复杂一些。 那最后一种情况,大家刚才咱们在分析角 a o d 的 时候,其实分析过这个表示方式,可能会有一些区别,对吧?所以分了两种情况。那接下来咱们在表示这个 d o e 的 时候,呃,表示角 c o e 的 时候,可不可能会也会有一些不同的情况呢?也会有的啊,这个 c o e, 大家发现这个 o e 呢,刚才是在这条虚线,就是这个 a o 延长线的右边,那可不可能跑到左边呢?跑到左边可能就比这个阿尔法这个角要小了。刚才是比这个阿尔法角要大啊,就是在他的外边了,所以咱们再来画一下,为了更稳妥一些,如果再往上转,那 o e 可能就 画到这个虚线的左边来了啊,那所以此时呢,咱们再来把这个画一下啊,他是假如说他 o e 就 跑到左边来了啊, o e 是 d o b 的 这个平分线啊,这画一个 o e, 然后接下来这是一百二十度, 还是一样的。因为平分,所以咱们假设这个角为 alpha, 这个大角也为 alpha。 然后接下来呢,还是去表示题里边的角啊。第一个 c o e 啊,角 c o e 仍然是六十度,加 alpha 没问题啊,是不变的。然后接下来再表示角 a o d, a o d a o d, 是 这个角啊,还是一样的。咱们从一百八十度里边把这个该减的角减掉就可以了啊,就是把下面这个大小减掉就可以了。下面这个大角怎么求呢?这是阿尔法,再把下面这一小点求出来就行。下面这一小点啊,用这个右边的这个角去入手, 这整个是一百八,上边是一百二,所以这一段是六十度,这个这一部分是六十度,所以这个小角就是阿尔法减六十度, 那阿尔法减六十度,那这个大角合起来,他就应该是二,阿尔法减六十度,所以角,呃, a o d 的 度数就用一百八去减去,这个阿尔法减六十度,那结果是一样的,仍然是二百四十度减阿尔法, 所以这个结论和刚才是一样的啊,也就是这个结论啊,刚才我框起来的,那最终的结果就是这两个了啊。 当然了啊,虽然站在这个就是每一个种情况都分析的这个前提下呢,这个题确实是非常难做,但是大家可以蒙一下嘛,对吧?呃,一共两个答案,这个第一个还是比较好蒙的,或者说第一个还是相对比较好求的。呃,所以 整体来说的话,这道题难度还是非常大的,尤其是这个最后一问啊,就是这两道题放在以往的这个月考题里边,或者放在其他年,呃,其他学校的一些这个月考题里边,都是可以作为这个压轴题存在的, 所以对于大家而言,嗯,还是有些难度的,大家下去以后好好再分析一下,关注我,布南老师,帮你解决所有数学问题。
42不难老师
猜你喜欢
最新视频
- 2.4万大萌芽


