天津初三解三角形过程

同学们，期末已经结束了吧，现在我们来看一下这个题目，初三的同学们，你们要注意了，你们还有不到半年的时间就要中考了，那么我们拿一道基础的题目，三角形和圆的综合题目，我们来找一找感觉， 我们现在分析一下，遇到这种题目，首先要告诫什么老师推荐，就是构建我推荐的方法，就叫真题思维。那么什么叫真题思维？就是去读已知，得已知，然后记住得到的这个已知一定是题目当中没有的，我们拿到这个已知去解这个题，这个就叫真题思维来，现在我们先来分析一下直径，我们看到直径能分析出什么， 是不是 o b 等于 o e， 我 们现在只能分析这个，后面告诉了我们什么点 a 点 b 是 圆 o 的 两个点。来记住这句话，一般同学都会把它忽略，但是同学这句话就告诉了什么 o a、 o d 可以 形成半径。 ok， 来我们继续，这里给了个切线 来，切线有了就说明什么，这里是切线的延长线，说明这里和它可以形成什么直角。所以说现在我们读了三个题目，三句话，我们读到了三个已知，拿着这三个已知我们去解题来，记住，同学，如果说一旦这个题目你发现你解不了， 大概率是你得到已知，你得到的少了，或者是得到的不对，方向错了，所以说一旦出现这种情况，没有任何的情况，我们没有任何思路，记住，从头我们再重新读一遍，把已知再重新的找一找， ok， 现在我们来看一下这个题目，第一问说了一下这里这个角度角 a、 d、 e 等于二十五度，它等于二十五度了。我们遇到这种题型，记住这种只要考切线了，而且还考角度了，并且这个角度是，这叫什么？这叫圆周角，它大概率是考什么？首先切线的性质，九十度、六十度、三十度之间的关系， 还有圆周角和圆心角的性质还有什么？这个题后面还给了一个等腰三角形，所以说等腰三角形这里也会遇到，所以说同学真题思维就是我们在这种题型的环境下，把我们能想的所有东西全部都想到，而且这些东西都叫下意识的东西。 ok， 现在我们看到了这个叫圆周角，所以说我们现在紧接着能想到什么？看到切线连半径或者连垂直，记住，这是我们说第一条。 ok， 我 们现在有了垂直，这里就等于九十度，所以说这里让我们去求角 c， 角 c 怎么求？ 我们再来看一下这个题目是不是可以用三角形的内角和用一百八十度减九十，再减这个角就等于角 c， 那 么这个角怎么求？是不是正好是我们这个角英文当中给了圆周角、圆心角，圆心角是等于圆周角的什么两倍， 所以说我们现在就可以得到，因为我们角 a、 d、 e 等于二十五度，所以说我们可以得到什么？角 a、 o、 c 就 等于五十度，这是什么？是不是圆心角是圆周角的两倍，所以说它可以等于五十度来，它等于五十度了之后一百八十度 减去九十，再减去我这个五十度，是不是就等于我的角 c 了？等于四十度来，同学，我这个过程是不全的，记住我们考试的时候一定要把过程写全来，所以这第一题同学你会了 吗？来，我们再用真题思维分析下第二个题目，第二个题目首先告诉了什么？这里是一个等幺，对不对？来，给到了我们一个等幺，一个 c e 等于二，这里等于二了，你会发现没有思路，为什么没有思路？ 他让你求的是半径，但是给到的跟半径没有什么关系。来，同学，你再看一看 c e 能找到什么关系来，关键点来了，这是我们读已知的非常关键，就是你一般情况下读到这种情况下你不知道什么叫已知，那么你就要去读问题，问题告诉你了，求半径。来，同学， c e 是 什么？ c e 是 不是这个三角形的一条边的一部分，对不对？来，它既然单独给你 c e， 说明了这个题一定要往这个三角形去考虑。来，这个三角形当中有谁是半径？是不是 o？ a 是 半径， o e 也是半径。 现在你得到了一个非常关键的点，就是在这个三角形里面有两条边，甚至有一条边的一部分是在半径上面。来这里等腰，三角形可以得到什么？ 可以得到两边相等，也可以得到两角相等，对不对？所以说角 b 等于角 c。 来，我们继续，那么我们现在来写一下，因为 a b 等于 a， c， 因为是等腰，对吧？所以说角 c 就 等于角 b， ok， 现在我们不知道它的角度，但是我们可以推， 怎么推导呢？我们现在来讲一下有一个非常关键的点，就是 a e， a e 是 一个非常多功能的弧，为什么？你看这个 a e， 它组成了角 c， 它组成了角 a o e， 它也组成了角 b， 所以 说 a e 这条弧是非常关键的，那么这条弧我们写在这里，因为我们的 a e 的 弧 等于 a e 的 弧，所以说我们找的是这条弧，要告诉老师。 ok， 所以 说来圆心角圆中角 a o c 就 等于二倍的角 b， 角 b 等于角 c， 所以 说角 a o c 就 等于二倍的角 c， 对 不对？来，我们刚才得到了一个九十度，我们得到九十度是谁？ o a c， 我 们知道 角 o a c 等于九十度，它等于九十度了，我们相当于剩下的两个角相加时也等于九十度，所以说角 a o c 加上角 c 等于九十度，前面这一部分等于二倍的它，所以说我们可以得到什么？ 三倍的角 c 等于九十度，对不对？所以说角 c 等于三十度，来三十度的角，三十度的角，在直角三角形当中， 三十度的角对应的边是不是其边的一半？所以说 a o 就 等于二分之一的 o c。 ok， 同学，聪明的你发现了， 思路出来了，对不对？所以说 o a 等于二分之一的 o c， 现在要干什么？我们要看一下问题，因为我们现在到现在这里就卡住了来，问题是让我们求半径，求什么？假设什么？所以说现在， 同学你现在考虑一下，那么你应该干什么？假设圆 o 的 半径为多少？为二或者为 x 都可以，这根据自己习惯来设。来，我们题目当中给什么？给 c e 了，对不对？ c e 等于二。来，因为 c e 等于二，所以说这一条边是二，这里也是二，这里是二加二，所以说这个小二就等于什么？二分之一的二加二，对不对？所以说我们把它写在下面， 等于二分之一的二加二，剩下的就是解方程，这里就等于二，等于二，对不对？所以说记住要最后写半径，然后写大话，这个题就解出来了，来培养核心思维，优成解放之路。这里是月球老师，我们下一下见。

同学们好啊，今天咱们来聊聊初中数学里一个超实用的工具，三角形三边关系。很多同学觉得它只是用来判断能不能组成三角形， 其实它还是解决线段最值问题的金钥匙。咱们都知道，三角形任意两边之和大于第三边，任意两边之差小于第三边，这个看似简单的性质，藏着求最大值和最小值的秘密哦。比如当题目里出现 pa 加 pb 最小或者 pop 最大这类问题时， 三角形三边关系就能帮上大忙。举个例子，要是想让 pa 加 pb 最小，咱们可以通过做对称点，把两条线段转化成三角形的两边之和，这时候最小值就等于第三边的长度。而求帕克最大值时， 同样可以构造三角形，利用两边之差小于第三边的性质，找到那个最大的差值。记住这个小技巧，以后遇到线段最值问题， 就能快速找到突破口。你们平时做这类题最喜欢用什么方法呢？评论区一起交流一下吧！

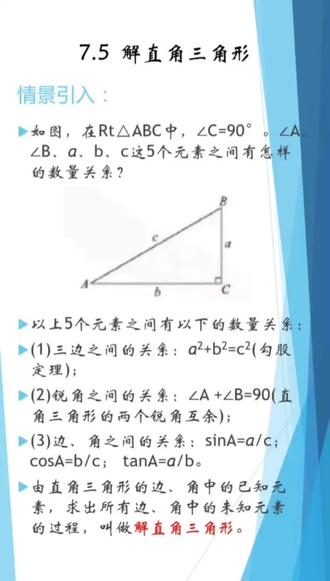
同学们大家好，本节课我们将学习第七章第五节。解直角三角形， 我们看如图，在直角三角形 abc 中，角 c 等于九十度。角 a、 角 b 和 abc 这五个元素之间有怎样的数量关系呢？看以上五个元素之间有以下的数量关系，三边之间的关系是 a 的 平方加 b 的 平方等于 c 的 平方。锐角之间的关系是角 a 加角 b 等于九十度。边和角之间的关系是三菱 a 等于四分之 a。 考三菱 a 等于 b 分 之 c， 它的 a 等于 b 分 之 a。 看由直角三角形的边角中的已知元素求出所有角，所有边角中的未知元素的过程。我们叫做什么？解直角三角形， 我们来看条例题。例题一，在直角三角形 a、 b、 c。 中，角 c 等于九十度，角 a 等于三十度， a 等于五。解这个直角三角形， 看在直角三角 a、 b、 c。 中，角 c 等于九十度，角 a 等于三十度，所以角 b 等于九十度。减去角 a 等于九十度。减三十度等于六十度。三、 a 等于四分之 a， c 等于 a 除以三根， a 等于五，除以三根。三十度等于十，它的 b 等于 a 分 之 b， 所以 b 就 等于 a 乘以它的 b 等于五，乘以它的六十度，等于五倍的根号。三、 再来看例题二，说在直角三角形 a、 b、 c 中，角 c 等于九十度， a 等于一百零四， b 等于二十点四九，那么求 c 的 值。二、求角 a、 角 b 的 大小 看在直角三角形 a、 b、 c 中，根据勾股定律可以得到 c 等于根号下 a 方加 b 方等于根号下一百零四的平方。加上二十点四九的平方。用计算计计算可以得到 c 约等于十 一百零六点零零二。有提议可知它应该等于 b 分 之 a 等于二十点四九分之一百零四。用计算计 算得可以得到角 a 约等于七十八点八五度，角 b 等于九十度，减去七十八点八五度，等等于十一点一五度。 再看例题三，如图在直在三角形 a、 b、 c 中， a、 c 等于八角 b 等于四十五度，角 a 等于三十度。求 a、 b 看过点 c 做 cd 垂直于 id， 垂直于 d。 在 直角三角形 a、 d、 c 中， a、 d 等于 a、 c 乘以考三英三十度等于 八，乘以二分之根号三等于四倍的根号三 cd 等于 a、 c 乘以二分之一，等于 c。 在 直角三角形 bc、 d 中，角 b 等于四十五度， 所以 b、 d 等于 c、 d。 所以 a、 d、 a、 b 就 等于 a、 d 加上 d、 b 等于四倍的根号三加四。 再来看例题四，若如图，圆 o 的 半径是十，求圆 o 的 内接正五边形的正内接正五边形 a、 b、 c、 d 的 边长。 还因为五边形 a、 b、 c、 d 是 正五边形，所以角 a、 o、 b 等于五分之三百六十度，等于七十二度。过点 o 作 o， h 垂直于 a、 b 垂直为 h。 在 直角三角形 i、 h、 o 中，因为角 i、 h、 o 等于九十度，角 i、 o、 h 等于二分之一，乘以 二分之一的二分之一倍的角 a、 o、 b 就 等于三十六度为 o， i 等于十，所以 h 等于 o， i 乘以三英三十六度，所以正五边形 a、 b、 c、 d 的 边长就等于 a、 b 就 等于二倍的 h 等于二，乘以十，乘以三英三十六度，约等于十一点八。 通过这节课学习，同学们要掌握课本第一百零九页的定义有直角三角形的边角中的已知数 未知元素的过程叫做解直角三角形。通过今天的学习，同学们有什么收获？会正确的运用所学的知识吗？好，今天的课就到这里布置一下课后作业，课后完成课本第一百一十页 第一百一十二页习题，七点五的第一题，第二题和第三题。好，同学们再见。

哈喽宝宝们，今天给大家讲一下解三角形的一道题，我们看这个题，在三角形 a、 b、 c 中，角 a、 b、 c 的 对应边分别为 a、 b、 c， 且三 a 乘 cosine 加 cosine 乘以三 a， b 等于二倍 cosine 乘 cosine d， 问求角 a 大 小。那首先我们看这个式子，三 a 乘 cosine， 就 前面这一部分，是不是能想到正弦和角公式就是 sin 括号 a 加 b 是 不是就等于上面这个 sin a 乘 cosine b， 再加上 cosine 乘 sin b， 对 吧？那我们原式是不是可以写成 sin a 加 b 等于 sin a 加 b 是 不是就等于二倍 sin c 乘 cosine a， 那 sin a 加 b 又能换成什么呢？三角形 a、 b、 c 中它 a 加 b 加 c 是 不是等于 pi， 那 a 加 b 是 不是等于 pi 减 c， 这是一样的吧。那 sin a 加 b 是 不是等于 sin 派减 c， 三派减 c 是 不是就等于三 c？ 那 所以前面就变成三 c 等于二倍三 c 乘 cosine， 然后除上二倍三 c 呢？ cosine a 是 不是就等于二分之一？它在三角形中那肯定是一百八十度吗？ a 属于零到 看之前，所以 a 等于三分之半，然后看第二个。若 a 等于高三，三角形 a、 b、 c 的 面积为四分之三倍，高三求 b 加 c 的 值。那这个也很很简单讲，我们由三角形面积公式是什么呢？ 他有很多公式，这个我们他有 a， 有 个 a 的 角，能求 bc 的 值。三 s 三角形 abc， 他 是不是等于二分之一 bc 乘上三 a？ 用这个公式，然后我们剩下的依次代入就行了。三 a 是 不是三 a 就 等于三三 a， 三分之派等于二分之根号三，然后这边就变成了四分之三倍。根号三等于二分之一乘 bc， 再乘上二分之根号三，然后这边就变成了四分之三倍。根号三等于四分之根号三。 bc， 那 我们能得到 bc 是 不是等于三的？而 b 方加 c 方的值， a 方是不是等于 b 方加 c 方减去二 bc 乘 cosine a， 那 b 方加 c 方能求吗？ 因为 a 等于根号三， cosine a 是 不等于二分之一 b， c 等于三。代入根号三的平方等于 b 方加上 c 方减二乘三，再乘二分之一就等于三，就等于 b 方加 c 方减三。 所以说 b 方加 c 方，我们能得出来六。我们有 b 方加 c 方的值，还有 b， c 的 值，用完全完全平方公式就能求出 b 加 c 的 值。 b 方加上 c 方，是不是就等于 b 加 c 的 平方减去 二倍的 bc 啊？ b 方加 c 方等于六，然后二 bc 带进去，那就是 b 加 c 的 平方，它是等于十二的。又因为 a 和 b 它都是边长吗？所以说不可能是负的。所以说 b 加 c 就 等于二倍根号三，这个就是计算，相当于计算多一些。好了，拜拜啦，有什么问题可以留言哈。

这是一道出三数线的几何体。已知在平行四边形 a、 b、 c、 d 中点 f 是 b、 c 的 中点， a、 f 交 b、 d 于点 e。 最后让我们求三角形 a、 b、 e 和四边形 e、 f、 c、 d 它们的面积之比。 梳理一下已知条件，已知四边形 a、 b、 c、 d， 它是一个平行四边形，所以 a、 d 和 b、 c 平行且相等。 平行可以得出来，角一和角三是相等的，因为他们是内错角，角二和角四是相等的，因为他们也是内错角。 两直线平行，内错角相等。在三角形 a、 e、 d 和 f、 e、 b 中有两个对应角，他们相等，那么这两个三角形就是相似的。下来我们可以除出他们的相似比， 因为 bc 等于 a、 d、 f 是 它的终点， b、 f 比上一个 bc 就是 一个一比二， b、 f 比上一个 a、 d 就 等于一比二。这两个三角形的相似比就是一比二。 又因为两个相似的三角形，它们的面积之比就等于它们相似，比的平方面积之比就是一比四。假如我们设 b、 e、 f 这个面积是 a， 那 么啊，三角形 a、 e、 d 这个面积就是四 a。 下来我们看一下三角形 a、 b、 e 这个面积怎么求？我们观察到 a、 b、 e 三角形 a、 b、 e 和三角形 b、 e、 f 这两个三角形，它们的底在一条直线上，而他们的顶点都是 b， 那 么他们底边上的高 就是同一个高，他们底边上的高就是相等的。设他们的高是 h， 那 么三角形 b、 e、 f 和三角形 b、 a、 e， 他 们的面积之比就等于 e、 f 比上一个 a、 e， 而 e、 f 比上 a、 e， 就是 这两个三角形的相似比，就等于一个 一比二。我们设的 b、 e、 f 这个面积是 a， 那 么 a、 b、 e 这个面积就是二 a， 三角形 a、 b、 d 的 面积是二 a 加四 a， 也就是一个六 a， 那 么三角形 b、 c、 d 的 面积也就是一个六 a， 六 a 减去一个 a， 这个就是一个五 a， 那 阴影部分的面积就是二 a 比五 a 等于个二比五，它们的比例关系也就出来了。

今天带大家看一道直角三角形的实际应用题，包括利用等腰三角形的性质、三角函数和辅助线构造直角三角形来计算点到水平面的距离。人形机器人的侧面是一图，如图二所示。题目中已经给出 a、 b 等于一百厘米， bc 等于 cd 等于四十厘米， ef 是 三十四厘米， a、 e 等于 ef， 角 a、 e、 f 等于一百二十度角 b、 c、 d 等于七十四度， a、 b 垂直 m、 n， 且 a、 b、 d 共线时，让我们求点 f 到水平地面 m、 n 的 距离是多少？我们可以首先过点 f 作 f， g 垂直 a、 b 于点 g 求 f 到水平地面 m、 n 的 距离，也就是求 g 到点 d 的 距离。 首先我们可以求 g、 b 的 长度， 那么 a、 e 的 长度是已知的，是三十四厘米，我们需要求 e、 g 这一段是多长。题目中已经给出角 a、 f、 e、 a、 e、 f 是 一百二十度，所以角 f、 e、 j 等于六十度，我们可以根据六十度的边的关系 来推。我们要求的 e、 j 是 六十度的邻边。题目中已知 e、 f 是 斜边，所以我们可以用 cos 六十度来求解。 cos 六十度等于二分之一等于 e j 比上 e、 f， 也就是 e、 j 比上三十四厘米， 可以推出两倍的 e、 j 等于三十四，也就是 e、 j 等于十七厘米。 所以 b、 j 的 长需要用 a、 b 减去 a， e 减去 e， j， 也就是一百厘米，减去三十四厘米，减去十七厘米，最后求出等于四十九厘米， 那我们需要求 b、 d 的 长度。题目中给出角 b、 c、 d 等于七十四度，并且 b、 c 等于 c、 d， 所以 三角形 b、 c、 d 是 一个等腰三角形，我们可以过点 c 做点 q， 过点 c 做 c q 垂直 b、 d 于点 q。 根据等腰三角形的性质， c、 q 是 角 b、 c、 d 的 角平分线，所以角 b、 c、 q 等于角 q c、 d 等于二分之一角 b、 c、 d 也就是三十七度。 因为三角形 bc q 和三角形 c、 q、 d 是 两个全等的三角形，所以我们需要求出 b q 的 长度 b q 也就等于 q d， 也就是 b、 d 的 一半。那我们首先来求 b q， b、 q 是 角 bc q 的 对边题目中已知 bc 等于四十厘米，是这个角的斜边，所以我们可以用 sine 三十七度来求解。在三十七度题目中已经给出是五分之三等于 b q 比上 b c， 也就是 b q 比上四十厘米，可以推出交叉相整五倍的 b q 等于一百二十，可以推出 b q 等于二十四厘米， 所以 b、 d 就 等于两倍的 b q， 也就是四十八厘米。最后 f 到水平地面 m n 的 距离，也就是 g、 d 之间的长度，也就是 b g 加上 b、 d 等于九十八，等于九十七厘米。

每次遇到解三角形的问题，你都信心满满，我们看一下这个题的第三问如何去做啊？一二两问，常规减法。呃，肯定应该没问题，我们直接来了啊！ b 解 c， a 加 b 等于 b 减 a， c， 那 把角放边以后，我们根据一些定律看一下啊。 bc 解 c 方等于 b 方解 a 方，那所以 b 方加 c 方减 a 方等于 bc。 根据 y 学定律， b 方加 c 方减 a 方等于二 bc cosine a， 所以 二倍的 cosine a 等于一， 所以 cosine a 等于二分之一，所以 a 角是六十度，那低温就解掉了。再看第二个求 b 的 曲值范围， 也是常规解法，这是前几年高考最常考的一个题。 b 比上三 b 等于 c 比上三 c， 继续对它整理 b 等于 c 倍的三 b 除以三 c 等于继续把三 b 换成三 a 加 c， 那 就是三。六十度加 c 比上一个三 c 等于二倍的二分之。根号三扣三 c 加上二分之一三 c 比上三 c， 那 继续对它展开整理，合并是根号三扣三 c 加上 三 c 比上三 c， 就 等于贪婪的 c 分 子。根号三加上一。所以接下来我们要去求贪婪的 c 的 取值范围，那先看 c 角的取值范围，由于它是锐角，所以是小于二分之派，大于六分之派， 那所以贪婪的 c 的 取值范围就是三分之根号三到整无穷， 那所以 b 就 属于一到四。我们再看第三问，先把第三问的图画一下，由于 g 点是 abc 的 重心，重心是中线的交点，那么他还有个性质是把这条线分成了二比一的两部分，所以 bg 就 等于三分之二的 b h 三分之二根号一下 c 方加上二分之 b 方，减去二， c 乘以二分之 b cosine a。 继续把 c 等于二， a 等于六十度代入整理，我们可以得到三分之一根号 b 减二的平方加上十二，它是大于等于三分之二被根号三， 那所以 b g 的 最小值就是三分之二倍根号三。记得点赞关注哦！

讲一下最新的五中稀缺的这个期末考试的第十题啊，我们来看一下题目。首先审题， c 呢等于 c， b 等于二。标一下二二角 a， c、 b 呢等于九十度，所以这样能得到一个等腰直角三角形 a、 c、 b， 因此 a、 b 呢等于二倍。根号二 点 d 呢，在 b、 c 上运动， d 是 动点 d。 在 运动的过程中呢，以 a、 d 为边，做一个正方形， 做一个正方形，过点 f， 再做 f， g 呢，垂直于 c 的 延长线，交它呢于点 g， 然后把 f、 b 呢给它连起来啊，交这个 d， e 呢于点 m， 这个 d， e 呢又跟这个 a、 b 呢交于点 n。 问，下列说法错误的是， 那这一题很显然它是一个怎么样反照这个二五年咱们的这个中考题出的一道这个压轴，对吧？我们这二五年的那个背景的话是一个刮豆模型，那这题依然还是一个呃，刮豆模型。所以这一题的话，就需要大家对刮豆模型呢有一个非常熟练的一个了解。 好，我们来看一下啊，这个刮动模型呢，我们就先不在这里面介绍了，有兴趣的同学。嗯，可以看我以前录的这个视频。我们来看一下这个刮动模型的话。呃，很显然这个点 d 呢是主动点， 点 e 呢是从动点好光度模型满足什么呢？就是主动点到定点的距离跟从动点到定点的距离比是一个定值。那这题很显然， a、 e 比上 a、 d， 就 这有个距离比， 这个距离比很显然等于根号二是一个定值。还有一个就是夹角的这个夹角，比如说主动点 和定点的连线，从动点和定点的连线，你看，以定点为顶点组成的这样的一个夹角，那这个夹角呢？也得是一个定角，那这题很显然它是一个四十五度，有了这两个条件，它才符合我们的这个刮动模型。 那刮动模型的话，熟悉的同学应该知道，就是主动点的轨迹它是一致的。现在主动点的轨迹呢， 是在一条直线啊，或者说他这是直线上面的一条线段，那么我点 e 呢？他应该也是直线上的一条线段，对吧？那么所以这样的话，我们就可以把从动点的轨迹给他，干嘛给他确定，我们要确定这个从动点的轨迹， 那从动点的轨迹呢？如何去确定呢？方法呢？有很多。那这题比较特殊，我们可以通过主动点的特殊位置去找从动点的特殊位置。 大家来看一下 d 点在特殊的位置时候，能推 e 点的这个特殊的位置，我们就把 d 放在哪个特殊位置，你比如说 d 可以 在 这个 c 的 时候，对吧？那如果 d 跟 c 重合，此时 a d 是， 是这个对不对？那很显然，那我的这个 d e 呢？是不是就呃等于这个 c b， 所以 这个当地在 c 的 时候，那 e 呢？是不是在这个地方？这帮我可以标个 e， 对 吧？好，那这时候我们再找 d 的 一个特殊位置， 那显然我们可以找当 d 在 b 点的时候，你是不是以 a d 为边？是不是再向外面再做一个？等腰直角三角形的时候，或者在外面再做一个这个，呃，正方形的时候，给它擦一下，那此时这个正方形画出来了，那刚好 应该是长这个样子啊，那刚好应该是长这个样子啊，那差不多呢，嗯， 在这啊，这个地方我图就不要画的特别准了啊，那很显然，那这是一几啊？这是一二，你看这三个点刚好在一条线上面，一一一二一三，我们刚才知道这个从动点的轨迹是一条直线，对吧？其实我只要找这条直线上面的两个特殊的点，就能把这条直线给它，缺什么给它基本确定了啊。 好，那这样的话，我们的一点的轨迹呢，就全部怎么样解决了？把这个图给它擦掉，五官的图都给它擦掉啊， 那这个一二的这个点的坐标呢，也比较特殊，也比较特殊，那我们来看一下啊，因为这个角是四十五度，这个角呢也是这个，呃，四十五度，所以这个三角形，这个三角形相当于就是一个等腰直角，是吗？三角形啊， ok， 那 我们现在把这条线呢再给它延长一点点，那整个 e 呢？就在这条直线上面干嘛动啊？这上面动。 好，嗯，我们来看一下啊， a 选项，他是说了当这个点 d 在 直线 bc 上面运动的时候，也就是说 a 选项有一个关键词，他把地点的这个运动的一个范围，从刚开始的这个边上面运动扩展到了这个直线上面运动， 所以现在这个 e 点的轨迹也是在整个直线上面动，而 a 选项让我们求 a e 加 c e 的 最小值，那很显然 a 选项求的是 a e 加上 c e， a e 加上 c e 的 话，它的一个是线段之和的最什么值？最小值，因此的话，那 a 选项很显然是一个将军印什么印码，而且是两定一动， 你看啊， a e 加上 c e 的 这个最小值，那很想我是不是做一下对称就可以了啊？那我就把 c 点关于它对称一下，我们把图给它标一下。 好，咱们把这个 c 呢给它对称过来，用个绿色的吧，对称过来，好，对称到这个地方，这边标一个 c e 撇， 那此时的话，我们的这个 c e 是 不是就变成了 c 撇 e， 然后直接连上 a c e 撇是不就可以了？也就是说，此时 a e 加上 c e 的 最小值，是不就等于 a c e 撇， a e 加上 c e 的 最小值，等于 a c e 撇，我们怎么去计算？那很显然我们还是要去。呃，添加辅助线，把它构造成一个直角三角形，我可以过 c 呢，往这边再做一条垂线啊， 这方我标个点 m 点 q 吧。 ok， 那 么现在我们开始一个计算，呃，咱们知道这个角呢，可能说是四十五度，那这个角呢，也是四十五度，所以 三角形这个地方呢，这个三角形它是一个等腰直角三角形，这条边呢是二，因此的话，那这个，呃，这条边的长度呢，就等于根号二。对称过来，这个长度也是根号二，这个方是垂直的，所以我们的 c c 一 撇呢，等于二倍根号二，是不等于二倍根号二， 而这个角呢等于四十五度，这个角呢也等于四十五度，所以我们的 c 一 撇 q， c 呢，它是一个等腰直角三角形，因此这条边呢， c 一 撇 q 等于二， c q 呢也等于二，所以我们再用勾股定顶，就能把它长度呢给它算出来了啊。那此时很简单，等于根号下， 应该是二的平方，再加上四的平方，所以答案呢，应该等于二倍杠五，所以这题的最小值呢，应该等于二倍杠五，并不是等于二倍根号二加二。如果你选了这个答案，你是估计没有看到这个关键词，它是在直线上面运动。好，这是 a 选项，所以当然呢，这题呢，就直接选 a 就 可以了。 这个和我们二五年的那个安徽中考题，他的那个第十题的压轴题的答案呢，也是 a 选项，如此一个类，一个意思啊，一个意思，但是他也是，呃，有一个审题的一个关键点。好，那这样的话，我们 a 选项呢，就不在这方继续讲了，继续我们看 b 选项， b 选项的话，它点 d 在 边 bc 上运动的时候，问我们正方形 a、 d， e、 f 面积的最大值，那 b 选项很简单， 这个正方形是不是等于 a d 的 平方，所以 a d 最大的时候呢，它整个面积就最大。那很想这个 a、 d 是 不是有一个直线形的距离，就是一个线段，那它距离最大的时候，肯定到 a b 的 时候是最大，所以那个 b 选项它是对的啊，所以这个 s 的 最大值呢，刚好等于二倍根号二括号的平方等于八。 c 呢？我们再看 c， c 是 点 d 在 这条边上运动的时候， b m 的 这个最大值是二分之一，我们知道这个地方是个垂直，所以这个图里面会形成一个一线三等角， 这有个一线三等角，这种题目在做一线三等角的题目的时候应该接触过，对吧？我要求一下 b m 的 这个最大值，那这个地方呢，我们就可以几何转代数啊，几何转代数， 那这条边呢，是二，我们可以设个圆就可以了。设这条边是 x， 那 这条边呢，等于二减 x， 把 b m 呢设成 y， 我 们知道这方有一个一线三角的相似，那熟知一线三角相似的乘积式的结论的同学，这方就可以直接写了啊， 或者你把比例式列出来，那我们直接写乘积式，应该两个 y 等于 x 乘上二减 x， 那 这方把 y 呢写出来，应该等于二分之一， 这个负的二分之一 x 的 平方再加上 x 配方就可以了。那就是负的二分之一 x 的 这个平方再减二， x 再加一，再减一，等于负的二分之一 x 减一，括号的平方再加上二分之一。所以 当这个 x 等于几时？等于一时，它的最大值呢？等于二分之一一，刚好呢，在这个取值范围上面，对吧？好，所以 c 答案呢，也是对的啊。这题比较难的是这个 d 选项啊，像有很多同学当时呢可能没有办法很好的处理这个 d 选项， d 选项呢，是一个模型， 这模型大家可以学一学啊，就是目前像咱们安徽的话，考的不是那么多啊，不是那么多，它是一个斜大于直的模型。斜大于等于直来讲一下啊，那 这个三角形是一个直角三角形，那这种题目呢，因为我们要求 a n， a n 刚好是这个直角三角形的斜边，对吧？我们遇到直角三角形的斜边，我们可以考虑取一下 a n 的 中点，取 a n 中点 o， 我 们取一下它的中点 o。 啊，这个地方的话，嗯，图不一定很准啊，就差不多这是点 o。 好， 这是它的中点，那显然的话， o d 是 不就是这个？呃， o n 的 这个 a n 的 一半，所以它是等于二分之一 a n。 好， 那这时候我们可以设个圆，把 o d 呢设成 x， 把 o a 呢也设成这个 x， 那么我这时候我再过 o， 那 向这再做一条垂线，在这再做一条垂线，把垂足呢标为点 h。 很 显然，此时我是不是形成了一个直角三角形 o d o h。 现在的话， o d 在 这里面是不是作为它的这个斜边，而 o h 呢，是作为它的这个什么边，这个直角边，显然这个 o d 的 话，它一定是大于这个 o h 的。 那什么时候能等于 o h？ 就是 当这个地点和这个 o 点，就是这个 h 点和这个地点刚好重合了，那此时 它的这个斜边呢，刚好肯定是等于这个 o h 的。 有时候这方有一个取等的过程，有一个取等的这个这个过程。好，那这时候我们就把这个 o d 和 o h 用我刚才射源的这个量给它表示进去啊，所以 x 呢，就大于等于。我们看一下， o h 等于呢，我们射的这条边是 x， 因此这个 o b 这条边呢，它应该等于二倍根号二，再减 x， 而这个地方 o h b 始终是一个等腰直角三角形，所以我的 o h 应该等于这条边，再除以根号二，所以它就大于等于 根号二分之二，再减多少减 x， 然后把这不等式解出来，那就根号二 x 大 于等于二倍根号二，再减 x， 把不等式解一下啊，那就根号二，加一倍的 x 大 于等于二倍，根号 x 应该大于等于二倍根号，除以根号加一分母由里化， 那又变成的是根号乘以这个根号，再怎么样减一啊？减一这括号打不下去了，那应该等于多少？所以的话应该是 x 大 于等于这个四减二倍根号，而我刚才说了这个 o d 呢，它是等于 a n 的 这个一半，因此 a n 的 话就应该大于等于八减四倍根号，所以 d 答案呢，它也是对的啊。所以这题大家重点学习一下 d 的 这个模型的一个处理的方法。