粉丝85.2万获赞533.7万
相关视频
 01:00
01:00 00:17
00:17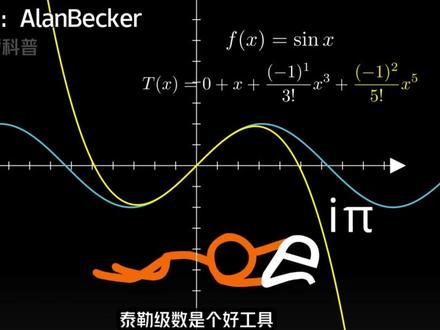 08:45查看AI文稿AI文稿
08:45查看AI文稿AI文稿听说你的朋友很厉害,那他一定看过艾伦贝克尔的数学动画吧。上回叔说到小城把带师部的余弦和带须部的政弦放在一起,得到了欧拉公式。为什么把这带师部的余弦和带须部的政弦放在一起就能得到欧拉公式呢? 嘿,那就老不堪一为敌的支书函数的秘籍数了。秘籍数又是什么?首先我们要知道级数是什么?级数是由一些以数字相加得到的组合,每一项都是按照一定的规律生成的,它可以使用线相相加,比如灯叉数列一加到一百, 也可以是无穷多项相加,比如公比为二分之一的无穷相等比数列之和。如果这些相加的结果趋近于一个有限的之,我们说起书是收敛的,可以计算出它的和。如果相加的结果没有确定的值或者趋向无穷的, 那么级数是发散的,没有有限的和。而蜜级数,他的每一项都是长数乘一遍两 a 克斯的蜜。我们注意到这些级数中有一些感叹号,他们表示的是阶程,阶程是一个增长数于小于等于他的所有增整数的成绩,比如 三的阶程就是三乘二乘一等于六。在我们讨论一亿为底的指数函数之前,让我们先来了解一下什么是自然底数。亿我在此前的视频分享过,以最早在银行复利的计算中被完整提出来,大约等于二点七一八二八, 还在科学上有许多重要的应用。那么以一为底的指数函数的秘籍数是怎么来的呢?这就不得不提到泰勒级数了。泰勒级数又是什么?看样子你是要打破砂锅问到底了。泰勒级数的推倒机与函数,在某一点的所有街道数。 这是一个数学上的概念,其基本思想是用一个无穷极数来逼近函数。哎哎,函数是什么?导数又是什么?我在之前的视频里分享过函数和导数的定义,现在用小学生都能听懂的语言再来简单介绍一遍。咱们可以把函数想象成一个机器,给他一个数, 他会根据一定的规则给咱们返回一个新的数。比如有一个函数叫作加二,如果咱们给他一个数五,他就会返回七, 因为五加二等于七。所以如果有一个函数来表示我们的未知随时间发生了变化,那么这个函数的倒数就表示我们的速度。 导书可以帮助我们了解函数是如何改变的,我们可以把它想象成一个速度记。举个例子,当我们在骑自行车时,我们的速度就是我们的位置函数的导数。这意味着,如果 我们骑的越快,速度越大,导数就越大。如果我们停下来不动,速度就是零,导数也就是零。比一届导数更高的导数作为高级导数,高级导数就是对函数的导数在求导。比如咱们还是在骑自行车,我们的加速度就是我们的速度,函数的导数 也就是我们的位置函数的二阶倒数。如果我们越来越快,那么加速度大于零,半阶倒数也就大于零。反之,如果我们越来越慢,那么加速度小于零, 八级导数也就小于零。如果我们的速度保持不变,加速度就是零,八级导数也就是零。有了以上的知识,现在我们回到泰勒奇数的推导。泰勒奇数是个好工具,它的核心思想是用一个无穷奇数来逼近某一个函数。假设有一个函数 a f x, 希望在点 a 处找到这个函数的金丝值,那我们可以从长数开始,然后慢慢添加越来越高阶的项,使得这个金丝再连一点的所有导数都与 a 辅 a 可死的相应导数相等。我们首先选择一个长数项, a 辅 a, 这样在 a x 等于 a 十,近四值就等于函数值。接下来我们添加一个信息项,这样在 a x 等于 a 十,近四函数的一阶导数就等于 f a x 的一阶导数。我们继续添加一个二次项,这样在 a x 等于 a 十, 这次函数的二阶倒数就等于 a 负 a x 的二阶导数。以此类推,我们可以继续添加更高阶的项。每个项都是 a 负 a 乘以 a x 减雷的恩次密除以闷的阶程,其中 a 负 a 零是 a 负 a x, 再 a x 等于 a 处的 a n 阶导数。这样我们就得到了泰勒奇术的一般心事。当泰勒奇术中的雷斗于零时, 我们就得到了麦克劳零级数。根据自然底数一的特性,我们能得到一等 x 次方的任意界导数都是他自身,所以一等 x 次方在 x 等于零处,等级导数都等于一的零次方。也就是以,把这些只带入到麦克劳零级数的公式中去, 我们就能得到以自然底数因为底的指数函数的密集数。然后我们按照欧拉的方法把 ax 替换重挨重 ax, 接着对展开始精心整理,把叙述的成计算出来 以后,把不包含蓄摔的象和宝宝还爱的象放在两个括号里,我们会得到两个技术。巧合的是, 左边这个不含蓄数挨的级数恰好是御写函数的麦克劳令展开始,右边帮含蓄数挨的级数恰好是这些函数的麦克劳令展开始。这真的只是巧合吗?不巧,用这些函数和预 函数替换上书籍数,我们就得到了欧拉公式的完整表达式。欧拉公式结识了指数函数、三角函数和复数之间的深刻关系。到西塔取不同的实数之时,意达埃西塔私房的结果是一个单位元上的点。 也就是说,勾拉公式可以用来表示副平面上以圆点为中心的单位圆上的点。这并不难理解, 因为组成欧拉公式是不合局部的余弦函数和正弦函数等,就是定义在单位元上的三角函数。如果负平面中的点位欧拉公式,那么所有点的模长都可以表示为可散音平方与散音平方和的平方感。众所周知, 这个等式横等于一,也就是说乌拉公式所表示的所有点到圆点的距离都是一,而这正是单位圆的定义。当我们把西塔等于派带落到这个公式,就得到了火柴人 动画中的欧拉很等式,这也是当小成把替核桃合并时,会变出另一个主角小艺,以及小艺得于赋予的缘故。现在我们回到前面跳过的剧情就能明白,小艺这个欧拉展开可不是乱展开,他是有备而来。接下来,小成知道符号是转了个头, 说明符号具有反向的作用。小虫学会这一招之后,在后续剧情中用符号追上了小艺,并且成功躲过致命一击。当小虫起身来追小艺的时候, 我们看到小易逃出派,改变自身指数上的弧度大小,画出一个半圆号逃离。为了解释这个半圆轨迹,我们来看看欧拉公式的完整形式。 此前我们已经介绍了欧拉公式在抚平面中表示的是一个单位元把一个元的弧度大小为二,派小一本身等于负一,在单位元的最左侧,当他的指数减去派时 值弧度等于零,起值位移对应的是大位元的最右侧。我们可以把这个过程看作是用来公式从派遣小为零的区间的变化,所以其对应的轨迹就是一个半圆。小常在追击小意的过程中,射手藏了称号和爱,等下马上就会用到这两个道具, 事实就是力量。为了更快追上小艺,小程拿出道具称号,对此审视下,程法肉眼可见的加速了,这种加速效果看起来跟是平加速一样,毕竟是平加速的按键,也是一个称号呢。烟抽着去一笔记,小程向小艺丢出符号, 成功让小易转向刹车。这种刹车方式和高铁的电制动非常类似,通过产生一个和电动机转向相反的电磁力曲作为制动力,使电机停止转动。哎嘿嘿,小易在刹车过程中还不忘踹开小程。接下来双 方发生的战斗式加减法的比劈,主打一个比大小小 成绩非小易之后发动二乘二的弓箭攻击。这里有个细节,从零到九的数字里只有死核七的底部是接纳,而其实之数,小易用减号挡住发射过来的数字四,并将数字四放到坟墓中去做壁画出一个八分之一圆弧, 这对应的就是欧拉公式从零到四分之派的轨迹。我们可以看到小一跑到空中后,小城再也没有集中过,比禁敌对空可比敌对地难多了。这时候小城掏出另一个道具哎 成在自己身上,也在空中画出了白圆的轨迹。通过前面的结论,我们已经知道成以爱的几何意义,就是逆时针旋转九十度,遗憾的是小成没办法将爱绑在 在自己身上,很快就落到了地面,让小一给逃走了。之后就是我们此前分析过的剧情,小城从爱出发把小一造了出来。后面的剧情就是艾伦贝克尔的数学动画中全片高潮的部分,数学知识密度相当之高。 泰蒙也会在下期视频中继续分享火柴人数学动画的解析,希望能对你有所帮助。
11.7万派蒙科普 00:51
00:51 01:55查看AI文稿AI文稿
01:55查看AI文稿AI文稿同学们好,今天是四月二号,每天学一点,坚持学一年。今天和大家分享一个欧拉公式,微加 f 减一等于二。任何一个简单多面体都满足微加 f 减一等于二。一个简单的公式就体现出了所有简单多面体的共同特征。 简单多变题指的是由若干个平面组成的几个题,比如四面体、三棱柱、长方体等等。所以含有曲面的几个题 不是简单多面题。其中 v 指的是零点数, f 指的是面数, face 一指的是棱数 a。 比如 四面体中,顶点数是四个,面数是四个,棱数是六个,四加四减六等于二。再比如,长方体中顶点有八个,面数有六个,棱数有十二个,八加六减十二也等于二。那么由若干个 n 边形组成的 分 b 几和题仍然满足 v 加 f 减一等于二。我们将面数继承 f 的面。先拿出一个面,此时一个 n 边形有 n 条棱, n 个顶点,此时 v 等于一等于 n。 拿出第二个面和前面组合,此时会减少一条棱,两个顶点, 所以此时一加一等于一。我拿出第三个面和前面组合,仍然减少一条往两个顶点, 此时微加二。当我们继续增加第四个面,此时微加三等于一。 我们拿出第五个面组合 v 加四等于一,我们拿出第六个面组合, v 加五等于一。因此我们发现了自然区的规律,当我们拿出倒数第二个面组合,此时一共有 x 一个面,满足 v 加 f 减二等于一。经过整理,发现 v 加 f 减一等于二。同学们,你能数出三等座的零点数、念数和能数来验证这个规律吗?评论区留下你的答案。
288崔老师(日历数学) 02:08查看AI文稿AI文稿
02:08查看AI文稿AI文稿今天上午的直播分享课呀,我们讲了立体图形的初步,在这里呢,老田分享一个欧拉公式,这个公式啊是关于棱柱、棱锥、顶点、面棱之间数量关系的一个公式。讲公式之前呢,我们先填写一个表格,我们看一下,摁,棱柱有多少个顶点?我们 知道 n 棱柱上下两个底面啊,都是一个 n 边形,那么这个底面呢,就有 n 条边和 n 个顶点,所以我们可以很容易写出,上面的底面有 n 个顶点,下边底面也有 n 个顶点,总共加起来啊,就是二 n 个顶点,那么有几个面呢?我们知道上下两个底面啊,这个数量是固定不变的, 唯独变化的就是 n 棱柱的侧面。因为底面啊是一个 n 边形,每一条边呢,都组成了一个侧面,所以就有 n 个侧面,所以 n 棱柱总共有 n 加二个面。那么有多少条棱呢?我们把 n 棱柱啊分成上中下三个部分,上底面 有 n 条棱,中间部分呢是 n 条立柱,下底面同样也有 n 条棱,所以加在一起正好是三 n 条棱。我们再来看一下棱锥, n 棱锥呢,我们知道他只有一个底面,也是 n 边形,也就是有 n 个顶点,但是他的上底面呢,变成了尖尖角的一个顶点,所以总共的顶点个数啊,就是 n 加一。那么 n 棱锥有几个面呢?我们知道 n 棱锥只有一个底面, 同样这个底面,这个 n 边形啊,每一条边形成了 n 个侧面,所以就是 n 加一个面。再来看一下 n 棱锥的棱数,我们可以看到竖起来的这个侧棱啊,总共有 n 条,再加上下底面的这个 n 边形, n 条棱呢?总共就是二 n 条棱。好了, 我用大写字母 v 来代表顶点数, f 代表面数, e 代表棱的条数。根据这个表格啊,我们很容易发现,无论是棱柱也好,棱锥也好, 好,他的顶点数量加上面的个数,减去棱的个数,哎,他等于一个长数。二,这个公式就是欧拉公式。其实比起欧拉公式啊,上面这个表格更加重要,因为你会发现,无论是能住也好,能追也好,我 只要给出你其中的一个变量,比如说顶点的个数,我很容易就能求出 n 等于几。那么有了 n 了,我就会很快求出另外两个变量的数量。关于欧拉公式,你理解了吗?
1277爱分享的老田 07:07查看AI文稿AI文稿
07:07查看AI文稿AI文稿大家好,这期讲欧拉公式,在漫长的数学历史长河当中,诞生了无数美丽的数学公式,他们宛如一颗颗璀璨的明珠,光彩夺目,而只有他被称为上帝公式,他就是欧拉公式。那我们来看一下他有什么特别之处啊。 它的形式是这样的,一的 i x 次方等于 cosine x 加上 i 乘以三 x, 其中一是自然长数, i 是虚数沙眼, cosine 呢,是三角函数。当 x 等于派的时候啊,公式就变成了一的 ipi, 次方等于负一,这个就是欧拉横等式。 这个等式包含了自然长数、虚数、圆周率和自然数。每一个单拿出来啊,在数学史上都是非常炸裂的存在。而欧拉公式竟然以一种极其简洁的形式,轻描淡写般把他们 结合了在一起,在以简洁唯美的数学世界里啊,难怪他会被称为上帝公式吧。事实上,与欧拉公式相近的公式,在此之前就已经被发现了。其实这也不奇怪,我讲虚数的那期视频呢,也有推导到类似的结果啊, 例如一七零七年,法国数学家蒂莫福就发现了一个这样的公式, cosine x 加减 i 乘以三 x 的 n 次方,它是等于 cosine n x 加减 i 乘以三 n x 的。 又例如,一七一二年,英国数学家罗杰科特斯在研究螺旋线无常的时候呢,就得出了一个这样的公式, l n cosinex 加上 i 乘三 x 呢,它是等于 ix 的 啊,这里注意一下啊, l n 这个符号呢,是后来欧拉取的啊,是表示自然对数的意思。在此之前,数学家们呢,都是用别的方法去表示自然对数的啊,这里我为了大家好理解,直接就用 用了 l n 啊,包括虚数 i 也是后来欧拉给的符号,在此之前呢,虚数都被写作根号负一,我为了方便表达啊,也是直接用了 i 的啊。 这个公式呢,可以说是无限接近欧拉公式了,只要两边同时取一为底的指数操作就可以了。不过科特斯在一七一六年突然离世,这一结果呢,也从未正式发表过。接下来为了说明欧拉公式,我得先讲一下这个自然长数是什么啊? 自然常数一,其实我们在高中的时候呢,就接触过了,他和 pi 一样,也是一个物理数来的,他约等于二点七一八二八。 自然长数又被称为欧拉数,但是欧拉数却不是欧拉发现的,是雅阁部博努力在研究存款复利的时候发现的。注意一下这里的博努力和流体力学的博努力啊,不是一个人, 流体力学的是丹尼尔博努力啊,他是雅格布的侄子。这里说明一啊,其实是有两个数学模型可以选的,一个呢,是一年之内无穷次存取 gc 啊,博努力用的就是这个。第二个呢,就是定期只存取一次啊,但是你可以存无穷多年, 不过不同年份的定期啊,就会对应到不同的利率,因为时间无穷细分这个事情对我来说呢,有点离谱啊,所以我这里用的就是第二个模型。 假如银行规定了一个这样的规则,存一年利率就是百分之一百,存两年利率就变成了百分之五十,也就是二分之一,存三年利率变为三分之一,而存 n 年呢,利率就变成 n 分之一, 复利的意思就是今年的本加息呢,会变成下一年的本啊。好,那么我们用一个具体的例子来说明啊,我有一块钱, 存一年之后,到手就是一加上一乘以百分百等于二。存两年,最后到手呢,就是一加上二分之一,加上一加上二分一,再乘以二分之一的,也就是一加二分一的二次方,等于二点二五。 存三年,最后到手的就是一加上三分之一的三次方,等于二点三七的,以此类推啊。存 n 年,最后呢,到手就是一加上 n 分之一的 n 次方。哎,这个时候好像发现存的越久,赚的就越多。如果我存无穷多年,那么本息会不会最后就是无穷多呢? 不会,他只会无限趋向于二点七一八二八点点点点,对吧?甚至呢都到不了二点七二。我们可以画一个一加上 x 分之一的 x 次方的函数图像啊,可以明显看到,函数值到了二点七一左右啊, 就上不去了。欧拉在他后来的注册中多次引用到了这个数,并且给了他一个符号一,所以这个数也被后人叫做欧拉数了。这个自然长数有什么特别的地方呢啊,我们来看一下啊,假如有一个指数函数是以一为底的,也就是 y 等于一的 x 次方, 我们随便找一个点吧,例如 x 等于二,那它的函数值呢,就是一的平方,在这一个点的倒数,也就是切线的斜率,它也是一的平方。 函数曲线与 x 轴围成的面积呢,它也还是一的平方。放眼整个数学界,这个函数的特性啊,也是独一份的啊, 当然,三角函数三 x 啊,求两次导之后呢,会变成自己的相反数啊,这个特性倒是和 e 的 x 方啊有点类似,感觉这两个函数冥冥之中就是有关联的。当然,对复数领域和三角函数领域研究颇深的 欧拉也是这样认为的。一七四八年,欧拉发表了一篇名为无限研究导论的论文,里面就引用了蒂莫夫的公式啊, 我们来看一下啊,两式相加除以二,就得到了 cosine 的 n x。 两式相减除以二 i 就得到了 cyan 的 n x。 欧拉大胆的把 x 取了无穷小,于是呢,就有了三眼 x 是等价于 x 的,扣上 x 呢,是等价于一的啊,那么式子呢,就变成了这样, 然后再取 n 为无穷大,令到 n x 等于 k 啊,那么就有 x 呢,是等于 k 除以 n 的。最终的式子呢,又变成了这样。 哎,大家看,这不就是我们刚刚讲过复利的计算形式吗?这个其实就是一的 i k 次方,而这个呢,就是一的负 i k 次方, 所以最后 q 三 k 和三 k 呢,就变成了这样。哎,我们看这两个式子,拿二式乘以 i 再加上一式, 于是乎,我们就得到了欧拉公式的最终形式码, q 三 k 加 i 三 k。 之前讲虚数的时候就提到过,它可以在副屏面上表示旋转,所以呢, e 的 i k 四方也是一样的。 举个例子,五乘以一的 i 三分之拍次方,这个数表示了负平面上五为半径,逆时针旋转了六十度所在的位置。 又例如一个负数一加 i 化成负指数,形式是怎样的呢?在负平面上画出来一加 i 的点在这,它的半径就是根号二全过的角度刚刚好是四十五度,也就是四分之派。用三角函数表示呢,就是根号二乘以 扣上四分派,加上 i 乘以三四分派,也就是根号二乘以一的 i, 四分之派次方。好。至此,欧拉公式就跟三角函数和旋转关联了到一起。 你想想啊,复离液激素还得用沙哑和抠上两种函数做基底去分解,如果用一的 ic 塔次方去做基底的话呢,一个就够了。好了,这期讲到这,下期我们讲复离液变换在复数域的展开,我们下期见。
1577有趣的理工男










