反三角函数正切函数奇偶性
粉丝41获赞446
相关视频
 03:05查看AI文稿AI文稿
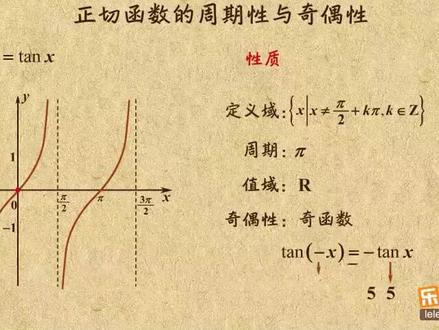
03:05查看AI文稿AI文稿这个视频咱来研究下正切函数的周期性与饥饿性。要看这些性质,咱先来看看正切函数的图像长啥样。正切函数可以用 y 等于 tangi xx 来表示,并且 x 的不能等于二分之派加 k 派, k 属于整数, 那在直角坐标系中, x 等于负二分之派,二分之派,二分之三派等等。这些地方太阳,并且 x 都没有取值。 接着回想下正前函数的诱导攻势, tang 巧, x 加派等于 tan 俊巧, x 发现没,他是一个周期函数,并且周期为派。利用这一点,那负二分之派到二分之派之间刚好是一个派,也就是一个周期。只要画出这个周期里的图像,那其他周期的也就知道了。 接着咱就用单位员来画画这个周期里的图像,把负二分之派到二分之派之间进行八等分,这些 对应的弧度分别是,负八分之三派,负四分之派,负八分之派,零等等等等。一直到二分之派,你已经学过正切直对应这个焦点处的垂线到中边的这一段,所以当 x 等于零时, tang xx 的就是零,显然图像得过远点。 当 x 等于八分之派时, tang 加 x 就是这么多,显然这个点一定在图像上。当 x 等于四分之派时,对应的 tang 加 x 就是这么多,等于这段半径一,那显然四分之派一这个点一定在图像上。 当 x 等于八分之三派时,对应的贪军抢 x 就是这么多。显然这个点也在图像上。当 x 等于二分之派时,贪军抢 x 就没有取值了。像这样,你把负二分之派到零之间的所有 x 也标到坐标轴上,接着依次找到他们对 对应的函数值,然后描出这些点,再把这些点用光环的曲线连接起来,就得到正切函数在负二分之派到二分之派上的图像了。根据正切函数的周期性,把图像向右拼一个派,就得到二分之派到二分之三派的图像了。 同样的,还可以向左平移一个派就得到负二分之三派到负二分之派的图像了。如果一次平移下去,就得到 y 等于摊俊叉 x 在 r 上的图像了。画好了图像,来看看这图像有啥性质定义就不用说了, x 不等于二分之派加 k 派, k 属于整数 周期,刚刚也讲过,就是派。再看看职狱, x 接近二分之派时, tang zhang xiangjiang 的取向正无穷, x 的接近负二分之派时, tang jiang xiangjiang 的取向父无穷。所以 xiang 二是全体识数,还有 机偶性。显然这个图像关于原点对称,所以是基函数,也就是 tangjinjangfux 等于 fu 的 tangjinjiangxx, 比如 tangjinjangxx 等于五,那 tangjinjinjanghuxx 就等于副的五。 好了,回顾刚才的内容,我主要讲了正期函数的图像以及他的性质。他的图像可以通过负二分之派到二分之派之间的这段,根据周期是派依次平易得到。 他的定义是 x 的不等于二分之派加 k 派直域是全体实数,并且是个饥寒数。怎么样,你学会了吗?如果学会了就速速刷题去吧!
1873初高中数学老师 09:15
09:15 01:03
01:03














