roll中值定理万能公式
粉丝5.9万获赞80.7万
相关视频
 04:52查看AI文稿AI文稿
04:52查看AI文稿AI文稿一招教你把双中指的中指定理变简单!中指定理的题型呢,是我们考研当中的重点题型,那么接下来我们来看一道双中指的中指定理如何来证明。那么这道题说 ff 在 b 区间连续开区间可导, 而且 f a 等于 f b 等于一证明存在,可 c e 踏属于开区间 a 到 b, 使得这样一个式子成立。可 c e 踏,这不叫双中指吗?双中指,而且两个中指都属于区间 a 到 b, 并没有强调可 c e 踏是不同的两个点啊,所以咱们这叫重复型的双中指。 两个种植的话,什么用两次种植定理?那根据要正的式子的变形来决定左边用什么,右边用什么。您发现 既有可 c 又有一踏,第一步是先分加让等号,一边全是可 c 等号,另外一边呢,全是一踏,所以那这个式子变成了一个 e 的一踏次,然后 f e 踏加上一个 f e 撇 e 踏,等于把这个 e 的副可 c 次移到右边去,这就是 e 的可 c 次,那么正它成立的话,同学,很显然这是某一个函数在可 c 的倒数啊, 哪个函数?求导是 e 的可 c 次呀?很显然这边对应的函数是谁呀? f x f x 用拉格朗日出现 f 一盘可 c, 说明右边的拉格朗日, 左边的话,同学,我们来看谁求导是这样一个式子呀, e 的 x fx 求导啊,如果说我瞪不出来,其实你也可以用还原法把它构造出来左边这一块的话呢,咱们是不是可以把它写成 e 的 x f x 加上一个 f e p x, 把一踏改成 x, 然后呢,直接让左边这一块等于零,指数行数永远不等于零啊,相当于是这个式的 等于零,那么这个是等于零,我们把它变成两边都很容易积分的形式,它是不是可以变成 f e 撇 x 除以 f x 等于负一,可以变成两边都很容易积分的形式啊, 同时积分,这就是烙印 f x 啊,这个位置负 x 啊,加上一个烙印 c, 我们说还原法是得 c 得辅助啊,那这个烙印 c 留在这边就可以了。我们把这个 x 移过来,两个烙印合并烙印 f x, 加上一个 line e 的 x 等于 line c, 这不就是 line e 的 x 乘以 f x 等于 line c 吗?得 c, 得辅助,说明这就是 c 呀, 这就是 c, 说明左边的这个辅助函数其实就是一个 e 的 x, 这不就是一个 f x 吗?当然我们右边的话呢,为了和这个不重复的话,我们可以改成一个什么呀, g x g x 就 e 的 x, e 的 x, 用拉个朗日可以产生这个,而左边这个 f x 呢,用 e 的 x 乘以 f x, 我们就可以产生左边这个式子。所以这个题的话呢,就是右边拉个朗日,左边拉个朗日,左边拉右边拉。那证明,首先令这个大 f x 是一个 e 的 x 乘以 f x, 然后呢? g x 是一个谁呀?是一个 e 的 x。 好,首先对我们的大 f x, g x 在区间 a 到 b 分别用拉个朗日,那从而就推出存在一个一踏属于区间 a 到 b, 使得大 f 一撇一,它等于大 f b 减去大 f a 比上 b 减 a 呀,这是把这个大 f 用拉给老师啊,那您 把这个化减一下,即大 f, 就是这个函数啊,那这个函数在 e 它的倒数那不就是一个 e 的 e 它次 f e 它加上一个 f, 一撇 e, 它等于大 f b, 那么就是一个 e 的 b 次 f, b 减 e 的 a 次 fa 比上一个谁呀? b 加 a 到这以后,同学注意, fafe 都是一样,那都是一的话,这不剩 e 的 b 次减 e 的 a 次除以 b 加 a 吗?这是把这个大 f 用的什么呀?拉个老知,那接下来把这个 gx, 那就这个函数 也用拉个朗字,那从而退出存在一个可 c, 所以区间 a 到 b, 使得 g 一撇,可 c 等于 g b 减去一个 g a 比上一个 b 减 a。 好,我们把刚才这个式子叫一 式,那么这个式子咱们化解一下吧。那第一撇可 c 就是 e 的可 c 次呀,等于 g b g b 是 e 的 b 次 g a, e 的 a 次比上一个 b 减 a。 好了,同学,咱们把这个式子叫第二个式子, 那么一式是个,这二式呢?是个这由一二从而推出一的一踏次 f, 一踏加上一个 f, 一撇一踏等于一的可是一次,那换句话说就是你要正的这个式子双中值的这个 结论就成立了呀。所以这个题最后就结尾了,要学会分加,如果是双中指,让等号一边全是可 c 等号,另外一边全是一踏,观察两边的式子适合用什么样的中值定理。好吧,同学,这个题咱们就分享到这里。
989考研数学娜姐 10:20查看AI文稿AI文稿
10:20查看AI文稿AI文稿同学们好,我是东北大学数学系杨中斌,主讲高等数学。 前面我们讲了求如何来求函数的导数。今天我们讲导数的应用。为了证明几个非常重要的定理,我们先介绍为一分中指定理。 我一分钟的定定包括三个落尔中定定,那个郎中定定和柯西中的定定。现在我们介绍落尔中定定。落尔中的定定中 需要用到一个非常重要的分码定理 射 y 抖音。 f。 在 ab 区间上。可微。可 c 是 ab 先生的一个点。如果函数 fx 在可 c 六处取得 最大值或者是最小值,折这一点的倒数一定等于零。例如 在 ab 区间上,函数 fx。 图像如此。在可 c 这点。很显然这个函数取得了最大值。 我们把函数在某一定的导数等于零,这样点成为函数的注点。例如 证明不是一般性不仿蛇。函数 fx 在可 c 这边取得最大值。 由于函数在这一点可打,所以我们取一点可 c 加,当然也属于 ab 区间。由于他这点取得最大值,所以 f 可 c 加上得到 x 就小于 f。 可 c 有导数的定义,求 诱导术。由于这一点可惜真的是最大值,所以这一点极限一定是小于 等于零。而又由于左极限又是大于等于零,而这个函数在这点又是可倒的,所以他的倒数一定等于零。所以这 这就是我们通常说的,如果函数 fx 在 ab 区间上可倒, 这可这是极致点,那么极致点的倒数一定等于零。有了非法定理,我们有处理非常重要的定理就是落而中定点。 它的内容。如果函数 fx 在 ab 区间上满足 b 区间连续开区间可导,而且在两个端点的函数值相等的话,那么在开区 ab 内一定存在一点可税,这一点的导数等于零。在几和上, 实际上就说明这个函数在这一点有一条水平的期限。由于 fx 在 ab 区间上连续,必定存在着最大值和最小值。但是呢,有两种情况。 如果最大值和最小值相等,由 fx 一定是一个长数,而长数的倒数都等于零,所以任何一点的倒数都等于零。如果最大值不等于最小值, 则 fx 由于 fa 等于 fb, 那么最大值和最小值不可能在端点出现。那么我们不妨假设最大值在 中间出现,那么则由于费马定点, fx 有最大,在可 c 处有最大者,所以这一点倒数一定等于零。 要注意,你路耳中的三个条件是缺一不可的。如果其中的任何一个不满足,这个路耳中的你有可能不成立。例如,如果函数 fx 在十一点处间断, 那么他一定不存在着倒数等于零的点。第二个,如果函数 mx 在 c 出不可倒,那么他也是不可能存在着倒数等于零的点。如果两个端点的函数 数值不相等,大家通过这个图可以看到也不存在着倒数等于零的点。所以我们通常说努尔终等的三个条件是一个充分条件,但他不是必要的。 又如何使用落尔中地理的由落尔中地理的结结论我们可以看到,由于存在着某一点的导数等于零,所以实际上我们就可以得到 判定一个函数在这一点是否存在着注点,或者说是否存在着 倒数等于零的点。如果看到一个方程的话,实际上可以看到一个倒还是方程是否有根。例如这 abc 是 任意的常数 a 四倍的 ax 放加上三倍的 bx 方加上二 c, 最等于 a 加 b 加 c。 要得证明这个方程至少有一个小于一的正根。由于要证明方程有根,所以我们通常情况下构造一个函数,而构造一个函数。我们说前面有一个零点定理,曾经讲过, 可以使用零点零来证明方程是否有根。而更有根据导函式方程,我们可以用使用路耳中的点算。所以我们各位可以构造一个函数 fx 等于 a x 字棒加上 b x 二字棒加 c x 平方减客户 a 加 b 加 c x, 然后验证 这个函数是否满足入耳中的条件。很显然,由于这些都是初等函数,而初等函数在必须兼施连续开局,兼施可打猎。 而这个函数在两个端点的函数值,大家知道把零带进去结果等于零,把一带进去,结果也是零。所以我们同桌在函数在两个端点的函数值相等,那么由落而终点点可以得到至少成了一点可信, 属于零一。在这个世界上,这人倒数一定等于零,这样就能证明了。可这就是这个方程的 跟逆入 fx 在 ab 区间上联系。在开区域。是啊, 可打的两个端点的函数值相等,要么证明存在一点可税,使得这一点的倒数值等于这一点的函数值。 而刚才我们这边的一个是一个具体的函数,现在呢?是一个抽象的方程。 第一个抽象发展也可以使用刚才我们说的构造一个圆函数,那么又如何通过这个方程来构造圆函数呢?我们知道如果你把瞌睡换成 x, 如果你把可这也换成 x, 这样十一难就相当于够了一个方程啊。那么就想这个函数,或者说这个方程的左边是哪一个函数的导数呢? 我们可以在两边都乘以一的负一个视频啊,当乘以一的负一个视频,大家可以看着这个函数,正好可以看的是一的负 x 乘以 fx 导数。那么好了,那我们就构造这样一个函数, 这函数 fx 是等于一点负 x 成为 fx, 然后验证这个函数是否满足入耳中国定的三个条件。 很显然,由于小 fx 在必须联系开区间可到伊的 fx 是一个具体函数,所以我们说这个函数应该满足 洛尔重力前两个条件。那么施罗马中第三个条件呢?我们来可以把 x 得可得, x 得 a 或 x 等于 b 带入海市中心。可以看出来 f, a 和 f, b 都等于零。两 这个函数就满足入耳中国定理的三个条件。存在着一点可税,使得这点导数一定等于零。然后把这点导数等于零带入到函数中间去,就可以得到这个方程。 由于一的负可税是永远不等于零的,所以我们得到指望成。 所以我们就说落耳中的你他可以来证明方程是否有根。但是我们说的构造一个函数,他构造的是一个元函数。 而原函数的构造就要大家使用一下导书里面的一些具体的表达式。而在很多求导过程中间,我们需要大家记住一些 求道理以后的心事。
44土木人小涛哥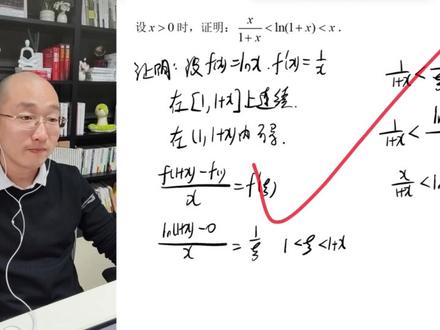 04:30查看AI文稿AI文稿
04:30查看AI文稿AI文稿刷证明题之前一定要知道题眼在哪,这样的刷题才有效,知道了题眼就知道了解题思路,挑战一分钟讲明白数学第四十八天,咱们期末考试啊,有一个特点,如果说是这种三册的不等式,一般情况下用的都是拉格朗日终止, 那拉个朗日中日定理他有一个特点,他就是一定要有一个相同应试的减法。我们来回忆一下啊。拉个朗日中日定理说的是这个样子,叫做 b 区间连续开区间可倒,然后能推出来 f e 接到可 c 等于 f b 减 f, a 比上 b 减 a, 体验就在这两个 f 相减,就叫做相同映射的减法。 f 我们叫函数,也叫做映射,哎,中间是一个减号,所以叫做相同映射的减法。我们举个例子,比如说平方叉,平方叫做映射,叉叫做减法,所以他就叫相同映射的减 减法。 a 方减 b 方叫做相同应设的减法。再比如说根号 a 减根号 b, 也是相同应设的减法。再比如说 乱方 a 减去乱方 b, 也叫做相同应酬的减法。在咱们的期末考试里边,比较爱考的是乱 a 减去乱 b, 但是往往题目里边你看不见乱 a 减乱 b, 他的出题方式就是把这个式子有可能会写成乱 a、 b、 b, 这是第一种,之前我们讲过一个视频,你可以往前翻。还有一种,他只给你写一个 log, 那另外的一个 log 去哪了呢?他其实把它隐藏了,他为什么隐藏呢? 因为他是要写成浪一的,浪一等于零,他可以不写,那他怎么隐藏的,我们就要怎么给他拿出来来这道题我们写一下证明,写证明题之前我给你们分析一下啊,看这是不是浪一加 x, 其实他这道题并不是浪一加 x 中间这个部分应该是乱一加 x 减去乱一,这个就叫做相同应设的减法了。好,你看这是不是叫做 fa 减去 fb, 那如果我们再除上一个 a 减 b, 是不就是这两个东西相减,是不叫做除以 x? 它的结果等于什么呢?是不等于 f 一接到可塞,那 f。 同学们,好,我们是不叫做相同映射的减法,我们要把这个映射拿出来,那这个映射 fx 是不是就等于浪 x? 好,那你告诉我, f 一接到 x 就等于 x 分之一吧, 所以 f 一接到可 c 就等于可 c 分之一吧。我们就按照这个思路往下写解题过程来。同学们,从上往下写叫做我们的解题思路,从下往上写叫做我们的解题过程。我们是不是应该这么写辅助函数出来设 f x 等于浪 x, 好写, 写完了,这个紧跟着两句话, b 区间连续开区间。可导,那你这个区间应该写谁呢?你看啊,我们是不是要写成浪一加 x 和浪一,所以我们就要这么写,在一到一加 x 上, 连续在一到一加 x 内得到。有的说,老师,这个 x 是谁呢? x 是大于零的。哎,我们只需要把一带入进去,一加 x 带入进去,你看是不就能得到 f 一加 x 减去 f 一比上他俩的叉是不是就是 x 等于的就是 f e 接到可 c 了吧?接下来我们就计算就可以了, f e 加 x 就等于 low e 加 x, f e 就等于零。把一带到这里面,其实就是等于零,分母是 x, 那么把 x 给它往里带,等于 f 一击倒可 c, 我们在这写一下, f 一的倒等于的是 x 分之一,所以 f 一到可 c 就等于可 c 分之一,那么可 c 是处在谁到谁之间,因为我们是在 f 一加 x 和 f 一就是在这两个点之间,或者你也可以直接看这,所以它就处在一到一加 x 之间。好,那这面的 解题思路我就给它去掉了,那么这里是不就有一个不等式了?因为题目里面写的是可 c 分之一,所以我们就要求一下可 c 分之一的取值范围,那就把它取到数了,那这两个也要取到数,并且这两个位置也要交换,那就变成了一加 x 分之一,分之一, 这面就是一分之一,一分之一就是等于一的。再然后我们把可 c 分之一给它写成这个样子即可,就变成了 lone, 一加 x 比上 x 来,左边就是一加 x 分之一,右边就是一。写完 完这个式子之后,你观察一下我们要证明的结论和我们写的式子有什么不同,不同点就在于这个中间没有 x, 所以我们要在不等式的三侧同时乘 x, 那就变成了一加 x, 左侧就是一加 x, 分成 x, 右侧就是 x。 你看看这道题是不是直接就证明出来了?做完。
973高数不高-刘赫
猜你喜欢
- 1.9万韦奈奈এ
- 85.9万GGBond的小课堂
















