八上数学轴对称剪纸问题怎样做
粉丝8250获赞2.4万
相关视频
 10:36
10:36 03:32
03:32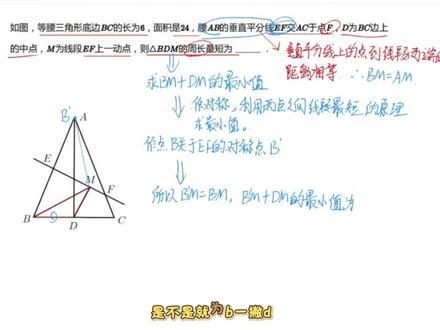 17:35查看AI文稿AI文稿
17:35查看AI文稿AI文稿一节课趁早加上数学第三次月考球对称对决问题二,掌握所有必考点和难点,学完轻松秒题。一,整个题十分,所有笔记已经给大家整理好了,话,接上一个视频,这节课我们继续精讲轴对称模型例题,大家有什么问题可以发在评论区里面啊。 好,那我们这题就先过了,那我们看,接着看第二个例题, 来,我们一起读下题吧。他说,如图,角 a, o, b 等于三十度点 p 位于角 a, o b 里面, o, p 等于三点 m, n, 分别是射线 o, a, o, b 上的动点。要我们求什么?要我们求这个三角形 p, m, n 的最小值,那我们看一下, 我们要求这个三角形的最小最小周长吧,周长的最小值吧,哎,那是不是我们这个模型啊,类似于我们的这个这个模型吧,对吧?那我们看我们这个模型怎么处理的,是不是分别做对称点, 分别关于这个 l 一和 l 二做对称吧。好,那我们这题让我们也就和那个模型,那样我们就倒着我们那个模型做, 那么怎么做呢? 那我们就是先分别做点, 我们我们要求出他的最小周长,我们 首先得把最小的周长的这种情况给画出来吧,对吧?那所以说我们先把这个最小的周长这种情况画出来,等下我们分别分别做 点 p, 关于 o a, 关于 o b 的 对称点 cd, 然后我们连接 cd, 连接 cd, 分别交 o, a, o, b, 迷恋 m n 吧。好,然后我们连接, 然后我们连接我们的这个 o, p, o, c, o, d, p, m, p, n。 好了,我们看, 那我们先连接一下吧。首先我们要做点 p 关于 o b 的对视点, 点 p 关于点 p 关于这个 o b 的对线点,那这个撇一撇吧, 大概是就是在这个位置吧。而我们这个,呃,点 p 关于 o b 的对线点是这个 c 吧,我们就取为点 p 关于 o a 的对线点,我们这个点就取为点 a 吧, 啊?点 c 啊,然后上面这个点我们就取为点 d 吧。 好,那我们到这一步,我们看,那我们看怎么,那什么时候他是这个最小的呢?是不? 这是我们直接连接 cd 的时候,对吧? 对吧?好, 那然后我们继续看,然后因为我们这个点 p 关于 o a 的对称点, 因为点 p 关于 o a 的对线点为 c 吧,关于 o b 的对线点 为例吧,那所以说我们的这个 pm 就等于 c m 吧, o p 就等于 o c 吧,我们这个角 c o a 就等于角 p o a 吧,对吧?对吧? 那是,那然后又因为什么呢?然后又因为我们这个点 p 关于 o b 的对线点 为 d 吧?是不是为 d? 好了,为 d 的话呢?它们中间有关于这个 o b 的中心点为 d 的话,那我们所以说我们这个 p n 就等于 dn 吧,然后 o p 就等于 o d 吧,然后我们的这个角 d o b 就等于角 p o b 吧。好,那所以说我们的这个 o c 就等于 o d, 等于 o p, 等于三百,对吧? 好,那所以说我们是不是就可以求出,所以说我们这个角 c o d 就等于 角 c o d 的话,是不是就等于角 c o a 加角 p o a, 加角 p o b, 然后加角 d o b 就等于什么呢?就等于二倍的角 p o a 加二倍的角 p o b 吧,那是不是就等于二倍的角 等于六十度吧?哎,那它等于六十度,那所以说,那所以说我们这个三角形 c o d 啊, c o d 啊,我们这里连接一下,所以说我们这个三角形 c o d 的话, 所以说我们这个三角形 c o d 的话,它是就是等边上, 为什么, 对吧?好,那所以说我们是不是就可以得到 c d 等于 o, c 等于 o d 等于三吧? 好了,所以我们这个三角形 p m n 的周长最小值, 周长最小值,是不是就是应该是等于 p m 加 p n, 然后加 m n 吧, 然后就是等于我们的这个 c m 加 m n 加 d n 的吧,那应该是大于等于 大于等于 c d 吧,那也就等于三吧。那所以说这个周长最小的周长就是多少呢?最小的周长的话,那就是我们的这个三吧。啊,那这个三就是我们的最小周长了。 好,那同学们可以截个图啊,如果说还有什么没弄明白的问题,欢迎发在评论区讨论啊。 好,那我们来看。接着来看第三条第三题,他说如图,等腰三角形底边的边长为六,面积 是二十四幺 a b 的垂直平分线, e f 交 a c 于点, f 点 d 为这个 b c 上的终点, m 为线段, e f 上的一个动点。好,那这个题要我们求什么呢?他说折三角形 b, d, m 的周长最短为多少?我们看一下三角形 b, d m 哎,三角形 b, d m 的周长最短,那是不是这个三角形啊?对吧? 那么看这个题,我们先明确一个问题啊,它要我们求这个三角形 b, d, m 的最长最短吧,那我们看一下,是这个红色的,这才三条,三条线段吧。好,那这三条线呢?我们发现一个什么问题呢?是不是这个 b d 的话是定值吧,对吧? 那我们是不是可以就把这个求三角形 b d m 的周长最短转化,为什么呢?转化为求 b m 加 d m 的 最小值吧,可不可以转化为,可不可以转化为这个, 对吧?因为我们 b d 是固,因为 b d 是定值吧,那所以说我们就可以把这个求三角形 b d m 的周长最短转化为求 b m 加 d m 的最小值吧。 那我们把 b m 加 d m 这最小值求出来之后,我们是不是这个周长最短已经能求出来了?好,那,那求 b m 加 d m 的最小值,那我们怎么办呢?是不 做对称就行了,做对称 然后利用什么呢?利用两点之间线段, 现代最短的 求最小值吧,对吧?好,那我们看怎么做对称? 我们观察一下,那我们是做点 b 的对视点还是做点 d 的对视点啊?哎,我们发现这里,我们看发现一个什么问题啊? 他说这个幺 a b 的垂直平分线吧, e f 吧。哎,那就说明我们这个 e f 是幺 a b 的垂直平分线吧。哎,那垂直平分线有什么特点?垂直平分线有一个重要的特点啊, 垂直平分线上垂直平分线上的点到脚两到脚两边的距离相等吧,就说垂直平分线上的点到到线段两端的距离相等吧, 对吧?垂直平分线上的点到线段两段的距离相等吧。那这又意味着我们这个, 那我们是不是就可以根据垂直屏幕线的这条性质推出什么了?那所以说我们这个 b m 是等于 a m 的吧,对吧?那 b m 等于 a m, 那我们垂直平分线我们之前有说过吧?垂直平分线是天然的轴对称模型吧?那我们因为,因为我们这个 b m 始终等于 a m, 那我们是不是就可以 把点 b 对称过去?那点 b 的对称点点 b 关于 e f 的对称点,是不是就点 a 了?对吧?那所以说我们这里的话,那就怎么了?那就是做点 b 关于 e f 的 b 撇,那这个 b 撇的位置是不是就是在点 a 这里,对吧? 好,那什么时候他们就选了,那是不是我们直接,直接连接,直接连接 b, 一撇 d 就行了,对吧? 那所以,所以,那我们的这个,所以我们这个 b e p m 就是等于 b m 的吧? 那这个 b e 撇 m 加 d m 的 它的最小值就为什么呢?是不是就为 b 一撇 d, 那也就是等于 a d 的吧,对吧?好,那所以, 所以我们三角形 b d m 的周长 最短,为什么呢?最短的话就是不相当于等于 a d 加 b d 吧,因为 a d 的话,这个我们这里求的是最短的情况吧, 对吧?那最短的情况下,是不是相当于就是为 a d 加 b d 啊?对吧?好,那么那我们现在是不是只要求出 a d 就行了?现在只要求出 a d 就行了吧?好了,我们看怎么求出 a d 啊? 哎,他这里是不是说底边长为六,面积是二十四吧,那我们这个 a d 就相当于就是高吧, 对吧?那就因为二分之一 e c 乘以个 a d 是等于 二十四吧,然后 b c 是等于六的,那所以我们可以解得 a d, 可以解的 a d 就等于八吧,对吧?所以解的 a、 d 等于八,然后 b、 d, 然后这个我这里再加一个,然后我们 d 为, 那所以说我们 a、 d 等于八,然后我们 b、 c、 b、 d 的话, b、 d 的话就等于二分之一乘六吧,就等于三吧,哎,那所以说我们这个 a、 d 加 b、 d 的话就等于八,加三等于十一吧,对吧?好,那所以说,那所以说我们 这个题的结果就是什么呢?哎,那所以说我们这题结果就是十一吧,对吧?那我们是不是就间接的求出我们这个三角形 b、 d、 m 周长的最小值了吧? 好,大家看还有什么疑问没有?有疑问的话大家可以发在评论区里面, 大家一定要把这个思路理清楚啊。其实这个求周长最短问题本质上就是求这个线段线段和最短的问题啊, 求周长最短的问题就是求,其实你,你好好看一下,本质上其实也就是求我们线段和最短的问题啊,也就是我们一开始学的那个, 就是我们一开始学的那几个模型啊。好,那我们这节课就先到这里了。
46刘哈哈数学















