初二几何格点问题
粉丝9857获赞1.0万
相关视频
 01:49查看AI文稿AI文稿
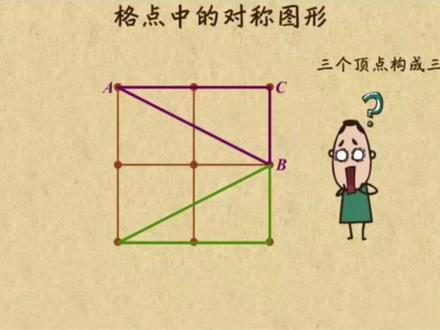
01:49查看AI文稿AI文稿这个视频我来讲讲格点中的对称图形,比如,我让你在这个格点中找三个顶点,构成一个三角形,使得这个三角形与 abc 轴对称,你会画吗? 哎,有小伙伴随手就画了一个,果然符合要求。找出一个的确不难,难的是找到所有的情况,你还有办法吗?嘿嘿,我来教你吧!你想想, abc 的顶点都在格点上,所以对称点也在格点上, 咱不妨以 c 点为例,看看他的对称点位置有可能在哪。如果 c 撇在这,那这两点连线的垂直平分线就是对称轴,对称一下显然不行。 那 c 一撇在这,这一条就是对称轴,对称一下,哎,符合要求。 c 一撇在这,那这一条就是对称轴,对称一下,这卡 来不行。如果 c 一撇在这,那这条就是对称轴。对称,哎,符合要求。接着看, c 一撇在这,他就是对称轴,对称一下还是不行。 c 撇在这,这个就是对称轴,对称一下,哎,符合要求。再看这,如果 c 撇在这,那他就是对称轴,还是对称也符合要求。 好了,数数看,一共有四种情况,符合要求。全了吗?嘿嘿,当然没有喽,如果 c 撇在这个位置,就有这个三角形,符合要求。注意喽, c 撇和 c 重合的情况千万不要漏掉,加上这个一共是五个三角形。 好了,总结一下,在格点中找轴对称图形,你就先找到某个顶点的所有可能对称点,利用对称点找到对称轴,逐一媒体就能数出答案。另外提醒一下,不要忘记对称点还是本身的情况怎么样,明白了吗?明白的话就速速去刷题吧!
108布尔学习法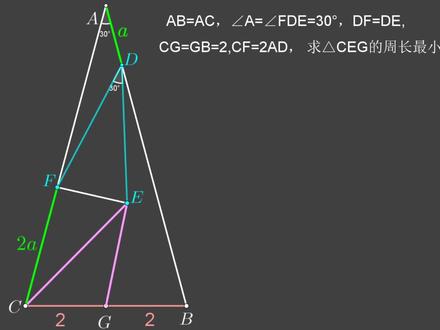 04:26查看AI文稿AI文稿
04:26查看AI文稿AI文稿这是锦江师大一中初二必卷填空的一道压轴题,我们先来看一下题目意思, abc 是 一个等腰三角形, ac 等于 ab, 角 a 等于三十度, d 和 f 分 别是 ab 和 ac 上的两个动点,且满足 cf 等于二倍的 ad。 再将 d、 f 沿着 d 点逆时针旋转三十度,得到了 d e, j 是 b, c 的 中点连接, c, e 和 j, e 要求 c g e 这个三角形周长的最小值, c、 g 的 长度,它等于二,是固定不变的。实际上我们只需要去算这两条紫色线段和的最小值。那首先我应该去想 e 点的轨迹是什么?如果 e 点的轨迹是在一条直线上,那这不就是将军引马吗? 怎么去证明这个 e 点的轨迹呢?是这道题的一个难点。首先可能有同学认为啊,这是一个刮豆原理,其实它并不是啊,因为这个 d 它是一个动点,它并不是一个定点。如果这个 d 是 一个定点,那么这个题它就是属于刮豆原理的题型。 可以先把 b、 e 给连接起来。在 ab 的 这一侧出现了两个三十度角,并且 f、 d 和 e、 d 是 相等的, 所以这里考察对一线三等角全等模型的一个知识点,这里给大家展示一下啊一线三等角全等模型的一个证明过程。所以接下来可以在 d、 b 上截取一点 h, 使角 e、 h、 d 等于三十度。 因为角一加角二等于一百五十度,角二加角三也等于一百五十度,所以角一就等于角三 三十度等于三十度, df 等于 d、 e, 所以 就可以证明出这两个三角形全等。这两个三角形全等就有对应边相等,所以 af 等于 h d。 假设这两条边记作 b, 又因为 ab 等于 ac, 而 ac 等于二, a 加 b, 那 么 ab 也应该等于二, a 加 b, 所以 就可以求出 h、 b, h、 b 的 长度,就是 a。 因为全等,所以 a、 d 等于 he 也等于 a, 所以 就可以得到三角形 h、 e、 b。 这是一个等压三角形,在这个等压三角形中,因为它的一个外角是三十度,所以这两个底角都是十五度。 就因为在 a、 b、 c 这个等腰三角形中,我们可以算出底角是七十五度,从而算出角 e、 b、 c 等于六十度。因为 c、 b 这条线段是一条固定的线段,而角 c、 b、 e 等于六十度, 说明 e 就 在 b、 e 这一条射线上运动。我们可以来看一下运动的一个过程, 现在就变成了将军引马问题要计算二,加上这两条紫色线段合的最小值,需要去做对称,选 c 或者这点其中一个点,去做 b、 e 这条射线的一个对称点,这里我选择这点去做 b、 e 的 一个对称点, 这一始终等于这一撇儿 e 现在所求就转化成了二加上 c、 e 再加上 e 这一撇儿。当 c、 e 这一撇儿这三点共线的时候,取最小值,也就是要运动成这个样子的时候最小。 为了大家看的更清楚,我把这个部分进行放大,接下来求出 c 这一撇儿。 因为是翻折过去的,或者说这两个三角形全等,所以 b 这一撇等于 b j 等于二, 并且角 e、 b、 j 也等于角 e, b、 j 等于六十度,所以角 c、 b、 j 一 撇,这个角合起来就是一百二十度。遇到一百二十度的时候,它的补角是六十度,是一个特殊的角, 所以可以过这一撇去做 c b 这条直线的一个垂线,构造直角三角形。 三角形 b m 这一撇是三十度、六十度、九十度的直角三角形。三边比为二,比一比根号三,所以 b m 等于一, m 这一撇等于根号三。最后求 c g 一 撇。在这个直角三角形中,利用勾股定律求斜边。最终答案为二,加上二倍的根号期。
 04:47查看AI文稿AI文稿
04:47查看AI文稿AI文稿哈喽,大家好,我是石老师,今天我们来学习一次函数几何压轴问题。对于一次函数,很多时候啊,大家对于简单的图像性质都是有所了解的,但是一旦它涉及到特殊图形的存在性,很多同学就无从下手,那我们今天就来讲其中 一个特殊图形的涂在线,是什么图形呢?是等腰三角形。我们就来看一下,当一次函数它和等腰三角形结合起来考察的时候,我们应该怎么去处理 好。首先我们还是边读题边翻译题目。在平面这条坐标系 x o y 中 o 是 坐标原点直线 y 等于五分之十二, x 加十二,与 s 轴交于 a, 与 y 轴交于 b, 也就是说 ab 这条直线是 y 等于五分之十二, x 加十二, 那 b 点它的坐标我们就知道了,是零到十二,对不对?好,那 a 点的坐标我们也能读出来是负五到零。 现在若点 c 在 坐标轴上,哎,他说在坐标轴上有没有说是 s 轴或者是 y 轴呀?没有对不对?所所以说明这个坐标轴 s 轴也是可以的, y 轴也是可以的。且三角形 abc 是 以角 abc 为顶角的。等腰三角形 a、 b c a、 b c 这个角为顶角。等腰三角形啊,这个角为顶角,那谁是底角呢? b a c 和 b c a 对 不对?也就是说它的隐含意思就是这个等腰三角形里边, b a 它等于 bc, 对 吧?好,它是等腰三角形,则 点 c 的 角坐标为多少?好,那此时我们来看一下,既然要求 b a 等于 bc, 那 我们是不是就可以看作以点 b 为圆心,以 b a 长为半径的一个圆, 哎,我们做一个圆,我们看它和坐标轴交于哪些点,是不是就可以了,对吧?好,这时我们找等腰线和思路,首先我们要知道 谁和谁是相等的,找到谁和谁相等,我们就可以。嗯,把它转化成以它为圆心,然后他们的长为半径做一个圆,然后和如果说在这个坐标轴上有焦点,那这个焦点就是他的另一个动点。 好,那你看 o a 长度是五, o b 长度是十二,哎,勾股定律,我们知道 b a 长度就是十三,那我们此时现在就以点 b 为圆心,以十三为半径做一个圆,它会是得到什么样子呢?做一个圆,大概是 大概,它它它,它是不是大概应该是这个样子啊?这个圆做的可能不太不太规范, 这表格可能有一些不太规范,大概是这个样子的,对不对?好,那我们来看一下它和它到底有哪些焦点呢?首先第一个焦点 很明显是在这点,对不对?对称过来的,然后它这个是十三,那它这个也应该是十三,十三,十二,这是十三,这是十二,那这里就应该也是五,所以说点 c 的 第一个坐标就诞生了,就是五斗零,对吧? 那我们来看点 c 的 第二个坐标呢?哎,我们一直向上,向上,所以我们发现它和外轴有一个交点在这里,对不对啊?好,这是 c 二,这是第二个点坐标,我们发现啊, c a b a 等于 bc 二,是不是?然后他们又是一个等腰三角形,它是十三,那这里也是十三了,对不对?好, 因为这时候我们知道 c 二和 b 之间的距离是十三,并且呢, b 的 坐标是零到十二, c 二在它的上面,那就是十二,加上十三应该就等于二十五,所以说 c 二的第二个坐标就是,哎,零到二十五。 好,接着我们继续检查,哎,他过来,过来的时候是不是和 x 又有一个焦点,但是此时这个焦点是 a 点,再过来的时候他和 y 轴又有一个焦点,对不对?我们令它为 c 三,那此时我们发现 b a 是 十十三,那 bc 三也是十三,对吧?那 b 的 坐标是十二,零到十二,那我们知道 十二减去十三,它就等于负一,所以说 c 三的坐标就找到了点, c 的 三个坐标是 五到零,零到二十五和零到负一。好,这就是一次函数和等幺四幺形结合的时候。我们的方法是什么呢?就是看他的 让他让,看他是以谁让,哪两个边是相等的,哪两个边相等,那我们以这个公共点为圆心,然后以他们已知的边长为半径,然后作圆,然后去找他这个动点 c 就 可以了。好吧,同学们听明白了吗?
19初中数学史老师
猜你喜欢
- 6393王老师爱叨叨
















