河南高考立体几何真题及答案
关于例题几何大题,与其花时间研究那些偏题、怪题,还不如把历年的高考真题做一遍。学长给大家整理了二零一六年到二零二零年的例题几何大题包含解答过程,有想法的同学可以做一遍,高考之前最好做三遍, 做完之后总结每道题的知识点和解析方法,并做横向比较。这是拿下例题几何大题的一个好办法。 风雨花丛中,未必 在遥远天 边 one time high。
粉丝34.1万获赞330.2万
相关视频
 00:57查看AI文稿AI文稿
00:57查看AI文稿AI文稿河南本月最重要的两次联考,一次是青铜名大联考,一次是这份 top 二十名校联考试卷,难度低于青铜名,主要难题几乎都集中在立体几何题上,所以这份试卷比较适合近期立体几何丢分较多的中档生进行巩固提升练习。 单选压轴第八题是一道值得积累的球类问题,几何法分析可以间隙用坐标计算也可以,后者计算量更大。多选题中,第十题是一道不错的平面向量与三角函数结合的基础题。 第十一题以空间四棱锥为在体,结合空间向量求解线面角和二面角涉及参数 k 的 不同,曲值计算量较大,对空间坐标系构建合法向量求解能力要求高。中上难度 填空题第十四题是双曲线与两条平行角已知的直线相交,求三角形面积,需先求焦点坐标,再利用直线垂直关系判断三角形形状,有创新性。 对于本次试卷的大题来说,最值得做的是第十七题,此题是一道十分简洁的空间几何好题。第二问使用间隙和三角函数射速标进行计算。最后两道压轴大题都比较常规。
131高考升学资料库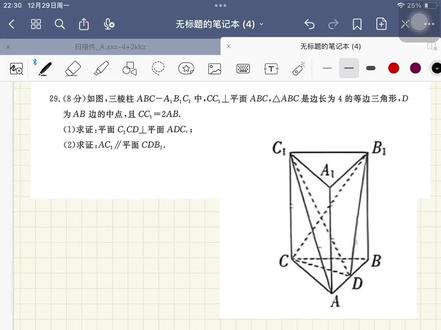 04:06查看AI文稿AI文稿
04:06查看AI文稿AI文稿hello, 同学们,大家晚上好,今天晚上给大家更新一期例题几何。那么今天这个题目呢?第一问是让你证明一个面面垂直,第二问是证明线面平行。先来看题目中的已知条件, c、 c 一 垂直于 abc, 这个是线面垂直,那么根据线面垂直的定义,我们知道 c、 c 一 就会垂直于底下这个面的任意一条直线啊,这个后续我们要用到的。好。第二个,这个三角形是一个等边三角形,并且 d 是 终点 哦,这个等腰三角形顶点和我们中点的连线,是不是和我这个底边是垂直的关系啊?好,先来看第一问,那么根据我们刚才的这个推论啊,因为三角形 abc 为等边 三角形,并且 d 为 ab 中点, 所以我们知道 a、 d 是 不是就是垂直于 c、 d 的? 我为什么要写 a、 d 呢?因为你看现在这个,如果把 c、 c、 d 看成是一个平面的话啊,那么我这个 a、 d 好 像就像是它的一条垂线, 我要证明 a、 d 是 它的一条垂线,仅仅只垂直于 c、 d 是 完完全全不够的。因为线面垂直的判定定理要求我们要在这个平面内找到两条相交的直线和它垂直,是不是才可以啊?所以我们又可以再用到第一个条件。哎,就是说我们刚开始说的 c、 c 一 垂直于平面 abc 啊,那么又因为我这个 a、 d 它是不是包含于平面 abc 的 啊?平面两字我省略没写啊,那所以说 这个 c、 c、 e 就 垂直于我们的 a、 d。 好, 你看现在的两个条件哈,一个是 a、 d 垂直于 c、 d, 一个是 a、 d 垂直于 c c、 e, 这两条线是不是都是我的平面 c、 c、 d 上的,并且它俩还相交啊?又因为 c、 d 交上 c、 c、 e 于点 c, 并且呢,这个 c、 d、 c、 c、 e 都包含于平面 c、 e、 c、 d 啊,所以我们就证明了 a、 d 啊,它是垂直于 c、 e、 c、 d 的, 或者说 a、 d 就是 这个平面的一条垂线哦,既然垂线找到了,那过这条垂线的任意一个面是不都和这个平面是垂直的?嗯,那你看,现在我这个 a、 d, 很 明显它是包含于平面 a、 d、 c、 e 的 好,所以就证明了我们的题目 c、 e、 c、 d 啊,是垂直于 a、 d、 c、 e 啊。你在书写的过程中,一定要把这个平面两次加上哈。好,这第一问 好,再来看第二问,第二问呢?是线面平行。那根据线面平行的判定定律,我们知道,要想证明一条线平行于一个面,我必须在这个面内找到一条线和它平行才可以啊。那么现在呢,没有现成的这个平行线,所以我们要去做一个辅助线。 做辅助线有两个原则啊,一个是连对角线,再一个就是去构造中点,去找三角形的中位线。好,现在很明显还有一个正方形的对角线没有连起来啊,那就是 b、 c、 e。 当我连接这条对角线之后, 它与 b、 e、 c 相当于点 o, 这个点 o 是 不刚好是一个中点啊?那你再去连接你的 o、 d 的 时候,会发现它这个 o、 d 刚好就是三角形 a、 b、 c、 e 的 中位线。好 连接 b、 c、 e 啊, b、 c、 e 交上 b、 e、 c 于点 o、 o 为,嗯,谁的终点? b、 c、 e 终点,又因为 d 为 b a 终点, 哎,所以这个 o、 d 是 不是就是平行于 a、 c、 e 的 好,下面平行除了平行之外,我还要写一个不包含,一个包含好。又因为 啊,我这个 a c 一 啊,它不包含于平面 c, d, b 一, 但是 o, d 包含于平面 c, d, b 一, 所以就证明了 a c 一 啊,平行于平面 c, d, b 一。 这就是这个题的一个完整的解析步骤。
113小脸喵讲数学 02:10查看AI文稿AI文稿
02:10查看AI文稿AI文稿为什么高考选择题全蒙 c 居然比你瞎算正确率还要高呢?真相很简单,因为高考选择题机器阅卷,只看答案,对了就得分,试过的都懂,考试遇到不会的选择别慌,今天教你数学选择题超绝秒杀大招,即学即用,学霸埋头算半天,你五秒就能出答案,啥都不会也能白捡二三十分,基础烧好直接杜绝马虎式分, 直接上干货。碰到两条件推结论的题,不用画图,不用做辅助线,一招秒杀!先记牢例题,平行线面平行面面平行 线线垂直线面垂直面面垂直。再分清强弱定律,阶梯直接套。结论,同类平行是线线平行面面平行为强定律。异类平行是线面平行为弱定律。异类垂直是线面垂直为强定律。同类垂直是线线垂直面面垂直为弱定律。那核心结论,双强得强,一强一弱得弱,双弱必错来看高考真题, 比如这道高考真题, a 选项 l 平行阿尔法 l 平行那么大,都是一类平行弱定律,双弱必错。 b 选项 l 垂直于阿尔法 l 垂直于那么大,均是一类平行强定律,双强得强 b 正确 c 选项 l 垂直于阿尔法强定律 l 平行于那么大弱定律,一强一弱该得弱。结论, 阿尔法平行于阿尔法弱,双弱一错。答案直接选 b。 再来一道 a 选项 m 平行阿尔法 n 平行阿尔法双弱定律 b 选项 m 平行阿尔法 m 平行那么大 s 双弱 b 错 c 选项 m 平行 n 同类平行强定力垂直于阿尔法 e 类垂直强定力双强条件。结论, n 垂直于阿尔法 e 类垂直强定力,双强得强 c 正确 b 选项 m 平行阿尔法弱定力,法则垂直于那么大弱定律双弱 b 错,答案就是 c。 接下来我们上一点强度这类题,让你用两个论断做条件,下一个做结论。写正确命题,照样秒减。先判三个论断强弱,一 l 垂直于 m 类垂直弱定力。二 m 平行阿尔法 e 类平行弱定力三 l 垂直阿尔法 e 类垂直强定力。牢记两弱一错的逻辑,只能用一强一弱推,另一弱 直接秒出二加三推一或者一加三推二秒出正确答案。这不是超简单的,我已经整理好高考常考的八十多个秒杀模型,覆盖向量、含 数、圆锥曲线等所有高频题型,每个模型都配了真题加描卷步骤,考场直接套着用。想要学习的同学后台告诉我,你的年纪。进入高三加数学,最后高考一分压千人,一分钟都不能浪费,只要找对方法,越难的题越有捷径。每天吃透一个秒杀模型,数学想练习真的很简单,一定要抓紧去!
201高考提分易老师 30:17查看AI文稿AI文稿
30:17查看AI文稿AI文稿看解答题的第十七题,考的是空间立体图形吧,我们在初中的时候啊,是不是喜欢考平面图形, 在平面中考线线平行是吧,线线垂直,求线段的长度,然后考察三角形全等啊,三角形相似等等,这初中选考的内容,那高中时候呢,就喜欢考空间图形, 空间图形主要考察线面平行,线面垂直,面面平行,面面垂直,然后选考二面角等等。那这一题呢,主要是考察是线面平行和二面角。 我们先看第一题,第一小问啊,第一小问,若 a, d 啊,垂直于 p b, 证明 a, d 平行于平面, p b, c, a, d 平行于平面 p b, p d, c, p b, c 这个平面 p b, c, 然后 a, d 啊,是这条线,我们看一下题目吧,我看一下那个开头,那个开头给了哪些条件吧,这个四等锥把 p a, b, c, d, 然后 p a 呢,是垂直于底面 a, b, c, d 的 p a 啊,垂直于底面 a, b, c, d, 那 么 p a 就 垂直底面上的任意一条直线吧。 然后 p a 等于 ac 等于二, p a, p a 等于 ac 等于二,等于 ac 等于二 pb 啊, bc 等于一, ab 等根号三, bc 等于一, ab 啊,等于根号三。根据这个条件啊,根据这个条件,我们能够求出啥?这不角 b 等于九十度啊, 根据这个条件和这个条件, a, c 等于二,我们能够得出角 b 等于九十度,角 b 等于九十度。根据勾股定律,角 b 等于九十度,是吧?然后我们再来看,若 a, d 啊, a, d 垂直于 pb, a, d 垂直于 pb, a, d 垂直于 p p b, 这这这个这长的 p b 证明 a, d 平行于平面 p b, c 这题啊,是不是很明显用到线面平行的判定力里啊, 就是这平面外的一条直线啊,与平面内的一条直线平行吧,那么这条平面外的这个直线是不是平行于这个平面?所以我们就要找和 a、 d 平行的一条在这个平面 p b, c 上的一条直线吧。 哇,你看这个图啊,是不是很明显啊,这个 bc 有 可能是平行的呀, bc 是 有可能平行于 ad 的 吧,那我们这时候你就要详细的看一下 bc 是 不是平行于 ad。 好 吧,我们根据已知条件,已知条件如果,那我们已知条件,我们知道了,角 b 等于九十度吧,如果,如果角这个角,这个 d, a, c, d, a, b 也等于九十度的话, 那么 ad 就 平行于 bc 了吧,所以我们主要是证明下这个角 d, a, b 等于九十度,也就是啊, d a 要垂直于 ab 吧,要证明这个这个吧, 我们如何这样?我们看这四等锥啊,这四等锥 pa 啊,是垂直于里面 a, b, c, d 的 pa 是 垂直于 a, b, c, d 的,是吧,那么 pa 是 不是垂直于 d a, 那 p a 因为啊,第一题啊,因为啊,因为 p a 垂直于底底面 a, b, c, d, 那 所以啊, p a 就 垂直于 p a 就 垂直于啊,还有个条件啊,然后 a, b 是 不是含有这个皮底面? 韩语这个底面 a, b, c, d, 那 么 p a 就 垂直于, 不是 ad 啊? ad ad 韩语这个底面,那么 p a 就 垂直于 ad 吧, p a 垂直于 ad, 你 再来看他题目又说了, ad 是 不是垂直于啊,又,因为啊, ad 垂直于 pb 吧, ad 垂直于 pb 这条斜的线,那所以啊, ad 就 垂直于平面, 啥 ad 啊,就垂垂直于平面 p a b 哇,用英文啊,英文 a b 是 不是韩语?平面 p a b 那 所以啊, a d 就 垂直于 a b 吧。 好吧, a d 垂直 ab 哎,这个条件怎么是算求出来了啊?那又因为又因为啊,角 abc 等于九十度啊,是根据勾股定来的吧?这是根据勾股定律算出来的吧。 那所以啊,就所以啊,就 a d 就 平行于 bc, 对 吧?平行于 bc, 那 又因为又因为啊,又因为 bc 是 不含于平面 pbc 是 吧? a d 啊,不含于平面 pbc, 那 所以啊, a d 就 平行于平面 p b c ok, 你 就这第一小问。第一小问,先求两个线平行,然后根据判定定理求出线面平行。好,这是第一小问。第二小问, 若 a d 垂直 dc 把这个去掉,这不是垂直了?第二个 a d 啊,垂直 a d 这个吧, a d 啊,垂直 dc a d 垂直 dc。 好, 那就这个角是九十度吧, 这个角等于九十度。角 a d, c 等于九十度,且二面角 a c, p d 的 正弦值为七分之,根号四十。这个角 a a c p a c, p d 啊,这个按面角的正弦值为七分之,根号四十二。 这种怎么求呀?这不第一反应啊。第一反应是啥?这不建立空间直角坐标系啊。空间直角坐标系 为什么要建直角坐标系呢?因为这种方法可以避免,避免啊,直接去求二面角,如果你直接去求这二面角,是不是一下子很难看出来啊?一下子很难看出来。你不知道哪个角?不知道哪个角是二面角吧?你,你是不是还要去找这二面角是比较麻烦的,所以我们第一反应是用空间直角坐标系, 用向量的方法是比较简易,而且这一题啊,是不是也非常好,非常容易去做这个空间直角坐标系啊,因为很多垂直就已经告诉你了吧, 那我们这一题啊,我们就先采用第一种方法建立空间直角坐标系,好,它告诉你 a, d 垂直于 d, c, a, d 垂直于 d, c, 那我们,那我们就,我们就可以以这个为 x 轴吧,我们以啊以 d, c, 以 d, c 为 x 轴,以啊 a, d 为 y 轴, 好吧, a, d 为 y 轴,然后过 d 点,过 d 点去做平行于 p a 的 线。直线 啊,这个 v z 轴 v, z 轴,然后就过 d 点做 平行于 p, a 的 直线, 为 c 轴, c 轴为什么要做平行于 p a 的 直线啊?因为 p, a 是 不是垂直于底面 a, b, c, d, 那 么这时候 z 轴啊,就垂直于底面 a, b, c, d 吧,那这个,那这三个轴呢?就是我们想要的轴, 我们设,我们求的是 a, d 吧,我们设 a, d, a, d 等于 a, 长度等于 a, 这时候我们是不是要求各点的坐标呀?二面角 a, c, p, d, 那 我们看 a, 求 a, c, p 和 d 的 坐标吧,你看 a 点坐标等于什么? a 点坐标是不是等于零? a, 零,然后 c 点坐标, 四点坐标,我们不知道哎,但是我们知道这个三角形啊,这是 d 点,这是 a 点,这是 c 点,我们设的是哪个? a, d, 这是九十度啊,这 a, d 是 等,这不等于 a, a, c 等于多少? ac 是 不等于 ac 等于 ac 的 平方,是不等于 ab 的 平方,加上,哎, ac 告诉你了, ac 告诉你了, ac 告诉你了, ac 等于二, a, c 的 长度等于二,那么 d, c 的 长度就是四减 a 的 平方吧。好,那么 c 点坐标就是根号下四减 a 的 平方 啊, c 点,然后零零,那 p 点坐标是啥? p 点坐标是这个点就是在 x 的 轴上是零吧,那 y 轴上是不是就等于 a, z 轴上等于二吧,因为 p a 的 长度等于二, 然后 d 点坐标就是圆点,就零零零。好,我们求出所有点的坐标了,那么这时候我们先看,先看平面啊,先看平面 a, c, p, 先看平面 a, c, p, 我 们是求出两个,两个求出两个,那个向量呀, 求出两个向量吧,我们先看 a, c 啊, a, c 向量等于多少?先看 a, c 等于根号下 四减 a 的 平方负 a 吧。零,哇,这 a, c 的 坐标,再求一个 ap 吧, ap 等于 零,零二吧,零零二,好,我们设设 m i n 吧, i n 等于 x y 一 z 一 为平面 a, c p 法向量,那我们能够求出啥?求出 n 等于啥? 具体过程草纸啊,那 z 肯定是等于零, z 肯定是等于零八, z 肯定是等于零,那我们求出啊,我们假设我们令 x 等于一,那 y 就 等于是不是 a 分 之根号下四减一的平方,这是 n 的 坐标,我们再看平面 里面啥? c, p, d 吧,看里面 c, p, d, 我 们求坐标,我们选两个吧,选 d p, 先选一个 d p, d p 等于什么?零 a 二呀,再选一个 c p 吧, c p 等于 负的根号下四减 a 的 平方 a 吧,有个二,好吧,同样,我们设 m 等于 x 一 y 哦, x 二 y 二 z 二为平面 c p, d 的 反向量, 这时候我们求出 m 等于多少其中一个向量 m 零二 零二非。好吧,这是,这是 m 的 向量,我们只是求出其中一个向量,那么这时候它告诉你了这个二面角正弦值,正弦值为七分之,刚好四十四十二,那么它余弦值多少?假如这两个向量之间假说这两个向量之间假角是 r 法, 我假设这个二面角是 r 法,这个二面角是 r 法,那么 cos 还 r 法, cos 还 r 法等于啥?是不等于这两个向量? m 乘 n 比上 n 向量的长度乘以 m 向量的长度呀,对吧? 他是是吧?要准确说,我还是要打个绝对值吧。加个绝对值符号就等于把它带进来,那就是等于啊, 乘以乘以就是零零,然后就是,是不是两倍的根号加四减一的平方比上 a 就 比上这绝对值啊,这现在也不用绝对值了,因为 a 是 也是正值,然后乘以根号加 一,加上 a 的 平方分之四减 a 的 平方是不是乘以根号加 二的平方?加 a 的 平方。哇,就等于化减,上面先不动吧。四减 a 的 平方比上 a 啊,不加上这根号多少啊?一加上 a 的 平方分之四,就 a 的 平方分之四吧,因为一已经约掉了,是不?乘以四加 a 的 平方, 这等于多少?这 a 是 不是跟这约掉了?这四跟这约掉了吧,就等于根号一下四减 a 的 平方比上根号一下,四加 a 的 平方等于等于多少?正弦值有了吧。那 cosine r 等于多少? 等于七分之根号七吧。哇,这没问题啊,这一减去四十九分之四十二,就四九分之七开,根号就根号七分之一,那就是七分之根号七,哇,等于七分之根号七, 两边同平方可以吧。就四减 a 的 平方比上四加 a 的 平方等于七分之一,那就四减 a 的 平方啊,七倍的四减 a 的 平方,就等于四加 a 的 平方,就二十八减七, a 的 平方,等于四加 a 的 平方, 是吧?八一的平方,那 a 等于多少? a 等于根号三吧。好,这种向量方法是不是很快就能够算出结果了? 这做这题目的时候,大家一定要细心,因为这个坐标他很容易就给他列错了,这坐标很容易就给他列错了。然后求向量时候呢,也特别容易错, 求发向量的时候一定要细心啊,发向量的时候一定要细心。好,那这就是向量版向量的方法,比较容易想到, 比较容易想到。好,那下面呢,我们看第二种方法吧,我们求一下二面角,把这都擦掉,把这第二根擦掉吧。 第二种方法呀,我们可以直接把这个二面角求出来吧,可以直接求出这个二面角,但是可能要花点时间看,我们是 这个二面角 a, c, p d 的 这个二面角吧, a, c, p, d, a, p c 和 d 二面角。哎,我们的常规思路啊,我们是不是想过这个 a 点,过 a 点,我们尝试一下,我们可以尝试一下过 a 点啊,去做这个 p c 的 垂线,假如为 e 点吧,然后我们连接 d e, 如果 d e 啊,如果 d e 啊, d e 也垂直于 p c 的 话,那么这个角 d, e, a 就是 我们,就是我们啊所要求的二面角吧,是吧? 但是我们啊,观察了很久,发现啊,这第一没有办法证明。这个第一啊,垂直于 pc, 这没有办法证明的,就这种方法,它不可取,不行,不可取,那不能这样做,换一种,换一种, 还有种思路啊,还有思路啊,因为我们是 a c b d 嘛。那有同学啊,会会啊,从 d 点啊,去做一条直线会先啊,先从 d 点做一条直线,或做个线段垂直于 pc 还是为 e 点啊,然后它连接 a e, 然后证明啊,证明 a e, 然后垂直 pc, 然后这时候呢,角 d e a d e a 就是 我们要的二面角,是吧?那这时候你发现啊,这 a e 垂直于 pc, 是 不还是没办法证明它怎么怎么垂直 pc 啊? a e, 你 没有办法证明 a e 是 垂直于 pc 的, 这种方法其实也是不可取的哇,你看了很久也看不出来这两个垂直,再换,再来尝试,再来尝试。其实啊,学数学啊, 它不是你突然就得,你要经过很多次尝试, 不是有些题吗?不是你一眼就能看出来的,你一定要是经过很多次尝试,反复试错,你才能够找到正确的办法。 其实学数学啊,就是将你能够想到的所有方法都使用一遍,总有一种方法能够解决你的问题,因为大家要清楚啊,我们他这考试范围一定是不会超出你所学的知识, 所以大家在平时一定要去多尝试,多尝试,用各种不同的方法去求解。这样这样的时候呢,到考试的时候,你就能够很快就能够判断出这一题要用什么办法,要做到做到这种程度了 哇,能做到这种程度,会为你啊节省很多时间,会提高你做题的效率和速度,你们看还能怎么做啊,还能怎么做? 哎,聪明的同学,你想到了,其实我可以做啊,从 d 点,从 d 点垂直于 a e 的 一个线段,假设为一点啊,假设为一点啊,我们,然后呢,再过一点啊,去做垂直于 p c 这个线段,假设我们交 f 点啊,这时候啊, e f 是 垂直于 pc 吧,所以我们是不是只需要这样 d f 也垂直于 pc 就 可以了?我们连接一下 d f, 我 就说我不一定要从 a 点做垂直于 pc 吧,我可以从这个其他点吧,是从一点吧,一点也可以吧,就是说我们可以从啊 p a c 啊,不 p p a c c 啊看一下啊, a c p 啊,对啊,对对,就 a c p, 就 说在 a c p 啊这个平面上, a c p 这个平面上, 我们做二面角,我们不一定要找这个端点吧,不一定要找这个端点垂直于 pc 吧,我们可以从可以找这个三角形中的任意一个点吧,比如说我们这个时候就找,找到了这个 e 点,是吧? e 点,我们假设我们做这个 e 点,然后垂直于 pc, 这种也是可以的吧, 那么我们知道啊, e f 是 垂直于 pc 的, 因为是我们自己做的吗?做的是垂垂线,那这时候我们只需要证,证什么证? d f 垂直于 pc, 我 们只需要证明这个,那么我们就能够得出啊,角 d f e 就是 我们所要的二面角吧。哇,我们现在主要看怎么证 d f 垂直于 pc 来看这个思路啊,我们啊,如果啊,如果,如果 pc 垂直于平面, d e f, 那 么 p c 是 不是就垂直于 d f 呀? 那 pc 垂直于平面 def 吗? pc 是 垂直的吧,因为啊, pc 首先啊,它是不是垂直于 e f 呀?是吧, pc 垂直 e f, 然后呢? 然后什么 看啊?然后啊,看这个 d e, d e 是不是垂直于 a c 啊?然后 d e 是 不是也垂直于 pa 啊? pa 是 不能够推出 d, e, d e 垂直于平面 p a, c 是 吧,那么是不是就能够推出来 d, e 是 垂直于 pc 的? 把这个填充放这来 放这俩是不是就能够得出?跟着这两个垂直是不是就能够得出 pc 啊?垂直于这个平面 d, e, f 是 吧,那么就能够得出 pc 垂直于 d f, 所以 啊,那么就正出来了呀。那这个角,这角 d e f 角 d, e, f 就是 我们要求的二面角吧。角 d, e, f 这个角就是二面角,那这是,这个是这个三角形啊,这个三角形我先画一下, 这是 d 吧,这 e 吧,这因为 d, e 啊,它垂直于平面 p a, c 的, 所以这个角才是九十度, d, e 是 九十度,这是 f。 好 吧,我们要求的是什么?哦,这,这个,这个是 m 面角吧, 我们要求的是 a, d 的 长度, a, d 的 长度,我们再画一下 a, d 的 长度, 假这个三角形啊,这是 a 点,这是 d 点,这 c 点,我们要求是 a, d 的 长度。我们假设 a d 为 x, 可以 吧? ac 的 长度已经告诉你了吧,等于二,那 dc 的 长度是不是等于四减 x 的 平方? 哎,我们知道这点值,这三引,三引,这个假设这个角,假设这个,我们另外 r 法吧,这样写起来比较方便一点。加,这是三 r 法是不告诉你了,等于七分之根号四十二,那我们是不是能得出 cosine r 法等于七分之根号七呀? 那么这样 tan 比上 cosine 根号四十二,比上根号根号七吧, 等于多少?根号六嘛。这弹性耳法就等于根号六。弹性耳法等于多少呀? 弹性耳法等于多少?弹性耳法,这个角啊,是不等于 d e 比上 e f? 那 我们现在要求的就是 d e 和 e f 的 长度吧, d e 和 e f 的 长度 啊,这一点,是不是在这个地方,一点是垂直他的吧,这个这一点一点是吧?长度是二,是他的吧?第一, 好吧,那根据这已知条件,我们能不能求啊? d e 等于什么?这角是不是等于九十度啊? a d 垂直 dc 吧, a d 垂直 dc 他 不告诉你了, a d 垂直 dc, 那 么根据三角形的面积公式,那么二分之一 x 乘以根号下四减 x 平方,是不等于二分之一 a c 啊,乘以 d e 是 吧? 等于二分之 a c 等于二吧,乘以 d e, 那 d e 就 不出来了。 d e 是 不是等于二分之 x 乘以根号下四减 x 的 平方 哇,这 d e, 那 么接下来就是求的是 e f 吧, e f e f 的 长, e f 这个地方在图上可以这这个地方 e f 的 长,也就是对应在这个地方 e f 等于什么? e f ef, 我 们再看一下这个这个大的图啊,我们求 ef, 我 们是不是可以先求出 cf 啊,或者是 ec 啊? 是吧?那 cf 可能是求不出来,是不是可以先求出 ec 啊?是不是先求 ec, 我们再看这这大图像,这 p a 等于几啊?等于二吧, ac 也等于二,那所以这个角是不等于这个角等于四十五度呀?哇,那么角,角什么角? e c f 等于四十五度吧?角 e c f 等于四十五度, e f 又是垂直于 ef, 又是垂直于 pc 的, 那么角是吧?角 f ec 也是四十五度吧。那么 ef 是 不是就等于 fc? ef 就 等于 fc, ef 是 不是就等于 fc 啊? 是吧? ef 等于 fc 是 不等于根号二倍的 fc 啊, 这能理解吧?因为弹性四十五度啊,是不等于弹性四十五?不啊,弹啊,不,不是弹性四十五度啊,因为三啊,四十五度啊,是不等于 ef 比上 fc 等于二分之根号二吧。那这样我们就能够求出 e c 等于根号二倍的 fc e c 等于根号二倍的 f c。 那 这时候我们是不是求 e c 就 好了呀? e c 如果出来的话,那 f f c 就 出来了, f c 出来了, e f 就 出来了,是吧?那么 e c 等于啥? e c 等于啥? e c 是 不是等于这一段 e c 等于啥? 我们 d e 是 不出来了, d e 出来了吧?你看哦,你看哦, e c 哦, e c 的 平方是不等于 d c 的 平方减去 d e 的 平方 啊,那就等于啊, d c 的 平方是不是四减 x 的 平方?四减 x 的 平方吗?这不减去啊, d e 的 平方是二分之 x 乘以根号下四减 x 的 平方,括号的平方,是吧?哎,那这 e c 不 就是开根号吗? e c 就是 根号下这个是吧? 那,那我们这个时候贪定而发,等于 d e 比上 e f d e 啊,就等于啊 d e。 我 们刚才求这个式子, x 乘以四减 x 的 平方比上二,然后比上 e f e f 等于 e f 等于 f c 是 吧? 那根号二倍的 f c 呢?又等于 e c 那 所以 f c 啊。哦哦,我们是 f c 哦, e f e f e f 等于 f c, 那 f c 就 等于 e c 除以根号二吧。那就 e f 就 等于 e c 除以根号二吧。 e c 等于这个,这个十字就是根号下 四减 x 的 平方,减去二分之 x 乘以根号下四减 x 的 平方,括号的平方是除以根号二呀。哇,这次式子化简啊,这下面这个式子,下面这个式子可以化简为化简为这个式子。 嗯,四减 x 平方比上两倍根号二,下面就画一个这个式子,然后就等于啊,就 x 根号下四减 x 平方比上二,然后比上四减 x 平方两倍根号二 就等于等于多少?等于根号六吧,根号六,那这样能够算出来 x 等于 根号三,好吧, x 等于根号三,这个就是啊,先求出二面角, 先找出二面角,然后再根据直角三角形啊,正弦定,等于先定理,然后进行求解进行算。 这种方法要比嗯向量法要复杂一点。如考试的时候啊,优先建议采用向量法,因为他比较快,考试时间有限嘛,找二面角可能还得找一段时间,所以就是考试时候优先建议使用向量法。 嗯,然后但平时的时候呢,就建议大家把所有的方法都试一下。那如果考试时候碰到那种题目啊,他不能用,他不能用啊,向量是吧?没办法直接去做直角坐标系的话,那你可能就要找出二面角了。 那么这就是以上部分,就是第十七题的所有内容。
 11:15查看AI文稿AI文稿
11:15查看AI文稿AI文稿所有立体几何的问题,我们都要立体图形平面化。好,我们来看这个第八题。 这道第八题的话,它是一条立体几何的问题,立体几何不见隙,这实际上是一个趋势,我们要会去分析这种类型的问题,我们先看他的条件。在一个能长为二的正方体内有一个内切球,我们先画一个正方体。 好,它有个那些球 o 一 那些球啊,那么我们就知道它的球心是不是肯定是它这个正方体的正中心嘛?所以我们先把它的球心给它点出来 o 一, 你可以考虑把这个球画一画,画球其实很简单哎,你先画个圆, 然后再画个弧,然后在后面再点虚线,哎,是不是还行啊?哈哈,好,我们继续再看。 请问这个内切球的一个半径是多少?他说记他的半径为 r 一 来, r 一 是多少,应该很明显吧, 看得出来吗?它能长是二,对它是一。好, ok, 我 们继续再读。它说若球 o 二与正方体的三个面和球 o 一 都相切, 也就是说你这个 o 二,这个球啊,它是跟三个面和这个球一都相切的,它就缩在角落的,我们可以把它点出来, 往下划一点。好,这个是 o 二, 那你想这样的 o r 是 不是实际上可以在球的任何一个角落啊?在,在这个里面的任何一个角落,但是无论它在哪一个角落,它是不是实际上的结果应该都是一致的。 你想一下,它是球和球是一个相切的状态,球和球相切,它背后就是数量关系。什么数量关系? 就是球星之间的距离,应该是等于半径之和,那么我们就自然而然肯定会去考虑连接这个 o 一 和 o 二。好,我们连接起来, 你们要有一点点空间想象力。当我连接了 o 一 和 o 二之后,请问如果我把这条线延长,请他会不会到顶点?你们判断一下会不会? 会,当然会,当然会。它是穿过去的,相当于它是一个对角线,它是可以穿过去的,明白吗?好,继续。那么我们现在怎么去求它这个 o 二的半径呢? 所有立体几何的问题,大家记住这句话,所有立体几何的问题,我们都要立体图形平面化,什么意思?来看, 我们可以计算一下这段长度来,这段长度我们刚已经算过了, r 一 是多少一,好, ok, 继续。我要求的是 o 二的半径,我们可以设 o 二的半径为 r, 所以 我们就可以得到这段是 r, 那 么这段不知道,但是我们是不是可以知道这一段? 这段怎么求?你要知道相切跟面相切他也是一个等量关系。我们过 o 一 往下做垂线,请问这段长是多少?一好, ok, 连接这里是多少 根号二好, o 二往下做垂直,这是不是还是 r? 来,我们求线段长,要么是钩股,要么是相似。那么你看一下这个图形里面,我们应该用钩股还是用相似? 应该是相似吧,他有个很明显的 a 字形相似。好,可以的,那么我们就去写他的一个线段长度来。这段长怎么去求? 对,我们大的是不可以直接勾一根号二,根号三直接求,那么求出来之后这里又是一,所以这段长度就有了,他就等于根号三减一减二。 好, ok, 这一段又是儿,你有两段就可以写了吧?不需要再写下面这一个直角边了,所以我们就可以写小三角形里面的斜边 根号三减一减二。比上大三角形里面的斜边根号三就等于小三角形里面的直角边,而比上大三角形里面的直角边一,那我们就可以交叉相乘去解他的这个二了。好,对角相乘, 根号三二就等于根号三减一减二啊。以上根号三加一,二就等于根号三减一。除过去 分母有理化,上下同乘,根号三减一,底下就变成了二,上面就变成根号三减一的平方就变成四减两倍的一个根号三,所以算下来就等于二减去根号三。 哦,所以我们就得到了 r 就 等于二减根号三。那我们第一问 第一个问题就对了,二减根号三,但是他要我们选的是错的。好,我们 r 已经算出来了,我们怎么去计算 r 三? 那么第三个球他要要求跟你正方体的三个面以及圆 o 二都要相切,那么也就是说你的下一个球是不是应该是缩在这个角落了? 那我问你,他跟前面有区别吗?求的过程中完全没有区别,他是不是只是等比例的进行缩小了?所以你们能不能想象出来, r 三是不是实际上是在 r 二的情况下又成了一次二减根号三, 那他就是二减根号三的平方,那么也就是说我们就可以得到他的这个 r n 是 不是实际上就是一个等比竖列? 那么我们看他的这个 b 选项,他问 r n 是 不是等比竖列?当然是的,首项是一公比,是二减根号三,好,再来 c 选项, c 选项是不是本质上是一个竖列求和? 竖列求和我们一共讲过五种方式。第一个公式法,如果你是等差或等比,是不是直接求和就行了? 第二个,分组求和,如果他是等差加等比或类似,我们可以分组求和。第三个,如果他是等差乘等比,我们是不是错位相消?第四个,我们是不是还有列向求和?第五个,还有什么求和方法? 还有倒序相加,大家不要忘了还有倒序相加的方法,倒序相加他是用于你,如果第一项加最后一项等于第二项加倒数第二项等于第三项加倒数第三项,那么像这样的竖列,我们就可以用倒序相加, 他还有一个名字叫叫这个高斯求和,就像我们去求等差数列一样。但是你不要认为只有等差数列才能用这种方法去进行求和。有还是有的,比如说我们举个例子, 假设我给你一个函数,这个函数它关于,因为数列,我们是不是也可以理解成是函数,只不过它的定义域是正整数罢了?比如说这个函数,假设它是关于十逗号二中心对称的一个函数, 那么你们能不能理解我 f 一 加上 f 十九,来告诉我 f 一 加上 f 十九等于多少? 他们两个加起来除以二,是不是应该是等于二的,所以他应该是等于四来 f 二加上一个 f 十八等于多少? 四,他符不符合?第一项加最后一项等于第二项加倒数第二项符合吧?所以如果我要算他的前十九项和,我是不是就可以首项加末项乘以项数除以二。 那么你什么时候会有这样的一个意识呢?你想你常见到的中心对称的函数是什么样的?函数 很简单,反比例是不就是?那么我是不是只要把反比例函数经过适当的平移,让它平移到关于十二中心对称,那么我是不是就可以了? 大家能不能听得懂?比如说我可以编题目了,我编这个 f x 就 等于 x 分 之一,来告诉我它现在关于谁对称 零零是不是零零?好,那么也就是说我要对它向右平移十个单位,再向上平移两个单位来,向右平移十个单位,就是 x 左加右减 x 减十分之一,再向上平移加二。那么这时候我给到你的时候不会这样给到你,我给到你 x 减十分之 二, x 减十九。那么当我把数列的通项给到你,是这样的时候,我再让你去求它的前十九项和,你是不是就懂了?我应该要用倒序相加,因为它第一项加倒数第一项,等于第二项加倒数第二项, 大家听懂了没有?好, ok, 那 么这里不谈,因为这里它本身就是一个等比数列,所以我们要求它的前十项和,是不是只需要套公式就行了?来,我们写 s 十就等于一减 q, q 是 多少? 二减根号三, a 乘以一减 q, a 就是 一,一减 q 的 十次方。好,这用中国号,我们稍微化减化减, 底下算下来就等于根号三减一,上面算下来就等于一减去一个二减根号三的十次方, 二减根号三的十字方,我们又不可能算了,你连二的十字方算的都费劲,但二的十字方是一零二四啊,这个大家最好把它记一下。那么这个东西你肯定算不了,但是我们可以考虑稍稍微对他有理化一下,对他有理化分子分母同时乘以根号三加一, 那么底下就变成了二,上面就变成根号三加一,再减去一个根号三加一,乘以个二减根号三的十次方。来他这个 c 选项,问我他是否大于 二分之根号三加一呢?来判断一下对不对?来告诉我这个数是正数还是负数? 正数,那你减去一个正数,请问你还会有后面大吗?不会,所以 c 就 错了。所以这个题目其实没有那么难啊,大家要会 例题,几何不见系一直是趋势,大家不要畏惧这种题型。
24扬州董老师数学 05:42查看AI文稿AI文稿
05:42查看AI文稿AI文稿二六届七八联考第十一题,一道人格分裂的几何题,前半段难度平稳输出,后半段画风突变,抽象到你根本画不出图,你能想象出来不?这边都是溜平,溜平的里边是个呼。别慌,显哥带你摸清这道题的规则,破解这道多选题。他说正四棱锥啊,他的高为 h 四棱锥,他的顶点在正方体的内部,包括边界上运动啊。问 h 的 角度范围, 你鄙视谁?出题你鄙视谁?你是在鄙视我吗?他这是一个正方体,你不用画了对不对?你这是个正方体, 你想想屁点在正方体的表面上和内部运动,那当然体高最大的时候就是一呗,体高最小的时候是接近零呗。 所以这个 a 选项他有点病啊,病的不轻,所以怒开两分,我就做下一道题了,如果我是学渣,一个对不对?明白了不? b 选项,他说正四棱锥,他的侧棱长是二分之根三,我们画一画啊, 就当画了啊,就当画了,那所以他说侧棱长是二分之根三,然后呢?问体高是多少,那体高的话,那就应该是放在这个三角形当中来解决问题,那这个数的话,就应该是二分之根二, 那所以一勾五定里,那就是四分之三减四分之二,四分之一就二分之一啊,开根号是二分之一,所以这个选项错误的。也说 h 应该等于二分之一。 再说一遍,这个长度是二分之根三,这个长度是二分之根。二勾五定里,四分之三减四分之二,四分之一,开根号二分之一,所以这个选项错了。他说 p 在 正方体的正方体的中心上,底面的中心上,然后呢?外接球, 正能锥的外接球,这是我们高考考烂的东西,所以他这个在正方体上,底边那个中心上。来来来,大家思考一下,那是不是相当于我们假设外接球的球心 在这就是 o, 那 这个地方呢?显然球心到球面上的距离,这是半径,又因为他的体高是一,因为这个点在正方体的上,上底面上吗?啊?上底面上啊,所以呢,他的体高就是一,那所以这个长度就是一点二, 然后呢,这个长度呢,也是球的半径,所以是正能锥的外接球。他有个万能公式指出我们烫,所以我们现算就可以了。也就说一减二的平方就应该等于二方再加上一个 啊,二分之一,所以二方再减去个二二,再加上一个一,等一个二分之一啊,写反了。嗯,一减二的平方再加上一个二分之一,等一个二方,所以这量是二分之一,再加上它, 没错吧?所以呢,二方和二方约定了,二二就应该等于二分之三,所以二呢,就应该等于四分之三, 所以外接球的表面积是四派,二方就是十六分之九,所以答案是四分之九派,这个选项是正确的,明白了, ok, 好, 来我们讲讲第一个选项怎么做。我先画出一个正方起来,这道题你应该会,你会怎么想呢?好吧, 好,他说什么呢?屁,为这个正方体的内切球,既然他为他内切球,内切球的半径我们是知道的,内切球的半径就应该是一个二分之一,因为他体高是一。现在呢?呃,他说的是屁为他的内切球的球心就说白了是正方体的中心, 正方体的中心,这个没错,是吧?那正方体的中心的话啊,人家说这个正方体的正方体的内切球与这个正四棱锥公共部分的体积是多少? 圆了?这道题它里边有个内切球啊,内切球它与这个正四面体的公共部分是什么?你能想象出公,公共部分是什么?不? 能想象公部分,哎,你切过西瓜吗?切西瓜,这边切一刀,哎,就是这样的,哎,这边都是溜平,溜平的,里边是个乎啊。所以这个地方你想想,我要想求的话,我肯定不可能直接求出来,因为我们没学过呀, 我们又,他又不是什么公形,对不对?我们又不会双重积分,对不对?所以呢,我们就得想他占多个球, 听明白了吧?占多少球,那占多少球,那这个问题就解决了。你只要能想到这一点,这道题解决了。所以 d 选项考你的空间想象能力, 听懂吗?他是完全对称的,你得想他占多少个球,那你想想,这样的话,他占了一部分,那如果是这个点,哎,以他为底面啊,就是这个底面啊。就说白了,这个地方也同样有一个正四棱锥,哎,他与那些球交在一部分,是不是一样的体积? 那上底面是不是也同样道理?这边左侧面是不是也一样的理解了?不,所以你们猜占几分之一,只需要打分母就可以了。几分之一的内切球? 好,你可能还没听懂这样的话,是一个正四面体,他与这个内切球啊,切公共部分有一部分啊,是多少我不知道。然后呢?哎,我假设这条也有个正四面体,他与这个内切球他也有个公共部分,这个公共部分肯定是一模一样的。 一模一样的。那这个地方呢?他也有个内切球,对不对啊?也也有个正四面体,他与这个内切球公分一模一样的,所以就完了,就完了。这道题就完了,所以占六分之一个。六分之一个内切球的体积。 内切球的体积是三分之四 pi 二的三次方,三次方是八分之一,所以答案是六六三十六分之 pi。 好, 你能想到不?选 d 听到吗?想想西瓜啊,你直接求是求不出来的,所以得占多少个球?所以我就想全都是对称的就可以了。他正好把整个的那些球瓜分了,分成了六等份,所以这是十一题。 ok, 好, 十一题。
54赵礼显数学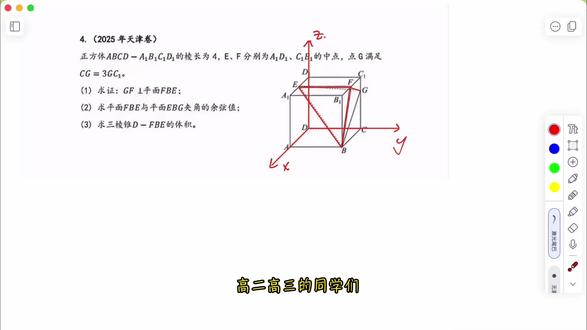 14:02查看AI文稿AI文稿
14:02查看AI文稿AI文稿高二高三的同学们,咱们今天拿天津高考的题目我们来看一下,在例题几何这里如何三步全部都用间隙的方式来用,那么我们说如果说间隙,我们在考场当中如何判断我们这个题是用间隙好还是用推导好?首先我们来看一下这个题目,这题首先告诉我们一个正方体, 那么点了一个棱长,那么首先真题思维告诉我们什么正方体棱长,我们要找什么?是不是有垂直?是不是每条边全部相等? ok, 后面继续有一个终点, 终点是贯穿于 e f, 那 么就相当于我这个 e f 是 不是平行于我的两条边,对不对?是不是这条边和这条边? ok, 那 么来我们继续看, 那么我们就最后有什么给了一个倍数关系,但是来我们看我们没有平行,没有垂直,我们有的垂直是什么?有的垂直是我们正方体的平行,以及 e f 和正方体边长的平行以及垂直,这是我们已经知道的,但是同学你会发现这个题目的已知真的非常的少, 我们能用的已知就是长度、垂直、平行以及终点还有倍数关系,那么在已知量非常少的情况下,老师推荐干什么?就用间隙,为什么?间隙虽然麻烦,它的麻烦的点在于我们,第一就是我们要先间隙怎样去做直角坐标系,但是这个题它好在了,我们用的是正方体, 正方体间隙是比较容易的。第二就是我们要写一些坐标,我们说写一些坐标的时候,可能我们写在点的时候看错了,所以说我们用什么方法,用三步做题法,三步做题法,详细的可以看我主页的置顶。 ok, 来,我们回归到这个题目, 我们还有一个点是什么?就是计算,所以说在例题几何里面,计算一定是一个非常大的一个重点。来,我们看一下这个题, 这题很明显,我们以 d 点为圆点,分别以 d, a, d, c 和 d, d, e, 我 们分别为 x、 y, z 轴建立空间直角坐标系,那么我们记住这句话一定要写全,而且要写完整。 ok, 每条边都是四,那么我们来写下 b 点, b 点,就是四四零,然后 e 点 二零四, ok, f 点二四四来 g 点零四三。 ok, 来,我们写完这四个点之后,我们来表示一下 e, f 向量, e, f, 我 们知道用后减前,所以说我们后面减,前面就是零四零。我们来继续 e, f, 我 们已经表示完了。之后我们来表示一下 e b 向量, e b 等于多少,还是用后减前,所以说 e b 就是 二四负四。 ok, 来,我们继续 f g 向量, f, g 还是用后减前。来。同学,这里我说一个简单的东西,我们这里先把它写完,就是负二零负一。 ok, 来,我们如果说不知道,我们用 b f, e, g, 因为你想什么,我们 g, f, f, b, e, 所以 说你如果要列点,老师建议你就找它上面所有这些点全部都表示出来,你可以在第一问的时候,就把每一个点就是从 a, 从 a、 b、 c, d, a, e, b, e, c, e, d, e, f, 还有 e, f, 还有 g, 它们每一个点全部都表示出来,那么你后面就可以不用写了,你就写由第一问得,或者是由已知得,那么我们就可以直接用我们的这些坐标,当然同学如果说你嫌他麻烦,你就用什么写什么就可以,但是千万不要忘记写 ok。 来,我们继续表示完这个之后我们找的是什么? 老师之前说过,如果说在推导方式里面找线面垂直要优先找什么?要优先找线垂直, ok, 线线垂直我们要找什么?是不是要找两条线相交,而且要有交点,并且我这条线,我平面外的这条线垂直于这两条相交的线,分别垂直, ok, 那 么我们才能推导出来,由线线垂直推导出我们的线面垂直。但是现在我们要找什么?我们用的是坐标方式,坐标方式要去证明线面垂直,我们要怎么找? 是不是我有这条线,我下面有一条面,我这个面和这个线垂直的,我的法向量要和我的这条线要干什么?是不是平行关系啊?所以说我现在应该是去假设我的法向量表示完我的法向量之后,我们 应该干什么?去找平行关系。所以说我们假设一下这个假设,我们的平面 f b e ok, f b e, 我 们的法向量 n 或者向量 m, ok, 我 们写 x y z, 当然你写 abc 也可以, x y z, 那 我们表示 x y z, 我 们把这个向量 m 代入到哪里?分别和 e f 和 e b 来代,因为我们这两个是垂直关系,所以说我们向量 m 是 发行量,发行量和 e f 是 垂直关系,所以说我们就等于四 b 等于零, ok, 我 们直接代入就行。下面也是向量 m 和什么呢?和 e b 进行一个相乘,等于二 a 加上四 b 减四 c 等于零, ok, 这是这两个,那么我们现在要干什么?我们是不是要求解我们的法向量?法向量如何求?让我们的某一个已知量,我们假设它为什么数?然后去求另外两个未知量,对不对?所以说我们假设我们令 a, 比如说 a, 我 们这里微到好算,我们比如取二,但是你也可以取一,可以取二分之一都可以。那么记住法向量取什么都可以,为什么可以取?因为法向量找的是倍数关系,比如说我这里写的是四一三,对吧?四一三加上它是它的法向量,那么你如果写出来是八二六,它 是不是也是法向量?它们之间成了一个二倍,但是它们还是法向量,它们是找了一个倍数关系来,我们继续。我现在 a 等于二, c 等于多少?我们把二代入,那么 b, b 等于多少? b 就是 零,所以说 c 就 等于一,那么 b 等于零。 ok, 我 们就写完了,我们把我们的法向量表示出来,向量 m 就 等于二零一, ok, 二零一。来,我们继续。那么我们现在要表示什么?是不是应该表示我们的 g f, 但是我们会发现 g, f 等于什么?或者是 f, g 等于什么? f, g 是 不是等于负的?我们的这什么 向量 m, 那 么我们向量 m 是 反向量,所以说他们之间是一个倍数关系,乘一个负一倍,所以说他们是一个什么?是一个平行关系,那么我们就可以得到一个平行关系,所以说我们就可以得到这条线,垂直于这个平面。 ok, 这就是第一个,来,我们继续说一下第二个,这里我们把另外一个题往后放一放, 来,我们来说一下第二问,第二问了个什么?问了一个这个平面和这个平面的加角的余弦值,所以说第二问问的是什么?是不是二面角?二面角我们要找什么?老师在上节课直播的时候也说了,二面角我们要找的是 cosine theta, cosine theta, 当然了, 如果说是一个线面角,我们的 cosine theta 是 可以直接找到 cosine theta 的 关系的,对不对?这里一定要区分好。 ok, 来,同学,如果说他这个题问的不是 cosine theta 的 关系的,对不对?这里一定要区分好。 ok, 来,同学,如果说他这个题问的不是余弦值,他问的直接是角度,那么你应该怎么找? 记住所有角度,在如果说你没有任何思路情况下,就考虑余限值就是 cosine 值,那么 cosine 值你只要考虑出来了,这个题大概率就不会错了。来,我们继续看一下第二问,第二问如何求?这里 e f b 或者 f b e 是 不是我们第一问的发向量?是不是我们刚才求的这里是不是它?所以说我们现在只需要求出来 e b g, e b g 在 哪里?让我们看一下 e b g 是 不是在这里啊? ok, 我 们会发现这个项链这个平面我们的法项不知道情况下,我们就要求一下,刚才我们已经表示了两个项链了,三个项链,那这几个项链我们也是可以再去疑问用到的,当然我们还需要取一些其他的来,我们看下这个图 是不是需要 e g 和 b g 对 不对?所以说我们来表示一下 e g 来一点 e g 后减前,所以说就等于负二四负一。来,我们来写下 b g 向量 b g 等于多少?也是后减前,从这里减去这里后减前,记住是 g 减 b, 来我们这里是多少?是负四,负四, 负四零三, ok, 我 们 b, g 和 e g 全部都表示出来了,我们现在应该表示什么?是不是表示我们的平面 b, e, g 的, 或者是 e b g 的 发向量,那我们来表示一下平面 e, g 的 发向量等于多少呢?比如说我们让它等于 n, 向量 n 等于 x, 一 y 一 z 一, ok, 这里我们一定要和上面这里 x, y, z 进行一个区分,然后避免它们符号重复。来,我们来表示一下,向量 n 就 等于向量 n 乘以 e g, 或者向量 n 乘以 g, e 都可以,这里我前面写的是 e, g, 我 们这里就写 g e, 但是同学如果说你表示的是 g, e, 但是前面这里是 e, g, 你 就乘以个负一就行,它们是一个相反关系。来,我们继续,这里就是负二, x 加上四 y 减 z 减 z 就 等于零,然后向量 n 乘以 b g, 向量 b 对, 等于负四, x 加三 g 等于零, ok, 这两个式子我们进行,还是原来的方法, x 就是 让 x 等于多少呢?所以我们看一下, 可以找到一个六,我们找六,那么我们把 x 代入,那么 z 和 y 不 就行了吗? z 等于八, y 等于五, ok, 来,我们的法向量向量 n 就 等于六五八, ok, 有 了这个反应量之后,我们应该找什么?来,我们看一下这个提问,找余弦值,所以说余弦值公式,记住这里我们不知道它的夹角,所以说我们要先在前面先写一下平面 f, b, e 和我们的平面 f b e, 这里我们已经重复了,这里我们重新写一下,这里应该是平面 b e、 g 它们的夹角,比如说夹角为 c 它, ok, 夹角为 c 它了,那么我们找的是什么?是不是 cosine c, 对 不对?那么我们应该找的是 cosine f g 和什么?和我们的法向量 f g 是 什么呀? f g 不 就是刚才我们找的倍数的关系啊,对吗?你想我乘一个倍数,那么其其实这个 f g 不 就是它的法向量,对不对?来,我们继续,那么我们直接代入公式就行,就是 f g, 然后乘向量 n, 然后比上 f g 的 模长, 乘 n 的 模长,乘 n 的 模长,然后就等于二十比上根号五,乘根号一二五, ok, 等于多少?等于五分之四, ok, 那 么这个题我们就出来了,但是同学老师建议你在这里我们再写一句答话,就是谁的平面和谁的平面的加着余弦值为多少,这就我们在这里写一句答话,以防万一,万一老师到时候就是看判卷,这里我们出现了一个错误,把这里扣掉了一分,比较冤。来,我们再看一下第三问, 第三问这里说的是什么?第三问,这里问的是一个体积,来,所有体积,别管是什么图形,它是不是都是底面积乘以高呀?当然不同的图形它底面积乘以高之后,它还会有一些变化,这个没有关系,但是它整体上是不是都是底面积乘以高? ok, 知道了这个之后我们怎么求?我们是不是应该要先求出来它的底面积,再求出来它的什么它的高?来,我们看一下这些说的是什么? d, d 在 这里, d 在 这里, f b e f b e 在 这里,所以说它找的是什么?来,我们换一个颜色,觉得好看, 来 d, 点到一点,我们这里到这里, ok, 我 们找的是什么?一个三棱锥,三棱锥底面是什么?底面是三角形,所以说高 高应该是什么?是不是点到面的距离公式,或者是点到直线的距离公式?我们知道你看这里因为是个斜边,所以说你可以用推导,你也可以用垂直,你也可以用垂直关系进行一个推导,你还可以用什么 点到平面的距离公式进行一个求解。所以说我们现在应该先求平面 b e f 的 什么面积来,我们刚才已经求开了,我们的 e f 垂直于平面。什么? e f 是 不是垂直于我们这里这个平面?所以说我这个直线垂直于它,我的 f b 又是在我的 b c c 一 b 一 这个平面内,所以我可以得到什么?我可以得到我的 e f 和我的 f b 是 相互垂直的, 那我这里相互垂直,所以说我这里找面积不就很好找了吗?来,我们进行一个求解。我们先来写一下,刚才我记得是 e f, 我 们知道 e f 是 垂直于平面, b c 一, 应该是 b c c 一。 ok, 这里我们重新写一下,应该是 b c c 一 b 一, ok, 我 们知道了这个之后,我们知道 f b 是 在哪个平面内的?是不是在我的 b c c e b 以内的? ok, 我 们知道了这两个之后,我们来看一下我们是不是可以推导出来我的 e f 垂直于我的 f b 吧,所以说我可以推导出来我的 e f 垂直于我的 f b, ok, 之后我有垂直,我为了是找什么?我不就是为了找我的面积公式吗?所以说我找的面积是什么? 来看一下是不是 b e f, ok, b e f 等于多少?等于二分之一,因为我垂直关系,所以说我就找的是 e f 乘 b f 来,二分之一乘多少,这里是四,后面这里应该用勾不定理 来看一下,应该是四,二根号来,应该是四的平方,乘二的平方应该是加了二的平方,就等于这里应该是十六,十六加四 再乘以,前面应该是,嗯,二倍的根号五,再乘二,应该就是四倍的根号五,四倍的根号五。来,这个是我们的面积公式。来,我们还需要什么?我是不是还需要我有一个高到我这个平面的一个距离公式? 所以我找的是什么?我可以找 d e, 我 也可以找 d b, 都可以,你觉得哪个方便,你就求哪个就可以。来我们这里先表示一下 d e 向量 d e 等于多少?来,我们看一下这里后减前,所以我们应该是二零四, ok, 那 么我们找的是什么?我们不就找的是地点到我这个平面的距离公式,对不对?来,距离公式小 d 等于多少?是不是我随便找的?第一的这条向量和什么和 f g 来比较? f g 的 模长, ok, 等于多少? 根号五分之八就是八倍的根号五比八,对,应该是比五,这里我们写的有点乱,我重新写一下,就是八倍的根号五比五, ok, 这个是我们这个式子,但是这个写完了吗?这个没有写完,这里是什么?这里是高, 我们还需要什么?体积应该是三分之一底面积乘以这个距离,也就是这个高应该是多少?三分之一乘以多少,乘以八倍的根号五比五乘以四倍,根号五等于多少?这应该是五个五四四八,三十二,应该是 三十二,下面应该是三。 ok, 这个题就已经写完整了,当然我们最后还可以写一句答话,把这个题再丰富一下,那么这个题同学你就可以拿到满分了。 我们会在一月初有一个为期一个月的期末冲刺时间,那么如果同学你感兴趣,欢迎来咨询,欢迎来加粉丝群。我们有寒假课,我们也有期末冲刺班, 当然期末冲刺班如果不够的同学,比如说同学,如果同学你报了一个月,但是我们期末我们就上了二十天,没有关系,剩下的时间会自动顺藤,在我们的寒假班里 会免费提供给,比如说我们三十天的课程,我们有二十天还没有上,那么寒假班我们会免费给大家提供十天的课程,培养真题思维,优城启航之路,我们猜一下。
 05:14查看AI文稿AI文稿
05:14查看AI文稿AI文稿这是刚结束的二零二四年新高考一卷的立体几和解答题,我们一起看一下这道题难不难。首先看一下题目四人追 p a、 b、 c, d 中 p a 垂直于底面 a、 b、 c d, p a 等于 a, c 等于二, b, c 等于一, a, b 等于根。三、 我把条件标在题目上,可以看出角 a、 b、 c 为一个直角。接下来我们看一下第一问。若 a 的垂直与 p b 证明 a 的平行与 p b、 c, 这是 a 的,它是垂直与 p b 的 证明。因为 p、 a 垂直于底面 a、 b、 c, 所以 p a 是垂直于 b、 c 的。 又因为 a、 b 方加上 b, c 方等于 a、 c 方,所以 a、 b 垂直于 b, c, 又因为 p a 交 a, b 等于 a, 那么 b、 c 就垂直于平面 a、 p、 b 同样,我们证明一下 a 的 p a 是垂直于 a 的, p b 也是垂直于 a 的。 p a 交 p b 等于 p 点,所以 a 的垂直于平面 a p、 b 因为 b、 c 也垂直于平面 a、 p、 b 垂直于同一个平面,两条直线平行,所以 b、 c 是平行于 a 的。又因为 b、 c 是属于平面 p、 b、 c, 所以 a 的平行与平面 p、 b、 c。 这是第一问。接下来我们看一下第二问。在题干中的条件下,这里又给出了 a 的垂直与的 c, 这里是一个直角且二面角 a 杠 c、 p 杠灯的正弦值为七分之,根号四十二,求 a 灯。我们先建立坐标系,如图所示,建立 a 杠 x y z 空间坐标系。 我们先过 der 点做 a、 c 的垂线垂足为一。我把三角形 a、 d、 c 的平面图画在下面,过 der 点 做 a、 c 的垂线垂足为一,并设 a 的等于 t。 我们可以从这个平 前面图形看一下,这一个边为 tac 是等于二的,这里又是直角。根据摄影定理, a 的方式等于 ae 乘以 ac 的,所以这里的 t 方等于 ae 乘以二, 所以可以得到 a, e 四等于二分之 t 方。勾固定理可以得到 a, e 四等于根号下 t 方减去四分之一倍 t 的四次方的。所以这时我们就可以找点的坐标 p 点的坐标零零二, c 点的坐标零二零 de 点的坐标 x 是负的,得一长度, y 的坐标是 a 一的长度二分之梯方, z 轴是等于零的, p, c 向量是等于零二负二 二 d c 向量根号下 t 方减去四分之一 t 的四次方,二减去二分之 t 方零,然后射出平面 d、 c, p 的法向量。 根据发销量垂直于 p, c 都是建立方程组 减得法销量 n 一是等于, 同理,我们可以得到平面 p a、 c 的发香量, 四为一零零。因为我们由法销量得到二面角的余弦值,所以我们先根据正弦值算出余弦值。因为三 inset 是等于七分之根号下四十二,这里可以看出这一个二面角为锐角, 所以扩散 inset 等于根号下一减。 say inset 方等于七分之根号七。那接下来我们可以用两个法相量表示它的二面角了。 所以扩散与 c 塔等于 n 一乘以 n 二的数量级,除以 n 一的模和 n 二的模等于七分之根七代入 n 一, n 二项量可化减的 t 的四次方减去七倍 t 方加上十二等于零。可以选择 t 方等于三或者 t 方等于四及 t 等于 根,三或者 t 等于二。但是 a 都是直角边, ac 是斜边等于二,要舍去最终 a 都是等于根三的,这是这一道题目。
1351我是小余 08:39查看AI文稿AI文稿
08:39查看AI文稿AI文稿十七题,如图四棱锥 p 杠 a、 b、 c、 d 中 pa 垂直于底面 a、 b、 c、 d, 然后他说 pa 等于 ac 等于二, bc 等于一, ab 等于根号三。然后第一问,说 ad 垂直于 p、 b、 c 的, 那我们看一下怎么证明。我们要证明一个直线平行,一个平面是不是可以通过直线与直线平行来证明啊?你看 a、 d 和这个平面 p、 b、 c, 它看上去 a、 d 和这个平面 p、 b、 c 中哪条直线平行呢?是不是和 b、 c 看上去是平行的?那我们看一下它俩平不平行。 我们知道这里面四能追踪 pa 是 垂直于底面 a、 b、 c、 d 的, pa 垂直于底面 a、 b、 c、 d。 所以 我们是不是就可以得出 pa 是 垂直于 ad 的? 狄文还说 ad 是 垂直于 pb 的, 也就是说我们写下来, 也就是说 pa 垂直于 ad, ad 又垂直于 pb, 那我们看 pa 和 p、 b 是 相交于点 p 的, 并且都存在于平面 p、 a、 b 内,是不是我们就可以得出 ad 是 垂直于平面 p、 a、 b 的, 对吧? ad 垂直于平面 p、 a、 b, 那 我们就可以得到 ad 是 垂直于 ab 的, 也就是角 d, a、 b 是 等于九十度的。 那我们再看一下题里还有什么条件。题里说 ab 等于根号三, bc 等于一, ac 等于二,这是什么?这是不是一个勾股定律啊?根号三的平方加一的平方等于二的平方,对不对?所以角 abc 也是九十度, 那角 d、 a、 b 等于九十度,角 abc 等于九十度,它俩相加等一百八十度,是不是说明 a、 d 是 平行于 bc 的? 又因为 b、 c 属于这个平面 p、 b、 c 内,所以我们就可以得出 ad 是 平行平面 p、 b、 c 的? 第一问证明结束,那我们再来看一下第二问,第二问说 ad 垂直于 d、 c, 我 们标出来 a, d 垂直于 d、 c, 且二面角 a c, p d 的 正弦值为七分之,根号四十二,让我们求 a、 d 的 长度。 那一遇到正弦值这种问题,我们是不是直接联想到要用数量机啊?那要用向量的数量机的话,是不是我们就要建立空间直角坐标系啊?那我们建议知道了 a、 d 是 垂直于 dc 的, 那我们是不是就可以以点 d 为圆点 d, a 为 x 轴, dc 为 y 轴,然后以垂直于这个底面 abcd 的 直线为 z 轴建立空间直角坐标系是最好的, 那我们来把图像画一下先,坐标系建好了,那我们想求数量积,是不是要先把这几个点的坐标表示出来呀?分别是点 a, 点 p, 点 c, 还有点 d。 那 么知道点 d 是 什么?点 d 的 坐标是圆点零,逗号零。 那点 a 的 坐标呢?这道题让我们求 a、 d 的 长度,那我们可以设设 a、 d 的 长度等于 a 是 吧?那么点 a 的 坐标什么?点 a 的 坐标就是 a, 逗号零,逗号零。 那点 c 的 坐标是什么呢?我们知道 a、 d 是 垂直于 d, c 的, a, c 等于二,所以我们可以根据勾股定律求出 d、 c 的 长度,那么 d, c 等于什么? d, c 就 等于根号下四减去 a 的 平方, 所以点 c 的 坐标是什么?所以点 c 的 坐标就是零,逗号根号下四减 a 方,逗号零。那我们再来看一下点 p, 我 们知道 pa 是 垂直于底面 abcd 的, 也就是说 pa 这条直线是平行于这轴的,所以我们就可以得到点 p 的 坐标是什么?点 p 的 坐标就是 a 逗号零,逗号二。 那现在四个点的坐标都求出来了,那是不是我们可以通过求这几个平面,平面 a, p、 c, 还有平面 d、 p、 c 它们的法向量,通过它们的法向量做数量积来求得正弦值啊?那我们先来看一下这个在这个平面 a、 p、 c 中吧。在平面 a、 p、 c 中的向量表示出来,我们看一下向量 a、 c 等于什么?向量 a、 c 等于 负 a, 逗号根号下四减 a 的 平方逗号零,向量 a、 p 呢?用 p 的 坐标减去 a 是 等于什么?等于零逗号零逗号二。那我们设平面 a、 p、 c, 它的法向量 n 一 的坐标为 x 一, 逗号 y 一, 逗号 z 一。 那我们知道平面的法向量与它在平面内的向量的数量积应该为零,那我们就来算一下吧。我们算一下向量 n 一 和向量 a、 c, 它的数量积等于什么?等于负 a 一 乘以 x 一, 加上根号下四减 a 方乘以 y 一, 它的数量积为零。那法向量 n 一 和 ap 的 数量积呢?就等于二倍的 z 一 等于零,那么就可以连立方程组, 对吧?连立方程组,那么得到 z 一 是等于零的。我们设这个 y 一 等于一,那我们最后就可以求出发向量 n 的 坐标是什么? n 应该等于,那 x 一 就是 a 分 之根号下四减 a 的 平方多少一,多少零, 这是平面 a、 p、 c 的 法向量。那我们再看一下平面 d、 p、 c, 那 我们看一下 d、 c 的 向量是什么?向量 d、 c 等于零,逗号根号下四减 a 的 平方逗号零 dp 的 向量坐标是 a, 逗号零逗号二。那我们设平面 d、 p、 c, 它的法向量 n 二的坐标是 x 二,逗号 y 二,逗号 z 二,所以向量 n 二与 d、 c 的 数量积等于根号下四减 a 方倍的 y 二等于零。 法向量和 d、 p 的 数量积是什么?就是 a 倍的 x 二加上二倍的 z 二等于零,那么连立方程组就可以得到法向量 n 二的坐标,它等于什么? y 二等于零。我们设 x 二等于一的话,就可以得到法向量的坐标是一逗号零,逗号负的二分之一。 那现在两个平面的法向量我们已经求出来了,我们是不是可以通过这两个法向量的数量积,再除以它们各自的模长,是不是就可以得到这两个平面的夹角的余弦值啊? 那我们写在上面,我们知道两个平面的夹角 cosine c, 它应该等于 n 一 和 n 二的数量积比上 n 一 的长度乘以 n 二的长度。 由于题里给的它是正弦值啊,所以我们画成余弦值的时候,我们要加一个绝对值, 那我们来看一下吧。 n 一 在这里, n 二在这里,它们俩数量积等于什么?它们俩数量积等于 a 分 之根号下四减 a 的 平方 的绝对值比上它们各自的魔长。 a 一 的 n 一 的长度是什么? n 一 是 a 方分之四减 a 方,加一乘以 n 二的长度是什么? n 二是一加上四分之 a 方, 最后化简出来,等的是根号下四加 a 方分之四减 a 方, 那么知道正弦值是七分之。根号四十二,也就是等于根号下 e 减去七分之四十二的平方,就是四十九分之四十二,等于的是根号下七分之一, 那我们来化解一下,最后求出来 a 是 等于根号三的,也就说最终 a、 d 的 长度等于根号三,这就是这道题最后的结果。
86祝名Arya 05:56查看AI文稿AI文稿
05:56查看AI文稿AI文稿大家好,这是一个立体几何的题目,现在我们看一下,然后他说有一个正方体啊, a b, c, d, 然后他的棱长是四,然后 e、 f 呢?分别是这个 a、 e, d, e, c, e b 的 中点, 然后其中呢这个 c g 啊等于三 c, e g, 然后这里有三问了,第一问是证明这个 g f 垂直于这个平面 e b f, 第二问呢是求这个平面 e、 b, f 跟这个平面 e b g 的 这个余弦值。第三个呢是求这个三等锥 d, b, e、 f 的 这个体积。 现在我们把这个已知条件跟这个题目要求啊一条条列出来,这样便于我们来那个把控这个题目的这个整体大局。 然后首先这个已知条件,第一啊给这个正方体,正方体楞长是四,然后第二个是 e 是 终点,然后 f 是 终点,这个 g 呢在这个 c 上切满足这个 c g, 呃,等于三 c e j, 然后第五个就是这个要求了,要求就是证明,刚才我们都说过了,证明这个 g f 垂锥平面 e b f, 然后再就是求这个二面角的这个预旋,第三个是求这个三棱锥的这个体积。 现在我们看这个题目这个要求啊,然后我们就可以有一个大体的思路了,这个是典型的这一个空间向量跟坐标题,坐标法题啊,因为这个题,这个特别是这个正方题,这个很规则,这个一线一一看,我们就可以把这个立体几何问题转化成为这个解析几何的问题, 然后题目他说这个垂直,证明这个垂直的话,然后那个我们就涉及到这个点击为零的这个问题,然后这个平面夹角呢?然后我们就可以用这个法向量夹角,然后这个体积呢,就可以用这个混合机跟这个行列式的这个方法来记。 首先我们建立坐标系,这个因为这个坐标系很简单,然后这里就不注意数了,建立起坐标系之后,这所有的点都有它自己的坐标了。 现在我们看这个具体题目啊,证明这个 g、 f 垂直于平面 e、 b、 f, 实际上,实际上就是要证明这个 g、 f 垂直于这个平面 e、 b、 f 里面的两条直线, 而且要证明这两条这这两条相交的直线,然后我们选这个 f e 跟这个 f b, 然后具体证明,我们这里就不注出了,因为我这里写的很详细,然后同学们可以点暂停,一步一步,然后看一下。 第二个是求这个平面 e、 b、 f 跟这个求求平面 e b g 这个夹角的这个余弦。然后我们首先刚才我们也说过了,这个两平面夹角等于两平面法向量夹角,所以说我们就是先求取出这两个法向量来,然后 这样的话,两个法向量 n 一 n 二这两个法向量具体求一下,然后具体怎么求,我们这里就不追书了,这里写的很详细了,然后算这加角余弦,因为法向量求出来之后,直接套公式就可以了,套这个公式就可以了,然后最后求出来这个余弦值是五分之四, 这里求这个三楞锥的体积啊,我们是用的混合机公式,这混合机公式是什么呢?这就是这个混合机公式, 然后这个三棱锥的这个体积等于六分之一,然后这是这三棱锥的这三条,三条那个边了三条向量是这么个关系, 因为这个公式啊,这是那个一个现有的公式,同学们可以直接背过。关于这个公式推导啊,我在某个题目里面讲过,这里就不赘述了, 然后套用这个公式的话,反正这个公式你看有,有什么我们求什么就可以了,因为这个是解析几何题,这个所有的点的坐标我们都知道的,所以说最后就是带进去算就可以了,算出来之后这个体积是三分之三十二。 现在我们看这个题目,从这个题目我们能学到哪些?这个就是有用的知识点,或者是核心知识点。首先 这种立体几何,像这种解析几何的这种转变,这这这种思维啊,你得有,特别是这个题目,这个题目你看他问的这么多,然后又求这么直线垂直某个平面,特别是还出现求这个两个平面的这个夹角,又求这个体积, 这样的话我们把它转化成为解析几何就比较简单了。这就是这个题目里面涉及了这个向量法的这个三大翻译规则。首先规则 a, 然后比如说垂直,垂直表示什么呢?就是点击为零, 这两个向量垂直,然后可以跟这个点击为零,这个是充分必要条件。这个规则 b, 规则 b 是 什么呢?这个平面夹角就跟其实就等于它这个法向量夹角,这样的话就转化成为求它的法向量了。 然后再就是带入这个余弦公式,这个规则 c, 这个体积就是等于这个混合机这个行列式的形式。这三楞锥的体积啊,我们就可以用这个公式直接套这个公式就可以了。 其中啊这个 abc 是 什么呢?就是从同一个顶点出发的这个三条棱的这个向量, 这里这个直观理解实际上就是怎么来推出这个题集公式的,同学们可以看一下这个直观理解。
28Mr.王大拿 05:44查看AI文稿AI文稿
05:44查看AI文稿AI文稿如图,在三棱锥中,平面 a、 b、 d 垂直于平面 b、 c、 d, a、 b 等于 a、 d 点 o 为 b、 d 的 中点啊, a、 b 等于 a、 d 点 o 为 b、 d 的 中点。根据等腰三角形的三线合一啊,我们可以证明 a、 o 呢,是垂直于 b、 d 的 啊。又因为这两个平面是垂直的,我们根据面面垂直的性质,就两个平面如果互相垂直, 那么其中一个平面内,你比如在这一题中就是 i、 o 了啊,垂直于他们交线啊,这个交线就是 b、 d 的 直线,就是 i、 o, 那 么和另外一个平面就 b、 c、 d 是 垂直的, 所以说根据这个面面垂直的性质,我们可以推出 i、 o 垂直平面 平面 b、 c、 d 啊,然后第一位证明 i、 o 垂直于 c、 d 啊。接着这个分析,因为 c、 d、 c、 d 包含于平面 b、 c、 d, 然后根据线面垂直的性质啊,所以这个 i、 o 呢,是垂直于 c、 d 的。 第二问,如果三角形 o、 c、 d 是 边长为一的等边三角形 o、 c、 d 边长为一,那角度都是六十度,边长都是一 好,那么 b、 o 也是一,因为 o 是 b、 d 的 中点呀,那么角 b、 o、 c 就是 一百二十度,那么角 o、 b、 c 和角 o、 c、 b 呢,都是三十度。 做题的时候,我们就可以用铅笔把这些数据给它标一下啊,那么角 b、 c、 d 就是 一个直角,三十加六十就九十啊, 点 e 呢?在棱 a、 d 上,那么 d、 e 等于二倍的 e i 哎,也就是 e, i 呢,比上 d, e 等于一比二 啊,等于一比二,这比例关系啊,且二面角 e、 b、 c、 d 的 大小为四十五度, e、 b、 c、 d 的 大小为四十度啊,求三棱锥 a、 b、 c、 d 的 体积。 那么由前面的分析,我们知道这个三棱锥它的底面积 b、 c、 d 的 面积好求 啊,这三十度,六十度,九十度, b、 d 等于二, c、 d 等于一,那 b、 c 就是 根号三样啊,底面积二分之一乘以底乘以高,那么再求,再求出什么 i o 的 长,那么 i o 的 长也就是这个三棱锥体积的高。 好,我们看一下这个条件怎么用。首先看一下这个二面角,把这个二面角 e、 b、 c、 d 给它做出来, 我们先由一点哈,就是它无非就是考核面面垂直的性质,由一点向 b、 d 做垂线,比如交于 f 点,那么根据面面垂直的性质,我们知道 e、 f 和底面 b、 c、 d 是 垂直的,然后过 f 点呢,再做 bc 的 垂线 点 g 啊,然后再连接这个 eg, 我 们现在证明这个角 egf 就是 这个二面角的平面角, 就只要证明 eg 和 bc 也垂直就行了啊, eg 和 bc 也垂直就行了,我们看 bc 是 垂直于 g、 f 的, bc 还垂直于 ef, 所以 bc 垂直于平面 e、 g、 f, 那 么进而可以推出啊, b、 c 也是垂直于啊 g、 e 的, 所以这个角 g、 e、 g、 f 就是 这个二面角的平面角,它是四十五度 啊,它是四十五度,然后再根据这个什么比例关系,我们就可以把这个 g、 f 给它算出来啊,这个比例关系,你看 a、 e 比 e、 d 等于一比二,那么 o, f 比 f、 d 呢?也是一比二呀 啊,那么所以说这个 o、 d 相当于一加二是三分,那 b、 o 呢,也是三分,那么 b、 f 呢?哎,就是,嗯,三加一等于四分 啊,那 b、 d 呢?啊,就是六分,然后根据啊,根据三角形 b、 g、 f 相乘于三角形 b、 c、 d, 我 们就可以把 g、 f 算出来, g、 f 算出来以后,它等于 e、 f, e、 f 也有了, e、 f 有 了以后,我们再根据就是三角形 d、 f、 e 相似于三角形 d、 o、 n, 我 们就可以算出什么 i、 o 的 长,也就是这个三棱锥,它什么底面的高,哎,它的高啊。 所以这一题呢,我们要把这个就是一个,就是说我们做这种题的时候,要用铅笔把数据标一标,写一写去分析一下啊。第一个,那么第二个知识点要熟练,你比如说面面垂直的性质 啊,还有这里证明二面垂直的判定与性质,知识点要熟练啊。






